Abstract
We describe here a collection of heuristics for producing "nice"- drawings of directed graphs, and a simple dual-mode software tool for testing and evaluating them. In playing mode, the heuristics are applied in random sequence over a set of drawings, in the manner of an asynchronous team (A-team). As new drawings are added to the set, others are deleted based on a multi-valued aesthetic evaluation function. By inspecting the "pedigree" of the best solutions found in playing mode, the user can obtain insights into the best order in which the heuristics should be applied. Then the user can test these insights in the working mode, where the heuristics are applied in a fixed sequence.Some of the heuristics that we describe here are similar to the steps of Sugiyama's D-ABDUCTOR graph-drawing package; and indeed we can obtain results similar to those of D-ABDUCTOR, by applying our heuristics in the proper sequence.
graph drawing; aesthetic criteria; visualization; multivalued optimization; A-team
Heuristics and pedigrees for drawing directed graphs* * Partially supported by CAPES, FAPESP and CNPq + research done while author was working at Instituto de Computação, Universidade Estadual de Campinas 1 We added vertex 8 adjacent with vertex 27 in our drawings.
Instituto de Computação
Universidade Estadual de Campinas, Brasil
stolfi@dcc.unicamp.br
Instituto de Informática
Universidade Federal de Goiás, Brasil
hadn@inf.ufg.br
C. F. X. de Mendonça+ * Partially supported by CAPES, FAPESP and CNPq + research done while author was working at Instituto de Computação, Universidade Estadual de Campinas 1 We added vertex 8 adjacent with vertex 27 in our drawings.
Departamento de Informática
Universidade Estadual de Maringá, Brasil
Abstract
We describe here a collection of heuristics for producing "nice"- drawings of directed graphs, and a simple dual-mode software tool for testing and evaluating them. In playing mode, the heuristics are applied in random sequence over a set of drawings, in the manner of an asynchronous team (A-team). As new drawings are added to the set, others are deleted based on a multi-valued aesthetic evaluation function. By inspecting the "pedigree" of the best solutions found in playing mode, the user can obtain insights into the best order in which the heuristics should be applied. Then the user can test these insights in the working mode, where the heuristics are applied in a fixed sequence.Some of the heuristics that we describe here are similar to the steps of Sugiyama's D-ABDUCTOR graph-drawing package; and indeed we can obtain results similar to those of D-ABDUCTOR, by applying our heuristics in the proper sequence.
Keywords: graph drawing, aesthetic criteria, visualization, multivalued optimization, A-team.
1 Introduction
An automatic graph drawing module is a necessary component of many information systems. Experience shows that abstract relations are better understood when displayed in graphical form; and most abstract relations can be naturally represented by directed graphs. Many general-purpose graph drawing packages and utilities can be found in the literature, such as GIOTTO [1], "Graph Browser" [14], DAG [7] and DRAG [23], ISI Grapher [12], EDGE [11], and D-ABDUCTOR [16], to cite just a few.
In order to be effective, however, the drawing of a graph must obey certain aesthetic and clarity criteria, that take into account the way the human eye and brain process visual input. The criteria that define a "nice"- graph may depend on the application, but usually include minimizing the number of line crossings and the size of the drawing, uniformizing the spacing of nodes and lengths of edges, etc. In the case of directed graphs, it is also desirable to have most edges oriented in a fixed general direction (say top to bottom, or left to right), so as to minimize the need for explicit arrowheads. Unfortunately, for almost any combination of criteria that one would like to use in practice, the problem of producing the "nicest possible"- drawing of an arbitrary graph is very difficult, often NP-hard.[5]. Therefore, practical graph-drawing systems such as the ones mentioned above are based on heuristic procedures, whose results are hopefully nice but not always the nicest possible.
The package D-ABDUCTOR by Sugiyama et al.[16, 17, 18] is a typical example. Its method consists of four steps executed sequentially. In each step a different algorithm is used to optimize some aspect of the drawing: the y-coordinates of the vertices, the horizontal order of the vertices in each y-layer, the x-position of each vertex in each layer (preserving their order), and so on. The result is not necessarily optimal, because these aspects are not independent: the best assignment of y-coordinates depends on the x-coordinates, and vice-versa. Nevertheless the D-ABDUCTOR system is quite popular, because it is fast and usually produces fairly nice results.
The main contribution of this article is a set of heuristics (described in section 4) which we have found effective in drawing directed graphs (as defined in section 2). Some of the heuristics are similar to the main steps of D-ABDUCTOR; indeed, we have obtained results comparable to those of D-ABDUCTOR by applying them in a particular sequence; these experiments are detailed in section [6]
We also describe in section [5] a simple software testbed that assists the user in evaluating and combining those heuristics. The software operates in two modes, playing and working. In working mode in which the user directly specifies a sequence of heuristics to be applied. In playing mode the heuristics are applied at random to a fixed-size pool of solutions, in the manner of the so-called asynchronous team or A-team model [19, 2, 3] with a multi-valued goal function [4, 13]
Theory predicts, and experience confirms, that an A-team is an inefficient way to combine heuristics. In our case, we found that a fixed sequence of heuristics, properly chosen, produced better drawings than any A-team, and was enormously faster (by three orders of magnitude, even on small graphs). This, incidentally, is the approach embodied in D-ABDUCTOR, and the reason for its popularity.
However, an A-team allows heuristics to cooperate and iterate in arbitrary ways, with a bias towards combinations that produce good solutions. It is therefore helpful for understanding how heuristics interact with each other, and for discovering general rules-of-thumb for combining them in effective ways. Thus, the "pedigree"- of the solutions generated in playing mode often suggests effective "programs"- for use in working mode. To support this claim, we describe our experience with our graph-drawing heuristics, described in section [6].
2 Terminology
2.1 Graphs
A graph G = (V,E) consists of a finite set V of vertices, and a set E of edges, which are ordered pairs of distinct vertices.
If e=(u,v) is an edge of G, we say that u and v are the endpoints of e, that u is the origin, v is the destination, and that u and v are adjacent or neighbors of each other. The neighborhood of a vertex x is the set of all of its neighbors.
2.2 Graph Drawings
Following Sugiyama's approach, we will restrict our attention to graph drawings where each vertex is placed on a point of the integer grid, and each edge is drawn as an y-monotone polygonal line whose corners lie on such points.
More precisely, we define a polyline as a sequence of distinct points p0,p1,..., pn with integer coordinates pi = (xi,yi), such that the ordinates y0, y1,..., yn are consecutive integers, increasing or decreasing. By definition, the links of the polyline are the open straight-line segments pi pi+1, implicitly oriented from pi to pi+1. The points p0 and pn are the origin and destination of the polyline, while p1, p2, ...pn-1 are its joints. A joint will be called a bend if the two adjacent segments are not collinear.
By convention, in our illustrations the x-coordinates increase from left ot right, and the y-coordinates increase from top to bottom. We therefore say that a link or polyline is descending if yi+1< yi, and ascending if yi < yi+1. In keeping with tradition, we consider descending edges to be more "natural"- than ascending ones.
We define a drawing of a graph G=(V,E) as an assignment of each vertex v to a distinct point v* of the integer grid Z2, and of each edge e=(u,v) to a valid polyline e*, whose endpoints are u* and v*. The joints of these polylines must be all distinct, and must not coincide with any of the vertex points v*.
A drawing of a graph G=(V,E) can be interpreted as another graph G'=(V',E'), where the set V' consists of all the points v* together with the joints of all polylines e*; and the set E' consists of the pairs (pi,pi+1) for all segments pi pi+1 in those polylines. To avoid confusion, we will refer to the elements of V' and E' as nodes and links, reserving the terms vertices and edges for the elements of G.
In the illustrations of this article, the nodes of G' that correspond to vertices of G are drawn as numbered ovals; all other nodes of G' (the joints) are left unmarked. To reduce clutter and make the drawings easier to read, we do not draw arrowheads on the edges; instead, we use solid lines for descending edges and dotted lines for ascending ones.
The set of all points of the integer grid with the same y coordinate is called layer y of the grid, and the set of all nodes of G' assigned to those points is layer y of the drawing. Note that the lowest-numbered layer is at the top in our figures. It follows from all the definitions that each link of the graph G' connects two nodes from adjacent layers. Also, every joint node on layer y has exactly one neighbor in layer y+1 and one in layer y-1.
2.3 Edge crossings
We define an edge crossing as a point of intersection between the two polylines e* and f* that represent two distinct edges e, f of G. Recall that polylines do not include their endpoints, links are open and span at most two layers, and the joints in a drawing are all distinct. It follows that the edge crossings correspond to pairs of links (a,b) Î E' ´ E' that intersect in their interiors.
Note that these conditions on the graph G' guarantee that the topology of the original graph G can be recovered without ambiguity from a drawing of G', provided the vertices are drawn as sufficiently small dots and the links as sufficiently narrow straight lines.
3 Aesthetic criteria
In order to compare drawings and algorithms, or to program a computer to automatically search good drawings, we need some well-defined measure of the quality of a drawing. Unfortunately, this notion is subjective and dependent on the application being considered.
An aesthetic indicator or score is a numerical function of the drawing that measures or counts some type of aesthetic defect which is generally undesirable (for the given application) and ought to be minimized. The following quantities, in particular, fit this definition is most contexts:
1. The number of edge-edge crossings.
2. The number of ascending edges.
3. The number of bends on edges.
4. The total length of all edges.
There are obvious conflicts between the above indicators. For instance, minimizing the number of crossings may require opening up the drawing and/or representing edges by longer paths. Typically, there is no single drawing of G that optimizes two independent aesthetic scores; so the problem of finding the "nicest drawing"- does not have a well-defined solution, much less an algorithm.
3.1 Penalty functions
A popular solution to this difficulty is to combine all the relevant aesthetic indicators into a single combined score, by weighted averaging, or some other mathematical function. Then the goal can be formally defined as finding a drawing G' with minimum score.
However, this approach merely pushes the difficulty to the user, who must select the weights or scoring function best suited to the application. Unfortunately the user generally doesn't know a priori what is the relative importance of each indicator (e.g., whether one extra crossing will look uglier than three extra bends). In fact, the best set of weights often depends on the graph itself. Typically the user and/or the implementer have to adjust the weights by trial and error, which is extremely time-consuming and rarely converges to the best settings.
3.2 Multi-valued comparison
Another solution, that does not require parameter tuning, is the multi-valued scoring approach of [4, 13]. In this approach, the merit of a solution A is measured not by a single score but by a score vector q(A) = á q1(A),q2(A),...,qm(A)ñ , where each qi is an aesthetic indicator; and no assumptions are made about the relative importance of the components. The score vectors thus define only a partial ordering of the solutions: we say that a solution A is better than a solution B (written A Ì B) if qi(A) £ qi(B) for all i, and qk(A) < qk(B) for at least one index k. Obviously, if these conditions hold, then A will get a lower mark than B under any combined score that is a monotone function of the individual score components.
In the multi-valued approach, a solution A is considered "good" if it is minimal under the Ì relation among all known solutions; that is, there is no other known solution B with BÌ A. It follows that if A and B are known good solutions, then either they have exactly the same score vector, or they are incomparable: there is some component qi by which A is better than B, and some other component qj by which the opposite is true. In the graph-drawing problem, for instance, A may have less crossings but more ascending edges than B.
By the same token, an heuristic is considered "useful"- if it can reduce one of the scores qi, even at the cost of increasing the others.
Finally, in drawing programs that explore various alternatives, the goal is not a single solution that minimizes an arbitrary combined score, but rather a set of solutions that are all minimal under Ì , and hence mutually equivalent or incomparable.
In general, the result set will contain not only a solution Ai that minimizes criterion qi, for each i, but also many "compromise"- solutions. For example, the result set may have solutions with score vectors (0,5,5), (5,0,5), (5,5,0), and (4,4,4). Note that the last one is better than each of the other three under some criterion, but is not optimal under any criterion (or even under any weighted average of the criteria).
In multi-valued optimization, the user still has the problem of selecting one solution among the ones returned. However since the non-minimal solutions have been eliminated, the output set generally contains many goodif not optimal solutions, so even a random choice may be acceptable. Moreover, the user can choose based on subjective criteria, without having to express them as a mathematical formula.
4 Heuristics for drawing directed graphs
We now describe a small set of heuristics that have been found quite effective in drawing directed graphs. First, however, we need to define some basic operations.
4.1 General-purpose graph-drawing tools
The following procedures are used by several of the heuristics to modify the current drawing G'. Actually these procedures assume only that G' is a sub-drawing of G a subgraph of some valid drawing of G.
-
shiftnodes(p1,...,pm;x1,...,xm): given a set of nodes
p1,...,
pm of
G', this procedure tries to move them to new abscissas
x1,...,xm, without changing their
y-coordinates.
This operation may entail shifting some other nodes of G' horizontally, in order to make space for the nodes pi. Also, each node pi may be placed at some abscissa that is not exactly at xi, but only close to it. (This happens, in particular, if the operation is asked to shift two nodes in the same layer to the same abscissa xi.)
-
addedge(u,v): given two vertices
u and
v of
G (not
G'), this procedure adds a polyline to the graph
G', from node
u* to node
v* which must lie on different layers.
The pair e=(u,v) must be an edge of G, but its polyline e* must be missing in G'. The inserted polyline will resemble an integral sign ò, with vertical stem. More precisely, the polyline will be a single link, if u* and v* are in adjacent layers. Otherwise, if u* and v* are k layers apart, it consists of a string of k-2 vertical links (at an abscissa ´ roughly midway between the abscissas of u* and v*), preceded and followed by two additional links incident to u* and v*.
Note that some existing nodes of G' in the intervening layers may have to be shifted horizontally, in order to make space for the joints of the new polyline.
-
movevertices
(v1,...,vm; p1,...,pm). this procedure tries to reassign the vertices
v1,...,vm of
G (not
G') to points
p1,...,pm of the integer grid. This reassignment must not cause two neighboring vertices to lie on the same layer of
G'.
Let pi = (xi,yi) for each i. First, the procedure deletes all the polylines of G' that represent edges of G incident to v1,...,vm. Then it relocates node v*i to any vacant spot on layer yi. and it performs shiftnodes (v*,x). Finally, the procedure performs addedge(e) for every edge e of G incident to v.
Note that the vertex vi will always end up in layer yi, but its abscissa may be somewhat removed from xi, depending on the crowding conditions around pi.
These operations are not entirely deterministic: coin flips are used in several cases to break ties, or just to ensure a minimum of "genetic diversity"- in the drawings generated by the heuristics.
4.2 The heuristics
Each heuristic operates on a current drawing G' of the graph G. By definition, an heuristic succeeds when it modifies G' even if the modified drawing is worse than the original in all scores. Otherwise the heuristics fails.
Some of these heuristics use a reference layer y, which is either the maximum or minimum y-coordinate of the vertices, or is the median layer the y coordinate which separates the vertices of G (but not necessarily the nodes of G') as evenly as possible.
-
NewRandom: The heuristic
NewRandom creates a random drawing for the graph
G. The heuristic assigns each vertex to a different layer in the range
[0..
n-1], at the same abscissa
x=0, and then uses
addedge to connect them with polylines.
-
AdjustY: This heuristic tries to displace each vertex
vi of
G to an "optimum"- layer
y'i
The heuristic begins by setting yi to the initial ordinate of vertex vi, for all i. Then, for each vertex vi in turn, the heuristic first determines the widest possible interval of ordinates Yi = [lo(Yi)..hi(Yi)] where that vertex could be placed without creating new ascending edges. Note that this interval always contains the current ordinate yi. The heuristic then sets yi to some ordinate yi' in the interval Yi, avoiding any layers that contain neighbors of vi in G.
When computing the interval Yi, the heuristic assumes that any vertex vj examined previously has already been moved to its chosen layers yj. Specifically, lo(Yi) is one more than the maximum yj for all in-neighbors vj of vi that are currently placed above vi (i.e. have yj < yi). The bound hi(Yi) is defined symmetrically.
After computing all ordinates yi, the heuristic uses movevertices to place each vertex vi at the point pi = (xi,yi), where where xi is its original abscissa.
There are several variants of this heuristic, distinguished by the order in which vertices are processed, and the criterion used to choose the new layers yi':
-
AdjustYPack: processes the vertices in order of increasing distance from a reference layer
y, and choose
yi as the ordinate in the interval
[lo(Yi)..hi(Yi)] that is closer to the median
y. The effect of this heuristic is to "squeeze"- all the vertices towards the reference layer
y.
-
AdjustYFlip: Processes the vertices in random order, and chooses the new layer
yi at random in the range
[lo(Yi)..hi(Yi)]. (However the procedure only chooses
y'i< yi if
vi has some neighbor
vj with
yj< yi; and similarly for
y'i > yi.).
-
AdjustYMean: Processes the vertices in random order, and selects each
yi as a weighted average of the ordinates
yj the neighors of
vi in
G. (Actually, each neighbor ordinate is modified by an offset d
i that is
-1 for out-neighbors, and
+1 for in-neighbors.) Each term has weight 1 if the corresponding polyline in
G' is descending, and 2 if it is ascending.
-
AdjustYMedian: Similar to
AdjustYMean, except that the weighted median is used instead of the weighted mean, and ties are broken by a sum-of-distances criterion. This variant has the effect of displacing the vertex
vi vertically, as far as possible, in the direction where most of its neighbors lie.
In all these variants, a random displacement in [-1..+1] may be applied to the chosen yi, taking care not to leave the interval Yi or placing two adjacent nodes in the same layer.
Note that, as the vertices are inserted into the chosen layers, the x coordinates of all nodes may be substantially disturbed.
These heuristics will not increase the number of ascending edges, and will generally reduce the overall height and total edge length of the graph. However, they may increase its width, and create new crossings and bends.
-
FixEDirs: this heuristic checks whether every edge
(u,v) of
G is drawn as a descending polyline. Whenever it finds an ascending edge (with
v higher than
u), the heuristic tries move
v from its current layer to a new layer just below
u; or to move
u to the layer just above
v. In the first case, in order to avoid new ascending edges, the heuristic will also displace other nodes connected to
v. More precisely, if it decides to displace a vertex
v from its current layer
y to a layer
y'>y, the heuristic will also move all out-neighbors of
v currently in layers
[y+1..y'] to the layer
y'+1 or beyond; and so on recursively. The symmetrical correction applies when
u is moved up.
In either case, the correction is performed only if it does not create any new ascending edges; that is, only if there is no directed path from v to u that consists entirely of descending edges.
If the graph G is acyclic, repeated applications of this heuristic will eventually remove all ascending edges.
-
AdjustX: For each layer
y of
G, and each
pi of
G in that layer, the heuristic computes a new abscissa
xi, taking into account the abscissas of the neighboring nodes in layers
y+1 and
y-1. The heuristic then uses
shiftnodes to place each
pi at the corresponding
xi.
The new abscissas xi for each layer are computed in two stages. First, the heuristic tries to improve the left-to-right order of the nodes in the layer. To that end, it tests each node the layer in turn, checking whether moving that node to some other position in the left-to-right order would reduce the number of link crossings. (Note that this heuristic may not find the optimum order). In a second stage, the abscissas of the nodes are recomputed, while preserving their order, so as to minimize a weighted sum of the squares of the link lengths. Note that this criterion tends to place each node near the barycenter of its neighbors.
In the second stage, extra penalty terms are used (a) to discourage bends, (b) to encourage vertical links in general, and (c) to discourage vertical links incident to nodes with even in- or out-degree (so as to encourage more symmetric drawings). In spite of this complexity in the cost function, the fixed ordering of the nodes allows the optimum abscissas to be computed in quadratic time, by dynamic programming.
-
SmoothX: this heuristic is similar in purpose to
AdjustX, but its method is simpler, and more similar to the barycentric adjustment of Sugiyama and Missue [17, 18]. For each layer
y of
G, the heuristic computes a new tentative abscissa
x for each node
w of
G in that layer, by taking a weighted mean of the abscissas of the neighboring vertices of
G. More precisely, if
w is a vertex of
G, then the average is taken over all neighbors of
w in
G. Otherwise,
w is a joint in a polyline that represents some edge
(u,v) of
G (not
G); in that case the "neighbors"- of
w are by definition
u and
v.
Again we have several variants of the AdjustX and SmoothX heuristic, differing by the order in which layers are processed:
-
AdjustXDown,
SmoothXDown: processes the layers sequentially, in order of increasing
y-coordinate.
-
AdjustXUp,
SmoothXUp: ditto, in order of decreasing
y-coordinate.
-
AdjustXOut,
SmoothXOut: ditto, in order of increasing distance from the median layer
y.
5 Exploring the heuristics
The heuristics described above interact in complex ways, and sometimes have antagonical effects. For instance, when the AdjustY heuristic is applied for the first time, it usually has the effect of moving all vertices to new layers, and re-routing all edges, with drastic effects on the horizontal order and placement of the nodes. Therefore, any previous applications of AdjustX before the first AdjustY are basically wasted effort.
As described in the introduction, our graph drawing tool provides a playing mode in which the heuristics are applied in random order to a fixed-size pool of drawings (of the same graph G). Each successful application of a heuristic generates a new drawing, which is added to the pool, while some other drawing is discarded to make room for it. This arrangement follows the asynchronous team or A-team approach, a "meta-heuristic"- for combinatorial optimization that was introduced by Talukdar, Souza and others [2, 20, 3, 21]. Basically, an A-team is an organization of autonomous agents in which each agent communicates with the others in an asynchronous way, using a shared memory, and producing a cyclic data flow. It can also be seen as a simplified and abstracted form of the genetic algorithm [9,24] in this case, without crossover since we did not implement a heuristic to combine two or more drawings.
In ouwr team, the probability of a drawing A to be discarded from the pool is proportional to its rank rA in the Ì partial order (section 3). The rank is defined as the maximum r such that the pool contains a chain of drawings A0Ì A1Ì ... Ì Ar, with Ar = A. Thus, instead of obtaining a single drawing that happens to be optimum by one particular criterion, we obtain a collection of drawings that span the gamut of Ì -minimal solutions.
The team starts with the heuristic NewRandom, which writes initial drawings into the memory. After that, the other agents run reading drawings from the memory and producing and writing new ones into it. This processing continues until a stop criterion be reached, for example, a time limit or an expected quality of the produced drawings.
At the end of the playing-mode run, the tool writes the drawings that remain in the pool, and their histories. The history of a drawing shows the sequence of heuristic applications that produced it, and, for each heuristic, its cost (running time) and the score of the resulting drawing.
A playing-mode run produces also a set of plots like the one in figure 1, showing the evolution of each score during the simulation, as a function of time. Each horizontal gray line represents a drawing that was generated some heuristic, and extends horizontally from the time of its creation to the time it was deleted from the pool. Its ordinate is its score.
Each diagonal line represents the execution of some heuristic, indicated by the line's color (not visible in the reproduction). The line usually bridges two gray lines, representing the input drawing (leftmost endpoint) and the output drawing (rightmost endpoint). However, heuristics that take no input, like NewRandom, are shown starting from a dot; and heuristics that fail are shown ending in one. (In these two cases, the y-position of the dot is not significant).
These results are very important since they provide an insight how the agents do work and cooperate in the team. Once these pieces of information have been collected we can use them in the working mode of our tool.
After the playing mode there are many questions to arise which may include: What happens if I increase this the pedigree with the execution of a particular heuristic? Is a particular subsequence in the pedigree necessary? Can I reduce a subset of the pedigree sequence and get the same result? Are there any better drawings with same heuristics?
To answer such questions the user must get first some insight about the heuristics inspecting the pedigrees of the good and bad solutions and than try some different recipes in the working mode. In this mode the user can tell exactly which order, intensity and number of times a set of heuristics will be run. The same recipes are used in both modes, however in playing mode the order is disregarded. A good start is the recipe found in the pedigrees of good solutions. Further information may be collected from the pedigrees of destructed solutions since they are samples of bad recipes, specially when several times a sequence is repeated just before destruction, in this case we say that such sequence is a disease.
Therefore, the playing mode is an initial or training stage that provides us a starting "cake recipe" of some ways to use the heuristics (and most of the time how to do not use the heuristics). One can see that the history of the pedigree of good solutions are good since they have survived the destruction policy during the early processing. Experience shows that a pedigree which is good for one graph does not apply to another graph.
An approach containing only the playing mode was applied to drawing straight line general graphs [10] obtaining satisfying results at the expense of expending several days to draw a few graphs. In most cases it takes about an hour to test the validity of an idea in playing mode.
Thus, after the user gets some insight about how heuristics interact he will never use the playing mode again. In the next section the best drawings were obtained and refined in the working mode. The insight were acquired after a series of trial and error in the playing mode sometimes getting a set of mediocre results.
6 Results
One necessary limitation of heuristic methods is that they can only be evaluated empirically, by comparing their results on "typical"- problems (which of course depend on the application).
Here we show some results obtained by playing and working mode recipes on selected graphs. The tests were performed with teams consisting of recipes of the heuristics described in section 4, applied in round-robin fashion (playing mode) to a pool of 10 solutions. It follows some results obtained by the application of the same recipes found in the pedigree of good solutions and some recipes found by intuition. The machine used was a SPARCStation 4 100 Mhz.
Figure 2 displays drawings of a C-syntax graph used by Sugiyama [15]; the output of his algorithm is shown in figure 2
Figures1 * Partially supported by CAPES, FAPESP and CNPq + research done while author was working at Instituto de Computação, Universidade Estadual de Campinas 1 We added vertex 8 adjacent with vertex 27 in our drawings. 3(a) ( a) and 3(b) ( b) show the best drawings for two A-team recipes obtained in playing mode.
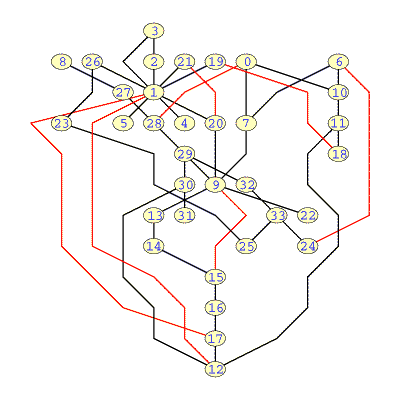
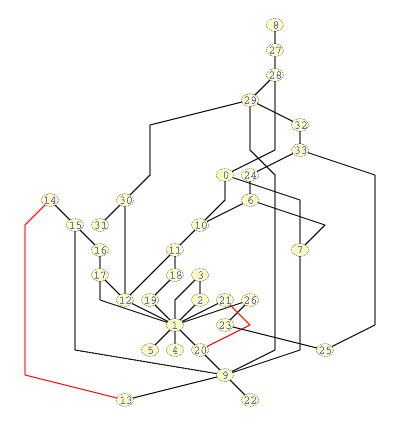
Figures 4(a) and 4(b) show drawings obtained in working mode after refining the pedigree of the drawing of figures 3(a) ( a) and 3(b) ( b) , respectively. The time to refine the pedigree recipes of both drawing was about a couple of minutes and the score of each solution are (24 crossings, 2 ascending arcs, 30 bends, 150.98 edge length and cost = 236.953ms) and (14 crossings, 4 ascending edges, 19 bends, 116.64 edge length and cost = 702.526ms), respectively.
(a)
(b)
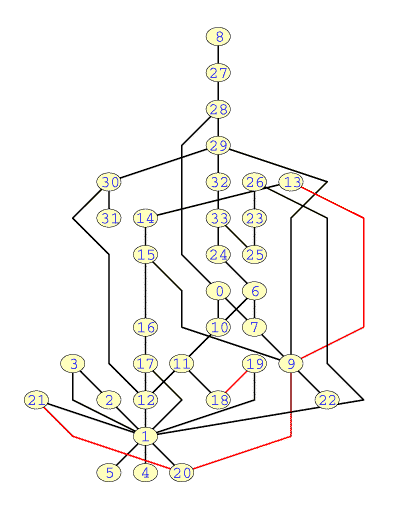
Figure 4 - Drawings of the C-syntax graph in working mode.
Figures 5(a) and 5(b) show drawings obtained in working mode of C-syntax Graph. The drawings consist of third and fourth refinement of a cooked pedigree found by intuition. The refining time took about 10 minutes and the score of each solution are (32 crossings, 2 ascending arcs, 32 bends, 174.68 edge length and cost = 1208.389ms) and (24 crossings, 3 ascending edges, 29 bends, 153.89 edge length and cost = 573.809ms), respectively.
(a)
(b)
Figures 6(a) and 6(b) show drawings obtained in working mode of Forrester's World Dynamics Graph [18]. The drawings consist of first and fourth refinement of a cooked pedigree found by intuition. The refining time took about 20 minutes and the score of each solution are (165 crossings, 7 ascending arcs, 80 bends, 702.92 edge length and cost = 3989.507ms) and (106 crossings, 7 ascending edges, 69 bends, 469.97 edge length and cost = 2127.546ms), respectively.
(a)
(b)
Figure 7 shows a drawing obtained in working mode of Unix Systems Family Tree [18]. The drawings consist of the first refinement of a cooked pedigree found by intuition. The refining time took less than a minute and minute and the score of the solution is(19 crossings, 0 ascending edges, 8 bends, 92.90 edge length and cost = 453.649ms).
To illustrate a pedigree in the working mode we give the pedigree recipe and score of drawing of figure 4(a) in figure 8. The fields in each line are <time, heuristic, [/ intensity], [@ internal repetition number]> and the last line contains the score of the pedigree: number of crossings, number of ascending edges, number of bends, sum of the length of all edges and running time in a SPARCStation 4 100 Mhz.
7 Conclusion
The heuristics we described, when suitably composed, can produce useful drawings of complex graphs. The best sequence of heuristics obviously depends on the graph. Like a training photographer that switch the camera to automatic to learn how to adjust the machine and later turn to manual to take better pictures, our tool provides two modes a playing mode for beginners and a working mode for experts. We have found instructive to observe the behavior of the heuristics when combined at random, as in an A-team (the playing mode of our tool). However, in this mode very little control is left to the user. After the user acquire insight about how the heuristics interact it may turn the tool in working mode.
For instance, even a cursory inspection of figure 1 shows that the NewRandom heuristic (which is rather expensive, due to the large area of the graphs it produces), quickly becomes ineffective. On hindsight, it is obvious that a freshly generated random drawing is much worse than drawings that have gone through many heuristics and have survived many rounds of selective deletion. Thus the random drawing is almost certain to rank last among the solutions in the pool, and hence is almost certain to be deleted within a few generations, before it has a chance to be processed. (Incidentally, this observation illustrates the basic inefficiency of the A-team model).
Moreover, a closer look at the pedigrees of the solutions found in the pool at the end of the run produced other valuable (and, in retrospect, equally obvious) insights, like the observation (section 5) that AdjustX and SmoothX are useful only after all instances of AdjusY and FixEDirs as in Sugiyama's method. This observation also hints that a more intelligent edge insertion procedure (say, one that finds the path with least crossings) might allow the layers to be finely adjusted at later stages, without undoing the work of AdjustX and SmoothX.
Therefore, the A-team approach is not enough by itself. It demands much time to produce good drawings and allows some bad combinations of the heuristics, which are not useful. However, the history of the best drawings (the pedigree solutions) produced tells us how to run the heuristics in a effective way, leading us to the working mode of our tool.
An approach containing only the playing mode was applied to drawing straight line general graphs [10] obtaining satisfying results, therefore, we believe that the tool proposed in this article may be applied for other classes of graphs with other aesthetic criteria.
Acknowledgements
We would like to thank professor Peter D. Eades for many useful suggestions.
References
[1] C. Batini, M. Talamano, and R. Tamassia. Computer Aided Layout of Entity-Relationship Diagrams. Journal of Systems and Software, pages 163173, 1984.
[2] P. S. de Souza and S. N. Talukdar. Genetic Algorithms in Asynchronous Teams. In Proc. of the Fourth International Conference on Genetic Algorithms, Los Altos, CA, 1991.
[3] P. S. de Souza and S. N. Talukdar. Asynchronous Organizations for Multi-Algorithm Problems. In Proc. ACM Symposium on Applied Computing, Indianapolis, IN, February 1993.
[4] R. F. Rodrigues e P. S. de Souza. Asynchronous Teams: A Multi-Algorithm Approach for Solving Combinatorial Multi-Objective Optimization Problems. In Proceedings of the 5th Workshop of the DGOR-Working Group Multicriteria Optimization and Decision Theory, Germany, May 1995.
[5] P. Eades and R. Tamassia. Algorithms for drawing graphs: An annotated bibliography. Report CS-09-89, Department of Computer Science, Brown University, Providence, RI, February 1989.
[6] J. W. Forrester. World Dynamics. Wright-Allen, Cambridge, MA, 1971.
[7] E. R. Gansner, S. C. North, and K. P. Vo. DAG A Program that Draws Directed Graphs. Softw. Pract. Exp., 18(11):10471062, 1988.
[8] D. J. Gschwind and T. P. Murtagh. A Recursive Algorithm for Drawing Hierarchical DirectedGraphs. Technical Report CS-89-02, Department of Computer Science, Williams College, 1989.
[9] Michalewicz, Zbigniew. Genetic algorithms + data structures = evolution programs, 3rd rev. And extended ed., New York: Spring-Verlag, 1996
[10] H. A. D. Do Nascimento, Uma Abordagem para Desenho de Grafos Baseada na Utilização de Times Assíncronos, Master Thesis, Instituto de Computação, Universidade Estadual de Campinas, Campinas, SP, Brasil; May 1997 (portuguese), also H. A. D. Do Nascimento, C. F. X. De Mendonça and P. S. De Souza, Sinergia em Desenho de Grafos Usando Springs e Pequenas Heurísticas. in Proc. of XXIII Seminário Integrado de Software e Hardware (SEMISH'96), pages: 403414; Recife, PE, Brazil; August 1996 (portuguese).
[11] F. Newbery Paulish and W. F. Tichy. EDGE: An Extendible Graph Editor. Softw. Pract. Exp., 20(S1):1/63S1/88, 1990. also as Technical Report 8/88, Fakultat fur Informatik, Univ. of Karlsruhe, 1988.
[12] G. Robins. The ISI grapher: A Portable Tool for Displaying Graphs Pictorially. Technical Report ISI/RS-87-196, Information Sciences Inst., University of Southern California, 1987. also in Proc. Symboliikka '87 Helsinki Finland August 1987.
[13] R. F. Rodrigues. Times Assíncronos para a Resolução de Problemas de Otimização Combinatória Multiobjetivo. M. Sc. thesis, Instituto de Computação, Universidade Estadual de Campinas, Campinas SP, Brazil, in print 1996.
[14] L. A. Rowe, M. Davis, E. Messinger, C. Meyer, C. Spirakis, and A. Tuan. A Browser for Directed Graphs. Softw. Pract. Exp., 17(1):6176, 1987.
[15] K. Sugiyama and K. Misue.Visualization of Structural Information: Automatic Drawing of Compound Digraphs. IEEE Transactions on Software Engineering, 21(4):876892, 1991.
[16] K. Sugiyama and K. Misue. A Generic Compoud Graph Visualize/Manipulator: D-ABDUCTOR. Lecture Notes in Computer Science (Proc. DIMACS Workshop Graph Drawing, 1995), 1027:500503, 1995.
[17] K. Sugiyama, S. Tagawa, and M. Toda. Effective Representations of Hierarchical Structures. Research Report 8, IIAS-SIS, Fujitsu Limited, Numazu, Shizuoka, Japan, 1979.
[18] K. Sugiyama, S. Tagawa, and M. Toda.Methods for Visual Understanding of Hierarchical Systems.IEEE Trans. Syst. Man Cybern., SMC-11(2):109125, 1981.
[19] S. N. Talukdar and P. S. de Souza. Asynchronous Teams. In Proc. Second Siam Conf. on Linear Algebra: Signals, Systems, and Control, San Francisco, CA, Nov. 1990.
[20] S. N. Talukdar and P. S. de Souza. Scale Efficienty Organizations. IEEE Int. Conference on Systems, Man and Cybernetics, October 1992.
[21] S. N. Talukdar and P. S. de Souza. Objects Organizations and Super-Objects McGraw Hill, 1993.
[22] R. Tamassia, G. Di Battista, and C. Batini. Automatic Graph Drawing and Readability of Diagrams. IEEE Trans. on Sys., Man., and Cybernetics, 18(1), January 1988.
[23] H. Trickey. Drag: A Graph Drawing System. In Proc. Internat. Conf. On Electronic Publishing, pages 171182. Cambridge University Press, 1988.
[24] J. Utech, J. Branke, H. Schmeck, and P. Eades, An Evolutionary, Algoritm for Drawings Directed Graphs, In Proc. of The International Conference on Imaging Science, Systems, and Technology (CISST'98), Las Vegas, Nevada: CSREA Press, pages 154160, July 1998
- [1] C. Batini, M. Talamano, and R. Tamassia. Computer Aided Layout of Entity-Relationship Diagrams. Journal of Systems and Software, pages 163–173, 1984.
- [2] P. S. de Souza and S. N. Talukdar. Genetic Algorithms in Asynchronous Teams. In Proc. of the Fourth International Conference on Genetic Algorithms, Los Altos, CA, 1991.
- [3] P. S. de Souza and S. N. Talukdar. Asynchronous Organizations for Multi-Algorithm Problems. In Proc. ACM Symposium on Applied Computing, Indianapolis, IN, February 1993.
- [4] R. F. Rodrigues e P. S. de Souza. Asynchronous Teams: A Multi-Algorithm Approach for Solving Combinatorial Multi-Objective Optimization Problems. In Proceedings of the 5th Workshop of the DGOR-Working Group Multicriteria Optimization and Decision Theory, Germany, May 1995.
- [5] P. Eades and R. Tamassia. Algorithms for drawing graphs: An annotated bibliography. Report CS-09-89, Department of Computer Science, Brown University, Providence, RI, February 1989.
- [6] J. W. Forrester. World Dynamics Wright-Allen, Cambridge, MA, 1971.
- [7] E. R. Gansner, S. C. North, and K. P. Vo. DAG – A Program that Draws Directed Graphs. Softw. – Pract. Exp., 18(11):1047–1062, 1988.
- [8] D. J. Gschwind and T. P. Murtagh. A Recursive Algorithm for Drawing Hierarchical DirectedGraphs. Technical Report CS-89-02, Department of Computer Science, Williams College, 1989.
- [9] Michalewicz, Zbigniew. Genetic algorithms + data structures = evolution programs, 3rd rev. And extended ed., New York: Spring-Verlag, 1996
- [10] H. A. D. Do Nascimento, Uma Abordagem para Desenho de Grafos Baseada na Utilização de Times Assíncronos, Master Thesis, Instituto de Computação, Universidade Estadual de Campinas, Campinas, SP, Brasil; May 1997 (portuguese),
- [11] F. Newbery Paulish and W. F. Tichy. EDGE: An Extendible Graph Editor. Softw. – Pract. Exp., 20(S1):1/63–S1/88, 1990. also as Technical Report 8/88, Fakultat fur Informatik, Univ. of Karlsruhe, 1988.
- [12] G. Robins. The ISI grapher: A Portable Tool for Displaying Graphs Pictorially. Technical Report ISI/RS-87-196, Information Sciences Inst., University of Southern California, 1987. also in Proc. Symboliikka '87 Helsinki Finland August 1987.
- [13] R. F. Rodrigues. Times Assíncronos para a Resolução de Problemas de Otimização Combinatória Multiobjetivo. M. Sc. thesis, Instituto de Computação, Universidade Estadual de Campinas, Campinas – SP, Brazil, in print 1996.
- [14] L. A. Rowe, M. Davis, E. Messinger, C. Meyer, C. Spirakis, and A. Tuan. A Browser for Directed Graphs. Softw. Pract. Exp., 17(1):61–76, 1987.
- [15] K. Sugiyama and K. Misue.Visualization of Structural Information: Automatic Drawing of Compound Digraphs. IEEE Transactions on Software Engineering, 21(4):876–892, 1991.
- [16] K. Sugiyama and K. Misue. A Generic Compoud Graph Visualize/Manipulator: D-ABDUCTOR. Lecture Notes in Computer Science (Proc. DIMACS Workshop Graph Drawing, 1995), 1027:500–503, 1995.
- [17] K. Sugiyama, S. Tagawa, and M. Toda. Effective Representations of Hierarchical Structures. Research Report 8, IIAS-SIS, Fujitsu Limited, Numazu, Shizuoka, Japan, 1979.
- [18] K. Sugiyama, S. Tagawa, and M. Toda.Methods for Visual Understanding of Hierarchical Systems.IEEE Trans. Syst. Man Cybern., SMC-11(2):109–125, 1981.
- [19] S. N. Talukdar and P. S. de Souza. Asynchronous Teams. In Proc. Second Siam Conf. on Linear Algebra: Signals, Systems, and Control, San Francisco, CA, Nov. 1990.
- [20] S. N. Talukdar and P. S. de Souza. Scale Efficienty Organizations. IEEE Int. Conference on Systems, Man and Cybernetics, October 1992.
- [21] S. N. Talukdar and P. S. de Souza. Objects Organizations and Super-Objects McGraw Hill, 1993.
- [22] R. Tamassia, G. Di Battista, and C. Batini. Automatic Graph Drawing and Readability of Diagrams. IEEE Trans. on Sys., Man., and Cybernetics, 18(1), January 1988.
- [23] H. Trickey. Drag: A Graph Drawing System. In Proc. Internat. Conf. On Electronic Publishing, pages 171–182. Cambridge University Press, 1988.
- [24] J. Utech, J. Branke, H. Schmeck, and P. Eades, An Evolutionary, Algoritm for Drawings Directed Graphs, In Proc. of The International Conference on Imaging Science, Systems, and Technology (CISST'98), Las Vegas, Nevada: CSREA Press, pages 154–160, July 1998
Publication Dates
-
Publication in this collection
16 Dec 1999 -
Date of issue
July 1999









