Abstract
If G is a graph, its clique graph K(G) is the intersection graph of all its (maximal) cliques. The complex G<FONT FACE=Symbol></FONT> of a graph G is the simplicial complex whose simplexes are the vertex sets of the complete subgraphs of G. Here we study a sufficient condition for G<FONT FACE=Symbol></FONT> and K(G)<FONT FACE=Symbol></FONT> to be homotopic. Applying this result to Whitney triangulations of surfaces, we construct an infinite family of examples which solve in the affirmative Prisner's open problem 1 in Graph Dynamics (Longman, Harlow, 1995): Are there finite connected graphs G that are periodic under K and where the second modulo 2 Betti number is greater than 0?
clique graphs; clique convergence; Whitney triangulations; clean triangulations; simplicial complexes; modulo 2 Betti numbers
ARTICLES
On the homotopy type of the clique graph* * Dedicated to Prof. J. L. Szwarcfiter in his 60 th Anniversary. ** Partially supported by CONACyT, Grant 400333-5-27968E.
F. LarriónI,1 * Dedicated to Prof. J. L. Szwarcfiter in his 60 th Anniversary. ** Partially supported by CONACyT, Grant 400333-5-27968E. ; V. Neumann-LaraI,1 * Dedicated to Prof. J. L. Szwarcfiter in his 60 th Anniversary. ** Partially supported by CONACyT, Grant 400333-5-27968E. ; M. A. PizañaII
IInstituto de Matemáticas, U.N.A.M., Circuito Exterior, C.U. México 04510 D.F. MÉXICO., {paco, neumann}@matem.unam.mx
IIUniversidad Autónoma Metropolitana, Depto. de Ingeniería Eléctrica., Av. Michoacán y Purísima s/n México 09340 D.F. MÉXICO., map@xanum.uam.mx, http://xamanek.uam.mx/map
ABSTRACT
If G is a graph, its clique graph K(G) is the intersection graph of all its (maximal) cliques. The complex G of a graph G is the simplicial complex whose simplexes are the vertex sets of the complete subgraphs of G.
of a graph G is the simplicial complex whose simplexes are the vertex sets of the complete subgraphs of G.
Here we study a sufficient condition for G and K(G)
and K(G) to be homotopic. Applying this result to Whitney triangulations of surfaces, we construct an infinite family of examples which solve in the affirmative Prisner's open problem 1 in Graph Dynamics (Longman, Harlow, 1995): Are there finite connected graphs G that are periodic under K and where the second modulo 2 Betti number is greater than 0?
to be homotopic. Applying this result to Whitney triangulations of surfaces, we construct an infinite family of examples which solve in the affirmative Prisner's open problem 1 in Graph Dynamics (Longman, Harlow, 1995): Are there finite connected graphs G that are periodic under K and where the second modulo 2 Betti number is greater than 0?
Keywords: clique graphs, clique convergence, Whitney triangulations, clean triangulations, simplicial complexes, modulo 2 Betti numbers.
1 Introduction and terminology
All our graphs are simple. If G is a graph, a complete of G is a complete subgraph of G and a clique is a maximal complete of G. The clique number w(G) is the maximum order of a clique of G. We shall often identify induced subgraphs with their vertex sets. In particular, we shall often write x Î G instead of x Î V(G).
We say that G is locally H if the subgraph NG(x) induced in G by the (open) neighbourhood of any vertex a; Î G is isomorphic to H. We say that G is locally  , = {H1,H2,...} if for every x Î G, NG(x) @ Hi for some Hi 6
, = {H1,H2,...} if for every x Î G, NG(x) @ Hi for some Hi 6  . Cn and Pn are, respectively, the cyclic and path graphs on n vertices. We say that G is locally cyclic if it is locally {Cn :n > 3}.
. Cn and Pn are, respectively, the cyclic and path graphs on n vertices. We say that G is locally cyclic if it is locally {Cn :n > 3}.
The clique graph K(G) of G has all cliques of G as vertices, two of them being adjacent iff they (are different and) share some vertex of G. We call K the clique operator. Iterated clique graphs are inductively defined by K0(G) = G and Kn+1(G) = K(Kn(G)). G is K-periodic if G @ Kn(G) for some n > 1. Extensive bibliography on clique graphs can be found in [14].
A graph G is clique-Helly if whenever X = {qi,...,qn } Í V(K(G)) is a family of pairwise intersecting cliques, then  X ¹ Æ. We say that Q = {q1,...,qn } Î V(K2(G)) is a star of G if
X ¹ Æ. We say that Q = {q1,...,qn } Î V(K2(G)) is a star of G if  Q ¹ Æ, otherwise it is a necktie of G. Obviously, a graph is clique-Helly iff it has no necktie.
Q ¹ Æ, otherwise it is a necktie of G. Obviously, a graph is clique-Helly iff it has no necktie.
If G is a graph, G is the simplicial complex whose simplexes are the completes of G. We say that two simplicial complexes are homotopic (
is the simplicial complex whose simplexes are the completes of G. We say that two simplicial complexes are homotopic (
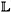 ) when their geometric realizations are homotopic (|
) when their geometric realizations are homotopic (| |
| 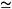 |
|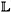 |). The behaviour of topological invariants of G
|). The behaviour of topological invariants of G under several graph operators (including the clique operator) has been studied in [9, 10, 11]. In particular, Prisner proved in [10] that if G is clique-Helly, G
under several graph operators (including the clique operator) has been studied in [9, 10, 11]. In particular, Prisner proved in [10] that if G is clique-Helly, G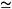 (G)
(G) . Our main result (Theorem 2.4) states that this is also true for many non-clique-Helly graphs. As an application of this, we will show (Theorem 2.5) that if G is free of tetrahedra and induced octahedra, then GK(G)
. Our main result (Theorem 2.4) states that this is also true for many non-clique-Helly graphs. As an application of this, we will show (Theorem 2.5) that if G is free of tetrahedra and induced octahedra, then GK(G) .
.
An interesting particular case is when the realization | | is a compact surface (with or without border), i.e.
| is a compact surface (with or without border), i.e.  is a triangulation of a compact surface. If G is the underlying graph (or 1-skeleton) of a surface triangulation
is a triangulation of a compact surface. If G is the underlying graph (or 1-skeleton) of a surface triangulation  , every face of
, every face of  is a triangle of G but the converse may not be true. We shall be interested in surface triangulations where every triangle of G is a face of
is a triangle of G but the converse may not be true. We shall be interested in surface triangulations where every triangle of G is a face of  : such a triangulation is a Whitney triangulation [17]. Thus, if
: such a triangulation is a Whitney triangulation [17]. Thus, if  is Whitney it is determined by G, and we tend to identify G with
is Whitney it is determined by G, and we tend to identify G with  , and sometimes even with |
, and sometimes even with | |. If
|. If  is Whitney, (except for the tetrahedron K4) the cliques of G are precisely the faces of the triangulation. Whitney triangulations have other names and have been studied before [2, 5, 8, 16, 17]. In particular, the description of the dynamical behaviour under the clique operator of the regular Whitney triangulations has been completed in [8]. As a corollary to our Theorem 2.5, we will have that the only Whitney triangulation of a compact surface which is not homotopic to its clique graph is the octahedron. We shall use the following two theorems:
is Whitney, (except for the tetrahedron K4) the cliques of G are precisely the faces of the triangulation. Whitney triangulations have other names and have been studied before [2, 5, 8, 16, 17]. In particular, the description of the dynamical behaviour under the clique operator of the regular Whitney triangulations has been completed in [8]. As a corollary to our Theorem 2.5, we will have that the only Whitney triangulation of a compact surface which is not homotopic to its clique graph is the octahedron. We shall use the following two theorems:
Theorem 1.1 [8] G is the underlying graph of a Whitney triangulation of a closed surface (resp. compact surface) if and only if G is locally cyclic (resp. G is locally {Cn,Pm: n > 3, m > 2}).
Theorem 1.2 [8] For every Whitney triangulation G of a closed surface with minimum degree at least 7 we have K(G) 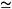 K3(G).
K3(G).
We refer to [1], [10] and [13] for undefined concepts.
2 Homotopy
If  . is a hypergraph,
. is a hypergraph,  * denotes its dual hyper-graph, and
* denotes its dual hyper-graph, and  ¯ is the smallest simplicial complex containing the hyperedges of
¯ is the smallest simplicial complex containing the hyperedges of  as simplexes. The following reformulation is due to Prisner [9, 10]:
as simplexes. The following reformulation is due to Prisner [9, 10]:
Theorem 2.1 (Dowker, [3]) For every hyper-graph ,
,  ¯ and
¯ and *¯ are homotopic.
*¯ are homotopic.
If G is a graph,  (G) is its clique hypergraph:
(G) is its clique hypergraph:  (G) has the same vertex set as G and its hyper-edges are the cliques of G. It follows immediately from the definitions that G
(G) has the same vertex set as G and its hyper-edges are the cliques of G. It follows immediately from the definitions that G =
=  (G)¯.
(G)¯.
The star hypergraph S(G) of G has the same vertex set as K(G) and the hyperedges are the cliques Q = {q1,q2,...,qr } of K(G) satisfying  Q ¹ Æ. It follows that
Q ¹ Æ. It follows that  (G)*¯ = S(G)¯ and that S(G)¯ Í K(G)
(G)*¯ = S(G)¯ and that S(G)¯ Í K(G) . The equality S(G)¯ = K(G)
. The equality S(G)¯ = K(G) holds precisely when G is clique-Helly.
holds precisely when G is clique-Helly.
Then, as pointed out by Prisner [10, Proposition 2.2], it follows from Dowker's theorem that G and K(G)
and K(G) are homotopic for every clique-Helly graph G. A reformulation of this result will be useful to us:
are homotopic for every clique-Helly graph G. A reformulation of this result will be useful to us:
Theorem 2.2 (Prisner, [10]) For every graph G, we have G =
=  (G)¯
(G)¯ 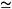
 (G)*¯ = S(G)¯ Í K(G)
(G)*¯ = S(G)¯ Í K(G) . In particular, if G is clique-Helly, then G
. In particular, if G is clique-Helly, then G
 .
.
Prisner provided examples of graphs G (namely the n-dimensional octahedra, for n > 3) such that G and K(G)
and K(G) are not homotopic. As we shall see shortly, this property of the octahedra is tightly connected to the fact that octahedra contain neckties without a center.
are not homotopic. As we shall see shortly, this property of the octahedra is tightly connected to the fact that octahedra contain neckties without a center.
Definition 2.3 If X is a complete of K(G) satisfying  X ¹ Æ, then q0 Î K(G) is called a center of X if:
X ¹ Æ, then q0 Î K(G) is called a center of X if:
Y Í X and  Y ¹ Æ imply
Y ¹ Æ imply  (Y È{q0}) ¹ Æ .
(Y È{q0}) ¹ Æ .
Note that X È {q0 } is always a complete of K(G). Also, when such an X is a clique of K(G), X must contain all its centers.
Many non-Helly graphs G satisfy G
K(G) , Indeed we shall show that for many non-Helly graphs G, S(G)¯ is a strong deformation retract of K(G)
, Indeed we shall show that for many non-Helly graphs G, S(G)¯ is a strong deformation retract of K(G) .
.
Let's rename  = S(G)¯ and
= S(G)¯ and  = K(G)
= K(G) . We know that
. We know that  Í
Í  . Note that the 0-simplexes of
. Note that the 0-simplexes of  and
and  are the same. In order to easily define the required mappings, we take the barycentric subdivision
are the same. In order to easily define the required mappings, we take the barycentric subdivision  ' of
' of  relative to
relative to  as used in [12, page 19].
as used in [12, page 19].
Equivalently, we define the complex  ' whose vertices are those of
' whose vertices are those of  (denoted by qi) plus a (formal) barycenter b(s) for each s Î
(denoted by qi) plus a (formal) barycenter b(s) for each s Î 
 , and whose simplexes are of the form {q1,...,qn , (s1),..., b(sm )} and satisfy:
, and whose simplexes are of the form {q1,...,qn , (s1),..., b(sm )} and satisfy:
1. {q1,...,qn}Î .
.
2. sjÎ 
 for all j.
for all j.
3. siÎ s1 for all i.
4. sjÍ sj+1 for ali j.
and then we may prove that this is indeed a subdivision of  using Theorem 3.3.4 in [13]. Of course, we still have
using Theorem 3.3.4 in [13]. Of course, we still have  Í
Í  '.
'.
The idea behind this is to grab the offending simplexes (those in 
 ) by its barycenters and retract them into S. Now we can prove our main result:
) by its barycenters and retract them into S. Now we can prove our main result:
Theorem 2.4 Let G be a graph. Assume that any complete X of K(G) with
X = Æ has a center which belongs to every necktie containing X. Then S(G)¯ is a strong deformation retract of K(G) . In particular, G
. In particular, G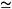 K(G)
K(G) .
.
Proof. For every simplex s in 
 select, using the hypothesis, a fixed center q(s) of s belonging to every maximal simplex (i.e. necktie) that contains s. Also, for each s Î
select, using the hypothesis, a fixed center q(s) of s belonging to every maximal simplex (i.e. necktie) that contains s. Also, for each s Î 
 , define
, define
s =  {Q Î K2 (G) : s Í Q}
{Q Î K2 (G) : s Í Q}
Note: s Í  Î
Î 
 , and s Í s' implies q(
, and s Í s' implies q( ) Î
) Î  Í
Í  .
.
Now define the map j1 :  ' ®
' ®  by j1 (qi) = qi and j1 (b(sj)) = q(
by j1 (qi) = qi and j1 (b(sj)) = q( j). Then for any simplex of
j). Then for any simplex of  ' we have that j1{q1,...,qn , (s1),..., b(sm)} = {q1,...,qn, (
' we have that j1{q1,...,qn , (s1),..., b(sm)} = {q1,...,qn, ( 1),..., b(
1),..., b( )}. This is a simplex of
)}. This is a simplex of  because there is a clique Q of K(G) such that qi Î Q and sjÍ Q for all i = l,...,n and j = 1,..., m (take a Q with smÍ Q). Therefore qi,q(
because there is a clique Q of K(G) such that qi Î Q and sjÍ Q for all i = l,...,n and j = 1,..., m (take a Q with smÍ Q). Therefore qi,q( j ) Î Q for all i and j. It follows that j1 :
j ) Î Q for all i and j. It follows that j1 :  ' ®
' ®  is a Simplicial map, so | j1| : |
is a Simplicial map, so | j1| : | '| ® |
'| ® | | is continuous.
| is continuous.
We claim now that Im(j1 i) =  : As q1Ç ¼ Ç qn¹ Æ and {q1,...,qn} Í s1Í
: As q1Ç ¼ Ç qn¹ Æ and {q1,...,qn} Í s1Í  1, we obtain that q1Ç ¼ Ç qn q(
1, we obtain that q1Ç ¼ Ç qn q( 1)¹ Æ. Using that
1)¹ Æ. Using that  1 Í
1 Í  2 Í ¼ Í
2 Í ¼ Í  and q(
and q( j ) Î
j ) Î  j for all j, it follows by induction that {q1,...,qn , (
j for all j, it follows by induction that {q1,...,qn , ( 1),..., b(
1),..., b( )} is a simplex of
)} is a simplex of  . Now we know that Im(|j1| ) = |
. Now we know that Im(|j1| ) = | | and that the restriction of |j1|to |
| and that the restriction of |j1|to | | is the identity in |
| is the identity in | |.
|.
On the other hand, consider the canonical homeomorphism j0 : | | ® |
| ® | '|. Let j = j1 o j0. Note that for all x Î |
'|. Let j = j1 o j0. Note that for all x Î | | there is a simplex s Î
| there is a simplex s Î  such that x, j(x) Î |s| (any maximal simplex s Î
such that x, j(x) Î |s| (any maximal simplex s Î  satisfying x Î |s| will do). Then it follows that j
satisfying x Î |s| will do). Then it follows that j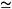 1
1 via the homotopy H(x, t) tx + (1 t)j(x) (see, for example [6, Prop. 1.7.5]). Since j|
via the homotopy H(x, t) tx + (1 t)j(x) (see, for example [6, Prop. 1.7.5]). Since j| = 1
= 1 , we have that H(x,t) = x for all x Î |
, we have that H(x,t) = x for all x Î | |. Therefore |
|. Therefore | | is a strong deformation retract of |
| is a strong deformation retract of | |.
|.
An interesting consequence is the following:
Theorem 2.5 If G is a graph free of induced octahedra and w(G) < 3, then G
K(G)
Proof. Without loss of generality we assume G to be connected and non-trivial. Then we observe that every clique of G is a triangle or an edge.
Let X be a complete of K(G) satisfying  X = Æ, and let Z = {q1,...,qr} be a minimal subset of X also satisfying
X = Æ, and let Z = {q1,...,qr} be a minimal subset of X also satisfying  Z = Æ.
Z = Æ.
Since Z is minimal and necessarily r > 3, we may take x23Î  (Z {q1}), x13Î
(Z {q1}), x13Î  (Z {q2}) and x12Î
(Z {q2}) and x12Î  (Z {q3})- Hence, q0 = {x12, x13 , x23} is a clique of G. This very construction was used by J. L. Szwarcfiter in his celebrated characterization of clique-Helly graphs [15].
(Z {q3})- Hence, q0 = {x12, x13 , x23} is a clique of G. This very construction was used by J. L. Szwarcfiter in his celebrated characterization of clique-Helly graphs [15].
It follows that q1 = {x12, x13 , a}, q2 = {x12, x13 , b} and q3 = {x13 , x23, c} for some three (different) vertices a, b, c Î G. Since q1 Ç q2 Ç q3 = Æ it follows that Z = {q1, q2, q3 }.
Let Q Î K2(G) be a necktie containing Z, and let q Î Q. If q n qo = Æ, then q = {a, b, c} and the set of vertices {x12, x13 , x23, a, b, c} induces an octahedron in G, contradicting our hypotheses. If |q Ç q0| = 1, say q n q0 = {x12}, then q Ç q3 = {c} and {x12, x13 , x23 , c} would contradict w(G) < 3. Therefore |q Ç q0| > 2 for every q Î Q.
Since the set {q Î K(G) : |q Ç q0| > 2} is a complete of K(G) it follows that Q = {q Î K(G) : |q Ç q0| > 2}. Now the condition on the clique number implies that q0 is a center of Q. Then Q is the unique necktie containing Z, so it is also unique containing X. Therefore go is a center of X which belongs to every necktie containing X, and we apply the previous theorem.
The following result is an immediate consequence:
Corollary 2.6 The only Whitney triangulation of a compact surface (with or without border) which is not homotopic to its clique graph is the octahedron.
Now let's denote the i-ih modulo 2 Betti number of a complex  by
by 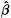 i(
i( ). Take any locally {Ct : t > 7} graph H. By Theorem 1.1 if is a Whitney triangulation of a closed surface, so we have
). Take any locally {Ct : t > 7} graph H. By Theorem 1.1 if is a Whitney triangulation of a closed surface, so we have 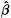 2(H
2(H ) = 1. Since H
) = 1. Since H
 we have
we have 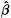 2(K(H)
2(K(H) ) = I. Then Theorem 1.2 tells us that G := K(H) is .K''-periodic, thus solving Prisner's open problem 1 in [11].
) = I. Then Theorem 1.2 tells us that G := K(H) is .K''-periodic, thus solving Prisner's open problem 1 in [11].
As a concrete example, it is shown in [8] that I ´ K3 is a locally C10 graph (here I is the icosahedron and {(a, b), (a', b')} Î E (A ´ B) iff {a, a'} Î E (A) and {b, b'} e E(B) ). In fact, Brown and Connelly [2] proved that for every t there is at least one finite locally Ctgraph. Next, we shall construct an explicit infinite family of locally C7 graphs.
3 Whitney triangulations
Let's start with an infinite graph T: V(T) =  Å
Å  and put N = {±(1,0),±(0,1),±(1,-1)}, then define {x, y} Î E(T) if and only if y x Î N.
and put N = {±(1,0),±(0,1),±(1,-1)}, then define {x, y} Î E(T) if and only if y x Î N.
Each vector u Î  Å
Å  gives rise to a translation x
gives rise to a translation x  u + x which is an automorphism of T. Every finite locally C6graph triangulating the torus is a quotient T/G where G is the translation group generated by the translations given by two linearly independent vectors u, v Î
u + x which is an automorphism of T. Every finite locally C6graph triangulating the torus is a quotient T/G where G is the translation group generated by the translations given by two linearly independent vectors u, v Î  Å
Å  . The group G must satisfy the following admissibility condition: for every g Î G and v Î V(T), the distance in T from v to g(v) is at least 4 (otherwise, the resulting triangulation is not Whitney, see [7]).
. The group G must satisfy the following admissibility condition: for every g Î G and v Î V(T), the distance in T from v to g(v) is at least 4 (otherwise, the resulting triangulation is not Whitney, see [7]).
Let u = (4,1), fix r > 2, and let vT = (2r,4r). Let Gr be the translation group defined by u and vr, and let  rbe the parallelogram defined by these two vectors. The locally C6graph Gr = T/Gr defines a Whitney triangulation of the torus with 14r vertices: Gris obtained by identifying the parallel edges of
rbe the parallelogram defined by these two vectors. The locally C6graph Gr = T/Gr defines a Whitney triangulation of the torus with 14r vertices: Gris obtained by identifying the parallel edges of  r.
r.
Now consider the 2r vertices w1, w2, w2r of Grwhich correspond to the vertices (2,1),(3,3),...,(2r + 1,4r - 1) in  r, i.e. wi = (i + 1,2i 1). The vertices of GTare the disjoint union of the closed neighbourhoods N[wi] of these vertices, and removing these vertices from Grwe obtain a locally P5 graph
r, i.e. wi = (i + 1,2i 1). The vertices of GTare the disjoint union of the closed neighbourhoods N[wi] of these vertices, and removing these vertices from Grwe obtain a locally P5 graph 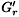 of order 12r. Let us call
of order 12r. Let us call 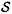 rthe surface triangulated by
rthe surface triangulated by 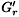 , which is a torus with 2r open disks removed. All the vertices of
, which is a torus with 2r open disks removed. All the vertices of 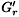 lie in the border of
lie in the border of 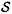 r. The connected components of the border of
r. The connected components of the border of 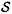 rare the hexagons H1, H2,...,H2r which were the open neighbourhoods of the removed vertices w1, w2,..., w2rof Gr.
rare the hexagons H1, H2,...,H2r which were the open neighbourhoods of the removed vertices w1, w2,..., w2rof Gr.
Consider the locally P4 graph 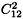 in figure 3. This graph gives us a Whitney triangulation of a cylinder, all the vertices lie in the border whose connected components B1 and B2 are induced hexagons of
in figure 3. This graph gives us a Whitney triangulation of a cylinder, all the vertices lie in the border whose connected components B1 and B2 are induced hexagons of 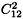 .
.
Now, take the surface
r(with its Whitney triangulation given by the graph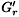 ) and r different copies of the cylinder (with the Whitney triangulation given by
) and r different copies of the cylinder (with the Whitney triangulation given by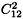 ). For the first copy, identify B1 with HI and B2with Hr+1in an orientable manner, so a handle is glued to Sr. For the second copy, identify B1 with H1and B2with Hr+1, so a second handle is glued to
). For the first copy, identify B1 with HI and B2with Hr+1in an orientable manner, so a handle is glued to Sr. For the second copy, identify B1 with H1and B2with Hr+1, so a second handle is glued to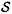 r. Continuing in this way, we obtain at the end a closed surface
r. Continuing in this way, we obtain at the end a closed surface 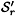 which is a sphere with r + 1 handles. The graph
which is a sphere with r + 1 handles. The graph 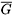 r obtained from
r obtained from 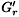 and the r copies of
and the r copies of 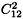 by the above method has 12r vertices and is the 1-skeleton of a triangulation of our surface
by the above method has 12r vertices and is the 1-skeleton of a triangulation of our surface 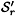 .
.
As we want
rto be locally C7 we have to take care so that the triangles in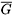 rare exactly the triangles already present (16r in
rare exactly the triangles already present (16r in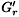 and 12 in each copy of
and 12 in each copy of 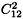 ). This fails when two vertices x Î Hi and y Î Hi+rwith d(x,y) < 3 in
). This fails when two vertices x Î Hi and y Î Hi+rwith d(x,y) < 3 in 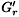 are identified with adjacent vertices in the i-th copy of
are identified with adjacent vertices in the i-th copy of 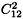 . Since d(Hi, Hr+i ) = r, there is no problem for r > 3.
. Since d(Hi, Hr+i ) = r, there is no problem for r > 3.
In case r = 2, there is an essentially unique way to glue the 2 copies of  in such a way that no new triangles are created, and this produces a triangulation of the orientable closed surface of genus 3 (the ''triple torus''). We verified this by computer using GAP [4]. It can be shown that the double torus does not admit a locally C7 triangulation.
in such a way that no new triangles are created, and this produces a triangulation of the orientable closed surface of genus 3 (the ''triple torus''). We verified this by computer using GAP [4]. It can be shown that the double torus does not admit a locally C7 triangulation.
Notice that for r > 3 the construction allows more freedom at the time of gluing (so in principle more than one example may have been constructed at each genus g > 3) and that even non-orientable surfaces are obtained gluing one handle in a non-orientable manner. So we have proved:
Theorem 3.1 Every orientable surface of genus at least 3, and every non-orientable surface with even Euler characteristic c< 6 admits a locally C7 triangulation G. For any such G, K(G) is a positive answer to Prisner's open problem 1 in [11].
- [1] Claude Berge. Hypergraphs. North-Holland Publishing Co., Amsterdam, 1989. Combinatorics of finite sets, Translated from the French.
- [2] Morton Brown and Robert Connelly. On graphs with a constant link. In New directions in the theory of graphs (Proc. Third Ann Arbor Conf., Univ. Michigan, Ann Arbor, Mich., 1971), pages 19-51. Academic Press, New York, 1973.
- [3] C. H. Dowker. Homology groups of relations. Ann. of Math. (2), 56:84-95, 1952.
- [4] The GAP Group, Aachen, St Andrews. GAP - Groups, Algorithms, and Programming, Version 4.2, 2000. (http://www-gap-system.org).
- [5] Nora Hartsfield and Gerhard Ringel. Clean triangulations. Combinatorica, 11 (2): 145-155, 1991.
- [6] P. J. Hilton and S. Wylie. Homology theory: An introduction to algebraic topology. Cambridge University Press, New York, 1960.
- [7] F. Larrión and V. Neumann-Lara. Locally C§ graphs are clique divergent. Discrete Math., 215(1-3):159 170, 2000.
- [8] F. Larrión, V. Neumann-Lara, and M. A. Pizaña. Whitney triangulations, local girth and iterated clique graphs. Discrete Math., 258(1-3):123-135, 2002.
- [9] Erich Prisner. Homology of the line graph and of related graph-valued functions. Arch. Math., 56(4):400-404, 1991.
- [10] Erich Prisner. Convergence of iterated clique graphs. Discrete Math., 103(2): 199-207, 1992.
- [11] Erich Prisner. Graph dynamics. Longman, Harlow, 1995.
- [12] C. P. Rourke and B. J. Sanderson. Introduction to piecewise-linear topology. Springer-Verlag, Berlin, 1982. Reprint.
- [13] Edwin H. Spanier. Algebraic topology. Springer-Verlag, New York, 1981. Corrected reprint.
- [14] Jayme L. Szwarcfiter. A survey on clique graphs. In Recent Advances in Algorithms and Combinatorics. C. Linhares and B. Reed, eds., Springer-Verlag. To appear.
- [15] Jayme L. Szwarcfiter. Recognizing clique-Kelly graphs. Ars Combin., 45:29-32, 1997.
- [16] W. T. Tutte. A census of plane triangulations. Cañad. J. Math., (14):21-28, 1962.
- [17] H. Whitney. A theorem on graphs. Ann. Math., 32(2):378-390, 1931.
Publication Dates
-
Publication in this collection
16 Dec 2003 -
Date of issue
2001





