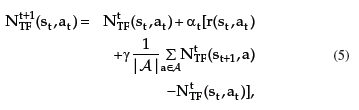Abstract
Reinforcement Learning is carried out on-line, through trial-and-error interactions of the agent with the environment, which can be very time consuming when considering robots. In this paper we contribute a new learning algorithm, CFQ-Learning, which uses macro-states, a low-resolution discretisation of the state space, and a partial-policy to get around obstacles, both of them based on the complexity of the environment structure. The use of macro-states avoids convergence of algorithms, but can accelerate the learning process. In the other hand, partial-policies can guarantee that an agent fulfils its task, even through macro-state. Experiments show that the CFQ-Learning performs a good balance between policy quality and learning rate.
machine learning; reinforcement learning; abstraction; partial-policy; macro-states
Compulsory Flow Q-Learning: an RL algorithm for robot navigation based on partial-policy and macro-states
Valdinei Freire da Silva* * e-mail: valdinei.freire@gmail.com ; Anna Helena Reali Costa
Laboratório de Técnicas Inteligentes - LTI, Departamento de Engenharia de Computação e Sistemas Digitais - PCS, Escola Politécnica da Universidade de São Paulo - EPUSP, São Paulo - SP, Brasil
ABSTRACT
Reinforcement Learning is carried out on-line, through trial-and-error interactions of the agent with the environment, which can be very time consuming when considering robots. In this paper we contribute a new learning algorithm, CFQ-Learning, which uses macro-states, a low-resolution discretisation of the state space, and a partial-policy to get around obstacles, both of them based on the complexity of the environment structure. The use of macro-states avoids convergence of algorithms, but can accelerate the learning process. In the other hand, partial-policies can guarantee that an agent fulfils its task, even through macro-state. Experiments show that the CFQ-Learning performs a good balance between policy quality and learning rate.
Keywords: machine learning, reinforcement learning, abstraction, partial-policy, macro-states.
1. Introduction
A common class of tasks in mobile robotics is planning an action policy to reach a desired goal state, usually through maximisation of a value function which designates sub-objectives and helps choosing the best path. For instance, the shortest path, the path with the shortest time, the safest path, or any combination of different sub-objectives5, 20. The definition of a task in this class may contain, besides the value function, some a priori knowledge about the domain, e.g., environment map, environment dynamics, goal position. Such knowledge allows a robot planning, while the lack of such knowledge obliges the robot either to learn it previously or to make use of heuristic strategies, such as moving to goal direction while avoiding obstacles19.
While the problem of mapping the environment has received great attention from the robotics community, mainly under the simultaneous localisation and mapping approach3,1, less attention has been given to learn the environment dynamics. Given a map and the robot localisation, if a goal position is given, it is possible through path planning to determine a path free of obstacles from the robot position to such goal. However, even if a priori knowledge is considered about moving directions in the Euclidean space so that an action policy can be computed, minor variations in the environment dynamics, such as slippery, oblique, or crushed ground, are not captured as well as are not inferred more generic sub-objectives.
Reinforcement Learning (RL)21 is a learning method that can be applied to the task of learning the dynamic environment and planning an action policy altogether. In RL, an autonomous agent learns an action policy based on its own experience. This policy is inferred from a process of trial and error, which is guided by the agent itself and received reinforcements that indicate a partial evaluation of executed actions, besides perceiving transitions among different situations - formally states - evidencing the environment dynamics. The sequence of received reinforcements determines the value of each executed trajectory. Reinforcements can indicate walked distance, time elapsed or any desirable local situation faced by the robot.
Whereas the robotic task of reaching a goal state in an environment populated with obstacles can be solved through planning, robots based on RL can learn and recover from big changes in the environment, like the appearance of new obstacles, or small ones, like the appearance of oil in the ground or of crushed ground2. Moreover, RL does not need to start learning from the scratch, some partial solution can be considered so that an RL algorithm fills the gaps or a sub-optimal solution can be considered so that an RL algorithm improve it.
Within the last fifteen years, many works about RL have been published18, 10, 22, 4, 14 extending Sutton's article22, which brought a mathematical formalism to RL. However, most methods depend strongly on the size of the state space in which the learning process is done, and gives rise to a trade-off between policy quality and learning speed.
Recent works in RL are attempts at finding methods that accelerate the learning rate without degenerating the policy quality. In such methods three objectives are pursued: scalability, so that no exponential increase occurs in the complexity of solving tasks when increasing the size of state space; knowledge transfer, so that most of common knowledge can be shared among different tasks; and stability, so that a method can be applied to different domains.
In this paper we propose a method that concerns scalability and knowledge transfer properties, so that an increase in the learning speed for a specific task in mobile robotics can be reached. On the other hand, we restrict our algorithm to a specific domain, that of reaching a goal state within an environment that contains obstacles where robots cannot walk through. The proposed method uses a discretisation of the state space combined with a previously learnt partial-policy7, both defined in accordance to the complexity of the environment structure. This method is implemented in the CFQ-Learning algorithm, which stands for Compulsory Flow Q-Learning.
We use both, temporal and spatial abstraction, in order to accelerate the learning process. Spatial abstraction is applied through low resolution discretisation of the state space11, 16 and similar states are grouped such that they share characteristics which will be learnt equal to all of them. Temporal abstraction is applied through macro-actions8, which are a sequence of actions or a sub-policy that are applied to more than one step, so that less chance for the robot choosing actions is left. However, since there are discontinuity in the state space because of obstacles, we may use a high resolution discretisation near such discontinuity, or a macro-action to over come the obstacles. We have chosen the second case, using a compulsory flow as partial-policy, which takes control of the robot near obstacles to get round them.
Based on theoretical and experimental analysis, we show that the CFQ-Learning performs a better balance between policy quality and learning speed than the Q-Learning algorithm does when applied to a discretised continuous state space.
The remaining of this paper is organised as follows. Section 2 presents the RL formalisation together with Q-learning, the most usual RL algorithm, then, the task domain of interest is presented followed by reinforcement learning algorithm that can solve it. In Section 3 we define formally the partial policy, named compulsory flow, and describe how to learn such flow. We then present the CFQ-Learning algorithm in Section 4, which uses the compulsory flow and a discretisation of the state space defined for the current task environment to learn action policies. In Section 5 we compare the performance of the CFQ-Learning algorithm with the Q-Learning algorithm when different discretisations of the state space are considered. We describe the experiments performed and present the results obtained. Finally, Section 6 summarises our conclusions.
2. Reinforcement Learning and Task Domain
In works concerning RL, Markovian Decision Processes (MDPs)17 are adopted as simplified models of real problems. MDP models are built under a well-established mathematical formalism, which compensates the simplifying conditions used to describe the environment, as there are optimal algorithms to solve problems expressed as MDPs17.
An MDP is defined by a tuple <A, S, P(st+1|st, at), r(s, a)> where A is a finite set of possible actions a, S is a finite set of possible states s, P(st+1|st, at) represents transition probabilities and r(s, a) is a bounded expected reinforcement function17.
2.1. Q-Learning algorithm
The basic idea behind RL is that the learning agent can learn how to solve an MDP task through repeated interactions with the environment. Note that all that is known by the agent is the set of actions A and the set of states S, whereas the functions P(s'|s, a) and r(s, a) must be learnt through interaction within the environment.
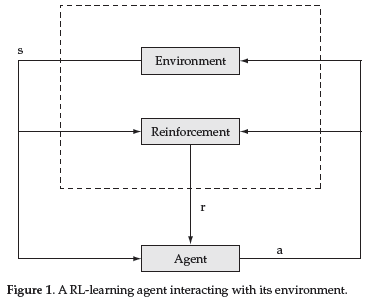
The environment is described by the set of possible states S, and the agent can perform any action from A. Each time it performs an action a in some state s, the environment reaches a new state and the agent receives a reinforcement r that indicates the immediate value of this state-action transition (see Figure 1).
The agent must find out a stationary policy of actions a*t = π* (st) that maximises the expected value function Vπ(st), which represents the expected reinforcement incurred for a policy π, and π*(st) = arg maxπ [Vπ(st)].17 It is common to assume the discounted-reinforcement value function, which makes use of a discount factor γ  (0,1] that forces recent reinforcements to be more important than remote ones. Vπ (st) is thus defined by:
(0,1] that forces recent reinforcements to be more important than remote ones. Vπ (st) is thus defined by:
The RL problem modelled as an MDP can be solved by the Q-Learning algorithm24, which finds an optimal policy incrementally without considering the transition probabilities of the environment model. Q-Learning is based on the TD(0) algorithm22, and estimates a value function Q(s,a) for each state-action pair. This value function is recursively calculated by:
where αt is the learning rate and γ is the discount factor.
During the learning process, at the time of choosing action αt it is necessary to select one between two strategies: exploration, which diversifies the policy in order to reach unknown state-action pairs and may improve the best current known policy, or exploitation, which chooses the best current known policy. Frequently a combination of both strategies is used (ε-greedy), where an exploration rate ε is defined9.
2.2. Task domain
Goal-state tasks have many applications in robotics - going to a desired room, holding an object, changing the environment, and so on. Frequently it is required that the robot plans the best possible path to solve the task within a continuous state space. Although RL algorithms can sub-optimally solve these tasks (for instance, by considering a high-resolution grid world and using an unitary cost for each action choice), too much time can result to obtain a reasonably good policy, resulting in an inefficient alternative in many cases.
The interest here resides in applications where a set of goalstate tasks are defined for the same kind of environment, so that it is worth acquiring in advance some knowledge about this kind of environment, and then reuse this knowledge in future tasks, where different goal positions or different environments are defined.
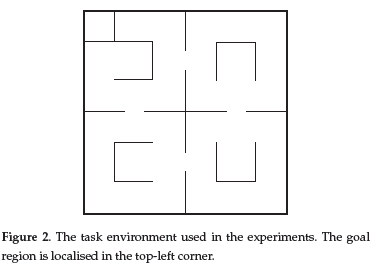
A mobile robot navigating in an one-floor house is a kind of environment that is considered in this paper. Figure 2 shows the environment used in the experiments described in Section 5, where a mobile robot can move in any direction.
The domain considered in this paper can be defined in a continuous space. In this space we can define a set of continuous states X that represents every possible position of the robot in the environment. One of the characteristics of such space is the notion of neighbourhood. For example, if a position in a plane is considered, the Euclidean distance can be considered to define a neighbourhood of each position, meaning that the robot can reach a state in this neighbourhood in the near future.
Although the continuous state space presents some important characteristics when planning, the solution discussed in this paper - RL algorithms - are only applied to discrete spaces. This way, we can consider a high resolution discrete space S that represents the continuous space of the domain through a map s(x): X → S. We must also consider a set of discrete actions A. The chosen discretisation should respect the following constraints:
1. The set of continuous states that is mapped into the same discrete state must be compact, i.e., if s(xi) = s(xj) = s then s(αxi+ (1 - α)xj) = s for all α
(0,1). This guarantees that the notion of neighbourhood is maintained in the discrete state space when we consider the continuous mean position of every continuous state mapped into the same discrete state;
2. The agent moves only to neighbour states in the discrete state space, i.e., P(st + 1= s' | st= s, at) > 0 if and only if s and s' are neighbours. This guarantees that the notion of neighbourhood in the continuous state space can be extended to the discrete state space; and
3. There are actions that can move the agent, with higher probability, to any direction in the state space, except to places where obstacles exist, i.e., for all neighbouring states s, s'
S, there is an action a
Asuch that P(st + 1= s' | st= s, at= a) = maxs"
S P(st + 1 = s" | st= s, at= a). This implies that if the set of discrete states allows k neighbour states, then | A| > k. This guarantees that the agent can move from any state to its neighbours.
Figure 3 shows two patterns of discrete states that respect such constraints. In the hexagon pattern, there are 6 possible actions, whereas in the quadratic pattern, there are 8 possible actions.
2.3. Q-Learning and continuous space
The Q-Learning algorithm, as described in Section 2.1, is restricted to discrete spaces (states and actions), and when applied to a continuous state (or action) space, a discretisation process is necessary. It is usual to use a uniform discretisation of the space (states and actions) as are shown in Figure 3, such that a discrete action is chosen and performed (for a constant period of time, until the agent makes a transition between discrete states, or until another condition occurs) in a considered discrete state, which encompasses the current real state.
In a continuous space, when applying a continuous control u(x(t)), its respective value function Vu(x(t))(x(t)) is obtained such that:
where x(t) is the current state, r(x,u) is the current reinforcement per time and γ is the discount factor.
In the discretisation process, a set of continuous states is associated with a discrete state s, s: X→S, where X is the set of continuous states and S is the set of discrete states. The function s(x) relates each continuous state x to a discrete state s = s(x) and for each discrete state in S, it is supposed that the value function of all its continuous states has similar values and similar optimal policy, which means that if s(x1) = s(x2) then V*(x1) V*(x2) and π*(x1)
V*(x2) and π*(x1)  π*(x2).4 In general, the set of discrete actions A is chosen in such way that the agent can move to all its discrete neighbours, as it was seen in section 2.2, the reinforcement function r(s,a) is derived from the continuous state space, and the value function is recursively calculated by Munos and Moore11:
π*(x2).4 In general, the set of discrete actions A is chosen in such way that the agent can move to all its discrete neighbours, as it was seen in section 2.2, the reinforcement function r(s,a) is derived from the continuous state space, and the value function is recursively calculated by Munos and Moore11:
where αt is the learning rate, γ is the discount factor, stx(t) is the discrete state st mapped from the continuous state x(t), and τ is the time taken to execute action at.
As a result of the discretisation process, finite cardinality is obtained. However, the performance of the Q-Learning algorithm is completely dependent on such cardinality and in the way the discretisation is made. If cardinality is high, a good policy can be obtained, but the learning speed is low, whereas if cardinality is low, the learning speed is high, but the learned policy is of lower quality. Then a trade-off between learning speed and policy quality must be considered for the discretisation process. When a discretisation is used, the convergence of Q-Learning algorithm is also corrupted, since it is not possible to guarantee a stationary transition function P(s'|s,a), but it will depend on the policy executed, or, more specifically, the previous discrete state occurred.
In most domains, a uniform discretisation is not the best solution, since the environment structure is not considered. Munos and Moore11 presented an algorithm that makes a non-uniform discretisation based on the value function variance of continuous states belonged to the same discrete state and on the influence of the value function of a discrete state in other discrete states. However, the system dynamics is considered to be known and deterministic. Reynolds16 proposed an adaptive algorithm based on policy to the non-uniform discretisation process, which acquires the dynamics of the environment whilst executes on-line discretisation of the state.
One reason for having discontinuity in optimal value functions and policies is the existence of obstacles and prohibited state transitions in the environment. Both methods cited above discretises the space in a more useful way, when compared to the uniform discretisation frequently used. However, when applied to an environment with many obstacles, high resolution is used near obstacles, since they produce high variations in the value function and in the policy, what decreases the learning speed.
We propose an alternative way to deal with this problem. The idea is to previously define i) an obligatory partial policy, named compulsory flow, that should be performed by the learning agent when near obstacles, and ii) a low-resolution discretisation of the state space based on the environment structure together with constraints on the action policy to be used in regions free of obstacles. Once the compulsory flow and the low-resolution discretisation of the state space are defined, this information can be reused in the policy learning process for different tasks defined for the same environment. Based on these definitions (compulsory flow and low-resolution discretisation), we contribute a new algorithm, called Compulsory Flow Q-Learning, aiming at a better balance between learning speed and policy quality.
3. Compulsory Flow
Partial policy is a mapping from a environmental region to a subset of possible actions13, 7, 15 and it helps incorporating a priori knowledge into RL learning methods. Differently from previous work in the literature, we consider a priori partial policy that reach a desired domain-dependent behaviour in the environment. In this paper, this action subset has only one possible action for each state. In order to define the compulsory flow, a high-resolution state space discretisation is used. Although it can spend lots of time to determine the compulsory flow, it is calculated only once for each environment. The same environment structure can be used for different tasks and the compulsory flow can be reused so that the learning speed can be increased.
Also, we will see that the compulsory flow can be defined locally, meaning that it is not sensitive to the global environment, but to situations faced by the robot. The compulsory flow is a partial policy used when the agent is near obstacles, so that the robot can get around obstacles6. In this sense, hardcoded partial policy can be used to implement get-around behaviour, being the only requirement that the agent keeps some inertial movement.
The compulsory flow is defined by the tangential-flow region RTF and the tangential-flow policy πTF , where
, where 
 is a function that defines an action a for each st, which is reached by performing at-1 in st-1. The previous action at-1 is used in order to guarantee inertial behaviour, trying to keep the same movement direction when avoiding obstacles.
is a function that defines an action a for each st, which is reached by performing at-1 in st-1. The previous action at-1 is used in order to guarantee inertial behaviour, trying to keep the same movement direction when avoiding obstacles.
Definition 1: Let NTF(s, a) be the expected number of actions performed by an agent to reach an obstacle when executing the action a in the state s and then following a random policy; at-1 and at be the last action executed and the new action to be performed, respectively;  be the number that determines the size of RTF; and a be the vector which represents action a in the continuous space; then it is defined:
be the number that determines the size of RTF; and a be the vector which represents action a in the continuous space; then it is defined:
Tangential-flow region RTF: si RTF if and only if
RTF if and only if  , that means, sis near some obstacle, and
, that means, sis near some obstacle, and
Tangential-flow policy πTF(.):

where  represents the inner product of
represents the inner product of 
 . This means that the angle between the vector πTF(sª ) and the vector a is less than 90º, what keeps the agent in a similar movement direction given by
. This means that the angle between the vector πTF(sª ) and the vector a is less than 90º, what keeps the agent in a similar movement direction given by  and near the boarder of RFT, making the agent getting around obstacles.
and near the boarder of RFT, making the agent getting around obstacles.
Figure 4 illustrates a tangential-flow region (gray region) and the corresponding tangential-flow policy when the agent starts at point 1, performs an action ai =at-1that drives it into RTF and activates πTF(.)(see Definition 1), which avoids collision with the wall by conducting the agent through the compulsory flow until point 2, when it is released and a new action ai can be chosen to be performed. When the agent is released from a compulsory flow will be explained in the next section.
In order for a learning agent to autonomously define (by exploration) the tangential-flow region RTF for an unknown environment, we propose the use of the following modification of the Q-Learning update rule:
where αt is the learning rate and γ is the discount factor. We use average instead of maximisation. The same rule can be adapted for different RL-algorithms. The reinforcement function must be defined to detect obstacles, as it is used in this work, but it can be used to detect other undesirable regions, such as cliff12, strong magnetic field, high temperature, moist, etc.
Figure 5 shows the value  obtained by using the described modification of the Q-Learning algorithm (Equation 1) with r(st, at) = 0 when hitting an obstacle and r(st, at) = 1 otherwise, and discount factor γ = 1. The tone of gray represents how far the agent is from reaching a obstacle walking randomly (black is closer, white is further). The tangential-flow region RTF of this environment can be obtained by defining a desired
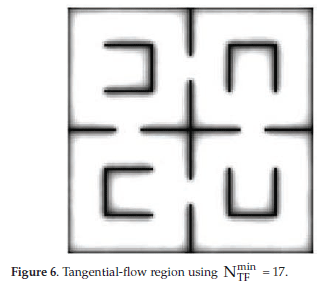
obtained by using the described modification of the Q-Learning algorithm (Equation 1) with r(st, at) = 0 when hitting an obstacle and r(st, at) = 1 otherwise, and discount factor γ = 1. The tone of gray represents how far the agent is from reaching a obstacle walking randomly (black is closer, white is further). The tangential-flow region RTF of this environment can be obtained by defining a desired  . Figure 6 shows the tangential-flow region RTF obtained with
. Figure 6 shows the tangential-flow region RTF obtained with  = 17.
= 17.
Notice that, regions with similar structure (corners, U-like form, gates) present similar tangential-flow region. This characteristic is important so that an agent can learn the tangential-flow region even before taking any action in the environment where a task must be done. The learning of the tangential-flow region and consequently the tangential-flow policy can be learnt before hand if all typical situations can be experimented by the agent and that such policy be defined in the space of local situations.
It is worth noticing again that the tangential-flow policy is just one possible compulsory flow. As it was already mentioned, a hard-coded behaviour of getting around obstacles can be programmed in the agent, even with other prohibited regions. Also, the compulsory flow can be used not only to get around regions where the agent cannot get through, but it can be used as away of guaranteeing that the agent does not damage itself.
4. Compulsory Flow Q-Learning
The CFQ-Learning algorithm addresses applications where previous information about the structure of the environment can be gathered and reused. It may happen when the robot has had already access to the environment in previous task or if the environment is of some kind previously known.
In our approach, while a high-resolution discretisation is used for the a priori definition of the compulsory flow for a task environment, a low-resolution discretisation is used in the CFQ-Learning algorithm to learn the task policy, what increases the learning speed while still keeping the agent safe in dangerous regions.
Similarly to the discretisation process described in Section 2.3, a set M of macro-states m is defined by a function m: S → M, where in general the region in a macro-state m  M is much larger than the region in a discrete state s
M is much larger than the region in a discrete state s  S. The set of actions A for macro-states is the same as that defined for discrete states.
S. The set of actions A for macro-states is the same as that defined for discrete states.
The CFQ-Learning algorithm considers as input: 1) the set S of high-resolution discrete states with the function s : X → S, where X is the set of continuous states; 2) the set M of lowresolution macro-states with the function m: S → M; 3) the set A of discrete actions; and 4) the tangential-flow region RTF and policy πTF with the function NTF: S × A → R.
In the algorithm there are three levels of states: 1) the continuous level X, that is where the real interaction of the agent with the environment occurs; 2) the high-resolution discrete level S, that is where the CFQ-Learning algorithm controls the real agent; and 3) the low-resolution discrete level M, that is where the policy is learnt.
When an action a is chosen in S-level, a correspondent action  is performed in X-level for a discrete time tn - tn-1.
is performed in X-level for a discrete time tn - tn-1.
When an action a is chosen in M-level, the agent can operate in two modes: 1) obstacle free --this mode is used in regions free of obstacles and the action a is executed in the S-level; and 2) compulsory flow --this mode is used when the agent reaches the tangential-flow region and the action determined by πTF is executed. The agent enters in mode 1 every time a macro-state transition occurs or when the action α takes the agent away from obstacles and there is not a great change in the movement direction (angle between the directions of the previous and the actual actions is less or equal than 90º). The agent enters in mode 2 every time the agent enters in the tangential-flow region.
The idea behind the CFQ-Learning algorithm is that, once an action a is chosen to be performed at the macro-state m, the action a will be executed whilst the agent is in the same macro-state and this action a does not drive the agent into the compulsory-flow region RTF (previously defined for the environment). Every time the agent invades the RFT region, the compulsory flow πFT(.) drives the agent until it can either perform the original action a again or a macro-state transition occurs. In the latter case, the learning agent chooses a new action. The compulsory flow πFT(.) is defined on the basis of the NTF(s, a) previously calculated and stored for being used in the current environment.
Table 1 describes the proposed CFQ-Learning algorithm. Variable tmacro keeps the entrance step of the macro-state, variable Rmacro keeps the cumulative reinforcement within current macro-state and amacro keeps the first action chosen when entering current macro-state (amacro is the action that causes all the sequence of actions within current macro-state, i.e., the action that can fire a partial policy).
As said in the Section 2.3, each possible action ai  A represents a movement in some direction in the state space X. The quality of a policy learnt using CFQ-Learning depends on the sets A and M. Let p*(s) be the number of states visited from the state s when applying an optimal policy and P(s) be the number of states visited from the state s when applying an optimal policy learnt under CFQ-Learning. The error (P(s)-p*(s)) can be minimised if the set A represents well all directions of movements: the larger the number of possible actions, the smaller the distance between P(s) and p*(s), once it will be easier choosing an action similar to the optimal policy. The same happens to the discretisation process, because it can help minimising the bounding error, enlarging macro-states when possible (for instance, narrow corridors) or making them smaller when there are no obvious sub-optimal actions.
A represents a movement in some direction in the state space X. The quality of a policy learnt using CFQ-Learning depends on the sets A and M. Let p*(s) be the number of states visited from the state s when applying an optimal policy and P(s) be the number of states visited from the state s when applying an optimal policy learnt under CFQ-Learning. The error (P(s)-p*(s)) can be minimised if the set A represents well all directions of movements: the larger the number of possible actions, the smaller the distance between P(s) and p*(s), once it will be easier choosing an action similar to the optimal policy. The same happens to the discretisation process, because it can help minimising the bounding error, enlarging macro-states when possible (for instance, narrow corridors) or making them smaller when there are no obvious sub-optimal actions.
5. Experimental Results
In the previous section nothing has been said about the CFQ-Learning algorithm convergence or optimal policy found under CFQ-Learning. Experiments have been conducted to empirically show that a high quality policy can be found, i.e., close in performance to optimal policy, and that in fact a convergence occurs to such high quality policy. CFQ-Learning is compared with a modified version of Q-Learning, here called Coarse Q-Learning, using the same low-resolution discretisation of the state space.
The Coarse Q-Learning algorithm used in these experiments is applied to the same set of macro-states used by the CFQ-Learning algorithm. In coarse Q-Learning, once an action is chosen inside a macro-state, the same action is executed until a transition between macro-states occurs or the agent collides with an obstacle. In the first case a new action is chosen after the macro-state transition. In the latter case, a random action is selected.
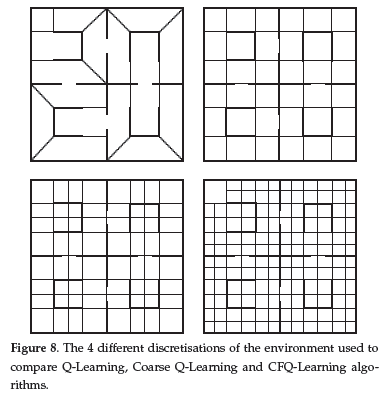
In order to evaluate the algorithm here defined, we choose to experiment in a discrete simulated environment. Figure 7 shows the original high-resolution state space, which has 10,000 states (100 × 100), whereas Figure 8 shows four different discretisations for the same environment used to compare CFQ-Learning and Coarse Q-Learning. These discretisations were made respecting the three properties of the set of macro-states M in Section 2.2.
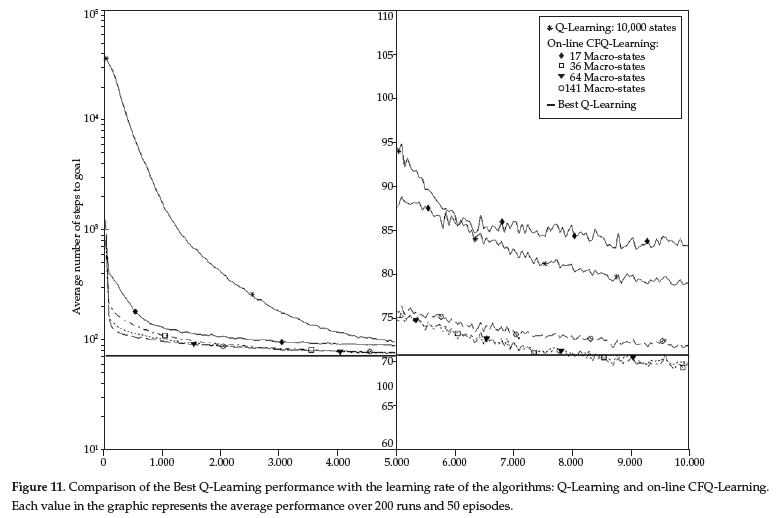
Parameters used in the experiments are: discount factor γ = 0.99, learning rate α = 0.3 decreasing in each episode with rate 0.9999 and exploration rate ε = 0.2 decreasing in each episode with rate 0.99975. The Best Q-Learning results (bold line in Figures 9, 10 and 11) were found following the procedure: 1) execute Q-Learning for 90,000 episodes in the high-resolution discretisation (100 × 100) and finds the "best policy"; 2) apply the "best policy" to 10,000 episodes and calculates the average performance among those 10,000 episodes; and 3) repeat this procedure for 200 runs and calculate the average performance among those 200 runs. This result is shown in graphics as the "Best Q-Learning", which is used as a reference to a very good performance.
Figure 9 shows the results using Coarse Q-Learning for different discretisations compared with high-resolution Q-Learning (100 × 100). It is possible to see the great dependence of the policy quality on the number of states. The number of steps to reach the goal region taken by the Coarse Q-Learning using 36 macro-states is more than 2 times greater than the number of steps taken by the high-resolution Q-Learning, after 10,000 episodes. If the number of macrostates used is 16, the result is 5 times worse.
Experiments were conducted with CFQ-Learning and its on-line version (when there is no knowledge about the environment and the tangential-flow policy must be obtained during the learning process). In the first steps of on-line CFQ-Learning, for all s  S and a
S and a  A, NTF(s, a) =
A, NTF(s, a) = + ε, where ε > 0, what means that, any state s is not in the tangential-flow region Rand the tangential-flow policy πTF does not take control of the agent. As the agent collides with obstacles, the Equation 1 is applied and the function NTF(.) is learnt, defining the real tangential-flow region and policy. In this version of CFQ-Learning the macro-state policy and the tangential-flow policy are learnt concurrently.
+ ε, where ε > 0, what means that, any state s is not in the tangential-flow region Rand the tangential-flow policy πTF does not take control of the agent. As the agent collides with obstacles, the Equation 1 is applied and the function NTF(.) is learnt, defining the real tangential-flow region and policy. In this version of CFQ-Learning the macro-state policy and the tangential-flow policy are learnt concurrently.
Differently from Coarse Q-Learning, CFQ-Learning obtains a policy with results closer to high-resolution Q-Learning. Figure 10 and Figure 11 show the results for CFQ-Learning and on-line CFQ-Learning, respectively. Both of them show that CFQ-Learning does not have a great dependence on the number of states: even when 16 states are considered, the number of steps is only 20 percent worse than the number of steps obtained by Q-Learning. When CFQ-Learning and on-line CFQ-Learning are compared, the greatest differences are in the first 1,000 episodes, when on-line Q-Learning is learning the tangential-flow policy and tangential-flow region, whereas the final performance of the policies is similar.
It is worth mentioning that the policy to be considered as the best Q-Learning is not really optimal, since it was learnt and there is no guarantee of its convergence. Also, the value shown in Figures 9, 10 and 11 is a sample of learnt policies. Then, it is allowed statistic variance, occurring that some policy reach better result than the best Q-Learning policy.
6. Conclusion
In this paper we presented a new learning algorithm, which makes use of high-resolution state-space discretisation in the control process, while using low-resolution discretisation in the policy-learning process. Using this algorithm the learning agent is capable of reaching the goal and finding out a good policy faster than by using algorithms based on high-resolution discretisation of the state space.
The proposed CFQ-Learning algorithm worked very well in the experiments conducted, having a performance close to the optimal policy, even when using low resolution discretisation of the state space. Although it is necessary to have a previous knowledge about the environment, such knowledge can be extract during the execution of the first tasks in the environment and reused later on in order to accelerate the learning process for future tasks.
In cases where it is not possible defining the tangentialflow region and policy a priori different solutions can be adopted. It is possible to use sensors (sonars, laser) to sense the distance and the direction of the robot to the undesirable regions and then, based on this sensing, to create the compulsory flow. It must be defined a priori the tangential-flow region based on distance and the tangential-flow policy to get around undesirable regions. Another option is to learn NTF(s, a) in the sensor space, which can be generalised for different parts of the environment or even different environments. This sensor space depends only on the regions nearby the agent and their relative positions, not considering the global position of the agent in the environment.
Ackowledgements
This research was conducted under the CAPES/GRICES Project MultiBot (Grant no. 099/03), FAPESP project Logprop (Grant no. 2008/03995-5) and CNPq project Ob-SLAM (Grant no. 475690/2008-7). Valdinei F. Silva is grateful to FAPESP (proc. 02/13678-0) and Anna H. R. Costa is grateful to CNPq (Grant No. 305512/2008-0).
Received: July 7, 2009; Accepted: August 27, 2009
-
1Bailey T and Durrant-Whyte H. Simultaneous localisation and mapping (slam): Part ii -state of the art. Robotics and Automation Magazine 2006; 13(3):1-10.
-
2Bianchi RAC. Uso de heurísticas para a aceleração do aprendizado por reforço [PhD thesis]. São Paulo, SP: Universidade de São Paulo; 2004.
-
3Durrant-Whyte H and Bailey T. Simultaneous localisation and mapping (slam): the essential algorithms. Robotics and Automation Magazine 2006; 13(2):1-9. (part I)
-
4Foster D and Dayan P. Structure in the space of value functions. Machine Learning 2002; 49(2/3):325-346.
-
5Jarvis R. Robot path planning: complexity, flexibility and application scope. In: Proceedings of the 2006 international symposium on Practical cognitive agents and robots; 2006; Perth, Australia. New York, SP: ACM; 2006. p. 3-14.
-
6Lee H, Shen Y, Yu CH, Singh G and Andrew Y. Ng: quadruped robot obstacle negotiation via reinforcement learning. In: Proceedingsof the IEEE International Conference on Robotics and Automation; 2006; Orlando, Florida. Los Alamitos, CA: IEEE Computer Society Press; 2006. p. 3003-3010.
-
7Marthi B, Russell SJ, Latham D and Guestrin C. Concurrent hierarchical reinforcement learning. In: Kaelbling LP and Saffiotti A. (Eds.). Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence; 2005; Edinburgh. San Francisco, CA: Morgan Kaufmann; 2005. p. 779-785.
-
8Mcgovern A, Sutton RS and Fagg AH. Roles of macro-actions in accelerating reinforcement learning. In: Proceedings of the Grace Hopper Grace Hopper Celebration of Women in Computing; 1997; San Jose, CA. Palo Alto, CA: Anita Borg Institute for Women and Technology; 1997. p. 13-18.
-
9Mitchell TM. Machine learning San Francisco: WCB/McGraw-Hill; 1997.
-
10Moore AW and Atkeson CG. Prioritized sweeping: reinforcement learning with less data and less real time. Machine Learning 1993; 13(1):237-285.
-
11Munos R and Moore A. Variable resolution discretization in optimal control. Machine Learning 2002; 49(2/3):291-323.
-
12Murarka A, Sridharan M and Kuipers B. Detecting obstacles and drop-offs using stereo and motion cues for safe local motion. In: Proceedings of International Conference on Intelligent Robots and Systems; 2008; Nice, France. Los Alamitos, CA: IEEE Computer Society Press; 2008. p. 702-708.
-
13Parr R and Russell S. Reinforcement learning with hierarchies of machines. In: Proceedings of 10 Advances in Neural Information Processing Systems; 1998; Denver, CO. Cambridge, MA: The MIT Press; 1998.
-
14Precup D, Sutton RS and Singh SP. Theoretical results on reinforcement learning with temporally abstract behaviors. In: Proceedings of the Tenth European Conference on Machine Learning; 1998; Berlin. New York: Springer; 1998. p. 382-393.
-
15Ramon J, Driessens K and Croonenborghs T. Transfer learning in reinforcement learning problems through partial policy recycling. In: Proceedings of the 18 European Conference on Machine Learning; 2007; Warsaw. New York, NY: Springer; 2000. p. 699-707.
-
16Reynolds SI. Decision boundary partitioning: variable resolution model-free reinforcement learning. In: Proceedings of the 17 International Conference on Machine Learning; 2000; Palo Alto, CA. San Francisco, CA: Morgan Kaufmann; 2000. p. 783-790.
-
17Ross SM. Applied probability models with optimization applications San Francisco: Holden-Day; 1970.
-
18Rummery GA and Niranjan M. On-line q-learning using connectionist systems Cambridge: Cambridge University; 1994. (technical report CUED/F-INFENG/TR 166).
-
19Selvatici AHP and Costa AHR. A hybrid adaptive architecture for mobile robots based on reactive behaviors. In: Proceedings of the 15 International Conference on Hybrid Intelligent Systems; 2005; Rio de Janeiro. Los Alamitos: IEEE Computer Society; 2005. p. 29-34.
-
20Strandberg M. Robot path planning: an object oriented approach. [PhD Thesis]. Sweden: Royal Institute of Technology; 2004.
-
21Sutton RS and Barto AG. Reinforcement learning: an introduction. Cambridge: MIT Press; 1998.
-
22Sutton RS. Learning to predict by method of temporal differences. Machine Learning 1988; 3(1):9-44.
-
23Sutton RS. Integrated architectures for learning, planning and reacting based on approximating dynamic programming. In: Proceedings of the 7 International Conference on Machine Learning; 1990; Austin, TX. San Francisco, CA: Morgan Kaufmann; 1990. p. 216-224.
-
24Watkins JCHC. Learning from Delayed Rewards [PhD thesis]. Cambridge: University of Cambridge; 1989.
Publication Dates
-
Publication in this collection
17 Dec 2009 -
Date of issue
Sept 2009
History
-
Accepted
27 Aug 2009 -
Received
07 July 2009