Abstract
A model is presented for the description of the concentration behavior of organometallic and sulfurated compounds in hydrodemetallation and hydrodesulfurization catalytic processes, where catalyst effectiveness decreases with time. Due to the complexity of the mixture, an approach based on pseudocomponents was adopted. The system is modeled as an isothermal tubular reactor with axial dispersion, where the gas phase (hydrogen in excess) flows upward concurrently with the liquid phase (heavy oil) while the solid phase (catalyst) stays inside the reactor in an expanded (confined) bed regime. The catalyst particles are very small and are assumed to be uniformly distributed in the reactor. The heavy oil fractions contain organometallics and sulfurated compounds, from which the metals and sulfur are to be removed, the metals as deposits in the catalyst pores and the sulfur as gas products. Simulations were carried out where the concentration profile inside the reactor was calculated for several residence times.
modeling and simulation; hydrodemetallation; hydrodesulfurization
Modeling and simulation of hydrodemetallation and hydrodesulfurization processes with transient catalytic efficiency
E.M. Matos, and R. Guirardello
Faculdade de Engenharia Química, Departamento de Processos Químicos,
Universidade Estadual de Campinas (UNICAMP), C.P. 6066, CEP 13081-970,
Phone: (+55) (019)788-3955, Fax: (+55) (019)788-3965, Campinas - SP, Brazil
E-mail: guira@feq.unicamp.br
(Received: March 3, 1999 ; Accepted: February 4, 2000 )
Abstract - A model is presented for the description of the concentration behavior of organometallic and sulfurated compounds in hydrodemetallation and hydrodesulfurization catalytic processes, where catalyst effectiveness decreases with time. Due to the complexity of the mixture, an approach based on pseudocomponents was adopted. The system is modeled as an isothermal tubular reactor with axial dispersion, where the gas phase (hydrogen in excess) flows upward concurrently with the liquid phase (heavy oil) while the solid phase (catalyst) stays inside the reactor in an expanded (confined) bed regime. The catalyst particles are very small and are assumed to be uniformly distributed in the reactor. The heavy oil fractions contain organometallics and sulfurated compounds, from which the metals and sulfur are to be removed, the metals as deposits in the catalyst pores and the sulfur as gas products. Simulations were carried out where the concentration profile inside the reactor was calculated for several residence times.
Keywords: modeling and simulation, hydrodemetallation, hydrodesulfurization.
INTRODUCTION
The presence of metals in crude oil and heavy fractions is highly undesirable because oil products such as fuels will have a low yield, produce toxic oxides when burned, cause corrosibility and produce ashes that can damage engines. A reduction in the amount of metals in the oil is accomplished by the process of hydrodemetallation (HDM), where the molecules that contain metals lose these atoms by reactions of hydrogenation. The products of HDM reactions can accumulate in the catalyst pores, causing the formation of deposits which end up obstructing those pores irreversibly, blocking access to the catalyst sites and leading to a progressive loss of catalytic activity (Wei, 1991). These deposits are metal sulfides and active demetallation catalysts, which are less active than the original catalyst (Pereira, 1990).
The presence of sulfurated compounds in crude oil and heavy fractions is also undesirable. It can lead to corrosibility in oils and lubricants and poisonous emissions such as SO2 and H2S when the fuel is burned. The reduction in sulfur content is accomplished by the hydrodesulfurization process (HDS), where the molecules that contain sulfur lose that atom by reactions of hydrogenation. Although the HDS reactions may not lead to intraparticle deposition, which could decrease the catalytic activity, the HDS kinetics is greatly influenced by deposits formed by HDM reactions, since they occur within the same catalyst, usually CoO and MoO3 or NiO and MoO3 supported by alumina (Speight, 1981), and the metal sulfide deposits formed by hydrodemetallation are poor desulfurization catalysts (Pereira, 1990).
The reactor considered in this work is an isothermal tubular reactor, with the excess hydrogen flowing concurrently upward with the heavy oil, while the catalyst remains inside the reactor in an expanded bed regime (confined bed). Operating pressure and temperature are in the range of 50 to 110 atm and 400 to 600 °C.
MATHEMATICAL MODEL
Main Assumptions
The model in this study is based on some assumptions about the process:
(a) the process is isothermal: for any degree of mixing (represented by the Peclet number), the reactor has a uniform temperature;
(b) the reactor is plug flow: the radial velocity profile is flat through the reactor for the liquid and gas phases;
(c) the reactor is plug flow: the radial concentration profile is flat and concentrations change only with axial position;
(d) hydrogen is in excess and is completely dissolved in oil:
-
the rate of reactions does not depend explicitly on the partial pressure of hydrogen;
-
there is no need for a mass balance for hydrogen;
(e) a pseudocomponent approach is assumed: although there are many different kinds of molecules bearing metal and sulfur, an equivalent concentration of metal and sulfur in the oil can be used in the mass balances;
(f) solid catalyst particles are small compared to gas bubbles: the catalyst is completely surrounded by the liquid phase.
These assumptions may introduce some error with respect to the actual process and their validity needs to be verified against experimental data.
Mass Balance Equations
The reaction process is assumed to be influenced by diffusion inside the catalyst particles, with a pseudo-first-order reaction for both metal and sulfur (hydrogen is in excess, so it does not appear in the rate expression). All other assumptions cited previously are also used in the development of the mass balance equations.
The mass balance for metals is given by

(1)

(2)
with the boundary conditions given by

(3)

(4)
The internal surface area of the catalyst per unit of volume, ap, for cylindrical pores with a bimodal pore structure, is given by

(5)
This is the initial internal area and the decrease in the surface area of the pores due to metal deposition is already included in the definition of the effectiveness factor  .
.
Equations (1) and (2) can be rearranged to give

(6)

(7)
where  is a function of Ms and time.
is a function of Ms and time.
The mass balance for sulfur results in similar equations:

(8)

(9)
with the boundary conditions given by

(10)

(11)
Equations (8) and (9) can be rearranged to give

(12)

(13)
where  is a function of Ms and time.
is a function of Ms and time.
Using some dimensionless variables, the mass balance equations can be rearranged to give

(14)

(15)

(16)
where j = m for hydrodemetallation and j = s for hydrodesulfurization and

(17)

(18)

(19)

(20)
The concentration of mass per unit volume can also be expressed in terms of mass fraction using the following equations:

(21)

(22)
Effectiveness Factor
The effectiveness factor for the hydrodemetallation and hydrodesulfurization reactions in the catalyst particles are defined by the ratio of the particle reaction rate to the initial particle rate in the absence of intraparticle diffusion resistance (Pereira, 1990). Since the intrinsic rate is given per unit of surface area, the result is

(23)

(24)
For the metal deposition, the effectiveness factor can be calculated using the perturbation method approach (Pereira, 1990). For a fixed value of Ms and for small values of q(q<<1), the effectiveness factor can be approximated by

(25)
where

(26)

(27)

(28)

(29)

(30)
Equations (25) through (30) are based on the assumption that the metal concentration at the external surface of the particle catalyst is fixed (Pereira, 1990). Since in this model the metal concentration changes with axial position and time, for equation (28) it was assumed that the solid phase (catalyst) is completely and perfectly mixed in the reactor (but not the gas and liquid phases), so the catalyst particles are exposed to an average concentration 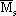 (Matos, 1997). This average value is used only in equation (28), and it is calculated using the values of Ms from z = 0 to z = L.
(Matos, 1997). This average value is used only in equation (28), and it is calculated using the values of Ms from z = 0 to z = L.
For the hydrodesulfurization process, the effectiveness factor can also be calculated using the perturbation method approach, considering that hydrodesulfurization and metal deposition occur within the same pores (Matos, 1997). For small values of q (q<<1), the effectiveness factor can be approximated by

(31)
for  and
and

(32)
for  where
where

(33)

(34)

(35)
NUMERICAL SOLUTION
The set of ordinary differential equations from the model were solved numerically using the orthogonal collocation method. This method was chosen due to the smoothness of solution of this particular model and the boundary conditions at different points.
The basic procedure for the method of collocation is to propose a polynomial trial function for the dimensionless concentration profiles  and
and  as follows:
as follows:

(36)
where P(x) is the dimensionless concentration profile (concentration over the initial concentration) and x is the dimensionless length (axial coordinate over the reactor length). Each concentration profile is described by a polynomial. Since each one has nine undetermined coefficients, it requires nine collocation
points, two at the boundary points and seven at internal points.
Applying the trial function at the boundary points, rearranging the coefficients and then applying the resulting function to the set of differential equations results in a set of residual functions given by

(37)
Where

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)
for organometallics:

(46)
for sulfur compounds:

(47)
The internal collocation points are selected according to orthogonality conditions, which depend on the interval and the weight functions (Villadsen and Stewart, 1967). In this case, the orthogonality condition is given by

(48)
where the interval is [ 0,1] and the weight function is  , since 0 and 1 are also collocation points (boundary conditions). The classes of functions that satisfy (48) are the Jacobi polynomials Gn(p,q,x) with p=3 and q=2 (Abramowitz and Stegun, 1972). Since in this work we are using seven internal points, they will be the roots of G7(3,2,x), given by (Abramowitz and Stegun, 1972)
, since 0 and 1 are also collocation points (boundary conditions). The classes of functions that satisfy (48) are the Jacobi polynomials Gn(p,q,x) with p=3 and q=2 (Abramowitz and Stegun, 1972). Since in this work we are using seven internal points, they will be the roots of G7(3,2,x), given by (Abramowitz and Stegun, 1972)

(49)
whose roots are presented in Table 1.
NUMERICAL RESULTS
The model was tested numerically with a program in Pascal. The values for the parameters in the model were set arbitrarily and are presented in Table 2. All data are assumed to be at the temperature and pressure of operation. The results are shown in Figures 1 and 2.
Equations (37) through (44) were solved using the orthogonal collocation points presented in Table 1. In order to test the influence of the collocation points, these equations were also solved using points arbitrarily set at x1 = 0.1, x2 = 0.2, x3 = 0.3, x4 = 0.5, x5 = 0.7, x6 = 0.8 and x7 = 0.9. There was no noticeable change in the results presented in Figures 1 and 2, which indicates that a polynomial of degree 8 (equation 36) is adequate to represent the solution for the situation tested, independently of the set of collocation points used.
The use of an average metal concentration 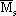 in equation (28) required an iterative procedure for the calculation of the concentration profiles in the reactor, where
in equation (28) required an iterative procedure for the calculation of the concentration profiles in the reactor, where  was used as the initial value.
was used as the initial value.
DISCUSSION AND CONCLUSIONS
Since catalyst effectiveness decreases with time, due to the deposition in the pores which leads to a smaller catalyst area, it is expected that conversion decreases with time in all parts of the reactor. This can be seen in Figures 1 and 2, which show that the loss of effectiveness increases with time, as expected.
The final conversion is influenced by several different factors. For example, although the reaction rate constant was assumed to be smaller for HDS than for HDM, it was assumed that  , so the effectiveness factor was larger for HDS than for HDM, which resulted in a higher conversion for HDS than for HDM, as can be seen in Figures 1 and 2.
, so the effectiveness factor was larger for HDS than for HDM, which resulted in a higher conversion for HDS than for HDM, as can be seen in Figures 1 and 2.
The steep decrease in catalyst effectiveness over time observed in these simulations is due to the very high concentration of metals arbitrarily assumed (0.08 %). Using lower metal concentrations catalyst life will increase and effectiveness will decrease slowly.
The results indicate that the model can describe the expected behavior of a reactor with decreasing catalyst effectiveness. The proposed strategy can also be used to fit experimental data in order to simulate reactor behavior.
ACKNOWLEDGMENTS
The authors would like to thanks FAPESP, Fundação de Amparo à Pesquisa do Estado de São Paulo, for the funding that supported this research.
NOMENCLATURE
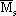
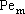
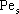
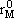
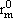
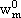
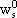
REFERENCES
Handbook of Mathematical Functions, edited by M. Abramowitz and I. A. Stegun, Dover Publications, Inc., New York (1972).
Matos, E. M., Modelagem e Simulação da Cinética Química do Tratamento das Frações
Pesadas do Petróleo, Campinas - SP, Masters thesis, Chemical Engineering,
Universidade Estadual de Campinas (1997).
Pereira, C. J., Metal deposition in hydrotreating catalysts. 1. A regular perturbation
solution approach. Ind. Eng. Chem. Res., 29, 512 - 519 (1990).
Speight, J. G., The desulfurization of heavy oils and residua, 1st edition, chapters 1-3
(1981).
Wei, J., Modeling of catalytic hydrodemetallation. Revue de Líntitut Français du Pétrole.
Vol. 46, N 4, Juillet - Août (1991).
Villadsen, J. V., Stewart, W. E., Solution of boundary-value problems by orthogonal collocation. Chemical Engineering Science, Vol. 22, pp. 1483-1501 (1967).
- Handbook of Mathematical Functions, edited by M. Abramowitz and I. A. Stegun, Dover Publications, Inc., New York (1972).
- Villadsen, J. V., Stewart, W. E., Solution of boundary-value problems by orthogonal collocation. Chemical Engineering Science, Vol. 22, pp. 1483-1501 (1967).
Publication Dates
-
Publication in this collection
06 July 2000 -
Date of issue
June 2000
History
-
Accepted
04 Feb 2000 -
Received
03 Mar 1999






