Abstract
One of the most important byproducts of the orange juice industry is the oil phase. This is a mixture of terpenes, alcohols, and aldehydes, dissolved in approximately 96% limonene. To satisfactorily use oil phase as an ingredient in the food and cosmetics industries separation of the limonene is required. One possibility is to use a fixed bed of silica gel to remove the light or aroma compounds from the limonene. The aroma substances are then extracted from the bed of silica gel using supercritical carbon dioxide. This work deals with the modeling of the desorption step of the process using mass balance equations coupled with the Langmuir equilibrium isotherm. Data taken from the literature for the overall extraction curves were used together with empirical correlations to calculate the concentration profile of solute in the supercritical phase at the bed outlet. The system of equations was solved by the finite volume technique. The overall extraction curves calculated were in good agreement with the experimental ones.
orange oil; oil phase; desorption; supercritical fluids; mass transfer modeling; solid matrices; carbon dioxide
MODELING THE SUPERCRITICAL DESORPTION OF ORANGE ESSENTIAL OIL FROM A SILICA-GEL BED
E.A.Silva1, L.Cardozo-Filho2* * To whom correspondence should be addressed , F.Wolff2 and M.A.A.Meireles3
1Departamento de Engenharia Química,Universidade do Oeste do Paraná, UNIOESTE, R.
Faculdade, 2550; CEP 87020-900, Toledo, PR, Brazil; E-mail: edsonas@deq.uem.br
2 Departamento de Engenharia Química,Universidade Federal de Maringá, UEM, Av. Colombo,
5790, 87020-900, phone: 55 44 226-2727, Maringá - PR, Brazil; E-mail: cardozo@deq.uem.br;
3LASEFI, Departamento de Engenharia de Alimentos, FEA, UNICAMP,
Campinas - SP, Brazil; E-mail: meireles@fea.unicamp.br
(Received: March 29, 2000 ; Accepted: April 23, 2000)
Abstract - One of the most important byproducts of the orange juice industry is the oil phase. This is a mixture of terpenes, alcohols, and aldehydes, dissolved in approximately 96% limonene. To satisfactorily use oil phase as an ingredient in the food and cosmetics industries separation of the limonene is required. One possibility is to use a fixed bed of silica gel to remove the light or aroma compounds from the limonene. The aroma substances are then extracted from the bed of silica gel using supercritical carbon dioxide. This work deals with the modeling of the desorption step of the process using mass balance equations coupled with the Langmuir equilibrium isotherm. Data taken from the literature for the overall extraction curves were used together with empirical correlations to calculate the concentration profile of solute in the supercritical phase at the bed outlet. The system of equations was solved by the finite volume technique. The overall extraction curves calculated were in good agreement with the experimental ones.
Keywords: orange oil, oil phase, desorption, supercritical fluids, mass transfer modeling, solid matrices, carbon dioxide.
INTRODUCTION
Brazil is the leading producer of concentrated orange juice on the international market. São Paulo state is the largest producer in Brazil. Concentrated frozen juice has been traditionally produced by concentration of cold-pressed orange juice under vacuum in multistage evaporators. The vapor that leaves the first evaporator contains the volatile compounds responsible for the characteristic orange flavor, a mixture of water, limonene and volatile substances with low molecular weight from a variety of chemical families, such as aldehydes, alcohols, terpenes, and the like. This mixture is sent directly to the system of essence recovery containing a fractionation column and a series of condensers and gas washers, from which two products are obtained: the oil phase and the aqueous phase. Both phases have chemicals that are partially responsible for the characteristic orange flavor. Therefore, both products can have important applications in the food, cosmetics, and pharmaceutics industries to aromatize a variety of goods. The oil phase has the most obvious applications because of its very large content of limonene. Indeed, in the citrus industry it is commercialized as limonene because its limonene content may amount to as much as 96% (Marques, 1997).
Due to its high limonene content, the oil phase is subjected to oxidation that forms, for instance, a -terpineol, thus modifying the oil-phase flavor. Ultimately, the oxidation process considerably lowers the oil phase price. On the other hand, the oxygenated compounds that form the mixture are the main substances responsible for the characteristic orange flavor. Therefore, deterpenation of the oil-phase is of great interest to the citrus industry. Some studies have been done on a process of adsorption of the oxygenated compounds in a bed of silica gel, followed by desorption with organic solvents. The organic solvent present in the concentrated mixture of oxygenated compounds must then be removed. An alternative process was studied by Marques (1997). In the proposed process the organic solvent desorption step was substituted by a supercritical fluid (SCF) desorption step. The SCF desorption developed by Marques (1997) consisted of a low-density SCF (Step I), followed by a high-density SCF (Step II). Marques (1997) confirmed that the bed of silica gel retained no limonene. On the other hand, ethanol, linalool, a -terpineol, trans-2-hexenal, nonanal, decanal, citronellal, neral, b -sinensal, a -sinensal, and ethyl butyrate were completely retained by the silica gel. During Step I of the SCF desorption the following substances were partially removed: linalool, octanal, nonanal, decanal, neral, geranial, ethyl butyrate, a -pinene, d -3-carene, b -mircene, and valencene. The other chemicals were partially removed only during SCF desorption Step II.
The supercritical fluid extraction (SCFE) of chemical species from a solid substratum includes contacting the solid phase with the supercritical fluid. The solid phase can be a vegetable plant material or a bed of porous adsorbent material, as is the case in oil-phase deterpenation. In either situation, the solid is usually called a solid substratum or solid matrix. The substratum forms a fixed bed through which the supercritical fluid flows, solubilizing the solute. This type of process is semi-continuous because, although the fluid phase flows continuously, the solid phase is also continuously being depleted in the solute.
It is generally accepted that the objectives of a mathematical modeling of any process are to identify and describe the major phenomena using an equation or set of equations capable of providing reasonable description of the overall process. Preferably, the chosen equation or set of equations should be kept as simple as possible with a limited number of parameters to allow the problem to be solved with the information available. All this, which is common knowledge, also applies to the modeling of processes carried out at high pressure, since in addition to the difficulties traditionally encountered in process modeling, here the experimental information available to the process engineer is still limited.
SCFE from a solid substratum can be modeled using two approaches: i) modeling the process that occurs with the individual particles, followed by integration on the bed volume to obtain an overall solution, or ii) modeling the process using mean properties for the fixed bed. The second approach is very useful for cylindrical beds with concentration profiles predominantly in the axial direction and negligible variations in the radial direction. The balance equations are written for an element of the bed and the solution obtained by integrating along the length of the bed. Nevertheless, to get the concentration profile, in either case it is also necessary to carry out integration in variable time, because the overall process occurs in transient regime. A good picture of the physical problem is required in order to write the balance equations and to choose the appropriate simplifications.
The mass-transfer as well as the thermodynamic limitations of the process must be known to provide a solution that can be used for process design. The mass transfer balance equations for the solid and fluid phases, and the rate of interfacial mass transfer must be combined with the phase equilibrium relationships in order to get the final solution to the problem. Therefore, the following information is required: i) a model to describe the species concentration profiles in the fluid phase located in the pores of the solid particles, ii) the mass transfer equation that describes the diffusion of the species in the solid phase, iii) a phenomenological equation to describe the interfacial mass transfer, which is in general written in terms of the resistance in the film surrounding the solid particles.
The objective of this work was to model the desorption step of the deterpenation of the orange oil phase by the process proposed by Marques (1997). The method of finite volume was employed to solve the system of equations that describes the process. Overall extraction curves data from the literature (Marques, 1997) were used to get the required information to solve the balance equations.
MATHEMATICAL MODELING
The mathematical formulation of SCF desorption is similar to any desorption problem, as extensively discussed in the literature. To study the deterpenation of the orange oil-phase mixture using low-pressure desorption followed by SCF desorption, the model for diffusion in homogeneous solid applied to fixed bed extractors was chosen. To do so, it is necessary to know the mass transfer and the dispersion coefficients for the fluid phase, the effective diffusion coefficient for the solid phase, and the adsorption isotherm.
Raghavan and Ruthven (1983) solved the problem of sorption from a homogenous solid for a bed formed of spherical particles, using the method of orthogonal collocation. Madras et al. (1994) solved a similar problem using the method of orthogonal collocation with finite elements. The hypotheses used for their model were the system was isothermal, the flow was unidirectional in the axial direction, dispersion was important only in the axial direction, the physical properties of the phases were constant, local equilibrium prevailed in the pores of the particles, and the isotherm was nonlinear. These assumptions adequately describe the SCF extraction from solid substratum (Brunner, 1994).
Figure 1 shows the SCF extractor, formed of a bed of spherical porous particles, and indicates the mechanisms of mass transfer. The bed of porous particles contains oxygenated compounds inside the particles and in its void space. The solvent flows axially and extracts the oxygenated compounds from both places. The amount of oxygenated compounds extracted depends on the temperature and pressure of the system, as well as on the dynamics of the system.
The mass balance equations for the fluid phase for the bed element indicated in is

(1)
with the following initial and boundary conditions:
 in
in
(2)
 in z = 1
in z = 1
(3)
 in z = 0
in z = 0
(4)
For the solid phase, assuming that local equilibrium is achieved, the differential mass balance is given by

(5)
with the following initial and boundary conditions:
 ,
,
(6)

(7)

(8)
where Y is the solute concentration in the bulk fluid phase, X is the solute concentration in the fluid phase inside the pores of the particles, z is the axial direction, r is the particles radii, t is the dimensionless time, e is the bed porosity, L is the bed length, q is the solute concentration in the solid phase, and Pe and Bi are the Peclet and Biot numbers, respectively.
The Langmuir isotherm will be used to describe local equilibrium between fluid and solid phases as follows:

(9)
where qmax and b are the Langmuir parameters.
The system of equations formed by Eq. 1 to Eq. 5 together with the initial and boundary conditions given by Eq. 2 to Eq. 4 and Eq. 6 to Eq. 8 was solved using the finite volumes technique (Maliska, 1995).
Applying the method of finite volume using the Weighted Upstream Differenciation Scheme (WUDS) (Maliska, 1995) for the approximating functions in the fluid phase, Eq. 1 and in the bed internal elements in the axial direction, we have

(10)
where

(11)

(12)

(13)

(14)
Constants an, as, bn, and bs are the coefficients of the interpolating function of the WUDS.
The same methodology will be applied to the contour elements of Eqs. 1 to 3. Then, for the condition in z = 0, we get

(15)
where

(16)
Analogously, for the condition in z = 1,

(17)
with

(18)
In a similar fashion, for the solid phase we obtain the following from Error! Reference source not found.:

(19)
where

(20)

(21)

(22)

(23)

(24)
Constants ae, aw, be, and bw are the coefficients of the interpolating function of the WUDS. Applying the same methodology to the contour elements of Eqs. 5, 7, and 8 for the condition in r = 0, we get

(25)
with

(26)
For the condition at r = 1, we get

(27)
where

(28)

(29)
Eqs. 10 and 19 were developed generically; therefore, they may be applied to any internal bed element. Conversely, Eqs. 15, 17, 25 and 27 are specific and can be used only for contour elements. The system of equations just developed must be solved simultaneously. To this end, the variables were redefined in a new set of equations. The grid spacing is shown in Error! Reference source not found..
For the intermediate elements, i.e., k = 2,3,4,.., ne - 1, the following expression was obtained for the solute concentration in the fluid phase:

(30)
For k = 1, i.e., z = 0, the expression for the solute concentration in the fluid phase is given by

(31)
For k = ne, i.e., z = 1 the concentration of solute in the fluid phase is given by

(32)
For the solute concentration in the solid phase, the differential equation in terms of the overall coordinates in the grid layout, corresponding to the level k, is given by

(33)
with i = 2,3,..., nr - 1.
For i=1, i.e., r = 0 (particle center), we have

(34)
For the surface of the particle, i = nr, i.e., r = 1 we obtain

(35)
The system formed by Eqs. 30 to 35 can be grouped and written as

(36)
where j = 1,2,...., n and n = ne(nr + 1).
To solve the above system of differential equations with the corresponding initial and boundary conditions, the IVPAG sub-routine from the IMSL (Fortran 4.0) was employed.
CALCULATION OF THE KINETIC PARAMETERS
In order to numerically solve the problem just discussed, knowledge of the following parameters was required: the coefficient of effective diffusion in the pores of the particles, Def; the coefficient of axial dispersion in the beds fluid phase, DL; and the mass transfer coefficient for the fluid phase, kf. These parameters were calculated from correlations found in the literature.
The coefficient of effective diffusion in the pores of the particles was calculated using the following correlation suggested by Smith (1981):

(37)
where  is the tortuosity factor,
is the tortuosity factor,  is the particle porosity, and D12 is the binary diffusion coefficient of the solutein the solvent. The tortuosity factor,
is the particle porosity, and D12 is the binary diffusion coefficient of the solutein the solvent. The tortuosity factor,  , varies from 2 to 8. In the present work the value used was 3.5, based on the suggestion of Madras et al. (1994). The binary diffusion coefficient was calculated using the following empirical correlation of He and Yu (1997):
, varies from 2 to 8. In the present work the value used was 3.5, based on the suggestion of Madras et al. (1994). The binary diffusion coefficient was calculated using the following empirical correlation of He and Yu (1997):

(38)

(39)

(40)

(41)
The axial dispersion coefficient for the bed was calculated using the empirical correlation of Tan and Liou (1989):

(42)
For the mass transfer coefficient, very few correlations specifically developed for a high-pressure system are available in the literature. One exception is the correlation developed by Lee and Holder (1995) for SCF/solid systems. This correlation takes into account both forced and natural convection. And, as discussed for other systems (Ferreira et al., 1997), natural convection can be of importance depending on system temperature and pressure. As the data of Marques (1997) were measured at conditions similar to those used by Ferreira et al. (1997), the Lee and Holder (1995) correlation shown below was chosen to calculate the fluid-phase mass transfer coefficient:

(43)
To evaluate the dimensionless numbers of Grashof, Reynolds, and Schmidt, the dynamic solvent viscosity was evaluated using the method of Chung (Reid et al., 1987).
RESULTS AND DISCUSSION
Deterpenation of the orange oil phase was carried out by Marques (1997) at three conditions (C 1, C 2, and C 3) for Step I and two conditions (C 4 and C 5) for Step II as shown in Error! Reference source not found.. The composition of the orange oil phase is given in Error! Reference source not found.. Bed porosity was e = 0.30 and that of the particle was e p = 0.45. Steps I and II occurred in series; therefore, the results for the overall process depend on the combinations of conditions used for each step.
The model for desorption proposed earlier is suited to binary systems. The orange oil phase is a mixture of chemical substances, as discussed before. In order to use the proposed model for the multicomponent system of interest, the oil phase was treated as a pseudopure component. The Kay mixing rule was used to evaluate the properties of the pseudopure substance. The composition of the oil determined by gas chromatography coupled with mass spectrometry (CGMS) was used (Error! Reference source not found.). The critical properties, acentric factors, and normal boiling temperatures of the pure compounds that form the orange oil phase were obtained from the literature or estimated as indicated (Error! Reference source not found.). The kinetic parameters (Def, DL and kf ) estimated by the correlations indicated previouslyt are shown in Error! Reference source not found..
The parameters for the Langmuir isotherm (qmax and b) were estimated using the experimental data of Marques (1997) and the following objective function:

(44)
where

(45)
At first, considering the experimental procedure of Marques (1997), the saturation concentration was assumed to be equal to the concentration of the first fraction of the experimental extraction curve. As can be observed in Error! Reference source not found., the results for Step I and Step II are satisfactory (Error! Reference source not found.) for condition C1. For conditions C2 and C3 the convergence criterion was not met.
To improve the system modeling, the saturation concentration was estimated simultaneously with the Langmuir parameters, thereby minimizing the objective function given by Eq. 44. With this increase in the degree of freedom for the model, the convergence criterion was met for all experimental conditions. As shown in Error! Reference source not found., the model quantitatively described the experimental data in spite of all the simplifying assumptions made in developing the model.
CONCLUSIONS
The proposed mass transfer model satisfactorily described the experimental behavior in the process of deterpenation of the orange oil phase designed by Marques (1997). Since the model was written in a generic fashion, it is worthwhile investigating its applicability to other SCF extraction from solid substratum.
From the results it is possible to conclude that the Kay mixing rule and the empirical correlations used were adequate. Evaluating process parameters from information available in the literature permitted a reduction in the numbers of parameters to be estimated from the experimental data available. This procedure helped achieve a better understanding of the mechanisms associated with the SCF desorption of the oxygenated compounds of the orange oil phase.
The values for the estimated Langmuir parameters behaved as expected. The increase in temperature was accompanied by an increase in qmax and a decrease in b.
NOMENCLATURE
Dimensionless Numbers
Subscript
Greek letters
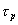
Model Discretization Constants
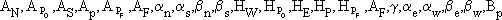
REFERENCES
Barros, B.N.; Scarminio, I.S.; Bruns, R.E.; Planejamento e Otimização de Experimentos. Editora da Unicamp, Campinas, São Paulo, Brazil, 1995.
Brunner, G., Gas Extraction: An Introduction to Fundamentals of Supercritical Fluids and the Applications to Separation Process, Darmstadt-Steinkopff, Germany, 1994.
Chen, T.L.; Asu, J.T., Prediction of Breakthrough Curves by the Application of Fast Fourier Transform, AIChE Journal, 33, No. 8, 1387 (1987).
Daubert, T.E.; Danner, R.P.; Sibul, H.M.; Stebbins, C.C, DIPPR Data Compilation of Pure Compound Properties, Project 801 Sponsor Release, Design Institute for Physical Property Data, AIChE, New York, NY, July, 1993,
Ferreira, S.R.S.; Meireles, M.A.A.; Nikolov, Z., Mass Transfer Correlations for SCFE of Black Pepper Essential Oil, Proceedings of the 4th International Symposium on Supercritical Fluids, B, 731 (1997).
He, Chao-Hong; Yu, Yong-Sheng, Estimation of Infinite-Dilution Diffusion Coefficients in Supercritical Fluids, Ind. Eng. Chem. Res., 36, 4430 (1997).
King, M.B.; Bott, T.R., Extraction of Natural Products Using Near-Critical Solvents, Blackie Academic & Professional, Chapman & Hall, Madras, India, 1993.
Lee, C. H.; Holder, G. D., Use of Supercritical Fluid Chromatography for Obtaining Mass Transfer Coefficients in Fluid-Solid Systems at Supercritical Conditions, Ind. Eng. Chem. Res., 34, 906 (1995).
Lide, D.R.; Kehiaian, H. V., CRC Handbook of Chemistry and Physics, 77th Edition, CRC Press, New York, 1996-1997.
Madras, G.; Thibaud, C.; Erkey, C.; Akgerman, A., Modeling of Supercritical Extraction of Organics from Solid Matrices, AIChE Journal, 40, No. 5, 777 (1994).
Maliska, R. C., Transferência de Calor e Mecânica dos Fluidos Computacional, Livros Técnicos e Científicos S.A., Rio de Janeiro, 1995.
Marques, D.S., Desterpenação de Óleo Essencial de Laranja por Cromatografia Preparativa de Fluido Supercrítico. M.Sc. thesis, UNICAMP, Campinas, São Paulo, Brazil, 1997.
Perry, R.H.; Green, D., Perrys Chemical Engineers Handbook, McGraw-Hill, 7th Edition, 1999.
Raghavan, N.S.; Ruthven, D.M., Numerical Simulation of Fixed Bed Adsorption Column by the Method of Orthogonal Collocation, AIChE Journal, 29, No. 6, 922 (1983).
Reid, R.C.; Prausnitz, J.M.; Poling, B.E., The Properties of Gases and Liquids, 4th Ed., McGraw-Hill Book Company, NY, 1987.
Smith, J. M., Chemical Engineering Kinetics, McGraw-Hill, New York (1981).
Tan, Chung-Sung; Liou, Din-Chung, Axial Dispersion of Supercritical Carbon Dioxide in Packed Beds, Ind. Eng. Chem. Res., 28, 1246 (1989).
- Barros, B.N.; Scarminio, I.S.; Bruns, R.E.; Planejamento e Otimizaçăo de Experimentos. Editora da Unicamp, Campinas, Săo Paulo, Brazil, 1995.
- Brunner, G., Gas Extraction: An Introduction to Fundamentals of Supercritical Fluids and the Applications to Separation Process, Darmstadt-Steinkopff, Germany, 1994.
- Chen, T.L.; Asu, J.T., Prediction of Breakthrough Curves by the Application of Fast Fourier Transform, AIChE Journal, 33, No. 8, 1387 (1987).
- Daubert, T.E.; Danner, R.P.; Sibul, H.M.; Stebbins, C.C, DIPPR Data Compilation of Pure Compound Properties, Project 801 Sponsor Release, Design Institute for Physical Property Data, AIChE, New York, NY, July, 1993,
- Ferreira, S.R.S.; Meireles, M.A.A.; Nikolov, Z., Mass Transfer Correlations for SCFE of Black Pepper Essential Oil, Proceedings of the 4th International Symposium on Supercritical Fluids, B, 731 (1997).
- He, Chao-Hong; Yu, Yong-Sheng, Estimation of Infinite-Dilution Diffusion Coefficients in Supercritical Fluids, Ind. Eng. Chem. Res., 36, 4430 (1997).
- King, M.B.; Bott, T.R., Extraction of Natural Products Using Near-Critical Solvents, Blackie Academic & Professional, Chapman & Hall, Madras, India, 1993.
- Lide, D.R.; Kehiaian, H. V., CRC Handbook of Chemistry and Physics, 77th Edition, CRC Press, New York, 1996-1997.
- Madras, G.; Thibaud, C.; Erkey, C.; Akgerman, A., Modeling of Supercritical Extraction of Organics from Solid Matrices, AIChE Journal, 40, No. 5, 777 (1994).
- Maliska, R. C., Transferęncia de Calor e Mecânica dos Fluidos Computacional, Livros Técnicos e Científicos S.A., Rio de Janeiro, 1995.
- Marques, D.S., Desterpenaçăo de Óleo Essencial de Laranja por Cromatografia Preparativa de Fluido Supercrítico. M.Sc. thesis, UNICAMP, Campinas, Săo Paulo, Brazil, 1997.
- Perry, R.H.; Green, D., Perrys Chemical Engineers Handbook, McGraw-Hill, 7th Edition, 1999.
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E., The Properties of Gases and Liquids, 4th Ed., McGraw-Hill Book Company, NY, 1987.
- Smith, J. M., Chemical Engineering Kinetics, McGraw-Hill, New York (1981).
Publication Dates
-
Publication in this collection
18 Oct 2000 -
Date of issue
Sept 2000
History
-
Received
29 Mar 2000 -
Accepted
23 Apr 2000











