Abstract
A mathematical model for prediction of monomer conversion, of particle number and of the evolution of the particle size distribution (PSD) in dispersion polymerization is developed. Despite being completed very early during the polymerization process (monomer conversion <1%), nucleation of new particles is the most important factor affecting the PSD. In order to describe the particle nucleation phenomena, the mechanism of homogeneous coagulative nucleation is considered. According to this mechanism, polymer chain aggregates can either coagulate and grow, to give birth to new polymer particles (particle nucleation), or be captured by existing polymer particles. Two sets of population balance equations are used: one for the aggregates, and a second one for the stable polymer particles. It is shown that the model is able to describe the dispersion polymerization of styrene in ethanol and the formation of micron-size monodisperse polymer particles.
Dispersion polymerization; particle size distribution; population balance
MATHEMATICAL MODELING OF DISPERSION POLYMERIZATIONS STUDY OF THE STYRENE POLYMERIZATION IN ETHANOL
P.H.H.Araújo1 and J.C.Pinto2
Programa de Engenharia Química / COPPE, Universidade Federal do Rio de Janeiro,
Cidade Universitária, CP: 68502, 21945-970, Fax: (0xx21) 590-7135,
Phone: (0xx21) 590-2241, Rio de Janeiro - RJ, Brazil
Email: pinto@peq.coppe.ufrj.br
(Received: October 19, 1999 ; Accepted: April 4, 2000)
Abstract - A mathematical model for prediction of monomer conversion, of particle number and of the evolution of the particle size distribution (PSD) in dispersion polymerization is developed. Despite being completed very early during the polymerization process (monomer conversion <1%), nucleation of new particles is the most important factor affecting the PSD. In order to describe the particle nucleation phenomena, the mechanism of homogeneous coagulative nucleation is considered. According to this mechanism, polymer chain aggregates can either coagulate and grow, to give birth to new polymer particles (particle nucleation), or be captured by existing polymer particles. Two sets of population balance equations are used: one for the aggregates, and a second one for the stable polymer particles. It is shown that the model is able to describe the dispersion polymerization of styrene in ethanol and the formation of micron-size monodisperse polymer particles.
Keywords: Dispersion polymerization, particle size distribution, population balance.
INTRODUCTION
Dispersion polymerization in polar organic media is a unique way to produce micron-size monodisperse polymer particles in a single process step. Monodisperse polymer particles are required for a number of practical applications, including the production of toners, preparation of instrument calibration standards, development of column packing materials for chromatography, and performing of biomedical and biochemical analysis (Sudol, 1997). Batch dispersion polymerization is usually started with the preparation of a homogeneous mixture containing monomer, organic solvent, soluble polymeric stabilizer, and initiator. The solvent selection depends on its miscibility with the constituents of the reaction environment: monomer, stabilizer and initiator are expected to dissolve completely in the solvent, while polymer is expected to precipitate during polymerization. Polymerization is initiated in solution by an initiator that is soluble in both the solvent and monomer. After precipitation, polymer particles are nucleated and form a distinct phase, which must be stabilized by the soluble polymeric stabilizer to avoid complete coagulation of the polymer material. The formation of new particles can be understood in terms of the homogeneous coagulative nucleation, where polymer chain aggregates formed during homogeneous nucleation either coagulate or are captured by existing polymer particles. New polymer particles are formed through coagulation and growth of aggregates.
The production of micron-size monodisperse polymer particles requires the tight control of the nucleation conditions. The nucleation period must be short and neither nucleation nor coagulation must occur after a specified time window. The nucleation of new polymer particles must be completed for monomer conversion levels below 1%. In spite of that, particle nucleation is the most important factor affecting the PSD. Different models have been presented in the open literature to describe the kinetics of dispersion polymerization (Ahmed and Poehlein, 1997; Sáenz and Asua, 1999), but none of them analyze the nucleation step. Therefore, just particle growth is taken into consideration to allow the calculation of the PSD evolution, which means that particle nucleation rates are assumed to be known. Using a geometrical progression of population bins, Paine (1990) presented a simple mechanistic model to predict particle size based on the coagulative nucleation mechanism. According to Kawaguchi et al. (1995), though, experimental results cannot be explained quantitatively yet in terms of Paines model. In spite of that, Paines model may be effective for some practical applications, given its underlying principles and deeper qualitative understanding of the particle formation process.
In the present work, a mathematical model is developed for prediction of conversion, of particle number and of the evolution of the particle size distribution (PSD) in dispersion polymerizations. The model is based on the homogeneous coagulative nucleation and comprises two sets of population balance equations: one for polymer chain aggregates and a second one for the stable polymer particles. Simulations are carried out for the styrene dispersion polymerization in ethanol.
MATHEMATICAL MODEL
The model is implemented for the batch dispersion polymerization of styrene in ethanol, using PVPK-30 (polyvinylpyrrolidone) as steric stabilizer, and AIBN (2,2-azobis isobutyronitrile) as initiator. Initiator concentration is equal to 1.0 wt % in respect to monomer. Initial monomer concentration is equal to 12.6 wt %. Polymerization temperature is equal to 70 oC. This system is commonly used to produce monodisperse polymer particles (Saénz and Asua, 1995).
According to Saénz and Asua (1998), experimental results suggest that radicals are produced in both the polymer and the continuous phases through the usual thermal decomposition of the initiator. Radicals dissolved in the continuous phase grow through the incorporation of dissolved monomer molecules and form oligoradicals. When the size of oligoradicals reaches a limiting value, oligoradicals precipitate and form a polymer chain aggregate. The fraction of radicals that precipitate is limited by the rate of termination with other radicals, by the entry rate into polymer particles and aggregates, and by chain transfer reactions. Aggregates can coagulate among themselves or be captured by existing polymer particles. New polymer particles are formed through coagulation and growth of aggregates. Inside the polymer particles, reaction is initiated by radicals formed through thermal decomposition of the initiator dissolved in the polymer mass and by radicals that are captured from the continuous phase. The most important assumptions used to write down the model equations are:
i) Monomer and initiator concentrations in the different phases are in thermodynamic equilibrium;
ii) Polymerization occurs in both continuous phase and polymer particles;
iii) The quasi-steady state assumption is valid for radicals;
iv) Radical desorption from polymer particles is negligible;
v) Volume contraction is negligible.
The first assumption is used because mass transfer rate are much higher than polymerization reaction rates. The second assumption is based on experimental data, while the third one is a rather standard assumption used to describe free-radical polymerizations. The forth assumption is due to the quite small surface area / volume ratio of polymer particles produced through dispersion polymerizations, when compared to emulsion polymerizations. The fifth assumption is a fair approximation of the actual experimental conditions, as the initial monomer holdup fraction is small and equal to 12.6 wt %.
Mass Balances
The mass balance for the initiator is:

(1)
where [I] is the mass concentration of initiator in the reactor vessel and kd is the rate constant for initiator decomposition.
The mass balance for the monomer may be written as:

(2)
where VR is the reactor volume; VII is the volume occupied by the continuous phase; [MA], [MA]II, [MA]III are the mass concentrations of monomer in the reactor, in the continuous phase and in the polymer phase respectively; ñm is the average number of radicals per particle; Np is the total number of polymer particles and aggregates in the reactor; 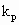 and
and 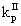 are the propagation rate constants in the polymer and in the continuous phase respectively; NA is the Avogadros number; [RTOT] is the concentration of radicals in the continuous phase.
are the propagation rate constants in the polymer and in the continuous phase respectively; NA is the Avogadros number; [RTOT] is the concentration of radicals in the continuous phase.
Equations for Thermodynamic Equilibrium
Monomer concentrations in the continuous and polymer phases are calculated with the iterative algorithm proposed originally by Omi et al. (1985). Equilibrium equations are written in terms of the partition coefficient ( ). For monomer, equations are:
). For monomer, equations are:

(3)

(4)
where VIII is the volume of the polymer phase.

(5)
For solvent, equations become:

(6)

(7)
where [S], [S]II and [S]III are the mass concentrations of solvent (ethanol) in the reactor, in the continuous phase and in the polymer phase respectively;  is the partition coefficient for the solvent (ethanol), obtained through the following equation (Pinto, 1990):
is the partition coefficient for the solvent (ethanol), obtained through the following equation (Pinto, 1990):

(8)
where [A]II is the molar monomer concentration in the continuous phase. The volume of the continuous phase (monomer + solvent) and of the polymer phase (monomer + solvent + polymer) are computed through an iterative procedure using the following recursive equations:

(9)

(10)
where [P]III is the mass concentration of polymer in the particle phase; rA, rS and rP are the densities of monomer, solvent and polymer respectively.
In order to calculate the monomer concentration, Equations (3-10) must be solved by the following iterative procedure:
-
Assume initial values for V
II and V
III;
-
[M
A]
III and [S]
III are calculated with Equations (5) and (7);
-
[M
A]
II and [S]
II are calculated with Equations (3) and (6);
-
V
II and V
III are calculated with Equations (9) and (10);
-
Return to 2 until convergence is reached.
The equilibrium equation for the initiator can be written in terms of a partition coefficient, as written for monomer and solvent. However, as this value is not available in the literature, it is assumed here that all initiator is dissolved in the continuous phase. Therefore, polymerization inside the polymer particles is assumed to be caused mainly by capture of growing radicals.
Radical Balance in the Continuous Phase
The quasi-steady state assumption is applied for radicals in the continuous phase. The concentration of all radicals in the continuous phase [RTOT] is given by:

(11)
where [Rh] is an oligoradical with h mers.
For radicals containing a single mer, it is possible to write:

(12)
where [I]II is the mass concentration of initiator in the continuous phase; PMI is the molecular weight of initiator; 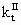 is the termination rate constant in the continuous phase; ke is the entry rate coefficient. In Equation (12), the numerator accounts for the formation of radicals by initiator decomposition. The first and second terms in the denominator of Equation (12) account for the loss of R1 by propagation and termination, respectively. The last term in the denominator of Equation (12) accounts for the loss by entry into polymer particles and aggregates. Entry is assumed to occur through diffusion, so that the entry rate coefficient may be given by:
is the termination rate constant in the continuous phase; ke is the entry rate coefficient. In Equation (12), the numerator accounts for the formation of radicals by initiator decomposition. The first and second terms in the denominator of Equation (12) account for the loss of R1 by propagation and termination, respectively. The last term in the denominator of Equation (12) accounts for the loss by entry into polymer particles and aggregates. Entry is assumed to occur through diffusion, so that the entry rate coefficient may be given by:

(13)
where Rpinch is the radius of a particle swollen by monomer; Dc is the diffusion coefficient of monomer in the continuous phase and fi is a factor used to take into account the fact that the diffusion coefficient of an oligoradical with i mers is lower than the diffusion coefficient of the monomer. Those two variables are assumed to be Dc = 1.5.10-5 cm2/s and fi = 4.0.10-2.
For radicals with 2 or more mers:

(14)
where,

(15)
The concentration of all radicals in the continuous phase [RTOT] is given by:

(16)
Equations (12-16) are solved iteratively, to allow the computation of [R1] and [RTOT].
Average Radical Number per Volume of Polymer Particle
Dispersion polymerization is used to produce micron size polymer particles. These particles are very large (when compared to emulsions, for instance) and contain a high number of radicals per particle (ñ>>0.5). Therefore, the "pseudo-bulk" kinetics may be assumed. However, according to Saénz and Asua (1999), the high internal viscosity of the polymer particles promotes the cage effect. This means that radicals generated within the polymer particles are likely to terminate before any significant growth can be attained, as diffusion of radicals through the polymer mass is seriously impaired. This also means that radicals present within the polymer particles come mainly from the continuous phase. As the entering chain is relatively long, it may be difficult for radicals to diffuse towards the core of the particle. This may cause the development of radical concentration distributions along the particle radius, as believed to occur in conventional emulsion polymerization by anchoring of the hydrophilic part of the entering radical to the particle surface. Under such circumstances, the radical number (ñ) per particle diameter (dp in cm) can be given by:

(17)
where K is assumed to be a constant equal to 3.0.1011 cm-2.
Population Balance of Aggregates
Polymer chain aggregates are nucleated by precipitation of oligoradicals of length equal to or longer than a critical length jcrit. Aggregates can coagulate among themselves or be captured by existing polymer particles. The population balance for polymer chain aggregates can be written as:

(18)
where the first and second terms of the right hand side of Equation (18) account for aggregates of mass l that disappear after coagulation with aggregates and with stable polymer particles respectively; while the fifth term of the right hand side of Equation (18) accounts for aggregates of mass l that are formed after coagulation of two aggregates.
The lower and upper limits for aggregate polymer mass (l) are amn and bmx respectively. The lower and upper limits for polymer mass of stable particles (m) are bmn and cmx respectively. NTp is the total number of aggregates.  is the total number of stable polymer particles.
is the total number of stable polymer particles.  is the coagulation rate constant for coagulation between aggregates and
is the coagulation rate constant for coagulation between aggregates and  is the coagulation rate constant for coagulation between aggregates and stable particles. The expression for aggregate nucleation may be given by:
is the coagulation rate constant for coagulation between aggregates and stable particles. The expression for aggregate nucleation may be given by:

(19)
The rate of growth of polymer chain aggregates due to propagation is:

(20)
where h(l,t) is the density of the aggregate size distribution, given by:

(21)
where n(l,t) is the number of aggregates of mass l at time t.
Total Number of Aggregates
If Equation (18) is integrated to include all particle aggregates of all sizes, Equation (22) can be obtained for the total number of aggregates:

(22)
where the first and second terms of the right hand side of Equation (22) account for aggregates that disappear after coagulation with other aggregates and stable particles respectively; the third, for generation of aggregates due to homogeneous nucleation; the forth and fifth, for aggregates that disappear after formation of new stable polymer particles through coagulation and propagation respectively.
Population Balance of Stable Polymer Particles
Polymer particles are formed through coagulation and growth of aggregates with mass bmx. Stable polymer particles also grow due to coagulation with aggregates and propagation of oligoradicals inside the particle. The population balance for the stable polymer particles is

(23)
obs.: a - if m = bmn the integral is equal zero; if amn+bmn < m <2.bmn, the integration limits are amn and m-bmn.
where the third term of the right hand side of Equation (23) accounts for growth through coagulation with aggregates of a stable polymer particle of mass m.
The nucleation of new stable polymer particles is caused by coagulation of the aggregates and by propagation of an aggregate of mass bmx as:

(24)
obs.: b - the integral is valid only for particle sizes between bmn and 2.bmn.
The growth rate due to propagation is given as:

(25)
Finally, defining the density distribution of stable polymer particles, f(m,t):

(26)
where n(m,t) is the number of polymer particles of mass m at time t.
Total Number of Polymer Particles
As performed previously, Equation (23) can be integrated over the size domain to allow the computation of the total number of stable polymer particles as:

(27)
where the first and second terms of the right hand side of Equation (27) account for the new stable polymer particles that are formed after coagulation of aggregates and propagation of an aggregate of mass bmx respectively.
Model Parameters
In order to calculate the coagulation rate coefficients, one may use an extension of the standard DLVO model developed by Gilbert (1995). According to the DLVO Theory, the movement of small particles suspended in a fluid may be described by a potential field that is composed of the electrical interactions among the charges distributed over the particle surfaces and of the attractive van der Waals particle interactions. The rate of coagulation may be described as the rate of diffusion across the maximum in this potential field. A possible disadvantage for using this approach is the relatively large number of parameters required by the DLVO model. From a practical point of view, most of them cannot be estimated based solely on the measurement of kinetic and PSD data.
The parameters used for model computations are listed in Table 1. Kinetic constants for propagation and termination are assumed to be the same in both phases. Based on the DLVO Theory, the difference between the coagulation rate constants for aggregates ( ) and for stable polymer particles (
) and for stable polymer particles ( ) is mainly due to the size differences between the two particle populations. According to the DLVO, the coagulation constant is expected to be proportional to
) is mainly due to the size differences between the two particle populations. According to the DLVO, the coagulation constant is expected to be proportional to  , where ri and rj are the radius of the swollen particles subject to coagulation. As the diameters of two aggregates that coagulate are much more uniform than the diameters of a large stable particle and a small aggregate, the coagulation rate constant for aggregate coagulation is also much lower. The size range of aggregates (amn, bmx) was defined in order to obtain spherical particles with diameter between 4 nm (jcrit meric units) and 80 nm. The size range of stable polymer particles (bmn, cmx) was defined in order to obtain spherical particles with diameter between 80 nm and 5 mm.
, where ri and rj are the radius of the swollen particles subject to coagulation. As the diameters of two aggregates that coagulate are much more uniform than the diameters of a large stable particle and a small aggregate, the coagulation rate constant for aggregate coagulation is also much lower. The size range of aggregates (amn, bmx) was defined in order to obtain spherical particles with diameter between 4 nm (jcrit meric units) and 80 nm. The size range of stable polymer particles (bmn, cmx) was defined in order to obtain spherical particles with diameter between 80 nm and 5 mm.
A finite difference discretization scheme was used to allow the numerical solution of the population balance equations, as described by Araújo (1999). The resulting set of algebraic -differential equations was solved with the help of the integrator DASSL (Petzold, 1982).
MODEL RESULTS
One of the objectives of dispersion polymerization of styrene in ethanol is the preparation of monodisperse polymer particles with diameters in the range of 1-10 mm for applications that require high quality latex. The uniformity of a particle size distribution may be characterized through the polydispersity index (PDI). A particle population may be regarded as monodisperse when the PDI is lower than 1.02 (Saénz and Asua, 1995). The PDI may be calculated as follows:

(28)
where dn and dw are number and weight average diameters; dp(x) is the diameter of a particle with mass x; and n(x) is the number of particles with mass x.
In Figure 1.a it is possible to observe the evolution of the average particle diameter and of the PDI during polymerization. At the beginning of reaction, the PDI is large, as the particles are small and the relative difference between the largest and smallest particles is also high. The particles grow at similar rates, so that the absolute difference between the sizes of these particles does not change significantly. Therefore, the relative difference between particle sizes and the PDI decrease. The final PDI of 1.014 indicates that the final distribution is monodisperse. The final average particle diameter (dp) obtained through simulation is 2.6 mm, which is in accordance with experimental data (Run A4) obtained by Saénz and Asua (1995) at similar conditions. At 88% monomer conversion Run A4 led to a PDI of 1.02 (monodisperse) and to a dp of 2.4 mm. At the same monomer conversion level, the model led to a PDI of 1.018 and to a dp of 2.5 mm.
Nucleation occurs during a very short time period and a large number of aggregates are formed. These aggregates grow though propagation and coagulation up to the critical size, when aggregates become stable polymer particles. In Figure 1.b it is possible to observe that the total particle number (for both aggregates and stable polymer particles) decreases slowly down to an almost constant value during the polymerization, after a short period of fast increase of the number of particles. This occurs because a large number of stable polymer particles are formed since the very beginning of the polymerization, which then absorb through coagulation most of the aggregates formed and avoid the nucleation of new stable polymer particles. After that, the model shows that the number of aggregates decreases. Despite of that, the rate of homogeneous nucleation increases, because the total particle area decreases with the aggregate coagulation, which causes the increase of the probability for an oligoradical to reach the critical value (jcrit) and nucleate new aggregates before being absorbed by the particles. The increase of the rate of nucleation does not affect the total particle number because the new aggregates coagulate almost immediately after nucleation. Reaction is completed after 1400 minutes of reaction.
Figure 2 presents the evolution of the particle size distribution (PSD) of stable polymer particles as a function of conversion. The graphic is plotted for number fraction and the distributions are normalized. Stable polymer particles start to be formed after 8.2 minutes of reaction through coagulation of aggregates. Stable particles grow mainly through coagulation with aggregates at the beginning, and afterwards growth is caused mostly by propagation. Particle growth leads to shifting of the PSD towards higher size values.
Figure 3 presents experimental PSD data (Run A4) at 88 % of conversion obtained by Saénz and Asua (1995) and the PSD obtained with the model at 88.9 % of conversion. It is possible to observe the very good agreement between experimental data and the model.
Although this work presents a useful model to allow the understanding of the behavior of PSDs during dispersion polymerizations, which is able to describe the production of monodisperse polymer particles through homogeneous coagulative nucleation, it is certain that more experimental data is needed for calculation of model parameters. For instance, the detailed development of the coagulation model is a key factor for proper description of the final shape of the PSD obtained.
CONCLUSIONS
A mathematical model that predicts conversion, particle number and particle size distribution in dispersion polymerization was developed. The model is based on first principles and presents the same behavior observed experimentally for the dispersion polymerization of styrene in ethanol used for the production of monodisperse particles (Saénz and Asua, 1995). This work illustrates the importance of using mathematical modeling to quantitatively analyze kinetic data as a unique way to elucidate the mechanisms involved in complex processes, although more experimental data are still necessary in order to calculate the parameters for the coagulation model.
ACKNOWLEDGMENTS
The authors thank CNPq Conselho Nacional de Desenvolvimento Científico e Tecnológico and CAPES Coordenação de Aperfeiçoamento de Pessoal de Nível Superior for providing scholarships.
NOMENCLATURE
Variables
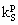
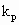
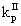
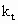
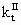
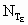
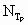
Subscript
Superscript
Greek Letters
- Ahmed, S.F., Poehlein, G.W., "Kinetics of Dispersion Polymerization of Styrene in Ethanol. 1. Model Development",. Ind. Eng. Chem. Res., 36, 2597 (1997).
- Araújo, P.H.H., "Distribuiçăo de Tamanhos de Partícula em Sistemas Heterogęneos de Polimerizaçăo", DSc. Thesis, PEQ/COPPE/UFRJ, Rio de Janeiro (1999).
- Brandrup, J., Immergut, E.H., "Polymer Handbook", Ed. J. Wiley, 3a ed., New York (1989).
- Cutter, L. A., Drexler, T. D., "Simulation of the Kinetics of Styrene Polymerization", in Computer Applications in Polymer Science, 13 (1982).
- Gilbert, R.G., "Emulsion Polymerization - A Mechanistic Approach", Academic Press, London (1995).
- Hui, A. W., Hamielec, A. E., "Thermal Polymerization of Styrene at High Conversions and Temperatures", J. Appl. Polym. Sci., 16, 749 (1972).
- Kawaguchi, S., Winnik, M.A., Ito, K., "Dispersion Copolymerization of n-Butyl Methacrylate with Poly(ethylene oxide) Macromonomers in Methanol-Water. Comparison of Experiment with Theory", Macromolecules, 28, 1159 (1995).
- Lenz, R.W., "Organic Chemistry of Synthetic High Polymers", Interscience Publishers, New York (1967).
- Omi, S., Kushibiki, K., Negishi, M., Iso, M., "Generalized Computer Modeling of Semi-Batch, n-Component Emulsion Copolymerization Systems and its Application", Zairyo Gijutsu, 3, 426 (1985).
- Paine, A.J., "Dispersion Polymerization of Styrene in Polar Solvents. 7. A Simple Mechanistic Model to Predict Particle Size", Macromolecules, 23, 3109 (1990).
- Petzold, L.R., "A description of DASSL: A Differential Algebraic System Solver", Sandia National Laboratories, Report # SAND82-8637 (1982).
- Pinto, U.B., "Estudo do Sistema Ternário Poliestireno/Estireno/Etanol Aplicado ŕ Polimerizaçăo por Precipitaçăo de Estireno em Etanol", M.Sc. Thesis, PEQ/COPPE/UFRJ, Rio de Janeiro (1990).
- Reid, R.C., Prausnitz, J.M., Poling, B.E., "The Properties of Gases and Liquids", Ed. McGraw-Hill, New York (1987).
- Sáenz, J.M., Asua, J.M., "Dispersion Polymerization in Polar Solvents", J. Polym. Sci. Chem., 33, 1511 (1995).
- Sáenz, J.M., Asua, J.M., "Kinetics of the Dispersion Copolymerization of Styrene and Butyl Acrylate", Macromolecules, 31, 5215 (1998).
- Sáenz, J.M., Asua, J.M., "Mathematical Modeling of Dispersion Copolymerization", Coll. Surf. Phys. Engngn. Asp., 153, 61 (1999).
- Stevens, C. J., "Mathematical Modeling of Bulk and Solution Free Radical Polymerization in Tubular Reactors", Ph. D. Thesis, University of Winscosin, Madison (1988).
- Sudol, E.D., in: J.M. Asua (Ed.), "Polymeric Dispersions: Principles and Applications", Kluwer Academic, Dordrecht (1997).
Publication Dates
-
Publication in this collection
16 Mar 2001 -
Date of issue
Dec 2000
History
-
Received
19 Oct 1999 -
Accepted
04 Apr 2000





