Abstract
Gas-liquid solubility of hydrogen in methanol and ethanol systems with electrolytes was studied in the temperature range from 305.15 K to 498.15 K and pressures from 4 to 10 MPa. The experimental method used was the Total Pressure Method, which eliminates sampling and analysis of the phases, determining their composition at equilibrium using the following experimental data: moles of solute and solvent in the system; pressure, temperature and volume of the system at equilibrium; together with thermodynamic equations for fluid-phase equilibria. The salts used were lithium chloride and potassium acetate. The solubility of hydrogen increases with increasing temperature and pressure and the presence of salts causes a decrease in the solubility of hydrogen, when compared with the results of systems without salts, characterizing a "salting-out" effect, which is greater in conditions of lower temperature and pressure, specially for potassium acetate.
Solubility; hydrogen; alcohols; electrolytes; high pressures
SALT EFFECT IN THE SOLUBILITY OF HYDROGEN IN N-ALCOHOLS AT PRESSURES UP TO 10 MPa AND TEMPERATURES UP TO 498.15 K
J.V.H.dAngelo* * To whom correspondence should be addressed and A.Z.Francesconi
Departamento de Engenharia Química , Escola de Engenharia, UFMG, Rua Espírito
Santo35, 6o andar,Centro, CEP: 30160-030, Phone: (0 31) 2381783/2381780,
Fax: (0 31) 2381789, Belo Horizonte - MG, Brazil
E-mail: jota@deq.ufmg.br
Departamento de Engenharia de Sistemas Químicos, Faculdade de Engenharia Química,
UNICAMP, C.P.6066, CEP 13083-970, Campinas - SP, Brazil
E-mail: francesconi@desq.feq.unicamp.br
(Received: November 25, 1999 ; Accepted: April 06, 2000 )
Abstract - Gas-liquid solubility of hydrogen in methanol and ethanol systems with electrolytes was studied in the temperature range from 305.15 K to 498.15 K and pressures from 4 to 10 MPa. The experimental method used was the Total Pressure Method, which eliminates sampling and analysis of the phases, determining their composition at equilibrium using the following experimental data: moles of solute and solvent in the system; pressure, temperature and volume of the system at equilibrium; together with thermodynamic equations for fluid-phase equilibria. The salts used were lithium chloride and potassium acetate. The solubility of hydrogen increases with increasing temperature and pressure and the presence of salts causes a decrease in the solubility of hydrogen, when compared with the results of systems without salts, characterizing a "salting-out" effect, which is greater in conditions of lower temperature and pressure, specially for potassium acetate.
Keywords: Solubility, hydrogen, alcohols, electrolytes, high pressures.
INTRODUCTION
In the industry of fine chemicals, a,b-insaturated alcohols are very important products, related with the production of flavors, pharmaceuticals, perfumes, cosmetics and many others. The catalytic hydrogenation reactions for converting aldehydes into these alcohols usually take place on a "slurry" reactor, where three phases are present: reactants, solvents and the products of the reaction (liquid phase), catalyst (solid) and hydrogen (gaseous).
Alcohols that are used as solvents for the reaction products have some influence in the selectivity and velocity of the reaction and in the catalyst activity. This influence is associated with the solubility of hydrogen in the solvents used. So the knowledge of the solubility of hydrogen in alcohols that may be used as solvents in the reaction medium is of great importance. Salts may be used together with the solvent to prevent polimerization reactions and also to keep the liquid-phase lightly alkaline. They may be present in the solution as impurities too. In this case, it is important to know how it affects the solubility of hydrogen in order to decide if a separation process for purification may be necessary or not.
The aim of this work was to study the solubility of hydrogen in methanol and ethanol, wich are solvents commonly used in those catalytic hydrogenation reactions of aldehydes, and how it is affected by the presence of salts added to the liquid-phase, comparing the results with the ones obtained for binary systems, without salt, in order to evaluate the salt-effect over the hydrogen. The influence of a salt may be very significant on phase-equilibria since it interacts with one or more species present in the system, altering their activity and so the distribution of the components in the phases at equilibrium.
Relatively few data of the solubility of hydrogen in alcohols at high temperatures and high pressures are available in scientific literature. For systems containing electrolytes, these data are even more scarse. So, extending the range of experimental pressure and temperature, beyond the one used in the reactions mentioned before, this work intends to contribute to diminish this lack of information. These results are also useful for testing and developing models for calculating thermodynamics properties.
EXPERIMENTAL METHODOLOGY
Apparatus
The experimental apparatus used for measuring the solubility of hydrogen in alcohols in systems containing electrolytes is a commercial equipment produced by LECO® Co., named "Barnes Volumetric Hydrothermal System", model RA-1A-1. A scheme of this apparatus is shown in Fig. 1. The equilibrium cell is a stainless steel mechanically agitated autoclave (volume 1128 cm3), which was placed inside an electrical heated furnace, with a maximum operation temperature of 673 K. To improve agitation, steel spheres (dead volume 6.2 cm3) were used inside the cell. The temperature at the extern wall of the autoclave was measured with a K type thermocouple connected to a digital controller (Eurotherm, model 847, resolution 0.1 K). The temperature inside the autoclave was measured with a J type thermocouple connected to a digital temperature indicator (Shimaden, model SD20, resolution 0.1 K). Both thermocouples were calibrated by measuring the boiling point of seven different chemicals, comparing the values indicated by them with the ones presented by a Pt-100 resistance thermometer (Guildline, model 9540, resolution 0.001 K), used as reference. The estimated uncertainty of the temperature measurement was ± 0.3 K. The autoclave was connected to a Bourdon gauge covering the range 0-40 MPa. This manometer was calibrated by measuring the pressure of saturated steam at several temperatures. The estimated uncertainty of the pressure measurement was ± 0.035 MPa.
Materials
Hydrogen (analytical grade, supplied by White Martins) was used without further purification. The purity of the alcohols was checked by three different ways: gas chromatography, measurement of refractive index and measurement of density. For all alcohols used (from Merck) no impurity peaks were found in the chromatography analysis. Table 1 shows the results of refractive index and density measured in this work, compared with values taken from literature for the alcohols used. All solvents were used without further purification except degassing, which was done by boiling them during a period of approximately 5 minutes in a beaker (Barnes, 1963). After this time, the beaker was sealed and them put into an ice bath for cooling, before use. The salts used (both from Merck) were heated in a stove for at least 15 hours, at a temperature of 423.15 K, to eliminate humidity and bound water. Them they were left in a desiccator for cooling before use. The minimun content specified by the fabricant for these salts is 99.0 mass %.
Experimental method
The experimental method used is similar to that of Cukor and Prausnitz (1972), Olson (1977), Graaf et al. (1992) and Breman et al. (1994). Known amounts of the components (hydrogen, alcohol and salt) are introduced in a vessel (equilibrium cell) of known volume. By measuring accurately these amounts and also pressure, temperature and volume of the system at equilibrium, and using thermodynamic relations of phase equilibria and a material balance; the composition of the phases at equilibrium can be determined and so the gas-liquid solubility, which is given by the mole fraction of the solute in the liquid phase, x2. This method is known as Total Pressure Method and its description and data reduction is given in details by Breman et al. (1994). This method is used only for binary systems. In this work, the ternary system (hydrogen + alcohol + salt) was considered a pseudo-binary constituted only by the gas and the solvent. This consideration is valid since the mole fraction of the solvent in the liquid phase is high (not less than 0.88) and that no salt is present in the gas phase.
Basically, the experimental procedure consists of evacuating the equilibrium cell and then fill it firstly with an amount of solution (degassed solvent with dissolved salt), previously prepared, in which the concentration of salt is known. Both quantities of solution and hydrogen are accurately measured from a differential mass of a beaker (for the solution), and of a small pressurized cylinder (for the gas), before and after feeding, using a semi-analitical balance (Mettler-Toledo, model A 300-51-126, inaccuracy of ± 0.005 g).
After the components were fed and locked-up inside the autoclave, the setpoint of the temperature controller is adjusted to a desired temperature and the rocking mechanism to agitate the system is turned on. Once attained equilibrium in the system at the desired point, the pair temperature-pressure of the system is written down. The setpoint is changed again, increasing temperature stepwise, until the highest temperature desired is reached. The system was assumed to be in equilibrium if during an interval of at least 40 minutes the values of temperature and pressure were constant within 0.3 K and 0.035 MPa, respectively, without showing any trends with time.
DATA REDUCTION
In this work, following the procedure used by Breman et al. (1994), the gas-liquid solubility of solute (2) in solvent (1) is also expressed by a so-called "pseudo Henrys coefficient", given by H2,1 PS, at a reference pressure which is the solvent saturation pressure, P1sat, and at the temperature of the system.
When equilibrium is attained in the system, the following relation holds for both components [Prausnitz et al., 1986]:

(1)
where P = absolute pressure of the system; yi = vapor-phase mole fraction of component i;  = vapor-phase fugacity coefficient of component i; xi = liquid-phase mole fraction of component i; fio = fugacity of component i at a reference state and g i = liquid-phase activity coefficient of component i. Taking as a reference state for the solute (hydrogen), the infinite dilution at the saturation pressure of the solvent at system temperature and taking into account the normalization of the activity coefficient of the solute by the unsymmetric convention (denoted by g2*® 1 as x2® 0), Eq. (1) can be written for the solute:
= vapor-phase fugacity coefficient of component i; xi = liquid-phase mole fraction of component i; fio = fugacity of component i at a reference state and g i = liquid-phase activity coefficient of component i. Taking as a reference state for the solute (hydrogen), the infinite dilution at the saturation pressure of the solvent at system temperature and taking into account the normalization of the activity coefficient of the solute by the unsymmetric convention (denoted by g2*® 1 as x2® 0), Eq. (1) can be written for the solute:

(2)
where H2,1 = Henrys coefficient of solute (2) in solvent (1); R = universal constant of ideal gases and  = partial molar volume of solute at infinite dilution. The exponential term of Eq. (2) is called the Poynting correction factor and is used to correct the effect of pressure over the fugacity of liquid phase of the solute.
= partial molar volume of solute at infinite dilution. The exponential term of Eq. (2) is called the Poynting correction factor and is used to correct the effect of pressure over the fugacity of liquid phase of the solute.
Substituting the product g2*H2,1 by the so called pseudo Henrys coefficient, Eq. (2) can be rewritten as:

(3)
Using the Peng-Robinson (1976) equation of state for evaluating the fugacity coefficient of the solute ( ), the equation of Wagner [Reid et al., 1987] for calculating the saturation pressure of the solvent, the modified equation of Rackett presented by Spencer and Danner (1972) for calculating molar volume of saturated liquid and the equation presented by Breman et al. (1994) for calculating the liquid density of solvent at increased pressure and also making a material balance for each component in both phases, the composition of the phases at equilibrium can be obtained from the primary experimental data at equilibrium (P, T, V, n1T and n2T) via an iterative method [Breman et al., 1994], where: T = absolute temperature; V = volume of the system (equilibrium cell); niT = total number of moles of component i fed in the system. This iterative method gives, as results, the number of moles of each component in both phases (liquid and vapor). Then the mole fraction of salt in the liquid phase is calculated considering the number of moles of alcohol and hydrogen in the liquid phase, given by the iterative method and the total number of moles of salt fed in the system, considering that all the salt is in the liquid phase.
), the equation of Wagner [Reid et al., 1987] for calculating the saturation pressure of the solvent, the modified equation of Rackett presented by Spencer and Danner (1972) for calculating molar volume of saturated liquid and the equation presented by Breman et al. (1994) for calculating the liquid density of solvent at increased pressure and also making a material balance for each component in both phases, the composition of the phases at equilibrium can be obtained from the primary experimental data at equilibrium (P, T, V, n1T and n2T) via an iterative method [Breman et al., 1994], where: T = absolute temperature; V = volume of the system (equilibrium cell); niT = total number of moles of component i fed in the system. This iterative method gives, as results, the number of moles of each component in both phases (liquid and vapor). Then the mole fraction of salt in the liquid phase is calculated considering the number of moles of alcohol and hydrogen in the liquid phase, given by the iterative method and the total number of moles of salt fed in the system, considering that all the salt is in the liquid phase.
The pseudo Henrys coefficient can then be calculated using Eq. (3). This coefficient is inversely proportional to the liquid-phase mole fraction of hydrogen. Analyzing its behavior as a function of temperature some conclusions arise about the solubility of hydrogen in alcohols in systems containing salts. Comparison of these data with the ones from binary systems (without salts) helps to understand the salt effect on the solubility of hydrogen in alcohols.
RESULTS AND DISCUSSIONS
The relevant physical properties of the pure components used in this study are presented in Table 2. Table 3 shows the molar charge of solvent (1), solute (2) and salt (3) for each experiment. Figures 2 to 4 show the behavior of the pseudo Henry´s coefficient as a function of the temperature of the system.
For all systems studied the solubility of hydrogen increases with increasing temperature and pressure, as can be seen by the behavior of the curves of the pseudo Henrys coefficient. Prausnitz et al. (1986) suggested that as a general rule, the solubility of a gas rises with increasing temperature whenever x2 is small and it falls with increasing temperature whenever x2 is large. Breman et al. (1994) also observed such behavior in systems containing hydrogen as a solute.
It was expected that the presence of an electrolyte in the system would reduce the solubility of hydrogen in the solvent, since that component is responsible for introducing ionic forces that alter the structure of the components of the liquid phase, causing a reduction in the number of "available" solvent molecules to solubilize the hydrogen. The solvent molecules probably form solvation complexes with the ions of the dissociated salt. In order to verify this effect of solubility reduction, the results were compared with some selected data obtained for the binary systems in the work of dAngelo (1998). Tables 4 and 5 show the results of this comparison. In these tables, the percentage reduction of hydrogen solubility in the alcohols, due to salt effect, is expressed by the symbol "¯ " and calculated by Eq. (4) as:

(4)
Analyzing the results presented in Tables 4 and 5, apparently, in the case of the system methanol-hydrogen-potassium acetate, at 8 mass % of salt in the initial solution, the salt effect is not sufficient to alter meaningfully the solubility of hydrogen. At the concentration of 10 mass % and 15 mass % of salt, this effect is very pronounced. For the systems with methanol it was observed a salting-out effect for the hydrogen in the liquid phase. This effect was observed in solutions of polar solvents by Al-Sahhaf and Kapetanovic (1997).
The comparison between the binary and ternary systems (with salt) also allows to conclude that the reduction of the solubility of hydrogen in alcohols, due to the addition of an electrolyte, is greater in the regions of low temperature and pressure. This is probably due to the fact that higher temperatures and pressures collaborate to increase the solubility and then, as they become greater, their effect over the solubility superposes the salt effect. The reduction in the solubility of hydrogen was proportional to the concentration of the salt in the solvent for all the systems.
When comparing the results for the systems that used potassium acetate with the ones containing lithium chloride, at the same salt concentration, it was observed that the reduction in the solubility of hydrogen was greater for the first salt cited, in similar conditions of temperature and pressure. This fact can be explained by the size of the salt molecule, which in the first case is bigger and so it would need more alcohol molecules to solubilize it, reducing the number of "available" molecules to solubilize the hydrogen.
Table 6 shows the uncertainties estimated for each variable measured experimentally. Considering them, a calculation from a worst case approach assuming all erros sources contributing maximally in the same direction to the overall error, has allowed to estimate the uncertainty in the values of the liquid-phase mole fraction of hydrogen as about ± 0.002. This value corresponds to a maximum relative deviation of ± 20% and a minimum relative deviation of ± 2%, among experimental data for all systems in this work.
Comparison with other solubility data for the systems studied in this work with data from literature was not possible since as far as we are concern these data do not exist, in the range of temperature and pressure of the experiments. Studies about modeling the behavior of such systems are going on and will be published latter.
CONCLUSIONS
The salt effect over the solubility of hydrogen in methanol and ethanol, using lithium chloride and potassium acetate as electrolytes was studied in this work, comparing the results obtained with data of solubility for binary systems. The solubility of hydrogen in all the systems studied increased with increasing temperature and pressure. Both salts used presented a salting-out effect for the hydrogen in the liquid phase. This effect is more pronounced in the range of low temperatures and pressures. When comparing the salts used, systems containing potassium acetate have shown a greater salting-out effect than the ones with lithium chloride, in similar conditions of temperature and pressure, at the same concentration of salt in the solution.
NOMENCLATURE
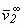
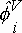
REFERENCES
- Al-Sahhaf, T.A., Kapetanovic, E., Salt effects of lithium chloride, sodium bromide, or potassium iodide on liquid-liquid equilibrium in the system water + 1-butanol, J. Chem. Eng. Data, 42, 74-77 (1997).
- Barnes, H.L., Ore solution chemistry. I. Experimental determination of mineral solubilities, Economic Geology, 58, 1054-1060 (1963).
- Breman, B.B., Beenackers, A.A.C.M., Rietjens, E.W.J., Stege, J.H., Gas-liquid solubilities of carbon monoxide, carbon dioxide, hydrogen, water, 1-alcohols (1 £ n £ 6), and n-paraffins (2 £ n £ 6) in hexadecane, octacosane, 1-hexadecanol, phenantrene, and tetraethylene glycol at pressures up to 5.5 MPa and temperatures from 293 to 553 K, J. Chem. Eng. Data, 39, 647-666 (1994).
- Cukor, P.M., Prausnitz, J.M., Solubilities of gases in liquids at elevated temperatures. Henrys constant for hydrogen, methane, and ethane in hexadecane, bicyclohexyl, and diphenylmethane, J. Phys. Chem., 76, 598-601 (1972)
- DAngelo, J.V.H., Estudo Experimental da Solubilidade do Hidrogênio em Álcoois, de 298,15 a 523,15 K e de 4 a 10 MPa, em Sistemas com e sem Elétrolitos e Modelagem da Fase Líquida, Doctoral Thesis, FEQ/UNICAMP, Campinas (1998).
- Graaf, G.H., Smit, H.J., Stamhuis, E.J., Beenackers, A.A.C.M., Gas-liquid solubilities of the methanol synthesis components in various solvents, J. Chem. Eng. Data, 37, 146-158 (1992).
- Olson, J.D., Solubility of nitrogen, argon, methane, and ethane in ethylene oxide, J. Chem. Eng. Data, 22, 326-329 (1977).
- Peng, D-Y., Robinson, D.B., A new two-constant equation of state, Ind. Eng. Chem. Fundam., 15, 59-64 (1976).
- Prausnitz, J.M., Lichtenthaler, R.N., Azevedo, E.G., Molecular Thermodynamics of Fluid Phase Equilibria, 2nd. edition, Prentice-Hall, New Jersey (1986).
- Reid, R.C., Prausnitz, J.M., Poling, B.E., The Properties of Gases and Liquids, 4th edition, McGraw-Hill Book Company, Cingapure (1987).
- Spencer, C.F., Danner, R.P., Improved equation for prediction of saturated liquid density, J. Chem. Eng. Data, 17, 236-241 (1972).
- Weast, R.C., Astle, M.J. editors, CRC Handbook of Data on Organic Compounds, 4th edition, CRC Press, Boca Raton (1987).
Publication Dates
-
Publication in this collection
16 Mar 2001 -
Date of issue
Dec 2000
History
-
Accepted
06 Apr 2000 -
Received
25 Nov 1999











