Phenomenological model of the clavulanic acid production process utilizing Streptomyces clavuligerus

PHENOMENOLOGICAL MODEL OF THE CLAVULANIC ACID PRODUCTION PROCESS UTILIZING STREPTOMYCES CLAVULIGERUS

A.Baptista-Neto, E.R.Gouveia, A.C. Badino-Jr^* and C.O. Hokka

Departamento de Engenharia Química, Universidade Federal de São Carlos,

C.P. 676, 13565-905, Phone: [phone], Fax: [phone]

São Carlos, SP - Brazil

E-mail: [e-mail]

(Received: November 3, 1999 ; Accepted: April 18, 2000)

Abstract - The kinetics of clavulanic acid production process by Streptomyces clavuligerus NRRL 3585 was studied. Experiments were carried out in a 4 liters bioreactor, utilizing 2 complex media containing glycerol as the carbon and energy source, and peptone or Samprosoy 90NB (soybean protein) as nitrogen source. Temperature was kept at 28°C and the dissolved oxygen was controlled automatically at 40 % saturation value. Samples were withdrawn for determination of cell mass (only peptone medium), glycerol and product concentrations. Gas analyzers allowed on line determination of CO₂ and O₂ contents in the exit gas. With Samprosoy, cell mass was evaluated by determining glycerol consumption and considering the cell yield, Y_X/S, as being the same for both cases. Oxygen uptake and CO₂ production rates were strongly related to growth and substrate consumption, allowing determination of stoichiometric constants in relation to growth, substrate, oxygen, product and carbon dioxide.

Keywords: clavulanic acid, Streptomyces clavuligerus, kinetic model

INTRODUCTION

Clavulanic acid is a strong b-lactamase inhibitor and only recently started to be administered together with penicillins to overcome problems related to antibiotic resistant pathogenic bacteria (Butterworth, 1984). It is produced in synthetic or complex media by some species of Streptomyces, as S. jumonjinensis, S. katsurahamanus and, mainly, Streptomyces clavuligerus which is unable to consume glucose (Zhang e Demain, 1992). In spite of its economical and therapeutic importance, information regarding process conditions is scarce and no quantitative kinetic data are reported so far.

Streptomyces sp. is an aerobic filamentous bacteria known as producer of several antibiotics, as it is the case of Streptomyces clavuligerus, producer of cephamycin C (Yegneswaran et al., 1991), cephalosporin (Rius and Demain, 1997) and clavulanic acid (Lee and Ho, 1996).

To avoid limitation Lee and Ho (1996) carried out studies to find the best carbon source for growth and clavulanic acid production. The authors observed that palm oil provided better productivity than obtained when utilized glycerol or sucrose as carbon source.

Although the best productivity values are reported with palm oil as carbon source, there are many authors, as Gouveia et al. (1999), Romero et al. (1986), Mayer and Deckwer (1996), that utilized glycerol as main carbon source. Other carbon sources, as maltose and dextrins, are easily metabolized by Streptomyces clavuligerus (Pruess and Kellet, 1983). Also, Garcia-Dominguez et al. (1989) describe the utilization of starch as carbon source.

Several studies using different nitrogen sources are reported in the literature. Belmar-Beiny and Thomas (1991) utilized malt extract and bacteriologic peptone; Romero et al. (1986), aminoacids, Mayer and Deckwer (1996), soybean flour or soybean extract and peptone, and Gouveia et al. (1999) utilized Samprosoy 90NB, a protein hydrolyzate from soybean.

Streptomyces clavuligerus develops exuberantly using soybean medium (Kadima et al., 1995) explaining the high production obtained by Mayer and Deckwer (1996) and Gouveia et al. (1999).

On the other hand, process modeling is essential for the implementation of cost optimization techniques and control strategy development. It is worth mentioning the work of Brass et al. (1997) concerning L-cartine and 6-hydroxinicotinic acid production bioprocess, when a remarkable time and cost reduction are achieved by means of optimization techniques based on kinetic model simulations.

In the literature, there are many studies on bioprocess modeling techniques and different approaches are extensively described by Bailey and Ollis (1986).

Regarding secondary metabolites, antibiotics being the most important example, Demain (1971) suggests that derepression of the enzyme responsible for the secondary metabolism, or accumulation of an internal inducer promotes production during idiophase, after the phase of rapid growth (trophophase). Models accounting for this phenomenon usually assume the transformation from repressed cells to derepressed cells when easily metabolized substrate level becomes lower than a critical concentration. Models developed by Araujo et al. (1996) and Cruz et al. (1999) are based on this assumption.

Concerning mathematical models dealing with clavulanic acid production bioprocess, Gudi et al. (1994) proposed inferential estimation strategies to estimate biomass concentration by on-line measurement of carbon dioxide evolution rate. In their study the product was not taken into account as the work aimed at on-line growth parameter estimation. Water soluble medium components were utilized to allow biomass separation for the estimation of its protein content. Tarbuck et al. (1985) proposed a kinetic model for estimation of the bioprocess progress. A defined medium and a complex soluble medium were utilized to allow biomass determination. In both works, state variables and specific rates were measured and monitored on-line, but no estimations of kinetic constants were reported.

In this work a kinetic model, assuming a stoichiometric equation, is proposed to explain the clavulanic acid production bioprocess, including kinetic parameters and yield coefficients determination. Two different media, with two different nitrogen sources were utilized, one with a protein extract from soybean and the other with soluble peptone. In the latter medium cell mass could be evaluated as all components were soluble, while in the former one, insoluble substances were present, and cell mass was determined indirectly.

MATERIALS AND METHODS

Microorganism

The strain Streptomyces clavuligerus NRRL 3585, kindly provided by the Institute of Antibiotics of the Universidade Federal de Pernambuco, Recife, PE, Brazil, was utilized throughout. Spore suspension containing approximately 10⁸ spores/ml was maintained in cryovials at -50ºC in freezer using glycerol (20% w/v) as cryoprotector.

Culture Media

Two distinct nitrogen sources were utilized: bacto-peptone and Samprosoy 90NB (a soybean protein hydrolyzate) kindly provided by Ceval Alimentos S/A, Esteio-RS, Brazil.

Germination media were composed of (in g/l): glycerol (20.0), bacto-peptone (32.0) or Samprosoy 90NB (37.0); pH 7.0. Two main fermentation media, also with different nitrogen source had the following composition (in g/l): glycerol (15.0), bacto-peptone (42.0) or Samprosoy 90NB (47.0), K₂HPO₄ (0.8) and pH 6.5. Both main fermentation media had the same total nitrogen concentration, 6.5 g/l.

Experimental Procedure

Two batch cultivations with different medium composition were conducted in a 4 liters Bioflo III fermentor (New Brunswick Scientific Co. Inc., USA). For each fermentation, spores were initially germinated in eight 500 ml Erlenmeyer flasks, with 50 ml germination medium. Flasks were inoculated with 1 ml of the spore suspension from the cryotubes and incubated in a rotary shaker (New Brunswick Sci.) for 24 hours at 28ºC and 250 rev/min. The contents of the flasks (400 ml) were transferred to the fermentor with 3.6 liters of fermentation medium, making up 4 liters of fermentation broth. The cultivations were carried out at 28ºC and the dissolved oxygen was controlled automatically at 40 % of air saturation value by changing agitation speed and keeping the aeration rate at 0.5 vvm. Samples were withdrawn each 3 hour for analytical determinations. For the gas balance method, air flowrate was measured by Cole Parmer mass flow meter and the oxygen (YO₂) and carbon dioxide (YCO₂) molar fractions in the outlet gas were measured by the gas analyzers Rosemount, models 755 and 880A, respectively.

Analysis

Cell concentration (Cx) was evaluated in peptone medium as dry matter obtained by vacuum filtration and drying at 105ºC for 24 hours. In Samprosoy 90NB medium, due to the presence of insoluble substances, cell mass was evaluated indirectly by determining glycerol consumption and considering the growth yield coefficient, Y_X/S, as being the same for Samprosoy and peptone media.

Glycerol concentration (Cs) was determined by HPLC (High Performance Liquid Chromatography, Waters), calibrated with 0.125, 0.25 and 0.5 g/l glycerol solutions. NaOH (10^-5 M) solution was used as the mobile phase. The equipment operated at 38ºC with 1ml/min flowrate. A Shodex KS 802 (Lonpak - division of Millipore, USA) column was utilized.

Clavulanic acid concentration (Cp) was determined by HPLC according to Foulstone and Reading (1982) with modifications proposed by Gouveia et al. (1999).

STOICHIOMETRY AND KINETIC MODELLING

Stoichiometry

According to Shuler and Kargi (1992), a material balance over biological reactions can be written when the composition of substrates, products and cellular material are known. Accurate determination of the cellular material composition is a major problem. For Streptomyces clavuligerus growth in which extracellular products are neglected, the following simplified biological conversion is proposed:

C₃H₈O₃ + a O₂ + b NH₃®

® c CH_1.666N_0.2O_0.27 + d CO₂ + e H₂O

(1)

where C₃H₈O₃ is molecular formula of glycerol, the main carbon source and CH_1.666N_0.2O_0.27 represents a typical bacteria composition (Atkinson and Mavituna, 1983).

Elemental balances on C, H, O and N yield the equations:

C: 3 = c + d

(2)

H: 8 + 3× b = 1.666× c + 2× e

(3)

O: 3 + 2× a = 0.27× c + 2× d + e

(4)

N: b = 0.2× c

(5)

Equations 2 through 5 constitute four equations for five unknown variables a, b, c, d and e and, therefore, one additional equation should be considered to solve the equation system.

One of them, the respiratory quotient (RQ), defined as the moles of CO₂ produced per mole of oxygen consumed, is written as:

(6)

Yield coefficients, Y_i/j, can be obtained relating rates of product formation to the limiting consumption rates of other components as follow:

(7)

(8)

(9)

where r_i represents the reaction rate of consumption or formation of component i, Qo₂ is the specific oxygen uptake rate (mmol.l^-1.h^-1) and m is the specific growth rate (h^-1).

If one of these yield coefficients is estimated experimentally, all variables of equation 1 can be determined.

Kinetic Modeling and Numerical Procedure

For the modeling, it was assumed that the microorganism grows in glicerol according to Monod model and that the cellular death begins after glycerol is practically depleted (bellow a critical concentration Cs₁). Concerning production, it was assumed that catabolic repression acts during part of the growth phase. Clavulanic acid formation began when glycerol concentration reached a critical value, Cs₂, higher Cs₁. Cellular death and product degradation were considered to follow first order rates in relation to cellular (Cx) and product (Cp) concentrations, respectively. The effect of dissolved oxygen concentration was not considered in the model because dissolved oxygen (DO) was controlled above the critical concentration to avoid limitation.

The rate equations describing the kinetic model are presented as follows:

(10)

(11)

(12)

where:

f(Cs₁) - is a "step function", initially equal to zero, that assumes value equal to 1 for concentrations below a critical concentration, Cs₁, when the cellular death begins.

f(Cs₂) – is also a "step function", initially equal to zero, during action of catabolic repression. It assumes value equal to 1 when glicerol concentration falls bellow a critical value, Cs₂.

Maximal specific growth rate (m_max) and growth yield coefficient (Y_X/S) were determined by independent equations as shown bellow, utilizing the experimental data of exponential growth phase.

(13)

(14)

where the subscript "0" indicates the beginning of the exponential phase.

Death constant (k_d) of the equation 10 was also obtained by an independent equation, considering the final experimental data of the batch cultivation in peptone medium, when only cellular death occurred.

(15)

where the subscript "i" indicates the beginning of the death phase.

Regarding estimation of the other kinetic model parameters, a nonlinear regression method (Marquardt, 1963) was utilized together with DDASSL algorithm (Petzold, 1989), for the numerical resolution of the set of three differential equations representing the model.

As mentioned above, in Samprosoy 90NB medium, it was not possible to determine cell concentration (Cx) directly. It was simulated by the model using the glycerol consumption data, in Samprosoy 90NB, and considering growth parameters (m_max, K_S and Y_X/S) and death constant (k_d) obtained with peptone medium. Initial condition (Cx₀) was an additional parameter estimated by Marquardt’s procedure. The criterion for the best fitting and parameter optimization was the minimization of the sum of the squares of residuals (SSR).

RESULTS AND DISCUSSION

Kinetic Parameter Estimations and Model Adjustment

As described above, kinetic parameter of the growth rate equation (m_max and Y_X/S) and for cell death rate (k_d) were determined independently by equations 13, 14 and 15 from the experimental Cx and Cs data obtained during the cultivation with medium containing peptone as the nitrogen source (soluble medium). Figures 1 and 2 show equations 13 and 14 fitted to the experimental data and the values of m_max and Y_X/S obtained by linear regression with 95% confidence level. The value of k_d=0.038± 0.001 h^-1 was determined similarly by plotting ln(Cx/Cx_i) versus t-t_i (data not shown).

After m_max, Y_X/S and k_d determination, the remaining kinetic parameters of the proposed model, represented by equations 10 through 12, were evaluated. The parameters from equation 10, K_S and f(Cs₁), as well as the parameters from equation 12; b, f(Cs₂) and k_p; were determined by non-linear regression utilizing simultaneously Marquardt algorithm (Marquardt, 1963), for parameter optimization and the DDASSL method (Petzold, 1989) for the numerical resolution of the set of differential equations. Mention should be made here that the estimates were made sequentially, i.e., for the cultivation with peptone (soluble), as a first approach, the remaining parameters from equation 10 were calculated so that it provided the best fit between the calculated and experimental values of Cx and Cs. The time course of cell concentration, Cx, for the cultivation with Samprosoy medium (presence of insoluble substances) was estimated according to the procedure described in previous item, considering initial cell concentration, Cx₀ as a parameter to be determined by the optimization method.

Further the production phase parameters, shown in equation 12 (b, f(Cs₂) and k_p) were also estimated by non-linear regression utilizing the simulated values of Cx and Cs, along with the adjusted equations 10 and 11, as well as the experimental Cp data obtained during the cultivation. This procedure was applied to the cultivations in peptone and Samprosoy media. Table 1 presents the adjusted values of the parameters for the two cultivations carried out. Figures 3 and 4 illustrate the comparison between the calculated and experimental values of the variables.

Figures 1 and 2 show the accuracy of the m_max and Y_X/S determination by independent equations 13 and 14. It is worth mentioning that these values are close to that reported in reference literature (Atkinson and Mavituna, 1983; Yegneswaran et al., 1991). Regarding K_S, a rather high value was found (3,48 g.L^-1), however figure 3 shows excellent fitting of the proposed model to the experimental values, both for glycerol consumption (Cs) and cell growth (Cx). Classical Monod model considering cell death shows to be suitable to describe the kinetics of Streptomyces clavuligerus growth in glycerol. It is interesting to note that the proposed methodology of inserting a "turnkey", f(Cs₁), to trigger the cell death, showed that the critical concentration Cs₁ is very low, almost zero, indicating that the cell death process starts after substrate depletion. Regarding initial cell mass concentration (Cx₀), the value estimated for the cultivation with Samprosoy medium was very close to that commonly found in cultivation with peptone. This fact indicates that the proposed strategy succeeded in simulating the time course of cell mass concentration during the process where direct determination of cell mass was not possible.

Concerning equation 12, describing clavulanic acid production, it can be observed that the value of the constant b estimated for the culture utilizing Samprosoy as nitrogen source was much higher than that found when peptone was used. It demonstrates that Samprosoy 90NB is an excellent nitrogen source for clavulanic acid production by Streptomyces clavuligerus, in accordance with the work of Gouveia et al. (1999). Furthermore, it can be observed that the estimated values for the glycerol critical concentration, Cs₂, bellow that the clavulanic acid synthesis starts, were very similar for both cultivations, regardless of the nitrogen source utilized. However the values were rather high, 11.14 and 11.84 g.L^-1 respectively, indicating that probably repression by glycerol is not the regulatory mechanism for clavulanic acid biosynthesis, at least in the glycerol concentration range studied (Cs<16 g.L^-1). Probably an inducer of the enzymes responsible for clavulanic acid synthesis accumulates during the phase of rapid growth.

Stoichiometry

Yield coefficients were determined by linear regression of experimental data obtained from on-line and off-line measurements in cultivation utilizing peptone medium. Respiratory quotient (RQ) and oxygen yield coefficient () were determined by linear regression of the Equations 6 and 8 to the experimental data. Specific oxygen uptake rate () was obtained through gas balance method and the specific growth rate (m) was determined by the differential method (m =1/Cx× dCx/dt) utilizing the experimental data of Cx as function of the time for the cultivation in peptone medium. Figures 5 and 6 show the results obtained.

Maximal value of the specific uptake rate (@ 8 mmol.g^-1.h^-1) obtained when m»m_max=0.207 h^-1 is in agreement with the value obtained by Scott et al. (1988) during the Streptomyces clavuligerus cultivation in shake flasks, that reported a value of 7.8 mmol.g^-1.h^-1. According to Shuler and Kargi (1992), is typically 0.9 to 1.4 g.g^-1 for most yeasts and bacteria growing in glucose. The value obtained in the present work, =1.32 mol.mol^-1=0.855 g.g^-1, is also in agreement with literature.

By introducing in equation 6 the value of respiratory quotient (RQ), obtained experimentally as shown in Figure 5, it can be written that d=0.814×a and the system of equations 2 through 5 can be solved. For comparison, Table 2 presents experimental and calculated values of some important yield coefficients. Calculated values were obtained by solving the system of equations (stoichiometry) and the experimental values obtained from the Figures 2, 5 and 6, where it is observed that the simple stoichiometry (Equation 1) explains reasonably well the growth of Streptomyces clavuligerus in glycerol medium.

CONCLUSION

The proposed kinetic model describing the clavulanic acid production bioprocess explained quite well the initial hypothesis taken into account. Clavulanic acid production showed to be sensitive to the nature of nitrogen source. When Samprosoy 90NB, a soybean derivative, was utilized the production level was twice as higher as that utilizing peptone. For the cultivation in medium containing peptone, the experimental data enabled to propose a pseudo-stoichiometric equation for cell growth. However, no stoichiometric equation regarding clavulanic acid biosynthesis could be considered because the fraction of substrate being transformed into product could not be determined.

ACKNOWLEDGEMENTS

We would like to thank Financial support from CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) and FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo, Brazil), Proc. 98/12.271-7.

NOMENCLATURE

a stoichiometric coefficient b stoichiometric coefficient c stoichiometric coefficient Cp clavulanic acid concentration (g.L^-1) Cs glycerol concentration (g.L^-1) Cs₁ critical concentration of glycerol when the death starts (g.L^-1) Cs₂ critical concentration of glycerol when the production starts (g.L^-1) Cx cellular concentration (g.L^-1) Cx_o initial cellular concentration (g.L^-1) d stoichiometric coefficient DO dissolved oxygen (%) e stoichiometric coefficient f(Cs₁) step function (-) f(Cs₂) step function (-) k_d death constant (h^-1) k_p product degradation constant (h^-1) K_S saturation constant (g.L^-1) specific oxygen uptake rate (mmol.L^-1.h^-1) maximal specific oxygen uptake rate (mmol.L^-1.h^-1) r_i reaction rate of consumption or formation of component "i" (g.L^-1.h^-1) RQ respiratory quotient (mol.mol^-1) S substrate t time (h) t_i time when the cellular death begins (h) t_o time when the exponential growth phase starts (h) Y_i/j yield coefficient of product "i" in relate to the substrate "j" Yco₂ carbon dioxide molar fraction in outlet gas (-) Yo₂ oxygen molar fraction in outlet gas (-) X cells b specific rate of clavulanic acid production (mg.g^-1.h^-1) m specific growth rate (h^-1) m_max maximal specific growth rate (h^-1)

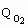
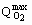
• Araujo, M.L.G.C., Giordano, R.C. and Hokka, C.O., Comparative studies on cephalosporin C production process with free and immobilized cells of Cephalosporium acremonium ATCC 48272, Chemical Engineering Science, 51, 2835 (1996).
• Atkinson, B. and Mavituna, F., Biochemical engineering and biotechnology handbook, Macmillan Publishers Ltd., UK (1983).
• Bailey, J.E. & Ollis, D.F. Biochemical Engineering Fundamentals, 2^nd ed., MacGraw-Hill Book Company, New York (1986).
• Belmar-Beiny, M.T. and Thomas, C.R., Morphology and clavulanic acid production of Streptomyces clavuligerus: Effect of stirrer speed in batch fermentations, Biotechnology and Bioengineering, 37, 456 (1991).
• Brass, J.M., Hoeks, F.W.J.M.M.; and Rohner, M., Applications of modelling techniques for the improvement of industrial bioprocess, Journal of Biotechnology, 59, 63 (1997).
• Butteworth, D., Clavulanic acid: Properties biosynthesis, and fermentation, In Biochemical of Industrial Antibiotics, ed. by Vandamme, E. J., New York, Marcel Dekker, 225 (1984).
• Cruz, A.J., Silva, A.S., Araujo, M.L.G.C., Giordano, R.C. and Hokka, C.O., Modeling and optimization of cephalosporin C production bioprocess in a fed-batch bioreactor with invert sugar as substrate, Chemical Engineering Science, 54, 3137 (1999).
• Demain, A.L., Overproduction of microbial metabolites and enzymes due to alteration of regulation, Advances in Biochemical Engineering, 1, 113 (1971).
• Garcia-Dominguez, M.; Martin, J.F. and Liras, P., Characterization of sugar uptake in wild-type Streptomyces clavuligerus, which is impaired in glucose uptake, and in a glucose-utilizing mutant, Journal of Bacteriology, 171, No 12, 6808 (1989).
• Gouveia, E.R.; Baptista-Neto, A.; Azevedo, A.G.; Badino, A.C. and Hokka, C.O., Improvement of clavulanic acid by Streptomyces clavuligerus in medium containing soybean derivative, World Journal of Microbiology and Biotechnology, 15, No. 5, 623 (1999).
• Gudi, R.D.; Shah, S.L. and Gray, M.R., Multirate state and parameter estimation in an antibiotic fermentation by delayed measurements, Biotechnology and Bioengineering, 44, 1271 (1994).
• Kadima, T.A.; Jensen, S.E. and Picard, M.A., Production of d-(L-a-aminoadipyl)-L-cysteinyl-d-valine by entrapped ACV-synthetase from Streptomyces clavuligerus, Journal of Industrial Microbiology, 14, 35 (1995).
• Lee, P.C. and Ho, C.C., Production of clavulanic acid and cephamycin C by Streptomyces clavuligerus in palm-oil medium, World Journal of Microbiology & Biotechnology, 12, 73 (1996).
• Marquardt, D.W., An algorithm for least-squares estimation of nonlinear parameters, J. Soc. Indust. Appl. Math, 11, 431 (1963).
• Mayer, A.F. and Deckwer, W.D., Simultaneous production and decomposition of clavulanic acid during Streptomyces clavuligerus cultivations, Appl. Microbiol Biotechnol., 45, 41 (1996).
• Petzold, L., Differential algebric system solver (DDASSL) subroutine, Computing and Mathematics Research Division, Lawrence Livermore National Laboratory, Livermore, California (1989).
• Pruess, D. L. and Kellett, M., Ro 22-5417, A new clavam antibiotic from Streptomyces clavuligerus, The Journal of Antibiotics, 36, No. 3, 208 (1983).
• Rius, N. and Demain, A.L., Regulation of lysine e -aminotransferase by carbon source and lack of control by phosphate in Streptomyces clavuligerus, Applied Microbiology and Biotechnology, 48, No. 6, 735 (1997).
• Romero, J.; Liras, P. and Martín, J.F., Utilization of ornithine and arginine as specific precursors of clavulanic acid. Applied and Environmental Microbiology, 52, 892 (1986).
• Scott, R.I.; Sladen, S.; Maidment, M.; Rashid, T.; Pratsis, C. and Perry, D., The effects of oxygen on b-lactam biosynthesis by alginate entrapped Streptomyces clavuligerus Journal of Chemical Technology and Biotechnology, 41,145 (1988).
• Shuler, M.L. and Kargi, F., Bioprocess engineering: basic concepts, Simon & Schuster Company, New Jersey (1992).
• Tarbuck, L.A.; Ng, M.H.; Leigh, J.R. and Tampion, J., Estimation of the progress of Streptomyces clavuligerus fermentations for improved on-line control of antibiotic production, In: Modeling and control of biotechnological process, Noordwijkerhout (1985).
• Yegneswaran, P.K.; Gray, M.R. and Thompson, B.G., Experimental simulation of dissolved fluctuations in large fermentors: Effect on Streptomyces clavuligerus, Biotechnology and Bioengineering, 38, 1203 (1991).
• Zhang, J. and Demain, A.L., "Regulation of ACV synthetase activity in the beta-lactam biosynthetic pathway by carbon source and their metabolites", Archives of Microbiology, 158, 364 (1992).

*

To whom correspondence should be addressed

Publication Dates

• Publication in this collection
  16 Mar 2001
• Date of issue
  Dec 2000

History

• Accepted
  18 Apr 2000
• Received
  03 Nov 1999