ANALYSIS OF TRICKLE BED AND PACKED BUBBLE COLUMN BIOREACTORS FOR COMBINED CARBON OXIDATION AND NITRIFICATION

ANALYSIS OF TRICKLE BED AND PACKED BUBBLE COLUMN BIOREACTORS FOR COMBINED CARBON OXIDATION AND NITRIFICATION

I.Iliuta^1*, S.C.Bildea², M.C.Iliuta³ and F.Larachi¹

¹Department of Chemical Engineering & CERPIC, Laval University, Québec, Canada G1K 7P4,

Fone: 1-418-656-2131 Ext. 4790, Fax: [phone], E-mail: [e-mail]

2University Politehnica of Bucharest, Department of Chemical Engineering,

Polizu 1, 78126 Bucharest, Romania

3University Politehnica of Bucharest, Department of Applied Physical Chemistry,

Polizu 1, 78126 Bucharest, Romania.

(Received: March 15, 2001 ; Accepted: November 21, 2001)

Abstract - Biological removal of nitrogen and carbon by combined nitrification-oxidation in gas-liquid trickle-bed reactors (TBRs) and packed bubble columns (PBCs) was analyzed theoretically using a transient two-dimensional model. The model describes TBR and PBC performances at steady state as well as their transient response to a pulse or step increase in inlet methanol and NH₄⁺-nitrogen concentrations. The hydrodynamic parameters were determined from residence time distribution measurements, using an imperfect pulse method for time-domain analysis of nonideal pulse tracer response. A transient diffusion model of the tracer in the porous particle coupled with the piston-dispersion-exchange model was used to interpret the residence time distribution curves obtained. Gas-liquid mass transfer parameters were determined by a stationary method based on the least-squares fit of the calculated concentration profiles in gas phase to the experimental values. Analysis of steady-state performances showed that under like operating conditions, the TBR outperforms the PBC in terms of conversions. A pulse change in the inlet methanol or NH₄⁺-nitrogen concentration causes a negligible transient change in the outlet methanol concentration and a negligible or high transient change in the outlet NH₄⁺-nitrogen concentration. A step change in the inlet methanol concentration causes the negligible transient change in the methanol outlet concentration and a relatively important transient change in the NH₄⁺-nitrogen outlet concentration. A step increase in the NH₄⁺-nitrogen inlet concentration induces a drastic transient change in the NH₄⁺-nitrogen outlet concentration but a negligible transient change in the methanol outlet concentration.

Keywords: carbon oxidation, nitrification, trickle bed reactors, packed bed columns, modelling.

INTRODUCTION

Conventional gas-liquid fixed bed bioreactors using immobilized biocatalysts have become increasingly popular in hosting a broad spectrum of biochemical processes, such as in fermentation and in wastewater treatment.

Numerous theoretical studies on the behavior of immobilized enzyme (or cell) fixed bed bioreactor performance have been reported in the literature. For instance, Kobayashi and Moo-Young (1971) evaluated the impact of axial dispersion and external mass transfer resistance on conversion in fixed beds and compared the size of reactors needed to obtain a given conversion for different degrees of backmixing. Vieth et al. (1976) provided an extensive review on the different aspects of modelling and design of immobilized enzyme reactors. Godia et al. (1987) examined the performance of a fixed bed bioreactor with yeast immobilized in carrageenan gel beads, taking into account the external and internal mass transfer. Papathanasiou et al. (1988) examined the transient behavior of immobilized fixed bed bioreactors. Hassan and Beg(1987) and Atiqullah et al.(1990) analyzed the performance characteristics of fixed bed biofilm wastewater treaters using various reaction kinetics with and without substrate inhibition. Hartmans and Tramper (1991) modelled the trickle bed bioreactors as a series of ideal continuous-stirred tank reactors and calculated their number and size to give the desired conversion. Diks and Ottengraf (1991) and Heckmat and Vortmeyer (1994) modelled first- and zero-order bioreactions inside the biofilm using the biocatalytic effectiveness factor approach. Ockeloen et al. (1996) developed an extension to Diks and Ottengraf's model by including Monod kinetics. In the dynamic models of Deshusses et al. (1995), Shareefdeen and Baltzis (1995) and Zarook et al. (1997), biomass growth was not considered and a constant biofilm thickness was assumed. Unlike these models, the dynamic trickle bed biofilter model presented by Allonso et al. (1997) includes biomass growth and a variable biofilm thickness along the reactor. Iliuta(1997) analyzed TBR and PBC performance during phenol biodegradation. Recently, fixed bed bioreactors have been modelled under shock loadings of feed concentration and temperature when simultaneous organic oxidation and nitrification reactions are occurring (Beg et al., 1995, 1996, 1997). Okkerse et al. (1999) developed a dynamic model that describes the degradation of volatile acidifying pollutants as well as the biomass accumulation in trickle bed biofilters for waste gas purification. A trickle bed bioreactor model was developed by Lobo et al. (1999) and used to show how the bioreactor size depends on the rate-limiting step, the absorption factor, the substrate fractional conversion and the gas-liquid contacting pattern. Xiu et al. (2001) presented a mathematical model for immobilized enzyme-catalyzed kinetic resolution of racemate in a fixed bed bioreactor in which the enzyme-catalyzed reaction was coupled with intraparticle diffusion, external mass transfer and axial dispersion.

The present paper's aim is to examine the steady-state performances of TBR/PBC biofilm reactors as well as their dynamic response to a pulse or step increase in inlet concentration. Simultaneous carbon oxidation and nitrification were chosen as test reactions for a typical wastewater loaded with oxygen-demanding carbon- and nitrogen-containing compounds. Methanol (CH₃OH) and ammonium ions (NH₄⁺) were the model reactants. Nitrogen is dealt with via the so-called nitrification process (Beg et al., 1997) by transforming ammonia into more oxidized nitrites or nitrates, which ultimately can be converted into molecular nitrogen by a subsequent denitrification.

The combined carbon oxidation and nitrification involve simultaneous diffusion and consumption of methanol, NH₄⁺-nitrogen and oxygen within the biofilm. Thus, a transient bioparticle model is proposed which accounts for (i) external mass transfer resistance between liquid bulk and bioparticles and (ii) simultaneous diffusion and reaction of methanol, NH₄⁺-nitrogen and oxygen inside the bioparticles.

Gas-liquid mass transfer parameters for air/carbon dioxide/water systems are evaluated by means of the axial dispersion model and least-squares fit of the calculated CO₂ concentration profiles in the gas phase versus experimental values. The hydrodynamic parameters are determined in separate studies from residence time distribution measurements, using an imperfect pulse method and time-domain analysis of nonideal pulse tracer responses.

MATHEMATICAL MODEL

A mathematical model including the major hydrodynamic and mass transport parameters of gas-liquid cocurrent packed-bed biofilm reactors is developed to simulate the concomittant bio-oxidation of organic carbon and bionitrification of ammonium-nitrogen from a methanol-ammonium containing model wastewater. Air and the wastewater are fed cocurrently downwards into the trickle bed reactor configuration and cocurrently upwards in the packed-bubble column configuration. The representational flow structure of the gas-liquid system on the pellet scale is sketched in Figure 1 for both configurations. It consists of the following contacting regions:

a) The dry biofilm directly in contact with the flowing air. This region, whose corresponding areal fraction is 1-· h_e, occurs only for the cocurrent downflow configuration at low liquid irrigation flow rates. For the cocurrent upflow configuration, the biofilm is completely wetted by the ascending liquid so that h_e is equal to one regardless of the prevailing fluid flow rates;

b) The wet biofilm in contact with the static liquid holdup, e_L,st; this particularly occurs at the contact points of the pellets, where the static liquid menisci form preferentially;

c) The wet biofilm in contact with the dynamic liquid holdup, · e_L,d;

d) The static-to-dynamic liquid holdups contact interface.

In setting up the model, the following basic assumptions are considered:

a) The liquid bulk flow is described by the axial dispersion model, while the gas flow is assumed to be that of a plug flow.

b) The transfer of gaseous oxygen takes place across the liquid dynamic-gas interface and the dry biofilm-gas interface (represented by the arrows in Figure 1);

c) The transport of organic carbon, ammonium-nitrogen and oxygen takes place from the dynamic and static liquid to the biofilm surface;

d) There is simultaneous diffusion and reaction of organic carbon, ammonium-nitrogen and oxygen within the biofilm;

e) The model is based on the unsteady-state mass balances of oxygen, methanol and ammonium-nitrogen in the gas and liquid bulks and bioparticles.

The oxygen mass balance in the gas phase, assuming plug flow, yields

Assuming a piston-dispersion-exchange pattern in the liquid, the transient methanol, NH₄⁺-nitrogen and oxygen concentrations in the dynamic and stagnant zones of the liquid phase are given by

where j = methanol, NH₄⁺-nitrogen and oxygen

In the case of two-phase downflow, the external wetting efficiency was estimated using the phenomenological model developed by Iliuta et al. (1999a). For two-phase upflow, the solids were assumed to be fully wet externally.

Initial and boundary conditions for eqs (1 - 5) are as follows:

@ t = 0 :

@ z = 0 :

@ z = H :

where the subscript ss stands for steady state.

In the present model for simultaneous organic oxidation and nitrification, three substrates (organic carbon, NH₄⁺-nitrogen and oxygen) are considered to be simultaneously transported from the dynamic liquid phase through the external film onto the surface of the biofilm, followed by diffusion and reaction within the biofilm. Formulation of the equations describing the simultaneous transport and reaction of methanol, NH₄⁺-nitrogen and oxygen within the biofilm are based on the following assumptions:

1) the biofilm is homogeneous with regard to biofilm density and operates at pseudo-steady state so that the biofilm properties such as biofilm thickness and density are constant (Beg et al., 1997; Diks and Ottengraf, 1991);

2) the microorganisms are uniformly distributed over the surface of solid particles, forming a uniform biofilm. The bioparticles are assumed to be spherical in shape. Although there exists a size distribution, the size of these bioparticles can be well represented by their average diameter (Beg et al., 1997; Tang et al., 1987; Tang and Fan, 1987; Wisecarver and Fan, 1989);

3) the growth-limiting nutrients are methanol, NH₄⁺-nitrogen and oxygen; all other nutrients are present in excess;

4) there is no physiological change in the microbes when immobilized onto the solid support surface, so the kinetic expression of cell growth and substrate consumption obtained from a suspended cell culture can be applied equally well to the immobilized system (Beg et al., 1997; Tang et al., 1987; Tang and Fan, 1987);

5) the effects of outward diffusion of the metabolic products are negligible;

6) the reaction terms consist of interactive Michaelis-Menten kinetics modified for two-substrate systems (Watanabe et al., 1992). The stoichiometric relationships are

where

1) the effects of depletion of methanol, NH₄⁺-nitrogen and oxygen due to adsorption in the biofilm are negligible;

2) the diffusivities of methanol, NH₄⁺-nitrogen and oxygen in the biofilm are assumed constant and independent of the radial position in the biofilm and of the concentrations of methanol, NH₄⁺-nitrogen and oxygen for a given biofilm thickness.

According to the above assumptions, the simultaneous transport and consumption of methanol, NH₄⁺-nitrogen and oxygen within the biofilm can be given by

The corresponding boundary and initial conditions for eqs. (14, 15, and 16) are given as

@ r = r_p:

@ r = r_f:

@ t = 0:

where c_c,ss (r), c_NH,ss (r) and C_O,ss (r) are the concentration profiles of methanol, NH₄⁺-nitrogen and oxygen within the biofilm at steady state.

The partial differential equations of the model are coupled and nonlinear, involving both time and space coordinates, and are subject to nonhomogeneous boundary conditions. Moreover, for the system to be solved, constitutive relationships are needed for the hydrodynamic parameters, mass interchange coefficients and reaction rate equation.

Gear's method is used to solve the system of two-dimensional parabolic partial differential equations. This method efficiently handles difficulties associated with solution of stiff and nonstiff nonlinear parabolic partial differential equations. A spatial discretization within the biofilm is generated by the method of orthogonal collocation (Finlayson, 1972; Villadsen and Michelsen, 1978) (the number of collocation points specified for the biofilm is 5). The reactor equations are discretized using the standard centered finite difference scheme (a spaced mesh with 20 points is used).

EVALUATION OF MODEL PARAMETERS

The performance of the bioreactor was simulated for 0.003 m solid particles as the support for cell immobilization. The characteristics of the solid particles and the fixed bed and the operating conditions are given in Table 1.

During the past few years, we have reported four studies on the hydrodynamic characteristics and gas-liquid mass transfer parameters of two-phase flow through fixed beds with porous particles. For two-phase downflow, the hydrodynamics was studied for superficial liquid velocities from 0.005 to 0.017 m/s (Iliuta et al., 1996a). In the case of two-phase upflow, the range of superficial liquid velocities studied was from 0.0021 to 0.0135 m/s (Iliuta et al., 1996b). The gas-liquid mass transfer measurements were carried out for superficial liquid velocities from 0.0028 to 0.0135 m/s (Iliuta, 1996; Iliuta and Thyrion, 1997). In addition, in this work, the hydrodynamics and the gas-liquid mass transfer were studied at low superficial liquid velocities (v_SL < 0.002 m/s). The laboratory-scale fixed bed reactor was a glass column with an inside diameter of 0.051 m, packed with porous particles (the packing characteristics are listed in Table 2). The packed height was 0.92 m. The description of the apparatus employed in this study was given previously (Iliuta et al., 1997).

The dynamic liquid holdup was measured at different flow rates of the phases by measuring the volume of the liquid drained after the inflow was stopped. The static liquid holdup was obtained from the difference between the external void volume of the bed and that of the liquid drained after the reactor had been totally flooded with liquid. During draining, the reactor was fed from the top with the same gas flow rate as that in the two-phase flow runs.

All liquid residence time distribution (RTD) measurements were conducted at room temperature and near atmospheric pressure. The tracer technique was chosen for determination of the needed liquid flow parameters. The change in electrical conductivity of a KCl tracer was simultaneously measured downstream/upstream of the injection point at both the top and the bottom of the bed using computer-monitored conductivity sensors. A brief tracer pulse was syringe-injected into the liquid inlet pipe. The signals of the sensors were amplified and transmitted to a computer by a data acquisition system. A residence time distribution model to describe the liquid flow in a fixed bed reactor packed with porous particles and operated under both partially and fully wetted conditions was proposed based on a simple representation of the liquid flow structure (Iliuta et al. 1999b). This model assumes that the external liquid stream is divided into two zones: a dynamic zone in which the liquid flows through the bed as a piston flow with axial dispersion and a stagnant zone in direct contact with the dynamic zone and the solid particle. The dynamic evolution of the tracer concentration in the particles was described in terms of diffusion phenomena. The tracer mass balance equations and boundary and initial conditions are the following

The model thus formulated involves three tuning parameters namely, the Péclet number (Pe), the Biot number (Bi_m,st) corresponding to static liquid-solid mass transfer and the number of transfer units (N) characterizing mass transfer between dynamic and static external liquid holdups. The remaining parameters are the static (e_L,st) and dynamic (e_L,d) liquid holdups, total (h_e), static fraction (h_st) and dynamic fraction (h_d) wetting efficiencies, Biot number (Bi_m,d) corresponding to dynamic liquid-solid mass transfer, and effective diffusivity (D^eff).

Pe, N and Bi_m,st were simultaneously identified from nonideal pulse tracer response data in time domain using a least-squares minimization between normalized experimental and model- predicted output responses. The partial differential equations (Eqs. 21-23) were reduced by orthogonal collocation (Finlayson, 1972; Villadsen and Michelsen, 1978) to ordinary differentialequations which were solved using a fourth-order Runge-Kutta method. Total wetting efficiency was estimated by the phenomenological model developed by Iliuta et al. (1999a). As shown in Figure 1, total wetting efficiency, h_e, splits into wetted fractions contributed by the dynamic (h_d) and static (h_st) liquid zones (h_e = h_d + h_st). These were estimated using the Rajashekharam et al. (1998) approximation. The effective diffusivities were taken from our earlier work (Iliuta et al., 1996b). The dynamic liquid-solid mass transfer coefficient was estimated with correlations from the literature: an average value was computed using the Specchia et al.(1976), the Goto and Smith (1975) and the Satterfield et al. (1978) correlations for two-phase downflow and the Specchia et al. (1978), the Delaunay et al. (1980) and the Mochizuki (1981) correlations for two-phase upflow.

The mass transfer experiments permitted evaluation of the volumetric liquid-side mass transfer coefficient using physical absorption of 5 to 10 % (v/v) CO₂ in to water. The mass transfer parameters were determined by a stationary method based on the least-squares fit of the calculated CO₂ concentration profiles in gas phase to the experimental values. Carbon dioxide concentration in the gas phase at the bed entrance and exit and at five other different intermediate heights of the packed bed was measured after phase separation by means of a gas chromatograph (Intersmat IGC 120ML). A one-dimensional model taking into account only the liquid mass transfer resistance was used to estimate the volumetric liquid-side mass transfer coefficient (Iliuta, 1996).

The liquid-solid mass transfer coefficients for methanol, NH₄⁺-nitrogen and oxygen were calculated using the same correlations as those used for determination of the hydrodynamic parameters.

The hydrodynamic and mass transfer parameters used in the simulations are listed in Tables 3 and 4. The diffusivities of methanol and oxygen within the biofilm were calculated using the correlation developed by Tang et al.(1987):

The kinetic constants describing the growth of the microbial culture were determined by Watanabe et al.(1992) (also see Table 5).

RESULTS AND DISCUSSION

Steady-State Behavior

The following analysis focuses on the description of the conversion of methanol and NH₄⁺-nitrogen in fixed bed bioreactors with two-phase upflow and downflow. To accomplish this task, several numerical experiments, covering a wide range of methanol and NH₄⁺-nitrogen concentrations, were performed.

Figure 2 shows the predicted methanol conversion plotted as a function of the inlet methanol concentration. A comparison of the performance of the two-phase downflow fixed bed bioreactor operating under the same conditions those as for the two-phase upflow bioreactor shows that the values for methanol conversion are very close, even if the gas-liquid mass transfer rate is much higher in the case of two-phase upflow. The oxygen gas-solid direct mass transfer (at low liquid velocities the bioparticle is partially wetted) and the low axial dispersion of the liquid phase in the case of two-phase downflow seem to offer a reasonable explanation of this behavior.

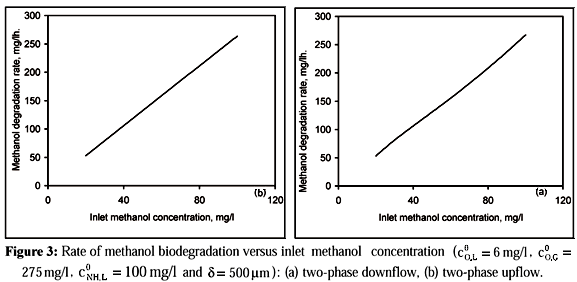
Figure 3 shows the rate of methanol biodegradation predicted from the model as a function of inlet methanol concentration. It can be seen that the rate of carbon oxidation in downflow is close to that in upflow and rises nearly linearly with inlet methanol concentration. This implies that the carbon oxidation is controlled by substrate concentration rather than by oxygen concentration.

Figure 4 shows the predicted NH₄⁺-nitrogen conversion plotted as a function of inlet methanol and NH₄⁺-nitrogen concentrations under the same conditions. This comparison of the performance of downflow versus upflow indicates that the downflow configuration yields much higher NH₄⁺-nitrogen conversions (except at high inlet methanol concentrations), even if the gas-liquid mass transfer rate is higher in the upflow configuration. Similarly to the aforementioned case of the carbon oxidation process, the oxygen gas-solid direct mass transfer and a lower liquid axial dispersion in downflow appear to be the major cause of this result. The closed performance of two-phase downflow and upflow configurations at high methanol concentrations is the result of the balance between oxygen consumption in the carbon oxidation and the nitrification processes.

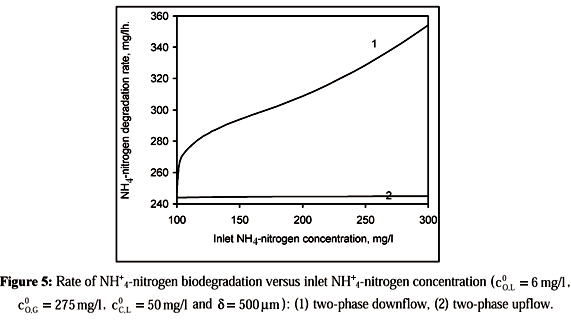
Figure 5 shows the NH₄⁺-nitrogen biodegradation rate as a function of inlet NH₄⁺-nitrogen concentration for two-phase downflow and upflow. In the downflow case, it can be seen that the NH₄⁺-nitrogen biodegradation rate increases with the increasing inlet NH₄⁺-nitrogen concentration. In the upflow case, an increase in the NH₄⁺-nitrogen inlet concentration causes a negligible change in the biodegradation rate.

The concentration axial profiles for methanol, NH₄⁺-nitrogen and oxygen at steady state are shown in Figure 6. In upflow, methanol (Figure 6a) and NH₄⁺-nitrogen (Figure 6b) concentrations at the reactor entrance are much lower than their feed (or inlet) concentrations, which is indicative of important backmixing effects in the liquid phase, i.e., high liquid axial dispersion coefficients. Moreover, in the first sections of the bioreactors, methanol and NH₄⁺-nitrogen concentrations are higher in downflow than in upflow. The higher gas-liquid mass transfer of oxygen in upflow could be the explanation for this behavior. Thus, in the first section of the bioreactor, the dissolved oxygen concentration is higher in upflow, as shown in Figure 6c. The results show that the organic substrate is consumed very rapidly near the inlet of the bioreactor, while most of the NH₄⁺-nitrogen is converted in the central region of the reactor.

Figure 7 demonstrates typical concentration profiles throughout the biofilm at various dimensionless axial distances for two-phase upflow. Near the inlet of the reactor, the dissolved oxygen concentration decreases rapidly to zero within the biofilm so a significant portion of the biomass is severely oxygen limited. Thus, the biodegradation rates of methanol and NH₄⁺-nitrogen are limited by an inadequate supply of oxygen. Near the reactor outlet, oxygen limitation is not as severe. The rate of gas-liquid mass transfer of oxygen is sufficient to sustain the biological reactions.

Dynamic Behavior

(a) Transient Response to Pulse Increase in Inlet Methanol and NH₄⁺-Nitrogen Concentrations

Model simulations were conducted to describe both relatively low- and large-pulse experiments.

Figure 8 is shows the pulse increase in the influent methanol concentration. A pulse change (from 50 to 100 or 300 mg/l) causes an insignificant transient change in the outlet methanol concentration (Figure 8a). The increase in methanol concentration is accompanied by a substantial increase in the methanol biodegradation rate. At the higher biodegradation rates, methanol is rapidly consumed. Its concentration falls to its original level; there is not enough substrate to sustain the high biodegradation rate and thus the reaction rate returns to its original value. This dynamic behavior is intuitively consistent with the concept that the biofilm is substrate-limited. Also, the pulse change in the inlet methanol concentration causes an unimportant transient change in the outlet NH₄⁺-nitrogen concentration (Figure 8b). This is because the change in the inlet methanol concentration induces an insignificant transient change in the oxygen concentration. It may be concluded that a pulse increase in the influent methanol concentration will have a negligible effect on the performance of fixed bed bioreactor.

Figure 9 shows the pulse increase in the influent NH₄⁺-nitrogen concentration. A pulse change from 100 to 300 or 500 mg/lleads to a negligible transient change in the outlet methanol concentration (Figure 9a) because this change induces an unimportant transient change in the oxygen concentration. When imposing a large-pulse change in the inlet NH₄⁺-nitrogen concentration, the system shows a relatively high transient change in the outlet NH₄⁺-nitrogen concentration (Figure 9b) and therefore requires more time to restore its steady-state operation.

Nitrification achieves steady state (when imposing a pulse increase in the influent NH₄⁺-nitrogen concentration) at a much slower rate than carbon oxidation (when imposing a pulse increase in the influent methanol concentration), which can be attributed to the difference in reaction rates.

(b) Transient Response to Step Increase in Inlet Methanol and NH₄⁺-Nitrogen Concentrations

The system response to a step increase in influent methanol concentration is shown in Figure 10. When imposing 50% or 100% step changes in inlet methanol concentration, the outlet methanol concentration remains low but at levels proportional to the amplification factor in the inlet composition (Figure 10a). In this case, the system is restored relatively quickly to its steady state. The increase in methanol concentration is accompanied by a substantial increase in the methanol biodegradation rate, and methanol is rapidly consumed. A 100% step increase in the inlet methanol concentration shows a relatively high transient change in the outlet NH₄⁺-nitrogen concentration (Figure 10b). In this case, the system requires a longer time to regain a new steady state.

The response of the system to a step increase in the influent NH₄⁺-nitrogen concentration is shown in Figure 11. The outlet methanol concentration is unaffected (Figure 11a), but a step increase in the inlet NH₄⁺-nitrogen concentration results in a drastic transient change in the outlet NH₄⁺-nitrogen concentration, such as that shown in Figure 11b. This dynamic behavior is intuitively consistent with the concept that the biofilm is oxygen limited.

CONCLUSION

Numerical simulations allowed analysis of the performance of two-phase cocurrent upflow and downflow fixed bed biofilm reactors under multisubstrate limitations involving simultaneous carbon oxidation and nitrification reactions.

Comparison of the performance of upflow and downflow configurations for simultaneous carbon oxidation and nitrification processes showed that under identical operating conditions downflow outperforms upflow in terms of conversion.

A pulse change in the inlet methanol concentration causes small transient changes in the outlet methanol and NH₄⁺-nitrogen concentrations. A large-pulse change in the inlet NH₄⁺-nitrogen concentration induces relatively important transient changes in the NH₄⁺-nitrogen outlet concentration but negligible transient changes in the methanol outlet concentration.

A step change in the inlet methanol concentration causes a negligible transient change in the methanol outlet concentration and a relatively important transient change in the NH₄⁺-nitrogen outlet concentration. A step increase in the NH₄⁺-nitrogen inlet concentration induces a drastic transient change in the NH₄⁺-nitrogen outlet concentration but a negligible transient change in the methanol outlet concentration.

NOMENCLATURE

a_c specific area of the packing (surface of the particles/volume of the bed) (m² m^-3) A_C

oxygen requirement in organic oxidation

A_NH

oxygen requirement in nitrification

Bi_m

Biot number, Bi_m,d = k_s,dr_{p /} D^eff, Bi_m,st = k_s,str_p/D^eff

c₀

moles tracer injected / (liquid flow rate . mean residence time of input response) (kmol m^-3)

c_d

tracer concentration in the dynamic zone of the liquid (kmol m^-3)

C_d

dimensionless tracer concentration in the dynamic zone of liquid (C_d = C_d / c₀)

c_j concentration of component j (j = O, C, NH) (kg m^-3) inlet concentration of component j (kg m^-3) c_p tracer concentration in the solid particle (kmol m^-3) C_p dimensionless tracer concentration in the solid particle (C_p=c_p/c₀) c_st tracer concentration in the stagnant zone of the liquid (kmol m^-3) C_st

dimensionless tracer concentration in the stagnant zone (C_st = c_st / c₀)

D_j molecular diffusivity of component j (m² s^-1) D^eff effective diffusivity of the tracer (m² s^-1) effective diffusivity of the component j (m² s^-1) D_L liquid axial dispersion coefficient (m² s^-1) d_p diameter of a sphere having the same external surface area as the particle (m) H bed height (m) ka

mass transfer coefficient between dynamic and stagnant liquid zones (s^-1)

K_C Michaelis constant for organic substrate (methanol) k_La volumetric liquid-side mass transfer coefficient (s^-1) K_NH Michaelis constant for ammonium-nitrogen K_OC Michaelis constant for oxygen in organic oxidation K_ONH Michaelis constant for oxygen in nitrification k_s,d liquid (dynamic)-solid mass transfer coefficient (m s^-1) k_s,st liquid (static)-solid mass transfer coefficient (m s^-1) m Henry constant N

number of transfer units (N=ka H/v_SL) (dimensionless)

Pe Péclet number (Pe=H_SL / D_L e _L,d) (dimensionless) r radial position within biofilm (m) r_f radius of the bioparticle (m) r_p radius of the support particle (m) R_c carbon oxidation rate (kg m^-3 s^-1) R_NH nitrification rate (kg m^-3 s^-1) R_O oxygen consumption rate (kg m^-3 s^-1) S cross-section area of the catalyst bed, m² t time (s) t_in mean residence time of the input response (s) v_SG superficial velocity of the gas (m s^-1) v_SL superficial velocity of the liquid (m s^-1) x dimensionless axial coordinate (x = z/H) X_C concentration of heterotrophs in the biofilm (kg m^-3) X_NH concentration of nitrifiers in the biofilm (kg m^-3) Y_C yield of biomass (carbon oxidation process) Y_NH yield of biomass (nitrification process) z axial coordinate (m)

Greek Letters

x dimensionless radial coordinate (x = r/r_p) d biofilm thickness (m) e bed porosity e_f porosity of biofilm e_G gas holdup e_L liquid holdup e_p particle porosity e_s solid holdup h_d dynamic wetted fraction of biocatalyst h_e total wetted fraction h_st static wetted fraction of biocatalyst m specific growth rate (s^-1) m_C,max maximum specific growth rate of heterotrophs (s^-1) m_NH,max maximum specific growth rate of nitrifiers (s^-1) q dimensionless time

Subscripts

C organic substrate d liquid dynamic zone f biofilm G gas int internal NH NH⁺₄-nitrogen L liquid O oxygen p solid particle s particle surface ss steady state st liquid stagnant zone w water

• Allonso, C.; Suidan, M. T.; Sorial, G. A.; Smith, F. L.; Biswas, P.; Smith, P. J. and Brenner, R. C., Gas Treatment in Trickle-Bed Biofilters: How Much Biomass Is Enough?, Biotechnol. Bioeng., 54, 583 (1997).
• Atiqullah, M.; Hassan, M. M. and Beg, S. A., Modeling of Axial and Recycle Backmixing Effects in a Biological Packed Bed Loop Reactor, Chem. Eng. J., 44, B15 (1990).
• Beg, S. A.; Hassan, M. M. and Chaudhry, A. S., Multi-Substrate Analysis of Carbon Oxidation and Nitrification in an Upflow Packed Bed Biofilm Reactor, Int. J. Environ. Stud., 49, 31 (1995).
• Beg, S. A.; Hassan, M. M. and Chaudhry, A. S., Effect of Sinusoidal Variation of Feed Concentration and Temperature on the Performance of a Packed-Bed Biological Reactor, Chem. Eng. Technol., 19, 43 (1996).
• Beg, S. A.; Hassan, M. M. and Chaudhry, A. S., Effect of Fasting Condition on Multi-substrate Carbon Oxidation and Nitrification System in an Upflow Packed-Bed Biofilm Reactor, Chem. Eng. Technol., 20, 162 (1997).
• Delaunay, G.; Storck, A.; Laurent, A. and Charpentier, J. C., Electrochemical Study of Liquid-Solid Mass Transfer in Packed Beds with Upward Cocurrent Gas-Liquid Flow, Ind. Eng. Chem. Process Des. Dev., 19, 514 (1980).
• Deshusses, M. A.; Hamer, G. and Dunn, I. J., Behavior of Biofilters for Waste Air Biotreatment. Experimental Evaluation of a Dynamic Model, Environ. Sci. Technol., 29, 1059 (1995).
• Diks, R. M. M. and Ottengraf, S. P. P., Verification Studies of a Simplified Model for the Removal of Dichloromethane from Waste Gases Using a Biological Trickling Filter (Part I), Bioproc. Eng., 6, 93 (1991).
• Finlayson, B. A., The Method of Weighted Residuals and Variational Principle, Academic Press, New York, 1972.
• Godia, F.; Casas, C. and Sola, C., Mathematical Modelization of a Packed-Bed Reactor Performance with Immobilized Yeast for Ethanol Fermentation, Biotechnol. Bioeng., 30, 836 (1987).
• Goto, S. and Smith, J. M., Trickle-Bed Reactors Performance, Part -1: Holdup and Mass Transfer Effects, AIChE J., 21, 706 (1975).
• Hartmans, S. and Tramper, J., Dichloromethane Removal from Waste Gases with a Trickle Bed Bioreactor, Bioproc. Eng., 6, 83 (1991).
• Hassan, M. M. and Beg, S. A., Theoretical Analysis of a Packed-Bed Biological Reactor for Various Reaction Kinetics, Chem. Eng. J., 36, B15 (1987).
• Heckmat, D. and Vortmeyer, D., Modelling of Biodegradation Processes in Trickle Bed Bioreactors, Chem. Eng. Sci., 49, 4327 (1994).
• Iliuta, I., Hydrodynamics and Mass Transfer in Multiphase Fixed Bed Reactors, Ph. D. diss., Université Catholique de Louvain, 1996.
• Iliuta, I.; Thyrion, F. C. and Muntean, O., Residence Time Distribution of the Liquid in Gas - Liquid Concurrent Downflow Fixed-Bed Reactors: Gas/Newtonian and Non-Newtonian Liquid Systems, Can. J. Chem. Eng., 74, 783 (1996a).
• Iliuta, I.; Thyrion, F. C.; Muntean, O. and Giot, M., Residence Time Distribution of the Liquid in Gas-Liquid Cocurrent Upflow Fixed-Beds Reactors, Chem. Eng. Sci. 51, 4579 (1996b).
• Iliuta, I., Performance of Fixed Bed Reactors with Two-Phase Upflow and Downflow, J. Chem. Techn. and Biotechn., 68, 47 (1997).
• Iliuta, I.; Thyrion, F. C.; Bolle, L. and Giot, M., Comparison of Hydrodynamic Parameters for Countercurrent and Cocurrent Flow through Packed Beds, Chem. Eng. Technol., 20, 171 (1997).
• Iliuta, I. and Thyrion, F. C., Gas-Liquid Mass Transfer in Fixed Beds with Two-Phase Cocurrent Downflow: Gas/Newtonian and Non-Newtonian Liquid Systems, Chem. Eng. Technol. 20, 538 (1997).
• Iliuta, I.; Larachi, F. and Grandjean, B. P. A., Catalyst Wetting in Trickle-Bed Reactors: A Phenomeological Model, Chem. Eng. Res. Design (Trans IChemE part A), 77, 759 (1999a).
• Iliuta, I.; Larachi, F. and Grandjean, B. P. A., Residence Time, Mass Transfer and Back-Mixing of the Liquid in Trickle Flow Reactors Containing Porous Particles, Chem. Eng. Sci., 54, 4099 (1999b).
• Kobayashi, T. and Moo-Young, M., Backmixing and Mass Transfer in the Design of Immobilized Enzyme Reactors, Biotechnol. Bioeng., 13, 893 (1971).
• Lobo, R.; Revah, S. and Viveros-Garcia, T., An Analysis of a Trickle-Bed Bioreactor: Carbon Disulfide Removal, Biotechnol. and Bioeng., 63, 98 (1999).
• Mochizuki, S., Particle Mass Transfer and Liquid Hold-up in Packed Beds with Upward Cocurrent Gas-Liquid Flow, Chem. Eng. Sci., 36, 213 (1981).
• Ockeloen, H. F.; Overcamp, T. J. and Grady Jr, C. P.L., Engineering Model for Fixed-Film Bioscrubbers, J. Environ. Eng., 122, 191 (1996).
• Okkerse, W. J. H.; Ottengraf, S. P. P.; Osinga-Kuipers, B. and Okkerse, M., Biomass Accumulation and Clogging in Biotrickling Filters for Waste Gas Treatment. Evaluation of a Dynamic Model Using Dichloromethane as a Model Pollutant, Biotechnol. Bioeng., 63, 418 (1999).
• Papathanasiou, T. D.; Kalogerakis, N. and Behie, L. A., Dynamic Modeling of Mass Transfer Phenomena with Chemical Reaction in Immobilized Enzyme Bioreactors, Chem. Eng. Sci., 43, 1489 (1988).
• Rajashekharam, M. V.; Jaganathan, R. and Chaudhari, V., A Trickle-Bed Reactor Model for Hydrogenation of 2, 4 Dinitrotoluene: Experimental Verification, Chem. Eng. Sci. 53, 787 (1998).
• Satterfield, C. N.; van Eek, M. W. and Bliss, G. S., Liquid-Solid Mass Transfer in Packed Beds with Downward Concurrent Gas-Liquid Flow, AIChE J., 24, 709 (1978).
• Shareefdeen, Z. and Baltzis, B. C., Biofiltration of Toluene Vapor under Steady-State and Transient Conditions: Theory and Experimental Results, Chem. Eng. Sci., 49, 4347 (1995).
• Specchia, V.; Baldi, G. and Gianetto, A., Solid-Liquid Mass Transfer in Trickle Bed Reactors, Proc. 4th Int./6th Eur. Symp. Chem. React. Eng., 7, 390 (1976).
• Specchia, V.; Baldi, G. and Gianetto, A., Solid-Liquid Mass Transfer in Cocurrent Two-Phase Flow through Packed Beds, Ind. Eng. Chem. Process Des. Dev., 17, 362 (1978).
• Tang, W. T.; Wisecarver, K. and Fan, L. S., Dynamics of a Draft Tube Gas-Liquid-Solid Fluidized Bed Bioreactor for Phenol Degradation, Chem. Eng. Sci., 42, 2123 (1987).
• Tang, W. T. and Fan, L. S., Steady State Phenol Degradation in a Draft-Tube, Gas-Liquid-Solid Fluidized-Bed Reactor, AIChE J., 33, 239 (1987).
• Vieth, W. R.; Venkatasubramanian, K.; Constandinides, A. and Davidson, B., Design and Analysis of Immobilized Enzyme Flow Reactors, Appl. Biochem. Bioeng., 1, 221 (1976).
• Villadsen, J. and Michelsen, M. L., Solution of Differential Equation Models by Polynomial Approximation, Prentice Hall, New York, 1978.
• Watanabe, Y.; Masuda, S. and Ishiguro, M., Simultaneous nitrification and denitrification in micro-aerobic biofilms. Wat. Sci. Tech., 26, 511 (1992).
• Wisecarver, K. and Fan, L. S., Biological Phenol Degradation in a Gas-Liquid-Solid Fluidized Bed Reactor, Biotechnol. Bioeng., 33, 1029 (1989).
• Xiu, G-H.; Jiang, L. and Li, P., Mass-Transfer Limitation for Immobilized Enzymes-Catalyzed Kinetic Resolution of Racemate in a Fixed-Bed Reactor, Biotechnol. Bioeng., 74, 29 (2001).
• Zarook, S. M.; Shaikh, A. A. and Ansar, Z., Development, Experimental Validation and Dynamic Analysis of a General Biofilter Model., Chem. Eng. Sci., 52, 759 (1997).

Publication Dates

• Publication in this collection
  13 May 2002
• Date of issue
  Mar 2002

History

• Accepted
  21 Nov 2001
• Received
  15 Mar 2001