The modelling of a textile dyeing process utilizing the method of volume averaging

TRANSPORT PHENOMENA UNIT OPERATION

The modelling of a textile dyeing process utilizing the method of volume averaging

A.A.Ulson de Souza^I; S.Whitaker^II

^IDepartamento de Engenharia Química e Engenharia de Alimentos, Universidade Federal de Santa Catarina, Phone: (+55) (48) 331-9448, Fax: (+55) (48) 331-9687, Cx. P. 476, 88040-900, Florianópolis - SC, Brazil E-mail: [e-mail]

^IIDepartment of Chemical Engineering and Material Science, Phone (+1) [phone], Fax (+1) [phone] University of California at Davis, CA 95616, U.S.A. E-mail: [e-mail]

ABSTRACT

In this work the modelling of a process of textile dyeing of a single cotton thread is presented. This thread moves at a constant velocity within a homogeneous dye solution under steady state conditions. The method of volume averaging is applied to obtain the mass transfer equations related to the diffusion and adsorption process inside the cotton thread on a small scale. The one-equation model is developed for the fiber and dye solution system, assuming the principle of local mass equilibrium to be valid. On a large scale, the governing equations for the cotton thread, including the expression for effective diffusivity tensor, are obtained. Solution of these equations permits the dye concentration profile for inside the cotton thread and in the dyeing batch to be obtained and the best conditions for the dyeing process to be chosen.

Keywords: textile, dyeing, modeling.

INTRODUCTION

The problem under study is illustrated in Figure 1, which shows a uniform cotton thread (w-region), moving at a constant velocity, u_o, within a homogeneous dye solution. The w-region is composed of fibers (s-region) and the dye solution inside the thread (b-phase). The concentration of dye in the thread at x = 0 is C_Aw^o, and the concentration in the h-region at y ~ ¥ is a constant value, C_A^¥.

A small scale can be identified inside the s-region as shown in Figure 1. On this small scale, two phases can be characterized: liquid in the microfibers, g-phase, and solid, k-phase (Plumb and Whitaker, 1988a, b, 1990). The k-phase refers to the cotton microfibers (Trotman, 1975; Holme, 1986), where the adsorption process occurs.

g - k SYSTEM AVERAGING

The governing differential equations and boundary conditions for the mass transfer process in both the g-phase and the k-phase, illustrated in Figure 1, are given by

It is assumed that in the interface the diffusive flux from the g-phase to the k-phase is equal to the adsorption rate.

The k-phase is assumed to be a rigid phase and the adsorption isotherm is a linear function expressed as

Here C_Ag represents the molar concentration of chemical species under study (mol/m³), C_As represents the surface concentration (mol/m²), and Dg is the g-phase molecular diffusivity of species A (Whitaker, 1992). The entrances and exits of the g-phase at the boundary of the s-region are represented by variable . Variable is used to represent the entire interfacial area within that region. The g-phase and the k-phase and the s-b system move at the same velocity in relation to the coordinate system; these two scales are confined to within the cotton fibers.

The intrinsic average concentration is defined by

The spatial averaging theorem (Howes and Whitaker, 1985) for volume can be expressed as

in which A_gk represents the interfacial area g-k contained within averaging volume .

The integration of Eqs. (1) through (4) in volume , using the spatial averaging theorem as presented by Ochoa-Tapia et al. (1993) and Whitaker (1999), results in the volume-averaged form of Eq. (1), given by

A key aspect of the process of spatial smoothing isthat the boundary condition given by Eq. (2) is combined with the governing equation. The area average concentration can be replaced by the intrinsic average concentration, when the following length-scale constraints, l_g << r_s and << l, are satisfied (Ochoa-Tapia et al., 1993; Whitaker, 1999).

Here av_gkrepresents the surface area per unit volume, given by

and the spatial deviation concentration can be expressed as

The Closure Problem

At this point a representation for the spatial deviation concentration needs to be developed.

Subtracting Eq. (8) divided by e_g from Eq. (1), one can obtain

The interfacial boundary condition for the deviation concentration can be expressed as

Since the source only influences the field over a distance on the order of l_g, we can generally replace the boundary condition imposed at with a spatially periodic condition for (Whitaker, 1999). So, when the spatially periodic model is used and is much greater than one, the boundary value problem can be rewritten as

Closure Variables

The boundary value problem for deviation concentration is solved by the method of superposition, where a proposed solution is given by

Whitaker (1999) proves that y = constant is the only solution. Since this additive constant will not pass through the filter, the value of y plays no role in the closed form of the volume averaged diffusion equation.

Here b and the scalar s are the closure variables and y is an arbitrary function (Whitaker, 1999). The two closure variables can be determined according to the following two boundary value problems:

Problem I

Problem II

Closed Form

The closed form of the governing equation for the intrinsic average concentration, <C_Ag >^g, can be obtained by substitution of Eq. (18) into Eq. (8). The resulting equation can be expressed as

where the effective diffusivity tensor is defined by

and vector u is defined by

Here the diffusive tensor, D_eff, depends only on the geometry of the porous medium (Whitaker, 1999).

One can use Eq. (23) and Eq. (27) for estimating the order of s and u. Using these results in Eq. (25), Whitaker (1999) demonstrated that the advective term can be neglected for the case of diffusion in porous solids. The final form of the local average diffusion and transport equation is given by

s-b SYSTEM AVERAGING

In this section we will develop the spatially smoothed equations associated with volume , shown in Figure 1. The length scales related to this averaging volume are identified in Figure 1. The boundary value problem associated with the local volume averaging procedure is given by

in the s-region

The s-Region

Integration of Eq. (29) over , illustrated in Figure 1, results in

in which the nomenclature for the s-region has been simplified by using the relationship , where

By using the averaging theorem and following the same procedure as that adopted previously and assuming that the restriction l_s << r_w is satisfied, Eq. (34) can be expressed as

Here j_s represents the volume fraction of the s-region contained in the volume .

The Closure Problem

Analogously to the previous procedure, here a representation for the spatial deviation concentration is required. The use of the spatial deviation concentration defined by Gray (1975) and applied to the s-region results in

The spatial deviation concentration equation can be obtained by subtracting Eq. (36) divided by j_s from Eq. (29), and the resulting equation can be simplified when the following restrictions are satisfied: . Under these circumstances Eq. (36) can be rewritten as

The b-Phase

The volume averaging form of Eq. (33) in volume , using the averaging theorem, is given by

The deviation concentration for the b-phase is given by .

The Closure Problem

One can see that the subtraction of Eq. (41) divided by j_b from Eq. (33) results in the governing equation for the deviation concentration, which is given by

By analysis of the order of the terms in Eq. (42), and assuming the length-scale constraints given by l_b << r_w and <<1, one can conclude that the nonlocal term can be considered negligible compared to the diffusion term and the closure process can be considered quasi-steady. Under these circumstances, Eq. (42) can be rewritten as

One-Equation Model

Making the assumption that the principle of local mass equilibrium (Quintard and Whitaker, 1993; Whitaker, 1986 a, b) is valid, we can write

Here <C_A>^* is the spatial average concentration defined as

The following definitions

can be used with Eqs. (36) and (41) to give

Here we have defined the overall effective diffusivity as

Closure Variables

Considering that the local closure problem has a unique nonhomogeneous term proportional to the gradient of the spatial average concentration evaluated on the centroid, one can write

where b_b and b_s are the closure variables.

The following boundary value problem needs to be solved:

One can show that y = x = constant. This constant will not pass through the filter represented by area integrals in Eq. (49), as suggested by Whitaker (1999). So the value of this constant plays no role in the closed-form equation.

The Closed Form

Substituting the expressions given by Eq. (50) and Eq. (51) for the spatial deviation concentrations in Eq. (49), taking into consideration solution of the boundary value problem, one can obtain

where

THE w-h SYSTEM

The w-Region

At this point we need to consider the w-region motion related to the h-phase and for this circumstance the time derivative of average concentration of species A in the w-region can be expressed as

By simplification Eq. (59), we can write

The subscript on the left side of Eq. (60) does not indicate what is being held constant, but instead indicates the velocity of the observer who is measuring the concentration. On the basis of Eq. (60) the governing equation for the w-region can be written as

The h-Phase

The governing equation for the h-phase is given by

One can assume that the boundary layer solution for the hydrodynamic problem in the h-phase is acceptable, and in this circumstance the velocity profiles obtained by Sakiadis (1961a, b, c) can be used in Eq. (62).

CONCLUSIONS

The model of a single cylinder cotton thread, developed using the method of volume averaging for the adsorption dyeing process, represents a fundamental approach in this area. Two scales were considered in order to formulate this problem. The k-phase, inside the s-region, is composed of microfibers where the adsorption process occurs. The w-region, containing the s-b system, moves at a constant velocity. The method of volume averaging is applied to obtain the mass transfer equations related to the adsorption process on the small and the large scale. The one-equation model is developed for the b - s system, assuming the local mass equilibrium. The simulation results and validation of this model as well as the effective mass diffusivity obtained by solution of closure problems will be presented in a subsequent paper.

ACKNOWLEGEMENTS

This work was done when Antônio Augusto Ulson de Souza was a postdoctoral student at University of California, Davis, with financial support from the Fundação Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, CAPES, Brazil.

NOMENCLATURE

_gk

Interfacial area of the g-k system, m²

_ge

Area of entrances and exits for the g-phase, m²

_sb

Interfacial area of the s-b system, m²

_se

Area of entrances and exits for the s-region, m²

_be

Area of entrances and exits for the b-phase, m²

A_gk

The g-k interfacial area contained within the averaging volume,

_s, m²

A_ge

Area of entrances and exits for the g-phase contained within the averaging volume,

_s, m²

A_sb

The s-b interfacial area contained within the averaging volume,

_w, m²

av_gk

The g-k interfacial area per unit volume, m^-1

C_A^¥

Concentration in the h-phase outside the boundary layer, kgmol/ m³

C_Ag

Point concentration in the g-phase, kgmol/ m³

<C_Ag>^g=C_s

Intrinsic averaged concentration in the g-phase, kgmol/ m³

_Ag

Spatial deviation concentration in the g-phase, kgmol/ m³

C_Ab

Point concentration in the b-phase, kgmol/ m³

C_Ah

Point concentration in the h-phase, kgmol/ m³

<C_Ab>^b

Intrinsic regional averaged concentration for the b-phase, kgmol/ m³

<C_s>

Superficial regional averaged concentration for the s-region, kgmol/ m³

<C_s>^s

Intrinsic regional averaged concentration for the s-region, kgmol/ m³

_s

Spatial deviation concentration in the s-region, kgmol/ m³

_Ab

Spatial deviation concentration in the b-phase, kgmol/ m³

<C_A>^*

Intrinsic spatial averaged concentration for the s-b system, kgmol/ m³

D_g

The g-phase molecular diffusivity, m²/s

D_eff

The g-phase effective diffusivity tensor, m²/s

D_b

The b-phase molecular diffusivity, m²/s

D_h

The h-region molecular diffusivity, m²/s

Effective diffusivity tensor for the s-b system , m²/s

I

Unit tensor

<K>

The averaged adsorption equilibrium constant, m

Keq

Adsorption equilibrium constant, m

_w

Characteristic length of the w-region, m

_s

Characteristic length of the s-region, m

_b

Characteristic length of the b-phase, m

_g

Characteristic length of the g-phase, m

l _i

Lattice vectors describing a spatially periodic porous medium, m

Long length for volume averaged quantities associated with the w-h system, m

n_gk

Outwardly directed unit normal vector pointing from the g-phase toward the k-phase

n_sb

Outwardly directed unit normal vector pointing from the s-region toward the b-phase

r_s

Radius of the g-k system averaging volume,

_s, m

r_w

Radius of the s-b system averaging volume,

_w, m

t

Time, s

t*

Characteristic time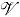, s

_s

Small-scale averaging volume, m³

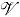_w

Large-scale averaging volume, m³

u _o

The w-region velocity vector, m/s

v_h

The h-phase velocity vector, m/s

V_g

Volume of the g-phase contained within

_s, m³

V_s

Volume of the s-region contained within

_w, m³

d_C

Mass boundary layer

d_H

Hydrodynamic boundary layer

e_g

The g-phase volume fraction in the g-k system

j_s

The s-region volume fraction in the s-b system

j_b

The b-phase volume fraction in the s-b system

<e>

The averaged porosity

Received: October 25, 2001

Accepted: July 3, 2003

• Gray, W.G., A Deviation of the Equations for Multiphase Transport, Chemical Engineering Science, 30, 229-233 (1975).
• Holme, I., The Effects of Chemical and Physical Properties on Dyeing and Finishing, in C. Preston (ed.), The Dyeing of Cellulosic Fibres, Chap. 3, Dyers Company Publications Trust (1986).
• Howes, F.A. and Whitaker, S., The Spatial Averaging Theorem Revisited, Chemical Engineering Science, vol. 40, pp. 1387-1392 (1985).
• Ochoa-Tapia, Chem. Engng. Sci., c.48 (1993).
• Plumb, O.A. and Whitaker, S., Dispersion in Heterogeneous Porous Media I. Local Volume Averaging and Large Scale Averaging, Water Resources Research, 24, 913-926 (1988a).
• Plumb, O.A. and Whitaker, S., Dispersion in Heterogeneous Porous Media II. Predictions for Stratified and Two-dimensional Spatially Periodic Systems, Water Resources Research, 24, 927-938 (1988b).
• Plumb, O.A. and Whitaker, S., Diffusion, Adsorption and Dispersion in Porous Media: Small-scale Averaging and Local Volume Averaging, in J. H. Cushman (ed.), Dynamics of Fluids in Hierarchical Porous Media, Chap. 5, Academic Press, New York (1990).
• Quintard, M. and Whitaker, S., One and two-equation Models for Transient Diffusion Processes in Two-phase Systems, in Advances in Heat Transfer, 23, 369-465, Academic Press, New York (1993).
• Sakiadis, B. C., Boundary-layer Behavior on Continuous Solid Surfaces: I. Boundary-layer Equations for Two-dimensional and Axisymmetric Flow, A.I.Ch.E. Journal, 7, 26-28 (1961a).
• Sakiadis, B.C., Boundary-layer Behavior on Continuous Solid Surfaces: II. The Boundary-layer on a Continuous Flat Surface, A.I.Ch.E. Journal, 7, 221-225 (1961b).
• Sakiadis, B.C., Boundary-layer Behavior on Continuous Solid Surfaces: III. The Boundary-layer on a Continuous Cylindrical Surface, A.I.Ch.E. Journal, 7, 467-472 (1961c).
• Trotman E. R., Dyeing and Chemical Technology of Textile Fibres, Charles Griffin & Co. LTD, London (1975).
• Whitaker, S., Transient Diffusion Adsorption and Reaction in Porous Catalysts: The Reaction Controlled, Quasi-steady Catalytic Surface, Chemical Engineering Science, 41, 3015-3022 (1986a).
• Whitaker, S., Local Thermal Equilibrium: An Application to Packed Bed Catalytic Reactor Design, Chemical Engineering Science, 41, 2029-2039 (1986b).
• Whitaker, S., The Species Mass Jump Condition at a Singular Surface, Chemical Engineering Science, 47, 1677-1685 (1992).
• Whitaker, S., Theory and Application of Transport in Porous Media: The Method of Volume Averaging, London, Kluwer Academic, 219p (1999).

Publication Dates

• Publication in this collection
  04 Dec 2003
• Date of issue
  Oct 2003

History

• Accepted
  03 July 2003
• Received
  25 Oct 2001