Abstract
Aiming at simulating air-heating systems, two algorithms were developed for the calculation of finned elliptical-tube heat exchangers, whose basic difference lies in the kind of hot fluid employed: saturated steam or hot liquid. In both cases, a crossflow unit, in which the cold fluid is mixed and always flows on the shell side, is considered. The hot fluid may exhibit multiple passes in the tubes and is assumed unmixed, except for the region between the passes. A comparison between calculated results and operating data on industrial exchangers indicated the adequacy of the algorithms developed. The codes were then introduced into the ASPEN Plus shell, enabling simulation of the steady-state operation of the whole drying-air heating system of a powdered milk plant. Moreover, a sensitivity analysis of this system was conducted for one of its operating parameters and the existence of an optimal value for this variable was clearly shown.
heat exchanger; elliptical tubes; fins; ASPEN
TRANSPORT PHENOMENA UNITY OPERATION
Analysis and simulation of the drying-air heating system of a Brazilian powdered milk plant
C. P. Ribeiro Jr. ; M. H. C. Andrade* * To whom correspondence should be addressed
Departamento de Engenharia Química, Universidade Federal de Minas Gerais, Rua Espírito Santo 35, Centro, Phone +(55)(31) 3238-1780, Fax +(55)(31) 3238-1789, CEP 30160-030, Belo Horizonte - MG, Brazil. E-mail: cano@deq.ufmg.br
ABSTRACT
Aiming at simulating air-heating systems, two algorithms were developed for the calculation of finned elliptical-tube heat exchangers, whose basic difference lies in the kind of hot fluid employed: saturated steam or hot liquid. In both cases, a crossflow unit, in which the cold fluid is mixed and always flows on the shell side, is considered. The hot fluid may exhibit multiple passes in the tubes and is assumed unmixed, except for the region between the passes. A comparison between calculated results and operating data on industrial exchangers indicated the adequacy of the algorithms developed. The codes were then introduced into the ASPEN Plus shell, enabling simulation of the steady-state operation of the whole drying-air heating system of a powdered milk plant. Moreover, a sensitivity analysis of this system was conducted for one of its operating parameters and the existence of an optimal value for this variable was clearly shown.
Keywords: heat exchanger, elliptical tubes, fins, ASPEN.
INTRODUCTION
Drying is the last step in the process of powdered milk production, and since the Second World War, the spray drying technique has been used in the vast majority of the dairy industries. This technique consists in transforming the liquid feed stream into a large number of small droplets, which are exposed to a heavy flow of hot gas in a drying chamber.
In the dairy industries, atmospheric air is used as the drying gas. It is filtered and then heated prior to being fed into the dryer at a temperature which ranges from 150 to 220ºC (Varnam and Sutherland, 1994; Schuck, 2002). Indirect heating systems, comprising high-efficiency finned-tube exchangers and saturated steam, are normally employed, though units with hot oil as the heating fluid can also be found. As an alternative, air can be heated by direct contact with combustion gases from a burner (Jansen and Elgersma, 1985; Kelly et al., 1989). Despite the substantially lower capital investment and the high thermal efficiency associated with direct heating, it is not recommended due to the likely contamination of powdered milk brought about by the nitrogen oxides from the combustion gases, which can result in the formation of cancerous chemicals, such as nitrosamines (Caric, 1994). A more detailed description of the air-heating systems in the dairy industry is given by Knipschildt and Andersen (1994).
Considering both the required outlet temperature and the amount of air to be treated, it is easy to see that these heating systems are characterised by high energy consumption. Therefore, any improvement in their operating conditions that leads to energy savings would be of considerable interest (O'Donnell et al., 1996; Schuck, 2002; Velic et al., 2003). In this work, a study was conducted on the industrial air-heating system installed at Embaré Indústrias Alimentícias S. A., a Brazilian dairy company located in Lagoa da Prata, Minas Gerais. This system, illustrated in Figure 1, provides two drying systems with hot air and is composed of six heat exchangers and a flash tank. All the exchangers have a rectangular shell and elliptical tubes, inside which the hot fluid flows.
Units EX-201 and EX-202 work in series and are fed with saturated steam at 13.2 kgf/cm2, supplying hot air to the smaller drying system, which is responsible for one-third of the total amount of powdered milk produced in the plant. The other exchangers are related to the main drying system. Only the last two units, EX-103 and EX-104, use steam at 21.5 kgf/cm2 as heating fluid. The condensate from these exchangers, together with that formed in both EX-201 and EX-202, feeds the flash tank, TQ-101, in which part of the feed (high-pressure liquid) vaporises on account of the low operating pressure of the tank (2.5 kgf/cm2). The steam produced in TQ-101 is the heat source for EX-102, whereas the liquid fraction from this tank is the hot fluid for the first exchanger in the arrangement, EX-101.
The ASPEN Plus environment (Evans et al., 1979), which has already been employed to simulate other industrial plants (Douglas and Young, 1991; Ong'iro et al., 1996; Rachid and Caño Andrade, 2001; Ribeiro and Caño Andrade, 2003), was chosen for analysis of the system described above. Since a built-in model block for simulating rectangular shell exchangers with finned elliptical tubes is not available in ASPEN, one was developed in this work and subsequently introduced into the simulator.
DESCRIPTION OF ALGORITHMS
The two codes developed for simulating finned elliptical-tube exchangers consider a crossflow unit with a rectangular shell, where the cold fluid flows and is assumed to be completely mixed. In the tubes, the fluid is assumed to be unmixed and may have more than one pass. All fins are rectangular in shape. The main difference between the two codes is the kind of heating fluid: hot liquid or saturated steam.
Regardless of the nature of the hot fluid, the heat-transfer rate in the unit, Q, is given by the classic equation (Incropera and DeWitt, 1996):
where U is the overall heat-transfer coefficient, AT is the total area of the finned tubes, LMTD is the logarithmic mean temperature difference and f its correction factor for the actual flow pattern in the exchanger.
In order to calculate the overall heat-transfer coefficient one must take into account the mean fin efficiency, 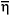 . Considering the total area of the finned tubes and neglecting the heat-transfer resistances owing to conduction through the tube wall, fouling and contact resistance between the tube and fins, U is estimated by the following equation (Hashizume, 1986):
. Considering the total area of the finned tubes and neglecting the heat-transfer resistances owing to conduction through the tube wall, fouling and contact resistance between the tube and fins, U is estimated by the following equation (Hashizume, 1986):
in which hsl and htb are the average heat-transfer coefficients on the shell and tube sides, respectively, Afin is the area of the fins, Aext and Aint are respectively the outer and inner surface area of the tubes.
From Figure 2, the different areas in eq. (2) can be quantified as follows:
where nfin is the number of fins per tube length, ntb is the number of tubes in the exchanger, L is the tube length and e is the eccentricity of an ellipse.
The mean fin efficiency was estimated by means of the expression developed by Suyi and Shizhou (1995) for the efficiency of rectangular fins in an elliptical tube as a function of the polar coordinate, q :
where
In eq. (9) and (10), I0 and I1 are respectively the modified Bessel functions of the first kind of order zero and one; K0 and K1 refer to the modified Bessel functions of the second kind of order zero and one, respectively (Boyce and Di Prima, 1994) and kfin is the thermal conductivity of the fins. Parameter r0 is the curvature radius of an ellipse:
where x(q) and y(q) are the parametric equations of the ellipse
and a(q) and b(q) are the parametric equations of the ellipse's evolute (Simmons, 1987)
Parameter rc is given by the following equation:
in which kn is the slope of the ellipse's curvature radius
According to the concept of mean value of a function over a given interval of its domain, it follows that
For the average heat-transfer coefficients, the value related to the shell side was estimated using the empirical correlation presented by Ilgarubis et al. (1988) for a bundle of finned elliptical tubes:
In eq. (21), Nu, Re and Pr are respectively the Nusselt, Reynolds and Prandtl numbers and S1 and S2 are the transverse and longitudinal bundle pitches. All physical properties should be evaluated at the fluid inlet temperature, and the reference velocity is calculated in relation to the minimum bundle cross section (Amin). The characteristic dimension for evaluating the dimensionless groups, Deq, is given by
where ntransv is the number of tubes in the transverse direction of the bundle.
For the tubes side, when the heating fluid is a hot liquid, the heat-transfer coefficient is calculated by the equation below, related to turbulent forced convection in cylindrical tubes (Incropera and DeWitt, 1996):
Here the liquid properties are evaluated at the mean film temperature and the characteristic dimension employed is the hydraulic or equivalent diameter of the elliptical tubes:
On the other hand, the heat-transfer coefficient associated with saturated steam condensation inside vertical tubes is calculated using the Nusselt theory on a vertical surface (Marto, 1991):
where kl, r l and ml are the condensate thermal conductivity, density and viscosity, respectively; rv is the steam density; g is the gravitational acceleration; g is the latent heat of vaporisation and Ts and Tw are respectively the saturation and wall temperatures.
However, if condensation takes place in either horizontal or slanted tubes, the equation presented by Fieg and Roetzel (1994) for laminar condensation in slanted elliptical tubes is utilised:
In eqs. (26) to (28), d is the condensate film thickness, y is the angle of the tube and Z is the dimensionless film thickness.
Both algorithms calculate the cold fluid outlet temperature by means of a heat balance, according to which the variation in fluid enthalpy is equal to the amount of energy transferred within the unit. Assuming ideal-gas behaviour for the cold fluid and adiabatic operation, we have
For the exchanger operating with saturated steam, it is assumed that there is no pressure drop on the tube side, so the steam temperature remains constant throughout the equipment, which leads to a unitary correct factor for the LMTD (Incropera and DeWitt, 1996). Assuming total condensation, an initial value for the cold fluid outlet temperature is generated. This initial value is used for evaluating the mean fin efficiency, and thus the overall heat-transfer coefficient can be determined by eq. (2). Upon substituting eq. (1) into eq. (29) and solving the resulting expression iteratively by Newton's method (Mathews, 1992), a new estimate for the cold fluid outlet temperature is obtained. With this new estimate, the value of 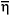 is recalculated by eqs. (9) to (20) and the iteration circuit is completed. Once the outlet temperature for the cold fluid converges, the amount of steam that actually condenses is determined by a heat balance.
is recalculated by eqs. (9) to (20) and the iteration circuit is completed. Once the outlet temperature for the cold fluid converges, the amount of steam that actually condenses is determined by a heat balance.
When a hot liquid constitutes the heat source, the temperature of adiabatic mixture is used as the initial value for the stream outlet temperatures. Assuming once again adiabatic operation, all energy supplied by the hot fluid has to be transferred to the cold one, hence, neglecting the effect of pressure on the liquid enthalpy:
By sustituting eq. (1) into eqs. (29) and (30) and solving the resulting system of non-linear equations using the Newton-Raphson method (Mathews, 1992), the outlet temperature of each fluid is calculated. In this case, the correction factor for the LMTD is evaluated with the aid of the equations presented by Bowman et al. (1940). All necessary integrals are evaluated numerically by the Gaussian quadrature method (Mathews, 1992). As a convergence criterion, the residue of all equations is required to be less than 10-6.
RESULTS AND DISCUSSION
Validation of the Algorithms
In order to validate the codes developed, an individual simulation of the units related to the heating system (Figure 1) was carried out. All exchangers have 36 x 14 mm (external dimensions) elliptical tubes, arranged in a triangular layout. Their walls are 2.0 mm thick. All fins are rectangular, with dimensions of 55 x 26 mm and a thickness of 0.23 mm. The hot fluid flows vertically in units EX-103 and EX-104 and horizontally in the others. In EX-102, the tubes have a 5º slope in relation to the horizontal axis. Additional design parameters of the simulated exchangers are listed in Table 1.
In the industrial plant, units EX-103 and EX-104 are, in fact, identical exchangers installed one immediately after the other. This is also the case for units EX-201 and EX-202. As a result, during the simulation each of these pairs was represented as a single unit, twice as wide as the original exchanger with twice as many tubes. The operating conditions of the units, which correspond to the input data for the individual simulation, are presented in Table 2.
The calculated air outlet temperatures are compared with averaged operating data from the industrial plant (Ribeiro, 2001) in Table 3. The biggest deviation, 6.7%, is associated with EX-101, which may be a consequence of the fact that, for this unit alone, one of the heat-transfer coefficients is estimated with an equation related to cylindrical tubes, inasmuch as no correlation for calculating the h value due to forced convection in elliptical tubes was found in the literature. Nevertheless, the agreement verified between calculated and operating values for the other exchangers attests to the validity of the algorithms developed.
Simulation of the Air-Heating System
In view of the results of the individual simulations, the codes developed were introduced into ASPEN to enable simulation of Embaré's air-heating system. The tank, TQ-101, was represented by the ASPEN built-in model block FLASH2, which performs rigorous multicomponent liquid-vapour equilibrium calculations. All physical property evaluations in the developed codes were carried out using only ASPEN models, so as to main the consistency of the calculations.
The input data for the simulation in this case are the operating pressure in tank TQ-101 and the conditions (temperature, pressure and flow rate) of the air streams fed into EX-101 and EX-201/2, apart from the data related to the steam streams in EX-201/2 and EX-103/4. Since the modular approach is adopted in ASPEN for the calculations (Motard et al., 1975), an initial value for the system tear stream, namely the cold fluid in EX-103/4, had to be provided in order to avoid convergence problems.
The results for the global simulation of the air-heating system are shown in Table 4. For the exchangers arranged in series, any deviation in the calculation for one piece of equipment will directly affect the results obtained for the next, so the absolute difference between calculated and operating outlet temperatures increases in the direction of the air flow. As a consequence, the deviations from the operating data are larger than those observed in the individual simulation of the units, but, nonetheless, quite acceptable as far as simulation of the industrial process is concerned, since the temperatures of the air streams which will actually be fed into the drying systems are predicted with an error less than 2.5%.
Sensitivity Analysis
Once developed, the module for simulating the air-heating system was employed to assess the effect of the pressure in tank TQ-101, P101, on the system's operation. Keeping all other parameters constant, simulations were conducted varying this pressure from 1.0 to 9.0 kgf/cm2. The results for air outlet temperature are presented in Figure 3.
In EX-101, the air temperature increases continuously as the pressure in tank TQ-101 increases. For the other two units, a steep initial rise in temperature is verified up to a pressure of about 2.0 kgf/cm2, where a maximum point is reached. From then on, any further increase in pressure leads to a decline in air outlet temperature. This behaviour points to the existence of an optimal operating value for the pressure in the tank, with which a minimum steam consumption for a given outlet temperature would be associated. In the simulations conducted, the highest temperature for the drying air was obtained for P101 = 2.33 kgf/cm2, a value similar to the plant's normal operating condition (P101 = 2.53 kgf/cm2), indicating, thereby, that the air heating system is actually working quite close to the region of minimum steam consumption.
As all other operating parameters are fixed, the total flow rate of condensate that is fed into TQ-101 is approximately constant, so the higher the pressure in the tank, the higher the flow rate of liquid water pumped as heating fluid into EX-101. This increment in the feed flow rate results in a higher heat-transfer coefficient on the tube side, and, since the resistance associated with convection on the tube side is significant, an increase in the U value is observed.
Moreover, a higher pressure in TQ-101 implies a higher saturation temperature for the liquid which leaves the tank and therefore a higher driving force for heat transfer in EX-101. The association of these two factors is responsible for the continuous increase in the air outlet temperature in EX-101 shown in Figure 3(a).
The flow rate of heating steam fed into EX-102, and consequently the available latent heat, decreases when P101 is raised (Figure 4). On the other hand, the amount of heat that can actually be transferred within this unit increases with P101 due to the increment in the LMTD value caused by the higher steam temperature, which is high enough to compensate for the rise in air inlet temperature. Initially, when P101 < 2.33 kgf/cm2, the amount of available latent heat remains greater than the amount of transferable energy, so the reduction in the former does not prevent the latter from increasing and the quality of the water stream that leaves EX-102 falls accordingly, as shown in Figure 4. For higher operating pressures in TQ-101, the opposite situation is verified and the amount of available latent heat becomes smaller than the amount of transferable heat, or in other words, the steam is totally condensed without using all of the available heat-transfer area. Due to the declining steam feed flow rate, the amount of energy actually transferred, and consequently the air outlet temperature, falls progressively.
The results obtained for EX-103/4 are directly related to what happens in EX-102. In EX-103/4, in view of the fact that the steam flow rate is a specified parameter, the available latent heat is fixed. For the P101 range studied, the amount of energy that can be transferred within the equipment is slightly larger than that available. Therefore, no change is verified for the amount of heat actually transferred in the equipment and the outlet temperature varies with the inlet temperature, an outcome which supports the strong resemblance between the temperature curves in Figures 3(b) and 3(c).
CONCLUSIONS
The integration of calculation codes developed in this work into the ASPEN Plus shell enabled the elaboration of a simulation model for the whole drying-air heating system of a powdered milk plant. The adequacy of this model was proven by means of a comparison between simulation results and operating data.
The model was used as a means of conducting a sensitivity analysis of this system for one of its operating parameters. The existence of an optimal value for this variable, associated with a minimum consumption of steam, was confirmed.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the financial support provided by FAPEMIG for the development of this work, as well as the authorisation conceded by Embaré Indústrias Alimentíciais S. A. for a study of part of their industrial plant.
NOMENCLATURE
total number of tubes in the exchanger, -
fin thickness, m
Received: February 13, 2003;
Accepted: November 27, 2003
- Bowman, R.A., Mueller, A.C. and Nagle, W.M., Mean Temperature Difference in Design, Transactions of the American Society of Mechanical Engineers, 62, 283 (1940).
- Boyce, W.E. and Di Prima, R.C., Equações Diferenciais Elementares e Problemas de Valores de Contorno. Guanabara Koogan, Rio de Janeiro (1994).
- Caric, M., Concentrated and Dried Dairy Products. In: Hui, Y.H. (Ed.), Dairy Science and Technology Handbook vol. 2. VCH, New York (1994).
- Douglas, P.L. and Young, B.E., Modelling and Simulation of an AFBC Steam Heating Plant Using ASPEN/SP, Fuel, 70, No. 2, 145 (1991).
- Evans, L.B., Boston, J.F., Britt, H.I., Gallier, P.W., Gupta, P.K., Joseph, B., Mahalec, V., Seider, W.D. and Yagi, H., ASPEN: An Advanced System for Process Engineering, Computers and Chemical Engineering, 3, 319 (1979).
- Fieg, G.P. and Roetzel, W., Calculation of Laminar Film Condensation in/on Inclined Elliptical Tubes, International Journal of Heat and Mass Transfer, 37, No. 4, 619 (1994).
- Hashizume, K., Heat Transfer and Pressure Drop across Finned Tubes. In: Cheremisinoff, N.P. (Ed.), Handbook of Heat and Mass Transfer vol. 1 - Heat Transfer Operations. Gulf, Houston (1986).
- Ilgarubis, V.A.S.; Ulinskas, R.V. and Butkus, A.V., Hydraulic Drag and Average Heat Transfer Coefficients of Compact Bundles of Elliptical Finned Tubes, Heat Transfer-Soviet Research, 20, No. 1, 12 (1988).
- Incropera, F.P. and DeWitt, D.P., Introduction to Heat Transfer. John Wiley & Sons, New York (1996).
- Jansen, L.A. and Elgersma, R.H.C., Direct Heating of Drying Air with Natural Gas in the Preparation of Milk Powder, Journal of the Society of Dairy Technology, 38, No. 4, 134 (1985).
- Kelly, P.M., Gray, J.I., Slattery, J., Direct Low-NOX Gas Combustion Heating of a Spray Dryer during Milk Powder Manufacture, , Journal of the Society of Dairy Technology, 42, No. 1, 14 (1989).
- Knipschildt, M.E. and Andersen, G.G., Drying of Milk and Milk Products. In: Robinson, R.K. (Ed.), Modern Dairy Technology vol.1. Chapman & Hall, London (1994).
- Marto, P.J., Heat Transfer in Condensation. In: Kakaç, S. (Ed.), Boilers, Evaporators and Condensers. John Wiley & Sons, New York (1991).
- Mathews, J. H., Numerical Methods for Mathematics, Science and Engineering. Prentice-Hall International, London (1992).
- Motard, R.L., Shacham, M. and Rosen, E.M., Steady-state Chemical Process Simulation, AIChE Journal, 21, No. 3, 417 (1975).
- O'Donnell, C.P., McKenna, B.M., Herlihy, N., Drying of Skim Milk: Opportunities for Reduced Steam, Drying Technology, 14, No. 3-4, 513 (1996).
- Ong'iro, A., Ugursal, I., Al Tawee, M.A. and Lajeunesse, G., Thermodynamic Simulation and Evaluation of a Steam CHP Plant using ASPEN Plus, Applied Thermal Engineering, 16, No. 3, 263 (1996).
- Rachid, R. Jr. and Caño Andrade, M.H., Steady-state Simulation of the Sour Water Treatment Plant of a Brazilian Refinery, Actas del 5ş Congreso Interamericano de Computación Aplicada a la Industria de Procesos CAIP 2001. Campos do Jordão, 187 (2001).
- Ribeiro, C.P. Jr. Modelling of Plate Heat-transfer Systems and Simulation of a Brazilian Powdered Milk Plant, Master's thesis, Federal University of Minas Gerais, Belo Horizonte (2001).
- Ribeiro, C.P. Jr. and Caño Andrade, M.H., Performance Analysis of the Milk Concentrating System from a Brazilian Milk Powder Plant, Journal of Food Process Engineering, 26, No. 2, 181 (2003).
- Schuck, P., Spray Drying of Dairy Products: State of the Art, Lait, 82, No. 4, 375 (2002).
- Simmons, G.F., Cálculo com Geometria Analítica, vol. 2. McGraw-Hill, São Paulo (1987).
- Suyi, H. and Shizhou, P., Convection and Heat Transfer of Elliptical Tubes, Heat and Mass Transfer, 30, No. 6, 411 (1995).
- Varnam, A.H. and Sutherland, J.P., Milk and Milk Products. Chapman & Hall, London (1994).
- Velic, D., Bilic, M., Tomas, S. and Planinic, M., Simulation, Calculation and Possibilities of Energy Saving in Spray Drying Process, Applied Thermal Engineering, 23, 2119 (2003).
Publication Dates
-
Publication in this collection
26 May 2004 -
Date of issue
June 2004
History
-
Accepted
27 Nov 2003 -
Received
13 Feb 2003






























