Calculation of liquid-liquid equilibrium of aqueous two-phase systems using a chemical-theory-based excess Gibbs energy model

THERMODYNAMICS

Calculation of liquid-liquid equilibrium of aqueous two-phase systems using a chemical-theory-based excess Gibbs energy model

P. A. Pessôa Filho^{I, II, *}; R. S. Mohamed^I

^IFaculdade de Engenharia Química, Universidade Estadual de Campinas, Caixa Postal 6066, CEP 13083-970, Campinas, SP - Brazil

^IIDepartamento de Engenharia Química, Escola Politécnica, Universidade de São Paulo. Cx P 61548, CEP 05424-970, São Paulo - SP, Brazil E-mail: [e-mail]

ABSTRACT

Mixtures containing compounds that undergo hydrogen bonding show large deviations from ideal behavior. These deviations can be accounted for through chemical theory, according to which the formation of a hydrogen bond can be treated as a chemical reaction. This chemical equilibrium needs to be taken into account when applying stability criteria and carrying out phase equilibrium calculations. In this work, we illustrate the application of the stability criteria to establish the conditions under which a liquid-phase split may occur and the subsequent calculation of liquid-liquid equilibrium using a chemical-theory-modified Flory-Huggins equation to describe the non ideality of aqueous two-phase systems composed of poly(ethylene glycol) and dextran. The model was found to be able to correlate ternary liquid-liquid diagrams reasonably well by simple adjustment of the polymer-polymer binary interaction parameter.

Keywords: Aqueous two-phase systems, thermodynamic modeling, Gibbs energy, liquid-liquid equilibrium.

INTRODUCTION

The occurrence of hydrogen bonding is responsible for large deviations in the random distribution of molecules (Kretschmer and Wiebe, 1954), which commonly used equations of state and liquid solution models are not able to describe. This difficulty can be overcome by modifying these thermodynamic models through chemical theory.

The term "chemical theory" refers to the approach according to which a hydrogen bond is treated, in thermodynamic modeling, as if it were a normal covalent bond. The origin of chemical theory goes back to Dolezalek (1908), according to whom any deviation from ideal behavior could be related to the formation of new species. The modern use of chemical theory to modify excess Gibbs energy models began with Kretschmer and Wiebe (1954), who used this theory to modify the Flory-Huggins equation (Flory, 1942). This work was later supplemented and put in a more complete form by Renon and Prausnitz (1967). Nagata and Kawamura (1977), Nagata (1985), Nath and Bender (1981ab, 1983), Brandani (1983) and Brandani and Evangelista (1984) have also used chemical theory to modify the UNIQUAC equation of Abrams and Prausnitz (1975). The main difference between these models lies in the way the chemical equilibrium between clusters formed through hydrogen bonding is calculated.

The first important chemical-theory-based model to modify volumetric equations of state was presented by Heidemann and Prausnitz (1976), who developed a van der Waals-type equation of state that incorporates association. Although with different simplifications, the hypotheses of Heidemann and Prausnitz were later used by Ikonomou and Donohue (1986), Anderko (1989, 1991), Wenzel and Krop (1990) and Shinta and Firoozabadi (1995), among others. A progressive departure from chemical theory in its strict sense can be observed in the sequence of these papers: chemical equilibrium among clusters is no longer calculated and some consequences of earlier work were assumed as working hypotheses with no rigorous verification of their validity. An attempt to return to the original concepts can be found in Pessôa Filho and Mohamed (1999).

In this work, we present an application of a chemical theory model, based on Kretschmer and Wiebe (1954), along with Michelsen’s stability analysis (1982ab), for the calculation of liquid-liquid equilibrium in aqueous two-phase systems.

Theoretical Considerations

Water is considered to be a self-associating compound whose multimers are in chemical equilibrium according to the series of chemical reactions defined by the equation

whose equilibrium constant is k_i. Although the self-association of water is more complex than stated in Eq. (1), this description is sufficient to improve the correlation of aqueous solution data up to the limit of experimental uncertainty, as will be seen. Using the reasoning of Kretschmer and Wiebe (1954), it is postulated that the Gibbs energy of the reactions represented in Eq. (1) does not depend on i when the reaction occurs between isolated molecules.

Following Kretschmer and Wiebe (1954) and Pessôa Filho and Mohamed (2001), the Flory-Huggins equation (Flory, 1942) is used as the working equation:

wherein f stands for the volumetric fraction, V represents the volume per amount of substance and c is the interaction parameter of the Flory-Huggins equation.

Thermodynamic models that employ chemical theory distinguish between two different compositions for the same mixture: an effective (or true) composition and an analytical (or apparent) composition, the latter being the composition calculated without accounting for association reactions. Chemical equilibrium constrains the value of the Gibbs free energy and allows it to be written in terms of the analytical compositions 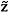, as neither self-association nor any kind of cross-association changes the number of degrees of freedom.

In order to test the stability of a general phase with composition z, the approach of Michelsen (1982a) is followed: an arbitrary phase separation is considered to occur, yielding a new phase whose composition is y. The Gibbs energy change upon this separation is analyzed for all values of y; stationary points of the tangent hyper plane are found to follow the relation:

in which j represents the self-associating compound or the inert; the apparent activity coefficients are and . The set of stationary points can be obtained by solving the above system of equations in Y_j. The corresponding values of 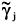can be calculated through the expression

Once the stationary point is calculated, stability can be verified by analyzing the values of Y_j; if S Y_k > 1, the phase 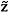is unstable. In summary, the stability analysis can be conducted for chemical theory models by replacing the true composition by the analytical composition and replacing the chemical potential of the associating compound by the chemical potential of its monomer, after which application of the method as presented by Michelsen (1982a,b) is straightforward.

RESULTS

Initial Calculations

Before liquid-liquid calculations could be carried out, the unknown parameters in the model, namely the Flory-Huggins interaction parameters and the self-association enthalpy and entropy, must be determined. The value of enthalpy and entropy of association in this work was taken from Nath and Bender (1981a), whose definition of the equilibrium constant coincides with that of Kretschmer and Wiebe (1954): D_ass H⁰ =-25.6 J.mol^-1 and D_ass S⁰ =-29.8 J. mol^-1.K^-1.

The Flory-Huggins parameters relating the interaction between polymers and water were obtained using water activity data and minimizing the residual standard deviation

wherein r is the number of experimental points, t is the number of parameters – just one in this case – and a_A is the water activity. The data were obtained from Grobmann et al. (1995) for aqueous solutions of PEG 6000, PEG 35000 and dextran 500 at 293K. The optimum values for the interaction parameter c for the dextran-water and PEG-water pairs were found to be c=-0.1180 and c=-0.3141, respectively. However, it must be stressed that the correlation of water activity data for PEG solutions was not as successful as for dextran solutions, as in the former case the average deviation between the experimental and calculated values was higher than the experimental uncertainty (values of residual standard deviation of 0.0064 for PEG solutions and 0.0022 for dextran solutions).

Liquid-Liquid Equilibrium Calculation

Prior to liquid-liquid equilibrium calculations, phase stability analysis was conducted. It was assumed that the composition of the phase whose stability was to be verified was located at the middle point of the experimental tie line. The stationary point was then found using Eq. (3) by upgrading the value of Y_j for each iteration using the following expression

wherein n and n-1 refer to the current and previous interaction, respectively. When analysis of the Y values showed that the phase was unstable, the corresponding 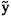value was taken as an initial guess composition of one phase, the composition of the other phase was calculated by mass-balance and liquid-liquid equilibrium was thus calculated by minimizing the total Gibbs energy.

Questions can be raised as to whether equation (6) may converge to multiple solutions, corresponding to local minima. This indeed can happen, though it has not been observed, despite the fact that the initial guess has been changed in order to cover a wide range of values. This can be due to both the relatively simple (although non linear) form of the Gibbs energy model and the low number of compounds present. Complete analysis of this subject can be found in McDonald and Floudas (1996) and Tessier et al. (2000), for instance.

The model presented was used to correlate 73 data sets for ATPS. These data, which have also been used in previous work for testing the reliability of an excess Gibbs energy model (Pessôa Filho and Mohamed, 2001), were obtained from Diamond and Hsu (1989a,b), Forciniti et al. (1991) and Zaslavsky (1995). In Table 1, we report the results on six systems for which experimental data were presented by Diamond and Hsu (1989a). The results obtained for these systems are typical and representative of those obtained with the other 68 systems considered in this work.

For comparison purposes, the Flory-Huggins equation in its original form was also used to correlate the same data. In both cases, the remaining optimal parameters were obtained through the minimization of the residual standard deviation

in which w is the mass fraction of the equilibrium phases and the summation excludes water. For the original Flory-Huggins equation, all interaction parameters were obtained by minimization of the objective function in Eq. (7), while for the chemical-theory-modified equation only the interaction parameter between the polymers was to be obtained. The question of whether the parameters obtained do correspond to the minimum value of this equation is of interest. For the modified model there is not much to consider: the fitting parameter is unique – it is mainly related to the calculated tie line length – and equation (7) is convex with respect to it. For the original equation, the number of parameters is larger, but their physical meaning somehow restricts their value. In this case, meaningless solutions were sometimes obtained and subsequently ignored. Complete analysis of this issue can be found, for instance, in Dominguez et al. (2002).

The values of the objective function presented in Eq. (7) are shown in Table 2.

It could be noted that the use of the chemical theory provided more reliable equilibrium calculations, despite the fact that the number of adjustable parameters obtained by direct fitting of liquid-liquid equilibrium data is lower. Let us consider system 5 in Table 1 as an example to illustrate the performance of both the original and modified Flory-Huggins expressions. The results obtained with these two equations are presented in Figures 1 and 2.

Equilibrium calculations with the chemical-theory-based model are in much better agreement with the experimental data than those obtained with the original model, despite the fact that the latter has three fitting parameters, while the modified equation has only one. It can also be concluded that, although the series of reactions represented by Eq. (1) does constitute a simplification of the real situation, it was sufficient to improve the performance of the original model to a large extent.

Solvation of PEG Molecules

The chemical-theory-modified model can be further improved by considering PEG molecules to exist in equilibrium in a solvated form according to the chemical reaction

whose equilibrium constant is k_P.

In this case, fitting three parameters to a simple curve that represents water activity of PEG solutions does not give reliable results due to the occurrence of multiple optimal points. In order to reduce the number of adjustable parameters, the number of water molecules in the solvation shell – the value j in Eq. (8) – and the value of the solvation constant were >set beforehand, and the interaction parameter PEG-water was then obtained by minimization of Eq. (5). Analysis showed that the optimal number of water molecules was equal to twice the number of oxygen atoms in the PEG molecule – each oxygen atom acts as donor of two electron pairs. As to the equilibrium constant, its value was high enough for the reaction (8) to be considered complete – a slightly better result was achieved for some finite values of the solvation constant, but the simplification of considering the reaction complete when calculating liquid-liquid equilibrium compensated for this restriction. In this case, the parameter for interaction between PEG and water was found to be c=-0.054. The water activity was also better correlated, with the value of the objective function in Eq. (5) decreasing to 0.0023.

The results obtained when considering this solvation of the PEG molecules were slightly better than those with only self-association being taken into account. The value of the objective function, Eq. (7), for the systems presented in Table 1 is shown in Table 3. The results of application of the model when including solvation obtained for system 5 are presented in Figure 3.

It is important to reiterate the fact that in this case the model allowed a good representation of both water activity and liquid-liquid equilibrium data.

CONCLUSIONS

The application of a chemical-theory-based Gibbs energy equation in the modeling of phase equilibrium data of aqueous two-phase systems is presented. The model is based on the Flory-Huggins equation modified by Kretschmer and Wiebe (1954). The stability test of Michelsen (1982ab) is used to verify the conditions for phase separation and to provide initial guesses for phase equilibrium calculations. The results obtained were remarkably better than those obtained with the original form of the Flory-Huggins equation, demonstrating that chemical theory can provide an adequate description of liquid-liquid equilibrium in these systems. Accounting for self-association of water and solvation of PEG molecules allowed a still better description of both water activity data and liquid-liquid equilibrium data of aqueous two-phase systems formed by PEG and dextran.

ACKNOWLEDGMENTS

Financial support from FAPESP and CNPq in the form of scholarships to P. A. P. F. and R. S. M. respectively is gratefully acknowledged. The authors wish to thank Prof. Dr. E. A. Miranda for his kind help and the valuable discussions.

NOMENCLATURE

Latin Letters A_i cluster formed by i monomer unities a_j activity of compound j G Gibbs energy [J] H⁰ standard enthalpy [J mol^-1] K constant [J mol^-1] M_j mass per amount of substance of compound j [g mol^-1] n amount of substance [mol] n_j amount of substance of compound j [mol] P polymer R gas constant [8.314 Pa m³ mol^-1 K^-1] r number of experimental points S⁰ standard entropy [J K^-1] T absolute temperature [K] t number of parameters V volume per amount of substance [m³ mol^-1] y composition of a hypothetical separated phase analytical composition of a hypothetical separated phase Y_j variable defined by Eq. (3) z composition of the system analytical composition of the system Greek Letters c interaction parameter of the Flory-Huggins equation f_j volume fraction of compound j analytical activity coefficient of compound j m_j chemical potential of compound j [J mol^-1] standard chemical potential of compound j [J mol^-1] s₁ residual standard deviation for water activity correlation, Eq. (5) s₂ residual standard deviation for phase equilibrium correlation, Eq. (7) Subscripts A self-associating compound ass association D inert compound Exponents calc calculated exp experimental p phase

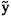
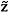
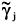
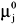
Received: March 19, 2003;

Accepted:

• Abrams, D.S. and Prausnitz, J.M., Statistical Thermodynamics of Liquid Mixtures: A New Expression for the Excess Gibbs Free Energy of Partly or Completely Miscible Systems, AIChE J., 21, 116-128 (1975).
• Anderko, A., A Simple Equation of State Incorporating Association, Fluid Phase Equilibria, 45, 39-67 (1989).
• Anderko, A., Phase Equilibria in Aqueous Systems from an Equation of State Based on the Chemical Approach, Fluid Phase Equilibria, 65, 89-110 (1991).
• Brandani, V., A Continuous Linear Association Model for Determining the Enthalpy of Hydrogen-Bond Formation and the Equilibrium Association Constant for Pure Hydrogen-Bonded Liquids, Fluid Phase Equilibria, 12, 87-104 (1983).
• Brandani, V. and Evangelista, F., The UNIQUAC Associated-Solution Theory: Vapor-Liquid Equilibria of Binary Systems Containing One Associating and One Inert or Active Component, Fluid Phase Equilibria, 17, 281-302 (1984).
• Diamond, A.D. and Hsu, J.T., Fundamental Studies of Biomolecule Partitioning in Aqueous Two-Phase Systems, Biotechnol. Bioeng., 34, 1000-1014 (1989a).
• Diamond, A.D. and Hsu, J.T., Protein Partitioning in PEG/Dextran Aqueous Two-Phase Systems, AIChE J., 36, 1017-1024 (1989b).
• Dolezalek, F., Zur Theorie der binären Gemische und konzentrierten Lösungen, Z. Phys. Chem., 64, 727-747 (1908).
• Dominguez, A., Tojo, J. and Castier, M., Automatic Implementation of Thermodynamic Models for Reliable Parameter Estimation Using Computer Algebra, Computers & Chemical Engineering, 26, 1473-1479 (2002).
• Flory, P.J., Thermodynamics of High Polymer Solutions, J. Chem. Phys., 10, 51-61 (1942).
• Forciniti, D., Hall, C.K. and Kula, M.-R., Analysis of Polymer Molecular Weight Distribution in Aqueous Two-Phase Systems, Fluid Phase Equilibria, 61, 243-262 (1991).
• Grobmann, C., Tintinger, R., Zhu, J. and Maurer, G., Aqueous Two-Phase Systems of Poly(ethylene glycol) and Dextran Experimental Results and Modeling of Thermodynamic Properties, Fluid Phase Equilibria, 106, 111-138 (1995).
• Heidemann, R.A. and Prausnitz, J.M., A van der Waals-Type Equation of State for Fluids with Associating Molecules, Proc. Natl. Acad. Sci. USA, 73, 1773-1776 (1976).
• Ikonomou, G.D. and Donohue, M.D., Thermodynamic of Hydrogen-Bonded Molecules: The Associated Perturbed Anisotropic Chain Theory, AIChE J., 32, 1716-1725 (1986).
• Kretschmer, C.B. and Wiebe, R., Thermodynamics of Alcohol-Hydrocarbon Mixtures, J. Chem. Phys., 22, 1697-1701 (1954).
• McDonald, C.M. and Floudas, C.A., GLOPEQ: A New Computational Tool for the Phase and Chemical Equilibrium Problem, Computers & Chemical Engineering, 21, 1-23 (1996).
• Michelsen, M.L., The Isothermal Flash Problem. Part I. Stability, Fluid Phase Equilibria, 9, 1-19 (1982a).
• Michelsen, M.L., The Isothermal Flash Problem. Part II. Phase Split Calculations, Fluid Phase Equilibria, 9, 21-40 (1982b).
• Nagata, I., On the Thermodynamics of Alcohol Solutions. Phase Equilibria of Binary and Ternary Mixtures Containing Any Number of Alcohols, Fluid Phase Equilibria, 19, 153-174 (1985).
• Nagata, I. and Kawamura, Y., Excess Thermodynamic Functions of Solutions of Alcohols with Saturated Hydrocarbons: Application of the UNIQUAC Equation to the Associated Solution Theory, Z. Physik. Chem. Neue Folge, 107, 141-158 (1977).
• Nath, A. and Bender, E., On the Thermodynamics of Associated Solutions. 1. An Analytical Method for Determining the Enthalpy and Entropy of Association and Equilibrium Constant for Pure Liquid Substances, Fluid Phase Equilibria, 7, 275-287 (1981a).
• Nath, A. and Bender, E., On the Thermodynamics of Associated Solutions. 2. Vapor-Liquid Equilibria of Binary Systems with One Associating Component, Fluid Phase Equilibria, 7, 289-307 (1981b).
• Nath, A. and Bender, E., On the Thermodynamics of Associated Solutions. 3. Vapor-Liquid Equilibria of Binary and Ternary Systems with Any Number of Associating Components, Fluid Phase Equilibria, 10, 43-56 (1983).
• Pessôa Filho, P.A. and Mohamed, R.S., A Chemical Theory Based Equation of State for Self-Associating Compounds, Thermochimica Acta, 328, 65-71 (1999).
• Pessôa Filho, P.A. and Mohamed, R.S., A Solvation-Based Thermodynamic Model for Aqueous Two-Phase Systems, Braz. J. Chem. Eng., 18, 449-458 (2001).
• Renon, H. and Prausnitz, J.M., On the Thermodynamics of Alcohol-Hydrocarbon Solutions, Chem. Eng. Sci., 22, 299-307 (1967).
• Shinta, A.A. and Firoozabadi, A., Equation of State Representation of Aqueous Mixtures Using an Association Model, Can. J. Chem. Eng., 73, 367-379 (1995).
• Tessier, S.R., Brennecke, J.F. and Stadtherr, M.A., Reliable Phase Stability Analysis for Excess Gibbs Energy Models, Chem. Eng. Sci., 55, 1785-1796 (2000).
• Wenzel, H. and Krop, E., Phase Equilibria by Equation of State. A Short-Cut Method Allowing for Association, Fluid Phase Equilibria, 59, 147-169 (1990).
• Zaslavsky, B.Y., Aqueous Two-Phase Partitioning, New York, Marcel Dekker (1995).

*

To whom correspondence should be addressed

Publication Dates

• Publication in this collection
  14 July 2004
• Date of issue
  Sept 2004

History

• Accepted
  13 Apr 2004
• Received
  19 Mar 2003