Abstract
Phase equilibrium calculations for fluids confined inside capillary tubes or porous media are formulated using the isofugacity equations. In this situation, the phase pressures are not equal and it is assumed that they are related by the Laplace equation. With this formulation, existing procedures for phase equilibrium calculations can be readily modified to include capillary effects. In this paper, we review some of the main authors who have studied the behavior of fluids inside porous media and perform bubble- and dew-point calculations for pure components and mixtures, using the Peng-Robinson equation of state to model the coexisting phases and several planar surface tension models. Comparisons with results from the literature indicate that the proposed formulation is adequate for representing phase equilibrium inside capillary tubes.
Phase equilibrium; Porous media; Surface tension; Confined fluids; Laplace equation
THERMODYNAMICS
Phase equilibrium calculations for confined fluids, including surface tension prediction models
R. O. Espósito; F. W. Tavares; M. Castier* * To whom correspondence should be addressed
Escola de Química, Universidade Federal do Rio de Janeiro, Phone: +(55) (21) 2562-7607, Fax: +(55) (21) 2562-7567, Cx. P. 68542, 21949-900, Rio de Janeiro - RJ, Brazil. E-mail: castier@eq.ufrj.br
ABSTRACT
Phase equilibrium calculations for fluids confined inside capillary tubes or porous media are formulated using the isofugacity equations. In this situation, the phase pressures are not equal and it is assumed that they are related by the Laplace equation. With this formulation, existing procedures for phase equilibrium calculations can be readily modified to include capillary effects. In this paper, we review some of the main authors who have studied the behavior of fluids inside porous media and perform bubble- and dew-point calculations for pure components and mixtures, using the Peng-Robinson equation of state to model the coexisting phases and several planar surface tension models. Comparisons with results from the literature indicate that the proposed formulation is adequate for representing phase equilibrium inside capillary tubes.
Keywords: Phase equilibrium; Porous media; Surface tension; Confined fluids; Laplace equation.
INTRODUCTION
Calculation of phase equilibrium of fluids confined by solid walls is important for several applications. For instance, petroleum fluids occur naturally inside porous media. In this situation, due to capillarity, phase interfaces may be curved with an abrupt change in pressure. In addition, interfaces do not occur at well-defined heights as in regular phase equilibrium calculations. Instead, for deep reservoirs, differences in pore size give origin to transition regions known as gas-oil contact (GOC) and water-oil contact (WOC) regions, which should be totally absent when only gravitational effects are considered (Wheaton, 1991).
In reservoir engineering, the influence of porous media on the behavior of gas-condensate systems has been difficult to distinguish because of the dubious ability of packed PVT cells to represent actual porous rocky matrixes. Some authors have studied phase equilibrium of hydrocarbon mixtures in such systems and could not observe any considerable difference in their behavior due to capillary effects, at least for the pore size they were able to work with in their laboratories.
Tindy and Raynal (1966) reported differences in bubble-point pressure for crude oils in conventional PVT cells and in porous media, but found none when dealing with a methane+n-heptane mixture in the same phase equilibrium cells.
Sigmund et al. (1973) used packed (1-mm spheres) and unpacked cells but did not observe different vapor compositions and liquid saturations for methane+n-butane and methane+n-pentane mixtures in a constant-composition expansion (CCE) process. They also made calculations for more severe curvatures, using experimental surface tension values to predict its influence on the methane+n-pentane system.
Lee (1989) presented other theoretical results on the process of constant-composition expansion (CCE) of a multicomponent gas-condensate fluid. Liquid- and vapor-phase compositions are obtained as functions of the vapor-phase pressure and the curvature. Lee (1989) also presented an interesting algorithm to consider effects of both capillarity and gravity, reporting profiles for liquid- and gas-pressure and composition with height.
Tester and Modell (1996) and Firoozabadi (1999) present clear formulations of the equilibrium conditions for curved interfaces, providing some examples that will be discussed later in this paper.
Moreover, porous media can be used to enhance fluid separation, as demonstrated by Al-Rub and Datta (1999). These authors used a semi-empirical model to predict the breakage of azeotropes in porous plates for systems with large differences in polarity, such as cyclohexane+ethanol in sintered stainless steel plates.
Shapiro and Stenby (1997, 2001) derived a generalized form of the Kelvin equation for nonideal fluid mixtures. The derivation is based on the integration of the Clausius-Clayperon equation for mixtures. Shin and Simandl (1999) used this generalized form of the Kelvin equation to predict the phase behavior of some binary mixtures in the pores of glass plates. Although they obtained theoretical results that agreed well with their experimental measurements, their model has given rise to controversy (Shapiro and Stenby, 2000) because of the improper use of the equation in calculations for mixtures. Even though Shapiro and Stenby (1997) made an important contribution to the formulation of the phase equilibrium of confined fluids, the derivation and application of their generalized Kelvin equation introduces unfamiliar parameters such as average compressibility and mixed volume.
Our objective in this work is to formulate a flexible algorithm for the calculation of the vapor-liquid equilibrium of confined fluids, including the effect of surface tension. This approach is based on the isofugacity criterion and on the Laplace equation to compute the pressure difference between the liquid and vapor phases, as done by Tester and Modell (1996) for pure components. Here, we extend this formulation to mixtures. Unlike most of the authors of previous articles using similar approaches, we use models for predicting surface tension as a function of composition and density of both coexisting phases instead of constant values for this property. This adds to the complexity of the problem because the surface tension is a function of composition and density of both phases, which in turn are calculated from an equation of state (EOS). Moreover, depending on the type of specification, the Laplace and the isofugacity equations need to be simultaneously solved. In most of the published articles with similar approaches, the specifications adopted allow the Laplace equation to be solved after the isofugacity equations are satisfied. The algorithm developed handles the simultaneous solution of both types of equations, with surface tensions predicted from models, and therefore is more general than those proposed in the publications reviewed.
FORMULATION
We assume a mixture of nc components with a vapor and a liquid phase in equilibrium inside a capillary tube of radius R with a contact angle q. The curvature radius, rc, is given by  . The surface tension of the mixture is denoted by s. The Laplace equation (Lee, 1989; Tester and Modell, 1996; Sychev, 1981) relates the pressures in the liquid (PL) and vapor (PV) phases:
. The surface tension of the mixture is denoted by s. The Laplace equation (Lee, 1989; Tester and Modell, 1996; Sychev, 1981) relates the pressures in the liquid (PL) and vapor (PV) phases:
Wettability effects can be introduced by specifying the value of angle q a priori. For example, for gas-condensate mixtures, capillary pressure, PC, given by PV PL, is positive, and therefore cosq > 0 if oil is the wetting phase. For complex porous structures, a mean curvature value can be used, for example, by means of the Leverett J-function (1941) and its later modifications (Garrouch, 1999; Wo et al., 2001).
Phase equilibrium also implies that the fugacities of each component i should be equal in the liquid (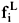 ) and the vapor (
) and the vapor (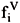 ) phases, even if the phases are at different pressures, i.e.,
) phases, even if the phases are at different pressures, i.e.,
It also holds that
In equation (2), we use the ideal gas reference state for each component at 1 bar and at the temperature of the system. The fugacities of each component i in the liquid or in the vapor phases are calculated using the Peng-Robinson EOS with the classical mixing rule.
where Kij is the binary interaction parameter.
In usual dew- and bubble-point calculations, the pressures in the two phases are equal. Therefore, one of the possibilities is to specify the temperature and mole fractions in one of the phases and solve the system of nc instances of equation (2) and equation (3) (or (4)) to determine the pressure and mole fractions of the other phase. In calculations of capillary condensation, one of the possibilities is to specify the temperature, mole fractions in one of the phases and one of the phase pressures (PV or PL). Equations (2) and (3) (or (4)) are solved for mole fractions and pressure of the other phase. This allows the calculation of the surface tension and then use of equation (1) to determine the R/cosq ratio. This sort of specification, used by Shapiro and Stenby (1997), therefore allows the uncoupling of the Laplace equation (eq. (1)) from the other system equations. However, another important problem occurs when none of the phase pressures is specified, i.e., when the specifications are the temperature, mole fractions in one of the phases, and the R/cosq ratio. In this case, the Laplace equation (eq. (1)) needs to be solved simultaneously with equations (2) and (3) (or (4)).
We solved this system of nonlinear equations using the Newton-Raphson algorithm with step-size control to prevent nonphysical values during the iterations, especially far from the solution. Analytical derivatives of all the necessary physical properties were automatically obtained using the Thermath program (Castier, 1999). It should be noted that, depending on the surface tension model, its analytical derivatives are rather involved, increasing the complexity of the algorithm. This will be addressed in the next section.
Surface Tension Models
Several models have been developed since the proposal of McLeod (1923) and Sugden (1932), who introduced the parachor equation for pure substances:
where P is the parachor of the compound and rL and rV are liquid and vapor densities, respectively. Pure-component parachors can be found elsewhere (Reid et al., 1987).
The surface tension of pure substances can be calculated independent of the densities, as in the case of the model of Miqueu et al. (2000). In this model, the surface tension of a pure species, s, is given by
where k is the Boltzmann constant, NA is the Avogadro number, and t = 1 T/Tc. The symbols Tc, vc, and w denote the critical temperature, critical volume, and acentric factor, respectively.
The McLeod-Sugden equation was extended to mixtures by Weinaug and Katz (1943):
Danesh et al. (1991) reviewed some of the major contributions for predicting the surface tension of multicomponent systems, observing that eq. (9) is still one of the most widely used for this purpose. Danesh et al. (1991) also proposed a modification of the surface tension exponent, which was assumed to be a function of the difference between the density of the liquid and the vapor phases:
where parameter E is given by
The molar densities depend on temperature, phase pressure, and mole fractions. Therefore, the derivatives of the surface tension model may depend on terms that come from the equation of state adopted for the system.
It should be emphasized that equations (8), (9), and (10) provide surface tension expressions for planar surfaces. When system dimensions reach the order of magnitude of tens of nanometers, interface curvature begins to affect surface tension, since the extension of the layer of transition between phases becomes of the same order of magnitude of molecular dimensions. Precise evaluation of this kind of influence remains a challenge in surface phenomena. The pioneering work of Tolman (1948, 1949) introduced a characteristic length (d), which represents the distance from the Gibbs surface of tension (Tolman, 1948) to another specific dividing surface within the transition layer for which the molar surface density vanishes (Tolman, 1949).With the Tolman length, it is possible to estimate the surface tension correction by means of the following relation (Tolman, 1949):
where splane is the surface tension for planar surfaces and sR is the corrected value.
Several authors (Blockhuis and Bedaux, 1992; Bykov and Zeng, 1999a, 1999b) have presented expressions for the computation of d and splane based on statistical mechanics approaches. Their results were corroborated by molecular dynamic simulations for pure-component systems. Malyshenko and Dunikov (2002) recently proposed a series expansion for pure-component surface tension correction in small-sized systems, as well as a simple expression for the Tolman length, which should be useful for engineering calculations.
The extension of Tolman's approach to mixtures should include a composition-dependent term in eq. (12). Robust constitutive equations for this extension to mixtures are not available in the literature reviewed. Therefore, in this work, we used equations (8), (9), and (10) for calculating surface tensions directly, without using the Tolman length to account for the effect of curvature. It should be noted that in the work of Sigmund et al. (1973), Lee (1989), Tester and Modell (1996), Firoozabadi (1999), and Shapiro and Stenby (1997), whose calculations were similar to ours, surface tension corrections due to the influence of curvature were also neglected. Moreover, these authors adopted constant surface tension values in their calculations, contrary to what is done in our work.
Indeed, curvature will indirectly affect our calculated surface tension values because of the coupling of isofugacity, Laplace, and surface tension model equations. However, such surface tension values should be regarded with caution, especially for small-sized systems with curvature radii on the order of tens of nanometers.
RESULTS AND DISCUSSION
We present results for pure species and for mixtures. In all cases, the Peng-Robinson EOS was used. Critical properties, acentric factors, and group parameters for calculating the parachors (when needed) were taken from Reid et al. (1987).
Example 1
Tester and Modell (1996) present a problem whose objective is to determine the radius of a spherical ethane bubble in liquid ethane at 1 bar and 270 K. In solving this problem, they assumed that the vapor pressure of ethane was 22.1 bar and its liquid molar volume and surface tension were 7.38×10-5 m3/gmol and 3.5 mN/m, respectively. Assuming the liquid to be incompressible, they obtained a pressure inside the gas bubble of 20.6 bar and a bubble radius of 3.571×10-9 m. We specified the same temperature, a radius of 3.571×10-9 m and imposed a contact angle q = 0, given that the pressure of the vapor phase is higher than that in the liquid. In accordance with Firoozabadi (1999), we then assume that a bubble in equilibrium within a liquid mass is analogous to a wetting liquid rising in a capillary tube. No phase pressures were specified. The surface tension was calculated using the correlation of Miqueu et al. (2000) (eq. 8). Our calculations resulted in a surface tension of 3.502 mN/m, and pressure values for the vapor and the liquid phases of 20.06 bar and 0.45 bar, respectively. As should be expected, the phase pressure difference (PV PL) is the same as that obtained by Tester and Modell (1996), i.e., 19.6 bar. The phase pressures are in good agreement with those of Tester and Modell (1996), even though they are not identical because, in our case, they were calculated using the Peng-Robinson EOS. For the sake of comparison, the vapor pressure of ethane at 270 K predicted by the Peng-Robinson EOS is 22.22 bar in the absence of any capillary effect.
Example 2
Let us consider the theoretical calculations of Sigmund et al. (1973) for the methane+n-pentane binary system. These authors used isofugacity equations with different phase pressures, using an equation of state for the vapor phase and an excess Gibbs free-energy model with Poynting correction for the liquid phase (Prausnitz and Chueh, 1968). The unsymmetrical convention was adopted for the activity coefficients. Specifying curvature, temperature, and liquid-phase composition, they could use the two equilibrium equations and the Laplace relation to obtain one independent mole fraction in vapor phase and both liquid- and vapor-phase pressures. Their algorithm is relatively simple because it uses experimental values of surface tension, which depend only on the specified liquid-phase composition (Stegemeier, 1959).
Here we used surface tension models, which increase the complexity of the procedure because of density and compositional derivatives, and the Peng-Robinson EOS to perform our calculations. The temperature was set at 310.93 K. Surface tensions were calculated using either the Weinaug and Katz (1943) parachor method or its modification by Danesh et al. (1991). In Figures 1 and 2 respectively the behavior of the gas-phase pressure and of the vapor-phase mole fractions are presented for different specifications of the liquid mole fractions. There is excellent agreement with the results of Sigmund et al. (1973). Our results using both methods for predicting the surface tension are nearly identical, and for this reason, they are not distinguishable in the figures. The results for calculated surface tension are compared to the experimental values of Stegemeier (1959) (Sigmund et al., 1973) in Figure 3. In this figure, it is possible to observe the effect of curvature radius on surface tension, even though it is not pronounced for the radii considered. For r=10-8 m, we found that negative liquid-phase pressure values may occur for methane mole fractions less than 0.12, which is the starting point of our curve. It should be remarked that cubic equations of state can show this behavior, as reported by Shapiro and Stenby (2001).
Example 3
In this example, we test our algorithm in a gas-condensate system presented by Lee (1989), whose complete characterization (including parachors) is reproduced in Tables 1 and 2. Lee (1989) performed several types of calculations, but the ones relevant for comparison with our work are those in which he specified the temperature, vapor-phase composition, and curvature, obtaining vapor- and liquid-phase pressures as well as liquid-phase composition. Curvature values were specified by arbitrarily varying the connate water saturation in an adequate Leverett J-function (Lee, 1989).
Specifying the same temperature (384.26 K), vapor-phase composition, and curvature values (r = ¥, 66, 10, 0.4, 0.1 mm) as those reported by Lee (1989), we calculated phase pressures and liquid compositions, using the modified Weinaug and Katz (1943) parachor equation of Danesh et al. (1991). We also set q = 0 (oil is the wetting phase).
Our results are compared to those of Lee (1989) in Table 3. As we used the same thermodynamic model (Peng-Robinson), differences in pressures and compositions could be attributed to the Taylor expansion used by Lee (1989) to approximate the liquid-phase chemical potentials, thereby obtaining a modified isofugacity condition (eq. 6 of Lee's paper). This equation may be thought of as a modified Kelvin equation to compute effects of composition and pressure. It is also unclear how Lee (1989) accounted for the effect of pressure on the parachor equation for surface tension. Nevertheless, it should be stressed that our results follow the same trend as those of Lee (1989): the vapor-phase pressure at the dew point increases as the radius is reduced, which is expected for retrograde systems. Agreement with the trends reported by Lee (1989) for the methane and C7+ liquid mole fractions was also observed.
Example 4
In this example, we deal with a binary mixture of methane and n-decane and specified the same temperature (310.93 K), liquid composition (99.894 mole % C1), and radii (ranging from 0.01 to 100 mm) as those presented by Firoozabadi (1999). Again, we set q = 0. In our calculations we used both the Weinaug and Katz parachor equation (1943) and its modification by Danesh et al. (1991). Our results for phase pressure and liquid-phase composition are presented in Figures 4 and 5. For the dew-point pressure and the methane mole fraction curves, our results with both surface tension models are lower than those reported by Firoozabadi (1999), who used a constant value for surface tension of 9.76 mN/m. However, all results show the same qualitative trend. For instance, for radii greater than 0.1 mm, variations in phase pressure and liquid composition are small in all cases. Our dew-point pressure (97.4 bar) at infinite radius is slightly lower than the value reported by Firoozabadi (1999) (98.2 bar) and both are lower than the experimental value of 100 bar. In Figure 6 we also show our surface tension values. Both parachor equations provide values of surface tension lower than 9.76 mN/m, which is the constant value used by Firoozabadi (1999). As previously mentioned, the calculated surface tension values for small-sized systems should be regarded with caution; the behavior of s models in Figure 6 are in qualitative agreement with the statements of Tolman (1949), who predicted that surface tension should decrease as we reduce the radius (at least for pure compounds).
Example 5
In this last example, we applied our algorithm to a binary methane+n-butane system studied by Shapiro and Stenby (1997), who presented the so-called modified Kelvin equation:
where PD is the dew-point pressure; vmix and vL are the mixed and liquid volumes, respectively; Zav is the average compressibility factor between PL and PD; and c is the relative pressure PV/PD. The mixed volume is given by
where  is the liquid mole fraction of component i at the noncapillary dew point and
is the liquid mole fraction of component i at the noncapillary dew point and 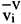 is the partial molar volume of component i in vapor phase.
is the partial molar volume of component i in vapor phase.
Demonstration of eq. (12) is somewhat complex, dealing with unfamiliar variables like mixed volume, relative pressure and average compressibility factor, but the calculations presented by Shapiro and Stenby (1997) using this approach are quite simple.
Knowing a "noncapillary" dew-point condition, i.e., PD, y, and its respective liquid-phase composition, Shapiro and Stenby (1997) varied the relative pressure arbitrarily, so that they could compute the respective PC values. Then, using the surface tension model proposed by Danesh et al. (1991), they could easily solve the uncoupled Laplace equation to obtain the curvature radii. They presented their results, plotting PC versus PV/PD and r versus PV/PD for three different dew-point pressures, namely, PD = 80, 100, and 120 bar.
According to the Peng-Robinson EOS, at 300 K, the dew-point pressure of a vapor phase of a methane+n-butane mixture containing 85.9 mole percent of methane is 120 bar. Therefore, we set the temperature at 300 K and varied curvature radius from 10-10 to 10-6m, specifying  = 0.859. For each curvature radius, we obtained the pressures of the two phases as well as the liquid-phase composition. We emphasize that our algorithm couples the Laplace equation with isofugacity equilibrium conditions. Again, we used the equation of Danesh et al. (1991) for calculating surface tension.
= 0.859. For each curvature radius, we obtained the pressures of the two phases as well as the liquid-phase composition. We emphasize that our algorithm couples the Laplace equation with isofugacity equilibrium conditions. Again, we used the equation of Danesh et al. (1991) for calculating surface tension.
Figure 7 presents some of our results in a r-versus-PV/PD graph. As we reduce the radius from 10-6m to approximately 10-9m, our profile shows (although only qualitatively) Shapiro and Stenby's (1997) monotonic behavior. Below this value, relative pressure reaches a maximum value and then drops to values lower than one. Shapiro and Stenby (1997) only predicted a monotonic behavior of the same type as that of the upper part of the curve shown in Fig. 7, probably because they specified a priori that the PV/PD ratio is always greater than 1. According to our calculations, as shown in Figure 7, there are two capillary radii which are solutions of the equilibrium equations in the region 1 < PV/PD < 1.04.
Figure 8 shows that surface tension varies over a relatively wide range (-95% to +55%) around the single value (0.206 mN/m) used by Shapiro and Stenby (1997). Again, the behavior of s follows the qualitative trend stated by Tolman (1949) (at least for pure compounds), i.e., it decreases as the radius of curvature decreases.
CONCLUSIONS
An algorithm coupling the isofugacity conditions for different phase pressures with the Laplace equation was proposed. It was used for calculation of phase equilibrium in systems whose surface tension was calculated by thermodynamic models, instead of adopting constant values. The algorithm is more general than others reviewed in this article, and allows more flexible specifications. Although there is no experimental data to validate the results reported either by us or by the authors reviewed, our results agree very reasonably with those of Tester and Modell (1996), Sigmund et al. (1973), Lee (1989) and Firoozabadi (1999). Of all the examples, there is qualitative discrepancy only in the case of the methane+n-butane system studied by Shapiro and Stenby (1997). We credit the deviations to the different kind of specifications, thermodynamic formulation, and in our case, the use of a model for calculating the surface tension instead of adopting a constant value. An interesting suggestion for future work is to derive an extension of Tolman's approach to mixtures and include it in the formulation presented here.
ACKNOWLEDGMENTS
The authors acknowledge the financial support of the following Brazilian agencies and/or programs: FAPERJ, CNPq, and PRONEX (Grant no. 124/96).
NOMECLATURE
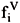
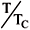
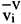
Greek Letters
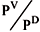
Received: January 6, 2004
Accepted: September 24, 2004
- Al-Rub, F.A.A. and Datta, R., Theoretical Study of Vapor-Liquid Equilibrium inside Capillary Porous Plates, Fluid Phase Equilibria, 162, 83 (1999).
- Blokhuis, E.M. and Bedaux, D., Pressure Tensor of a Spherical Interface, J. Chem. Phys., 97, no. 5, 3576 (1992).
- Bykov, T.V. and Zeng, X.C., A Patching Model for Surface Tension and the Tolman Length, J. Chem. Phys., 111, no. 8, 3705 (1999a).
- Bykov, T.V. and Zeng, X. C., A Patching Model for Surface Tension of Spherical Droplet and Tolman Length, J. Chem. Phys., 111, no. 23, 10602 (1999b).
- Castier, M., Automatic Implementation of Thermodynamic Models Using Computer Algebra, Computers and Chemical Engineering, 23, 1229 (1999).
- Danesh, A.S., Dandekar, A.Y., Todd, A.C., and Sarkar, R., A Modified Scaling Law and Parachor Method Approach for Improved Prediction of Interfacial Tension of Gas-Condensate Systems. SPE 22710, Dallas, TX, Oct (1991).
- Firoozabadi, A., Thermodynamics of Hydrocarbon Reservoirs, McGraw Hill Co., USA (1999).
- Garrouch, A.A., A Modified Leverett J-Function for De Dune and Yates Carbonate Fields: A Case Study, Energy and Fuels, 13, 1021 (1999).
- Lee, S-T., Capillary-Gravity Equilibria for Hydrocarbon Fluids in Porous Media. SPE 19650, San Antonio, TX, Oct (1989).
- Leverett, M.C., Capillary Behavior in Porous Solids, Trans AIME, 142, 152 (1941).
- Malyshenko, S.P. and Dunikov, D.O., On the Surface Tension Corrections in Nonuniform and Nonequilibrium Liquid-Gas Systems, Int. J. Heat Mass Trans, 45, 5201 (2002).
- McLeod, D.B., On a Relation between Surface Tension and Density, Trans. Faraday Soc., 19, 38 (1923).
- Miqueu, C., Broseta, D., Satherley, J., Mendiboure, B., Lachaise, J., and Graciaa, A., An Extended Scaled Equation for the Temperature Dependence of the Surface Tension of Pure Compounds Inferred from an Analysis of Experimental Data, Fluid Phase Equilibria, 172, 169 (2000).
- Prausnitz, J.M. and Chueh, P.L., Computer Calculations for High-Pressure Vapor-Liquid Equilibria, Prentice-Hall Inc, Englewood Cliffs, N.J. (1968).
- Reid, R.C., Prausnitz, J.M., and Poling, B.E., The Properties of Gases and Liquids, McGraw Hill, N.Y. (1987).
- Shapiro, A.A. and Stenby, E.H., Kelvin Equation for a Non-Ideal Multicomponent Mixture, Fluid Phase Equilibria, 134, 87 (1997).
- Shapiro, A.A. and Stenby, E.H., Comment on "Vapor-Liquid Equilibria in Porous Media", Fluid Phase Equilibria, 173, 159 (2000).
- Shapiro, A.A. and Stenby, E.H., Thermodynamics of the Multicomponent Vapor-Liquid Equilibrium under Capillary Pressure Difference, Fluid Phase Equilibria, 178, 17 (2001).
- Shin, Y. and Simandl, J., Vapor and Liquid Equilibria in Porous Media, Fluid Phase Equilibria, 166, 79 (1999).
- Sigmund, P.M., Dranchuk, P.M., Morrow, N.R. and Purvis, R.A., Retrograde Condensation in Porous Media, Soc. Pet. Eng. J., 93, April (1973).
- Stegemeier, G.L., Interfacial Tension of Synthetic Condensate System, Ph.D. dissertation, University of Texas at Austin (1959).
- Sugden, S., The Parachors and Valency. A List of Parachors, Brit. Assoc. Report (1932).
- Sychev, V.V., Complex Thermodynamics Systems, MIR publishers, Moscow (1981).
- Tester, J.W. and Modell, M., Thermodynamics and its Applications, Prentice Hall International Series, 3rd edition (1996).
- Tindy, R. and Raynal, M., Are Test-Cell Saturation Pressures Accurate Enough? Oil and Gas Journal, 128, Dec (1966).
- Tolman, R.C., Consideration of the Gibbs Theory of Surface Tension, J. Chem. Phys., 16, no. 8, 758 (1948).
- Tolman, R.C., The Effect of Droplet Size on Surface Tension, J. Chem. Phys., 17, no. 3, 333 (1949).
- Weinaug, C.F. and Katz, D.L., Surface Tension of Methane-Propane Mixtures, Ind. Eng. Chem., 239 (1943).
- Wheaton, R., Treatment of Variations of Composition with Depth in Gas-Condensate Reservoirs. SPE Res. Eng. May (1991), 239.
- Wo, S., Xie, X., and Morrow, N.R., A Statistical Model of Apparent Size Distribution and Drainage Capillary Pressure. Colloids and Surfaces, A: Physicochemical and Engineering Aspects, 187-188, 449 (2001).
Publication Dates
-
Publication in this collection
14 Mar 2005 -
Date of issue
Mar 2005
History
-
Received
06 Jan 2004 -
Accepted
24 Sept 2004
























