Parameter estimation for LLDPE gas-phase reactor models

PROCESS SYSTEMS ENGINEERING

Parameter estimation for LLDPE gas-phase reactor models

G. A. Neumann^I; T. F. Finkler^II; N. S. M. Cardozo^II; A. R. SecchiII, ^*

^IBraskem S/A, III Pólo Petroquímico, Via Oeste, Lote 5, CEP: 95853-000, Triunfo - RS, Brazil Phone: +(55) (51) 3457-5495 – Fax: +(55) (51) 3457-5450, E-mail: [e-mail] ^IIGrupo de Modelagem, Simulação, Controle e Otimização de Processos (GIMSCOP), Departamento de Engenharia Química, Universidade Federal do Rio Grande do Sul, Phone: +(55) (51) 3308-3528, Fax: +(55) (51) 3308-3277, Rua Sarmento Leite, 288/24, CEP: 90050-170, Porto Alegre - RS, Brazil. E-mail: [e-mail], E-mail: [e-mail], E-mail: [e-mail]

ABSTRACT

Product development and advanced control applications require models with good predictive capability. However, in some cases it is not possible to obtain good quality phenomenological models due to the lack of data or the presence of important unmeasured effects. The use of empirical models requires less investment in modeling, but implies the need for larger amounts of experimental data to generate models with good predictive capability. In this work, nonlinear phenomenological and empirical models were compared with respect to their capability to predict the melt index and polymer yield of a low-density polyethylene production process consisting of two fluidized bed reactors connected in series. To adjust the phenomenological model, the optimization algorithms based on the flexible polyhedron method of Nelder and Mead showed the best efficiency. To adjust the empirical model, the PLS model was more appropriate for polymer yield, and the melt index needed more nonlinearity like the QPLS models. In the comparison between these two types of models better results were obtained for the empirical models.

Keywords: Ethylene polymerization; Parameter estimation; Empirical model; Phenomenological model, LLDPE.

INTRODUCTION

Multivariate models for polymerization processes provide useful information about process and product characteristics and are therefore important to the polymer industry. Thus, correctly validated multivariate models are essential to the development of reliable optimization procedures and predictive controllers.

Depending on their nature, i.e., empirical, phenomenological, or hybrid, these models may give different levels of information. Phenomenological models have higher extrapolation capability than empirical models, which is advantageous for process optimization and product development. However, the development of phenomenological models may be too expensive when there is little available information about the phenomena that govern the process. On the other hand, empirical models require less investment in modeling, but need larger experimental datasets to generate models with good predictive capability.

Many studies on the modeling of polyolefin polymerization processes have been developed in the past several decades. Many of these studies have been focused on model description and parameter estimation, which represent important steps in the development of both phenomenological and empirical models.

Sato et al. (2000) studied the modeling and simulation of an industrial gas-phase ethylene polymerization process, based on McAuley's phenomenological model (McAuley and MacGregor, 1991), for use in melt index and density nonlinear control design.

Many published papers deal with application of modeling and parameter estimation in industrial nonlinear model predictive control design (Zhao et al., 2001; Soroush, 1998). Parameter estimation for a phenomenological model should include sensibility analysis to select the key parameters to be adjusted, like the analysis of Sirohi and Choi (1996). Bindlish et al. (2003) studied the parameter estimation problem for industrial polymerization processes. In their work, two kinetic parameters were estimated for Exxon's homo and copolymerization to use in monitoring and feedback control systems for these processes.

This work studies the parameter estimation step in the modeling of an industrial process for production of linear low-density polyethylene (LLDPE). This process consists of two gas-phase reactors connected in series. Phenomenological and empirical models for the prediction of yield and melt index in each reactor were considered and compared.

PHENOMENOLOGICAL MODEL

The industrial reactors were modeled as fluidized-bed reactors (Kunii and Levenspiel, 1991; Choi and Ray, 1985; Gambetta, 2001). According to the model proposed by Gambetta (2001), the fluidized bed can be divided into two regions: an emulsion phase and a bubble phase, connected by heat and mass transfer between them. The emulsion phase has a solid phase (polymer and catalyst), a gas phase at the minimum fluidization velocity, and a gas phase adsorbed by the solid phase. The bubble phase is composed of the excess gas required to keep the emulsion phase at the minimum fluidization velocity. In the disengagement section, only the gas phase is considered.

The kinetic model was developed for Ziegler-Natta catalysts for the following reactions: spontaneous activation of sites, chain initiation by the monomer, chain propagation, chain transfer to hydrogen, spontaneous deactivation, and deactivation by hydrogen (Gambetta, 2001). Mass balances for the main gases (ethylene, comonomers, solvent, and hydrogen) and polymeric species were used to obtain gas phase and polymer compositions, respectively. The momentum technique for the bulk polymer (the sum of live and dead polymer) was used to determine the molecular weight distribution (Neumann, 2001). Empirical correlations adjusted to experimental data had previously been used to obtain the melt index as a function of the weight average molecular weight predicted by the model.

The resulting system of algebraic-differential equations was implemented in C-language with input and output data manipulation and integration into the Matlab/Simulink® environment. Each reactor model has 22 states and the simulation time is about 25 seconds for 11 days of plant data (Pentium III 800 MHz 128 MB RAM).

Parameter estimation for the phenomenological model was accomplished using the weighted least squares method with Equation 1 as the objective function to be minimized.

where the subindices calc and exp are of the data calculated by the model and the experimental data of the plant, respectively. Prod is the resin yield, MI is the melt index, and w is the weight.

EMPIRICAL MODEL

The empirical model was obtained through PLS (partial least squares) decomposition and its nonlinear extensions, the QPLS (quadratic PLS) and the BTPLS (Box-Tidwell-based PLS). For detailed information about these three PLS versions, readers are referred to Finkler (2003), Wold (1966), Baffi et al. (1999), and Li et al. (2001). The three PLS techniques were implemented using the software Matlab®.

RESULTS

Two industrial process datasets were used, one for parameter estimation and the other for model validation.

Parameter Estimation for the Phenomenological Model

The objective function (Eq. 1) was minimized through the comparison of eight multivariate optimization algorithms without constraints to verify their efficiency in obtaining the minimum (number of evaluations of the objective function). The following techniques were compared: the flexible polyhedrons of Nelder and Mead [NM], Hooke and Jeeves's [HJ], Rosembrock's [RO], Powell's [PO], the complex [CO], Newton's [NE], Newton's with Levenberg-Marquardt's modification [LM] (Himmelblau, 1972), and the global optimization using adaptive random search (Secchi and Perlingeiro, 1989) [RS]. Two of these (NE and LM) are variable metric methods (which use the first and the second derivates of the objective function).

Parameter estimation was carried out in two stages. In the first stage, initial guesses for the parameters were obtained from a preliminary estimation with steady-state data. In the second stage, the variable metric algorithms (LM and NE) were included, using as initial guess the best set of parameters in the first stage. These algorithms were included only in the second stage because they are more sensitive to the initial guesses of the parameters, and in the first stage these initial guesses were very far from the minimum. The dataset used in all estimations was dynamic data from a period of 11 days of production.

In Table 1, a comparison between the optimization methods for the first stage of the estimation is shown. The value of the objective function is 12.8 for the initial set of parameters.

In Table 1, it is possible to verify that all methods reduce the value of the objective function on the same order of magnitude, in relation to the initial value. The difference between the methods is the number of evaluations of the objective function. Due to the time of one simulation, the optimization times were 112 hours for the slowest method (RO) and 1.5 hours for the fastest method (CO).

The analysis of estimations shows that the flexible polyhedron and complex methods had very fast convergence and low values of objective functions. The Rosembrock method was the slowest, but it was highly efficient, with a low value of S. The methods of Hooke and Jeeves and the random search showed values of S that were low, but higher than the minimum found and with the longest time. For this reason, these two methods were excluded in the second stage of estimations.

Table 2 shows the results of the second stage of estimation, where the minimum of S in Equation 1 is sought, taking the results of stage 1 with the NM method and small perturbations as initial guesses for the parameters. The variable metric methods were included in this stage.

Although the number of evaluations of S is large for the flexible polyhedron and complex methods, these showed good results. The variable metric methods showed the highest speed of convergence of all methods, as expected, but they resulted in higher values of the objective function than the other methods.

The set of kinetic parameters chosen at the end of the estimation stages was the result of the flexible polyhedron optimization in stage 2, because this result showed the minimum of the objective function.

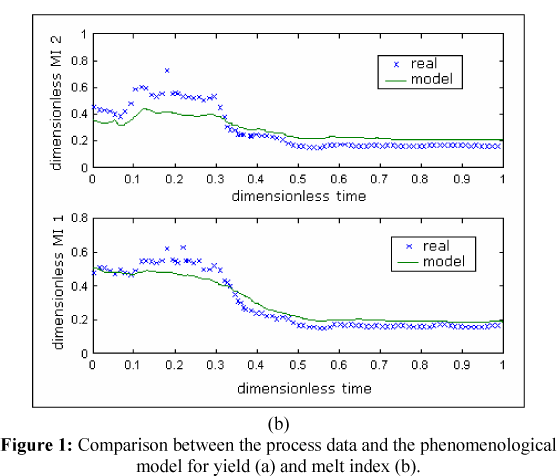
Figure 1a shows the values of yield of each reactor for the data set used in the estimation. Figure 1b shows the same results for the melt index.

It is possible to recognize the need for improving the model dynamics. The tendency of the prediction is different from that of the process data. This can be achieved by including a term of tendency in the objective function.

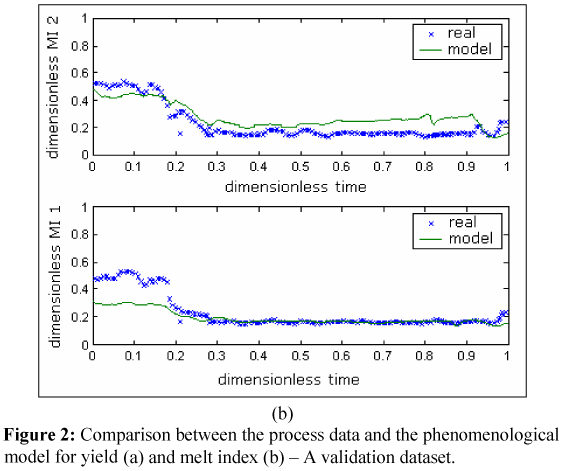
Another dataset of real plant data was used to validate the models. This set includes 12 days of data from a run of a different period from that of the data used in parameter estimation. Figures 2a and 2b show the comparison between plant validation data and model prediction of yield and melt index, respectively. In this case, it can also be noted that the dynamics can be improved. Even so, the prediction has values on the same level as that of the process data.

Empirical Model

Using the seven previously mentioned input variables, the PLS, QPLS, and BTPLS techniques were employed to identify the steady-state gains of the melt index and polymer yield using industrial plant data. The empirical models were generated using 70 stationary points which were selected from the same dataset as that used for the phenomenological model adjustment. Based on the estimated stationary gains and on the identified system dynamics, dynamic empirical models were built.

For both reactors, the polymer yield values predicted by the PLS, QPLS, and BTPLS empirical models are compared with the plant data in Figure 3. The simulations were performed with the software Simulink® using the stationary gains of the empirical models. The reported results suggest that linear PLS is the most appropriate model to predict the polymer yield.

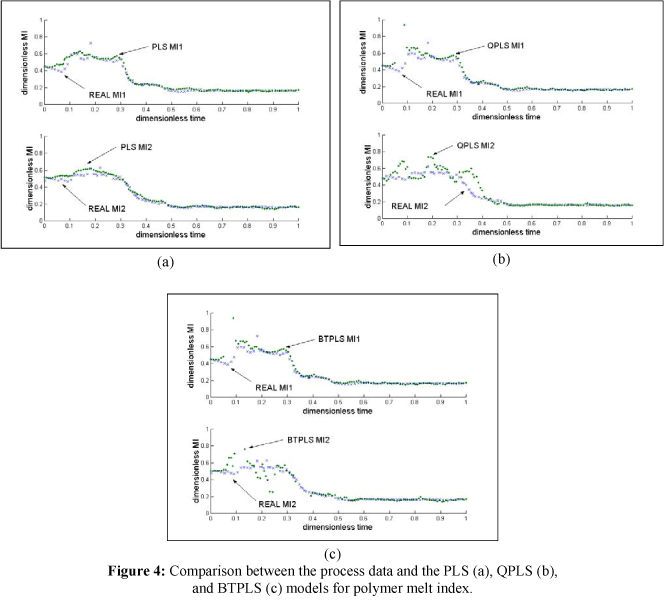
In Figure 4, the melt index values predicted by the empirical models developed are compared to the process data for both reactors.

Again, the linear PLS method had an outstanding fit, although it was verified that the QPLS model gave a better prediction. This can be explained by the fact that the dynamic behavior of the melt index had a more pronounced nonlinear contribution than the polymer yield. Table 3 shows a comparison of the correlation coefficients for the melt index of the two reactors.

The validation results confirm the conclusion that the QPLS model is the best empirical model for the melt index. Thus, the PLS model was selected to predict the polymer yield while the QPLS model was selected to predict the polymer melt index. For both reactors, these models were validated using the same dataset as that used to validate the phenomenological models. The results for the polymer yield and melt index are reported in Figure 5. As can be noted, the model predictions are still good, with better results for the melt index.

Comparison Between the Models

A comparison of the results of model predictions showed a better fit with the validation data for the empirical models. This is due to the fact that steady-state data were available to fit these models. For example, the predicted values for the resin yield and the melt index were acceptable at the steady-state, even with a linear PLS. For the dynamic data, the best results for the melt index were obtained with the QPLS model. This occurs due to the nonlinear nature of the IF.

The poor quality of the plant data may explain the inaccuracy of the phenomenological model. In this case, the use of hybrid models may be necessary.

CONCLUSIONS

Industrial process data were fit to models of different types for ethylene polymerization reactors. To adjust the phenomenological model, the optimization algorithms based on the flexible polyhedron method of Nelder and Mead were the most efficient in finding the minimum difference between the real data and the model predictions. To adjust the empirical model, the PLS model was more appropriate for polymer yield and the melt index needed more nonlinearity like the QPLS models. The comparison between these two types of models showed better results for the empirical models. Adjustments of the dynamics of the models are necessary, so both can be used for the development of advanced process control.

(Received: March 28, 2005 ; Accepted: March 09, 2007)

• Baffi, G., Martin, E.B. and Morris, A.J., Non-Linear Projection to Latent Structures Revisited: The Quadratic PLS Algorithm, Computers and Chemical Engineering, v. 23, p. 395-411 (1999).
• Bindlish, R., Rawlings, J.B. and Young, R.E., Parameter Estimation for Industrial Polymerization Processes, AIChE J., v. 49, n. 8, p. 2071-2078 (2003).
• Choi, K.Y. and Ray, W.H., The Dynamic Behaviour of Fluidized Bed Reactors for Solid Catalized Gas-Phase Olefin Polymerization, Chem, Eng. Sci., v. 40, p. 2261-2279 (1985).
• Finkler, T.F., Desenvolvimento de uma Ferramenta para Obtenção de Modelos Empíricos, Master's thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre (2003).
• Gambetta, R., Modelagem e Simulação de Reatores em Leito Fluidizado, Master's thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre (2001).
• Himmelblau, D.M., Applied Nonlinear Programming, McGraw-Hill Book Company (1972).
• Kunii, D. and Levenspiel, O., Fluidization Engineering, 2nd Edition, Butterworth-Heinemman (1991).
• Li, B., Martin, E.B. and Morris, A.J., Box-Tidwell based Partial Least Squares Regression, Computers and Chemical Engineering, v. 25, p. 1219-1233 (2001).
• McAuley, K.B. and MacGregor, J.F., On-line Inference of Polymer Properties in an Industrial Polyethylene Reactor, AIChE J., v. 37(6), p. 825-835 (1991).
• Neumann, G.A., Modelagem e Simulação de um Reator Tubular de Alta Pressão para Produção de PEBD, Master's thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre (2001).
• Sato, C., Ohtani, T. and Nishitani, H., Modeling, Simulation and Nonlinear Control of a Gas-Phase Polymerization Process, Comp. Chem. Eng., v. 24, p. 945-951 (2000).
• Secchi, A.R. and Perlingeiro, C.A., Busca Aleatório Adaptativa, XII Congresso Nacional de Matemática Aplicada e Computacional, São José do Rio Preto (1989).
• Sirohi, A. and Choi, K.Y., On-line Parameter Estimation in a Continuous Polymerization Process, Ind. Eng. Chem. Res., v. 35, p. 1332-1343 (1996).
• Soroush, M., State and Parameter Estimations and Their Applications in Process Control, Comp. Chem. Eng., v. 23, p. 229-245 (1998).
• Wold, H., Nonlinear Estimation by Iterative Least Squares Procedures, in F. David (ed.), Research Papers in Statistics, Festschrift For Lerzy Newman, p. 411-444, Wiley, New York (1966).
• Zhao, H., Guiver, J., Neelakantan, R., Biegler, L.T., A Nonlinear Industrial Model Predictive Controller Using Integrated PLS and Neural Net State-Space Model, Control Eng. Practice, v. 9, p. 125-133 (2001).

*

To whom correspondence should be addressed

Publication Dates

• Publication in this collection
  23 July 2007
• Date of issue
  June 2007

History

• Received
  28 Mar 2005
• Accepted
  09 Mar 2007