Abstract
This work presents a method to analyze hydrogen production by biomass gasification, as well as electric power generation in small scale fuel cells. The proposed methodology is the thermodynamic modeling of a reaction system for the conversion of methane and carbon monoxide (steam reforming), as well as the energy balance of gaseous flow purification in PSA (Pressure Swing Adsorption) is used with eight types of gasification gases in this study. The electric power is generated by electrochemical hydrogen conversion in fuel cell type PEMFC (Proton Exchange Membrane Fuel Cell). Energy and exergy analyses are applied to evaluate the performance of the system model. The simulation demonstrates that hydrogen production varies with the operation temperature of the reforming reactor and with the composition of the gas mixture. The maximum H2 mole fraction (0.6-0.64 mol.mol-1) and exergetic efficiency of 91- 92.5% for the reforming reactor are achieved when gas mixtures of higher quality such as: GGAS2, GGAS4 and GGAS5 are used. The use of those gas mixtures for electric power generation results in lower irreversibility and higher exergetic efficiency of 30-30.5%.
Hydrogen; Fuel cell; Gasification gas of biomass; Steam reforming; Thermodynamic analysis
THERMODYNAMICS AND SEPARATION PROCESSES
Hydrogen from biomass gas steam reforming for low temperature fuel cell: energy and exergy analysis
A. SordiI,* * To whom correspondence should be addressed ; E. P. SilvaII,III; L. F. MilanezIII; D. D. LobkovII,III; S. N. M. SouzaIV
IFederal Technology University, Paraná, Rua Alagoas 200, 86020-430, Londrina - PR, Brazil. E-mail: alexandresordi@utfpr.edu.br
IIUniversity of Campinas, UNICAMP, Physics Institute, Hydrogen Laboratory, P.O. Box 6039, 13083-970, Campinas - SP, Brazil
IIIUniversity of Campinas, UNICAMP, Faculty of Mechanical Engineering, Department of Energy, P.O. Box 6122, 13083-970, Campinas - SP, Brazil
IVState University of West Parana, UNIOESTE, 85806-300, Cascavel - PR, Brazil
ABSTRACT
This work presents a method to analyze hydrogen production by biomass gasification, as well as electric power generation in small scale fuel cells. The proposed methodology is the thermodynamic modeling of a reaction system for the conversion of methane and carbon monoxide (steam reforming), as well as the energy balance of gaseous flow purification in PSA (Pressure Swing Adsorption) is used with eight types of gasification gases in this study. The electric power is generated by electrochemical hydrogen conversion in fuel cell type PEMFC (Proton Exchange Membrane Fuel Cell). Energy and exergy analyses are applied to evaluate the performance of the system model. The simulation demonstrates that hydrogen production varies with the operation temperature of the reforming reactor and with the composition of the gas mixture. The maximum H2 mole fraction (0.6-0.64 mol.mol-1) and exergetic efficiency of 91- 92.5% for the reforming reactor are achieved when gas mixtures of higher quality such as: GGAS2, GGAS4 and GGAS5 are used. The use of those gas mixtures for electric power generation results in lower irreversibility and higher exergetic efficiency of 30-30.5%.
Keywords: Hydrogen; Fuel cell; Gasification gas of biomass; Steam reforming; Thermodynamic analysis.
INTRODUCTION
The fuel cell is an electrochemical device that converts the fuel chemical energy into electrical energy directly. The main classification of fuel cells is by type of electrolyte used and operation temperature. PEMFC uses NAFION® membrane as the electrolyte and gaseous diffusion electrodes with platinum (Pt) as catalyst, and the operating temperature is under 80ºC. Due to the low temperature, the PEMFC operates only with hydrogen of high purity (99.99%mol.mol-1), and the concentration of carbon monoxide in the gaseous flux should not exceed 10 µmol.mol-1.
The main sources for hydrogen production are: water, fossil hydrocarbons and biomass. Technologies utilized to remove the hydrogen of those sources are: water electrolysis and hydrocarbon reforming.
Hydrogen can be obtained from biomass mainly through two processes, both involving the reforming of methane. The first is the anaerobic degradation of organic matter, producing biogas mainly composed of methane (CH4) and carbon dioxide (CO2). The second is biomass gasification, a thermo-chemical process in which biomass is transformed into fuel gas, usually called producer gas or synthesis gas (GGAS).
The gasification gas of biomass is composed of H2, CO, CH4, CxHy, CO2 and N2. The molar fractions of these gaseous species in the GGAS composition depend on the design of the gasifier, the biomass composition and operational conditions. The potential of gasification gas to produce hydrogen depends, in turn, on its composition, mainly on its CH4 and CO contents. For electricity generation in a low-temperature fuel cell, such as the PEMFC, it is necessary a gas processing (reforming and purification) until there is only hydrogen in the output gaseous flow.
This work presents a methodology for the thermodynamic simulation of hydrogen production by reforming the gasification gas of biomass. Gas mixtures from different gasification processes were used in order to find which had the highest potential for hydrogen and electricity production. The "highest potential" mixture is understood as the one in which the reforming and purification of the gasification gas of biomass results in the minimum irreversibility for the total system.
PEMFC / GASIFICATION GAS SYSTEM
Figure 1 illustrates the model of the system for hydrogen and electricity production from gasification gas of biomass. The gas enters the reforming reactor at 850ºC and atmospheric pressure at position 1, and leaves at position 2 at a temperature that depends on its composition at the entrance. The reform gas must be cooled before passing through the shift reactor for the reaction of carbon monoxide with steam. After the shift reactor, the shift gas must be cooled and compressed. The last part of the system is hydrogen purification by a PSA cycle and electrical energy production in PEMFC stacks. Currently, the PEMFC stacks are built on a power scale ranging up to 250 kW. In this work the fuel cell power was calculated based on the gas flow of GGAS1 pilot plant. Position 7 represents the flow of pure hydrogen, and position 9 represents the flow of the exhaust gas mixture at the PSA exit.
THERMODYNAMICS OF THE FUEL CELL
According to Larminie and Dicks (2003), the thermodynamics of the fuel cell is represented by the reaction (1) and equations below. The Global reaction of hydrogen with oxygen from air is:
The maximum electrical work Wel that can be produced by the fuel cell is:
or:
Eq. (1) can be written on a molar basis as:
The available thermal energy is
In reaction (1) two electrons are transferred to a circuit external to the fuel cell. For each mol of hydrogen involved in the reaction, 2N electrons are transferred, where N is the Avogadro's number. If -e is the charge of an electron then the charge flow will be (DOE, 2002):
During the operation of the fuel cell, a difference of potential E appears between the cell electrodes. The electrical work wel is calculated by the equation:
If there are no irreversibilities present in the system, then the produced work will be equal to the Gibbs free energy of the reaction:
Equation (6) calculates the ideal voltage or reversible potential for a fuel cell operating with hydrogen. For standard conditions (298.15 K and 101.325 kPa), the following applies:
This results in 1.229 V for a fuel cell based in Rc.(1). However, several phenomena related to the kinetics of the electrochemical conversion in the electrodes result in losses (overpotentials) in the cell potential when the current intensity increases (Matelli and Bazzo, 2005). The overpotentials are known as: polarization by activation, ohmic polarization and polarization by concentration. The electrochemical efficiency quantifies the overpotential effects by the equation:
Where EOP is the real operating voltage of the fuel cell. According to Matelli and Bazzo (2005), the practical efficiency can be defined by the thermodynamic efficiency multiplied by the electrochemical efficiency:
For a fuel cell system operating with hydrogen from biomass gasification gas reforming, the overall efficiency is associated to the total power output and the gas lower heating value (LHV). This efficiency is named first law efficiency of the PEMFC/gasification gas system:
Where the electrical power of fuel cell is:
GASIFICATION GAS REFORMING AND PURIFICATION
The gasification gas of biomass has a hydrogen molar fraction that can be maximized by the reforming of the molar fractions of methane (CH4), hydrocarbons (CxHy), and carbon monoxide (CO).
For maximum conversion of these gaseous species into hydrogen two reactors are needed: one for hydrocarbon reforming and another for CO processing.
The process of reforming is defined as a thermochemical and catalytic conversion of a liquid, solid or gaseous fuel into a hydrogen-rich mixture. According to Silva (1991), most processes use light hydrocarbons for extracting hydrogen. Light hydrocarbons are those with molecular mass between methane and naphtha, and a boiling point below 250ºC. These compounds can react with water at temperatures of 650-900ºC. In the case of methane, a nickel/alumina catalyst is used.
The best known reforming methods are: steam reforming, partial oxidation, and auto-thermal reforming. In this work, steam reforming was considered. The global gasification gas reforming reactions are described by Rcs. (2) to (4).
The application of H2 for power generation in PEMFC requires that the anode inlet gas have a CO concentration lower than 10 µmol.mol-1, since CO is a poison to the fuel cell eletrocatalyst (Zalc and Löffler, 2002). If hydrogen is produced from hydrocarbons reforming (i.e. biomass gasification gas), purification is required in order to reduce the CO levels to cell requirements. This task is partially accomplished by a water gas shift (WGS) reactor (reaction 4) (Giunta et al., 2006). The final CO cleanup occurs in a preferential oxidation (PrOx) or in the pressure swing adsorption (PSA) unit.
The WGS reaction is moderately exothermic with a heat reaction, ΔH= -40kJ.mol-1. The high temperatures favor intrinsic kinetics while lower temperatures favor high equilibrium CO conversion.
Adiabatic operation with an inlet-outlet temperatures of 250-350ºC yields poor performance because the temperature of the process stream increases to a point at which equilibrium conversion is low (<80%). Isothermal operation with inlet-outlet temperature of 250ºC initially yields conversions lower than those obtained adiabatically, but the conversion curve continues to increase to an equilibrium conversion value of 90% (Zalc and Löffler, 2002).
Significantly better performance can be achieved by operating at a relatively high temperature and exploiting reaction kinetics when the gas composition is far from equilibrium and then lowering the temperature as thermodynamics begins to limit the CO conversion (Zalc and Löffler, 2002). This task is accomplished in two adiabatic stages using two different catalysts with intermediate cooling. The first reactor operates between 300 and 500ºC (high temperature stage HTS) and uses an iron-based catalyst (Fe/Cr). The second reactor operates at lower temperatures (180-300ºC) (low temperature stage LTS) and uses a copper-zinc catalyst supported on alumina Cu/Zn/Al (Francesconi et al., 2007).
Hydrogen final cleanup can be achieved by a PSA system, which is widely used for gas purification. PSA is generally employed for oxygen or nitrogen from air, and for hydrogen generated by processes such as hydrocarbon reforming. This technology has been in commercial use for hydrogen purification since 1966, and is currently widely used (Myers et al., 2002).
Basically, a PSA works by the action of an adsorbent bed selective for certain gaseous species. A gaseous mixture is introduced into the bed under high pressure, and the adsorbing solid selectively adsorbs certain components, allowing the non-adsorbed component to pass through the bed as a purified gas.
The PSA systems operate in cycles, where three steps are basic to any process: pressurization, adsorption and depressurization. In the depressurization occurs the adsorbent regeneration and desorption of components retained, and then the process returns to its initial condition. Therefore, the removal of species adsorbed is done by total pressure reduction, which gives the PSA systems a faster pace in cycles and greater production per unit volume of adsorbent bed than other types of adsorption processes (Neves and Schvartzman, 2005). The fastness and the operation with two or more sync beds allows input and output of products continuously, these features are essential for fuel cell systems.
The energy required for this separation of gaseous species is obtained from the mechanical work of compressing the gaseous mixture. Energy expended in this mechanical work is a significant component of the operational cost of a PSA system.
SYSTEM PERFORMANCE ANALYSIS
The methodology used to analyze the performance of the system was the energy and exergy balance. Initially the simulation of the gasification gas reforming was carried out, in which the final mixture composition, corresponding to the chemical equilibrium in a given thermodynamic condition, was calculated using Lagrange multipliers to find the minimization point of the total Gibbs free energy of the system. In this work, the EES (Engineering Equation Solver) was used in the simulation of the gasification gas reforming.
The hydrogen molar fraction in the mixture is a function of the temperature, pressure and the steam/carbon ratio (γ). In the present work, the pressure was 101.3 kPa, and the parameter γ was equal to 2 for CH4 reforming, 3 for C2H4, and 1 for CO reforming.
With regard to input conditions, the gasification gas may have compositions depending on the gasification process and biomass type. Table 1 illustrates the molar fractions of some gaseous mixtures produced by different gasification processes reported by Bain (2004). Initials in Table 1 stand for:
CFB: circulating fluidized bed
FB: fluidized bed
IFB: indirect fluidized bed
ICFB: indirect circulating fluidized bed
DRF: downdraft
UPF: updraft
Once the hydrogen molar fraction in the gaseous mixture in the shift reactor (shift gas) is calculated, the next step is the hydrogen purification by PSA. In the present work, a PSA system was considered with an operation pressure of 650 kPa, and a hydrogen recovery factor of 0.85 of the volumetric flow of the molar fraction of this species in the shift gas. These characteristics were chosen based on research and development data from the Hydrogen Laboratory of the University of Campinas Physics Institute.
Thermodynamic analysis of the system illustrated in Fig. 1 assumed the ideal gas model. Equations (12) and (13) represent the enthalpy and entropy calculations for an ideal gas mixture.
The mass and energy balances in reactors and heat exchangers are represented by Eqs. (14) to (16).
The exergy balance for a control volume is:
The definition of specific physical and chemical exergy, according to Szargut et al. (1988), is represented by Eqs.(18) and (19):
Where the total specific exergy is:
The reference environment proposed by Szargut et al. (1988), where standard temperature and pressure (298.15 K and 101.325 kPa) and the standard atmosphere composition can be found was used to define physical and chemical exergies.
Exergetic efficiency calculations adopted the input/output criterion defined by Kotas (1995) as ratio efficiency. The ratio efficiencies of the following control volumes were calculated: reforming and shift reactors, heat exchangers, PSA, PEMFC, and the system as a whole. Eqs.(21) to (26) represent these efficiencies, respectively.
RESULTS
Figures 2 and 3 show the molar fractions of the equilibrium composition of GGAS1 and GGAS2 reforming simulations respectively. The potential for hydrogen production is higher from GGAS2 than from GGAS1 because of its higher CH4 and CO molar fractions. The temperature at which hydrogen production reaches its peak depends on the amount of CH4, CO and inert gases such as N2 and CO2. The CH4 reforming reaction is enhanced by higher temperatures (650-850ºC), while the CO reforming reaction is enhanced by lower temperatures (250ºC) in an isothermal reactor as Zalc and Löffler (2002). Thus, gas cooling is necessary at the reforming reactor exit to allow the conversion of the remaining CO molar fraction in the shift reactor.
In order to allow the use of the gasification gas physical exergy at the reforming reactor, the gas pre-cleaning must be performed by the hot system. If the system is cold, the gaseous mixture must be heated up to the reforming operation temperature again, increasing the energy consumption of the hydrogen production system.
Tables 2 and 3 illustrate the results of thermodynamic simulation for PEMFC / GGAS system in Fig. 1.
Figure 4 shows that the largest contribution in the exergy destruction (irreversibility) occurs in the PEMFC. The process of electrical work transfer in the fuel cell is associated to the chemical potential gradient, and the generation of irreversibility is proportional to this gradient. The exhaust gas temperature of the PEMFC is very close to the ambient temperature, and therefore there is not much heat produced by the PEMFC available.
The gaseous mixture composition has an important effect on the system performance. For the gaseous mixtures in Table 1, Figure 5 shows the variation on reformer exergetic efficiency as a function of the nitrogen molar fraction in the gasification gas of biomass. The higher the amount of this inert gas is, the lower the reformer efficiency. In practice, the presence of inert gases has a negative influence on the reaction kinetics.
Although the effectiveness of the reforming process is very important for the performance of the system, the PSA has the most striking influence on the energy consumption. Hydrogen purification is the main determinant of energy consumption, due to the need to compress the gaseous mixture, and due to the use of part of the purified hydrogen for adsorption bed regeneration. Figure 6 shows that purification performance is proportionally better for higher molar fractions of hydrogen in the shift gas. This favorable condition is obtained in the reforming of GGAS2, GGAS4 and GGAS5 (Figure 7). These gaseous mixtures are produced by the gasification process with steam injection and indirect heating, which yields gases of a higher quality. In a pilot plant, steam production should be provided for the gasification process; part of the required heat can be obtained by burning the PSA exhaust gas.
Figure 8 shows the variation of the first and second law efficiencies of the fuel cell system as a function of the hydrogen molar fraction in the shift gas. The first law efficiency is an adequate parameter to measure system performance but is not adequate to measure the gas quality, since the lower heating value does not reflect the quality of the gaseous mixture for hydrogen production. The second law efficiency, on the other hand, is indicative of the gasification gas quality in the sense that the smaller the gas flow required to produce a given amount of hydrogen, the higher the system performance will be. For the construction of a pilot plant, the higher exergetic efficiency illustrated in Figure 8 results in components of a smaller volume. Figure 9 also indicates that the system will be smaller due to the lower irreversibility. A pilot plant with smaller volume components will have a correspondingly lower cost.
CONCLUSIONS
The simulation demonstrated that the hydrogen production varies with the operation temperature of the reforming reactor, and with the gas mixture composition. These two variables are inherently dependent because of the particular chemical equilibrium state for each thermo-chemical reaction of system species.
The temperature of 850ºC in output gasification reactor is sufficient for maximum methane conversion and hydrogen production. But hot gas cleaning should be used in gasification process so that gasification gas physical exergy can be utilized in steam reforming. In cold gas cleaning the cooling of the gasification gas to the environment temperature in the wet scrubber results in a thermal energy loss, which is a disadvantage of the cold cleaning. Gas reheating for the steam reforming reaction also causes the destruction of the exergy inherent to the heat transfer process, and makes the system more complex.
The exergetic efficiency of the reforming reactor also depends on the gas composition; for the lower quality gas (GGAS1) the efficiency was 85%. For GGAS2, which is the best quality gaseous mixture, the reactor efficiency presented a value of 92.5%.
Both the exergetic efficiency and the total irreversibility values of the power generation system with PEMFC were, respectively, 26.2% and 775 kW for GGAS1 and 30.5% and 575 kW for GGAS2. Therefore, to achieve the maximum performance of the hydrogen production and electricity generation in the fuel cell systems, the gasifier should be designed to obtain gas mixture similar to GGAS2.
The main responsible for the difference between the first and second law efficiencies of the PEMFC system is the hydrogen purification process (PSA). Thus, for a fuel cell / gasification gas system to be competitive when compared with the traditional thermal machines, further research and development in gas purification technology is necessary. On the other hand fuel cells operating at high temperatures like the SOFC (Solid Oxide Fuel Cell) and MCFC (Molten Carbonate Fuel Cell) are adequate to operate with gases from gasification because there is no need for hydrogen purification.
ACKNOWLEDGEMENTS
We are thankful to CAPES for the financial support of this work, and to the Hydrogen Laboratory and the Mechanical Engineering Faculty at UNICAMP.
NOMENCLATURE
(-)
cm2
(-)
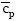
J.kmol-1.K-1
1.602 x10-19C
V
V
V
J.kmol-1
W
(-)
9.6487x107 C. kmol-1
(-)
(-)
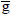
J.kmol-1
J
(-)
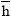
J.kmol-1
J
(-)
(-)
mA.cm-2
W
(-)
J.kmol-1
(-)
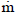
kg.s-1
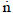
kmol.s-1
6.02 x1023
(-)
kPa
(-)
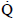
W
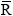
8,314 J.kmol.K-1
(-)
(-)
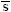
J.kmol-1.K-1
J.K-1
(-)
(-)
K)
J)
J.kmol-1
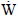
W
(-)
mol.mol-
%mol.mol-1
(-)
%
%
101.3 kPa and 298.15 K
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
101.3 kPa and 298.15 K
(Submitted: September 28, 2007 ; Accepted: July 4, 2008)
- Bain, R. L., Biomass Gasification Overview, NREL National Renewable Energy Laboratory. US DOE United States Department of Energy, p. 48 (2004).
- DOE - U.S. Department of Energy. Fuel Cell Handbook, EG & G Services Parsons, Inc. Science Applications International Corporation, West Virginia, USA, p. 352 (2002).
- Francesconi, J. A., Mussati, M. C., Aguirre, P. A., Analysis of design variables for water-gas-shift reactors by model-based optimization, Journal of Power Sources, v. 173, p. 467-477 (2007).
- Giunta, P., Amadeo, N. and Laborde, M., Simulation of a Low Temperature Water Gas Shift Reactor Using the Heterogeneous Model/Application to a PEM Fuel Cell, Journal of Power Sources, v. 156 (7) p. 489-496 (2006).
- Kotas, T. J., The Exergy Method of Thermal Plant Analysis. Krieger Publishing Company, Florida (1995).
- Larminie, J. and Dicks, A. Fuel Cell Systems Explained, John Wiley Sons (2003).
- Matelli, J. A., Bazzo, E., A Methodology for Thermodynamic Simulation of High Temperature Internal Reforming Fuel Cell Systems, Journal of Power Sources, v.142, p. 160-168 (2005).
- Myers, B. D., Ariff, G. D., James, B. D., Lettow, J. S., Thomas, C. E. and Kuhn, R. C., Cost and Performance Comparison of Stationary Hydrogen Fueling Appliances, The Hydrogen Program Office; Office of Power Technologies; U.S Department of Energy. 123 p. (2002).
- Neves, C. F. C and Schvatzman, M. M. A. M., Separação de CO2 por meio da tecnologia PSA, Química Nova, v.28, n. 4, p. 622-628 (2005).
- Silva, E. P., Introdução a Tecnologia e Economia do Hidrogênio. Campinas: Editora da Unicamp (1991).
- Szargut, J., Morris, D. R. and Steward, F. R., Exergy Analysis of Thermal, Chemical and Metallurgical Processes, John Benjamins Publishing Co. (1988).
- Zalc, J. M. and Löffler, D. G., Fuel processing for PEM fuel cells: transport and kinetic issues of system design, Journal of Power Sources, v. 111, p. 58-64 (2002).
Publication Dates
-
Publication in this collection
10 Mar 2009 -
Date of issue
Mar 2009
History
-
Accepted
04 July 2008 -
Received
28 Sept 2007





 , therefore the maximum thermodynamic efficiency of the fuel cell is defined as:
, therefore the maximum thermodynamic efficiency of the fuel cell is defined as: 




























