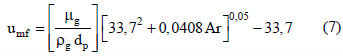Abstract
The paper presents experimental research of thermal conductivity coefficients of the siliceous sand bed fluidized by air and an experimental investigation of the particle size influence on the heat transfer coefficient between fluidized bed and inclined exchange surfaces. The measurements were performed for the specific fluidization velocity and sand particle diameters d p=0.3, 0.5, 0.9 mm. The industrial use of fluidized beds has been increasing rapidly in the past 20 years owing to their useful characteristics. One of the outstanding characteristics of a fluidized bed is that it tends to maintain a uniform temperature even with nonuniform heat release. On the basis of experimental research, the influence of the process's operational parameters on the obtained values of the bed's thermal conductivity has been analyzed. The results show direct dependence of thermal conductivity on the intensity of mixing, the degree of fluidization, and the size of particles. In the axial direction, the coefficients that have been treated have values a whole order higher than in the radial direction. Comparison of experimental research results with experimental results of other authors shows good agreement and the same tendency of thermal conductivity change. It is well known in the literature that the value of the heat transfer coefficient is the highest in the horizontal and the smallest in the vertical position of the heat exchange surface. Variation of heat transfer, depending on inclination angle is not examined in detail. The difference between the values of the relative heat transfer coefficient between vertical and horizontal heater position for all particle sizes reduces by approximately 15% with the increase of fluidization rate.
Fluidized bed; Heat transfer; Surface; Particle thermal conductivity; Siliceous sand; Experiment
FLUID DYNAMICS; HEAT AND MASS TRANSFER; AND OTHER TOPICS
Experimental investigation of thermal conductivity coefficient and heat exchange between fluidized bed and inclined exchange surface
B. StojanovicI,* * To whom correspondence should be addressed ; J. JanevskiII; M. StojiljkovicIII
IFaculty of Mechanical Engineering, University of Nis, Serbia, Aleksandra Medevedeva 14, 18000 Nis, Serbia. E-mail: banes@masfak.ni.ac.yu
IIFaculty of Mechanical Engineering, University of Nis, Serbia, Aleksandra Medevedeva 14, 18000 Nis, Serbia. E-mail: djoje@masfak.ni.ac.yu
IIIFaculty of Mechanical Engineering, University of Nis, Serbia, Aleksandra Medevedeva 14, 18000 Nis, Serbia. E-mail: mladens@masfak.ni.ac.yu
ABSTRACT
The paper presents experimental research of thermal conductivity coefficients of the siliceous sand bed fluidized by air and an experimental investigation of the particle size influence on the heat transfer coefficient between fluidized bed and inclined exchange surfaces. The measurements were performed for the specific fluidization velocity and sand particle diameters dp=0.3, 0.5, 0.9 mm. The industrial use of fluidized beds has been increasing rapidly in the past 20 years owing to their useful characteristics. One of the outstanding characteristics of a fluidized bed is that it tends to maintain a uniform temperature even with nonuniform heat release. On the basis of experimental research, the influence of the process's operational parameters on the obtained values of the bed's thermal conductivity has been analyzed. The results show direct dependence of thermal conductivity on the intensity of mixing, the degree of fluidization, and the size of particles. In the axial direction, the coefficients that have been treated have values a whole order higher than in the radial direction. Comparison of experimental research results with experimental results of other authors shows good agreement and the same tendency of thermal conductivity change. It is well known in the literature that the value of the heat transfer coefficient is the highest in the horizontal and the smallest in the vertical position of the heat exchange surface. Variation of heat transfer, depending on inclination angle is not examined in detail. The difference between the values of the relative heat transfer coefficient between vertical and horizontal heater position for all particle sizes reduces by approximately 15% with the increase of fluidization rate.
Keywords: Fluidized bed; Heat transfer; Surface; Particle thermal conductivity; Siliceous sand; Experiment.
INTRODUCTION
Ever since its emergence, the fluidization phenomenon has attracted the attention of numerous researchers. Its application in numerous technological operations stems from its excellent properties, which are reflected in: intensive mixing of solid particles, a high contact-surface between gas and solid particles, an almost constant temperature in the entire bed, as well as simple insertion and removal of the material from the bed. In the past several decades, numerous papers and studies of the process of fluidization and its application have been published, most of which are based on experimental research. The field of heat conduction has been of great interest to researchers, since the fluidized bed is characterized by high heat conductivity. Yet, despite a large number of papers which deal with this problem (Massoudi and Phouc, 2007), their authors' conclusions are highly disparate, sometimes even contradictory. The reasons for this dispersion of results lie in differing conditions in which these experiments are performed. These facts have motivated experimental research with the chief goal of determining thermal conductivity coefficients of the fluidized bed for particles of siliceous sand of differing fractions. Based on the obtained values of heat transfer coefficient, one can conclude that the tendency of heat transfer coefficient change remains the same, independent of the particle size. The tendency of heat transfer coefficient change with increase of fluidization rate is less significant for bigger particles. The influence of the most important parameters on the values of thermal conductivity coefficients of the fluidized bed has been analyzed through the experimental results obtained.
Due to very efficient contact between gas and particles, i.e., fluidized bed and immersed heat exchange surfaces or walls, fluidized beds have very intensive heat exchange. Heat transfer between the fluidized bed and the surfaces immersed in the bed is a function of the dynamic characteristics of the bed (Martin, 1984), most of all bubble movement and particle mixing intensity. However, it is evident that fluidization velocity and particle size are the most influential factors on exchanged heat quantity between surfaces.
Also, key factors in heat transfer between an immersed surface and fluidized bed are the particle motion in the vicinity of the heat transfer surface, contact time with the surface and particle concentration on the wall (Zarghami et al., 2007). Gas and particle motion above, over and on the lateral side of exchange surfaces is specific, so the changes in those zones are mostly investigated in the literature.
The complexity of the problem and majority of influencing factors, which are difficult to include into equations, cause the experimental determination of heat transfer coefficient to be accepted method.
THERMAL CONDUCTIVITY OF THE FLUIDIZED BED
Since specific thermal capacity of solid particles is volumetrically higher than specific thermal capacity of gases by several orders, moving particles are basic heat holders in the bed. In this case, the ordinary Fourier's equation can be used for describing the process of heat propagation in the fluidized bed, where the thermal diffusivity coefficient reflects the intensity of the mixing of material in the bed. Its value can be measured by a modified method of the instantaneous heat source, whose essence is as follows: a strong instantaneous thermal impulse is created in the fluidized bed by quickly pouring a small portion of previously heated particles of that same material into it. The moment of achieving maximal temperature τmax at a certain distance from the heat source is registered according to the equation (Geljperin, 1967):
where n=3, 2, 1 depending on whether heat source is a point, a line or a surface. The movement of bubbles enables the mixing of particles in the emulsion phase, both in the direction of the bed's height, and in the radial direction, whereby a certain amount of particles passes through any observed intersection of the bed. Since particles in the non-isothermal bed differ with respect to the value of enthalpy, a resulting flux of warmer particles will appear if their concentration is higher on one side of the observed intersection. Presupposing that the concentration of warmer particles per unit volume changes in the direction of the flow of particles only, their resulting thermal flux per unit surface can be expressed as:
If the following expression for enthalpy is introduced into expression (2):
we obtain:
where λ is thermal conductivity coefficient of the fluidized bed, which is defined as:
For determining the thermal conductivity coefficient in the axial direction, Borodulja and associates (1966) used a glass pipe, length of 1m, diameter of 80mm. On the upper surface of the bed, an instantaneous surface heat source was created by pouring a small portion (5-7% in volume) of particles heated in a furnace up to a temperature of 100-700ºC. The time of particle pouring was less than 0.5s. For measuring the temperature of the bed, two thermocouples were used; one of them was placed on the distributor, the other at half the height of the bed. Measurements were performed with several monodisperse and polydisperse fractions of different types of material for different heights of the stagnant bed. The processing of experimental data has shown that thermal diffusivity coefficient in the axial direction can be described by the following equation:
Determination of thermal conductivity coefficient in the radial direction is performed in a pipe with diameter 175mm. An instantaneous spot heat source was obtained by quickly pouring a small portion of warm sand particles along the axis of the apparatus through a glass pipe with diameter 25mm. For temperature measurement, a thermocouple was placed at the height of the pouring of particles from the pipe, at the distance of 60-70mm from its axis.
The research has shown that there is a highly intensive mixing of material in the fluidized bed in the axial direction. Axial thermal conductivity coefficient was within λa=(1100-6000)W/m.K. On the other hand, mixing of material in the radial direction was relatively small. Values of radial thermal conductivity coefficients were: λr=(50150)W/m.K.
In their published paper, Peters et al. (1953) tried to calculate the thermal conductivity coefficient by determining the temperature profile in the fluidized bed. The apparatus was in the shape of a parallelepiped, width 65mm, length 450mm, height 480mm, which was not completely filled with sand (dekv=0.23mm). As a source of heat, they used an electric heater consisting of a wire spiral, which provided heat evenly along the transverse section of the bed. Thermal isolation of the vessel prevented thermal loss through the wall from being higher than 7%. Calculated numerical values of thermal conductivity in the axial direction were within 1163-1977 W/m.K, while in the radial direction they were of the order of 12002000 W/m.K. Peters et al. (1953) state that those values are significantly increased and that they are practically impossible to obtain on the basis of such experimental conditions.
The research on thermal conductivity of the fluidized bed shows the existence of dispersion of results obtained by various authors (Kunii and Levenspiel, 1976) since they show complex dependence of thermal conductivity coefficients on various factors. Therefore, it is very difficult to give any approximation of obtained results by some global empirical dependence. For practical calculations, it is much more reliable to take absolute values of the coefficient λ at a given moment.
EXPERIMENTAL METHOD
The goal of experimental research on the fluidized bed in this paper is determination of thermal conductivity coefficients depending on operational characteristics of the fluidized bed: velocity, fluidization rate and the size of particles. Experimental research was conducted on a laboratory apparatus (Figure 1). The apparatus consists of a measuring part, above which there is a pipe for the supply of heated sand into the bed, a device for the supply of air, and a device for measurement, regulation, and registering of the process. Special attention was paid to the construction of the device for the supply of heated sand into the bed. Material, which was previously heated up to a temperature 250-350ºC, was instantaneously inserted into the fluidized bed by quick surface pouring through the pipe with diameter 45mm onto the bed surface.
A fan from the external environment supplies the air necessary for fluidization. The flow of air is measured by a standard apparatus, while a valve enables the desired flow of air. In order to stabilize the flow of air, the sections in front of and behind the apparatus are long enough. A chamber isolated by glass wool helps produce an even distribution of air on the intersection of the operational part of the apparatus. A distributor is placed at the inlet into the operational part of the apparatus, while a tapered extension, which prevents the removal of minor fractions, is placed above. Chromel-alumel thermocouples are used for temperature measurements. One of them is placed at the outlet from the bed. Another one, for the determining thermal diffusivity coefficient in the axial direction is placed immediately above the distributor (Figure 1a), i.e., for determining ar in the radial direction (Figure 1b).
In order to start the experimental determination of the thermal conductivity coefficient, certain measurements were performed. Siliceous sand with differing fractions was used as material for fluidization. Subsequent to sifting in standard sieves, fractions of siliceous sand with average particle diameter of 0.3mm, 0.5mm, and 0.9mm, were separated (Table 1). The following characteristics were determined for each fraction:
■ actual sand density ρp,
■ bulk sand density ρn,
■ equivalent particle diameter dp,
■ porosity at minimal fluidization rate εmf,
■ minimal fluidization rate Umf.
The minimum fluidization velocity was determined experimentally and its value coincides with the value from the equation (Srinivasakannan and Balasubramanian, 2002):
Bulk density of the particles was determined by pouring freely a certain quantity of sand into a calibrated vessel, while actual density was determined by a picnometer. The value of specific thermal capacity was taken from Naumann (1981).
As has been said, for determining thermal conductivity coefficient in the axial direction, two thermocouples are placed on the axis of the stagnant bed, whereby the first was placed at 43.5mm from the distributor, and the second on the surface of the bed. By adjusting the flow of air, the desired velocity of air at the working temperature is obtained. At this working velocity of air, with known minimal fluidization velocity, the fluidization rate was determined. In this established state, an already prepared portion of previously heated sand is very quickly inserted through the fixed pipe. During the movement of inserted hot sand through the fluidized bed, the thermocouples measured temperature in the bed, with registration on an acquisition system. For a set fluidization rate, separate bed temperatures were registered each 0.02s. What can be noted is that temperature in the bed increases, due to the movement of hot sand particles. At the same time, the time span between two maximal increases in temperature registered by the thermocouples is read. For a known distance between the thermocouples and read time, the value of the thermal diffusivity coefficient is calculated. Since thermal diffusivity is determined in the axial direction, it is assumed that, in equation (1), the value of n=1 (superficial material dosage). For a certain fluidization rate and the existing conditions, the experiment was repeated several times. The velocity of air was then increased and another experiment was performed, for the same sand fraction, in the way described above. After measuring a certain fraction, the operational part of the apparatus is emptied and another fraction is poured in and the same experiment repeated.
The values of thermal conductivity coefficient in the radial direction were determined by the same procedure as the values of axial conductivity. As has been described, the difference is in the positions of thermocouples, which were, in this case, in the same plane (Figure 1b), and with point source material dosage (n=3).
RESULTS AND DISCUSSION
For assessment of the intensity of mixing in the fluidized bed, coefficient of effective thermal conductivity is authoritative. In view of the interrelationship between thermal conductivity and thermal diffusivity coefficients, Figure 2 shows the dependence of averaged values of thermal conductivity coefficient on the velocity of the fluidization agent. Since thermal conductivity and thermal diffusivity are connected through specific thermal capacity of particles and the density of the fluidized bed, which depends directly on the porosity of the bed, the way in which the thermal conductivity coefficient changes with the fluidization rate is similar to the way in which the thermal diffusivity coefficient changes with the fluidization rate. The maximal value of thermal conductivity, which occurs at a fluidization rate of approximately N=2.5, once again points to the fact that, at that velocity of the fluidization agent, mixing of particles brings about more intense contacts and collisions of solid particles (Huilin et al., 2007). The occurrence of the maximum can also be accounted for by a decrease in the density of the fluidized bed and an increase in its porosity with the increase of gas velocity, which may cause differing characteristics of the change of thermal conductivity coefficient.
Generally, the obtained values of thermal diffusivity coefficient in the radial direction are smaller by an entire order (Figure 3). In contrast to the conductivity coefficient in the axial direction, inthis case what can be observed for all average equivalent diameters is the occurrence of the maximum of the thermal conductivity coefficient in the radial direction at a fluidization rate N=2.5. According to numerous researchers, local concentration of particles influences the heat transfer in the sense of its intensification when the annular distribution of particles across the transverse section of the column (with a solid core in the center, a rarefied bed around the core, and a dense ring next to the wall) deteriorates. At the same time, mixing of particles and the frequency of their mutual collisions increases, which enhances more intensive diffusion of heat. Certain fluctuations of the values of thermal diffusivity can be observed in the diagrams of dependence of thermal diffusivity coefficient on the fluidization rate. The cause of these fluctuations may be successive arrival of differently heated particle packages at the observation places and sometimes bubbles that pass through the bed. When bubbles go through the bed, at some moment, one of the two thermocouples may be inside a bubble, thus registering the temperature of air inside the bubble. Since the temperature of air inside a bubble is higher than the temperature of air and of solid particles in the emulsion phase, an increase of temperature will occur at that place at that moment.
By means of their interaction, all treated hydrodynamic parameters influence in a highly complex manner global heat transfer in the fluidized bed and, consequently, thermal conductivity coefficients. Domination of some of them occurs only in a limited range. The results obtained through the experiments point to the fact that porosity of the bed, i.e., concentration of particles, although a very important factor of heat transfer in the fluidized bed, is not independent of particle flux, relative particle and gas velocity, and reverse mixing.
Percentage error of the measuring instrument was determined based on the obtained values:
■ distance between the thermocouples - 1%
■ time - 0.4%
Based on the above values, the percentage average squared error of the measuring instruments was 1.077%, while the error of determining thermal diffusivity coefficient experimentally was 8.8%.
Bearing in mind that the obtained values of the heat transfer coefficient measurement error lie in the boundaries allowed for the experimental research, the results can be considered as trustworthy and accurate.
HEAT TRANSFER BETWEEN FLUIDIZED BED AND SURFACES IMMERSED IN THE BED
The most commonly used way of heat transfer in fluidized bed is the heat transfer between the fluidized bed and immersed surfaces of different shapes and sizes (Botterill, 1975).
The value of the heat transfer coefficient increases when the gas velocity is higher than the minimal fluidization velocity. It reaches its maximum for the gas velocity known as the optimal velocity of the fluidization. After this, it decreases with the increase of the velocity.
It is generally accepted that the overal surface- to-bed convective heat transfer coefficient can be considered to be made up of three additive components:
where hpc, hgc, hb are the particle convective, the gas convective and the bubble heat transfer coefficients, and (1-fo) is the time of contact of the emulsion phase with the heat transfer surface (Chen et al., 2005).
The time of contact of the particle package with the surface τ depends on both the time of contact of bubbles with the surface fo and the frequency of the transit of the bubbles at the considered point on the surface
where A is the coefficient which is defined as:
Rk and Rc in (10) are the resistance to heat transfer of the particle package and the contact thermal resistance of a gas film. Hamidipour et al. (2005) investigated particle-wall contact experimentally and found that the particle-wall contact time in a bed of sand particles decreases with increasing gas velocity in the bubbling regime of fluidization.
The greatest part of the total coefficient of the heat transfer is the particle convective heat transfer coefficient (Botterill, 1975, Baskakov et al, 1978):
It has been seen that the particle size has an important effect both on the value of the maximal heat transfer coefficient and on the change of the effect of certain mechanisms on the overal heat transfer. For this reason, the influence of the particle size on the heat transfer in the fluidized bed is the most common objective of the experimental research. The experimental results (Wang et al., 2004) show that, for small particles, dp<0.8 mm, the effects of thermophysical properties of particles on the heat transfer coefficient become important with decreasing particle diameter.
EXPERIMENTAL APPARATUS
Experimental investigation of heat transfer by convection between an immersed tube and the fluidized bed was carried out on the laboratory scale apparatus of 600 mm in height and the square cross-section of dimensions 160x160 mm.
The immersed heat exchange surface -an electric heater - is made of copper tube, of outer diameter 16 mm and length of 100 mm. Three thermocouples are built-in on the outer surface - on the front side, lateral and upper side - relative to the direction of the heater rotation to the fluidization air flow. The heater is fastened on the carrier in a frame with dimensions of 150x150 mm (Figure 4). The frame can be rotated around the horizontal axis, 100 mm above the distributor, enabling the change of heater inclination.
In order to get the same working conditions for each fluidization velocity, the heater inclination was changed and the temperature of the heater surface and the bed were measured at each angle. For a defined fluidization velocity, the inclination of the heater was changed gradually in 10º increments from the vertical position (angle of 0º) to the horizontal position (angle of 90º). For each angle of inclination the measurements were restored after reaching the stationary state. The procedure was repeated for every new fluidization velocity and all three particle sizes: 0.3, 0.5 and 0.9 mm. The stagnant bed height was 160 mm.
RESULTS AND DISCUSSION CONCLUSIONS
Defining the average values of the heat transfer coefficient between fluidized bed and immersed inclined exchange surfaces supposes defined local heat transfer coefficients (Baskakov et al., 1973), the distribution of which along the surface is very uneven, because of different aerodynamic conditions.
The measurement of the local heat transfer coefficient between the heater surface and fluidized bed was conducted in order to define the mean value of the heat transfer coefficient for the whole heater. Because of the symmetry of the flow around the cylinder, the mean value of the heat transfer coefficient is defined as the arithmetic mean value of local heat transfer coefficients:
In order to examine the influence of sand particle size on heat exchange between the fluidized bed and immersed surface for an inclined heater, investigations were conducted with particle diameters of 0.3, 0.5, and 0.9 mm.
The tendency of heat transfer coefficient change with increase of fluidization rate is similar for smaller and bigger particles - Figures 5, 6 and 7 (Baskakov et al., 1978), although this influence is less significant for bigger particles, because after reaching a fluidization rate of 2.5, the air velocity influences insignificantly the heat transfer coefficient distribution.
In order to make a better analysis of particle size and fluidization rate influence on heat exchange between fluidized bed and inclined surface, Figure 8 shows the dependence of relative heat transfer coefficient (h*=hφ/hº) on inclination angle for fluidization rates of 1 to 3.
The figure clearly underscores the tendency of the heat transfer coefficient change to stay the same, no matter what the particle diameter, but with the increase of particle diameter, the influence of heater inclination decreases. Thus, the difference between the values of relative heat transfer coefficient in vertical and horizontal position of the heater for particle diameter 0.3 mm decreases from 24% to 10%; for a particle diameter 0.5 mm from 23% to 10% and for particle diameter 0.9 mm from 20% to 8% with the increase of fluidization rate from N=1 to N=3,.
CONCLUSIONS
On the basis of results of experimental and theoretical research of thermal conductivity coefficients in the fluidized bed that have been conducted so far, as well as on the basis of the results of our own experimental research, it has been confirmed that the fluidized bed has very good thermal conductivity, which enables its application in numerous industrial processes of heat exchange.
The results obtained in experimental research have shown that thermal conductivity coefficients depend on the hydrodynamic structure of the fluidized bed. Although the change in thermal conductivity coefficients differs in the axial and radial directions, it generally depends on fluidization rate and the size of particles.
For all treated fractions of the sand, the values of thermal conductivity coefficient of the fluidized bed in the axial direction were within 450-3100 W/mK, which also represents the maximal value reached in all measurements. The obtained values of those same coefficients in the radial direction are within 19-110 W/mK, which provides a satisfactory level of agreement with the results of other authors.
Despite the complexity of the analysis of thermal conductivity through the fluidized bed, the results obtained provide a realistic picture that can be used in all future theoretical and experimental research on the process of heat conduction in the fluidized bed.
The results of experimental investigation confirm the direct dependence of heat exchange intensity on the aerodynamic conditions in fluidized bed. It is evident that the frequency and the period of contact of heat exchange surfaces with bubbles and particle packets depends on particle size, fluidization velocity and inclination of the heat exchange surface.
The tendency of the heat transfer coefficient change stays the same, independent of the particle diameter. However, the influence of heater inclination decreases with the increase of particle diameter. So it can be concluded that the influence of particle size on heat transfer coefficient for inclined surfaces can be neglected.
It can also be concluded that the influence of exchange surface inclination on heat transfer between the fluidized bed and immersed surfaces decreases with the increase of fluidization rate.
NOMENCLATURE
Symbols
a
Archimedes number
solid diffusivity
entalphy
Subscripts
Greek Letters
(Submitted: May 19, 2008 ; Revised: October 1, 2008 ; Accepted: October 15, 2008)
- Baskakov A. P., Berg B. V., Vitt O. K., Filippov N. F., Kirakosy V. A., Goldobin J.M., Maskaev V. K., Heat transfer to objects immersed in fluidized beds, Powder Technology, 8, 273-282 (1973).
- Baskakov, A. P., Bertg, B. V., Rizkov, A. F., Filippovkij, N.F., Processii teplo i massoperenosa v kipjascem sloje, Metalurgija, Moskva, pp. 144-151, (1978).
- Borodulja, V. A., Zabrodskij, S. S., Tamarin, A. I., Judickij, V. I., Isledovanie gidrodinamiki i temperaturnoprovodnosti psevdoozizenogo sloja, sb. Teplo-i massoprenos, Tom 5, Energia, Moskva pp. 75-85, (1966).
- Botterill, J. S. M., Fluid-bed Heat Transfer, Academic Press, London (1975).
- Ćatipović, M. N., Heat transfer to Horizontal Tubes in Fluidized Beds: Experiment and Theory, Ph.D. Thesis, Oregon State University, Corvallis, OR (1979).
- Chen, J. C., Grace, J. R., Golriz, M. R., Heat transfer in fluidized beds: design methods, Powder Technology, 150, 123-132 (2005).
- Davidson, J. F., Harrison, D., Fluidized Particles, Cambrige University Press, Cambridge (1963).
- Geljperin N. I., Osnovi tehniki psevdoozizenie, Moskva, 184 (1967).
- Groenewold, H., Tsotsas, E., Drying in fluidized bed with immersed heating elements, Chemical Engineering Science 62 (2007).
- Hamidipour M., Mostoufi N., Sotudeh-Gharebagh R., Chaouki J., Monitoring the particle-wall contact in a gas fluidized bed by RPT, Powder Technology 153, 119-126 (2005).
- Huilin, L, Yunhua Z., Ding J., Gidspow D. and Wei L., Investigation of mixing/segregation of mixture particles in gas-solid fluidized beds, ChemicalEngineering Science, vol. 62, (2007).
- Jovanovic, G. N., Catipovic N. M., Fitzgerald T. J. and Levenspiel O., Fluidization (J. R. Grace, J. M. Matsen, eds.), Plenum, New York, pp. 325-332 (1990).
- Kunii, D., Levenspiel О., Fluidization Engineering, 13, Wiley, New York (1969).
- Martin, H., Heat transfer between gas fluidized beds of solid particles and the surface of immersed heat transfer exchanger elements, Part I. Chemical Engineering and Processing, 18, 157-169 (1984).
- Massoudi, M., Phuoc T. X., Conduction and dissipation in the shearing flow of granular materials modeled as non-Newtonian fluids, Powder Technology, 175, 146-162 (2007).
- Nauman, E. B., Residence time distributions in systems governed by the dispersion-equation, Chemical Engineering Science, 36(6), 957-966 (1981).
- Peters, K., Orlichek A., Schmidt A., Wärmetransportfähigkeiten von Wirbelschichten, Chem. Ing. Tech., 25 (6), 313-316 (1953).
- Schlunder, E. U., Waermeubergang an bewegte kugelschutt ungen bei kurzfristigem kontact, Chemical Engineering Technology 43, 651-654, (1971).
- Srinivasakannan, C. and Balasubramanian, N., A simplified approach to the drying of solids in a batch fluidized bed, Brazilian Journal of Chemical Engineering, 19 (3), 293-298 (2002).
- Wang L., Wu P., Zhang Y. P., Yang J., Tong L. G., Ni X. Z., Effects of solid particle properties on heat transfer between high-temperature gas fluidized bed and immersed surface, Applied Thermal Engineering, 24, 2145-2156 (2004).
- Zarghami R., Mostoufi N., Sotudeh-Gharebagha R., Chaouki J., Analysis and modeling of particle-wall contact time in gas fluidized beds, Chemical Engineering Science, 62, 4573-4578 (2007),
Publication Dates
-
Publication in this collection
23 June 2009 -
Date of issue
June 2009
History
-
Reviewed
01 Oct 2008 -
Received
19 May 2008 -
Accepted
15 Oct 2008