Abstract
The study of non-Newtonian flow in plate heat exchangers (PHEs) is of great importance for the food industry. The objective of this work was to study the pressure drop of pineapple juice in a PHE with 50º chevron plates. Density and flow properties of pineapple juice were determined and correlated with temperature (17.4 < T < 85.8ºC) and soluble solids content (11.0 < Xs < 52.4 ºBrix). The Ostwald-de Waele (power law) model described well the rheological behavior. The friction factor for non-isothermal flow of pineapple juice in the PHE was obtained for diagonal and parallel/side flow. Experimental results were well correlated with the generalized Reynolds number (20 < Re g < 1230) and were compared with predictions from equations from the literature. The mean absolute error for pressure drop prediction was 4% for the diagonal plate and 10% for the parallel plate.
Food processing; Heat exchanger; Pressure drop; Non-Newtonian
FLUID DYNAMICS; HEAT AND MASS TRANSFER; AND OTHER TOPICS
Non-newtonian flow and pressure drop of pineapple juice in a plate heat exchanger
R. A. F. CabralI; J. A. W. GutII,* * To whom correspondence should be addressed ; V. R. N. TelisI; J. Telis-RomeroI
IDepartment of Food Engineering and Technology, Universidade Estadual Paulista, R. Cristóvão Colombo 2265, 15054-000, São José do Rio Preto - SP, Brazil. E-mail: javier@ibilce.unesp.br
IIDepartment of Chemical Engineering, Escola Politécnica, University of São Paulo, P.O. Box 61548, 05424-970, São Paulo - SP, Brazil. E-mail: jorgewgut@usp.br
ABSTRACT
The study of non-Newtonian flow in plate heat exchangers (PHEs) is of great importance for the food industry. The objective of this work was to study the pressure drop of pineapple juice in a PHE with 50º chevron plates. Density and flow properties of pineapple juice were determined and correlated with temperature (17.4 < T < 85.8ºC) and soluble solids content (11.0 < Xs< 52.4 ºBrix). The Ostwaldde Waele (power law) model described well the rheological behavior. The friction factor for non-isothermal flow of pineapple juice in the PHE was obtained for diagonal and parallel/side flow. Experimental results were well correlated with the generalized Reynolds number (20 < Reg< 1230) and were compared with predictions from equations from the literature. The mean absolute error for pressure drop prediction was 4% for the diagonal plate and 10% for the parallel plate.
Keywords: Food processing; Heat exchanger; Pressure drop; Non-Newtonian.
INTRODUCTION
Pineapple (Ananas comosus L.) is a popular fruit worldwide; however, in many developing countries the variety of pineapple products (canned fruit, canned juice or frozen juice concentrate) is still limited. Pineapple is of commercial and nutritional importance in the tropics, due to its excellent taste and as a natural source of vitamins and other important nutrients (Nicoleti et al., 2001). Thermal processing is required for the industrialization of pineapple pulp and juice for destruction of microorganisms and inactivation of enzymes. Adequate heat treatment levels must be reached with minimum alteration of nutritional and sensorial characteristics. For the correct design of continuous heat processing plants, it is essential to understand the flow properties of the product over a proper temperature range. The influence of temperature and solids content on the rheological properties of different liquid foods is available in the literature for various products, such as orange juice (Telis-Romero et al., 1999), fruit purees (Guerrero and Alzamora, 1997; 1998) and dairy products (Velez-Ruiz and Barbosa-Canovas, 1998; Flauzino et al., 2009). However, limited information was found in the literature for the flow properties of pineapple juice.
The study of non-Newtonian flow in plate heat exchangers (PHEs) is of great importance for the food industry, since various processes include this device, such as cooling and heating applications in milk, citrus juices and tropical fruit pulp pasteurization and concentration processes (Leuliet et al., 1987; Carezzato et al., 2007).
The main advantages of using PHEs are their arrangement flexibility, ease of maintenance and cleaning and high heat exchange rate. The conventional gasketed PHE consists of a stack of corrugated metal plates clamped together in a frame. Each plate has four corner ports, which in pairs provide access to the flow passages on either side of the plate. Sealing is accomplished with elastomeric gaskets so arranged that the two streams exchanging heat pass through alternate flow passages. The embossed patterns provide a substantially larger surface area and improve mechanical resistance of the plate pack. The corrugation geometry determines, to a great extent, the thermo-hydraulic performance of the exchanger. Nevertheless, the information available on this aspect is mostly proprietary. The corrugated pattern in general use is of chevron (herringbone) design. Successive plates are assembled with the chevron patterns pointing in opposite directions, thereby producing a complex three-dimensional flow passage (Shah and Focke, 1988; Saunders, 1988).
Previous investigations have shown that the corrugation angle is a major parameter influencing PHE thermal and hydraulic performance (Focke et al., 1985; Muley and Manglik, 1999). Moreover, the flow pattern inside the channel, which can be diagonal or parallel depending on the gasket type (see Figure 1), also influences the PHE performance, especially for wide plates (Bansal et al., 2001).
The objective of this work was to study the pressure drop of pineapple juice, a non-Newtonian fluid, flowing in a PHE with chevron plates. Density and flow properties of the pineapple juice were studied for different temperatures and solid contents. The friction factor was determined for diagonal and parallel flow patterns for a wide range of generalized Reynolds number and results were compared with the predictions of equations from the literature.
Rheological Behavior of Concentrated Juices
A large number of liquid foods exhibit non-Newtonian flow behavior and can be described by the Ostwaldde Waele model given by Eq. (1), also known as the power law model (Steffe, 1996).
In Eq. (1), σ is the shear stress, 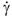 is the shear rate, k is the consistency coefficient and n is the flow behavior index. For Newtonian fluids, n = 1 and k assumes the value of the fluid viscosity, µ. This rheological model has been used to describe the rheology of apple juice, peach and pear puree (Saravacos, 1970), concentrated orange juice (Crandall et al., 1982), guava puree (Vitali and Rao, 1982), concentrated orange juice with low pulp concentration (Rao et al., 1984), frozen concentrated orange juice (Tavares et al., 2007) and soursup juice (Gratão et al., 2007).
is the shear rate, k is the consistency coefficient and n is the flow behavior index. For Newtonian fluids, n = 1 and k assumes the value of the fluid viscosity, µ. This rheological model has been used to describe the rheology of apple juice, peach and pear puree (Saravacos, 1970), concentrated orange juice (Crandall et al., 1982), guava puree (Vitali and Rao, 1982), concentrated orange juice with low pulp concentration (Rao et al., 1984), frozen concentrated orange juice (Tavares et al., 2007) and soursup juice (Gratão et al., 2007).
Some non-Newtonian fluids may present an additional resistance to flow, represented by the Herschel-Bulkley model (Saravacos and Kostaropoulos, 1995), presented in Eq. (2), where σ0 is the yield stress.
For liquid foods, the rheological parameters k, n and σ0 are mostly dependent on temperature, T, and solids content, Xs. The temperature dependence of k and σ0 usually follows an Arrhenius type correlation and the solids content effect can be incorporated into the model as a power or exponential factor (Giner et al., 1996).
Pressure Drop
For fluid flowing through a PHE, the pressure drop consists mainly of three components: the pressure drop within the channels due to friction and flow contraction/expansion; the pressure drop associated with the distribution ducts inside the PHE; and the pressure variation due to an elevation change. The pressure drop, ΔP, can be evaluated by using an analogy to tube flow as in Eq. (3), where ρ is the density, f is the Fanning friction factor, vc = Q/(Nbw) is the mean channel velocity, De is the equivalent diameter, Q is the volumetric flow rate, vp = Q/(π Dp2/4) is the mean inlet port velocity, g is the acceleration of gravity, P is the number of passes and N is the number of channels per pass (Shah and Focke, 1988; Miura et al., 2008). Empirically, the pressure drop associated with the distribution ducts is assumed to be proportional to the inlet velocity head through the plate port (second term on the right-hand side of Eq. (3)) and the proportionality coefficient λ = 1.3 recommended by Saunders (1988) was used in this work.
The equivalent diameter of the PHE channel is defined in Eq. (4) and the effective heat transfer area of a plate is defined in Eq. (5), where Φ is the area enlargement factor, which may be provided by the plate manufacturer.
For Newtonian and non-Newtonian flow, the Fanning friction factor can be correlated to the generalized Reynolds number for power law fluids, Reg, through a Hagen-Poiseuille like equation, as in Eq. (6), where α and β are empirical parameters. The generalized Reynolds number for tube flow is presented in Eq. (7); note that, if n = 1.0, the original Reynolds number, Re = ρvcDe/µ, is obtained (Darby, 2001).
MATERIAL AND METHODS
Material
Pineapple (Ananas comosus L.) fruits, variety Smooth Cayenne, were purchased from a local market in São José do Rio Preto (State of São Paulo, Brazil) and stored at 7ºC prior to use (AOAC, 1990). A batch of concentrated pineapple juice, with 63.8% solid content and 5.4% pulp content, was prepared in a pilot plant finisher with a single stage evaporator and sieved through a 1.6 mm-mesh. Experimental measurements were performed using concentrated juice diluted in distilled water to obtain soluble solids contents of 11.0, 17.7, 23.5, 33.2, 37.9, 43.2 and 52.4 ºBrix, which was determined with a digital refractometer (Marconi, Piracicaba, Brazil). Temperatures studied were 17.4, 36.7, 54.8, 76.2 and 85.8ºC.
Density and Rheological Behavior
The density of the reconstituted pineapple juice was determined in triplicates, by picnometry. A best fit equation for the temperature and soluble solids dependence was obtained with the software Statistica 8 (StatSoft, Tulsa, USA).
Rheological measurements were carried out using an AR 2000 rheometer (TA Instruments, New Castle, USA) with cone and plate geometry (60 mm disc, 4º angle) under controlled stress and temperature. During measurements, the exposed surfaces of the samples were covered with the solvent trap accessory of the rheometer to prevent evaporation. Shear rate range was 0.5 to 300 s1 and both upward and downward tests were performed in duplicate for each temperature and soluble solids content combination. The experimental procedure was previously tested by a rheological study of ethylene glycol and chlorobenzene (Telis-Romero et al., 2005; Polizelli et al., 2003).
Fitted rheological models for the dependence of shear rate on shear stress were obtained by the non-linear estimation procedure implemented in Statistica 8, minimizing the sum of squared errors. Likewise, best fit equations for the dependence of the obtained rheological parameters on temperature and soluble solids were obtained. The suitability of the equations was evaluated by the number of parameters, coefficient of determination (r2) and analysis of residuals.
Pressure Drop
The plate heat exchanger used is an adaptation of a M10 PHE (Alfa Laval, Lund, Sweden) with stainless steel chevron plates (θ = 50º, L = 619 mm, w = 323 mm, Dp = 100 mm, ε = 0.6 mm, Ap = 0.22 m2, Φ = 1.10), gaskets with variable thickness (b = 2, 4 and 6 mm) and a countercurrent symmetric single pass arrangement with 23 channels. Diagonal and parallel flow patterns were tested (see Figure 1). A schematic diagram of the experimental setup is shown in Figure 2, which was previously used for determination of the pressure drop for tube flow of orange juice (Telis-Romero et al., 1999), egg yolk (Gut et al., 2005; Telis-Romero et al., 2006) and milk cream (Flauzino et al., 2009).
Differential pressure transmitters LD-301 (Smar, São Paulo, Brazil) were used to obtain pressure drop data on the PHE. A 7500B data logger (HP Agilent, Santa Clara, CA) monitored temperatures and pressures. Various flow rates and inlet temperatures of pineapple juice with Xs = 11.0 and 24.0 ºBrix were tested in order to obtain a large range of pressure drop data.
Initial pressure drop tests were made with ethylene glycol (Newtonian behavior) in the PHE. Experimental results were compared with pressure drop calculated with Eq. (3), using the friction factor correlation f=11.25/Re0.631 from Saunders (1988) which is valid for θ=50º and 20 < Re < 300. Viscosity of ethylene glycol was obtained from Steffe (1996) and density was measured by picnometry for temperatures between 0 and 90ºC.
RESULTS AND DISCUSSION
Density
Density of pineapple juice was measured in triplicate and the mean experimental error was ±30 kg/m3. This property showed a linear dependence on both temperature, T, and soluble solids content, Xs. Equation (8) was fitted with r2 = 0.987 and the mean absolute error is 0.6% for density determination. The results are presented in Figure 3, where the density data of distilled water (Schwier, 1992) was included in the fitting of Eq. (8).
Rheological Behavior
Pineapple juice showed non-Newtonian pseudoplastic behavior in the temperature and soluble solids content range studied. Upward and downward results showed no time-dependent behavior. Figure 4 presents some of the obtained rheograms, which were analyzed according to the models of Ostwaldde Waele (Eq. (1)) and HerschelBulkley (Eq. (2)). Since no significant yield stress was detected, the Ostwaldde Waele (power law) model was fitted to all rheograms for determination of the consistency coefficient, k, and flow behavior index, n. As can be seen by the straight lines in Figure 4, the Ostwaldde Waele model adjusted well to the data in the shear rate range studied.
An Arrhenius type equation correlated the absolute temperature effect on k well and a positive linear dependence was observed between the logarithms of k and Xs. Accordingly, Eq. (9) was chosen to fit the experimental data (r2 = 0.997), where R = 8.31451 J/mol·K is the universal gas constant and the parameter 1.89× 104 J/mol is the activation energy (obtained from the non-linear parameter estimation of Eq. (9)). The results for the consistency coefficient and the fitted equation are shown in Figure 5. The consistency coefficient, as well as the apparent viscosity, increases with the juice concentration and decreases with temperature, as expected.
The behavior index showed a clear linear dependence with temperature. A linear dependence was also verified between log(n) and log(Xs). Therefore, Eq. (10) was used to fit the experimental data (r2 = 0.996). As expected, the behavior index decreases from unity (Newtonian behavior) with the increase of the juice concentration, as can be seen in Figure 6.
Pressure Drop
Figure 7 presents the results of the initial pressure drop tests with ethylene glycol (27 < Re < 216). As can be seen, there is a good agreement between experimental results and the prediction from Eq. (3) with the friction factor correlation from Saunders (1988). The mean absolute error of the pressure drop prediction is 6%.
The pressure drop was then determined for the heating of pineapple juice in the PHE (Xs = 11.0 and 24.0 ºBrix). Using the diagonal plates, 731 conditions were obtained, and 637 were obtained with the parallel/side plates. The flow rate of pineapple juice varied between 13 and 119 kg/s (0.4 < vc< 8.0 m/s), the inlet temperature was between 28 and 79ºC and the outlet temperature was between 39 and 81ºC. Consequently, the generalized Reynolds range was 40 < Reg< 1200 for diagonal plates and 20 < Reg< 1230 for parallel plates.
Equation (3) was used for the determination of the experimental friction factor. Density and rheological parameters were calculated at the inlet and outlet temperatures and mean values were used. Afterwards, parameters α and β in Eq. (6) were determined in order to minimize the squared error in f. The first results showed that the friction factor versus log(Reg) plot would be better fitted by two straight lines, instead of one, for the Reg range studied. The limiting value chosen for Reg was 300 (Saunders, 1988). The results of the model fitting are presented in Table 1, in Figure 8, which represent Moody-type diagrams, and in Figure 9, which presents parity charts for pressure drop determination.
As can be seen in Figures 8 and 9, it was possible to obtain a good correlation between the friction factor and the generalized Reynolds number for the pineapple juice flow in the corrugated channel of the PHE. The mean absolute error for the pressure drop prediction was 4% for the diagonal plate and 10% for the parallel plate. The initial tests with ethylene glycol showed that the correlations presented by Saunders (1988) give accurate predictions of the friction factor for Newtonian flow (Figure 7). However, the friction factors obtained for pineapple juice are consistently higher than those predicted by Saunders (1988), but with the same type of dependence on the Reynolds number.
It can be observed in Figures 8 and 9 that the dispersion of the points is larger for the flow in parallel plates. Moreover, the friction factor is slightly higher for parallel plates. These results could be attributed to the presence of air bubbles and flow maldistribution, which are more likely to occur in parallel/side plates than in diagonal plates.
CONCLUSIONS
Density and flow properties of pineapple juice were successfully determined and correlated with temperature (17.4 < T < 85.8ºC) and soluble solids content (11.0 < Xs< 52.4 ºBrix). The Ostwaldde Waele (power law) model described well the observed rheological behavior. The pressure drop of pineapple juice flowing through a PHE with 50º chevron plates was determined for various flow rates (13119 kg/s,) and temperatures (2881ºC). The obtained friction factors correlated well with the generalized Reynolds number (20 < Reg< 1230) for diagonal and parallel plates. The friction factor versus Reynolds number correlation chart showed a change of flow regime around Reg = 300; thus, two correlations were needed. The adjusted correlations are useful for pressure drop prediction with a mean absolute error under 10%.
ACKNOWLEDGMENTS
The authors wish to thank the São Paulo State Research Foundation, FAPESP, for financial support (Process 06/56015-2).
NOMENCLATURE
Greek Symbols
(Submitted: November 27, 2009 ; Revised: May 7, 2010 ; Accepted: May 14, 2010)
- AOAC, Official Methods of Analysis. 15th ed., Association of Official Agricultural Chemists, Washington DC (1990).
- Bansal, B., Müller-Steinhagen, H. and Chen, X. D., Comparison of crystallization fouling in plate and double-pipe heat exchangers. Heat Transfer Eng., 22, 13-25 (2001).
- Carezzato, A., Alcantara, M. R., Telis-Romero, J., Tadini, C. C. and Gut, J. A. W., Non-Newtonian heat transfer on a plate heat exchanger with generalized configurations. Chem. Eng. Technol., 30, (1), 21-26 (2007).
- Cheremisinoff, N. P., Properties and concepts of single fluid flows; In: Cheremisinoff, N. P., Encyclopedia of Fluid Mechanics, V, 1, Flow Phenomena and Measurement, Gulf, Houston, 285-351 (1986).
- Crandall, P. G., Chen, C. S. and Carter, R. D., Models for predicting viscosity of orange juice concentrate. Food Technol., 36, 245-252 (1982).
- Darby, R., Chemical Engineering Fluid Mechanics. 2nd ed, Marcel Dekker Inc., New York (2001).
- Flauzino, R. D., Gut, J. A. W., Tadini, C. C. and Telis-Romero, J., Flow properties and tube friction factor of milk cream: influence of temperature and fat content. J. Food Process Eng., in press (2009).
- Focke, W. W., Zachariades, J. and Olivier, I., The effect of the corrugation inclination angle on the thermohydraulic performance of plate heat exchangers. Int. J. Heat Mass Tran., 28, (8), 1469-1479 (1985).
- Giner, J., Ibarz, A., Garza, S. and Xhian-Quan, S., Rheology of clarified cherry juices, J. Food. Eng., 30, (1-2), 147-154 (1996).
- Gratão, A. C. A., Silveira-Jr, V. and Telis-Romero, J., Laminar flow of soursop juice through concentric annuli: Friction factors and rheology. J. Food Eng., 78, 1343-1354 (2007).
- Guerrero, S. N. and Alzamora, S. M., Effect of pH, temperature and glucose addition on flow behaviour of fruit purees - I. Banana puree. J. Food Eng., 33, 239-256 (1997).
- Guerrero, S. N. and Alzamora, S. M., Effect of pH, temperature and glucose addition on flow behaviour of fruit purees - II. Peach, papaya and mango purees. J. Food Eng., 37, 77-101 (1998).
- Gut, J. A. W., Pinto, J. M., Gabas, A. L. and Telis-Romero, J., Continuous Pasteurization of Egg Yolk: Thermophysical Properties and Process Simulation. J. Food Process Eng., 28, 181-203 (2005).
- Leuliet, J. C., Maingonnat, J. F. and Lalande, M., Etude de la perte de charge dans des échangeurs de chaleur à plaques traitant des produits non-Newtoniens. Revue Générale de Thermique, 26, (308-309), 445-450 (1987).
- Miura, R. Y., Galeazzo, F. C. C., Tadini, C. C. and Gut, J. A. W., The effect of flow arrangement on the pressure drop of plate heat exchangers. Chem. Eng. Sci., 63, 5386-5393 (2008).
- Muley, A. and Manglik, R. M., Experimental study of turbulent flow heat transfer and pressure drop in a plate heat exchanger with chevron plates. J. Heat Trans., 121, (1), 110-117 (1999).
- Nicoleti, J. F., Telis-Romero, J. and Telis, V. R. N., Air-drying of fresh and osmotically pre-treated pineapple slices: fixed air temperature versus fixed slice temperature drying kinetics. Drying Technol., 19, (9), 2175-2191 (2001).
- Polizelli, M. A., Menegalli, F. C., Telis, V. R. N. and Telis-Romero, J., Friction losses in valves and fittings for power-law fluids. Braz. J. Chem. Eng., 4, 455-463 (2003).
- Roa, M. A., Cooley, H. J. and Vitali, A. A., Flow properties of concentrated juices at low temperatures. Food Technol., 38, 113-119 (1984).
- Saravacos, G. D., Effect of temperature on viscosity of fruit juices and purees. J. Food Sci., 35, 122-125 (1970).
- Saravacos, G. D. and Kostaropoulos, A. E., Transport properties in processing of fruits and vegetables, Food Technol., 49, 99-109 (1995).
- Saunders, E. A. D., Heat Exchangers: Selection, Design & Construction, Longman, Harlow (1988).
- Schwier, K., Properties of liquid water. In: Hewitt G.F. (Ed.), Handbook of Heat Exchanger Design, Begell House, New York (1992).
- Shah, R. K. and Focke, W. W., Plate heat exchangers and their design theory. In: Shah, R. K., Subbarao, E. C. and Mashelkar, R. A. (Ed.) Heat Transfer Equipment Design, Hemisphere, New York, 227-254 (1988).
- Steffe, J. F., Rheological Methods in Food Process Engineering. 2nd ed., Freeman, East Lansing (1996).
- Tavares, D. T., Alcantara, M. R., Tadini, C. C. and Telis-Romero, J., Rheological properties of frozen concentrated orange juice (FCOJ) as a function of concentration and subzero temperatures. Int. J. Food Prop., 10, (4), 829-839 (2007).
- Telis-Romero, J., Telis, V. R. N. and Yamashita, F., Friction factors and rheological properties of orange juice. J. Food Eng., 40, 101-106 (1999).
- Telis-Romero, J., Thomas, C. E. P., Bernardi, M., Telis, V. R. N. and Gabas, A. L., Rheological properties and fluid dynamics of egg yolk. J. Food Eng., 74, 191-197 (2006).
- Telis-Romero, J., Polizelli, M. A., Gabas, A. L. and Telis, V. R. N., Friction losses in valves and fittings for viscoplastics fluids, Can. J. Chem. Eng., 83, 181-187 (2005).
- Velez-Ruiz, J. F. and Barbosa-Canovas, G. V., Rheological properties of concentrated milk as a function of concentration, temperature and storage time. J. Food Eng., 35, 177-190 (1998).
- Vitali, A. A. and Rao, M. A., Flow behavior of guava puree as a function of temperature and concentration. J. Texture Studies, 13, 275-289 (1982).
Publication Dates
-
Publication in this collection
04 Jan 2011 -
Date of issue
Dec 2010
History
-
Received
27 Nov 2009 -
Accepted
14 May 2010 -
Reviewed
07 May 2010



















