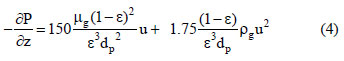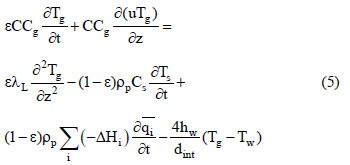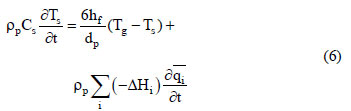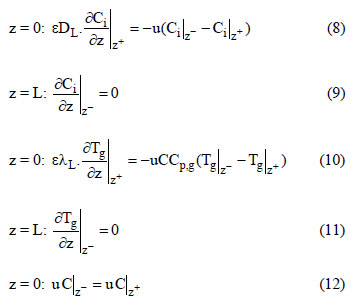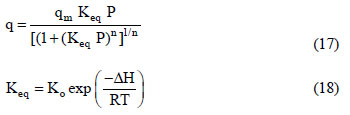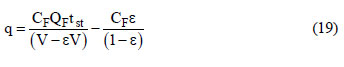Abstract
In this study, the fixed - bed adsorption of carbon dioxide and a carbon dioxide - nitrogen mixture on zeolite 13X was investigated. The adsorption equilibrium and breakthrough curves were determined at different temperatures - 301 - 306 K, 323 K, 373 K and 423 K. A model based on the LDF approximation for the mass transfer, considering the energy and momentum balances, was used to describe the adsorption kinetics of carbon dioxide and a carbon dioxide - nitrogen mixture. The model acceptably reproduced all of the breakthrough curves and can be considered as adequate for designing a PSA cycle to separate carbon dioxidenitrogen mixtures.
Adsorption; Carbon dioxide; Nitrogen; Zeolite 13X; Modeling
THERMODYNAMICS
Modeling of the fixed-bed adsorption of carbon dioxide and a carbon dioxide- nitrogen mixture on zeolite 13X
T. L. P. DantasI,III,* * To whom correspondence should be addressed ; F. M. T. LunaII; I. J. Silva Jr.II; A. E. B. TorresII; D. C. S. de AzevedoII; A. E. RodriguesIII; R. F.P.M. MoreiraI
IFederal University of Santa Catarina, Department of Chemical and Food Engineering, Laboratório de Energia e Meio Ambiente (LEMA), Phone: + (55) (48) 33319448, Ext. 211, Fax: + (55) (48) 33319687, Campus Universitário, Trindade, P.O. Box 476, 88040-900, Florianópolis-SC, Brazil
IIFederal University of Ceará, Department of Chemical Engineering, Grupo de Pesquisa em Separações por Adsorção, (GPSA), Phone: + (55) (85) 3366-9611, ext. 28, Campus do Pici, 60455-760, Fortaleza-CE, Brazil. E-mail: murilo@gpsa.ufc.br; ivanildo@gpsa.ufc.br; eurico@ufc.br; diana@gpsa.ufc.br
IIIUniversity of Porto, Faculty of Engineering, Department of Chemical Engineering, Laboratory of Separation and Reaction Engineering (LSRE), Associate Laboratory LSRE/LCM, Phone: (351) 22 508 1669, Fax: (351) 22 508 1674, Rua Dr. Roberto Frias s/n, P.O. Box 4200-465, Porto-Portugal. E-mail: arodrig@fe.up.pt
ABSTRACT
In this study, the fixed-bed adsorption of carbon dioxide and a carbon dioxide-nitrogen mixture on zeolite 13X was investigated. The adsorption equilibrium and breakthrough curves were determined at different temperatures-301-306 K, 323 K, 373 K and 423 K. A model based on the LDF approximation for the mass transfer, considering the energy and momentum balances, was used to describe the adsorption kinetics of carbon dioxide and a carbon dioxide-nitrogen mixture. The model acceptably reproduced all of the breakthrough curves and can be considered as adequate for designing a PSA cycle to separate carbon dioxidenitrogen mixtures.
Keywords: Adsorption; Carbon dioxide; Nitrogen; Zeolite 13X; Modeling.
INTRODUCTION
The emission of CO2 from power plants that burn fossil fuels is the major reason for the increase in the concentration of this gas in the atmosphere. The amount of carbon dioxide in the atmosphere is currently increasing globally by around six billion tons per year (Zhao et al., 2007).
The capture and storage of carbon dioxide is a technically feasible method of making significant reductions in carbon dioxide emissions. Capturing carbon dioxide involves separating the CO2 from other flue gases. The technological advances that are being developed around the world capture carbon dioxide from flue gases by using different schemes: postcombustion, pre-combustion and oxy-fuel processes.
Several studies have been conducted worldwide in the field of CO2 capture by adsorption, indicating that this technique is attractive as a post-combustion treatment of flue gas. Strategies like PSA (pressure swing adsorption) and TSA (temperature swing adsorption) processes have been proposed and investigated for adsorption in a cyclic process (Cavenati et al., 2006; Chou and Chen, 2004; Gomes and Yee, 2002; Grande and Rodrigues, 2008). Pressure swing adsorption technology has become an interesting alternative due to low energy requirements and cost advantages. The PSA processes can be operated at high temperatures and overcome the need to cool the fuel gas to ambient temperature prior to the removal of carbon dioxide (Gaffney et al., 1999).
The capture of carbon dioxide by adsorptive processes is mainly based on preferential adsorption of this gas on a porous adsorbent. Thus, the first and most important step is to find a suitable adsorbent. In industrial processes, zeolite 13X is frequently used as an adsorbent due to its high adsorption capacity (Lee et al., 2002; Siriwardane et al., 2001). For any such case, the basic information required is the adsorption equilibrium behavior of the pure components, in this case carbon dioxide. The design of a PSA system also requires the development of a model that can describe the dynamics of the adsorption on a fixed-bed with the selected adsorbent.
In this study, the adsorption of carbon dioxide and a carbon dioxide-nitrogen mixture on zeolite 13X packed in a fixed-bed was studied. The Linear Driving Force (LDF) model, considering the energy and momentum balances, was used to describe the kinetics of the carbon dioxide and the carbon dioxide-nitrogen mixture adsorption on zeolite 13X.
EXPERIMENTAL SECTION
The gases used for the carbon dioxide breakthrough curves were provided by White Martins S.A/Brazil: Helium 4.5 (99.99%) and standard mixtures of carbon dioxide/helium (20% CO2/He v/v) and carbon dioxide/nitrogen (20% CO2/N2 v/v). Pure CO2 (99.99%) and N2 (99.995%) were supplied by Air Liquid S.A. (Portugal). The adsorbent used was zeolite 13X (TradeShinli, China) and its characterization (BET area, pore size distribution and micropore volume), as well as information on the adsorption equilibrium of the pure carbon dioxide and pure nitrogen components, have been reported in a previous study (Dantas et al., 2008).
Fixed-Bed CO2 and CO2/N2 Mixture Adsorption
The experimental breakthrough curves were obtained by passing the appropriate gas mixture (20% CO2/He v/v or 20% CO2/N2 v/v) through the column packed with zeolite 13X. The solid adsorbent was pre-treated by passing helium over it at a flow rate of 5x10- 7 m3.s- 1 at 593K for 2 hours. These breakthrough curves were obtained at 301K, 323K, 373K and 423 K. The total gas flow rate was maintained at 5x10-7 m3.s- 1 for the CO2 breakthrough curves and at 10x10- 7 m3.s- 1 for the CO2/N2 breakthrough curves. The reversibility of the adsorption was studied in desorption experiments by passing pure helium through the packed column at a total flow rate of 5x10- 7 m3.s- 1. The gas flow was controlled by a mass flow unit (Matheson, USA). A Model CG35 gas chromatograph (CG Instrumentos Científicos, Brazil) equipped with a Porapak-N packed column (Cromacon, Brazil) and with a thermal conductivity detector (TCD) was used to monitor the carbon dioxide and nitrogen concentration at the bed exit, using helium as the reference gas. The column was located inside a furnace with controlled temperature. The experimental system (column and furnace) was considered to be adiabatic because it was isolated with a layer of 0.10 m of fiberglass and with a refractory material. The properties of the adsorbent and of the fixed-bed are given in Table 1.
Fixed-Bed CO2 Adsorption from a CO2/N2 Mixture in a Nitrogen-Saturated Fixed-Bed
The solid adsorbent was previously treated by passing nitrogen over it at a flow rate of 1.67x10- 5 m3.s- 1 at 593K for 12 hours. After this pre-treatment, the temperature of the fixed bed was adjusted to the desired value (306 K, 323 K, 373 K or 423 K) under a N2 atmosphere. The CO2/N2 mixture (10% CO2/N2 v/v) was then fed to the column at a total gas flow rate of 3.5x10- 5 m3.s- 1. The gas flow was controlled by mass flow controllers (Teledyne Brown Engineering, USA). At the end of the column, the carbon dioxide concentrations were periodically analyzed using a GA-40T Gas Analyzer (Madur Electronics, USA). The temperature inside the column was continuously monitored using a K-thermocouple placed at 0.17 m and 0.43 m from the bottom of the column. The column was located inside a convective furnace and thus the system was considered to be non-adiabatic. The characteristics of the fixed bed and the column are presented in Table 2.
MODEL DESCRIPTION
The model used to describe the fixed-bed dynamics was derived from the mass balance taking into account the energy balance. For the model used to describe the fixed-bed dynamics of the adsorption of the CO2/N2 mixture and of CO2 from the CO2/N2 mixture in a nitrogen-saturated fixed-bed, the momentum balance was also considered. The model was based on the following assumptions:
(i) The flow pattern is described by the axially dispersed plug flow model;
(ii) The mass transfer rate is represented by a linear driving force (LDF) model;
(iii) The gas phase behaves as an ideal gas mixture; and
(iv) Radial concentration and temperature gradients are negligible.
With these assumptions, the fixed-bed model is described by the following equations (Eq. 1-7). The mass balance for each component is given by Eq. (1) (Ruthven, 1984):
where ε is the bed porosity, Ci is the concentration of component i in the gas phase, DL is the axial dispersion coefficient, u is the superficial velocity, and ρp is the particle density. The rate of mass transfer to the particle for each component is given by Eq. (2):
where KL is the LDF overall mass transfer coefficient, qi* is the adsorbed equilibrium concentration, i.e., qi* =f(Ci) given by the isotherm, and 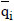 is the average adsorbed concentration. The total concentration C is given by:
is the average adsorbed concentration. The total concentration C is given by:
where P is the total pressure, Tg is the gas phase temperature and R is the universal gas constant. The Ergun equation considers the terms of the pressure drop and velocity changes:
where µg is the gas phase viscosity, ρg is the gas phase density and dp is the particle diameter.
The energy balance is:
where Cg is the molar specific heat of the gas phase, λL is the axial heat dispersion coefficient, Cs is the solid specific heat, (-ΔHi) is the adsorption heat for the ith component at zero coverage, hw is the internal convective heat coefficient between the gas and the wall, dint is the bed diameter, and Tw is the wall temperature. The solid phase energy balance is expressed by:
where hf is the film heat transfer coefficient between the gas and the adsorbent. For the column wall, the energy balance can be expressed by:
where ρw is the column wall density, Cp,w is the column wall specific heat, αw is the ratio of the internal surface area to the volume of the column wall, αwl is the ratio of the logarithmic mean surface area of the column shell to the volume of the column (Da Silva and Rodrigues, 2002), U is the overall heat transfer coefficient between the column wall and the external air, and T∞ is the furnace
external air temperature.
For an adiabatic system, the last term of Eq. (7) must not been considered. The boundary conditions are the following:
The initial conditions for the adiabatic system are:
The initial conditions for the non-adiabatic system are the following:
The mathematical model was solved with the commercial software gPROMS (Process System Enterprise Limited, UK), which uses the method of orthogonal collocation on finite elements for resolution. The bed was divided into fifty sections with three collocation points for each element of the adsorption bed.
Estimation of the Model Parameters
According to Ruthven and Farooq (1993) and Sircar and coworkers (1999), the kinetics of the diffusion of nitrogen into zeolite 13X is controlled by molecular diffusion in the macropores. In this study, it was considered that the diffusion of both nitrogen and carbon dioxide into the zeolite 13X is controlled by molecular diffusion in the macropores. In fact, when the LDF overall mass transfer coefficient was evaluated considering micropores, macropores and Knudsen diffusion, the fitting of the model to the experimental data was not satisfactory (Dantas, 2009).
The LDF overall mass transfer coefficient is related to the effective diffusivity of the macropore molecular diffusion-controlled system by the following relationship:
where rp is the particle radius, εP is the particle porosity, τP is the particle tortuosity, q0 is the value of q (concentration at the solid phase) at equilibrium with Co (adsorbate concentration in the feed at feed temperature Ti ) expressed in the appropriate units. The q0 value was determined by using the apparent Henry constant in the low pressure region, since Eq. 15 is appropriate when the adsorbent operates within Henry's law. The molecular diffusivity ( Dm,i ) is evaluated from the Chapman-Enskog equation. A particle tortuosity ( τp ) of 2 was assumed and a value of 0.37 for the particle porosity was used (Cavenati et al., 2004).
The axial dispersion coefficient was evaluated using the correlation of Wakao and Funazkri (1978):
where ε is the term corresponding to the stagnant o contribution to axial dispersion. For low Reynolds numbers, the value of this term has an important effect on the fixed-bed dynamics. For Reynolds numbers lower than 1 (Re < 1), a value of 0.23 was used for this term and, for higher Reynolds numbers (Re > 10), a value of 20 was used for this term. These values are consistent with those previously observed by other authors who used this correlation to model a fixed-bed adsorption process in the gas phase with similar Reynolds numbers (Cavenati et al., 2006; Delgado et al., 2006).
The gas phase viscosity was estimated from Wilke's equation (Bird, 1060). The mass and heat transport parameters were estimated according to correlations reported in the literature (Bird, 1960; De Wash and Froment, 1972; Incropera and De Witt, 1996). The correlations used to evaluate the mass and heat transport parameters are summarized in Table 3. The values for some of the physical and transport properties of the gas phase, used for the calculation of the breakthrough simulation parameters, are shown in Table 4.
RESULTS AND DISCUSSION
Adsorption Equilibrium of Carbon Dioxide and Nitrogen
The basic information required to describe the fixed-bed dynamics of the adsorption of carbon dioxide and a carbon dioxide-nitrogen mixture is the adsorption equilibrium behavior of the single components. The adsorption equilibria of the pure components on the zeolite 13X used in this study have been previously reported (Dantas, 2009). The CO2 and N2 adsorption equilibrium data were fitted using the Toth model (Eq. (17)) (Toth, 1971; Do, 1998) and the temperature dependence of the equilibrium was described according to the Van't Hoff equation (Eq. (18)).
In this study, the adsorbed equilibrium concentration of carbon dioxide on zeolite 13X was estimated as a function of the feed concentration from a mass balance in the fixed bed. For each experimental breakthrough curve, the adsorbed equilibrium concentration is given by:
where CF is the feed concentration, V is the bed volume, QF is the feed volumetric flow rate and tst is the stoichiometric time given by:  o equilibrium concentrations of nitrogen could not be measured due to the very fast breakthrough time, which generates large errors in the adsorbed equilibrium estimates.
o equilibrium concentrations of nitrogen could not be measured due to the very fast breakthrough time, which generates large errors in the adsorbed equilibrium estimates.
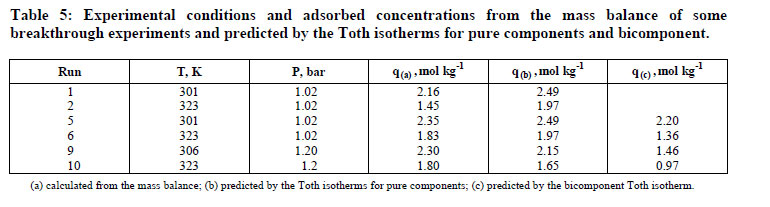
The resulting adsorbed equilibrium concentrations are given in Table 5. The differences between some of the values are attributed to the different methodologies used. It can be observed that the zeolite 13X adsorption capacity for CO2 in the CO2/He and CO2/N2 mixtures is very close to that predicted by the Toth isotherm using the fitting parameters previously reported (Dantas, 2009). This is to be expected if the active sites for N2 and CO2 are independent. The amount of CO2 adsorbed predicted by the multicomponent Toth isotherm has a higher deviation (28.58%) than that predicted by the pure gas Toth isotherm (14.53%).
Thus, the pure component equilibrium isotherms predicted very well the equilibrium of each component in the CO2/N2 mixture. Moreover, this solid adsorbed carbon dioxide to its total capacity. This assumption agrees with Siriwardane and coworkers (2001), who observed the same results for adsorption of CO2/N2 mixtures on 13X zeolite. Table 6 shows the equilibrium parameters of the Toth model for carbon dioxide and nitrogen adsorption on zeolite 13X.
Breakthrough Curve Modeling
Fixed-Bed CO2 Mixture Adsorption
For the carbon dioxide breakthrough curves, a set of experiments was performed changing the initial temperature of the bed (runs 1 to 4) and the results were simulated using the model described above. Because the feed consists of a small concentration of a single adsorbable component (carbon dioxide), the velocity through the bed was considered to be constant. As mentioned previously, the system was also considered to be adiabatic. Figure 1 shows a comparison between the experimental and theoretical curves obtained for CO2 adsorption on zeolite 13X under the conditions of runs 1 to 4. It can be observed that, when the temperature is increased, the carbon dioxide breakthrough times are shorter due to the exothermic nature of the adsorption. It was also observed that the simulated curves reproduce adequately the experimental data for the different feed concentrations and temperatures studied, suggesting that the assumptions on which the model is based could be valid for this system. The LDF overall mass transfer coefficients calculated and used in these simulations are shown in Table 7.
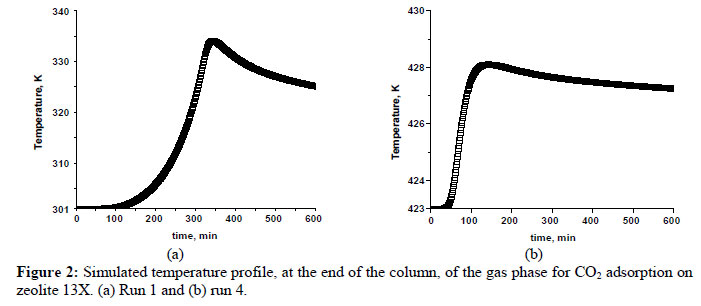
The simulated temperature profiles at the end of the bed are shown in Figure 2 for the conditions of run 1 and run 4 where the large and small temperature peaks are expected. It can be observed that the temperature peaks are very large. In Figures 2 (a) and 2 (b), the temperature peaks correspond to the differences of around 35 K and 5 K, respectively. This is due to the high heat of adsorption for carbon dioxide on zeolite 13X and heat effects during the adsorption process must therefore be considered.
Fixed-Bed CO2/N2 Mixture Adsorption
Figure 3 shows a comparison between the experimental and theoretical curves obtained for N2 and CO2 adsorption on zeolite 13X under the conditions of runs 5 to 8. In Table 7 is possible to observe the LDF Figure 3 shows a comparison between the overall mass transfer coefficient used for these carbon experimental and theoretical curves obtained for N2 and dioxide and nitrogen breakthrough curves.
The model reproduces very well all of the breakthrough curves, for all feed concentrations, including the experimental breakthrough curves obtained for nitrogen. It was observedthat the adsorbent is very selective toward carbon dioxide, as shownby the difference between the breakthrough times. Aspreviously stated, the theoretical curves for CO2 and N2 adsorption on zeolite 13X were simulated by considering the Toth equation for the pure components to describe the equilibrium. The simulation results show that the zeolite 13X capacity for CO2 adsorption isnotaffected by the presenceof N2.These results are in line with the observations reported byGoj et al. (2002) obtained by molecular simulation and by Harlick and Tezel(2003). The observations showedmixture isothermsin which the amount of CO2 adsorption is almost unchanged from the analogous single component isotherm. These results are attributed to the lateral interactions between carbondioxide molecules due to their higher quadrupole moment (Delgado et al., 2006).
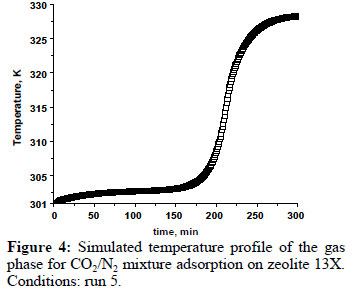
Figure 4 shows the simulated temperature profile for the carbon dioxide/nitrogenmixture adsorption on zeolite 13X, at the end of column, under experimental conditionsof temperature of301 K (run 5). The temperature peak correspond toa differencearound 30K, very similar to the temperature peak observed for the CO2 adsorption only. In the inset, it is possible toobserve that there is a first temperature peakat the beginning of the adsorption. This is to be expected, since, at the beginning, there is also nitrogen adsorption.
Fixed-Bed CO2 Adsorption from a CO2/N2 Mixture in a Nitrogen-Saturated Fixed-Bed
A set of experiments was performed changing the initial temperature of the bed to obtain the breakthrough curves of CO2 adsorption from CO2/N2 mixtures on zeolite 13X in a nitrogen-saturated fixed bed (runs 9 to 12). Figure 5 shows the experimental and simulated breakthrough curves for the CO2 adsorption. The model was suitable for describing the dynamics of CO2 adsorption. The LDF overall mass transfer coefficient used to simulate these breakthrough curves can be seen in Table 7.
The system is non-adiabatic and a variation in the fluidphase temperature was noted during the adsorption (Figure 6) at the differential positionof 0.17 m for run 9. The temperature peak is high, even considering that in this system there is a contribution from nitrogen desorption. This is because zeolite 13X is very selective toward carbondioxide; there is a largedifference between the heat ofadsorptionof carbon dioxide and ofnitrogenon thisadsorbent and the presence of nitrogen does not affect the CO2 adsorption. Moreover, the thermal effects must be considered for all of the CO2 adsorption systems discussed herein.
CONCLUSIONS
In this study, the fixed-bed adsorption of carbon dioxide on zeolite 13X was investigated. A model based on the LDF for the mass transfer, considering the thermal effects, was able to suitably describe the carbon dioxide breakthrough curves.
The fixed-bed adsorption of carbon dioxide from CO2/N2 mixtures on zeolite 13X was also studied. The adsorption dynamics were investigated at several temperatures and under different conditions: considering N2 adsorption and desorption. It was demonstrated that zeolite 13X adsorbed carbon dioxide and nitrogen to its total capacity and, thus, the equilibrium of CO2 and N2 adsorption for CO2/N2 mixtures can be very well described by the pure component adsorption isotherms. A model based on the LDF for the mass transfer, considering the energy and momentum balances, was able to describe adequately the adsorption kinetics of carbon dioxide and nitrogen.
The LDF overall mass transfer coefficient was related to the effective diffusivity for a macropore molecular diffusion-controlled system. The zeolite 13X used in this study has high selectivity for CO2 and it is suitable for CO2/N2 separation processes. The model proposed here can be used to design a PSA cycle to separate CO2/N2 mixtures, where pressure drop and thermal effects are very important.
ACKNOWLEDGEMENTS
The authors are grateful to CAPES for financial support and CAPES/GRICES for the International Brazil/Portugal Cooperation Project.
NOMENCLATURE
constant volume for the gas phase
i in the gas phase
the gas and the adsorbent
the gas and the column wall
coefficient of component i
component i
the solid phase) at
equilibrium with Co
component i
equilibrium of component i
at equilibrium
temperature
coefficient
Greek Letters
component at zero coverage
film temperature
area to the volume of the
column wall
mean surface area of the
column shell to the volume
of the
column wall
coefficient
conductivity
film temperature
Dimensionless Numbers
(Submitted: June 21, 2010 ; Revised: February 23, 2011 ; Accepted: April 30, 2011)
Permanent Address: Federal University of Paraná, Department of Chemical Engineering, Phone + (55) (41) 33613173, Fax: + (55) (41) 33613277, Centro Politécnico, 81531-980, Jardim das Américas, Curitiba-PR, Brazil. E-mail: tirzha@ufpr.br, regina@enq.ufsc.br
- Bird, R.B., Stewart, W. E., Lightfoot, E. N., Transport Phenomena. John Wiley & Sons, New York (1960).
- Cavenati, S., Grande, C. A., Rodrigues, A. E., Adsorption Equilibrium of Methane Carbon Dioxide and Nitrogen on Zeolita 13X. J. Chem. Eng. Data, v. 49, 1095-1101 (2004).
- Cavenati, S., Grande, C. A., Rodrigues, A. E., Separation CH4/CO2/N2 mixtures by Layered Pressure Swing Adsorption for upgrade of natural gases. Chem. Eng. Sci., v. 61, 3893-3906 (2006).
- Chou, C. T., Chen, C. Y., Carbon dioxide recovery by vacuum swing adsorption. Sep. Purif. Technol., v. 39, 51-65 (2004).
- Dantas, T. L. P., Separação de dióxido de carbono por adsorção a partir de misturas sintéticas do tipo gás de exaustão. Ph.D. Thesis, University of Santa Catarina (2009).
- Dantas, T. L. P., Rezende, R. V. P., Rodrigues, A. E., Moreira, R. F. P. M., Adsorção de CO2 e N2 sobre carvão ativado e zeólita 13X: Isotermas de Equilíbrio através de medidas gravimétricas. In: 7ş Encontro Brasileiro sobre Adsorção- 1ş Simpósio Sul-Americano sobre Ciência e Tecnologia de Adsorção (2008). (In Portuguese).
- Da Silva, F. A., Rodrigues, A. E., Propylene/Propane separation by vaccum swing adsorption using 13X zeolite. AICHE J., v. 47, 341-355 (2001).
- Delgado, J. A., Uguina, M. A., Gómez, J. M., Sotelo, J. L., Ruíz, B., Fixed-bed adsorption of carbon dioxide-helium, nitrogen-helium and carbon dioxide-nitrogen mixtures onto silicalite pellets. Sep. Purif. Technol., v. 49, 91-100 (2006).
- De Wash, A. P., Froment, G., Heat transfer in packed beds. Chem. Eng. Sci, v. 27, 567-576 (1972).
- Do, D. D., Adsorption analysis: Equilibria and kinetics. Imperial College Press, v. 2, London (1998).
- Gaffney, T. R., Golden, T. C., Mayorga, S. G., Brzzowski, J. R., Tayler, F. W., Carbon dioxide pressure swing adsorption process using modified alumina adsorbents, U.S. Patent, 5, 917, 136 (1999).
- Goj, A., Sholl, D. S., Akten, E. D., Kohen, D., Atomistic Simulations of CO2 and N2 Adsorption in Silica Zeolites: The Impact of Pore Size and Shape. J. Phys. Chem. B., v. 106, 8367-8375 (2002).
- Gomes, V. G., Yee, K. W. K., Pressure Swing adsorption for carbon dioxide sequestration from exhaust gases. Sep. Purif. Technol., v. 28, 161-171 (2002).
- Grande, C. A., Rodrigues, A. E., Electric Swing Adsorption for CO2 removal from flue gases. Int. J. Greenhouse Gas Control, v. 2, 194-202 (2008).
- Harlick, P. J. E., Tezel, F. H. Adsorption of carbon dioxide, methane and nitrogen: pure and binary mixture adsorption for ZSM-5 with SiO2/Al2O3 ratio of 280. Sep. Purif. Technol., v. 33, 199-210 (2003).
- Incropera, F. D., De Witt, D. P., Fundamentals of Heat and Mass Transfer, 4nd Ed., John Wiley & Sons: New York, U.S.A (1996).
- Lee, J. S., Kim, J. H., Kim, J. T., Suh, J. K., Lee, J. M., Lee, C-H., Adsorption Equilibria of CO2 on Zeolite 13X and Zeolite X/Activated Carbon Composite, J. Chem. Eng. Data, v. 47, 1327-1242 (2002).
- Ruthven, D. M., Principles of Adsorption and Adsorption Processes. John Wiley & Sons, New York (1984).
- Ruthven, D. M., Xu, Z., Farooq, S., Sorption kinetics in PSA systems. Gas Sep. Purif., v. 7, 75-81 (1993).
- Sircar, S., Rao, M. B., Golden, T. C., Fractionation of air by zeolites. Studies in Surface Science and Catalysis, v. 120, 395-423 (1999).
- Siriwardane, R. V., Shen, M-S., Fisher, E. P., Poston, J. A., Adsorption of CO2 on Molecular Sieves and Activated Carbon. Energy Fuels, v. 15, 279-284 (2001).
- Toth, J., State Equations of the Solid-gas Interface Layers. Acta Chim. Acad. Sci. Hung., v. 69, 311-328 (1971).
- Wakao, N., Funazkri, T., Effect of fluid dispersion coefficients on particle-to-fluid mass transfer coefficients in packed beds: Correlation of Sherwood numbers. Chem. Eng. Sci., v. 33, 1375-1384 (1978).
- Zhao, Z., Cui, X., Ma, J., Li, R., Adsorption of carbon dioxide on alkali-modified zeolite 13X adsorbents. Int. J. Greenhouse Gas Control, v. 1 (3), 355-357 (2007).
Publication Dates
-
Publication in this collection
01 Sept 2011 -
Date of issue
Sept 2011
History
-
Accepted
30 Apr 2011 -
Reviewed
23 Feb 2011 -
Received
21 June 2010