Abstract
This work reviews recent trends in the modeling of cellulose hydrolysis, within the perspective of application of kinetic models in a bioreactor engineering framework, including scale-up, design and process optimization. From this point of view, despite the phenomenological insight that mechanistic models can provide, the expectation that more detailed approaches could be a basis for extrapolations to different substrates and/or enzymatic pools is still not fulfilled. The complexity of the lignocellulosic matrix, the different mechanisms of catalytic action, the role of mass transfer limitations and the deviations from ideal mixing are important difficulties for the modeler, which will continue to impose more conservative approaches for scale-up. Nevertheless, the search for more robust models is a very important task, provided that the engineer is aware of their limitations. Data-driven, non-mechanistic models such as artificial neural networks, perhaps in combination with other approaches in the so-called hybrid models, is also a promising alternative.
Cellulose hydrolysis; Kinetics; Mathematical modeling; Bioreactor design
REVIEWS
Recent trends in the modeling of cellulose hydrolysis
R. Sousa Jr.* * To whom correspondence should be addressed ; M. L. Carvalho; R. L. C. Giordano; R. C. Giordano
Department of Chemical Engineering, Federal University of São Carlos, Phone: + (55) (16) 3351 8713, Fax: + (55) (16) 3351-8266, Rod. Washington Luís, Km 235, CEP: 13565-905, CP 676, São Carlos - SP, Brazil. E-mail: ruy@ufscar.br
ABSTRACT
This work reviews recent trends in the modeling of cellulose hydrolysis, within the perspective of application of kinetic models in a bioreactor engineering framework, including scale-up, design and process optimization. From this point of view, despite the phenomenological insight that mechanistic models can provide, the expectation that more detailed approaches could be a basis for extrapolations to different substrates and/or enzymatic pools is still not fulfilled. The complexity of the lignocellulosic matrix, the different mechanisms of catalytic action, the role of mass transfer limitations and the deviations from ideal mixing are important difficulties for the modeler, which will continue to impose more conservative approaches for scale-up. Nevertheless, the search for more robust models is a very important task, provided that the engineer is aware of their limitations. Data-driven, non-mechanistic models such as artificial neural networks, perhaps in combination with other approaches in the so-called hybrid models, is also a promising alternative.
Keywords: Cellulose hydrolysis; Kinetics; Mathematical modeling; Bioreactor design.
INTRODUCTION
Modeling the enzymatic hydrolysis of lignocellulosic materials is probably one of the most challenging subjects in (bio)reactor engineering science at present, and the substantial number of publications and reviews about this topic echoes this situation. Indeed, the complexity of (ligno)cellulosic substrates and the multiplicity of mechanisms involved in the synergistic action of the pool of cellulolytic enzymes create a dilemma for the modeler: taking into account the ever-growing mass of information regarding substrate characteristics (which are of course quite sensitive to pre-treatment conditions), enzyme action, substrate-enzyme interactions and so forth, or simply relying on empiricism? Validate fundamental models with dozens of parameters or use black-box models? In fact, both approaches will most certainly lack generality, but which would be more reliable for real-world reactor design, catalyst optimization and cost evaluation?
Zhang and Lynd (2004) reviewed the enzymatic hydrolysis of cellulose from the perspective of the development of an aggregate understanding of the action of the enzymatic pool. The key point in this approach is to incorporate within the model information regarding other substrate properties in addition to bulk concentrations. Thus, a classification scheme for models was proposed, based on the degree of detail of the description of substrate state variables and/or of the activities of the different enzymes: nonmechanistic, semimechanistic, functionally based and structurally based models.
Nonmechanistic models, which are not based on a definable enzyme/substrate interaction model, can be very useful for data correlation, although they do not enhance the phenomenological understanding of the system.
Semimechanistic models are based on a definable enzyme/substrate interaction model, but use only concentrations as the substrate state variable and/or with only one overall enzymatic activity. Besides their utility for data correlation, semimechanistic models may also be useful for identification of some essential features of the hydrolysis mechanism.
Functionally based models go further, including additional substrate state variables, such as crystallinity, and considering the action of multiple enzymes. Nevertheless, functionally based models can lead to an overwhelming number of parameters, demanding a large amount of experimental data for a consistent model-fitting and validation procedure that may discourage their application.
Finally, structurally based models, which use structural information of the lignocellulose matrix, can be useful to provide insights into the relationship between structure and function. The development of meaningful kinetic models based on structural information, however, is still a major challenge.
Zhang and Lynd (2004) suggested reinvigorating functional modeling of enzymatic hydrolysis, in order to make use of the large volume of information made available by the advancement of the methods for structural characterization of biomass.
Bansal et al. (2009), in a more recent work, reinforced the interest in having models that account for major substrate and enzyme properties. However, as the authors reemphasize, such models must be validated by experimental data that is more detailed than simple conversion vs. time profiles.
In short, the modeler faces at this point the "curse of dimensionality": more fundamental insight demands more complex models and, thus, more parameters to be estimated, growing exponentially. Then, the question posed to the bioreactor engineer is to optimize the complexity of the model, which is bracketed, on one side, by the quality of the available information and the experimental effort needed for model validation and, on the other side, by the use that will be made of the model.
We do not intend to present another extensive review of the subject, but only to sort out works in this area published during the last five years. The idea is to evaluate the latest trends in modeling of cellulose hydrolysis, but from the perspective of the application of kinetic models within a bioreactor engineering framework, where reactor design and process optimization are the ultimate goals.
MINI-REVIEW
Wang et al. (2004) proposed an empirical kinetic model for enzymatic degradation of cotton fibers. A nonlinear multivariate regression model (Equation (1)) was used to postulate the interaction among three independent variables (X1, X2 and X3) for predicting the conversion of substrate into total reducing sugars (TRS), the model output (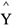 ). X1, X2 and X3 represent the effects of cellobiohydrolase, endoglucanase and β-glucosidase, respectively; X4, X5, X6 and X7 represent the synergistic effects between them.
). X1, X2 and X3 represent the effects of cellobiohydrolase, endoglucanase and β-glucosidase, respectively; X4, X5, X6 and X7 represent the synergistic effects between them.
The analysis suggests that the enzymatic degradation of cotton fiber is a progressive process. Cellulose fibers are first depolymerized or solubilized by the synergism between cellobiohydrolase I and endoglucanase I and then the oligomers obtained were randomly hydrolyzed into glucose by endoglucanase I and β-glucosidase. This is an example of how a datadriven model can provide information about the catalytic mechanism, since the significance of the cross-effects indicated the trend of action of the enzymatic pool. The authors argue that the model can be applied to the quantitative estimation of the effects of three main components of the cellulosic pool, cellobiohydrolase I, endoglucanase I and β-glucosidase separately or in combination, during the whole process of cellulose degradation. Of course, this claim must be put into perspective, since such a data-driven model would hardly be useful when the substrate or the enzymatic pool is changed.
Li et al. (2004) examined the enzymatic hydrolyses of various cellulosic pulps in stirred Erlenmeyer flasks. To enhance saccharification, the reaction was also carried out in a stirred tank reactor with continuous ultrasonic irradiation. A pseudohomogeneous Michaelis-Menten equation with inhibition was then used for fitting. Sugars would be produced from a hypothetical soluble substrate whose initial concentration would correspond to the final conversion of the substrate (Equation (2)). This approach reflects a difficulty that often does not receive attention in the published models: how to quantify substrate concentration for a polymer that is initially solid and gradually made soluble? In fact, the "substrate" is the hydrolysable glucosidic bonds, but how to quantify rigorously their molarity or mass concentration? It is very important that the assumptions made by the modeler concerning this point are clearly stated.
In Equation (2), T∞ denotes the ultimate value of the total sugars concentration, T. Hence, 0.9 (T∞ T) is the hypothetical substrate concentration in the pseudo-homogeneous MichaelisMenten mechanism (the factor 0.9 takes into account an average stoichiometry of the hydrolysis); k is the apparent rate constant, KM is the apparent Michaelis constant and KI is proposed to be the apparent competitive inhibition constant between total sugar and cellulase. E0 is the initial enzyme concentration; t is time. The model was validated against time courses of TRS and glucose liberation during the saccharification, either with or without ultrasonic irradiation. The authors found that the variation in the properties of the pulp and the intensity of ultrasonic irradiation changed the apparent rate constant k, but had no effect on the apparent Michaelis and competitive product inhibition constants.
Bezerra and Dias (2004) investigated the kinetics of an exoglucanase (Cel7A, from Trichoderma reesei) in the presence of cellobiose, with different enzyme/substrate (Avicel) ratios, in order to establish which of eight modified Michaelis-Menten hydrolysis models best explained the observed behavior. The kinetic parameters were estimated by non-linear least squares, employing integrated forms of Michaelis-Menten equations. It was found that the cellulose hydrolysis velocity, v, followed a model that takes into account competitive inhibition by cellobiose (as in Equation (3)).
Vmax is the maximal velocity, S is cellulose (transformed into potential cellobiose), P (product) is cellobiose; the subscript 0 is the initial concentration at t = 0. Km is the Michaelis-Menten constant and Kic is the (competitive) inhibition constant.
Other models, incorporating mixed inhibitions and improvements like inhibition by substrate increased only slightly the performance of the model.
In another work, Bezerra and Dias (2005) studied the effect of ethanol inhibition on Trichoderma reesei cellulases. To determine inhibition parameters for crude cellulase and for a purified exoglucanase (Cel7A), integrated Michaelis-Menten equations were used considering the presence of two inhibitors: cellobiose, as a hydrolysis product, and ethanol. Hydrolysis of cellulose by purified Cel7A showed competitive inhibition by both cellobiose and ethanol. Hydrolysis of cellulose by crude enzyme followed a model that also considered noncompetitive inhibition (as in Equation (4)).
I is the ethanol plus cellobiose concentration and Kiu is an (uncompetitive) inhibition constant. Ethanol was a more effective inhibitor of the crude enzyme than of exoglucanase Cel7A, but cellobiose inhibition was much more important than ethanol inhibition in both cases.
Carrillo et al. (2005) studied the kinetics of (sodium hydroxide) pretreated wheat straw hydrolysis using different concentrations of a commercial cellulase. As expected, compared to untreated wheat straw, the delignification pretreatment increased hydrolysis. The influence of enzyme concentration on the production of reducing sugars was studied by considering two different theoretical approaches:
In the first one, the hydrolysis model and its kinetic parameters were determined from initial velocities assuming a Michaelis-Menten mechanism, but with solid substrate and soluble enzyme. This implies that enzyme and substrate concentrations are exchanged in the Michaelis equations, the enzyme, instead of the product, being released to the medium at the end of the reaction sequence. Hence, the initial hydrolysis velocity can be expressed as a function of the initial enzyme concentration (as in Equation (5a)).
In this equation, v0 is the initial hydrolysis velocity, Vemax is the maximal velocity and Ke is the corresponding half-saturation constant.
In the second strategy, the Chrastil approach (1988 and 1988b, as in Equation (5b)) was used. All time constants for the rate of product formation are ranked, taking into account that, in a heterogeneous system, the time curves depend strongly on the heterogeneous rate-limiting structures of the substrate-enzyme system, including enzyme diffusion resistances. With this analysis, additional kinetic and structural characteristics may be inferred, which cannot be revealed from initial velocity analysis as proposed by HenriMichaelisMenten. The n and k' parameters offer quantitative information about the overall steric structure of the diffusion system and catalytic properties, respectively, and may be useful to follow the changes that necessarily occur in the substrate enzyme system while cellulose solubilization advances.
P and P∞ are the products which diffuse at time t and at equilibrium, respectively, k' is a rate constant proportional to the diffusion coefficient as defined by Fick's law, and n is a structural diffusion resistance constant dependent on the steric structure of the system. The parameter n reflects the apparent reaction order. When diffusion resistance is small, n tends to 1. If the system is strongly limited by diffusion resistance, n is small. One may conclude from this work that distinct approaches to the kinetic modeling may be complementary, helping to understand the changes in the dynamics of this system while the reaction proceeds. Actually, this is a difficulty often present when one tries to fit simple pseudohomogeneous Michaelis-Menten equations to long term batch experiments for cellulose hydrolysis.
Kadam et al. (2004) developed a multireaction semimechanistic kinetic model in which three hydrolysis reactions were modeled, one heterogeneous reaction for cellulose breakdown to cellobiose, another heterogeneous reaction for glucose formation from cellulose and one homogeneous reaction for hydrolyzing cellobiose to glucose. Cellulase adsorption onto lignocellulose was modeled by a Langmuir isotherm (as in Equation (6a)).
EiB is the bound enzyme concentration, EiF is the free enzyme concentration, Eimax is the maximum mass of enzyme that can adsorb onto a unit mass of substrate, and Kiad is the dissociation constant for the enzyme adsorption/desorption reaction. The products of hydrolysis, cellobiose, glucose and also xylose were considered to competitively inhibit the enzymatic reactions (see Equations (6b) - (6d)).
In these equations, r1 is the cellulose-to-cellobiose reaction with competitive inhibition by glucose, cellobiose and xylose; r2 the cellulose-to-glucose reaction with competitive inhibition by glucose, cellobiose and xylose inhibition; r3 the cellobiose-toglucose reaction with competitive glucose and xylose inhibition. S is the substrate concentration at a given time, CG is the glucose concentration, CCb is the cellobiose concentration, X is the xylose concentration, KiIG are the inhibition constants of glucose on the enzymes, KiIG2 are the inhibition constants of cellobiose on the enzymes, KiIX are the inhibition constants of xylose on the enzymes, K3M is the substrate (cellobiose) saturation constant, and RS is the substrate reactivity (dimensionless). In an attempt to represent all the transformations of the substrate during the enzymatic hydrolysis, they were lumped into one parameter, RS, which was correlated with the normalized substrate concentration (RS=S/S0). These model parameters were estimated from experimental data for pretreated corn stover and the model matched well the experimental data.
Zhang and Lynd (2006) presented a functionally based kinetic model for enzymatic hydrolysis of cellulose by the Trichoderma reesei cellulase system. The model represented the actions of endoglucanase I (EG1) and cellobiohydrolases (CBH) I and II. It also incorporated two substrate parameters: the degree of polymerization and the fraction of β-glucosidic bonds accessible to cellulase.
The action of endoglucanase is consistent with a mechanism postulating that free EG1 adsorbs to a cellulose molecule to form an enzymecellulose complex. The adsorption occurs randomly with respect to chain length and the adsorption equilibrium constant (in Equation (7a)) describes the distribution with respect to cellulose molecules of all lengths.
The quantity (i-1)Gi denotes the total concentration of β-glucosidic bonds in cellulose chains of DPi. Multiplying by the fraction of bonds accessible to cellulase, Fa, one has the concentration of accessible bonds in chains of DPi. In the second step of the mechanism, hydrolysis of cellulose molecules of DPi to smaller products is considered. Equation (7b) is an equation for the overall rate of formation of Gi due to the action of EG1.
Here Gi and Gk are cellulose molecules with a chain length (DP) of i and k, respectively, kEG1 is rate constant for EG1 cleavage of β-glucosidic bonds, subscript t is total enzyme, while f is free enzyme. Cellulose hydrolysis by cellobiohydrolases had rate equations that were functions of the degree of polymerization and of the fraction of β-glucosidic bonds accessible to cellulase.
This is an attempt at a rational, phenomenological approach, embracing structural information of the substrate. Nevertheless, its application is limited by the lack of information to estimate some necessary parameters. Therefore, the authors relied on rate equations for CBH proposed in a previous work (Okazaki and Moo-Young, 1978). Initial enzymelimited reaction rates simulated by the model were consistent with important behavior reported in the literature, like the effects of substrate characteristics, the degree of endo/exoglucanase synergy and enzyme loading on relative reaction rates for different substrates. In a more recent work, Zhou et al. (2009) developed a general formalism, which can be reduced mathematically to the Zhang and Lynd (2006) and Okazaki and Moo-Young (1978) models. However, the authors state [Zhou et al., 2009b] that several experimental assays are required to provide a more detailed quantitative validation of their morphology-based approach, which correlates observed hydrolysis rates with the mesoscopic substrate morphology. Time-dependent results for the accessibility fraction Fa and DP could be directly compared to model predictions and they would provide a more stringent test of the model, as well as further constraints on model parameterization.
In the work by O'Dwyer et al. (2007), glucose inhibition patterns for the Trichoderma reesei cellulase complex and lime-pretreated corn stover were identified. The ranges of substrate concentrations and enzyme loadings in which the linear form of a simplified HCH-1 model is valid were also identified. HCH-1 is a modified MichaelisMenten model with non-competitive inhibition and a fraction of insoluble substrate available to bind with the enzyme (as in Equation (8a)):
where CC is the cellulose concentration, E is the enzyme concentration, φ is the fraction of the cellulose surface that is free to be hydrolyzed, and k, α, and ε are parameters that describe the degree of substrate reactivity and hence are related to biomass structural features. For multiple inhibitors, the inhibition parameter i, which is the fraction of total enzyme not inhibited by product, is given as
where β1 and β2 are glucose (CG) and cellobiose (CCb) binding constants, respectively.
With a high enzyme loading, the HCH-1 model can be integrated and simplified in a way that conversion into sugar is linear with the logarithm of enzyme loading (as in Equation (8c)).
where x is sugar conversion. Experiments were carried out with an excess of cellobiase to ensure that the results were not influenced by cellobiose inhibition. A non-competitive inhibition pattern was identified for the corn stovercellulase system, validating the assumptions of the HCH-1 model.
In another work by O'Dwyer et al. (2008), the fact that plots of biomass digestibility can be linear with the logarithm of enzyme loading was further explored, assuming that the slope and intercept of these monolog plots may characterize biomass reactivity. Nonmechanistic feed-forward back-propagation neural networks (Annema, 1995; Hagan et al., 1996) were designed to predict biomass digestibility by simulating the 1, 6, and 72-h slopes and intercepts of glucan, xylan, and total sugar hydrolyses of 147 poplar wood samples with a variety of lignin contents, acetyl contents, and crystallinity indices.
An artificial neural network is an effective tool to represent nonlinear relations between input and output variables. They are black box models, not requiring a phenomenological description of how the output depends on the input. Instead, they learn from input-output data sets. A neural network is an array of nodes (neurons) linked by connections. The topology used in this work was the multilayer perceptron, supervised training network a very popular architecture for predictive models. Two or more neurons of this kind of neural net can be combined in a layer and they are interconnected. Each connection has a scalar weight associated with it, which modifies the strength of the signal. The function of the neuron is to sum the weighted inputs and pass the summation to neurons in the subsequent layer through a nonlinear transfer function. In this case, feedforward neural networks were used, where the information flows through the net only in one way. Supervised training of the neural net is simply the estimation of the weights, the model parameters, from a series of inputs and associated outputs.
O'Dwyer et al. (2008) demonstrated the potential of neural networks to predict biomass digestibility. According to Bansal et al. (2009), models that interpolate over a wide range of the predicted and independent variables can be useful for designing processes under various conditions. Of course, this approach is very sensitive to the quality of the empirical data bank used for training.
In heterogeneous catalytic systems, the interaction between reactant and catalyst can be different from the corresponding homogeneous situation, because of the peculiarity of the diffusion and molecular collision processes involved. The fractal theory, developed for processes with inherent irregularity and complexity, can be applied to heterogeneous catalysis. To better understand the heterogeneous enzymatic reactions, a "jammed" fractal Michaelis-Menten model was presented by Xu and Ding (2007), applying the general fractal formalism to the classical model of homogeneous enzymatic reactions coupled to a kinetic "jamming" effect caused by the overcrowding of enzyme/ substrate in confined space (like in vehicular traffic flow theory); see Equation (9).
where j is a "jamming" factor and f is a "fractal dimension". When E<<jS, the "jamming" effect becomes negligible; when f→0, the fractal effect becomes negligible. This kinetic model was applied to the hydrolysis of cellulose by cellobiohydrolase.
In the work by Bommarius et al. (2008), Avicel was subjected to three different pretreatments (acid, alkaline, and organosolv) and subsequent exposure to a mixture of cellulases. Addition of β-glucosidase to avoid the inhibition of cellulase by cellobiose accelerated cellulose hydrolysis. All pretreatments of Avicel were found to slightly increase its degree of crystallinity in comparison with the untreated material. Adsorption of cellulase on cellulose and "jammed" fractal Michaelis-Menten kinetics were considered. Adsorption of cellulase and β-glucosidase on cellulose was significant. The conversion vs. time behaviors of Avicel (pretreated and untreated) were found to be similar. Jamming of adjacent cellulase enzymes when adsorbed on a microcrystalline cellulose surface was evident at higher concentrations of enzyme.
In the work by Al-Zuhair (2008), a semimechanistic model based on a previous work by Gan et al. (2003) was derived to predict the rate of reducing sugar production, using Aspergillus niger cellulase for hydrolysis of two kinds of cellulose: amorphous carboxymethylcellulose and crystalline wood shavings. The experimental results were used to estimate the kinetic parameters. In the model, the complex structure of cellulose is divided into hydrolysable [Sc] and non-hydrolysable [Sx] regions. The non-hydrolysable regions are assumed to reversibly inhibit the reaction in a competitive manner. The fractions of the inactive and the active materials are defined by Equations (10a) and (10b).
where [St] is the total cellulose surface concentration and φ is the inert fraction coefficient, which is assumed to be constant for each type of cellulose (low for carboxymethylcellulose but high for wood shavings). The inert fraction coefficient, φ, represents the substrate crystallinity index used by Fan and Lee (1980). There was good agreement between experimental results and model predictions.
In the work by Liao et al. (2008), a kinetic model incorporating adsorption, enzymatic hydrolysis, and product inhibition was developed for enzymatic hydrolysis of differently pretreated fibers from dairy manure. Enzyme adsorption was modeled based on a Langmuir-type isotherm (with a change in the adsorption constant, represented by an empirical expression). Enzyme activity, instead of protein concentration, was used to describe the enzymatic hydrolysis in order to avoid the effect of manure protein on enzyme protein analysis. A first-order reaction rate, r, was applied to model the hydrolysis, with glucose inhibition (as in Equation (11)).
where Ceff is the concentration of cellulose available for the enzyme, Ceff =  CC, CC is the cellulose concentration, CC0 is the original cellulose concentration, λ is the constant relating the percentage of cellulose available for the enzyme, EC is the concentration of enzyme absorbed by cellulose, EC =
CC, CC is the cellulose concentration, CC0 is the original cellulose concentration, λ is the constant relating the percentage of cellulose available for the enzyme, EC is the concentration of enzyme absorbed by cellulose, EC = , Ead is the enzyme activity adsorbed by fiber, L is the lignin concentration, H is the hemicellulose concentration, CG is the glucose concentration, and KIG is the inhibition constant for glucose. The model satisfactorily predicted the behavior of enzyme adsorption, hydrolysis, and product inhibition for all sample manure fibers.
, Ead is the enzyme activity adsorbed by fiber, L is the lignin concentration, H is the hemicellulose concentration, CG is the glucose concentration, and KIG is the inhibition constant for glucose. The model satisfactorily predicted the behavior of enzyme adsorption, hydrolysis, and product inhibition for all sample manure fibers.
In their work, Zheng et al. (2009) presented a semimechanistic kinetic model (based on Kadam et al., 2004) to describe the enzymatic hydrolysis of creeping wild ryegrass. Their model incorporates two heterogeneous reactions of cellulose-to-cellobiose and cellulose-to-glucose and one homogeneous reaction of cellobiose-to-glucose. Adsorption of cellulase onto pretreated creeping wild ryegrass was modeled by a Langmuir adsorption isotherm. The model also incorporated the negative role of lignin (nonproductive adsorption) using a Langmuir isotherm adsorption of cellulase onto lignin. The model also considered the (competitive) inhibitions of cellulase by glucose and cellobiose. The model showed high accuracy for predicting cellulose hydrolysis trends.
Hodge et al. (2009) developed an optimization strategy for cellulose hydrolysis at solid percentages higher than 15%, when inefficient stirring and mixing in tank reactors may become a problem. Starting from a previously developed model (Kadam et al., 2004) for batch operation and considering modifications to account for effects of feeding in fed-batch operation, a feeding policy (profile) was developed to maintain the insoluble solids concentration at a manageable level throughout the reaction course. Therefore, sugar concentration within the tank reactor may be increased without using a high initial load of insoluble solids.
In the work by Morales-Rodríguez et al. (2010), optimization of fed-batch reactors for cellulose hydrolysis was studied. To this end, three different feedback (PI) control strategies were developed and evaluated using a first-principles model of the hydrolysis process. A (re-calibrated) model of Kadam et al. (2004) was used to test the performance of three control strategies: (1) insoluble solids control; (2) controller 1 + enzyme class I (CBH + EG) control; (3) controller 1 plus 2 and enzyme class II (BGD) control.
Control strategy 3 gave promising results regarding cellulose conversion and amount of added enzyme. The authors claim that the amount of enzyme can be reduced 107% with respect to the base case operation, which uses a predefined fed-batch feeding strategy (Hodge et al., 2009). Nevertheless, this conclusion was based on simulations, and experimental validation is necessary to verify whether the re-calibrated model is valid for all simulated conditions.
In ethanol production from cellulose, enzymatic hydrolysis and fermentative conversion may be performed sequentially, in a sequential hydrolysis and fermentation process (SHF) or in a simultaneous saccharification and fermentation (SSF) process. Drissen et al. (2009) affirm that choosing either is a trade-off between optimal enzyme temperatures and inhibitory glucose concentrations on the one hand (SHF) versus sub-optimal temperatures and ethanol-inhibited cellulose hydrolysis on the other (SSF). Drissen et al. (2009) extended a published kinetic model to consider enzyme inhibition by ethanol, thus allowing the comparison between SSF and SHF. Their model assumed three enzyme-catalyzed reactions for cellulose hydrolysis: cellulose-to-cellobiose (reaction 1), cellobiose-to-glucose (reaction 2) and cellulose-to-glucose (reaction 3). For reactions with cellulose as substrate, the active amount of enzyme was the adsorbed fraction (linear adsorption constant KL). For reactions yielding glucose, product inhibition was assumed (inhibition constants Ki,G and Ki,2). In addition, all enzymes were subject to thermal inactivation (constant KD). The nature of the cellulose substrate was assumed to be conversion-dependent, through a recalcitrance parameter (constant KREC). Finally, ethanol inhibition affected the rates of reactions 1 and 3 (inhibition constant Ki,EtOH).
Here CC is the cellulose concentration, CCb is the cellobiose concentration, CE is the enzyme concentration, CEtOH is the ethanol concentration, CG is the glucose concentration, eg is the β-glucosidase activity per g of protein in the enzyme preparation, etotal is the protein (enzyme) concentration per L reaction, kmax,i is the maximum specific rate constant, Km is the Michaelis constant for β-glucosidase, R is the gas constant, T is the absolute temperature, Ea is the activation energy. For modeling glucose consumption and biomass formation, standard Monod kinetics was assumed, expanded to include ethanol inhibition. The model predicted SSF processing to be superior. The superiority of SSF over SHF was confirmed experimentally, both with respect to ethanol yield from glucose and ethanol production rate.
A kinetic model was presented by Zhang et al. (2009) to predict simultaneous saccharification and co-fermentation of paper sludge by a commercial cellulase preparation and a xylose-consuming genetically modified yeast Saccharomyces cerevisiae. A semi-mechanistic rate equation for cellulose hydrolysis proposed by South et al. (1995) was used and parameters for paper sludge came from the data of Shao (2007). The parameters presented in Shao's model were based on cellulose hydrolysis only, but hemicellulose hydrolysis was of interest for the study by Zhang et al. (2009). Therefore, adsorption and some hydrolysis parameters were recalculated from Shao's data. Adsorption of cellulase, hydrolysis of glucan to cellobiose with inhibition by cellobiose and ethanol, and hydrolysis of cellobiose to glucose with inhibition by glucose were considered (as in Equations (13a)-(13d)).
To extend the preexisting modeling to SSCF, it was necessary to address xylan hydrolysis (by a simple correlation model, as in Equation (13e)).
where BG is the β-glucosidase concentration in solution, c the conversion-independent component of cellulose in the rate function, Cs the specific capacity of carbohydrate component for cellulase, CE the concentration of carbohydrateenzyme complex, CCb the cellobiose concentration, Ef the free cellulase concentration, Et the total cellulase concentration, Eth the ethanol concentration, CG the glucose concentration, Gn the cellulose component of the remaining substrate, k the cellulose hydrolysis rate constant, KC the rate constant for hydrolysis of cellobiose to glucose, KCG the inhibition of cellobiose hydrolysis by glucose, KS the Langmuir affinity constant, KSC the inhibition of cellulose hydrolysis by cellobiose, KSP the inhibition of cellulose hydrolysis by ethanol, m the exponent of declining glucan reactivity, and Xn the xylan component of the remaining substrate.
The net rate of glucose formation was determined by the rate of formation by enzymatic hydrolysis and the rate of consumption by fermentation. Glucose fermentation was accounted for by a Monod equation with one additional term representing competitive inhibition of sugar uptake from xylose and another additional term representing ethanol inhibition. The rate of formation of xylose was described by an approach similar to that used for glucose. The overall cell mass formation rate was determined from the predicted cell growth due to glucose and xylose consumption and the predicted cell death due to the endogenous metabolism and ethanol toxicity. Ethanol production rate was calculated on the basis of sugars consumed.
Experimental results showed that glucan and xylan enzymatic hydrolysis were highly correlated and that the low concentrations of xylose encountered during SSCF did not have a significant inhibitory effect on enzymatic hydrolysis. Ethanol was found to inhibit the specific growth rate and accelerate cell death. The cellulose adsorption capacity and cellulose hydrolysis rate constants were found to have the greatest impact on ethanol production (for a fixed substrate loading, enzyme loading, and fermentation time), among the enzymatic hydrolysis-related constants. Ethanol yield and maximum ethanol tolerance had the greatest impact among the fermentation-related constants.
In a companion paper, Zhang et al. (2009b) observed that their kinetic model could predict batch and fed batch fermentations well at solids concentrations up to 62.4 g L-1 but not at 82.0 g L-1. The authors concluded that a mass transfer limitation was responsible for the discrepancy between model and experimental data.
In the work by Shao et al. (2009), the model of South et al. (1995) for simultaneous saccharification and fermentation of cellulosic biomass was extended and modified to accommodate intermittent feeding of substrate and enzyme and a cascade reactor configuration.
Zhang et al. (2009) used artificial neural networks (Annema, 1995; Hagan et al., 1996), to describe the kinetics of enzymatic cellulose hydrolysis and compared with a quadratic polynomial (regression Equation (14)).
where Y is the response value of glucose concentration, X'1 is the cellulase activity, X'2 is the substrate concentration and X'3 is time. Three hydrolysis parameters served as input to the neural network model: cellulase activity, substrate concentration and time. The output was the glucose content. Experimental data were utilized to train the neural network using the classic backpropagation algorithm. The artificial neural network predictions showed better agreement with the reported experimental results than the quadratic polynomial.
The model by Levine et al. (2010) is based on a mechanistic description that includes distinct adsorption and complexation steps for the enzyme. Individual cellulases of a well-defined enzyme mixture are explicitly tracked; substrate concentration and the degree of cellulose polymerization are monitored and surface concentrations of each cellulose chain length are individually described. Representation of the substrate is focused on capturing the time course of cellulose surface area; as the cellulose particles shrink, new chains are exposed and the total cellulose surface area is reduced. Particles are composed of cellulose chains of varying length described by a Poisson distribution based on the initial degree of polymerization. The cellulose particles shrink as soluble cello-oligosaccharides are released from the surface. A material balance describes the rate at which the particle radius changes with time.
As soluble cello-oligosaccharides are released from the solid cellulose surface, fresh cellulose chains become part of the surface. A term is required in the equations for cellulose chain surface concentrations to account for this new chain exposure. Particles are assumed to be composed of a continuum of cellulose chains and their physical characteristics (e.g., sites per area and density) are assumed to remain constant as the particles shrink. The rate at which new chains are exposed is equal to the rate at which old chains are lost, since the number of sites per area is assumed to be constant. Individual chains have an exposure term that depends on the rate of loss of old chains and the initial degree of polymerization probability distribution function F. The cellulose chains on the surface are represented as a lattice of glucose units. In the case of lignocellulosic substrate, the representation of the surface can be modified to include non-hydrolyzable sites. Each enzyme that adsorbs onto this lattice occupies a certain number of sites.
The mechanism by which cellulases catalyze the hydrolysis of cellulose followed three steps: (1) adsorption, (2) complexation, and (3) reaction. Adsorption and complexation were treated as reversible steps, while the reaction step was irreversible. Adsorption and desorption of the cellulases were described using site and enzyme balances, which provide concentrations of cellulose surface sites and solution-phase enzymes. All cellulases are allowed to adsorb onto identical free sites on the cellulose surface. Adsorption and desorption are treated as elementary reactions, leading to balance equations for adsorbed, uncomplexed enzyme concentrations. The catalysis step is assumed to be slow, allowing complexation/decomplexation to be considered close to equilibrium. The equilibrium assumption for complexation leads to a simple relationship between the surface concentrations of adsorbed complexed enzyme, adsorbed uncomplexed enzyme, and surface cellulose chains. The difference in the equilibrium relationship for endoglucanase and cellobiohydrolase enzymes stems from the ability of endoglucanase to complex with any glycosidic bond on the cellulose chain, while cellobiohydrolases can only complex with a specific chain end (reducing or non-reducing). Using the equilibrium relationship and considering the above-mentioned mechanism (adsorption, complexation and reaction), balance equations for the surface concentration of solid cellulose chains of length i can be derived. Soluble cello-oligosaccharides are formed by enzymes acting on both soluble, short-chain sugars and on insoluble chains within the solid substrate. The equations describing the generation of soluble short-chain sugars assume a MichaelisMenten mechanism for the soluble phase reaction terms, and rely on assumptions similar to those for the solid phase reaction terms.
This model requires a variety of adsorption, kinetic, and physical parameters. Sets of experimental values were determined, or values from the literature were used. In the absence of reliable experimentally determined parameters, estimates were made by fitting the model to experimental data. The model explicitly tracks individual cellulases and key cellulose surface properties. Independent enzyme adsorption and complexation steps were incorporated in an attempt to capture the most important details of the enzymesubstrate interaction. Individual enzyme hydrolysis (EG2 or CBHI) and mixed enzyme hydrolysis scenarios were used to compare model results with experimental data from the literature. The model results were not consistent with all of the experimental data, however.
The cellulase enzymatic cocktail secreted by Trichoderma reesei has been intensively investigated with respect to its kinetics for cellulose hydrolysis. Nevertheless, β-glucosidase is very poorly secreted by T. reesei strains and complete hydrolysis of cellulose often requires supplementation with a commercial β-glucosidase preparation, such as that from Aspergillus niger. Possible differences between native T. reesei and supplemented β-glucosidases are usually not taken into consideration. In the work by Chauve et al. (2010), a comparative kinetic analysis between β-glucosidase from A. niger and β-glucosidase from T. reesei was performed. β-glucosidase from A. niger showed a lower specific activity than β-glucosidase from T. reesei and was also more sensitive to glucose inhibition. A Michaelis-Menten model considering competitive inhibition by glucose was validated and was able to predict the β-glucosidase activity of both enzymes.
In the work by Rivera et al. (2010), a data-driven technique based on artificial neural networks and design of experiments was applied in order to identify optimal enzyme combinations. This technique was used to construct a model of the combined effects of cellulase and β-glucosidase loads on glucose yield after enzymatic hydrolysis. The authors state that their dynamic model can be used not only for the prediction of glucose concentration profiles for different enzymatic loadings, but also to obtain the optimum enzyme loading that leads to high glucose yield.
One of the purposes of the study by Brown et al. (2010) was to compare models for the enzymatic hydrolysis of pretreated biomass. Experimental enzymatic hydrolysis data from AFEX (ammonia fiber explosion) treated wheat straw were modeled with two and three-parameter models from the literature. In order to evaluate the models, initial reaction rate data at 49ºC were considered. For three-parameter models, the HCH-1 model fitted best the experimental data; for two-parameter models, Michaelis-Menten gave better results. As expected, three-parameter models fit the data better than the two-parameter models. The best three models at 49ºC were compared using initial rate data at three temperatures (35, 42 and 49ºC). The HCH-1 model provided the best fit based on F values, the scatter plot and the residual sum of squares.
In the work by Ko et al. (2010), rice straw was collected to convert cellulose into ethanol through enzymatic hydrolysis followed by fermentation. In their research, the kinetic model parameters of cellulose saccharification were determined from real experimental data for cellulase hydrolysis. The fermentation model was based on the cybernetic approach (Di Serio et al., 2003) including both glucose and ethanol inhibition. A more fundamental modeling of the growth behavior of S. cerevisiae requires a detailed knowledge of the intracellular control mechanisms that the Monod classical model is not able to describe. The cybernetic modeling framework is based on the hypothesis that microorganisms optimize the utilization of available substrates to maximize their growth rate at all times (Ramkrishna, 2003). The values of the single growth rates of the different metabolic pathways are calculated by means of a modified Monod equation, where each growth rate is proportional to the concentration of a postulated "key" enzyme within the metabolic pathway. The cybernetic modeling framework replaces the detailed modeling of regulating processes with the cybernetic variables ui and νi, representing the optimal strategies for the synthesis and activity, respectively, of the enzymes of the metabolic pathway, i. The value of ui can be assessed by assuming that cell resources will be allocated in such a way as to obtain the maximum biomass growth rate. A law of resource allocation (as in Equation (15a)) can be derived from the economic theory of marginal utility. The marginal utility of a good or service is the relative satisfaction gained (or lost) by an increase (or decrease) in its consumption.
The variable controlling the inhibition/activation mechanism of the "key" enzyme i (νi) is determined by considering a null inhibition effect when the microorganism grows on the substrate that accelerates the biomass growth rate to the utmost, whereas the inhibition effect progressively increases at a decreasing growth rate (see Equation (15b)).
Ko et al. (2010) simulated the operations of the SSF and the SHF processes. It was shown that the SSF process can be better at reducing the processing time when the desired ethanol concentration is high. Since operating the SSF process initially under aerobic conditions can help biomass growth, the time interval of the aeration phase was also investigated. It was shown that for rice straw the optimal duration of the aeration phase is 7 h (if the ethanol productivity is used as the performance index to be maximized).
In their works, Andrić et al. (2010 and 2010b) stated that new bioreactor design strategies are required to alleviate product inhibition (quantified by the authors using the MichaelisMenten model incorporating non-competitive product inhibition), thus enhancing the efficiency of enzymatic cellulose hydrolysis. Running the enzymatic hydrolysis at medium substrate concentrations in separate reactors that allow continuous glucose removal was the solution proposed by the authors. Membrane reactors allowing continuous, complete glucose removal are suggested. According to the authors, current membrane reactors are still not suitable for large scale operation. It is emphasized that industrial realization of cellulosic ethanol production requires more focus on the operational feasibility of different hydrolysis reactor designs, notably for membrane reactors.
After this short overview of the more recent models for the enzymatic hydrolysis of lignocellulosic substrates, the question of their applicability for the design, optimization or control of bioreactors naturally arises. Given this variety of approaches, the response is certainly not straightforward. Table 1 is an attempt to summarize the different model characteristics from this point of view.
DISCUSSION
Table 1 is an attempt to show some recent models for cellulose hydrolysis, their attributes (and drawbacks) and the kind of information (experimental effort) they require to be applied. As it becomes apparent from this compilation, the complexity of the substrates and of the catalytic mechanism for this system is so high that considering all aspects in a generic, first-principles model is unfeasible at the present state of the art.
One point to be stressed is that it is very important to understand what one means by "substrate concentration". Often this information is not explicit in the publications.
Most of the models do not try to correlate rate and equilibrium constants with temperature, using Arrhenius or Van t´Hoff equations (Drissen et al, 2009, is one of the exceptions, considering thermal inactivation as well). The influence of pH on enzymatic rates of hydrolysis is not considered as well, probably because the number of parameters would increase accordingly and the authors prefer to model systems at constant temperature and pH.
Two different views for modeling this complex system are present in the recent literature. The first one can be named application-driven models for instance, the use of models to optimize the production of bioethanol. The tendency here is moving towards models of increasing complexity. Data-driven models, such as neural networks or multiple regression expressions, are being largely used. However, the higher the complexity of interactions that one wants to model, the lower the generality of the model itself. Hence, extensive experimental data are demanded in order to build a consistent, robust empirical model to be used for bioreactor design.
On the other hand, models that take into account more fundamental aspects of the enzyme(ligno)celllulosic substrate interactions are being published, too. They can provide a better insight into the mechanism of action of the enzymatic pool. Their application to engineering problems cannot be discarded, yet their real use is restrained by the availability of data needed to support the tuning of parameters and to characterize structural aspects of the substrate. Indeed, the need for structural and chemical characterization of the substrate, the occurrence of thermal inactivation, the role of mass transfer resistances and of deviations from ideal mixing in the heterogeneous reactor, all these phenomena make the use of these more detailed models for reactor design and scale-up very difficult. Once again, the lack of generality is present, since one would need information for each specific substrate/enzyme system not forgetting the huge variability of lignocellulosic substrates.
Certainly both tendencies will continue in the foreseeable future. We believe that engineering practice for design and scale-up will probably rely more on different empirical and semi-empirical approaches (nonmechanistic or semimechanistic): neural networks, regression analysis, and simple rate equations here including pseudohomogeneous, two or three parameter equations based on reaction mechanisms that we know are not the "real thing" that is happening, but that fit well to the data. Besides, distinct approaches of kinetic modeling may be complementary. Using combinations of their functional forms perhaps may be an alternative to represent the dynamics of this system while the reaction proceeds. This is actually a difficulty often present when one tries to fit simple pseudohomogeneous equations to long-term batch experiments.
Hybrid neural network-first principle models can also be considered for specific situations. Neural networks have been successfully used as "black-box" models of dynamic systems. Combining them with simplified (semimechanistic) first principles models, in order to form a combined (hybrid) model structure, may be an interesting solution. This methodology offers advantages over a completely "black-box" approach, since the semimechanistic part of the model would describe interactions based on physical considerations, while the neural network complements this model by estimating unmeasured process parameters. Such models are expected to perform better than completely "black-box" neural network models in process identification tasks.
But one cannot disregard the future use of structurally based models, provided the evolution of methods for structural characterization of the substrate makes feasible the industrial use of advanced techniques non-destructive spectroscopic methods, for instance. If this kind of information becomes available, the lack of empirical data may be overcome and the routine use of this kind of model may become a common practice.
From our review of recent papers, we may state that there is still room for works that systematically compare different model conceptions against real data.
CONCLUSION
As a conclusion, we observe that semimechanistic models considering Langmuir and/or Michaelis-Menten enzyme/substrate interactions are still largely applied (and improved, such as in the "jamming" fractal Michaelis-Menten). Inclusion of substrate structure-related state variables in addition to concentration and multiple enzymes can be considered in functionally based models. Unfortunately, the functionally based models can lead to a large number of parameters to fit to experimental data. Due to the increase in the number of parameters, such models need to be validated with experimental data other than conversion vs. time profiles. Many times, there is no rational basis to estimate some necessary parameters.
Nonmechanistic approaches, such as artificial neural networks, which perform correlations without requiring mechanistic assumptions of how the output depends on the inputs, are an attractive alternative, although lacking capacity for generalization. Some studies demonstrated the potential of neural networks. Such models are able to interpolate over a large range of the predicted and independent variables. Artificial neural networks showed better performance than quadratic polynomials.
Our intention with this mini-review was to draw a picture of recent approaches used for modeling cellulose enzymatic hydrolysis, mostly from a utilitarian point of view, namely, for applications in bioreactor engineering practice. With this in mind, the point to be addressed is: do the mathematical forms of the semi-mechanistic, mechanistic or functionally based models support generalization? Can they be applied for substrates and enzymatic pools different from those used by the authors which will most certainly be the case for real industrial processes? In our opinion, the answer is essentially no, at least at the present stage of the research.
Currently, all approaches require experimental validation for application in reactor design of specific processes. More structured models can inspire more confidence for extrapolations, but they require detailed information about substrate and/or enzymes, leading to a large experimental effort. Thus, scale-up procedures tend to be more conservative, relying on experimental data from pilot plants.
Finally, considering the rising demand for sustainability (lower water consumption and/or lower consumption of energy to concentrate the product, resulting in high solids loading), fed-batch operation can be a very interesting process alternative. Still, the question of imperfect mixing in the solid-liquid reactor should be studied in the future. To scale up to the industrial level, it is important to model the deviation of the bioreactor from ideality, a field that deserves future attention.
ACKNOWLEDGEMENTS
The authors would like to thank the support of FAPESP-BIOEN, CNPq and CAPES.
NOMENCLATURE
ethanol concentration
glucose concentration
enzyme concentration
concentration of enzyme absorbed by cellulose
β-glucosidase activity per g of protein in the enzyme preparation
bound enzyme concentration
free enzyme concentration
total cellulase concentration
protein (enzyme) concentration per L reaction
fraction of bonds accessible to cellulase
cellulose component of the remaining substrate
hemicellulose concentration
ethanol plus cellobiose concentration
fraction of total enzyme not inhibited by product
"jamming" factor
parameters that describe the degree of substrate reactivity
rate constant of EG1 β-glucosidic bonds cleaved
inhibition constant for glucose
inhibition constants of glucose on enzymes
inhibition constants of xylose on enzymes
apparent Michaelis constant
recalcitrance parameter
inhibition of cellulose hydrolysis by cellobiose
inhibition of cellulose hydrolysis by ethanol
product, cellobiose
products which diffuse at time t and at equilibrium, respectively
cellulose-to-glucose reaction with competitive inhibition by glucose, cellobiose and xylose inhibition
substrate, cellulose
cellulose hydrolysis velocity
initial hydrolysis velocity
xylose concentration
cellulase activity FPU
substrate concentration
independent variable, effect of endoglucanase
and β2 are glucose (CG) and cellobiose (CCb) binding constants, respectively
fraction of the cellulose surface that is free to be hydrolyzed
(Submitted: August 8, 2010 ; Revised: March 3, 2011 ; Accepted: April 16, 2011)
- Al-Zuhair S., The effect of crystallinity of cellulose on the rate of reducing sugars production by heterogeneous enzymatic hydrolysis. Bioresource Technol., 99, 4078 (2008).
- Andrić P., Meyer A. S., Jensen P. A., Dam-Johansen K., Reactor design for minimizing product inhibition during enzymatic lignocellulose hydrolysis: I. Significance and mechanism of cellobiose and glucose inhibition on cellulolytic enzymes. Biotechnol. Adv., 28, No. 3, 308 (2010).
- Andrić P., Meyer A. S., Jensen P. A., Dam-Johansen K., Reactor design for minimizing product inhibition during enzymatic lignocellulose hydrolysis: II. Quantification of inhibition and suitability of membrane reactors. Biotechnol. Adv., 28, No. 3, 407 (2010b).
- Annema, A., Feed-forward Neural Networks: Vector Decomposition Analysis, Modeling and Analog Implementation. Kluwer Academic Publishers, Boston (1995).
- Bansal, P., Hall, M., Realff M. J., Lee, J. H., Bommarius, A. S., Modeling cellulase kinetics on lignocellulosic substrates. Biotechnol. Adv., 27, No. 6, 833 (2009).
- Bezerra, R. M. F. and Dias, A. A., Discrimination among eight modified MichaelisMenten kinetics models of cellulose hydrolysis with a large range of substrate/enzyme ratios. Appl. Biochem. Biotech., 112, 173 (2004).
- Bezerra, R. M. F. and Dias, A. A., Enzymatic kinetic of cellulose hydrolysis. Appl. Environ. Microb., 126, 49 (2005).
- Bommarius, A. S., Katona, A., Cheben, S. E., Patel, A. S., Ragauskas, A. J., Knudson, K., Pu, Y., Cellulase kinetics as a function of cellulose pretreatment. Metab. Eng., 10, 370 (2008).
- Brown, R. F., Agbogbo, F. K., Holtzapple, M. T., Comparison of mechanistic models in the initial rate enzymatic hydrolysis of AFEX-treated wheat straw. Biotechnol. Fuels, 3, 6 (2010).
- Carrillo, F., Lis, M. J., Colom, X., Lopez-Mesas, M., Valldeperas, J., Effect of alkali pretreatment on cellulase hydrolysis of wheat straw: Kinetic study. Process Biochem., 40, 3360 (2005).
- Chauve, M., Mathis, H., Huc, D., Casanave, D., Monot, F., Ferreira, N. L., Comparative kinetic analysis of two fungal βglucosidases. Biotechnol. Fuels, 3, 3 (2010).
- Chrastil, J., Enzymic product formation curves with the normal or diffusion limited reaction mechanism and in the presence of substrate receptors. Int. J. Biochem., 20, No. 7, 683 (1988).
- Chrastil, J., Determination of the first order consecutive reaction rate constants from final products, Comput. Chem., 12, No. 4, 289 (1988b).
- Di Serio, M., Aramo, P., de Alteriis, E., Tesser, R., Santacesaria, E., Quantitative analysis of the key factors affecting yeast growth. Ind. Eng. Chem. Res., 42, 5109 (2003).
- Drissen, R. E. T., Maas, R. H. W., Tramper, J., Beeftink, H. H., Modeling ethanol production from cellulose: separate hydrolysis and fermentation versus simultaneous saccharification and fermentation. Biocatal. Biotransfor., 27, No. 1, 27 (2009).
- Fan, L. T. and Lee, Y. H., Major chemical and physical features of cellulosic materials as substrates for enzymatic hydrolysis. Adv. Biochem. Eng., 14, 101 (1980).
- Gan, Q., Allen, S. J., Taylor, G., Kinetic dynamics in heterogeneous enzymatic hydrolysis of cellulose: an overview, an experimental study and mathematical modeling. Process Biochem., 38, 1003 (2003).
- Hagan, M., Demuth, H., Beale, M., Neural Network Design. PWS Publishing, Boston (1996).
- Hodge, D. B., Karim, M. N., Schell, D. J., McMillan, J. D., Model-based fed-batch for high-solids enzymatic cellulose hydrolysis. Appl. Biochem. Biotech., 152, 88 (2009).
- Kadam, K. L., Rydholm, E. C., McMillan, J. D., Development and validation of a kinetic model for enzymatic saccharification of lignocellulosic biomass. Biotechnol. Progr., 20, 698 (2004).
- Ko, J., Su, W. J., Chien, I. L., Chang, D. M., Chou, S. H., Zhan, R. Y., Dynamic modeling and analysis of simultaneous saccharification and fermentation process to produce bio-ethanol from rice straw. Bioprocess Biosyst. Eng., 33, 195 (2010).
- Levine, S. E., Fox, J. M., Blanch, H. W., Clark, D. S., A mechanistic model of the enzymatic hydrolysis of cellulose. Biotechnol. Bioeng., 107, No. 1, 37 (2010).
- Li, C., Yoshimoto, M., Tsukuda, N., Fukunaga, K., Nakao, K., A kinetic study on enzymatic hydrolysis of a variety of pulps for its enhancement with continuous ultrasonic irradiation. Biochem. Bioeng. J., 19, 155 (2004).
- Liao, W., Liu, Y., Wen, Z., Frear, C., Chen, S., Kinetic modeling of enzymatic hydrolysis of cellulose in differently pretreated fibers from dairy manure. Biotechnol. Bioeng., 101, No. 3, 441 (2008).
- Morales-Rodríguez, R., Capron, M., Huusom, J. K., Sin, G., Controlled fed-batch operation for improving cellulose hydrolysis in 2G bioethanol production. 20th European Symposium on Computer Aided Process Engineering ESCAPE20 (2010).
- O'Dwyer, J. P., Zhu, L., Granda, C. B., Holtzapple, M. T., Enzymatic hydrolysis of lime-pretreated corn stover and investigation of the HCH-1 Model: inhibition pattern, degree of inhibition, validity of simplified HCH-1 Model. Bioresource Technol., 98, 2969 (2007).
- O'Dwyer, J. P., Zhu, L., Granda, C. B., Chang, V. S., Holtzapple, M. T., Neural network prediction of biomass digestibility based on structural features. Biotechnol. Progr., 24, 283 (2008).
- Okazaki, M. and Moo-Young, M., Kinetics of enzymatic hydrolysis of cellulose: Analytical description of a mechanistic model. Biotechnol. Bioeng., 20, 637 (1978).
- Ramkrishna, D., On modeling of bioreactors for control. J. Process Control, 13, 581 (2003).
- Rivera, E. C., Rabelo, S. C., Garcia, D. D., Maciel, R., da Costa, A. C., Enzymatic hydrolysis of sugarcane bagasse for bioethanol production: determining optimal enzyme loading using neural networks. J. Chem. Technol. Biotechnol., 85, 983 (2010).
- Shao, X., Lynd, L., Wyman, C., Bakker, A., Kinetic modeling of cellulosic biomass to ethanol via simultaneous saccharification and fermentation: Part I. Biotechnol. Bioeng., 102, No. 1, 59 (2009).
- Shao, X. J., Cellulosic Biomass to Ethanol: Kinetic modeling, scale up, and reactor design. PhD Thesis, Dartmouth College, USA (2007).
- South, C. R., Hogsett, D. A. L., Lynd, L. R., Modeling simultaneous saccharification and fermentation of lignocellulose to ethanol in batch and continuous reactors. Enzyme Microb. Technol., 17, 797 (1995).
- Wang, L. S., Zhang, Y. Z., Yang, H., Gao, P. J., Quantitative estimate of the effect of cellulase components during degradation of cotton fibers. Carbohydr. Res., 339, 819 (2004).
- Xu, F. and Ding, H., A new kinetic model for heterogeneous (or spatially confined) enzymatic catalysis: contributions from the fractal and jamming (overcrowding) effects. Appl. Catal. A-Gen., 317, 70 (2007).
- Zhang, J., Shao, X., Townsend, O. V., Lynd, L. R., Simultaneous saccharification and co-fermentation of paper sludge to ethanol by Saccharomyces Cerevisiae RWB222 Part I. Biotechnol. Bioeng., 104, No. 5, 920 (2009).
- Zhang, J., Shao, X., Townsend, O. V., Lynd, L. R., Simultaneous saccharification and cofermentation of paper sludge to ethanol by Saccharomyces Cerevisiae RWB222 Part II. Biotechnol. Bioeng., 104, No. 5, 932 (2009b).
- Zhang, Y., Xu, J. L., Yuan, Z. H., Modeling and prediction in the enzymatic hydrolysis of cellulose using artificial neural network. Fifth Intern. Conf. Natural Comput., Tianjin, China (2009).
- Zhang, Y. H. P. and Lynd, L. R., Toward an aggregated understanding of enzymatic hydrolysis of cellulose: noncomplexed cellulase systems. Biotechnol. Bioeng., 88, No. 7, 797 (2004).
- Zhang, Y. H. P. and Lynd, L. R., A functionally based model for hydrolysis of cellulose by fungal cellulase. Biotechnol. Bioeng., 94, No. 5, 888 (2006).
- Zheng, Y., Pan Z., Zhang, R., Jenkins, B. M., Kinetic modeling for enzymatic hydrolysis of pretreated creeping wild ryegrass. Biotechnol. Bioeng., 102, No. 6, 1558 (2009).
- Zhou, W., Schüttler, H. B., Hao, Z., Xu, Y., Cellulose hydrolysis in evolving substrate morphologies I. Biotechnol. Bioeng., 104, No. 2, 261 (2009).
- Zhou, W., Schüttler, H. B., Hao, Z., Xu, Y., Cellulose hydrolysis in evolving substrate morphologies II. Biotechnol. Bioeng., 104, No. 2, 275 (2009b).
Publication Dates
-
Publication in this collection
24 Nov 2011 -
Date of issue
Dec 2011
History
-
Accepted
16 Apr 2011 -
Reviewed
03 Mar 2011 -
Received
08 Aug 2010
























