Abstract
A computer simulation study of a laminar steady-state glass flow that exits from a channel cooled with water is reported. The simulations are carried out in a two-dimensional, Cartesian channel with a backward-facing step for three different angles of the step and different glass outflow velocities. We studied the interaction of the fluid dynamics, phase change and thermal behavior of the glass flow due to the heat that transfers to the cooling water through the wall of the channel. The temperature, streamline, phase change and pressure fields are obtained and analyzed for the glass flow. Moreover, the temperature increments of the cooling water are characterized. It is shown that, by reducing the glass outflow velocity, the solidification is enhanced; meanwhile, an increase of the step angle also improves the solidification of the glass flow.
Phase change; Computational fluid dynamics; Glass flow; Solid-liquid interface; Finite element
PROCESS SYSTEMS ENGINEERING
Simulation of the solidification in a channel of a water-cooled glass flow
G. E. Ovando ChaconI, * * To whom correspondence should be addressed ; S. L. Ovando ChaconV; J. C. Prince AvelinoII; A. Servin MartinezIII; J. A. Hernandez ZarateIV
IInstituto Tecnológico de Veracruz, Depto. Metal-Mecánica y Mecatrónica, Calzada Miguel Ángel de Quevedo 2779, Col. Formando Hogar, C.P. 91860, Veracruz, Veracruz, México. Phone: + 52 229 9341500, ext. 136. E-mail: ovachag@hotmail.com
IIInstituto Tecnológico de Veracruz, Depto. Metal-Mecánica y Mecatrónica, Calzada Miguel Ángel de Quevedo 2779, Col. Formando Hogar, C.P. 91860, Veracruz, Veracruz, México. Phone: + 52 229 9341500, ext. 136. E-mail: jcpa@itv.edu.mx
IIIInstituto Tecnológico de Veracruz, Depto. Metal-Mecánica y Mecatrónica, Calzada Miguel Ángel de Quevedo 2779, Col. Formando Hogar, C.P. 91860, Veracruz, Veracruz, México. Phone: + 52 229 9341500, ext. 136. alservinm@gmail.com
IVInstituto Tecnológico de Veracruz, Depto. Metal-Mecánica y Mecatrónica, Calzada Miguel Ángel de Quevedo 2779, Col. Formando Hogar, C.P. 91860, Veracruz, Veracruz, México. Phone: + 52 229 9341500, ext. 136. jorgeahz67@yahoo.com.mx
VInstituto Tecnológico de Tuxtla Gutiérrez, Depto. Química y Bioquímica, Carretera Panamericana, km 1080, C.P. 29000, Tuxtla Gutiérrez, Chiapas, México. Phone: + 52 961 6150380 E-mail: ovansandy@hotmail.com
ABSTRACT
A computer simulation study of a laminar steady-state glass flow that exits from a channel cooled with water is reported. The simulations are carried out in a two-dimensional, Cartesian channel with a backward-facing step for three different angles of the step and different glass outflow velocities. We studied the interaction of the fluid dynamics, phase change and thermal behavior of the glass flow due to the heat that transfers to the cooling water through the wall of the channel. The temperature, streamline, phase change and pressure fields are obtained and analyzed for the glass flow. Moreover, the temperature increments of the cooling water are characterized. It is shown that, by reducing the glass outflow velocity, the solidification is enhanced; meanwhile, an increase of the step angle also improves the solidification of the glass flow.
Keywords: Phase change; Computational fluid dynamics; Glass flow; Solid-liquid interface; Finite element.
INTRODUCTION
An important issue in fluid dynamics is the analysis of fluid flow and heat transfer in channels with phase change, being the topic of extensive study because it is present in many technical applications and natural processes. On the other hand, in the glass industry the mold design and operating conditions can be optimized for a wide range of casting conditions using knowledge obtained through the development of a mathematical model and conducting numerical experiments to predict the location of the solid liquid interface. Pilon et al. (2006) analyzed the flow and thermal structures in the molten glass bath of a typical glass melting furnace with a throat but without air bubblers or electric boosting. They considered the molten glass as an incompressible, homogeneous and Newtonian fluid; furthermore, the flow was assumed to be laminar. The variation of the glass composition along the tank was neglected and the heat flux distribution from the combustion space to the batch/glass melt was imposed. They showed the velocity profiles, indicating the predominance of the flow in the longitudinal direction. The combination of the heat losses through the side walls and the bottom created temperature gradients that generated cells. Rienstra and Chandra (2001) studied the glass flow in the pressing phase of manufacturing glass jars or parisons. They considered that the wall thickness and radius of the parison varies very slowly. By using a perturbation method based on the slender geometry and a low Reynolds number, they obtained an explicit analytical description of the velocity and pressure gradient of the glass flow. The model described highly viscous incompressible Newtonian glass flow during the pressing phase of the production and included a general slip boundary condition in the form of a linear relation between shear stress and slip velocity. Based on these results, they calculated the total force on the plunger, for a given plunger velocity, and solved an ordinary differential equation for the resulting plunger velocity when the force was prescribed. Representative examples showed a very good agreement of the flow velocity between the analytical solution and the numerical solution of a Stokes-flow model obtained with the finite element method. Mirbagheri et al. (2003) simulated the flow of an incompressible molten metal in a mould cavity. They developed a numerical code and proposed a new algorithm with free and solid boundary condition to investigate the heat transfer and the effect of the coating permeability during the mould filling using finite differences. This problem was modeled with the momentum equations, the continuity equation and the heat transfer equation for the liquid or solid zone; the heat transfer equation was used for the mushy region, while the free surface function and the backpressure function were utilized for low melting point metals. Velocity profile, temperature field and filling sequence were obtained from the simulations. To this end, the governing equations were discretized with the finite difference method and a semi-explicit solution of this approximation was obtained to compute the first guess for new time-level velocities using the initial conditions or previous time-level values for all advective, pressure and viscous accelerations. To satisfy the continuity, pressure was iteratively adjusted in each cell and the velocity changes induced by each pressure change are added to the velocity computed previously. In most cases, an over-relaxation factor was used to accelerate the convergence of the iteration. Shmueli et al. (2008) investigated the process of melting of a phase change material in a vertical tube. The numerical simulations were done with FLUENT and the flow patterns were obtained with a detailed distribution of heat transfer on the inner wall of the tube. The results of the simulation and the analysis of digital pictures, obtained in previous studies, reveal that the effect of convection in the liquid phase provokes non-radial heat fluxes from the wall to the melting. The conservation equations for air were solved in the domain bounded by the perimeter of the inner walls, phase change melting from below, and the upper boundary of the tube from above. Boundary conditions for the momentum equation were no-slip at all solid surfaces and slip at the upper boundary of the tube, while for the energy equation constant and uniform temperature were considered on the outside wall of the tube, zero heat flux at the bottom, and ambient air temperature at the upper boundary of the tube. Giannopapa (2006) developed a computational model to simulate the blow-blow forming process of glass containers, which characterized the glass flow and the heat transfer. He was able to track the geometry of the deforming interface of glass by applying structured and unstructured fixed meshes. The Navier-Stoke equations were used to described the motion of the hot glass, while the energy equations were used to described heat transfer between the glass and the mould. The governing equations were discretized with the finite element method. In this work they analyzed the propagation of glass during the forming process and the temperature profiles. Salinas (2006) studied numerically the solidification of aluminum alloy in a square cavity considering the flow of a incompressible Newtonian fluid with isotropic thermal properties where the phase change and the heat transfer by conduction and convection were considered. The mathematical model was based on a set of partial differential equations given by momentum, continuity and heat transfer equations. The discretization of the governing equations was done with the finite volume method combined with a SIMPLER scheme to join pressure and velocities. Transient results of the non-isothermal solidification were obtained where the streamlines and isotherms showed a complex flow with secondary vorticity. The goal of the present work is to analyze the phase change of a glass flow due to cooling with a water flow, providing insight into the flow patterns, interface formation and temperature behavior on the glass flow and mould wall. The present research is of particular relevance for the glass industry as we will be extending the current knowledge on how the geometry of the step channel affects the phase change and the fluid dynamics of the glass flow.
PROBLEM FORMULATION
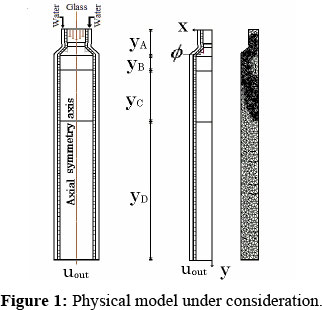
Schematic representation of the studied configuration is depicted in Figure 1, which consists of a short cylindrical channel that carries a liquid glass flow. At the same time, in order to control the solidification process, the channel wall is cooled with water flowing adjacent to the outer vertical side of the channel wall with thickness tw. The entrance temperature of the glass flow is fixed to Tin, while the entrance temperature and velocity of the water flow are fixed to Tw and Uw, respectively. In this work a two-dimensional axially symmetrical channel with an inclined backward-facing step is considered, where φ is the step inclination angle. The flow of glass enters in the superior boundary of the channel and exits at the inferior boundary of the domain with the outflow velocity denoted by Uout, to simulate the casting velocity when the fluid is solidified or the jet velocity when the fluid experiments no phase change. The solid layer is not attached to the walls when a phase change occurs but instead is removed with velocity Uout. This operation is a stage of the process of a glass bottle manufacturer.
No-slip boundary conditions were imposed at all solid walls. L is the distance from the entrance of the channel to the lower boundary of the domain. The walls of the short channel from the superior part of the channel to the step are assumed to be adiabatic. After the step, convection heat transfer coefficients are imposed along the domain boundary in order to take into account the heat exchange by convection of the glass and water with the wall. The flow region Ω chosen for the numerical simulations is a two-dimensional channel, where the flow, heat transfer and phase change are analyzed. The conservation equations that describe this problem for a steady-state incompressible fluid in this region are the momentum, continuity and energy equations:
where  is the velocity vector, u1 and u2 being the transversal and axial velocity components respectively; ν is the kinematic viscosity, p is the pressure, k is the thermal conductivity, Cp is the specific heat, and T is the temperature. At the wall the velocity is zero and pure conduction is considered.
is the velocity vector, u1 and u2 being the transversal and axial velocity components respectively; ν is the kinematic viscosity, p is the pressure, k is the thermal conductivity, Cp is the specific heat, and T is the temperature. At the wall the velocity is zero and pure conduction is considered.
The model includes the Boussinesq approximation and a damping force. Physically in the phase change region when the fluid temperature decreases the glass solidifies. As a consequence, a damping force drives the velocities to zero in the solid, so the body force is given as follow:
where g is the acceleration of gravity, β is the compressibility coefficient and ca is the fraction of liquid phase, given by:
cb is the permeability constant and ε is small number to prevent division by zero in the calculations. This term vanishes in the liquid phase region (ca=1). Tm=1223 K is the melting temperature and ΔT=20 K is the temperature interval where the liquid-solid mixtures coexist.
In the mushy region the specific heat capacity in the energy equation should be:
in order to incorporate the effect of the significant amount of latent heat released in the phase change region, δ is defined as follow:
while the enthalpy change is given by:
The velocity boundary conditions at the channel for the glass flow are:
The velocity boundary conditions at the channel for the water flow are considered to be no-slip boundary conditions, except in the following cases:
The temperature boundary conditions at the channel for the glass flow are:
The temperature boundary conditions at the channel for the water flow are:
At the solid-fluid interfaces the following boundary condition is imposed:
where n is the normal to the surface of the boundary and K is the solid-fluid thermal conductivity ratio. The thermophysical properties of glass used in the simulation are independent of temperature, see Table 1.
NUMERICAL METHOD
The numerical simulation was carried out using the finite element method. To this end, the space discretization step h, the finite element triangulation τh of the polygonal domain  , the space of polynomials P1 in two variables of degree less than or equal to one, and the space of continuous functions
, the space of polynomials P1 in two variables of degree less than or equal to one, and the space of continuous functions  defined in
defined in  were introduced. The functional spaces are approximated by the following finite dimensional spaces:
were introduced. The functional spaces are approximated by the following finite dimensional spaces:
Using the above finite dimensional spaces leads to the following approximation of Equations (1)-(3) in their variational forms; for more details see: Chorin (1973), Glowinski and Pironneau (1992), Turek (1999), Marechuk (1990), Glowinski (2003), Glowinski and Le Tallec (1989), Dean and Glowinski (1997) and Dean et al. (1998). The method consists of finding  with
with  ,
,  and
and  with
with 
 , such that:
, such that:
On the other hand, Γ1 and Γ3 are the Dirichlet boundary conditions of velocity and temperature, respectively;  and
and  are the finite element approximation of the velocity and temperature boundary function
are the finite element approximation of the velocity and temperature boundary function  and
and  , respectively. Similarly,
, respectively. Similarly,  and
and  are finite element approximations of the initial condition functions
are finite element approximations of the initial condition functions  and
and  , respectively.
, respectively.
Figure 2, shows the mesh convergence analysis for three different meshes with resolution of 19840, 18935 and 17245 net elements. The simulations were performed with an adaptive mesh for all cases in order to guarantee the mesh independence of the solution. The adaptive mesh allows for fast and accurate calculations because it concentrates the majority of the elements where the phase transition occurs. The steady state simulations were obtained with the thinnest mesh using a direct solver with a relative accuracy |ui+1-ui|/|ui+1| of 1.0×10-6. The numerical code had been previously validated with different problems. For example, for solidification process it was compared with the melting of ice in a square enclosure studied by Arid et al. (2012) the average Nusselt numbers in the steady state obtained with this code, for constant temperatures of 275 K and 277 K at the heated wall were 30.85 and 72.93, which coincide with the values reported (31 and 73) by those authors.
RESULTS AND DISCUSSION
The results presented here are for a short water-cooled channel. The inner flow of the channel is affected by the phase change and the heat flux from the glass flow to the cooling water, with 90°, 50° and 10° inclined backward-facing steps. The outflow velocities explored in this investigation are 8.65×10-5 m/s, 8.65×10-2 m/s and 8.65×100 m/s, which for glass as working fluid correspond to the Reynolds numbers (Re=UoutL / ν) of 0.00054, 0.54 and 54. At the entrance of the channel the glass temperature is fixed at Tin=1373 K, the inlet water temperature is fixed at Tw=310 K and the surroundings temperature is fixed at T0=300 K. The thickness of the channel wall is taken as tW=0.015 m.
General Thermal and Fluid Dynamic Behavior
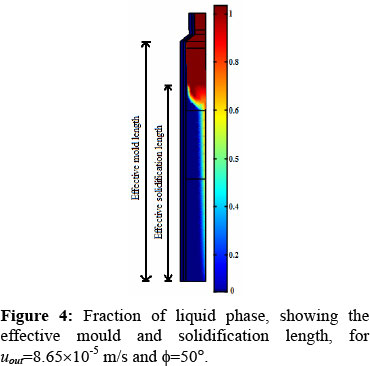
In general, it is found that the solidification zone is increased as the step angle is increased. Moreover, the cooling process is enhanced as the glass outflow velocity is reduced. Furthermore, when the solidification occurs a primary interface is observed which propagates almost in a transversal direction toward the middle-vertical line; a secondary interface elongates in the axial direction toward the exit of the channel, see Figure 3, indicating that in this zone the heat flux is given by convection. Moreover, the shape of the solidification front changes with the geometrical configuration of the channel. From the above result, it is established that the angle of the mould can be used as a means of control of the effective solidification length without making the liquid region control too difficult. This would be useful to minimize the severity of surface defects such as bleed bands and cold shuts. The appearance of these defects can been attributed to excessive effective mould length, so the mould length could be optimized on the basis of surface quality and minimization of the irregularities at the interface zone. Another interesting result of the simulation is that, at least for φ=50° and 90°, an inverse relation can be observed between the casting velocity and the effective solidification length, see Figure 4. This is an important result, because most of the surface defects on continuous casting process may be attributed to interactions between the primary and secondary interface associated with the cooling of the mould that largely depends on the effective solidification length.
It is noticeable that, with the variation of the step angle, the direct contact between the solidified glass and mould can be minimized, so the moulds design can be used to minimize the primary cooling and the extent of the primary solidification interface, improving the surface quality and internal structure of the glass. Hence, the φ parameter can be used to control the position of the heat flux instabilities, which can be of major importance to control the final properties of the material. The results also indicate that increasing the outflow velocity of the fluid, the total heat transfer decreases, as is expected, because there is no time to exchange heat with the cooling medium. As a result, there is no change of phase and the field temperature remains constant. For φ=10°, the temperature fields are practically the same for uout=8.65×10-5 m/s and uout=8.65×10-2 m/s. However, there are significant differences in the temperature fields for  and
and  in the range of uout=8.65×10-5 m/s and uout=8.65×10-2 m/s, which indicates that, reducing the step angle of the channel, it is possible to increase the total heat transfer from the glass flow to the cooling water.
in the range of uout=8.65×10-5 m/s and uout=8.65×10-2 m/s, which indicates that, reducing the step angle of the channel, it is possible to increase the total heat transfer from the glass flow to the cooling water.
On the other hand, it is found that the vortex formation is generated by two mechanisms; the first one is due to the solidification process, which decelerates the motion of the glass flow and occurs for the lowest outflow glass velocity. The solidified glass acts as a vorticity source and the vortices generated are attached to the vertical-middle line. This mechanism is characterized by a sharp change in the flow direction as the fluid meets the solid phase. The vortical structure is anti-clockwise and transversal stretched by the perturbation produced by the phase change of glass. This mechanism is observed for  , 50° and 90° and is of great relevance because this flow pattern tends to enhance the glass quality since the unmelted grains generated have enough time to melt. The second mechanism is due to the boundary layer separation when the fluid experiments a sudden change in the flow velocity at the step region; this occurs for the largest outflow glass velocity with
, 50° and 90° and is of great relevance because this flow pattern tends to enhance the glass quality since the unmelted grains generated have enough time to melt. The second mechanism is due to the boundary layer separation when the fluid experiments a sudden change in the flow velocity at the step region; this occurs for the largest outflow glass velocity with  and
and  . The vortical flow is axially stretched by the inflowing fluid, part of this flow moved upstream to form the flow recirculation beyond of the step region. This flow reversal is developed just behind the step as a consequence of the separation point in the step corner and the reattachment point on the wall of the short channel. The heat transfer phenomena are of great relevance in flows with detachment and reattachment points because this dynamical behavior affects the phase change mechanism, which gives, as a result, a global change of the material properties of the fluid to be solidified. At the zone of the entrance where the geometry expands, the boundary layer detaches due to the strong pressure gradient. For
. The vortical flow is axially stretched by the inflowing fluid, part of this flow moved upstream to form the flow recirculation beyond of the step region. This flow reversal is developed just behind the step as a consequence of the separation point in the step corner and the reattachment point on the wall of the short channel. The heat transfer phenomena are of great relevance in flows with detachment and reattachment points because this dynamical behavior affects the phase change mechanism, which gives, as a result, a global change of the material properties of the fluid to be solidified. At the zone of the entrance where the geometry expands, the boundary layer detaches due to the strong pressure gradient. For  , one clockwise vortex can be observed near the channel step, the fluid recirculates and mixing takes place at this region, the perturbation is propagated beyond the step, as the streamline suggests. At the core of the vortex, a low pressure zone is distinguished and a stagnation point can be identified, then a strong pressure gradient associated with the expansion flow as a result of the abrupt change in the transversal area is observed. For
, one clockwise vortex can be observed near the channel step, the fluid recirculates and mixing takes place at this region, the perturbation is propagated beyond the step, as the streamline suggests. At the core of the vortex, a low pressure zone is distinguished and a stagnation point can be identified, then a strong pressure gradient associated with the expansion flow as a result of the abrupt change in the transversal area is observed. For  , one clockwise vortex produced by the change of the channel transversal section can also be observed. The inflowing fluid stream splits into a strong central jet and a lateral flow with recirculation and vortex generation. It is seen that the stagnation region decreases and the intensity of the vortices becomes weaker with the reduction of the step angle.
, one clockwise vortex produced by the change of the channel transversal section can also be observed. The inflowing fluid stream splits into a strong central jet and a lateral flow with recirculation and vortex generation. It is seen that the stagnation region decreases and the intensity of the vortices becomes weaker with the reduction of the step angle.
Case
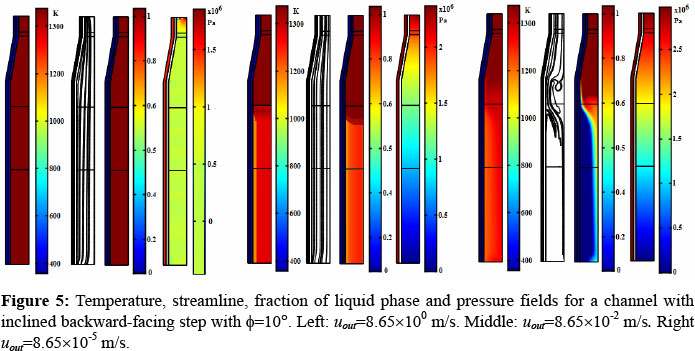
Temperature, streamline, phase change and pressure fields of the flow that exits from a water-cooled short channel with a 10° inclined backward-facing step are shown in Figure 5. At high glass outflow velocity Uout=8.65×100 m/s (Re=54), see left panel of the figure, the water temperature increases slightly from the imposed temperature of 310 K at the inlet flow of the cooling water to 313 K at the water outlet flow, indicating a low heat transfer rate from the glass flow which enters at the superior open boundary and exists at the inferior open boundary of the short channel. For this case no phase change can be observed and, from the streamlines, a uniform pattern of the flow inside the whole domain and a laminar glass flow due to the inertial effect, which is high enough to overwhelm the viscous effect, is identified. The pressure field shows changes at the entrance of the domain and then remains constant. For this velocity, the angle of the step does not affect the flow behavior and no vortices are present n the glass flow. In order to simulate the casting velocity or the jet outlet velocity of the fluid according to the phase change, three different outflow velocities Uout are imposed at the inferior boundaries of the domain. Decreasing the glass outflow velocity to Uout=8.65×10-2 m/s (Re=0.54), see middle panel of the figure, the water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 315 K at the water outlet flow, indicating a greater increase of the heat transfer rate from the glass to the water in relation to the previous case. For this condition, a uniform pattern of the flow is observed inside the whole domain, the glass temperature changes slightly after the step and remains almost constant through the domain, experimenting a slight change near the wall. As a consequence of this constant temperature the fraction of liquid phase is above 0.7 and no solidification can be observed through the whole domain. The slight variation of temperature and the phase change behavior can be associated with the uniform velocity of the fluid and no vortices are present in the glass flow so the exchange of heat with the cooling water is increased, in such a way that a higher total heat transfer is observed.
The pressure field indicates high pressure of the flow at the inlet and low pressure of the flow at the outlet due to the solidification tendency. For the lowest outflow velocity of uout=8.65×10-5 m/s (Re=0.00054), see right panel of the figure, the water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 322 K at the water outlet flow; the heat transfer rate from the glass to the water is high enough and solidification can be appreciated in the glass flow. Furthermore, a complex non-uniform recirculation pattern of the flow is observed in the liquid phase zone as the solid phase zone decelerates the movement of the fluid; the glass temperature is high at the entrance of the channel and decreases after the step, with strong temperature gradients that intensify the heat transfer from the glass to the cooling water. The flow also experiments a phase change, noting that the fraction of liquid phase is 1 at the entrance of the channel, which implies that a completely liquid phase is present at the inlet; however, after the step the fluid starts to solidify and, just over the wall of the cooling water duct, the glass flow is completely solidified. The temperature and phase changes are due to the high heat fluxes to the cooling water just after the step of the channel. The pressure field indicates high pressure at the inlet flow region and a reduction of the pressure from the step to the outlet of the domain. The pressure changes in the step region of the channel are due to the perturbation provoked by vortex formation.
Case
In order to investigate the influence of the step geometry on the fluid behavior, the step of the channel was increased. Temperature, streamline, phase change and pressure fields of the flow that exits from a short water-cooled channel with a 50° inclined backward-facing step are shown in Figure 6. At high glass outflow velocity Uout=8.65×100 m/s (Re=54), see left panel of the figure, the water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 314.3 K at the water outlet flow, indicating a low heat transfer rate from the glass to the water. For this case, uniform temperature and phase change due to the velocity of the glass flow is also observed; however, the interaction of the fluid with the channel step generates instabilities of the boundary layer located at the step wall and a clock-wise vortex can be appreciated. The pressure field shows a reduction around the channel step and a uniform behavior after the step since the glass temperature is constant and the fluid remains in the liquid phase. Decreasing the glass outflow velocity to Uout=8.65×10-2 m/s (Re=0.54), see middle panel of the figure, a uniform pattern of the flow at the liquid region of glass is observed. Moreover, the glass temperature and the glass phase change after the middle part of the domain, where the fluid decreases its temperature and starts to solidify. The water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 316.2 K at the water outlet flow; for this geometrical condition, the glass flow starts to solidify when Uout 5.53×10-1 m/s. At low outflow velocity Uout=8.65×10-5 m/s (Re=0.00054), see right panel of the figure, the mushy region can be clearly observed where the liquid and solid phase coexist and the latent heat of fusion is released during the solidification process.
The pattern of the flow inside the domain is characterized by vortical structures in the liquid region; the glass temperature is high at the entrance of the channel and low after the third part of the domain, with a strong temperature gradient near the mushy region. The glass is characterized by three different zones: liquid, mushy and solid zones, with the cooling process that takes place at the mushy zone being of great importance from the point of view of material properties. The temperature and phase changes are due to the high heat fluxes just after the step of the channel. The pressure field indicates a progressive change in the pressure of the flow inside the domain. The water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 328 K at the water outlet flow. The heat transfer rate from the glass to the water allows the solidification of the glass flow.
Case
Temperature, streamline, phase change and pressure fields for the simulation of glass flow with water cooling that exits from a short channel with 90° inclined backward-facing step are shown in Figure 7. For high glass outflow velocity uout=8.65×100 m/s (Re=54), see left panel of the figure, a large vortex can be appreciated, which is stronger than in the case of φ=50°. The size of the vortices is augmented due to the abrupt transition of the channel, the glass is liquid and its temperature is constant in the whole domain. The fluid experiments a significant reduction of pressure in the step region, while a constant pressure is observed at the outlet of the domain. The water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 314.8 K at the water outlet flow, indicating a low heat transfer rate from the glass to the water. Reducing the outflow velocity to uout=8.65×10-2 m/s (Re=0.54), see middle panel of the figure, there is a reduction of the temperature after the middle part of the domain which is associated with phase change. The water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 318.2 K at the water outlet flow. The heat transfer from the glass to the water provokes a phase change on the glass flow. When the outflow velocity is decreased to uout=8.65×10-5 m/s (Re=0.00054), see right panel of the figure, the temperature field is more complex than in the previous cases with the same outflow velocity. The glass experiments a large temperature gradient in the third part of the domain in which the solidification gradient changes rapidly; this complex interaction between the thermal-fluid dynamic and the geometry of the channel provokes rapid liquid-solid interface formation. As a result of this behavior of the phase-change region the material could modify its properties. The temperature field shows that the hot fluid is cooled rapidly just after the step. For this reason this configuration shows the highest solidification rate. The pressure is high in the inflow region and the streamline shows vortex formation in the liquid phase region. The water temperature increases from the imposed temperature of 310 K at the inlet flow of the cooling water to 331.7 K at the water outlet flow. For this geometry, thermal and fluid dynamic conditions result in a larger heat transfer rate from the glass to the water. As a result, a larger solidification zone is obtained for this case.
Temperature Profiles
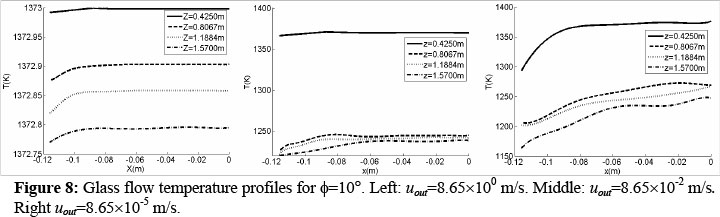
Figure 8 shows the temperature profiles for the simulation of glass flow with water cooling exiting from a short channel with 10° inclined backward-facing step for four different position of the axial coordinate. At high glass outflow velocity Uout=8.65×100 m/s (Re=54), see left panel of the figure, the glass temperature profiles change slightly for the four different positions, showing a uniform behavior in the transversal direction, and the temperature profiles exhibit values above the melting temperature. Decreasing the glass outflow velocity to Uout=8.65×10-2 m/s (Re=0.54), see middle panel of the figure, the glass temperature profile is uniform and above the melting temperature for z=0.425 m. Moving away from the entrance of the channel, the glass temperature starts to decrease toward the wall of the channel where the heat is transfered to the cooling water. Moreover, the glass temperature starts to approach the melting temperature. For the lowest glass outflow velocity of Uout=8.65×10-5 m/s (Re=0.00054), see right panel of the figure, the glass temperature behavior is more complex. At z=0.425 m, the glass temperature starts to decrease slowly; however, near the mould wall the glass temperature experiments an abrupt reduction of about 60 K. For the other three positions the temperature reduction is also significant. However, this variation is in a gradual fashion along the whole transversal direction. The longer the distance from the channel entrance, the bigger is the extension of the glass flow that reaches the melting temperature.
Figure 9 shows the temperature profiles for the simulation of glass flow with water cooling exiting from a short channel with 50° inclined backward-facing step for four different positions of the axial coordinate. At high glass outflow velocity Uout=8.65×100 m/s (Re=54), see left panel of the figure, the glass temperature variations are less than 1 K, also showing a uniform behavior in the transversal direction; the temperature values are above 1372.4 K indicating glass liquid phase. Decreasing the glass outflow velocity to Uout=8.65×10-2 m/s (Re=0.54), see middle panel of the figure, the glass temperature profile is uniform and above 1350 K for z=0.425 m. For z= 0.8067 m, the temperature at the central part of the domain is about 1290 K; it then experiments a linear decrease and finally stabilizes at 1225 K. Far away from the entrance of the channel the glass temperature stays uniform approaching the melting temperature. For the lowest glass outflow velocity of Uout=8.65×10-5 m/s (Re=0.00054), see right panel of the figure, the glass temperature is gradually reduced toward the mould wall for the four axial positions. However, at z=0.425 m the temperature of the glass is above the melting temperature. For the other three axial positions the glass temperature approaches the melting temperature and even below.
Figure 10 shows the temperature profiles for the simulation of glass flow with water cooling exiting from a short channel with 90° inclined backward-facing step for four different positions of the axial coordinate. At high glass outflow velocity Uout=8.65×100 m/s (Re=54), see left panel of the figure, the glass temperature shows a uniform behavior in the transversal direction; the temperature values are above 1369 K indicating glass liquid phase. Decreasing the glass outflow velocity to Uout=8.65×10-2 m/s (Re=0.54), see middle panel of the figure, the glass temperature profile is also uniform and above 1350 K for z=0.425 m. For z= 0.8067 m the temperature at the central part of the domain is about 1250 K, then it experiments a decrease and finally stabilizes at 1220 K. Far away from the entrance of the channel the temperature of the glass remains uniform, approaching the melting temperature. For the lowest glass outflow velocity of Uout=8.65×10-5 m/s (Re=0.00054), see right panel of the figure, the glass temperature is gradually reduced toward the mould wall for the four axial positions. However, at z=0.425 m the temperature of the glass is above the melting temperature at the central part of the domain; it then decreases to reach a temperature below the melting temperature near the mould wall. For the other three axial positions the glass temperatures are below 1100 K, which means a solid phase for these positions. Figure 11 shows the water flow temperature profiles for Uout=8.65×10-5 m/s. The left panel is for  ,and the right panel is for φ=90°, observing a linear decay of the temperature through the wall of the mould as a result of the heat transfer absorbed by the cooling water. For φ=10°, a higher temperature is observed at the side glass of the wall than in the case of φ=90°, where the glass temperature reaches about 940 K at the bottom end of the channel.
,and the right panel is for φ=90°, observing a linear decay of the temperature through the wall of the mould as a result of the heat transfer absorbed by the cooling water. For φ=10°, a higher temperature is observed at the side glass of the wall than in the case of φ=90°, where the glass temperature reaches about 940 K at the bottom end of the channel.
CONCLUSIONS
We have presented the phase change simulation of a glass flow passing through a two-dimensional symmetric short channel cooled with water. To this end the Navier-Stokes equations coupled with the energy equation were solved by using the finite element method and adaptive meshes. It has been demonstrated that the angle of the step of the channel can be used to control the effective solidification length; hence, the geometry of the channel has a significant influence on the final properties of the solidified glass. Reducing the Reynolds number and increasing the step angle of the channel, the cooling of the glass flow is enhanced and, as a result, the size of the solidification zone is increased. Two vortex formations are identified: the first one is related to the inertial effect of the glass flow and the second one is related to the solidification process, which acts as a vorticity source. The model captures the transversal propagation of the primary interface and the axial propagation of the secondary interface, which plays an important role due to the fact that it can be used to optimize solidification processes. On the other hand, the model is able to reproduce the linear temperature behavior through the wall of the channel. For φ=50° and φ=90° an inverse relation between the casting velocity and the effective solidification length can be observed. The temperature profiles show slight variation of the glass temperature at high velocities of the glass outflow. However, as the casting velocity is reduced, the glass temperature profiles become more complex. The study indicates that the interaction between the geometry of the channel and the thermal fluid dynamics largely influence the solidification process of a glass flow with water cooling. Although the application of the present study is limited due to the fact that it is made for constant properties, the fluid thermal dynamic behavior is potentially useful for understanding the phase change in a glass flow. The variations of the glass properties are the subject of ongoing research.
NOMENCLATURE
Greek Symbols
ACKNOWLEDGEMENTS
The research was supported by DGEST, CONACYT and PROMEP.
Submitted: June 25, 2013
Revised: December 17, 2013
Accepted: December 20, 2013
- Arid, A., Kousksou, T., Jegadheeswaran, S., Jamil, A. and Zeraouli, Y., Numerical simulation of ice melting near the density inversion point under periodic thermal boundary conditions. Fluid Dynamics & Materials Processing, 8, pp. 257-275 (2012).
- Chorin, A., Numerical study of slightly viscous flow. J. Fluid Mech., 57, pp. 785-796 (1973).
- Dean, E. J. and Glowinski, R., A wave equation approach to the numerical solution of the Navier-Stokes equations for incompressible viscous flow. C. R. Acad. Sci. Paris, 325, Serie I, pp. 789-797 (1997).
- Dean, E. J., Glowinski, R. and Pan, T. W., A Wave Equation Approach to the Numerical Simulation of Incompressible Viscous Fluid Flow Modeled by the Navier-Stokes Equations. Mathematical and Numerical Aspects of Wave Propagation. Edited by J. A. de Santo, SIAM, Philadelphia (1998).
- Giannopapa, C. G., Development of a computer simulation model for blowing glass container. 2006 ASME Conference Proceeding PVP, Vancouver, Canada, pp. 165-172 (2006).
- Glowinski, R., Numerical Methods for Fluids. Part 3. Handbook of Numerical Analysis, vol. IX, P. G. Garlet, and J. L. Lions, Eds., North-Holland, Amsterdam (2003).
- Glowinski, R. and Pironneau, O., Finite element methods for the Navier-Stokes equations. Annual Rev. Fluid Mech., 24, pp. 167-204 (1992).
- Glowinski, R. and Le Tallec, P., Augmented Lagrangian and operator-splitting methods in nonlinear mechanics. SIAM, Philadelphia (1989).
- Jimenéz, R. A., Análisis del sobrecalentamiento de los vertedores en una máquina de secciones individuales en la fabricación de envases de vidrio. M.Sc. Thesis, Veracruz Institute of Technology, Mexico (2002). (In Spanish).
- Marechuk, G. I., Splitting and Alternate Direction Methods. Handbook of Numerical Analysis 1, P. G., Garlet, and J. L., Lions, Eds., North-Holland, Amsterdam, pp. 197-462 (1990).
- Mirbagheri, S. M. H., Esmaeileian, H., Serajzadeh, S., Varahram, N. and Davami, P., Simulation of melt flow in coated mould cavity in the casting process. Journal of Materials Processing Technology, 142, pp. 493-507 (2003).
- Pilon, L., Zhao, G. and Viskanta, R., Three-dimensional flow and thermal structures in glass melting furnaces. Part I. Effects of the heat flux distributions. Glass Science and Technology, 75, pp. 55-68 (2006).
- Rienstra, S. W. and Chandra, T. D., Analytical approximation to the viscous glass-flow problem in the mould-plunger pressing process, including a investigation of boundary conditions. Journal of Engineering Mathematics, 39, pp. 241-259 (2001).
- Salinas, C. H., Alloy aluminum solidification in square section. Rev. Fac. Ing. Univ. Tarapacá, 14, pp. 16-25 (2006).
- Shmueli, H., Ziskind, G. and Letan, R., Investigation of melting in a vertical circular tube: Local heat fluxes. Proceedings of 2008 ASME Summer Heat Transfer Conference, Jacksonville, USA, pp. 1-5 (2008).
- Turek, S., Efficient Solvers for Incompressible Flow Problems: An Algorithmic and Computational Approach. Springe-Verlag, Berlin (1999).
Publication Dates
-
Publication in this collection
14 Nov 2014 -
Date of issue
Dec 2014
History
-
Received
25 June 2013 -
Accepted
20 Dec 2013 -
Reviewed
17 Dec 2013