Abstract
In this work, the vapor-liquid equilibrium experimental data for the systems of isopropyl chloroacetate + isopropanol, isopropyl chloroacetate + cyclohexane and isopropyl chloroacetate + benzene were measured by a modified Rose-type recirculating still under the pressure of 101.3 kPa. The thermodynamic consistency of the measured data was verified by the Herington and van Ness methods, respectively. The experimental data were correlated by the NRTL, Wilson, and UNIQUAC activity coefficient models, and the corresponding interaction parameters of the three models were obtained. The root-mean-square deviations between the experimental data and calculated results for the temperature and the mole fraction of the vapor phase were less than 0.58 K and 0.0066, respectively. In addition, the excess Gibbs energy was calculated for the three systems.
Keywords:
Vapor-liquid equilibrium; Isopropyl chloroacetate; Correlation; Thermodynamic model
INTRODUCTION
Isopropyl chloroacetate is a raw material and intermediate, which is widely used in the synthesis of nonsteroidal anti-inflammatory drugs, such as naproxen, ketoprofen and ibupofen. Generally, isopropyl chloroacetate can be synthesized by esterification of chloroacetic acid and isopropanol with a catalyst, such as cation exchange resin (Patwardhan and Sharma, 1990Patwardhan, A. A., Sharma, M. M. Esterification of Carboxylic Acids with Olefins Using Cation Exchange Resins as Catalysts. Reactive Polymers, 13, 161-176 (1990). https://doi.org/10.1016/0923-1137(90)90051-5
https://doi.org/10.1016/0923-1137(90)900...
), inorganic salts (Liu and You, 2013Liu, S., You, H. Effect of the Different Reaction Conditions on Synthesizing of Isopropyl Chloroacetate. European Chemical Bulletin , 2, 9-10 (2013). https://doi.org/10.1016/j.molliq.2018.11.047
https://doi.org/10.1016/j.molliq.2018.11...
), and ionic liquids (Liu et al., 2007). During the esterification process, the water-carrying agent is required to remove water continuously to increase the esterification yield. Ma et al. (2006Ma, J., Jiang, H., Gong, H., Sun, Z. Esterification of Chloroacetic Acid with Alcohols Catalyzed by Zinc Methanesulfonate. Petroleum Science and Technology, 24, 431-440 (2006). https://doi.org/10.1081/LFT-200043689
https://doi.org/10.1081/LFT-200043689...
) reported the synthesis of isopropyl chloroacetate using cyclohexane as a water-carrying agent in their work. Wang et al. (2003Wang, M., Tian, J., Liu, L., Jiang, H., Gong, H., Su, T. Synthesis and Characterization of Methane-Sulfonates and Their Catalytic Activities for Esterification. Chinese Journal of Inorganic Chemistry, 19, 731-734 (2003).) used benzene as a water-carrying agent to separate water from the esterification process. After the reaction, a mixture of isopropyl chloroacetate, unreacted isopropanol and water-carrying agent is obtained. To separate isopropyl chloroacetate from the mixture by distillation, vapor-liquid equilibrium (VLE) data are required.
Until now, some works have reported the preparation of isopropyl chloroacetate (Xu et al., 2011Xu, J., Zhang, J., Yin, X. Esterification Process to Synthesize Isopropyl Chloroacetate Catalyzed by Lanthanum Dodecyl Sulfate. Brazilian Journal of Chemical Engineering , 28, 259-264 (2011). https://doi.org/10.1590/S0104-66322011000200010
https://doi.org/10.1590/S0104-6632201100...
; Liu and You, 2012Liu, S., You, H. An Overview on Synthetic Methods of Isopropyl Chloroacetate. European Chemical Bulletin, 1, 103-106 (2012).). However, for separation of isopropyl chloroacetate from the reacted solution, the VLE data for the systems of isopropyl chloroacetate + isopropanol, isopropyl chloroacetate + cyclohexane and isopropyl chloroacetate + benzene have not been reported in the NIST database. Therefore, it is necessary to generate the VLE data for these systems, which can be useful for the separation and purification of isopropyl chloroacetate from the mixture by distillation.
In this work, the VLE data for the systems isopropyl chloroacetate + isopropanol, isopropyl chloroacetate + cyclohexane and isopropyl chloroacetate + benzene were measured under the pressure of 101.3 kPa. To ensure the reliability of the measured VLE data, the thermodynamic consistency test was performed by the Herington and van Ness method. The non-random two-liquid (NRTL) (Renon and Prausnitz, 1968Renon, H., Prausnitz, J. M. Local Compositions in Thermodynamic Excess Functions for Liquid Mixtures. AlChE Journal, 14, 135-144 (1968). https://doi.org/10.1002/aic.690140124
https://doi.org/10.1002/aic.690140124...
; Liu et al., 2019Liu, X., Xu, D., Diao, B., Zhang, L., Gao, J., Liu, D., Wang, Y. Choline chloride based deep eutectic solvents selection and liquid-liquid equilibrium for separation of dimethyl carbonate and ethanol. Journal of Molecular Liquids, 275, 347-353 (2019).), Wilson (Wilson, 1964Wilson, G. M. A New Expression for The Excess Free Energy of Mixing. Journal of the American Chemical Society, 86, 127-130 (1964). https://doi.org/10.1021/ja01056a002
https://doi.org/10.1021/ja01056a002...
; Li, 2014), and the universal quasi-chemical (UNIQUAC) (Abrams and Prausnitz, 1975Abrams, D. S., Prausnitz, J. M. Statistical Thermodynamics of Liquid Mixtures: A New Expression for the Excess Gibbs Energy of Partly or Completely Miscible Systems. AIChE Journal, 21, 116-128 (1975). https://doi.org/10.1002/aic.690210115
https://doi.org/10.1002/aic.690210115...
) activity coefficient models were used to correlate the experimental VLE data and the binary interaction parameters for the three models were regressed. In addition, the calculation of the excess Gibbs energy for the three systems from the VLE data was listed.
EXPERIMENTAL
Chemicals
Isopropyl chloroacetate, cyclohexane, isopropanol and benzene were commercial grade chemicals in this work. The mass purities of isopropyl chloroacetate, cyclohexane, isopropanol and benzene were 0.980, 0.995, 0.997 and 0.995, respectively, which were confirmed by gas chromatography (GC) and all the reagents were used directly. The boiling point temperatures for the chemicals were determined by a modified Rose-type recirculating still. The relevant information of the chemicals, such as CAS number, supplier, boiling temperature and so on, is given in Table 1.
Apparatus and procedure
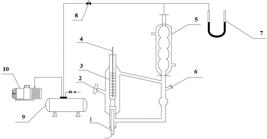
The apparatus used in this work was a modified Rose-type recirculating still which is presented in detail in Figure 1. The equilibrium temperature was determined by a mercury thermometer with the accuracy of ± 0.1 K. The pressure was measured by a mercury U-shaped manometer and the accuracy of the manometer was ± 0.1333 kPa. In each experiment, a liquid mixture of 50 ml was charged into the equilibrium still and heated. The vapor condensate was recirculated and mixed with the liquid in the still, which could make enough contact for the two phases. To reach the equilibrium state, the recirculation time for the two phases was maintained for at least 50 min at a constant temperature, then the equilibrium temperature was recorded. At the same time, 0.3 ml of the vapor and the liquid phases were withdrawn by syringe for analysis, respectively. All the samples were analyzed by GC.
The vapor-liquid equilibrium apparatus: 1, heating rod; 2, liquid phase sample port; 3, thermometer sleeve tube; 4, mercury thermometer; 5, condenser; 6, vapor phase sample port, 7, mercury U-shaped manometer, 8, needle valve, 9, buffer tank, 10, vacuum pump.
Gas chromatography (GC7900, Shanghai Tianmei Scientific Instrument Co., Ltd.) was used to analyze the samples, which was equipped with a flame ionization detector (FID) and a capillary column. The carrier gas was high-purity nitrogen with the purity of 99.999 wt%. The compositions of all samples were obtained by a T2000P GC workstation. The detailed operating conditions are shown in Table 2.
Analysis
Before analyzing the compositions of the samples, the area correction normalization method (Dai et al., 2014Dai, C., Lei, Z., Xi, X., Zhu, J., Chen, B. Extractive Distillation with a Mixture of Organic Solvent and Ionic Liquid as Entrainer. Industrial & Engineering Chemistry Research, 53, 15786-15791 (2014). https://doi.org/10.1021/ie502487n
https://doi.org/10.1021/ie502487n...
; Wu et al., 2018Wu, J., Xu, D., Shi, P., Gao, J., Zhang, L., Ma, Y., Wang, Y. Separation of azeotrope (allyl alcohol + water): Isobaric vapour-liquid phase equilibrium measurements and extractive distillation. Journal of Chemical Thermodynamics , 118, 139-146 (2018). https://doi.org/10.1016/j.jct.2017.11.009
https://doi.org/10.1016/j.jct.2017.11.00...
) was applied to calibrate the GC in this work. First, five different standard samples were prepared gravimetrically with an AR1140 electronic balance (Ohaus Corporation) with an accuracy of ± 0.0001 g. The five different standard samples with known compositions were analyzed by GC and the peak area of GC was calibrated. The samples of the vapor and liquid phases were analyzed at least three times, and the average values were recorded.
RESULTS AND DISCUSSIONS
Experimental VLE results
The experimental VLE data of isopropyl chloroacetate + isopropanol, isopropyl chloroacetate + cyclohexane and isopropyl chloroacetate +benzene were measured at the pressure of 101.3kPa and are listed in Table 3. The T-x-y profiles for the three systems are plotted in Figures 2-4.
Experimental VLE data for temperature T, liquid phase mole fraction x i , vapor phase mole fraction y i , activity coefficient γ, excess Gibbs energy G E , the results for cyclohexane (1) + isopropyl chloroacetate (2), isopropanol (1) + isopropyl chloroacetate (2) and benzene (1) + isopropyl chloroacetate (2) at 101.3kPa.a
T-x-y phase equilibrium for the system cyclohexane (1) + isopropyl chloroacetate (2) at 101.3 kPa: ●, experimental data; -, calculated by the NRTL model.
T-x-y phase equilibrium for the system isopropanol (1) + isopropyl chloroacetate (2) at 101.3 kPa: ●, experimental data; -, calculated by the NRTL model.
T-x-y phase equilibrium for the system benzene (1) + isopropyl chloroacetate (2) at 101.3 kPa: ●, experimental data; -, calculated by the NRTL model.
The equilibrium relationship of the system is represented by the following equation (Smith et al., 2001Smith, J. M., Van, N. H. C., Abbott, M. M. Introduction to Chemical Engineering Thermodynamics. sixth (ed). McGraw-Hill, New York (2001).):
Generally, the exponential term exp[Vi L((p - pi s)/RT)] is approximately equal to 1 under atmospheric pressure. In addition, the vapor phase could be regarded as an ideal gas, thus φi and φi s are equal to 1. Thus, Eq. 1 can be simplified as follows:
The pi
s can be calculated by the Wagner 25 equation (Forero and Velásquez, 2011Forero, G. L. A., Velásquez, J. J. A. Wagner Liquid-Vapour Pressure Equation Constants From a Simple Methodology. J. Chem. Thermodynamics, 43, 1235-1251 (2011). https://doi.org/10.1016/j.jct.2011.03.011
https://doi.org/10.1016/j.jct.2011.03.01...
; Gao et al., 2016bGao, J., Zhao, L., Zhang, L., Xu, D., Zhang, Z. Isobaric Vapor-Liquid Equilibrium for Binary Systems of 2,2,3,3-Tetrafluoro-1-propanol + 2,2,3,3,4,4,5,5-Octafluoro-1-pentanol at 53.3, 66.7, 80.0 kPa. Journal of Chemical and Engineering Data , 61, 3371-3376 (2016b). https://doi.org/10.1021/acs.jced.6b00429
https://doi.org/10.1021/acs.jced.6b00429...
):
and
The Wagner 25 parameters C 1i to C 4i , as well as the T ri and T ci for each pure component i, were taken from the Aspen Plus physical properties databank and listed in Table 4. In the meantime, the activity coefficient was calculated by Eq. 2, and the results are listed in Table 3.
To evaluate the non-ideality of the three binary systems, the excess Gibbs energy G
E (Acevedo et al., 1988Acevedo, I. L., Posfigo, M. A., Katz, M. Excess Thermodynamic Properties and VaporLiquid Equilibrium Data for the n-Butylamine + p-Dioxane System at 25oC. Journal of Solution Chemistry, 17, 977-986 (1988). https://doi.org/10.1007/BF00649741
https://doi.org/10.1007/BF00649741...
; Shi et al., 2017Shi, P., Gao, Y., Wu, J., Xu, D., Gao, J., Ma, X., Wang, Y. Separation of azeotrope (2,2,3,3-tetrafluoro-1-propanol + water): Isobaric vapour-liquid phase equilibrium measurements and azeotropic distillation. Journal of Chemical Thermodynamics , 115, 19-26 (2017). https://doi.org/10.1016/j.jct.2017.07.019
https://doi.org/10.1016/j.jct.2017.07.01...
) was calculated as follows:
The calculated results of G E are presented in Table 3 and Figure 5. As shown in Figure 5, the three binary systems exhibit positive deviations from Raoult′s law, which indicates the non-ideality of the solutions for three binary systems. Furthermore, the values of the excess Gibbs free energy for three binary systems follow the order of isopropyl chloroacetate + cyclohexane > isopropyl chloroacetate + isopropanol > isopropyl chloroacetate + benzene.
Excess Gibbs energy for the three systems at 101.3 kPa: ▲, cyclohexane (1) + isopropyl chloroacetate (2); ●, isopropanol (1) + isopropyl chloroacetate (2); ■, benzene (1) + isopropyl chloroacetate (2), --, calculated by the NRTL model.
Thermodynamic consistency tests
For the binary mixtures, the Herington and van Ness method were used to check the consistency of the experimental data.
The Herington method (Herington and Inst, 1951Herington, E. F. G., Inst, J. Tests for the Consistency of Experimental Isobaric Vapour-Liquid Equilibrium Data. Journal of the Institution of Petroleum, 37, 457-470 (1951).; Alinejhad et al., 2018Alinejhad, M., Shariati, A., Hekayati, J. Experimental Vapor-Liquid Equilibria and Thermodynamic Modeling of the Methanol + n-Heptane and 1-Butanol + Aniline Binary Systems. Journal of Chemical and Engineering Data, 63, 965-971 (2018). https://doi.org/10.1021/acs.jced.7b00766
https://doi.org/10.1021/acs.jced.7b00766...
) based on the Gibbs−Duhem theory was adopted which can be described as follows:
The ln(γ1/γ2) vs x diagram is shown in Figure 6 and T max and T min are the maximum and minimum boiling points, respectively. The criterion of the Herington test is that the absolute value of |D-J| should be less than 10. As shown in Table 5, the results of thermodynamic consistency for all three systems are all less than 10, which indicates that the experimental data of the three systems passed the thermodynamic consistency test.
ln(γ1/γ2) vs. x 1 plot for the three systems: ■, cyclohexane (1) + isopropyl chloroacetate (2); ●, isopropanol (1) + isopropyl chloroacetate (2); ▲, benzene (1) + isopropyl chloroacetate (2), --, calculated by the NRTL model.
The van Ness test method (Van Ness et al., 1973Van Ness, H. C., Byer, S. M., Gibbs, R. E. Vapor-Liquid Equilibrium: part I. An appraisal of data reduction methods. AIChE Journal , 19, 238-244 (1973). https://doi.org/10.1002/aic.690190206
https://doi.org/10.1002/aic.690190206...
; Gao et al., 2016aGao, J., Li, H., Xu, D., Zhang, L., Zhao, L., Li, C. Isobaric Vapor-Liquid Equilibrium for Binary Systems of Thioglycolic Acid with Water, Butyl Acetate, Butyl Formate, and Isobutyl Acetate at 101.3 kPa. Journal of Chemical and Engineering Data , 62, 355-361 (2016a). https://doi.org/10.1021/acs.jced.6b00686
https://doi.org/10.1021/acs.jced.6b00686...
) is expressed by the following equations:
The obtained VLE data can pass the thermodynamic consistency test if the values ofΔy andΔP are both less than 1. The test results are presented in Table 6. As seen from Table 6, the results of Δy andΔP are all less than unity, which indicates that the measured VLE data are thermodynamically consistent.
VLE data correlation
The measured experimental VLE data were correlated by the NRTL, Wilson and UNIQUAC activity coefficient models. For the UNIQUAC model, the structural parameters r and q are presented in Table 7. The expressions of the activity coefficient models are as follows:
NRTL:
αij = 0.3
Wilson:
UNIQUAC:
The interaction parameters of the above three models were obtained based on the maximum likelihood method by minimizing the following objective equation:
The obtained interaction parameters of the NRTL, Wilson and UNIQUAC models in Aspen plus simulator (2013) are listed in Table 8. The root-mean-square deviations (RMSD) were employed to evaluate the difference between the experimental and the calculated results. The RMSD (y i) and RMSD (T) are as follows:
The calculated RMSD values with the correlated parameters are presented in Table 8, which are less than 0.58 K and 0.006 respectively. As is shown in Table 8, the NRTL, Wilson and UNIQUAC models could correlate the VLE data for the three binary systems. Since the calculated results by the three model were graphically similar, the results correlated by the NRTL model were plotted in Figures 2-4.
According to the residuals of temperature and vapor mole fraction, the reliability of VLE data measured for each system has been checked (Orchillés et al., 2017Orchillés, A. V., Miguel, P. J., González-Alfaro, V., Llopis, F. J., Vercher, E., Martínez-Andreu, A. Isobaric Vapor-Liquid Equilibria for the Extractive Distillation of 2-Propanol + Water Mixtures Using 1-ethyl-3-methylimidazolium Dicyanamide Ionic Liquid. Journal of Chemical Thermodynamics , 110, 16-24 (2017). https://doi.org/10.1016/j.jct.2017.02.005
https://doi.org/10.1016/j.jct.2017.02.00...
; Mathias, 2017Mathias, P. M. Guidelines for the Analysis of Vapor-Liquid Equilibrium Data. J. Chem. Eng. Data, 62, 2231-2233 (2017). https://doi.org/10.1021/acs.jced.7b00582
https://doi.org/10.1021/acs.jced.7b00582...
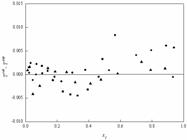
; Ma et al., 2018). Since the values of RMSD by the NRTL model were relatively larger than those of the Wilson and UNIQUAC models, the residuals of temperature and vapor mole fraction were calculated based on the difference between experimental values and the calculated values in the NRTL model. The residuals for the vapor mole fraction and temperature are less than 0.016 and 0.010 and are presented in Figures 7 and 8. As shown in Figures. 7 and 8, the distributions of the vapor phase mole fraction and temperature residuals are randomly distributed around zero. The fluctuations of the vapor phase mole fraction and temperature residual values are within the range between -0.016 and 0.012, and -0.005 and 0.010 respectively.
Residual plot of vapor mole fraction for the three systems: ■, cyclohexane (1) + isopropyl chloroacetate (2); ●, isopropanol (1) + isopropyl chloroacetate (2); ▲, benzene (1) + isopropyl chloroacetate (2).
Residual plot of temperature for the three systems: ■, cyclohexane (1) + isopropyl chloroacetate (2); ●, isopropanol (1) + isopropyl chloroacetate (2); ▲, benzene (1) + isopropyl chloroacetate (2).
CONCLUSIONS
The VLE data for the binary solutions of isopropyl chloroacetate + cyclohexane, isopropyl chloroacetate + isopropanol and isopropyl chloroacetate + benzene were generated at 101.3 kPa. The calculated excess Gibbs energy results indicate that the three systems show positive deviations from Raoult′s law. The thermodynamic consistency test for the experimental data was checked by the Herington and van Ness methods, and the measured VLE data passed the consistency tests. The thermodynamic models NRTL, Wilson, and UNIQUAC were adopted to fit the measured VLE data for the investigated systems and the binary interaction parameters of the models were regressed. The RMSD values for the mole fraction of vapor phase and the temperature were all less than 0.58 K and 0.0066, respectively.
ACKNOWLEDGEMENTS
This work was supported by the Shandong Provincial Key Research & Development Project (2018GGX107001), National Natural Science Foundation of China (21878178) and Project of Shandong Province Higher Educational Science and Technology Program (J18KA072).
REFERENCES
- Aspen Plus Software, Aspen Technology, Inc., Burlington, MA, 2013, Version 8.4.
- Abrams, D. S., Prausnitz, J. M. Statistical Thermodynamics of Liquid Mixtures: A New Expression for the Excess Gibbs Energy of Partly or Completely Miscible Systems. AIChE Journal, 21, 116-128 (1975). https://doi.org/10.1002/aic.690210115
» https://doi.org/10.1002/aic.690210115 - Acevedo, I. L., Posfigo, M. A., Katz, M. Excess Thermodynamic Properties and VaporLiquid Equilibrium Data for the n-Butylamine + p-Dioxane System at 25oC. Journal of Solution Chemistry, 17, 977-986 (1988). https://doi.org/10.1007/BF00649741
» https://doi.org/10.1007/BF00649741 - Alinejhad, M., Shariati, A., Hekayati, J. Experimental Vapor-Liquid Equilibria and Thermodynamic Modeling of the Methanol + n-Heptane and 1-Butanol + Aniline Binary Systems. Journal of Chemical and Engineering Data, 63, 965-971 (2018). https://doi.org/10.1021/acs.jced.7b00766
» https://doi.org/10.1021/acs.jced.7b00766 - Chen, R., Zhong, L., Xu, C. Isobaric Vapor-Liquid Equilibrium for Binary Systems of Toluene + Ethanol and Toluene + Isopropanol at (101.3, 121.3, 161.3, and 201.3) kPa. Journal of Chemical and Engineering Data , 57, 155-165 (2011). https://doi.org/10.1021/je200921u
» https://doi.org/10.1021/je200921u - Dai, C., Lei, Z., Xi, X., Zhu, J., Chen, B. Extractive Distillation with a Mixture of Organic Solvent and Ionic Liquid as Entrainer. Industrial & Engineering Chemistry Research, 53, 15786-15791 (2014). https://doi.org/10.1021/ie502487n
» https://doi.org/10.1021/ie502487n - Dorris, T. B., Sowa, F. J., Nieuwland, J. A. Organic Reactions with Boron Fluoride. VIII. The Condensation of Propylene with Acids. J. Am. Chem. Soc., 56, 2689-2690 (1934). https://doi.org/10.1021/ja01327a048
» https://doi.org/10.1021/ja01327a048 - Forero, G. L. A., Velásquez, J. J. A. Wagner Liquid-Vapour Pressure Equation Constants From a Simple Methodology. J. Chem. Thermodynamics, 43, 1235-1251 (2011). https://doi.org/10.1016/j.jct.2011.03.011
» https://doi.org/10.1016/j.jct.2011.03.011 - Gao, J., Li, H., Xu, D., Zhang, L., Zhao, L., Li, C. Isobaric Vapor-Liquid Equilibrium for Binary Systems of Thioglycolic Acid with Water, Butyl Acetate, Butyl Formate, and Isobutyl Acetate at 101.3 kPa. Journal of Chemical and Engineering Data , 62, 355-361 (2016a). https://doi.org/10.1021/acs.jced.6b00686
» https://doi.org/10.1021/acs.jced.6b00686 - Gao, J., Zhao, L., Zhang, L., Xu, D., Zhang, Z. Isobaric Vapor-Liquid Equilibrium for Binary Systems of 2,2,3,3-Tetrafluoro-1-propanol + 2,2,3,3,4,4,5,5-Octafluoro-1-pentanol at 53.3, 66.7, 80.0 kPa. Journal of Chemical and Engineering Data , 61, 3371-3376 (2016b). https://doi.org/10.1021/acs.jced.6b00429
» https://doi.org/10.1021/acs.jced.6b00429 - Gupta, B. S., Lee, M.-J. Isobaric Vapor-Liquid Equilibrium for the Binary Mixtures of Nonane with Cyclohexane, Toluene, M-xylene, or P-xylene at 101.3kPa. Fluid Phase Equilibria, 313, 190-195 (2012). https://doi.org/10.1016/j.fluid.2011.10.009
» https://doi.org/10.1016/j.fluid.2011.10.009 - Herington, E. F. G., Inst, J. Tests for the Consistency of Experimental Isobaric Vapour-Liquid Equilibrium Data. Journal of the Institution of Petroleum, 37, 457-470 (1951).
- Li, J., Hua, C., Xiong, S., Bai, F., Lu, P., Ye, J. Vapor-Liquid Equilibrium for Binary Systems of Allyl Alcohol + Water and Allyl Alcohol + Benzene at 101.3 kPa. Journal of Chemical and Engineering Data , 62, 3004-3008 (2017). https://doi.org/10.1021/acs.jced.6b00893
» https://doi.org/10.1021/acs.jced.6b00893 - Li, Y. Measurement and correlation of isobaric vapor-liquid equilibrium for the binary system of cyclopentane and tetrahydrofuran. Brazilian Journal of Chemical Engineering, 31, 815-820 (2014). https://doi.org/10.1590/0104-6632.20140313s00002623
» https://doi.org/10.1590/0104-6632.20140313s00002623 - Liu, D., Gui, J., Zhu, X., Song, L., Sun, Z. Synthesis and Characterization of Task‐Specific Ionic Liquids Possessing Two Brönsted Acid Sites. Synthetic Communications, 37, 759-765 (2007).
- Liu, S., You, H. An Overview on Synthetic Methods of Isopropyl Chloroacetate. European Chemical Bulletin, 1, 103-106 (2012).
- Liu, S., You, H. Effect of the Different Reaction Conditions on Synthesizing of Isopropyl Chloroacetate. European Chemical Bulletin , 2, 9-10 (2013). https://doi.org/10.1016/j.molliq.2018.11.047
» https://doi.org/10.1016/j.molliq.2018.11.047 - Liu, X., Xu, D., Diao, B., Zhang, L., Gao, J., Liu, D., Wang, Y. Choline chloride based deep eutectic solvents selection and liquid-liquid equilibrium for separation of dimethyl carbonate and ethanol. Journal of Molecular Liquids, 275, 347-353 (2019).
- Ma, J., Jiang, H., Gong, H., Sun, Z. Esterification of Chloroacetic Acid with Alcohols Catalyzed by Zinc Methanesulfonate. Petroleum Science and Technology, 24, 431-440 (2006). https://doi.org/10.1081/LFT-200043689
» https://doi.org/10.1081/LFT-200043689 - Ma, Y., Gao, J., Li, M., Zhu, Z., Wang, Y. Isobaric Vapour-Liquid Equilibrium Measurements and Extractive Distillation Process for the Azeotrope of (N, N-dimethylisopropylamine + acetone). Journal of Chemical Thermodynamics, 122, 154-161 (2018). https://doi.org/10.1016/j.jct.2018.03.019
» https://doi.org/10.1016/j.jct.2018.03.019 - Mathias, P. M. Guidelines for the Analysis of Vapor-Liquid Equilibrium Data. J. Chem. Eng. Data, 62, 2231-2233 (2017). https://doi.org/10.1021/acs.jced.7b00582
» https://doi.org/10.1021/acs.jced.7b00582 - Orchillés, A. V., Miguel, P. J., González-Alfaro, V., Llopis, F. J., Vercher, E., Martínez-Andreu, A. Isobaric Vapor-Liquid Equilibria for the Extractive Distillation of 2-Propanol + Water Mixtures Using 1-ethyl-3-methylimidazolium Dicyanamide Ionic Liquid. Journal of Chemical Thermodynamics , 110, 16-24 (2017). https://doi.org/10.1016/j.jct.2017.02.005
» https://doi.org/10.1016/j.jct.2017.02.005 - Patwardhan, A. A., Sharma, M. M. Esterification of Carboxylic Acids with Olefins Using Cation Exchange Resins as Catalysts. Reactive Polymers, 13, 161-176 (1990). https://doi.org/10.1016/0923-1137(90)90051-5
» https://doi.org/10.1016/0923-1137(90)90051-5 - Renon, H., Prausnitz, J. M. Local Compositions in Thermodynamic Excess Functions for Liquid Mixtures. AlChE Journal, 14, 135-144 (1968). https://doi.org/10.1002/aic.690140124
» https://doi.org/10.1002/aic.690140124 - Shi, P., Gao, Y., Wu, J., Xu, D., Gao, J., Ma, X., Wang, Y. Separation of azeotrope (2,2,3,3-tetrafluoro-1-propanol + water): Isobaric vapour-liquid phase equilibrium measurements and azeotropic distillation. Journal of Chemical Thermodynamics , 115, 19-26 (2017). https://doi.org/10.1016/j.jct.2017.07.019
» https://doi.org/10.1016/j.jct.2017.07.019 - Smith, J. M., Van, N. H. C., Abbott, M. M. Introduction to Chemical Engineering Thermodynamics. sixth (ed). McGraw-Hill, New York (2001).
- Van Ness, H. C., Byer, S. M., Gibbs, R. E. Vapor-Liquid Equilibrium: part I. An appraisal of data reduction methods. AIChE Journal , 19, 238-244 (1973). https://doi.org/10.1002/aic.690190206
» https://doi.org/10.1002/aic.690190206 - Wang, M., Tian, J., Liu, L., Jiang, H., Gong, H., Su, T. Synthesis and Characterization of Methane-Sulfonates and Their Catalytic Activities for Esterification. Chinese Journal of Inorganic Chemistry, 19, 731-734 (2003).
- Wilson, G. M. A New Expression for The Excess Free Energy of Mixing. Journal of the American Chemical Society, 86, 127-130 (1964). https://doi.org/10.1021/ja01056a002
» https://doi.org/10.1021/ja01056a002 - Wu, J., Xu, D., Shi, P., Gao, J., Zhang, L., Ma, Y., Wang, Y. Separation of azeotrope (allyl alcohol + water): Isobaric vapour-liquid phase equilibrium measurements and extractive distillation. Journal of Chemical Thermodynamics , 118, 139-146 (2018). https://doi.org/10.1016/j.jct.2017.11.009
» https://doi.org/10.1016/j.jct.2017.11.009 - Xu, J., Zhang, J., Yin, X. Esterification Process to Synthesize Isopropyl Chloroacetate Catalyzed by Lanthanum Dodecyl Sulfate. Brazilian Journal of Chemical Engineering , 28, 259-264 (2011). https://doi.org/10.1590/S0104-66322011000200010
» https://doi.org/10.1590/S0104-66322011000200010
NOMENCLATURE
- T Equilibrium temperature (K)
- p Pressure (kPa)
- N The point of the experimental data
- α Non-randomness parameter in the NRTL model
- r Area parameter of UNIQUAC
- q Volume parameter of UNIQUAC
- z Lattice coordination number in the UNIQUAC model
- θ Area fraction in the UNIQUAC model
- u Uncertainty
- x Mole fraction in the liquid phase
- y Mole fraction in the vapor phase
- φi Fugacity coefficient of the vapor phase
- φi s Fugacity coefficient at the saturated pressure
- γ Activity coefficient
- Vi L Liquid molar volume
- R Universal gas constant (8.314 J.K-1.mol-1)
- pi s Saturation vapor pressure
- pci Critical pressure of pure component
- a, b Binary interaction parameters
- σ Standard deviation
- i,j Component i, j
- cal Calculated property
- exp Experimental property
Publication Dates
-
Publication in this collection
13 Jan 2020 -
Date of issue
Oct-Dec 2019
History
-
Received
01 Mar 2019 -
Reviewed
24 Apr 2019 -
Accepted
03 June 2019