Abstracts
The process of Friction Stir Welding (FSW) is a welding method developed by the "The Welding Institute" (TWI) of England in 1991. The welding equipment consists of a tool that rotates and progresses along the joint of two restrained sheets. The joint is produced by frictional heating which causes the softening of both components into a viscous-plastic condition and also by the resultant flow between the sheets to be joined. Numerical Modeling of the process can provide realistic prediction of the main variables of the process, reducing the number of experimental tests, thus accelerating the design processes while reducing costs and optimizing the involved technological variables. In this study the friction stir welding process is modeled using a general purpose finite element based program, reproducing the material thermal map and the corresponding mass flow. Numerical thermal results are compared against experimental thermographic maps and numerical material flow results are compared with material flow visualization techniques, with acceptable concordance.
Friction stir welding (FSW); Three-dimensional modeling; flow; temperature; finite element
O processo denominado "Friction Stir Welding" (FSW) é um método de soldagem desenvolvido pelo "The Welding Institute" (TWI) na Inglaterra em 1991. O equipamento de soldagem consiste de uma ferramenta que gira e avança ao longo da interface entre duas chapas fixas. A junção é produzida pelo calor gerado por fricção o qual causa o amolecimento de ambos os componentes atingindo uma condição visco-plástica e também pelo escoamento resultante entre as laminas a ser unidas. A modelagem numérica do processo pode fornecer uma predição real das principais variáveis do processo, reduzindo o número de testes experimentais, acelerando, portanto os processos de projeto ao mesmo tempo em que reduz custos e permite a otimização das variáveis tecnológicas envolvidas. Neste trabalho, o processo de soldagem por fricção é modelado empregando um programa de propósito geral baseado no método dos elementos finitos, procurando reproduzir a distribuição térmica e o correspondente escoamento de massa. Os resultados numéricos térmicos são comparados com distribuições termográficas experimentais e os resultados numéricos de escoamento de massa são comparados com aqueles obtidos a partir de técnicas experimentais de visualização, atingindo uma concordância aceitável.
Friction stir welding (FSW); Modelagem 3D; escoamento; temperatura; elementos finitos
TECHNICAL PAPERS
3D modeling of material flow and temperature in Friction Stir Welding
Modelagem 3D do fluxo de material e da temperatura na soldagem "Friction Stir"
Diego SantiagoI; Santiago UrquizaI; Guillermo LomberaI; Luis de VediaII
IDto.de Ing. Mecánica, Univ. Nac. de Mar del Plata (CONICET), 7600 Mar del Plata, Buenos Aires, Argentina. dsantiago@fi.mdp.edu.ar, glombera@fi.mdp.edu.ar, santiagourquiza@fi.mdp.edu.ar
IIInstituto Sabato (UNSAM-CNEA), CIC, 1650 San Martín, Buenos Aires, Argentina ldevedia@cnea.gov.ar
ABSTRACT
The process of Friction Stir Welding (FSW) is a welding method developed by the "The Welding Institute" (TWI) of England in 1991. The welding equipment consists of a tool that rotates and progresses along the joint of two restrained sheets. The joint is produced by frictional heating which causes the softening of both components into a viscous-plastic condition and also by the resultant flow between the sheets to be joined. Numerical Modeling of the process can provide realistic prediction of the main variables of the process, reducing the number of experimental tests, thus accelerating the design processes while reducing costs and optimizing the involved technological variables. In this study the friction stir welding process is modeled using a general purpose finite element based program, reproducing the material thermal map and the corresponding mass flow. Numerical thermal results are compared against experimental thermographic maps and numerical material flow results are compared with material flow visualization techniques, with acceptable concordance.
Key-words: Friction stir welding (FSW); Three-dimensional modeling; flow; temperature, finite element.
RESUMO
O processo denominado "Friction Stir Welding" (FSW) é um método de soldagem desenvolvido pelo "The Welding Institute" (TWI) na Inglaterra em 1991. O equipamento de soldagem consiste de uma ferramenta que gira e avança ao longo da interface entre duas chapas fixas. A junção é produzida pelo calor gerado por fricção o qual causa o amolecimento de ambos os componentes atingindo uma condição visco-plástica e também pelo escoamento resultante entre as laminas a ser unidas. A modelagem numérica do processo pode fornecer uma predição real das principais variáveis do processo, reduzindo o número de testes experimentais, acelerando, portanto os processos de projeto ao mesmo tempo em que reduz custos e permite a otimização das variáveis tecnológicas envolvidas. Neste trabalho, o processo de soldagem por fricção é modelado empregando um programa de propósito geral baseado no método dos elementos finitos, procurando reproduzir a distribuição térmica e o correspondente escoamento de massa. Os resultados numéricos térmicos são comparados com distribuições termográficas experimentais e os resultados numéricos de escoamento de massa são comparados com aqueles obtidos a partir de técnicas experimentais de visualização, atingindo uma concordância aceitável.
Palavras-chave: Friction stir welding (FSW); Modelagem 3D; escoamento; temperatura, elementos finitos.
1. Introduction
The Stir-Welding or Friction Stir Welding (FSW) [1] is a technique that involves the joining of two thick sheets or plates using mechanical means. Figure 1 shows a schematic representation of the FSW process, the tool consists of a shoulder, normal to the axis of rotation of the tool and a small diameter probe connected to it. The tool shoulder, with larger diameter than that of the probe, prevents the material from being expelled from the workpiece to be welded. This minimizes the formation of voids in the welded area. On the other hand, the main part of process heat input is induced by friction between shoulder tool and plates. Usually the probe is "threaded" to increase the generation of frictional heating and a greater mixing effect on the materials.
Once the sheets or plates are butted on a common axis, the rotating tool is plunged into the welding workpiece until the shoulder is brought into close contact with the two parts to be joined. Once the probe is inserted, it moves in the welding direction. As the tool moves along the joint line, the heated and plasticized material is swept around the probe to the rear where it consolidates and forms the weld. It results in a solid-state high quality weld. Notice that the tool axis is typically tilted by several degrees (2º or 3º) from the vertical to facilitate consolidation of the weld.
Among the several papers about FSW it is worth mentioning those written by Flores et al [2]., Murr et al [3], and Liu et al [4] regarding the micro-structural aspects of aluminum alloy welding, and those written by Dawes and Thomas [5,6] describing the FSW process, summarizing its advantages and disadvantages. There are several works on numerical simulation in relation with this process. Gould et al [7] developed an analytical heat transfer model for FSW. The model is based on the well known Rosenthal equation [8] which describes a quasi stationary temperature field over a semi-infinite plate due to a moving heat source. Kovacevic et al [9,10] carried out thermal and thermo-mechanical analyses using finite elements. These analyses are based on a heat source model, not considering the thermo-mechanical coupling generated by plastic flow. It is worth mentioning that due to the characteristics of this problem, by using fully coupled thermal-mechanical viscoplastic flow models [11-13], good results can be expected where plastic deformations commonly occur. Besides, due to its geometric and kinematic characteristics, the problem is mainly three-dimensional, which together with the presence of high strain rate gradients around the probe imposes a high computational demand. In this sense, this kind of modeling was tackled by Colegrove et al [13]. using the "CFD package FLUENT", where a coupled thermomechanical viscoplastic model for aluminum material was solved obtaining good results as regards material flow distribution. Recently, Nandan et al [14,15] reported results of stainless steel FSW simulation by using this kind of models with good agreement between computed temperature field and experimental data, showing the versatility of the viscoplastic flow models to represent large deformation processes as in FSW. Nevertheless, none of the previously quoted papers contrast material flow simulation with experimental data.
In this work, coupled modeling of material flow and temperature field distribution was carried out for a steady state problem. The thermal model boundary conditions considered the convection heat loss and heat transfer through the tool and the base plate. Heat generation through viscous dissipation was also taken into account. Results obtained were contrasted with experimental data. Thermal results were compared with experimental data obtained by thermographic imaging. The modeled flow structure around the tool was analyzed comparing results with those existing in previously published works of experimental researchers [2-4] and also with our own data coming from photographic imaging corresponding to the contact surfaces of the joint, more specifically, in the vicinity of the leading zone were the joint was not yet full achieved. This technique allows to qualitatively asses the experimental flow patterns around the tool, avoiding the implementation of more sophisticated (e.g., particle tracing) techniques and facilitating the validation of these aspects of the numerical results.
2. Governing equations
2.1. Mechanical model
Neglecting inertial and volume forces, the equilibrium equation in a volume of material Ω with boundary ∂Ω can be written as [16]:
where σ is the Cauchy stress tensor . Tractions Tºi can be prescribed in a part of the boundary ∂Ωt(Neumann conditions), while the velocity components uºi can be specified in the rest of the surface ∂Ωu(Dirichlet conditions).This can be expressed as follows:
where ∂Ω = ∂Ωt ∂Ωu y ∂Ωt ∩ ∂Ωu =  , n is the unit outward normal to the contour ∂Ω, eiis the unit basis vector for a three-dimensional Cartesian coordinate system and u is the velocity vector. The deformation rate vector is related to the symmetric part of the gradient of the velocity field according to
, n is the unit outward normal to the contour ∂Ω, eiis the unit basis vector for a three-dimensional Cartesian coordinate system and u is the velocity vector. The deformation rate vector is related to the symmetric part of the gradient of the velocity field according to
Assuming the material is incompressible, then the following continuum equation must be fully observed on Ω
If a flow formulation for modeling the large plastic deformations involved in the stir-welding process is adopted, the stress tensor deviator S can be related to the deformation rate tensor D -which actually is a deviator by virtue of the incompressibility hypothesis - as given by:
where µ is the effective viscosity of the material and p the hydrostatic pressure. Besides, σe is the effective stress, say, the second invariant of the stress tensor, and σe is the effective deformation rate, say, the second invariant of the deformation rate tensor. These can be described as:
This work assumes a viscoplastic constitutive model where stresses depend on deformation rate and temperature. This is represented by [17]:
where α, Q, A and n are material constants, R is the gas constant and T is the absolute temperature. Material constants can be determined using standard compression tests. The mechanical model is completed after describing the appropriate boundary conditions.
2.2. Thermal Model
Temperature distribution is determined by solving the heat balance equation [16]:
where ρ is the density, Cp is the heat capacity, k the thermal conductivity, θ the temperature and γ the internal heat generation rate due to viscoplastic power dissipation. It is assumed that 90% of the plastic power converts to heat [18]. The term that corresponds to the rate of heat generation through mechanical work can be expressed as the product between stress and deformation rate, as follows:
with η the fraction of power not absorbed in microstructural defects.
Properties of pure aluminum were adopted, both for the mechanical parameters as well as for the temperature-dependent conductivity and specific heat. A thermal flow qº can be prescribed on a part of the boundary ∂Ω q, while the temperature θ º can be specified in the rest of the surface∂Ωθ.This can be written as:
Where ∂Ω = ∂Ω ∪ ∂Ωθ and n is the unit outward normal to the boundary ∂Ω.qThe contribution qº is due to the cooling of the surfaces by convection and also by the heat transmission through the contact interfaces, e.g., the "tool-plates" and the "base-plates" interfaces.
2.3. Geometric Model
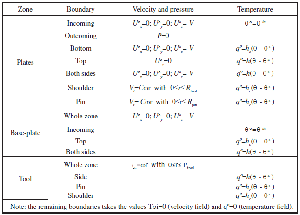
In this work, it is assumed a reference frame fixed to the welding tool, so that the plate moves towards the tool at a speed (V = 2.0 mm/s) and temperatures (σ ª= σ in = 25ºC) imposed on the entrance surface of the region under study. All boundary conditions are detailed in Appendix A Appendix A
The surface of the tool probe is spirally threaded. The effect of the ascending flow produced by such spiral is simulated imposing an upward velocity component on the probe surface. This velocity is a function of the spiral step (Pitch=1,2 mm/rev) and the tool rotation velocity (σ= 22,5 rev/s)
Data for the materials properties [19] and the constitutive law constants [17] of the model are shown in tables 1 and 2, respectively.
Also it is adopted that the material in contact with the tool has a 50 % relative slipping(C=0.5) as suggested by Ulysse [11], which produce realistic results and simplifies the model implementation. Figure 2 shows a perspective of the geometry of the problem and the dimensions used. The dimensions are based on a work of Cabot et al [19].
Figure 3 shows the different areas of the problem. Area 1 represents the steel base where the plates to be welded are placed and Area 4 corresponds to the tool. Areas 2 and 3 represent the plates to be welded, which have been meshed with low and high concentration of elements, respectively. Figures 4a and 4b show the assembled geometry. Figures 4c and 4d show the mesh details of densified regions corresponding to Areas 2 and 3.
3. Numerical model
The base plate was modeled using a Taylor-Hood tetrahedron [16] finite element mesh, i.e, P2-P1 tetrahedron elements with quadratic interpolation for velocity field and linear for pressure, which are div-stable [20] and also allows an adequate capture of the high tension gradients present in the neighborhood of the tool. The implemented mesh had approximately 85000 elements with 107000 velocity nodes (Figure 4). This case was solved using the general proposed solver code (Solver GP) developed by Urquiza et al [21,22].
The solution algorithm consists of two substeps: the first one values that depend on deformation rates obtained in the previous iteration. The discrete equations are derived from a classic Stokes problem formulation for viscous incompressible flow with the previously mentioned finite element interpolations. Also the addition of Chorin's [23] artificial compressibility is considered in order to attain better convergence rates. For each non-linear iteration, the corresponding linear algebraic equation system is solved through a LU preconditioned conjugated gradient method based on the scheme proposed by Saad in SparseKit [24]. On the other hand, the second sub-step solves the temperature field with quadratic interpolation derived from the corresponding advection-diffusion problem and assuming fixed the velocity field as provided by the first sub-step. The solution of the algebraic system is the same as in the first substep.
Even though a stationary solution is required, an implicit time advancement scheme was implemented, mainly used as preconditioner for the equation systems.
4. Results
4.1. Temperature fields
The temperature values obtained in the modeling were contrasted against experimental data measured by thermograph. The infrared thermal camera used is a Fluke Ti30, the images generated are 120x160 pixel size and contain a temperature measure for each pixel. The precision of the temperature measurement of this camera is ±2% at full scale. Thermograph data correspond to a weld made with the same process parameters used in this work. Those data were obtained at CAC-CNEA.
Comparisons between model prediction and experimental data are shown in Figure 5b. This graphic takes the temperature values of the top surface of the plates in two cross weld direction lines placed at 10mm and 14.4mm ahead of the tool rotation axis (see the white lines in Figure 5a). It can be observed a reasonably well agreement between temperature values obtained with the model and with those coming from experimental data. 6b illustrates the convective drag effect over the temperature field produced by the weld velocity.
As it is depicted in figures 5 and 6, the resulting temperature distribution in the tool is practically linear in a direction coincident with the rotation axis. Therefore, the tool mesh may be replaced by a Neumann condition on the Tool-Plates interface, reducing the computational cost of the problem.
4.2. Velocity fields and material flow
Figure 7 shows the Iso-surfaces of the velocity module corresponding to 3 mm/s (figure 7a), to 5 mm/s (figure 7b) and to 20 mm/s (figure 7c). Those figures illustrates that zones with velocities closer to the weld velocity (Vw= 2mm/s) are greater in size for the retreating side than for the advancing side. This is in agreement with the experimental work carried out by Murr [3], where it is reported a thermo-mechanically affected zone around the probe which is at least twice as large on the retreating side compared with that for the advancing side.
In figure 7c the velocity iso-surface corresponds to values ten times greater than the weld velocity. In this case the delimited zone is almost symmetrical. Therefore, it can be said that it represents approximately the boundary between the Thermo- Mechanically Affected Zone (TMAZ) and the Stir Zone (SZ) subjected to plasticization and agitation. This is in accordance with that reported by Guerra et al [25]. In this way, it will be possible to predict different microstrucutral regions (TMAZ, SZ) whose in turn determines the final properties of the welded joint. Consequently, this computational model has the potentiality to optimize the properties of the joints as a function of the different size of the microstructural regions occurring around the tool. This is an important aspect where modeling tools can contribute to improve the welded joints via a better control of the distribution of final material properties.
Figure 8 shows the path of the streamlines around the tool. The flow lines of this figure represent the paths of material particles that go through the affected zones in the neighborhood of the tool tip. Being the advancing direction WD coincident with the positive Z axis (+Z), the pathlines advance in the negative direction of that axis (-Z). The initial position of the flow line shown in figure8a correspond to the joint position (x=0) at 3mm of the bottom plates (y=3mm). This f low line clearly shows the ascending effect produced by the threaded surface of the pin. From the same figure it can be observed that once the flow line reaches the top surface, contacting the tool shoulder, it takes a descending path rotating several times before continuing its course. As a consequence, the material stays close to the surface of the tool pin remaining inside to the SZ (velocity module>20mm/ seg) during several revolutions. This type of flow patterns was observed by Guerra et al [25]. There, was recognized a "rotational zone" equivalent to SZ, where the material "is moved by entering onto the rotational zone, undergoing several revolutions, and finally dropping off in the wake of the nib".
Figure 8b shows an arrangement of flow lines coming from the joint position(x=0) along the whole thickness of the plates (0mm<y<6.25mm). It can be seen how the flow lines coming from the lower half of the plates enter to the SZ, while the others circumvent the SZ, going through the TMAZ before escaping from that zone on straight path along the welding direction. Also, it can be observed how the flow lines coming from the upper half of the plate are driven by the interaction with the tool pin while those coming from the lower half are driven by the interaction with the tool shoulder.
To compare the material flow obtained in the modeling with experimental results [19], the deformations produced in the material located in front of the tool were observed. In this zone the material of the surfaces to be joined has become greatly deformed but still remains unwelded. In this way it is possible to visualize the flow patterns without using particle tracers. Figure 9 illustrates these facts comparing pictures of the material located on the leading side (LS) of the tool with the corresponding surfaces generated by the modeled material flow lines. It is observed that the modeled plastically deformed zone (figure 9d) is larger than the one obtained experimentally (figure 9c), mainly around the tool shoulder. This difference can be attributed to the fact of applying a uniform relative slipping condition to the whole surface of the tool. Thus, it can be inferred that the velocities applied to the tool shoulder in the model are higher than the ones observed experimentally, generating a greater deformation zone. Also, from the results observed in figure 9d, can be estimated the thickness of the deformed zone in a direction perpendicular to the shoulder surface. As was stated by Kumar et al [26] the relative size of the deformed zones driven by the shoulder movement with respect to those driven by the pin are determinant for well behaved joints.
5. Conclusions
A three-dimensional computational model was presented through Finite Element modeling of the FSW process. The results are congruent with those observed experimentally, reproducing realistically the main characteristics of the flow patterns prevailing in the neighborhood of the tool.
With the flow line analysis were recognized two specific zones where the material undergoes different patterns of flow. It is noticeable the presence of a region adjacent to the welding probe with very strong gradients in the velocity field, and another zone, surrounding the former, where the flow velocities are considerably lower. Consequently, the material passing through one of these zones will be subjected to a very different thermomechanical history than the material going through the other. This in turn will influence in a distinctive manner the microstructural characteristics of the welded material in each region. As a result, the developed model has the potentiality to identify different process zones which can be helpful to predict and optimize the main process parameters of FSW. In this sense, this kind of computational models can contribute to reduce labors on designing and setting experimental trials.
Future efforts must be oriented toward improving the contact conditions on the interfaces where the material become in contact with the tool tip and the shoulder, in order to attain better adjustment of the volumes of material driven by the tool.
6. Acknowledgments
We are grateful to Pedro Cabot and Alberto Moglioni of CACCNEA for their advice and technical support on setting the experimental measurement employed in this work.
7. References
(Recebido em 05/10/2008; Texto Final em 11/07/2009).

Click to extend

- [1] THOMAS, M.W. et al., Friction Stir Butt welding. GB Patent Application No.9125978.8 Dec 1991. US Patent No.5460317, Oct. 1995.
- [2] FLORES, O.V. et al., Microstructural issues in a friction-stir welded aluminum alloy, Scr. Mater., v.38, p.703, 1998.
- [3] MURR, L.E.; LIU, G.; McCLURE, J.C. A TEM study of precipitation and related microstructures in friction-stir-welded 6061 aluminum, J. Mater. Sci., v.33, p.1243, 1998.
- [4] LIU, G. Et al, Micro- structural aspects of the friction-stir welding of 6061-T6 aluminum alloy, Scr. Mater., v.37, p.335, 1997.
- [5] DAWES, C. J.; THOMAS, W.M. Friction stir process for aluminum alloys, Welding Journal, v.75, p.41, 1996.
- [6] DAWES, C. J. An introduction to friction stir welding butt welding and its developments, Welding and Fabrication, Jan. 1995.
- [7] GOULD, J.E.; FENG, Z. Heat flow model for friction stir welding of aluminum alloys, J. Mater. Process. Manu., v.7, 1998.
- [8] ROSENTHAL, D.; SCHRMERBER, R. Thermal study of arc welding, Welding Journal, v.17, p.208, 1938.
- [9] CHEN, C. M.; KOVACEVIC, R. Finite element modeling of friction stir welding - thermal and thermomechanical analysis, Int. J. Mach. Tool. Manu., v.43, p.1319-1326, 2003.
- [10] SONG, M.; KOVACEVIC, R. Thermal modeling of friction stir welding in a moving coordinate system and its validation, Int. J. Mach. Tool. Manu., v.43, p.605-615, 2003.
- [11] ULYSSE, P. Three-dimensional modeling of the friction stir-welding process, Int. J. Mach. Tool. Manu., v.42, p.1549-1557, 2002.
- [12] SANTIAGO, D. et al., Numerical modeling of joints welded by "friction stir welding" process, Materials Research, v.7, n.4, p.569-574, 2004.
- [13] COLEGROVE, P.A.; SHERCLIF, H. R. 3-Dimensional CDF modelling of flow round a threated friction stir welding tool profile, J. Mater. Process. Tech., v.169, p.320-327, 2005.
- [14] NANDAN, R. et al, Numerical modelling of 3D plastic flow and heat transfer during friction stir welding of stainless steel, Science and Technology of Welding and Joining, v.11, p.526-537, 2006.
- [15] NANDAN, R. et al, Three-dimensional heat and material flow during friction stir welding of mild steel, Acta Materialia, v.55, p.883-895, 2007.
- [16] ZIENKIEWITZ, O. C.; TAYLOR, R.L. The finite element method. McGraw Hill, v.1-2, 1989.
- [17] SHEPPARD, T.; WRIGHT, D. S. Determination of flow stress: Part 1 constitutive equation for aluminum alloys at elevated temperatures, Metals Technology, p.215, June 1979.
- [18] JOHNSON, W.; KUDO H. K. The mechanics of Extrusion. Manchester University, 1962.
- [19] CABOT, P.; MOGLIONI, A.; CARELLA, E. Soldadura por fricción-agitación (FSW) de AA 6061 T6, Materia, v.8, p.187-195, 2003.
- [20] GUNSBURGER, M. Finite element methods for viscous incompressible flows. A guide to the theory, practice and algorithms. Academic Press, London, 1989.
- [21] URQUIZA, S.A.; VENERE, M. J. An application framework architecture for FEM and others related solvers, Mecánica Computacional, Argentina, v.21, pp 3099-3109, Oct. 2002.
- [22] URQUIZA, S.A. Hemodinámica computacional de sistema arterial humano: 2009. 236 pp. PhD thesis dissertation - Instituto Balseiro, Universidad Nacional de Cuyo, Bariloche, Argentina.
- [23] CHORIN, A.J. Math. Comp., v.22, n.7, p.45-762, 1968.
- [24] SAAD, Y. SPARSEKIT: a basic tool kit for sparse matrix computation (version 2), University of Illinois, 1994, available at: <http://www.users.cs.umn.edu/~saad/software/SPARSKIT/sparskit.html>
- [25] GUERRA, M. et al, Flow patterns during friction stir welding, Materials Characterizations, v.49, p.95-101, 2003.
- [26] K. Kumar, Satish V. Kailas. The role of friction stir welding tool on material flow and weld formation, Mat. Sci. Eng. A, v.485, p. 367-374, 2008.
Appendix A
Publication Dates
-
Publication in this collection
09 Nov 2009 -
Date of issue
Sept 2009
History
-
Received
05 Oct 2008 -
Accepted
11 July 2009