Determinação de fase vítrea em bauxitas refratárias

Amorphous phase determination in refractory bauxites

Determinação de fase vítrea em bauxitas refratárias

(Amorphous phase determination in refractory bauxites)

C. Pascoal¹, R. Machado², V. C. Pandolfelli3

¹Empresa Brasileira de Aeronáutica S.A. - EMBRAER

²CCDM, Universidade Federal de S. Carlos - UFSCar

³DEMa, Universidade Federal de S. Carlos - UFSCar

Rod. Washington Luiz, Km 235, C.P. 676, S. Carlos, SP, 13565-905

[e-mail] ou [e-mail]

Resumo

A refratariedade e a resistência ao choque térmico dos materiais estão intrinsecamente ligadas às fases que os compõem, de modo que a identificação destas fases através da técnica de difração de raios X é atualmente imprescindível para a completa caracterização de matérias-primas de produtos cerâmicos. Em 1969, H. M. Rietveld desenvolveu um software de refinamento por mínimos quadrados que permite a completa caracterização cristalográfica de um material mono ou multifásico. Apesar de possuir mais de trinta anos, a técnica ainda não é utilizada de maneira regular na análise quantitativa de matérias-primas naturais. O presente estudo busca utilizar o método de Rietveld em conjunto com outras metodologias, na quantificação da fase vítrea de bauxitas refratárias, analisando as vantagens e limitações desta técnica, bem como os resultados obtidos. Foram escolhidas a partir da literatura quatro técnicas cuja proposta comum é a determinação da fase vítrea em refratários e/ou outras classes de cerâmicas utilizando-se o método de Rietveld como base teórica. Uma quinta técnica, denominada dissolução química, foi utilizada como meio de comparação. Os resultados ilustram que, apesar dos esforços, nenhuma das técnicas estudadas pode ser utilizada de forma rápida e principalmente confiável para a determinação da quantidade de fase vítrea em refratários.

Palavras-chave: matérias-primas, refratários, caracterização química.

Abstract

The refractoriness and thermal shock resistance of any material is deeply related to the crystalline and amorphous phases present. In 1969, H. M. Rietveld developed a software that provides the complete characterization of single or multiphase materials. For nearly thirty years, since it was developed, the Rietveld Method has not been extensively used in quantitative analysis of natural raw material. This study has the objective to use this methodology along with other ones, in order to quantify the amorphous phase in refractory bauxites, considering its facilities and drawbacks. Four techniques were chosen to determine the vitreous phase in refractories raw materials, using the Rietveld method as theoretical basis. The fifth technique, named chemical dissolution in fluorydric acid, was used as a comparison method. The results illustrated that, despite the efforts, none of the techniques studied can be applied as a fast and reliable method to determine the amorphous content in refractories.

Keywords: raw-materials, refractories, chemical characterization.

INTRODUÇÃO

No campo dos refratários, a quantificação das fases cristalinas e amorfas de um material é essencial para prever as propriedades a altas temperaturas. As fases definem a refratariedade do material, bem como sua resistência ao choque térmico. O teor de fase vítrea está relacionado, entre outros aspectos, à resistência ao ataque químico do refratário e sua resistência à fluência.

O método de Rietveld tem sido amplamente empregado na determinação de estruturas cristalinas e análise quantitativa de fases. O programa utiliza um algoritmo baseado no ajuste por mínimos quadrados para refinar um modelo estrutural teórico em relação a difratogramas reais. Uma extensa bibliografia sobre o assunto pode ser encontrada, porém não é objetivo deste trabalho o aprofundamento teórico na técnica, que pode ser consultada nas diversas referências apresentadas [1-6].

Das técnicas selecionadas neste trabalho, a primeira a ser analisada é também a mais conhecida e utilizada na determinação do teor de fase vítrea em um material. O método do padrão interno requer a presença de um padrão de estrutura e concentração conhecidas [7]. É baseado na própria análise quantitativa de fases cristalinas proposta no método de Rietveld e considera [6] alguns princípios: 1) A intensidade dos picos de uma fase é proporcional a um fator de correção, obtido pelo refinamento de Rietveld; 2) Esta intensidade é também proporcional à massa da fase e 3) Se todas as fases presentes na amostra estão identificadas e são cristalinas, as frações em peso de cada fase podem ser obtidas e sua soma é igual à unidade. Considerando a presença de um padrão interno de concentração conhecida, os valores obtidos pelo refinamento de Rietveld podem ser corrigidos.

Cuidado especial deve ser tomado na escolha do padrão interno [7], que deve apresentar muitas linhas de difração para minimizar possíveis erros devido à orientação preferencial e extinção primária. A granulometria do padrão deve ainda ser controlada para evitar alargamento de picos devido à presença de partículas muito finas e/ou deformadas.

A segunda técnica utilizada, denominada "Matrix Flushing" foi desenvolvida como tentativa de determinar quantitativamente a concentração de fases cristalinas e amorfas utilizando também a difração de raios X [8]. Considerando um feixe de raios X monocromático atingindo uma amostra plana, a intensidade dos raios difratados pela amostra está relacionada à concentração da fase na amostra segundo a equação (A):

sendo:

I_i - Intensidade de raios X difratados por um plano (hkl) da fase i,

K_i - Constante, depende da geometria do difratômetro e da fase i,

X_i - Fração em peso da fase i,

n_i - Densidade da fase i,

m_i - Coeficiente de absorção mássica do composto puro i,

m_t - Coeficiente de absorção mássica da amostra, incluindo a fase i, o padrão interno e a referência, se existirem.

No desenvolvimento da técnica, Chung selecionou um composto puro, não presente na amostra a ser estudada, e o denominou agente fluxante. Conhecendo cada uma das fases cristalinas existentes, preparou também padrões contendo 50% de amostras puras de cada fase cristalina e 50% de coríndon. Com tais padrões, o autor propõe então a retirada dos fatores de absorção da equação de intensidade e a simplificação da equação acima para a equação (B), para uma mistura binária contendo coríndon e uma fase i:

sendo:

X_f - Fração em peso do agente fluxantes,

I_i - Pico de intensidade máxima da fase i na amostra desconhecida,

I_f - Pico de intensidade máxima da fase fluxante na amostra desconhecida ,

I_c - Pico de intensidade máxima da fase córindon amostra desconhecida,

A equação (B) determina uma relação simples entre a intensidade e a concentração de fase. Mais importante é que a equação não apresenta os efeitos de absorção, uma vez que todos estes fatores foram retirados. Esta equação pode ainda ser utilizada para análise quantitativa de qualquer composto multifásico.

A terceira técnica escolhida foi desenvolvida para análise de cristalinidade em vitro-cerâmicas, sendo também baseada no método de Rietveld com a utilização de um padrão interno. De acordo com os autores [9], a cristalinidade a é definida como a fração cristalina de uma amostra, pela proporção entre a soma das fases cristalinas (W_c) e o peso total da amostra (W). Com a utilização de um padrão interno, a equação evolui para:

sendo:

W_std^* - fração em peso do padrão interno, obtida pelo método de Rietveld;

W_std - fração em peso do padrão interno, obtida experimentalmente.

Desta maneira, a cristalinidade é determinada pela soma das frações em peso dos componentes cristalinos em relação à fração do padrão interno, (W_c/W_std*). Este valor pode ser obtido através da análise de Rietveld, e (W_std/W) pode ser obtido determinando-se os respectivos pesos da amostra e do padrão interno.

A quarta técnica selecionada, ou método do modelamento da estrutura amorfa, considera a estrutura da fase vítrea sendo próxima à de um sólido nanocristalino, em que não existe ordem de longo alcance. Desta maneira, foi utilizado [10] o modelamento da sílica vítrea proposto [11] para determinar a quantidade de fase vítrea em cerâmicas tradicionais. Nesse artigo é ressalvado que o modelo ainda não descreve exatamente a estrutura da sílica amorfa e necessita de melhorias. No entanto, o modelo é descrito como suficiente para determinação do teor de fase vítrea em cerâmicas [10].

Partindo da estrutura cristalina de um aluminossilicato de sódio, NaAlSiO₄, e alargando os picos de maneira a formar bandas de difração, foi possível a aproximação de um modelo "estrutural" para a sílica vítrea. Considerando a fase amorfa como uma fase nanocristalina, é possível a sua inclusão no programa de refinamento de Rietveld, com a conseqüente determinação da quantidade de fases cristalinas e amorfas em uma amostra.

No setor de refratários, a bauxita tem adquirido grande importância, uma vez que pode substituir parcial ou totalmente agregados de alumina eletrofundida em formados e monolíticos, devido a sua alta refratariedade e custo inferior. A partir da caracterização, espera-se gerar conhecimentos que possam repercutir no processamento desta matéria-prima, aumentando seu valor agregado e sua participação no mercado de refratários. Adicionalmente, o trabalho procura testar técnicas recentes de quantificação de fases no estudo de materiais complexos, como é o caso das matérias-primas naturais.

PROCEDIMENTO EXPERIMENTAL

Foram selecionadas amostras de bauxita de cinco diferentes fornecedores, denominadas: MSL (origem brasileira), Guyana RASC (origem guianesa), Alpha Star (origem americana), Guizhou e Shanxi, ambas de origem chinesa. Os padrões de referência utilizados nesta fase do trabalho - alumina, mulita, tialita, rutilo, carbeto de tungstênio e fluorita - foram cedidos pelo Centro de Caracterização e Desenvolvimento de Materiais - CCDM.

Para a seqüência de experimentos, foram retirados 100 g de cada uma das amostras a partir de quarteamento de cerca de um quilo de material proveniente dos cinco fornecedores. As amostras foram moídas em moinho de carbeto de tungstênio para passagem em malha #325 mesh. De 100 g de cada material foram separadas amostras de aproximadamente 3 g para realização dos ensaios de difração de raios X. Os difratogramas obtidos foram utilizados para determinação das fases cristalinas bem como para a detecção de fase vítrea pelo método do modelamento da fase amorfa proposto [10].

Para determinação da quantidade de fase vítrea através dos métodos padrão interno e grau de cristalinidade, 2 g de cada amostra foram misturados a úmido a 0,5 g de um padrão referência de fluorita, com auxílio de um bastão de vidro, durante dez minutos.

No caso do método matrix flushing, foram preparadas 5 amostras para serem utilizadas como padrão para determinação das intensidades de referência: 50%WC/50%Al₂O₃, 50%TiO₂/50%Al₂O₃, 50%Al₂TiO₅/50%Al₂O ₃, 50%CaF₂/50%Al₂O₃, 50%3Al₂O₃.2SiO₂/50%Al ₂O₃. A preparação destes padrões segue o procedimento descrito anteriormente para o método do padrão interno, sendo pesados 2 g de cada fase e misturados a úmido à mesma quantidade de alumina, com auxílio de bastão de vidro. Foram realizados vários ensaios de difração, cada qual em intervalos angulares que continham as máximas intensidades de cada fase cristalina. Os resultados de intensidade foram então utilizados, junto aos difratogramas contendo a amostra de interesse adicionada ao padrão de fluorita, para determinação da fase vítrea.

Os difratogramas foram coletados em modo passo a passo (0,05 grau/s), em intervalos 2q de 5º a 75º. Foi utilizado tubo de raios X de cobre, operando a 40 kV e 40 mA, com monocromador secundário mosaico de grafite. O feixe incidente é colimado com fendas de entrada e antiespalhamento de 3º de abertura. O feixe difratado é colimado com fendas de resolução e do monocromador de 0,6 mm. Ambos os feixes são equipados com fendas Soller.

Os dados foram analisados utilizando-se o programa DBWS-98XX, um upgrade dos programas DBWS de Rietveld. Os modelos de estrutura cristalina utilizados no refinamento para cada fase encontram-se nas referências [12-17]. Os dados para modelamento da estrutura cristalina das fases (parâmetros de rede, posições atômicas e fatores de ocupação) foram obtidos a partir de um CD-ROM específico para este fim: ICSD - Inorganic Crystal Structure Database.

Os parâmetros de refinamento selecionados incluem os fatores de escala, a função polinomial de quinta ordem que define a radiação de fundo, o deslocamento da amostra, os parâmetros de rede de cada fase, parâmetros que definem a largura e o perfil dos picos calculados, e funções de orientação preferencial e assimetria. A função perfil pseudo-Voigt foi a escolhida para o refinamento, devido à sua maior simplicidade. As posições e frações atômicas somente foram refinadas para as fases principais, devido à dificuldade de identificação das fases minoritárias em meio à radiação de fundo. Não foram considerados os coeficientes de absorção de cada fase.

O procedimento utilizado para determinação de fase vítrea via dissolução em ácido fluorídrico descrito a seguir foi utilizado por Knudsen e Thaulow [18]. Foram realizados dois testes distintos de dissolução. No teste inicial, cerca de 5 g de amostra foram misturados a 150 mL de uma solução de ácido fluorídrico de concentração 10%, por intervalos de tempo de 1, 2 e 4 horas à temperatura de 0 ºC. A baixa temperatura é fundamental para evitar a volatilização do ácido. Os resultados de perda de massa obtidos em função dos tempos de dissolução de uma, duas e quatro horas foram utilizados para traçar curvas de dissolução. A perda de massa extrapolada para o tempo zero hora corresponde ao teor de fase vítrea, evitando assim que o cálculo seja mascarado pela dissolução de fases cristalinas pelo ácido.

Para a dissolução em ácido fluorídrico foram misturados 0,4 g de amostra a 40 mL de solução de ácido fluorídrico 10%. Foram considerados os tempos de ataque de 1, 2 e 4 horas, com o banho à temperatura de 0 ºC, utilizando-se duas amostras de cada bauxita por tempo de ataque. Após a dissolução, as amostras foram filtradas, lavadas em 500 mL de água e secas em ar. Para determinação da perda de massa, os filtros contendo cada amostra foram queimados em cadinho de massa constante, para retirada do filtro de papel. O cadinho foi pesado e determinada então a variação de massa antes e após dissolução. A curva de dissolução foi traçada e o valor extrapolado para zero (na tentativa de desconsiderar a dissolução de fases cristalinas pelo ácido), para determinação do teor de fase vítrea.

RESULTADOS E DISCUSSÃO

As análises químicas para as bauxitas de diferentes origens são apresentadas na Tabela I.

O modelamento das fases pelo programa de Rietveld, para análise semiquantitativa de fases cristalinas, é relativamente fácil e rápido. A aquisição de dados cristalográficos, considerando as fases conhecidas e estequiométricas, não requer também muito tempo. O estudo do funcionamento do programa demanda cerca de dois meses de trabalho contínuo e monitorado por especialistas em cristalografia. A interface do software com o usuário não é tampouco amigável, e um bom conhecimento de estruturas cristalinas e teoria cristalográfica, bem como do próprio método de Rietveld, é imprescindível para a obtenção de resultados verossímeis e satisfatórios. Foram testados, para o caso das amostras Alpha Star e Guizhou, cerca de doze modelos de estrutura para a fase mulita encontrados em literatura, sem que nenhum deles se ajustasse perfeitamente à fase indicada. Uma das maiores dificuldades do método de Rietveld é o tratamento das fases minoritárias, cuja relação sinal/ruído é baixa e os picos confundem-se com a radiação de fundo no difratograma.

Para estas fases, e principalmente no caso da mulita, que é uma fase não estequiométrica, não é possível o refinamento das posições atômicas e fatores de ocupação, que na verdade são os determinantes da concentração dos átomos na estrutura.

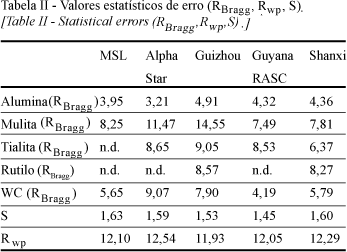
A Tabela II identifica os indicadores residuais do modelamento de Rietveld. Os valores de R_Bragg são obtidos para cada fase cristalina, sendo que os valores residuais R_wp e S são obtidos por cada amostra analisada via Rietveld.

Os indicadores residuais apontam a qualidade do refinamento, estimando a precisão e a aceitação dos resultados finais. O método de Rietveld utiliza vários indicadores, no entanto, apenas alguns são mais indicados [19]: (R_Bragg, R_wp e S) e mesmo assim só devem ser considerados dentro do contexto de coleta de dados, instrumento utilizado e tipo de amostra analisada.

O residual R_wp é um bom indicador do progresso de um refinamento em particular. O valor de R_Bragg é utilizado na indicação dos modelos para cada fase, sendo influenciado muito mais por parâmetros estruturais que por parâmetros instrumentais. Valores típicos de R_wp para refinamentos utilizando difração de raios X variam de 10% a 20%. Valores permissíveis para R_Bragg em análises de Rietveld via difração de raios X chegam aos 9%, mas valores ótimos próximos a 3% são facilmente alcançados para fases majoritárias de perfil simples, como no caso da alumina.

Valores de 'goodness of fit' (S) podem ser bons indicativos de comparação entre resultados, sendo que o valor mínimo esperado (ou seja, quando o refinamento está completo e o único erro presente é o ruído estatístico) é igual a 1, sendo que valores acima de 1,5 indicam provavelmente modelos de refinamento inadequados. No entanto, para amostras mais complexas, com presença de fases não totalmente cristalinas e fases minoritárias, valores mais altos de S podem ser aceitos.

Os valores de R_Bragg encontram-se relativamente altos para a fase mulita das amostras Alpha Star e Guizhou, já que a literatura considera aceitáveis valores em torno de nove. No caso da mulita para as amostras Alpha Star e Guizhou, estes altos valores de R_bragg reforçam a desconfiança sobre o modelo de estrutura escolhido para o refinamento. Para as fases restantes, os valores deste indicativo residual encontram-se dentro dos valores aceitáveis.

Outro parâmetro observado no indicativo de um bom refinamento é o parâmetro S, que correlaciona tanto parâmetros estruturais quanto de perfil e é determinado para cada amostra analisada. Em um refinamento perfeito, o valor de S é igual a 1, sendo que valores acima de 1,5 são indicativos de problemas no refinamento ou presença de muitas fases em concentrações baixas (que é o caso deste trabalho). Valores de S acima de 1,7 indicam estratégia de refinamento ou modelamento inadequado. Portanto os valores obtidos nos refinamentos realizados foram compatíveis, apresentando valores pertinentes. O indicador residual perfil-ponderado Rwp (determinado para cada amostra) também se encontra em níveis aceitáveis para o refinamento (10% a 20% para a difração de raios X).

Na determinação da quantidade de fases cristalinas, foram analisados quatro padrões de difração para cada amostra, a fim de fornecer um desvio padrão relativo para a técnica (Tabela III).

Os valores obtidos por Rietveld correspondem ao esperado [20], indicados na Tabela IV. As diferenças entre concentrações estão dentro de limites aceitáveis, considerando-se que bauxitas são matérias-primas bastante heterogêneas. Infelizmente não se tem conhecimento de dados para concentração de fases para as amostras Alpha Star e Guizhou.

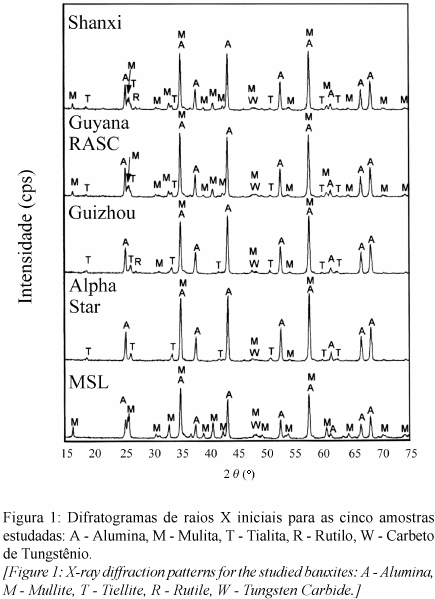
De acordo com os resultados de difração de raios X indicados na Fig. 1, pode-se observar que as amostras Alpha Star e Guizhou apresentam difratogramas semelhantes, com ausência da fase mulita e alta concentração de alumina. No caso da bauxita Guizhou, rutilo é ainda encontrado em pequena quantidade. A amostra brasileira MSL, por sua vez, não apresenta picos para a fase tialita, sendo composta majoritariamente por mulita e alumina. As bauxitas restantes, Guyana RASC e Shanxi, apresentam difratogramas semelhantes, com a presença de alumina como componente principal, seguida das fases secundárias mulita e tialita e, no caso da amostra Shanxi, apresentando ainda traços de rutilo.

A diferença entre os valores obtidos para as Tabelas III e IV pode ainda estar distribuída em solução sólida na tialita e alumina, ou ainda fazendo parte da fase vítrea presente nas amostras. No caso da amostra MSL, além da presença de Fe₂O₃ e TiO₂ em solução sólida, sugere-se ainda a presença de tialita como contribuição ao TiO₂, em concentração abaixo do limite de detecção da técnica de difração de raios X.

Método do Padrão Interno

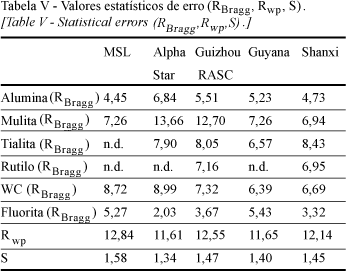
Os indicativos residuais para cada refinamento, em cada amostra, são ilustrados na Tabela V. Os valores obtidos para cada fase e a correção para a determinação do teor de fase vítrea estão indicados na Tabela VI.

A determinação de fase vítrea via adição de padrão interno e análise de Rietveld apresenta algumas desvantagens que acabam por comprometer a técnica. O modelo de refinamento deve ser adequado à estrutura cristalina de fases, e no caso da presença de fases não estequiométricas, como a mulita, a determinação de fases amorfas fica seriamente comprometida, levando a resultados errôneos. A escolha do padrão interno também deve ser cautelosa, visto que o mesmo não deve apresentar orientação preferencial e fenômenos de extinção primárias. No caso da fluorita, a tendência à orientação é alta (e a presença de poucos picos de difração, que é o caso, aumenta ainda mais esta tendência), o que também pode afetar os resultados para fase vítrea.

No caso das amostras Alpha Star e Guizhou, ambas apresentam falhas no modelamento da estrutura da mulita, que é distinta da fase presente nas demais amostras. A falha nestes casos impossibilita determinação precisa de fases, diminuindo a confiabilidade do método de Rietveld na análise de fases amorfas. Segundo estudos [21], o erro estimado na determinação chega a 28%, que é bastante considerável. Nas demais amostras, a determinação de fase vítrea apresentou valores adequados e esperados.

De acordo com o teor de álcalis presente nas amostras esperava-se valores bastante distintos dos obtidos, e uma ordem seqüencial como se segue: MSL < Guyana RASC < Guizhou » Alpha Star < Shanxi. Sendo assim, o método não se apresentou satisfatório para a determinação da fase vítrea para amostras de bauxita refratárias com teor da fase esperada de no máximo 15%.

Método "matrix flushing"

No método desenvolvido por Chung [8] foram utilizadas as intensidades de difração calculadas através do método de Rietveld na determinação da concentração de fases cristalinas e amorfas. Para tanto foram utilizados os programas DBWS98xx e DMPLOT. Os valores de intensidade obtidos a partir dos dois testes foram substituídos na equação (B), para determinação da concentração de fases. Os valores de fase vítrea são apresentados na Tabela VII.

Observando-se os resultados obtidos, conclui-se que a determinação de fase vítrea não é válida para este método, apresentando valores absurdamente altos para matérias-primas utilizadas em altas temperaturas.

Provavelmente uma das causas de resultados tão distorcidos seja o método de coleta dos valores de intensidade, através dos difratogramas em Rietveld. Fases minoritárias, como WC e rutilo, tem seus picos com baixa relação sinal/ruído, o que dificulta sobremaneira a determinação das respectivas intensidades. As fases mulita, alumina e tialita apresentam vários picos sobrepostos em reflexões bastante próximas, e deve-se ressaltar que Chung considera para o cálculo das concentrações somente os dois ou três picos mais intensos, que podem sofrer vários tipos de efeitos (orientação preferencial, absorção, entre outros) que mascaram o real valor da intensidade.

Método do Grau de Cristalinidade

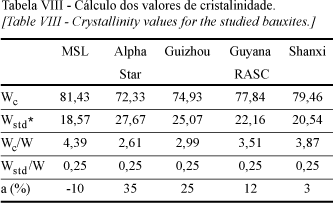
Para a obtenção dos resultados do método do grau de cristalinidade, foram utilizados os mesmos difratogramas referentes ao método do padrão interno. Sendo assim, os valores estatísticos de erro para o método de Rietveld nesta técnica são ilustrados na Tabela V. A Tabela VIII indica o grau de cristalinidade para cada amostra, de acordo com o procedimento de cálculo para este método.

Como pode ser observado, os valores não condizem com o resultado esperado na literatura (Tabela IV), e novamente valores absurdos são encontrados para a quantidade de fase amorfa presente nas bauxitas estudadas. Tais resultados já eram esperados, quando consideramos que este método é uma adaptação do método do padrão interno. Na realidade, os valores obtidos para ambos os métodos são relativamente próximos.

Método do modelamento da estrutura amorfa

Os resultados obtidos para o modelamento via estrutura da fase amorfa, bem como os indicativos residuais de cada fase são ilustrados nas Tabelas IX e ^X.

Os indicativos residuais ilustram um refinamento que necessita de melhorias, já que tanto os valores para a estrutura, quanto para o refinamento como um todo, apresentam-se bastante elevados. Isto ocorre principalmente pela impossibilidade do refinamento da radiação de fundo, que acaba por influir em todas as fases. Como dito anteriormente, a radiação de fundo (background) foi considerado constante, para que qualquer variação decorrente da radiação seja relacionada à fase vítrea.

Embora o método tenha produzido resultados mais próximos à realidade das amostras testadas, existe ainda um problema adicional: a radiação de fundo. Como a quantidade de fase vítrea é bastante reduzida, quando comparada a cerâmicas tradicionais, a intensidade da radiação de fundo influencia drasticamente os valores de teor de fase vítrea obtidos.

A utilização de um background linear não é suficiente para tornar o método preciso o bastante para sua utilização em refratários. Os autores indicam que valores abaixo de 5% de fase vítrea não conseguem ser mensurados com precisão suficiente. Acreditamos que neste caso se enquadrem as amostras de bauxita sul-americanas, que teriam então seus valores de fase vítrea superestimados em relação à realidade.

Método do ácido fluorídrico

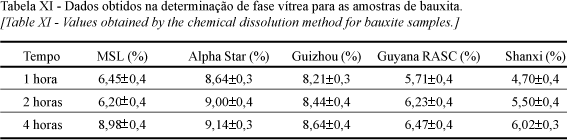
Durante o teste de dissolução, foi utilizada uma única solução de um mesmo ácido, para eliminar fatores de incerteza quanto à concentração da solução e do ácido puro. O filtro de papel foi queimado em cadinho de porcelana tarado, pois o mesmo tem o peso variado devido à absorção de umidade. A única incerteza deste ensaio é quanto à incineração do papel, pois durante sua ignição podem ser lançados para a atmosfera do forno partículas de amostra, falseando os resultados. A Tabela XI ilustra os valores obtidos neste ensaio, dados estes que são ilustrados na Fig. 2, que também apresenta as equações de tendência. A Tabela XII resume os valores de fase vítrea obtidos.

A partir dos resultados obtidos pode-se concluir que este é o método que se apresenta mais próximo dos dados reportados [20] (Tabela IV) na determinação de fase amorfa. Embora seus valores possam estar de alguma forma superestimados devido à dissolução de fases cristalinas, principalmente a mulita por apresentar SiO₂ em sua estrutura, acredita-se que seus valores estejam coerentes com o esperado.

Pode-se observar na Fig. 2 que as amostras, à exceção da brasileira MSL, apresentam curvas de dissolução quase paralelas em relação ao eixo das abscissas, o que indica uma perda de massa relativamente constante. No caso da bauxita MSL, devido à alta concentração de mulita, pode-se acreditar que a variação da massa ao longo do tempo de ataque deva-se à dissolução desta fase cristalina pelo ácido fluorídrico.

Em relação aos valores obtidos, a única surpresa seria o teor de fase vítrea para a amostra Shanxi, que, esperava-se, fosse elevado devido à diferença nos valores de sílica observados anteriormente. Por outro lado, considerando-se o teor de álcalis, esta amostra apresenta K₂O em quantidade significativamente menor que outras amostras chinesas, o que pode significar esta diferença na quantidade de fase líquida presente. Em comparação com as amostras sul-americanas, sua maior concentração de mulita indica uma maior corrosão desta fase nestas amostras, superestimando seu valor frente à bauxita Shanxi. Ou ainda as maiores temperaturas de calcinação para as amostras MSL e RASC propiciaram o aumento na concentração de fase amorfa.

Embora apresente coerência, este método é, no entanto, de difícil aplicação industrial. Inúmeras são as variáveis que afetam a medida de perda de massa, o que torna o ensaio não reprodutível. Durante a etapa experimental, algumas limitações foram reportadas: 1) A dificuldade para obter-se uma solução com concentração precisa em 10%, devido à impossibilidade de utilização de instrumentos de medida de vidro, como provetas e buretas; 2) A volatilidade do ácido, que exige que a solução seja descartada ao final do dia, limitando o tempo de ensaio; 3) A grande quantidade de amostras para obter-se um valor aceitável, sendo que para uma amostra são necessários nove ensaios de dissolução; 4) A necessidade de queima em cadinho tarado, o que acarreta em um aumento considerável no tempo de ensaio, sendo que para uma amostra são necessários cerca de dez dias, com a utilização de um único cadinho. Portanto, embora se tenha alcançado resultados satisfatórios com a última metodologia desenvolvida, a sua inviabilidade prática ainda propicia margem para inúmeros estudos e pesquisas nesta área.

CONCLUSÕES

A técnica de Rietveld para determinação de fases mostrou-se uma boa ferramenta para análise semiquantitativa de fases cristalinas. Sua metodologia fornece resultados mais precisos quando comparados ao método de comparação direta de intensidades. A aquisição de dados para o programa é relativamente simples, no entanto requer longo treinamento no software de análise. A principal deficiência da técnica diz respeito aos modelos aplicados. Fases não-estequiométricas, fato bastante comum em cerâmicas, não geram modelos precisos, que necessitam de refinamento para obtenção de um resultado satisfatório. No entanto este refinamento só é possível se a fase estudada apresenta-se em concentração relativamente alta na amostra, limitando a utilização da técnica a amostras puras, com fases sem extensas soluções sólidas.

Outro fator que limita a técnica de Rietveld é o coeficiente de absorção das fases de uma amostra. Embora o programa possua a alternativa de utilizar-se o coeficiente de absorção, sua determinação experimental é bastante demorada e inexata. No caso do presente estudo, em que as fases possuem elementos pesados como titânio e tungstênio, a correção de microabsorção é indispensável, e bastante trabalhosa. Outro fator limitante é a preparação da amostra. Embora o programa utilize funções que corrijam a orientação preferencial, uma preparação cuidadosa é necessária principalmente quando existam fases que apresentam orientação preferencial forte, que é o caso da tialita no presente estudo.

Embora o teor de fase vítrea seja uma das principais características que determinam o comportamento dos refratários a altas temperaturas, sua determinação ainda não possui método prático e confiável. Na tentativa de adaptar técnicas de determinação de fase vítrea em cerâmicas tradicionais para refratários, foram utilizados outros métodos baseados em Rietveld, para caracterização das amostras de bauxita. Conforme ilustram os resultados obtidos, nenhum dos métodos forneceu resultados satisfatórios. O principal fator limitante é sem dúvida o limite de detecção das técnicas, que são utilizadas para concentrações de fase vítrea acima de 20%. Outro problema característico é a soma de erros. Aos erros inerentes a Rietveld, somam-se os erros de preparação do padrão, ou ainda da preparação das amostras, ou ainda de outros modelos estruturais ainda em estudo. Conclui-se que não foi encontrado método analítico eficiente para determinação de fase vítrea em refratários.

A única técnica que produziu resultados coerentes, a dissolução em ácido fluorídrico, apresenta problemas experimentais que limitam sua aplicação, tais como o tempo e a complexidade da preparação, e as inúmeras variáveis de controle envolvidas, tais como concentração do ácido, controle da temperatura do banho, volatilidade do ácido fluorídrico e sua periculosidade, entre outros.

Os valores de fase vítrea obtidos pela técnica de dissolução encontram-se em concordância com o esperado em literatura. Amostras chinesas apresentam maior teor de álcalis, o que provavelmente indica superior fluência a altas temperaturas. Amostras sul-americanas apresentam menor teor de fase vítrea, devido ao menor teor de álcalis e conseqüentemente menor redissolução da mulita em líquido. Baseando-se nestes resultados, sua resistência à fluência a alta temperatura tende a ser superior. A amostra Shanxi apresenta-se também diferenciada quanto ao teor de fase vítrea, apresentando menor teor do que o esperado. A literatura afirma que o teor de K₂O na composição de bauxitas é o maior responsável pela formação de fase líquida e conseqüente dissolução da mulita. Sendo a concentração deste óxido menor na amostra Shanxi em relação às outras amostras chinesas, acredita-se na menor viscosidade da fase amorfa durante a calcinação, com menor dissolução de mulita e menor quantidade de fase vítrea após o resfriamento da matéria-prima.

AGRADECIMENTOS

Os autores agradecem a CAPES, FAPESP, e CNPq pelo auxílio na realização deste trabalho.

REFERÊNCIAS

(Rec. 03/07/01, Ac. 04/01/02)

• [1] H. M. Rietveld, "Line Profiles for Neutron Powder-Diffraction Peaks for Structure Refinement", Acta Crystallographica 22 (1967) 151-52.
• [2] H. M. Rietveld, "A Profile Refinement Method for Nuclear and Magnetic Structures", J. Appl. Crystallography 2 (1969) 65-71.
• [3] R. A. Young, A. Sakthivel, T. S. Moss, C. O. Paiva-Santos, A. C. Larson, "User's Guide to Program DBWS-98XX for Rietveld Analysis of X-Ray and Neutron Powder Diffraction Patterns", Georgia Institute of Technology, USA, (1995) 22 p.
• [4] R. A. Young, "Profile Shape Functions in Rietveld Refinements", J. Appl. Crystallography 15 (1982) 430-38.
• [5] R. A. Young, P. E. Mackie, R. B. Von Dreele, "Application of the Pattern Fitting Structure Refinement Method to X-Ray Powder Diffractometer Patterns", J. Appl. Crystallography 1 (1977) 262-69.
• [6] R. J. Hill, C. J. Howard, "Quantitative Phase Analysis from Neutron Powder Diffraction Data using the Rietveld Method", J. Appl. Crystallography 20 (1987) 467-74.
• [7] D. L. Bish, S. A. Howard, "Quantitative Phase Analysis using the Rietveld Method", J. Appl. Crystallography 21 (1988) 86-91.
• [8] F. H. Chung, "Quantitative Interpretation of X-Ray Diffraction Patterns of Mixtures. I. Matrix-Flushing Method for Quantitative Multicomponent Analysis", J. Appl. Crystallography 7 (1974) 519-525.
• [9] Y. Katsumasa, Y. Terashi, A. Nakayama, "Crystallinity Analysis of Glass-Ceramics by the Rietveld Method", J. Am. Ceram. Soc. 81, 11 (1998) 2978-82.
• [10] L. Lutterotti, R. Ceccato, R. Dal Maschio, E. Pagani, "Quantitative Analysis of Silicate Glass in Ceramic Materials by the Rietveld Method", Mater. Sci. Forum 278-281 (1998) 87-92.
• [11] A. Le Bail, "Modelling the Silica Glass Structure by the Rietveld Method", J. Non-Crystalline Sol. 183 (1995) 39-42.
• [12] L. Lutterotti, P. Scardi, "Simultaneous Structure and Size-Strain Refinement by the Rietveld Method", J. Appl. Crystallography 23 (1990) 246-52.
• [13] T. Ban, K. Okada, "Structure Refinement of Mullite by the Rietveld Method and a new Method for Estimation of Chemical Composition", J. Am. Ceram. Soc. 75 (1992) 227-30.
• [14] C. J. Howard, T. M. Sabine, F. Dickson, "Structural and Thermal Parameters for Rutile and Anatase", Acta Crystallographica 47 (1991) 462-68.
• [15] A. E. Austin, C. M. Schwartz, "The Crystal Structure of Aluminium Titanate", Acta Crystallographica 6 (1953) 812-13.
• [16] J. Leciejewicz, "A Note on the Structure of Tungsten Carbide", Acta Crystallographica 14 (1963) 200.
• [17] D. N. Batchelder, R. O. Simmons, "Lattice Constants and Thermal Expansivities of Silicon and Calcium Fluoride between 6 and 322 K", J. Chem. Phys. 41 (1964) 2324-29.
• [18] T. Knudsen, N. Thaulow, "Investigation of the Mineralogical Properties of Refractory-Grade Calcined Bauxite", Am. Ceram. Soc. Bull. 57, 7 (1978) 685-688.
• [19] C. Giacovazzo, H. L. Monaco, D. Viterbo, F. Scordari, G. Gilli, G. Zanotti, M. Catti, "Fundamentals of Crystallography", Oxford Science Publications, Oxford (1992) pp. 109-140.
• [20] H. Leupold, G. Vermeer, "Jari Brazilian Calcined Bauxite - Production and Application in High Alumina Refractories" MSL Minerals S.A., Proc. UNITECR'95, Japão (1995) 571-578.
• [21] I. C. Madsen, R. J. Finney, R. C. A. Flann, M. T. Frost, B. W. Wilson, "Quantitative Analysis of High-Alumina Refractories using X-Ray Powder Diffraction Data and the Rietveld Method", J. Am. Ceram. Soc. 74, 3 (1991) 619-24.

Datas de Publicação

• Publicação nesta coleção
  05 Ago 2002
• Data do Fascículo
  Jun 2002

Histórico

• Aceito
  04 Jan 2002
• Recebido
  03 Jul 2001