Fratura de refratários

Fracture of refractories

Fratura de refratários

Fracture of refractories

F. N. Cunha-Duncan; R. C. Bradt

Department of Metallurgical and Materials Engineering, The University of Alabama, Tuscaloosa, AL 35487-0202 USA

RESUMO

A fratura de refratários é considerada sob o ponto de vista tradicional de resistência mecânica além da perspectiva da mecânica da fratura. Resistência mecânica e tenacidade à fratura são relacionadas por meio do tamanho dos agregados em refratários, o que ilustra a importância dos aspectos microestruturais dos agregados refratários na resistência. O método de análise da integral-J e a técnica experimental da separação de cunha (wedge-spliting) são revisados devido ao fato destes serem convenientes para explicar o caráter não-linear da curva força-deslocamento para refratários. Este último aspecto é associado ao conceito de curva-R crescente, que é discutido sob o ponto de vista fenomenológico. Curvas-R crescentes estão diretamente relacionadas ao agregado refratário através dos mecanismos de tenacidade que são ativos na zona de processo de trinca, tanto na frente como atrás da trinca em propagação. Os processos de tenacificação de refratários são responsáveis pelas regiões não-lineares das curvas ou diagramas de tensão-deformação e força-deslocamento e das curvas-R crescentes. O dano por choque térmico, originalmente apresentado sob o ponto de vista convencional de resistência mecânica é abrangido no conceito de curva-R crescente. Concluiu-se que a natureza dos agregados de refratários, bem como seu tamanho e distribuição, tem importância decisiva no fenômeno de fratura em refratários. Isso é devido ao papel crucial que agregados assumem na região de propagação da trinca. A distribuição do agregado deve ser o foco do arranjo microestrutural para melhores características de fratura, quando todos os outros fatores são de igual importância ao refratário como um todo.

Palavras-chave: fratura, refratários.

ABSTRACT

Fracture of refractories is considered from the traditional strength point of view and from the perspective of fracture mechanics. Strength and fracture toughness are related through the aggregate sizing of refractories, which illustrates the importance of the microstructural aspects of the refractory aggregate to the strength. The J-integral analysis methodology and the wedge-splitting experimental technique are both reviewed, as they are useful to address the nonlinear load-displacement character of refractories. The latter is associated with the concept of a rising R-curve, which is discussed from the phenomenological point of view. The rising R-curve is directly related to the refractory aggregates through toughening mechanisms that are active in the crack process zone, both in the front of and behind an extending crack. The refractory toughening processes are responsible for the nonlinear portions of the stress-strain and load-displacement curves, or diagrams and the rising R-curves. Thermal shock damage, which is originally addressed from the conventional strength viewpoint is then considered within the rising R-curve concept. It is concluded that the refractory aggregates, their size and distribution in a refractory body, assume an absolutely critical role in refractory fracture phenomena. This is because of the crucial role that aggregates assume in he following wake region of a crack. The aggregate distribution must be the focus of microstructural design for improved fracture characteristics when all other factors are equal in a refractory body.

Keywords:fracture, refractories.

INTRODUÇÃO

A fratura é um problema crítico para refratários em uso. Este não é um campo sem progresso, como pode ser observado em estudos prévios [1, 2]. Contudo, este tópico é extremamente complicado para refratários industriais devido à existência de diversos compósitos com várias fases que são utilizados sob condições dinâmicas. Além do mais, os grandes volumes necessários para os revestimentos de vasos de processos metalúrgicos têm limitado muitos refratários comerciais ao uso de sistemas minerais que contêm impurezas, muitas das quais são silicatos. Durante o processamento de refratários, os silicatos desenvolvem-se ligando fases em contornos de grãos que frequentemente dominam o seu processo de fratura a temperaturas elevadas. Estas características especiais elevam os refratários a uma única posição técnica na hierarquia dos materiais, posição a qual é uma combinação de cerâmica, geologia, mineralogia e tecnologia da engenharia de compósitos. Infelizmente, esta mistura especial de ciência e tecnologia não é uma área particularmente ativa em pesquisa. Refratários se posicionam dentro de um leque da tecnologia industrial onde lucro é o objetivo em contraste ao entendimento dos fenômenos técnico-científicos.

A natureza compósita dos refratários separa o processo de fratura do refratário dos materiais monofásicos, partículas pequenas, das cerâmicas estruturais frágeis de alta resistência e aproxima a fratura do refratário à fratura de materiais compósitos processados. Por exemplo, semelhante aos compósitos de alta tecnologia, os refratários geralmente exibem curvas-R crescentes durante extensão ou propagação de trinca. Refratários comerciais são compósitos dinâmicos de alta tecnologia [3]. Entretanto, além do fenômeno de fratura frágil, pesquisadores devem entender o desenvolvimento da zona de propagação da trinca e da importância das curvas-R durante o processo de fratura. Infelizmente, o fenômeno da curva-R não foi bastante nem sistematicamente estudado em nenhum sistema refratário; portanto, muitas implicações desse fenômeno podem ser apenas inferidas sobre outros trabalhos, como por exemplo, aqueles de sistemas de simples estrutura cerâmica.

A fratura é um dos dois modos de ruptura mais comuns em revestimentos refratários de vasos modernos de processamento industrial. O outro é o ataque químico ou corrosão por material contido nos vasos de processamento, geralmente metais no estado fundido ou vidros a temperaturas muito elevadas. Com metais no estado líquido, o processo de corrosão é da camada de escória que protege o metal líquido da atmosfera. Geralmente estas reações entre escória/refratários são tão intensas e tão problemáticas que tipos especiais de refratários, diferentes daqueles do resto do revestimento do vaso de processamento, devem ser empregados nas linhas de escória de vasos metalúrgicos.

A fratura de refratários pode ser de diversos tipos, incluindo a simples sobrecarga mecânica que pode ocorrer como resultado do impacto durante o carregamento de rejeitos no vaso de processamento. A fratura devido à tensão térmica durante resfriamento ou aquecimento, particularmente o aquecimento inicial do vaso ou durante ciclos térmicos rápidos entre aquecimentos, é outro tipo de fratura. No caso de concretos refratários ou moldados, a fratura explosiva resultante da retenção de umidade/líquido é também uma grande preocupação [4]. Estas fraturas podem ser catastróficas e resultam na completa perda do revestimento refratário. Algumas vezes, o choque térmico apenas causa a formação de trincas e esfoliação (spalling) e uma significante redução do tempo de vida, ou campanha do revestimento. Contudo, a fratura não precisa necessariamente ser catastrófica. Ela pode apenas resultar no desenvolvimento de um modelo de trinca no revestimento do vaso de processo. Aquelas superfícies das trincas podem resistir e futuramente serem fechadas por tensões compressivas no revestimento do vaso causadas pela expansão térmica quando o vaso é aquecido a temperaturas elevadas durante operação.

RESISTÊNCIA DO REFRATÁRIO

Até hoje, depois de quase meio século de mecânica da fratura, a fratura de refratários permanece associada com o conceito de resistência, uma vez definido para estudantes universitários durante aulas curriculares de resistência dos materiais. A definição de resistência dos refratários é geralmente encontrada em termos de resistência à flexão em três pontos ou simplesmente resistência à flexão, frequentemente chamada de módulo de ruptura (MOR). No caso de refratários, existe um teste padrão simples para medida da resistência mecânica. Este é baseado na seguinte expressão:

onde s_f é a resistência à flexão em três pontos, L é a distância entre os apoios do teste (test span), b é a largura do corpo de prova e h é a altura do corpo de prova. A carga de fratura é P. Esta expressão indica a tensão trativa máxima que o corpo-de-prova prismático é submetido na sua parte inferior. Apesar de talvez 80-90% das resistências de refratários apresentadas na literatura serem obtidas com base em testes usando a equação (A), este método deixa muito a desejar, principalmente pela preparação do corpo de prova, distribuição de falhas no refratário e taxa de aplicação de carga durante o teste [5]. Alguns pesquisadores preferem utilizar outro teste de resistência, o teste de compressão diametral, também conhecido como teste Brasil. Neste teste um corpo de prova cilíndrico é carregado em compressão diametral para produzir uma fratura trativa interna alinhada com o diâmetro da amostra. Contudo, o teste Brasil não será discutido aqui.

Em princípio, a equação (A) é apenas aplicada quando a curva de força-deslocamento é completamente linear elástica até a ruptura, semelhante ao diagrama do meio apresentado na Fig. 1, que ilustra uma medida da integral-J de um corpo de prova não-entalhado. Infelizmente, raramente as curvas de força-deslocamento são determinadas durante as medidas normais de resistência dos refratários. Frequentemente, o deslocamento não é monitorado. É plausível supor que muitos dos resultados de resistência à flexão de refratários apresentados na literatura são suspeitos. Contudo, como consequência dos muitos anos de utilização dos resultados de resistência baseados neste tipo de flexão ou medidas de resistência flexural, engenheiros envolvidos na aplicação de refratários têm desenvolvido uma metologia para desenvolvimento de revestimento refratário baseada nos resultados provenientes desses tipos de testes. Este tipo de teste de resistência permanecerá, sem dúvida, como uma parte da fratura de refratários por um período de tempo indeterminado.

A equação (A) pode ser convertida à terminologia da mecânica da fratura utilizando a conhecida equação de Griffith, de maneira análoga à equação anteriormente discutida, pode ser apresentada como:

onde K_IC é a tenacidade à fratura, Y é um fator geométrico igual a p^-1/2 na clássica derivação de Griffith, e C é o tamanho crítico de trinca [6]. Quando os refratários rompem de maneira elástica frágil, onde a curva força-deslocamento é claramente linear elástica até a ruptura, ambas equações (A) e (B) representam satisfatoriamente a resistência do corpo. Contudo, quando refratários não rompem de maneira linear elástica, assim como quando uma extensa região não-linear se desenvolve antes da fratura, o uso dessas equações não é a melhor prática para determinação da resistência. Estas são, contudo, utilizadas com regularidade no campo de refratários, geralmente, sem considerações às suas limitações.

Antes de proceder com o verdadeiro processo de fratura em refratários, é importante apresentar de modo geral valores de resistência e tenacidade de refratários industriais. Isto certamente ajuda a esclarecer o leitor e ao mesmo tempo fornece um entendimento da importância das resistências dos refratários em serviço. Para a grande maioria dos casos, revestimentos ou sistemas refratários não suportam severas condições de carregamento. Sua função é principalmente revestir. Durante sua aplicação, refratários não possuem um papel estrutural importante. Por estas razões, refratários não precisam ser muito resistentes, apenas resistentes o suficiente para manter sua integridade. De fato, sob a perspectiva do dano por choque térmico, tal qual discutido a seguir, alta resistência pode ser um fator detrimental à resistência ao dano por choque térmico para muitas aplicações refratárias.

As resistências de vários tipos de refratários não serão apresentadas, contudo uma faixa genérica de valores será discutida, com o objetivo de estabelecer uma comparação relativa entre os materiais. Tipicamente, refratários apresentam resistência à flexão ou resistência flexural de acordo com a equação (A) na faixa de 10-40 MPa (~1500 a 6000 psi) à temperatura ambiente. É importante observar que refratários não são muito resistentes de acordo com padrões ou comparações. Frequentemente, o revestimento refratário dos vasos de processo são combinados com a estrutura de aço dos mesmos, ou suportados por suas superestruturas ancoradas. Na maioria das aplicações, os refratários devem pelo menos suportar seu próprio peso, o que na realidade não é muito significante. Em outras aplicações, os refratários devem ser projetados de modo a suportar tensões compressivas, onde os mesmos geralmente apresentam resistência um tanto superior.

Refratários são utilizados a temperaturas elevadas; portanto, há um interesse lógico na mudança de sua resistência com o aumento da temperatura. Quando a resistência do refratário é medida pelo método de flexão em três pontos e em função da temperatura, a resistência à flexão invariavelmente exibe um máximo valor que está associado ao enfraquecimento das ligações dos silicatos. Normalmente, o valor máximo de resistência não é muito elevado. Frequentemente, é verificado entre 600 ºC e 1400 ºC, dependendo do tipo de refratário, porcentagem de silicatos e da análise química de tais silicatos. A temperaturas mais elevadas, acima dessa resistência máxima, a resistência do refratário rapidamente diminui, exibindo distintamente curvas de força-deslocamento não-lineares. Portanto, refratários já não muito resistentes, tornam-se ainda menos resistentes a temperatures mais elevadas, mas com menor fragilidade. Além disso, a elevadas temperaturas, a dependência da taxa de carregamento à resistência se torna complexa. A combinação da taxa de carregamento e dos efeitos de temperatura sobre a resistência foram previamente discutidos [2, 5]. Esta não é uma interdependência simples, e varia consideravelmente para diferentes sistemas refratários.

Para entender os fundamentos que governam a resistência dos sistemas refratários, é importante perceber que apesar de muitos refratários serem considerados frágeis a baixas temperaturas (600 ºC), uma vez que a temperatura de resistência máxima é excedida, os refratários não permanecem tão frágeis. Os silicatos amolecem e desenvolvem um significante grau de "plasticidade". Fratura frágil de refratários não é um grande problema a temperaturas elevadas onde a distinta deformação plástica/viscosa aparece como um tipo de resposta sob a maioria das condições de carregamento. Além do mais, apesar de existirem na literatura registros de resistência de refratários a temperatures elevadas, estes valores de resistência reportados devem ser aceitos com algumas reservas e apenas aplicados para prever/desenhar situações com considerável cautela. Provavelmente, a maioria dessas resistências não foi medida adequadamente.

RELAÇÃO TENACIDADE À FRATURA / RESISTÊNCIA

Os estudos de Nakayama na década de 60 estão centralizados no teste de trabalho de fratura e sua aplicação em refratários. Conceitos de energia associados ao crescimento de uma única trinca até a fratura do refratário são introduzidos [7]. Nas décadas de 70 e 80, seguindo estudos iniciais desenvolvidos por Nakayama, pesquisadores concluíram que para entender a fratura de refratários era necessário realizar medições em trincas individuais ou únicas, ao invés do, ou em adição ao, conhecido teste de resistência à flexão. Isto foi feito aplicando-se a mecânica da fratura para uma única trinca. Sakai e Bradt revisaram e discutiram os resultados obtidos a partir de inúmeros corpos de prova sob a ótica da mecânica da fratura e relacionaram-nos com medidas de trabalho de fratura [8]. Existem várias maneiras de medir-sea tenacidade à fratura de refratários. Os valores de K_IC foram determinados para corpos de prova com uma única trinca na extremidade ou corpos de prova de flexão entalhados, onde o corpo de prova tradicional para o teste de flexão em três pontos foi simplesmente entalhado à metade da altura da seção transversal com disco de diamante. Com a utilização do corpo de prova para teste de flexão artificialmente trincado (disco de diamante), a tenacidade à fratura é então calculada de acordo com a seguinte expressão:

que mostra uma combinação aproximada das equações (A) e (B). Os parâmetros mantêm a mesma definição. O termo f{c/h} está relacionado à razão entre o comprimento da trinca e a espessura do corpo de prova, apesar da maioria dos pesquisadores usarem o entalhe reto à metade da espessura do corpo de prova. Diversos pesquisadores têm tabulado esta função [9, 10].

A tenacidade à fratura pode ser medida por este teste a baixas temperatures onde fraturas são predominantemente frágeis e a curva de força-deslocamento é essencialmente linear elástica à ruptura. Esta tenacidade pode ser representada graficamente em função da resistência medida de acordo com o teste de flexão em três pontos para um grupo ou classe de refratários, como argilas ou compostos de alta alumina. O resultado é uma linha reta que passa pela origem. A inclinação desta linha, assim como indicado pela equação (B), é a constante geométrica, Y, multiplicada pela raiz quadrada do comprimento crítico da trinca, C. Os comprimentos de trinca estimados pela inclinação de tais gráficos são geralmente iguais aos maiores agregados no refratário. Isto não é uma surpresa porque sempre se soube que as composições de refratários com maiores tamanhos de agregados têm menores resistências mecânicas que aquelas contendo apenas agregados finos. É evidente que as trincas intrínsicas ao corpo refratário são relacionadas as, ou na mesma escala de tamanho que, os maiores agregados no refratário. Este é um ponto importante para o entendimento da resistência de refratários e a função dos agregados numa composição refratária.

É adequado comentar os valores de tenacidade à fratura reportados para refratários, com a única intenção de verificar a sua susceptibilidade à fratura. Apesar de não ser apropriado agrupar os aluminosilicatos e refratários básicos, ou refratários moldados e tijolos, neste momento não é tão desastroso tecnicamente proceder dessa maneira, devido à ampla generalidade pretendida por este raciocínio. A razão é que refratários não são muito resistentes. A tenacidade à fratura de refratários geralmente se encontra na faixa entre 0,2 a 1,5 MPa.m^1/2, o que não representam valores de tenacidade muito grandes. Refratários moldados apresentam-se na extremidade inferior de tal intervalo e tijolos queimados na superior. Para fins de comparação, a tenacidade do vidro de janela é 0,75 MPa.m^1/2, enquanto que para a maioria dos ferros fundidos é cerca de 20 MPa.m^1/2, apesar de haver uma variação. Os aços mais tenazes apresentam valores maiores que 200 MPa.m^1/2 [6].

Os baixos valores de tenacidade à fratura são esperados, visto que refratários não são muito resistentes e suas trincas intrínsicas são consideravelmente grandes. A presença de grandes agregados (trincas) pode ser prontamente observada a olho nu em corpos refratários. Apesar da tenacidade à fratura não ser a completa situação para a fratura de refratários, seus baixos valores claramente demonstram que a resistência à iniciação de trincas em refratários não é muito alta. Formação de trincas e fratura devem ser seriamente levadas em consideração para refratários industriais em muitas de suas aplicações.

FRATURA À TENSÃO TÉRMICA

Quando a fratura ocorre como consequência das tensões térmicas geradas durante as mudanças de temperatura que o revestimento refratário sofre durante seu aquecimento inicial, ou durante ciclos térmicos das práticas operacionais do dia-a-dia, a extensão do dano durante a fratura é governada pelo critério de energia. Isto foi ilustrado por Hasselman em seus trabalhos clássicos [11, 12]. Geralmente para refratários, pode se esperar que a microestrutura experimente uma extensão de trinca quasi-estática durante qualquer tipo de choque térmico, mas o crescimento cinético de trinca também deve ser levado em consideração, apesar de ser provavelmente muito menor e menos provável. Expressões semelhantes explicam ambas situações. Para o crescimento cinético de trinca, Hasselman derivou e definiu o parâmetro de resistência ao dano por choque térmico cinético, R^''", como:

onde E é o modulo elástico e g_wof é o trabalho de fratura como originalmente medido por Nakayana [7] e subsequentemente por Tattersall e Tappin [13]. Hasselman, de maneira semelhante, definiu o parâmetro de resistência ao dano de crescimento quasi-estático de trinca, R_st, como:

onde a é o coeficiente de expansão térmica e os demais parâmetros os mesmos definidos anteriormente. Isto foi revisado por Rodrigues e Pandofelli especialmente para refratários moldados [14].

Apesar de não ser óbvio, as expressões (D) e (E) têm a mesma dependência geral do módulo elástico e da resistência mecânica. A tensão termo-elástica pode expressar de maneira simples para a limitação linear total em uma dimensão da seguinte forma:

elevada ao quadrado em ambos os lados, se torna:

Combinando equações (G) com (E) para E·a², é revelado que ambos R^''" e R_st são inversamente relacionados ao quadrado da resistência mecânica dividido pelo modulo elástico, E. Esta relação, s²/E, é essencialmente a energia de deformação elástica armazenada num elemento ao nível de tensão s [15]. Isto é a força motriz para fratura ou propagação da trinca. Não é supresa que se o crescimento da trinca no dano por choque térmico for cinético ou quasi-estático, a trinca deve ser ainda controlada pela energia de deformação elástica armazenada no sistema.

A análise acima explica porque a evolução da resistência mecânica de refratários industriais através da história não teve seu foco no desenvolvimento de refratários de alta resistência. A resistência ao dano por tensão térmica diminui com o aumento da resistência, quadrado da resistência. Refratários de alta resistência mecânica são mais susceptíveis ao dano por choque térmico. Fabricantes de refratários conhecem tal afirmação há um bom tempo, e seus engenheiros cerâmicos aumentaram a resistência ao dano por choque térmico de argilas com a adição de agregados grandes derivados de rejeitos moídos à mistura/composição do refratário. Engenheiros de refratários pioneiros frequentemente defendem que agregados grandes e duros funcionam como obstáculos às trincas provenientes de choque térmico [16]. Os agregados provavelmente comportam-se segundo esta regra, contudo é mais provável que o efeito benéfico de agregados de tijolos moídos foi principalmente um dos introdutores de grandes falhas na microestrutura refratária e, portanto, reduzindo a resistência mecânica e a energia de deformação elástica armazenada disponível para a propagação de trincas por choque térmico. Agora é reconhecido que os agregados grandes e resistentes também assumem um papel importante na criação de curvas-R crescentes em refratários e diminuem a extensão da propagação de trincas, ponto que será futuramente discutido. Não importa o quanto multifacetado seja a função do agregado, é óbvio que onde a resistência ao dano por choque térmico é levada em consideração, o mais resistente não é necessariamente o melhor.

FRATURA NÃO-LINEAR E A TÉCNICA DA INTEGRAL-J

A fratura frágil, linear elástica de refratários ocorre apenas à temperatura ambiente, ou a temperaturas elevadas moderadas. Até mesmo à temperatura ambiente, muitos refratários, especialmente moldados ou outros monolíticos, irão exibir uma extensa porção não-linear da curva de força-deslocamento antecedente à ruptura num teste normal de resistência à flexão, e muito provavelmente, num teste de mecânica da fratura com uma trinca artificial grande. A curva de força-deslocamento para um teste típico de resistência mecânica assemelha-se com o primeiro diagrama apresentado na Fig. 1. Esta forma não-linear é o resultado do fenômeno inelástico ocorrendo na região da trinca ou fratura, ambos na zona de processo à frente da trinca antecedendo a trinca principal (microtrincamento) e também na região seguinte de rastro atrás da frente da trinca do outro lado da superfície de fratura recém-formada (formação de ponte de agregado). Tipicamente, depois da região linear elástica durante carregamento inicial, uma extensa flexão da curva ocorre e uma região não-linear se desenvolve fazendo com que o valor máximo na curva força-deslocamento seja alcançado rapidamente. Esta característica de não-linearidade da curva força-deslocamento também acontece com vários materiais metálicos, mas isto é consequência da extensa zona plástica que se desenvolve nos arredores da região frontal da ponta da trinca durante escoamento e fluxo plástico de deslocamento. O ponto é que a curva tensão-deformação ou força-deslocamento não-linear é um fenômeno geral de força-deslocamento em materiais, não sendo restrito apenas para refratários industriais.

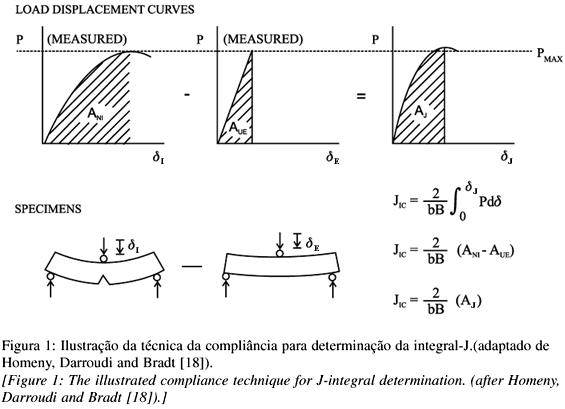
Para abordar este fenômeno inelástico não-linear, Rice formulou o conceito conhecido como integral-J [17]. A integral-J é baseada no caminho independente da integral de linha de energia que abrange a região da trinca. Isto foi inicialmente aplicado a metais para ampliar os conceitos de mecânica da fratura linear elástica e para tratar o problema de intenso fluxo plástico nas proximidades da ponta da trinca durante carregamento. Contudo, os princípios gerais desse conceito são universais e não são restritos a materiais específicos ou a algum mecanismo particular não-linear. Homeny et al. usaram este parâmetro para a fratura de refratários no final dos anos 70 [18]. Parece natural utilizar o conceito de integral-J e a metodologia experimental para fratura de refratários, mas esta metodologia nunca recebeu a aceitação universal esperada. Contudo, desde que é básico em princípio, e irá sem dúvida ganhar crédito no futuro, talvez em algum tipo relacionado de teste, o método experimental simples da compliância para determinação da integral-J é discutido neste trabalho.

A Fig. 1, adaptada de Homeny et al. [18], demonstra os princípios básicos da técnica experimental da compliância para determinação da integral-J. Um corpo de prova artificialmente trincado ou entalhado e outro idêntico, porém sem o entalhe, são necessários. O corpo de prova entalhado é carregado apenas até um pouco além de sua carga máxima, com o intuito claro de identificar o regime não-linear, e obter o registro de sua curva força-deslocamento. Então a área, A_NI, é determinada para o ponto de deslocamento de carga máxima. Em seguida, o corpo de prova idêntico sem o entalhe é carregado até o mesmo valor de P_MAX. A energia de deformação elástica armazenada no corpo de prova, A_UE, pode ser determinada e posteriormente subtraída da energia do corpo de prova entalhado. A diferença entre as duas é usada para calcular o valor crítico da integral-J, J_IC, no ponto de carga máxima atingida pelo corpo de prova entalhado. Esta é a técnica da compliância descrita por Rice et al. [17], Mindes et al. [19] e por Roedig et al. [20].

Esta técnica resulta no valor J_IC com unidades (J/m²) e, portanto, requer comparação com um valor de G_IC ao invés da intensidade de tensão baseada na tenacidade à fratura, K_IC. Quando Homeny, Darroudi e Bradt mediram os valores de J_IC e os valores de K_IC para os mesmos refratários de aluminosilicatos de acordo com a equação (C) e os converteram para valores de G_IC, eles observaram que os valores de J_IC consistentemente superam os valores de G_IC, frequentemente por um fator 4 ou maior. É óbvio que a técnica da integral-J é capaz de medir as demandas de energia da zona de processo de trinca em refratários. Além do mais, a integral-J tem um significado fundamental para a condição microestrutural associada com a carga máxima. Esses são problemas críticos no cerne do projeto microestrutural de refratários. Deve ser concluído que a integral-J tem grande potencial para contribuir com o entendimento do processo de fratura, na relação com o projeto microestrutural e inúmeros fenômenos relacionados aos materiais refratários.

Quando Homeny et al. compararam as energias obtidas pelo método da integral-J com duas vezes o total do trabalho de fratura, 2g_wof, para os mesmos refratários, este último era geralmente muito maior, frequentemente 4 ou 5 vezes maior [18]. É evidente que quando trincas grandes se desenvolvem nos corpos refratários, há uma considerável dissipação de energia nas proximidades da frente da trinca em avanço, provavelmente em ambas, as zonas de processo frontal e a região seguinte do rastro da trinca. O fato de que Homeny et al. fizeram estes experimentos em escala laboratorial, cujos corpos de prova tinham dimensões de apenas poucos centímetros, e que a zona de processo totalmente desenvolve em tais corpos de prova seria, provavelmente, maior que o próprio corpo de prova propriamente dito, sugere que a evolução da zona de processo em refratários é uma área interessante para futuras pesquisas. Certamente, uma área onde um grande entendimento irá beneficiar o desenvolvimento microestrutural refratário, especialmente para resistência mecânica e resistência ao dano por choque térmico.

TRABALHO DE FRATURA

O desenvolvimento do teste de trabalho de fratura e sua subsequente aplicação para refratários contendo argilas, desenvolvido por Nakayama e Ishizuka, foi um trabalho importante que redirecionou a pesquisa da fratura de refratários para o uso de uma única trinca grande semelhante ao estudo da mecânica da fratura para metais [21]. O teste do trabalho de fratura continua sendo um dos testes mais simples que pode ser aplicado a refratários. Contudo, semelhante aos comentários prévios relacionados ao tamanho do corpo de prova, é comprovado que o tamanho da zona de processo da região da trinca para refratários pode ser bastante grande e muitos corpos de prova para teste de trabalho de fratura em escala laboratorial não são grandes o suficiente para permitir o completo desenvolvimento da zona de processo de trinca. Ao contrário desta observação, o teste de trabalho de fratura será discutido devido à sua simplicidade e à extensão de seus princípios a modernos testes de fratura que estão em voga. Seus princípios são essenciais para entender a fratura de refratários, especialmente fratura a choque térmico e trincamento/esfoliação (spalling).

Um problema fundamental para o teste de trabalho de fratura é fornecer uma geometria que promova crescimento estável de trinca, ou seja, extensão de trinca que a máquina de ensaio seja capaz de monitorar completamente durante o crescimento de trinca através da microestrutura do corpo de prova. É também apropriado ter uma máquina de ensaios rígida, de baixa compliância capaz de promover crescimento estável de trincas. Nakayama obteve ambas condições, esta última por construir sua própria máquina. No caso do primeiro requerimento, Nakayama utilizou o simples corpo de prova para teste de flexão em três pontos com entalhe triangular na metade de seu comprimento, ou tipo entalhe-chevron, de forma que a ponta da seção triangular do corpo de prova estivesse para o lado de tensão durante ensaio à flexão. Quando feito de forma apropriada, isto promove uma curva força-deslocamento estável, à medida que a trinca cresce durante o ensaio. Este problema de estabilidade de trinca é importante e tem sido discutido extensivamente por Nakayama, Abe e Bradt [22]. A energia ou trabalho de fratura é simplesmente:

trabalho de fratura =

onde a integral, òPdu, é a área sob a curva força-deslocamento e A é a área transversal do ligamento restante do corpo de prova depois do entalhe. O fator 2 é incluído porque quando o corpo de prova é rompido, duas novas superfícies de fratura são criadas. Isto é semelhante às energias ou áreas abaixo das curvas na Fig. 1. Apesar do tipo de entalhe chevron ser preferido atualmente, qualquer forma triangular de ligamento do corpo de prova que promova a iniciação de crescimento estável de trinca a pequenas forças aplicadas é adequada.

Inicialmente, foi considerado que o trabalho de fratura era uma constante do material, assim como o módulo elástico ou tenacidade à fratura. O descobrimento das curvas-R crescentes, que será discutido mais adiante, e o conceito da zona de processo da região da trinca totalmente desenvolvida sobre uma trinca em avanço tem gerado considerável dúvida sobre esta idéia. Apesar desta discussão ser prematura para curvas-R e para tratar da zona de processo de trinca, ela é necessária. O trabalho ou energia para criar uma trinca é dependente do desenvolvimento da zona de processo de consumo de energia na região da trinca. Em refratários com curvas-R crescentes, a zona de processo é função do tamanho ou comprimento da trinca. Ela geralmente aumenta em tamanho com o aumento do comprimento da trinca, mas atinge um plateau no seu estágio de desenvolvimento mais completo. Na maioria dos testes de trabalho de fratura em escala laboratorial, o corpo de prova para ensaio não é suficientemente grande para gerar um plateau ou estado de equilíbrio da zona de processo da trinca à medida que a trinca está se extendendo. Portanto, a energia de fratura está continuamente aumentando com o crescimento da trinca. A menos que o pesquisador tenha corpos de prova para ensaio muito grandes, onde a condição de equilibrío da zona de processo de trinca seja atingida e, então, o trabalho de fratura é normalizado com base no comprimento de trinca unitário no valor do plateau ou região da zona de processo de tamanho constante, à medida de trabalho de fratura deve aumentar com o aumento do tamanho de trinca e também do corpo de prova. Este dilema se relaciona com a origem fundamental da curva-R crescente e também se aplica a outros materiais como, por exemplo, concretos estruturais.

É preciso discutir o uso do teste com corpo de prova com uma única trinca entalhada na extremidade, descrito previamente pela equação (C), para medidas de tenacidade à fratura de maneira experimental e, simultaneamente, extrair-se o trabalho de fratura. De fato, muitos pesquisadores preferem obter estes dois parâmetros a partir do mesmo corpo de prova durante um único ensaio. Devido à eficiência em obter-se dois dados experimentais a partir de um único teste, pesquisadores consideram este teste muito interessante. Muitos usam esta técnica com algum sucesso, pois muitos refratários estão microestruturalmente bem projetados para dissipar energia durante crescimento de trinca. Desta forma, há pouca ou nenhuma dificuldade em obter-se uma fratura estável de um entalhe reto. Se uma máquina de ensaios rígida for utilizada, o entalhe chevron não é necessário. Há muitos perigos em gerar dados dessa maneira. O mais importante é o rumo da propagação da trinca originalmente definido pelo entalhe feito com serra de diamante. Isto gera uma área de superfície de fratura mais larga que a área aparente do plano entalhado. Quando isso acontece, altos valores de trabalho de fratura são erroneamente obtidos. É evidente, que o entalhe triangular tem uma vantagem, um efeito dominante sobre a trinca propagante, ausente no entalhe reto. Assim como entalhes retos têm uma forte tendência a produzir trincas semi-estáveis, é possível que o tempo de resposta da máquina de ensaios não seja suficientemente longo para monitorar completamente o crescimento da trinca durante o ensaio com corpo de prova entalhado. Uma fração da energia dissipada pelo corpo de prova pode não ser registrada. Por essa razão, o autor não recomenda o uso do corpo de prova com uma única trinca entalhada na extremidade para gerar conjuntamente os resultados de tenacidade à fratura e de trabalho de fratura.

Assim como para resistência mecânica e tenacidade à fratura, é apropriado considerar de maneira geral alguns valores de trabalho de fratura para refratários, apenas para situar o leitor e os pesquisadores de refratários. Considerando o trabalho de fratura do vidro de janela, ou o de planos de clivagem de monocristais, os valores não são muito diferentes de suas energias livres de superfície termodinâmica, apenas 1 – 2 J/m². Para estes materiais, as energias para formação e propagação de trinca são virtualmente iguais. Com pequenos tamanhos de grão, cerâmicas avançadas estruturais de alta resistência têm valores de trabalho de fratura a cerca de 10 J/m². Refratários geralmente têm valores de trabalho de fratura muito maiores. À temperatura ambiente, os mais frágeis, refratários queimados densamente, têm valores de trabalho de fratura de cerca de 30 J/m² e os refratários microestruturalmente bem projetados têm valores de trabalho de fratura a cerca de 100 J/m² ou mais. Deve ficar claro que refratários são substancialmente mais resistentes ao crescimento de trinca que à formação de trinca, por um fator igual ou superior a 10.

Finalmente, quando os valores do trabalho de fratura são medidos em função da temperatura, os valores próximos da resistência máxima, ou talvez um pouco maior em temperatura são muito maiores. Os valores máximos de trabalho de fratura a temperaturas elevadas são frequentemente > 1000 J/m². Isto é predominantemente devido à presença de silicatos viscosos. Como esperado, o teste a temperaturas ainda mais elevadas, onde os silicatos são ainda mais fluidos, ou menos viscosos, revela um significante decréscimo nos valores do trabalho de fratura para apenas poucos J/m².

CUIDADOS DURANTE ENSAIOS DE FRATURA

A medida que o desenvolvimento de refratários passou a incluir o teste de fratura, tornou-se evidente que existem problemas na obtenção de resultados representativos para ensaios de corpos de prova em escala laboratorial. Isto ficou óbvio com os corpos de prova para trabalho de fratura, devido à diversidade de resultados obtidos em vários testes realizados no mesmo corpo de prova. Os resultados obtidos estavam compreendidos em uma ampla e inaceitável faixa de valores com grandes intervalos de confidência (confiança). Com um simples exame visual das superfícies de fratura foi possível relacionar os resultados dos ensaios ao caráter das superfícies de fratura. Foi constatado o importante papel desempenhado por agregados grossos no processo de fratura, frequentemente resultando em altos valores de trabalho de fratura quando o agregado se encontrava próximo da extremidade do entalhe chevron ou do ligamento triangular restante. Tornou-se evidente que o agregado grosso da microestrutura refratária não permitiria uma amostragem representativa do refratário para corpos de prova em pequena escala laboratorial. Sem dúvida, uma das razões é que sua presença não permite o desenvolvimento completo da região da zona de processo da trinca. Nem o microtrincamento ou a ramificação de trinca em frente da trinca em avanço, nem o fenômeno de formação de pontes na região do rastro da trinca atingiram uma configuração de equilíbrio . Um corpo de prova muito maior é claramente necessário para abranger adequadamente as estruturas refratárias de agregados grossos. É claro que tijolos, alguns com 1 m de extensão, são disponíveis para corpos de prova de muitos tipos de refratários.

Pesquisadores em VRD em Leoben, Áustria, promoveram teste de fratura de separação de cunha (wedge-splitting) onde corpos de prova muito maiores são utilizados, permitindo melhor amostragem e um grau muito maior de desenvolvimento da zona de processo de trinca [23, 24]. Apesar deste teste não ter recebido ampla aceitação até o momento, nem ter sido explorado por completo, ele traz a promessa de promover um entendimento considerável no que se refere ao processo de fratura de refratários. Infelizmente, muitos pesquisadores usando este teste com corpos de prova de separação de cunha (wedge-splitting) optaram por redefinir algumas das terminologias padrão de fratura e criaram certa confusão para aqueles que não são familiarizados com este campo de pesquisa. Testes sistemáticos e ordenados utilizando esta técnica para diferentes variações das microestruturas refratárias, e também em função da temperatura, estão em estudo para esclarecer os importantes mecanismos de fratura.

O teste de separação cunha (wedge-splitting) tem algumas características em comum com o método da compliância da integral-J, previamente discutido. Este merece uma descrição mais detalhada para aqueles que desejam empregá-lo em testes futuros de fratura de refratários. A Fig. 2 ilustra um esquema do corpo de prova para ensaio, adaptado de Buchebner e Hartmut [24]. É evidente que o nome do teste, separação de cunha (wedge-splitting), representa sua própria descrição. Ele apresenta um arranjo elaborado dentro de uma configuração de entalhe iniciado, com dois entalhes laterais para restringir o caminho da trinca no decorrer do teste. A amostra é carregada sob compressão, permitindo obter-se parâmetros de fratura a partir da análise da curva força-deslocamento. Devido ao tamanho do corpo de prova e da grande área superficial de fratura, normalmente não há dificuldade em promover-se fraturas completamente estáveis para refratários e, portanto, um registro confiável da energia total para propagação de trinca através do corpo de prova é facilmente obtido com um máquina de ensaios rígida.

A Fig. 3 ilustra curvas força-deslocamento típicas para corpos de prova refratários provenientes de ensaio de separação de cunha (wedge-splitting). Graficamente, tem-se um refratário de categoria "frágil" (talvez um corpo de argila excessivamente queimado) e um "tenaz" ou uma variedade que consome mais energia (por exemplo, com 70% alumina altamente microtrincado). Quando a curva força-deslocamento é integrada, análogo à equação (H) previamente descrita, é possível obter o trabalho de fratura total. Alguns pesquisadores usam esta técnica para definir a energia superficial de fratura específica e usam G_F ao invés do trabalho de fratura total, 2g_wof. Isto pode ser uma nomenclatura conveniente caso seja necessário relacionar este resultado à taxa de liberação de energia de deformação, G_C, ou talvez em forma de alguma variante de J_C . No entanto, a medida experimental é claramente o trabalho de fratura como definido por Nakayama [7].

Como as curvas força-deslocamento são tipicamente estáveis para corpos de prova de separação de cunha (wedge-splitting), estas exibem uma região elástica linear inicial e uma região não-elástica moderada, que é seguida por um valor de carga máxima, semelhante ao primeiro diagrama da Fig. 1 para a técnica da integral-J, seguido por um longo decréscimo de carga com aumento do deslocamento. Também é possível usar o máximo desta curva força-deslocamento para informações adicionais o que ainda requer demonstração. Alguns pesquisadores têm sugerido a integração da curva força-deslocamento até o ponto máximo como uma medida da taxa de liberação de energia de deformação, G_C, descrita como:

onde a integral é tomada até a carga máxima, P_max, e A é o ligamento restante ou a eventual área superficial de fratura. Esta técnica teria mais mérito se todos os corpos de prova universalmente testados fossem do mesmo tamanho. Contudo, deve ser relembrado que um procedimento similar é utilizado na técnica da compliância da integral-J onde a energia de deformação elástica armazenada no corpo de prova na carga máxima é subtraída para especificamente identificar a energia da zona de processo de trinca. Como a energia de deformação elástica armazenada varia com o tamanho do corpo de prova de ensaio e o tipo de material refratário, esta deve ser considerada independentemente da área observada sob a curva de força-deslocamento. Isto sugere que a simples atribuição da carga máxima à G_C não é fundamentalmente correta. Contudo, o valor de G_C determinado dessa maneira talvez seja uma aproximação satisfatória para propostas dentro de uma classe única de refratários, como por exemplo refratários mag-cromo ou alumina-magnesia-carbono.

Uma técnica particularmente interessante e prática de usar os resultados do teste de separação de cunha (wedge-splitting) é utilizar a razão da área sob a curva de fratura estável desde o carregamento inicial até o ponto máximo, referido como G_C acima, e da área total da curva força-deslocamento estável que fornece G_F. A razão entre as duas grandezas pode ser usada para definir a razão de flexibilidade, tenacidade ou ductilidade, como:

Esta razão terá um valor alto, >10, para refratários com alto consumo de energia durante a propagação da trinca relativo à energia necessária para a formação da trinca. Esta razão não significa nada além, na verdade menos ainda em bases fundamentais pelo problema com G_C, que a conhecida razão que relaciona o trabalho de fratura e a energia superficial de fratura do corpo de prova com uma única trinca entalhada na extremidade:

onde o valor de K_IC é o determinado pelo teste com corpos de prova contendo uma única trinca entalhada na extremidade, tal qual detalhado anteriormente e descrito pela equação (C). E representa o módulo elástico do refratário. Quando os problemas separados de energia para propagação e formação de trinca são expressos como descrito acima, torna-se óbvio o interesse das pesquisas direcionadas para a indústria com o objetivo de obter-se ambos K_IC e g_wof a partir de um único corpo de prova, como por exemplo o teste com corpos de prova com uma única trinca entalhada na extremidade. O uso do corpo de prova de separação de cunha (wedge-splitting) também parece ser possível.

É aconselhado observar que qualquer uma das duas razões expressas pelas equações (J) e/ou (K) é uma medida da energia necessária para propagação de trinca dividida pela energia necessária à formação da trinca. Quanto mais alto o valor dessa razão, melhor a resistência ao dano por choque térmico do refratário e maior a capacidade do refratário de adaptar-se às deformações térmicas e mecânicas em serviço. Este último é frequente pois a microestrutura do refratário é capaz de acomodar processos de significante trincamento internos e ainda manter a sua integridade mecânica. Este último, indiretamente relaciona-se à longa extensão da curva força-deslocamento, tanto no teste de trabalho de fratura quanto no de separação de cunha (wedge-splitting). Assim, como observado por Buchebner e Hartmut [24], isto é aconselhável para aplicações como fornos rotativos de cimento onde o perfeito arredondadamento do revestimento de aço é trocado de acordo com o tempo de vida relacionado aos processos de degradação natural.

A ZONA DE PROCESSO DE TRINCA PARA REFRATÁRIOS

Parece evidente que fenômenos muito interessantes de absorção de energia ocorrem nas proximidades de trincas de refratários e que estes consomem uma grande quantidade de energia à medida que a frente da trinca avança [25]. Estes eventos ocorrem em duas regiões diferentes, a zona de processo em frente da trinca em avanço e a região seguinte do rastro que acompanha a frente da trinca em avanço. Uma vez que a trinca começa a se propagar, esta desenvolve uma zona de processo frontal de equilíbrio, contudo a região atrás da trinca continua a crescer. O fato de que trincas grandes são mais difíceis de serem propagadas que trincas pequenas sugere que a região seguinte do rastro é mais importante para a resistência ao crescimento de trinca [26].

A Fig. 4 ilustra um esquema da zona de processo total ao redor da trinca, tanto à frente como atrás da frente da trinca em avanço. À frente da trinca, acredita-se ocorrer toda a "ação", o microtrincamento prevalece e há geralmente uma considerável ramificação da trinca, associada principalmente com a junção das microtrincas na região. O tamanho da região de processo frontal varia de refratário para refratário, mas uma simples estimativa usando a aproximação assim como Dugdale sugere que a região da frente da trinca ou a zona de processo frontal deve ser bem ampla, muito maior que a maioria dos corpos de prova de escala laboratorial quando totalmente desenvolvida. Isto indica que os resultados de um corpo de prova de pequena escala laboratorial provavelmente não geram números absolutos, porque a zona de processo de trinca, frente e trás, está apenas parcialmente desenvolvida. Devido a estes efeitos de tamanho, testes em escala laboratorial devem apenas fornecer valores para comparação entre diferentes microestruturas de refratários testadas com o mesmo tamanho de corpo de prova e sob às mesmas condições de ensaio. Evidentemente, que se o módulo elástico de diferentes corpos de prova refratários varia amplamente, problemas adicionais são introduzidos usando algumas dessas técnicas. Isto é devido às diferentes quantidades de energia de deformação elástica armazenadas nos corpos de prova e devem ser levadas em consideração no caso de processos ou eventos microestruturais de absorção de energia, assim como eles estão relacionados às curvas força-deslocamento.

A outra região importante à frente da trinca em propagação nos refratários é a região atrás da frente da trinca. Em materiais frágeis, a extensão da abertura da trinca, COD, não é muito grande assim como também não é a extensão da abertura da ponta da trinca, CMOD. Elementos microestruturais do refratário, como, por exemplo, os agregados grandes, são capazes de interagir através das superfícies recém-formadas de trinca. Aparentemente, os fenômenos que ocorrem na região seguinte de rastro da trinca são os mais importantes durante o processo de fratura, ou os fenômenos relacionados a trincamento nos refratários. Certamente, eles são aqueles que contribuem para os fenômenos de curvas-R, descritos na próxima sessão. Talvez muitoa coisa aconteça logo atrás de uma trinca em avanço, contudo em refratários, os dois mais importantes são a formação de ponte de agregados refratários e o ligamento de silicatos, ambos ilustrados no esquema da Fig. 4.

As pontes de silicatos na superfície da trinca formam-se apenas em consequência da fratura do refratário a temperaturas elevadas, onde silicatos vítreos tornam-se viscosos e podem fluir e formar ligamentos entre as superfícies de fratura recém-criadas. Claro, é necessário que estes ligamentos tenham resistência para que sejam capazes de manter as superfícies em formação da trinca juntas. Isto ocorre apenas em uma faixa limitada de temperatura. A altas temperaturas, a viscosidade dos silicatos diminui e sua resistência diminui, evitando que eles liguem as superfícies da trinca. Provavelmente, esta é a razão porquê existe uma máxima resistência em função da temperatura e um máximo para o trabalho de fratura em refratários contendo silicatos. A formação de extensa ligação das superfícies de fratura da trinca dessa natureza é comum. Esta é a razão para o uso de fibras em compósitos de alta tecnologia e também para o uso de fibras metálicas em refratários moldados. Esses materiais também podem trincar, contudo eles apresentam boa capacidade de retenção de sua integridade..

A regra da formação de pontes de agregados atrás da frente da trinca em avanço é fundamental para a resistência ao crescimento da trinca em materiais refratários. Homeny e Bradt demonstraram a importância da distribuição de agregados com referência direta à resistência ao dano por choque térmico, comparando as distribuição de tamanhos de agregados contínua e espaçada [27]. Apesar da importância fundamental desses componentes microestruturais ser conhecida há muitos anos, só recentemente ela foi compreendida em toda sua extensão, quando verificou-se que os agregados agem na região do rastro depois da frente da trinca ter passado. Os detalhes dos mecanismos de formação de pontes de agregados que contribuem para a resistência ao crescimento da trinca ainda não são totalmente reconhecidos ou completamente entendidos. Pelo menos três deles foram propostos, incluindo a formação de pontes através das superfícies recém-criadas da trinca, a presença de agregados atrás da trinca, o que requer a formação de pontes e os efeitos de fricção de remoção dos agregados de um dos lados da trinca passante. O último, obviamente, ocorre com regularidade quando a superfície da fratura do refratário é examinada e grandes agregados ressaltados são gerados como consequência do desvio de trincas que resulta por circular os agregados. Este último processo ocorre apenas quando os agregados são mais resistentes que a matriz que os liga. Talvez esta última observação tenha conduzido os pioneiros em refratários a perceber os agregados como freios de trincas [16]. De qualquer forma, é aconselhada a presença de agregados grandes e resistentes, não apenas para favorecer o desvio da trinca, mas também para consumir energia durante a formação de pontes seguindo a trinca.

Existem muitas maneiras para melhorar a resistência do refratário ao crescimento de trincas sob o ponto de vista de desenho estrutural e microestrutural de agregados. A primeira e mais importante é a distribuição de tamanhos de partículas da fração de agregado da composição do refratário [27]. É evidente que para haver a formação de pontes, o agregado deve ter no mínimo a mesma dimensão da abertura da trinca, COD, ou talvez ser maior que a abertura da boca da trinca, CMOD, para que o agregado possa formar pontes a grandes distâncias atrás da frente da trinca em propagação. Isto tem conduzido ao conceito de refratários com agregados muito grandes em revestimentos para refratários moldados. Os interstícios entre as partículas de agregado desses materiais são infiltradas com massa refratária escoante. Isto funciona bem em áreas como fundos de panela de aciaria.

Uma extensão natural do conceito de tamanho de agregado é o seu aspecto geométrico. É evidente que agregados angulares devem ter um efeito mecânico de fechamento maior que agregados esféricos. A experiência com a adição de fibras em moldados indica que o comprimento e a razão de aspecto são importantes. Provavelmente, maiores razões de aspecto melhoram a resistência ao crescimento de trinca, contudo a mistura desta geometria de fibra ao refratário moldado ou cimento não é muito fácil. Agregados resistentes e de superfície áspera são os mais indicados.. A química do ligamento com os silicatos nos refratários é também muito importante. Atualmente já se reconhece que os fenômenos que ocorrem atrás da frente da trinca em avanço, na região seguinte do rastro da trinca são os efeitos mais importantes para a resistência ao crescimento de trinca em refratários. Resta identificar e quantificar os fenômenos capazes de produzir microestruturas refratárias de maior resistência ao crescimento de trinca.

CURVAS-R PARA REFRATÁRIOS

As consequências do comportamento de curva-R crescente para refratários são conhecidas já há algum tempo. Adams et al [26] foram os primeiros a experimentalmente demonstrar este fenômeno para uma série de refratários de aluminosilicatos ao observar que trincas longas eram mais difíceis de crescer do que trincas curtas. De modo simples, a resistência ao crescimento da trinca aumenta durante seu próprio crescimento em função do aumento da probabilidade de interação na grande região seguinte do rastro da trinca. A curva-R é a curva-Resistência, ou seja, a curva de resistência ao crescimento de trinca.

A Fig. 5 ilustra o conceito de curva-R crescente que contrasta com a curva-R plana ou frágil, típica de vidros, ou corpos de prova cerâmicos de pequeno tamanho de grão. A curva-R plana assim como observada para materiais perfeitamente frágeis é representada pela linha pontilhada horizontal da Fig. 5. A resistência ao crescimento de trinca, o valor R, é constante com o comprimento da trinca, o eixo horizontal. Nesse instante, o valor R é apenas 2g_f, onde g_f é a energia da superfície de fratura. O diagrama mostra o crescimento da trinca ou região extendida da trinca à direita do zero como DC. O tamanho inicial da trinca no corpo de prova de teste é designado como C_i e posiciona-se na extremidade esquerda do eixo horizontal. A linha pontilhada registrada como G é a taxa de liberação de energia de deformação. Para um material perfeitamente frágil, ela intercepta a curva-R plana em C = 0. Neste caso, o critério de fratura de G = R é verificado e o material se rompe catastroficamente, produzindo uma curva de força-deslocamento semelhante à do diagrama do meio da Fig. 1, perfeitamente linear elástico à fratura.

Entretanto, para um material com curva-R crescente, como ilustrado pela linha sólida que se curva para cima, originada no ponto de intersecção das duas linhas pontilhadas no eixo vertical de G e R, uma vez que G = R e o crescimento de trinca se inicia, o valor de R aumenta. R imediatamente excede G e a trinca é capturada; quando R > G, a trinca não se propaga. Uma série de muitas linhas G, começando da linha pontilhada até a linha sólida, ocorre para carga crescente da trinca. Contudo, a natureza crescente da curva-R imediatamente faz com que R exceda G toda vez que R = G, e um tipo de processo de crescimento de trinca quasi-estático ocorre com aumento de tensão. Eventualmente a curva-R crescente assume caráter assintótico para um valor de zona de processo de trinca completamente desenvolvida (em frente e atrás da frente da trinca) e a curva-G é capaz de se aproximar e ultrapassar esse valor tangencialmente. O critério de rompimento é então determinado pela igualdade das inclinações das duas curvas. A fratura ocorre quando(dG/dc) > (dR/dc) assim como demonstrado no diagrama de crescimento de trinca da Fig. 5.

Pode ser visto que a presença da curva-R crescente tem dois efeitos evidentes na fratura do refratário. Primeiramente, é criada a necessidade de uma tensão mais alta para atingir o critério de fratura. Isto aumenta a resistência do refratário antes de seu rompimento catastrófico. Em segundo lugar, é gerado um tipo de comportamento não-linear durante o carregamento à fratura. Esta região não-linear é claramente marcada como DC_NL para o crescimento de trinca não-linear da Fig. 5. Isto corresponde à região não-linear da curva convencional força-deslocamento, o desvio do comportamento linear elástico que antecede a carga máxima. Esta é a região não-linear que Gogotsi et al. usaram para definir a razão de fragilidade, a qual mais tarde os mesmos utilizaram para resistência ao dano por choque térmico [29]. A extensão da resistência mecânica aumenta e a extensão da região não-linear depende do refratário e da temperatura na qual é medida. Ela também depende da zona de processo de trinca e dos agregados ali presentes e que afetam a formação de pontes na região seguinte do rastro depois da frente da trinca ter passado e determinam a taxa de crescimento para a curva-R naquele refratário.

Em geral, curvas-R não são obtidas para refratários pois muitos pesquisadores não as entendem ou simplesmente acreditam que a determinação das mesmas é muito problemática. Apesar de tudo, a integração da curva-R determina apenas o trabalho de fratura total, então não há motivo para preocupar-se com os detalhes. A razão é que se a curva-R é determinada por completo, então deve ser possível correlacionar diretamente os fenômenos das curvas-R com características microestruturais específicas dos refratários à medida que a trinca avança e interage com tais características. Sakai e Bradt [29] descreveram uma técnica gráfica simples para determinação completa da curva-R e como esta, pode ser derivada da curva estável força-deslocamento, assim como aquela apresentada na Fig. 4 para corpos de prova de separação de cunha. As curvas força-deslocamento de corpos de prova de separação de cunha parecem se enquadrar perfeitamente para a determinação de curvas-R. Caso os resultados da curva força-deslocamento sejam analisados, as relações das características de curva-R crescente ou em nível para a microestrutura do refratário, características de seus agregados, deve sem dúvida provar ser muito interessantes, e reveladores de aspectos surpreendentes sobre o processo de crescimento de trincas em refratários.

DETERMINAÇÃO GRÁFCIA DE CURVAS-R

Métodos gráficos simples são apresentados para a determinação da curva-R. Estas técnicas incluem o método de carregamento-descarregamento, a medida do comprimento de trinca in situ e a curva universal adimensional força-deslocamento. Nesta revisão, a técnica de carregamento-descarregamento é descrita para ilustrar os princípios de determinação gráfica da curva-R. As demais técnicas foram discutidas por Sakai e Bradt [29].

A Fig. 6 ilustra a representação gráfica desta técnica. Considerando o teste de força-deslocamento para um corpo de prova típico de mecânica da fratura, carregado até o ponto A, após a trinca atingir certo comprimento inicial. O corpo de prova é então descarregado. A trajetória de descarregamento é uma linha reta até o ponto B, que não coincide com a origem. Caso o corpo de prova seja recarregado até o ponto C provocando um crescimento adicional da trinca, Dc, e mais uma vez descarregado até zero, a trajetória de descarregamento é novamente uma linha reta até o ponto D, outro ponto que também não coincide com a origem. Estes pontos que não coincidem com a origem são resultados de deformações residuais irreversíveis que ocorrem nas proximidades da ponta da trinca. A área envolvida pela região ABDC, Dp_R, é a medida da energia adicional consumida durante o processo de carregamento de A até C e a criação da área de trinca nova, DA. Caso o valor de DA seja consideravelmente pequeno, e dividindo Dp_R por DA, a resistência de crescimento da trinca é obtida para aquele aumento de crescimento de trinca e pode ser especificado como R_C [12],

A área ou energia, Dp_R, que foi consumida para criar a nova área da trinca, DA, pode ser separada em duas áreas complementares, assim como ilustrado na Fig. 6b. Uma energia é a área triangular Dp_G, envolvida por AEB e a outra energia é a área Dp_ir, envolvida por ACDBE. A energia de deformação elástica armazenada, DU_e, nos pontos A e C do diagrama, é equivalemente às duas áreas triangulares ABQ e CDX, respectivamente. As áreas, Dp_G e Dp_ir, podem ser relacionadas à energia não-linear de tenacidade à fratura, G_C [13], e à energia irreversível para o crescimento de trinca, f_ir [14] da acordo com

e

A resistência ao crescimento da trinca, R_C (A), de um corpo de prova com área de trinca, A, e da área superficial total de fratura, S, é relacionada ao trabalho de fratura, g_wof, [15] de acordo com

Para estimar precisamente o tamanho da trinca, a relação quantitativa da compliância de A versus o comprimento da trinca, c, deve ser determinada antes do teste de fratura. Assim, o gráfico de R_C versus DC pode ser construído para mostrar a curva-R.

Uma dificuldade com o método de carregamento-descarregamento são as trajetórias de descarregamento "artificiais" ao longo de AB e CD. Durante o descarregamento, a dissipação de energia pode ser acompanhada por histerese na zona de processo da frente da trinca e na região seguinte do rastro da trinca. Isto pode ser influenciado por efeitos de interação friccional intensos entre as superfícies de trinca da fratura principal. Esta última dissipação de energia pode tornar-se relevante para alguns refratários com várias fases, especialmente para aqueles com grãos muito grandes que produzem superfícies de fratura ásperas. Por estas razões, o valor da compliância obtido a partir da inclinação das trajetórias de descarregamento pode ser um pouco diferente daquele que foi avaliado experimentalmente para um corpo de prova com entalhe, ou de um valor teórico. Esta energia de dissipação artificial e da deformação residual pode criar alguns erros na avaliação de Du_ir e da nova área da trinca, DA. A magnitude destes erros varia para diferentes materiais e talvez para diferentes corpos de prova do mesmo material. Apesar dessas pequenas dificuldades, o método de carregamento-descarregamento tem a vantagem de possibilitar a determinação dos parâmetros não-lineares de energia da fratura em função do comprimento de trinca usando apenas um corpo de prova. Maiores detalhes estão disponíveis no artigo de Sakai e Bradt [29].

A CURVA-R CRESCENTE E A RESISTÊNCIA AO DANO POR CHOQUE TÉRMICO

É visível que a aproximação do balanço de energia ao dano por choque térmico originalmente proposto por Hasselman [11] cerca de meio século atrás, relaciona diretamente o consumo de energia por processos não-lineares na zona de processo da região da trinca ao conceito de uma curva-R crescente. Obviamente, se a trinca consome mais energia como consequência de uma curva-R crescente, ela então não irá propagar-se por grandes distâncias e o dano por choque térmico resultante será diminuído. Em termos de mecânica da fratura, a curva-R crescente faz com que R > G, resultando na captura da trinca com menor penetração no corpo refratário. Este evento (R > G) repetitivo é o que Hasselman se referiu como crescimento de trinca quasi-estático. A perda de resistência não é tão grande quanto para o material com curva-R plana, porque não há crescimento cinético de trinca. Infelizmente, em situações industriais, como observado na Fig. 5, o valor de G depende da tensão, s, que é um parâmetro dependente de tempo durante as variações de temperatura, como, por exemplo, os ciclos térmicos de refratário de vaso de processamento revestido. Isto complica consideravelmente a análise, contudo não descarta a necessidade de refratários resistentes ao crescimento de trinca para aumento de resistência ao dano por choque térmico e o fato de que a curva-R crescente é almejada para materiais refratários.

Sem introduzir diagramas adicionais para extensão ou crescimento da trinca no campo de tensão térmica transiente, a função da curva-R crescente no aumento da resistência ao dano por choque térmico pode ser visualizada de maneira análoga ao diagrama de G,R versus DC da Fig. 5. Quando uma trinca de choque térmico encontra uma curva-R acentuadamente crescente de resistência ao crescimento de trinca, esta reage apenas como qualquer outra trinca. Ela será capturada quando R > G, um fato que repetidamente acontece com o incremento da extensão da trinca. O resultado é que ao invés de crescimento cinético de trinca e grande decréscimo na resistência após o evento de tensão térmica, a resistência mecânica do refratário é apenas gradualmente diminuída, até mesmo durante os choques térmicos mais severos. O crescimento da trinca ocorre de maneira quasi-estática, assim como Hasselman originalmente previu, muito tempo antes de curvas-R, ou medidas para qualquer sistema cerâmico serem elaborados. Refratários micro-estruturalmente bem projetados nunca devem exibir crescimento cinético de trinca, nem perda precipitada de resistência em testes severos de choque térmico. Até mesmo a perda de resistência mecânica com aumento da intensidade do choque térmico é sempre gradual para refratários bem projetados. Algumas vezes, não há praticamente nenhuma degradação de resistência para os refratários com resistência muito baixa. Isto ocorre, por exemplo, para os refratários da classe de 70% alumina altamente microtrincados, que apresentam extensas regiões não-lineares na curva força-deslocamento. Caso as suas curvas-R fossem medidas, elas seriam crescentes e muito acentuadas, propícias para a captura da trinca.

As relações entre os conceitos e fenômenos não-lineares das curvas força-deslocamento durante os testes de resistência, a existência da curva-R crescente e o aumento da resistência ao dano por choque térmico são conhecidos há várias décadas. As primeiras ligações foram aquelas propostas por Gogotsi e co-autores no final dos anos 70, há aproximadamente um quarto de século [28, 30]. Infelizmente, naquele tempo as idéias não eram levadas a sério porque a época era da mecânica da fratura "pura" aplicada a cerâmicas, incluindo refratários, e Gogotsi tinha uma técnica mecânica única envolvendo uma definição não-conventional da fragilidade de cerâmicas através de curvas de resistência não-lineares. Entretanto, Gogotsi e co-autores claramente relacionaram a característica não-linear das medidas de resistência com uma boa ou melhor resistência ao dano por choque térmico. Entretanto, ele não relacionou isto às curvas-R, pois o conceito de curva-R não era conhecido naquele tempo.

O próximo trabalho significante sobre o assunto surgiu por volta de 1990, mais de uma década depois que os conceitos não-lineares foram propostos por Gogotsi. Steinbrech e co-autores claramente demonstraram que as contribuições principais para a curva-R crescente em corpos cerâmicos de alumina estavam atrás da frente da trinca, na região seguinte do rastro [31]. Na mesma época, Swain começou a tratar o efeito de curva-R sobre o dano por choque térmico [32, 33]. Sakai e Ichikawa relacionaram diretamente os fenômenos de microtrincamento em avanço à frente da trinca e formação de pontes de trinca atrás da frente da trinca com o aumento no trabalho de fratura [34]. Em meados de 1990, todos os fundamentos foram estabelecidos para associar diretamente a curva força-deslocamento não-linear com os fenômenos da zona de processo da região da trinca a curvas-R crescentes, conduzindo a melhores resistências ao choque térmico de cerâmicas e refratários. Hoje em dia, quase uma década depois, as medidas experimentais relacionadas a esses conceitos ainda não são parte das atividades diárias para o desenvolvimento de refratários, mas é claro que estas devem se tornar, e eventualmente serão. Isto é apenas uma questão de tempo.

Nos registros da conferência NATO sobre choque térmico de cerâmicas avançadas [35], existem muitos trabalhos tratando da relação entre o aumento da resistência ao dano por choque térmico e os efeitos não-lineares de curvas-R crescentes. Infelizmente, estes trabalhos são de natureza totalmente teórica ou aplicados a materiais cerâmicos estruturais avançados, e não a refratários reais. São poucos os exemplos de cerâmicas avançadas capazes de gerar curvas-R crescentes tão acentuadas quanto aquelas para a maioria dos refratários microestruturalmente bem projetados. Até hoje, aproximadamente uma década depois de todos os princípios básicos terem sido definidos e confirmados, pelo menos de maneira parcial para cerâmica avançadas, estudos paralelos necessários para sistemas refratários de uso prático ainda não foram finalizados.

Parece evidente, até mesmo para o leitor sem tanta experiência, que o projeto microestrutural de refratários deve estar focalizado de maneira a optimizar o caráter não-linear da curva força-deslocamento, assim também como a taxa de crescimento da curva-R. É óbvio que um caminho para este objetivo está no projeto da distribuição de agregados para maximizar a formação de pontes na região seguinte do rastro de uma trinca em extensão. Esta é uma metodologia clara para melhorar a resistência ao dano por choque térmico de refratários. No caso de refratários, este projeto microestrutural está diretamente relacionado ao caráter do agregado, sua distribuição de tamanhos, sua resistência mecânica e seu tipo de ligação à matriz do refratário. Apesar de existirem muitas generalidades que devem ser aplicadas a todas as distribuições de agregados no refratário, tal qual selecionar agregados grossos mas consistentes com a manufatura do refratário, e obter-se outras propriedades a níveis adequados para desempenho industrial, deve ser esperado que cada sistema refratário terá cartacterísticas próprias. A mesma distribuição de agregados que maximiza o aumento das curvas-R para tijolos ou outras formas queimadas, provavelmente não irá otimizar da mesma forma produtos moldados. Talvez cada classe de refratários irá requerer um estudo sistemático detalhado dos efeitos das características dos agregados nas curvas-R de cada sistema. A comunidade técnica de refratários tem avançado lentamente no entendimento de curvas-R crescentes e sua mais importante função no desenvolvimento de refratários de maior resistência ao choque térmico.

SUMÁRIO E CONCLUSÕES

A fratura de refratários foi discutida por duas aproximações: resistência mecânica convencional e mecânica da fratura, considerando várias técnicas para medidas experimentais. A resistência e a tenacidade à fratura dos refratários estão relacionadas ao tamanho do agregado no refratário. Os agregados, seus tamanhos e distribuições, bem como suas características de ligação são críticos para trincas intrínsicas em refratários e afetam diretamente a resistência de refratários.

Foi observado que agregados tem uma função importante nos mecanismos de formação de pontes de trinca na região seguinte do rastro de uma trinca em propoagação nos refratários. Isto conduz a curvas-R crescentes, que estão relacionadas às características das curvas não-lineares tensão-deformação e força-deslocamento dos refratários. Estas características dos refratários resultam em melhor resistência ao dano por choque térmico. Quando todos os processos de "tenacidade" de trinca de refratários são considerados, é evidente que os agregados dominam a formação de pontes de trinca na região seguinte do rastro da trinca. Entretanto, deve ser concluído, que os agregados, seus tamanhos e distribuições, assim como suas resistências, geometrias e tipo de ligação com a matriz são críticos para as propriedades relacionadas à fratura de refratários.

Rec. 27/05/03, Ac. 18/11/03

• [1] R. C. Bradt, "Fracture Testing of Refractories, Past, Present and Future", pp. 661-668 in Vol. I of Proc. 2^nd Int. Symp. on Refractories, TARJ, Tokyo, Japan (1987). Reprinted in Taikabutsu 40, 1 (1988) 14-18 and in Am. Ceram. Soc. Bull. 67, 7 (1988) 1176-1179.
• [2] R. C. Bradt, "Elastic Moduli, Strength and Fracture Characteristics of Refractories", pp. 165-192 in "Microstructure and Properties of Refractories" edited by J.P. Singh and S. Banerjee, Key Engineering Materials, Vol. 88, Trans Tech Publications, Aedermannsdorf, Switzerland (1993).
• [3] R. C. Bradt, "Twenty First Century Refractories, Dynamic High-Tech Composites", 15-21 in Proc. of the 2^nd Chinese Int. Ref. Symp., edited by X. Zhong, et al. (1992). Also published in Chinese in the J. Chin. Cer. Soc. 21, 2 (1993) 169-175.
• [4] W. H. Gitzen and L. D. Hart, "Explosive Spalling of Refractory Castables Bonded with Calcium Aluminate Cement", Am. Ceram. Soc. Bull. 40, 8 (1961) 503-507, 510.
• [5] A. G. Crouch and K. H. Jolliffe, "The Effect of Stress Rate on the Rupture Strength of Alumina and Mullite Refractories", Proc. Brit. Cer. Soc. 15 (1970) 37-46.
• [6] R. W. Hertzberg, pp. 229-542 in "Deformation and Fracture of Engineering Materials", J. Wiley & Sons, New York, NY (1976).
• [7] J. Nakayama, "Bending Method for Direct Measurement of Fracture Surface Energy of Brittle Materials", Jap. J. Appl. Phys. 3, 7 (1964) 422-423.
• [8] M. Sakai and R. C. Bradt, "Fracture Toughness Testing of Brittle Materials", Int. Mat. Reviews 38, 2 (1993) 53-78.
• [9] W. F. Brown, Jr. and J. E. Srawley, "Plane Strain Crack Toughness Testing of High-Strength Metallic Materials", pp. 13-15 in ASTM STP 410, ASTM, Philadelphia, PA (1967).
• [10] D. Munz and T. Fett, 25-27 in "Ceramics: Mechanical Properties, Failure Behaviour, Materials Selection", Springer-Verlag, Berlin, Germany (1999).
• [11] D. P. H. Hasselman, "Elastic Energy at Fracture and Surface Energy as Design Criteria for Thermal Shock", J. Am.. Ceram. Soc. 46, 10 (1963) 535-540.
• [12] D. P. H. Hasselman, "Unified Theory of Thermal Shock", J. Am.. Ceram. Soc. 52, 11 (1969) 600-604.
• [13] H. G. Tattersall and G. Tappin, "Work of Fracture and its Measurement in Metals and Ceramics", J. Mater. Sci. 1, 3 (1966) 296-301.
• [14] J. A. Rodrigues and V. C. Pandofelli, "Thermal Treatment Temperature and its Influence on the Thermal Shock Parameters of Refractory Castables", Interceram 51 (May 2002) 186-189.
• [15] E. P. Popov, pp. 111-115 in "Engineering Mechanics of Solids", Prentice Hall, Upper Saddle River, NJ (1999).
• [16] I. Dulberg, personal communication, J. H. France Refractories, Snow Shoe, PA (1970).
• [17] J. R. Rice, "A Path Independent Integral and the Approximante Analysis of Strain Concentration by Notches and Cracks", J. Appl. Mech. 35, 6 (1968) 379-386.
• [18] J. Homeny, T. Darroudi and R. C. Bradt, "J-Integral Measurements of the Fracture of 50% Alumina Refratories", J. Am.. Ceram. Soc. 63, 5-6 (1980) 326-331.
• [19] S. Mindes, F. V. Lawrence and C. E. Kesler, "The J-Integral as a Fracture Criterion for Fiber Reinforced Concrete", Cem. Concr. Res. 7, 6 (1977) 731-742.
• [20] M. Roedig, G. Kleist, H. Schiffers and H. Nickel, "The J-Integral Applied to Carbon", pp. 51-62 in Proc. of the Fifth London Int. Carbon and Graphite Conf., Vol. I, Society of Chemical Industries, London (1978).
• [21] J. Nakayama and M. Ishizuka, "Experimental Evidence for Thermal Shock Damage Resistance", Amer. Cer. Soc. Bull. 45, 7 (1966) 666-669.
• [22] J. Nakayama, H. Abe and R. C. Bradt, "Crack Stability in the Work-of-Fracture Test, Refractory Applications", J. Am.. Ceram. Soc. 64, 11 (1981) 671-675.
• [23] H. Harmuth, "Stability of Crack Propagation Associated with Fracture Energy Determined by Wedge Splitting Specimen", Theor. and App. Fract. Mech. 23, 2 (1995) 103-108.
• [24] G. Buchebner and H. Harmuth, "Magnesia-Hercynite Bricks an Innovative Burnt Basic Refractory", pp. 201-203 in Proc. UNITECR 1999, Berlin, Germany, German Refractories Association, Berlin, Germany (1999).
• [25] R. C. Bradt, "Problems and Possibilities with Cracks in Ceramics", pp. 349-360 in Science of Ceramics, 11, Swedish Ceramic Society, Goteborg, Sweden (1981).
• [26] T. A. Adams, D. .J. Landini, C. A. Schmacher and R. C. Bradt, "Micro-and Macro-Crack Growth in Alumina Refractories", Am.. Ceram. Soc. Bull. 60, 7 (1981) 730-735.
• [27] J. Homeny and R. C. Bradt, "Aggregate Distribution Effects on the Mechanical Properties and Thermal Shock Behavior of Model Monolithic Refractory Systems", pp. 110-130 in Adv. in Ceramics, Vol. 13, "New Developments in Monolithic Refractories", R.E. Fisher editor, Am.. Ceram. Soc., Westerville, OH (1985).
• [28] G. A. Gogotsi, Y. L. Grushevsky and K. K. Strelov, "The Significance of Non-Elastic Deformation in the Fracture of Heterogeneous Ceramic Materials", Ceramurgia 4, 2 (1978) 113-118.
• [29] M. Sakai and R. C. Bradt, "Graphical Methods for Determining the Nonlinear Fracture Parameters of Silica and Carbon Refractory Composites", pp. 127-142 in Fract. Mech. of Ceramics, Vol. VII, edited by R. C. Bradt et al., Plenum Publishing Corp., New York, NY (1986).
• [30] G. A. Gogotsi, "The Significance of Non-Elastic Deformation in the Thermal Shock Fracture of Heterogeneous Ceramic Materials", pp. 279-291 in "Thermal Shock and Thermal Fatigue Behavior of Advanced Ceramics", edited by G. A. Schneider and G. Petzow, NATO ASI Series E: Applied Sciences, Vol. 241, Kluwer Academic Publishers, Dordrecht, The Netherlands (1993).
• [31] R. W. Steinbrech, A. Reichi and W. Scharwachter, "R-Curve Behavior of Long Cracks in Alumina", J. Am.. Ceram. Soc. 73, 7 (1990) 2009-2015.
• [32] M. V. Swain, "R-Curve Behavior and Thermal Shock Resistance of Ceramics", J. Am.. Ceram. Soc. 73, 3 (1990) 621-628.
• [33] E. H. Lutz and M. V. Swain, "Interrelation between Flaw Resistance, R-Cuve Behavior and Thermal Shock Strength Degradation in Ceramics", J. Am.. Ceram. Soc. 74, 11 (1991) 2859-2868.
• [34] M. Sakai and H. Ichikawa, "Work-of-Fracture of Brittle Materials with Microcracking and Crack Bridging", Int. J. Fracture 55, 1 (1992) 65-80.
• [35] "Thermal Shock and Thermal Fatigue Behavior of Advanced Ceramics", edited by G. A. Schneider and G. Petzow, NATO ASI Series E: Vol. 241, Kluwer Academic, Dordrecht, The Netherlands (1993).

Datas de Publicação

• Publicação nesta coleção
  01 Abr 2004
• Data do Fascículo
  Dez 2003

Histórico

• Recebido
  27 Maio 2003
• Aceito
  18 Nov 2003