Slope stability analysis at highway BR-153 using numerical models

Abstract

An existing cut slope on Highway RS-471/BR-153 is studied. The slope is composed of the Serra Geral Formation's material: a highly altered volcanic breccia and above it a slightly altered and very fractured rhyolite. A numerical analysis of the slope is carried out in two dimensions. Fracturing of the rhyolite necessitates the use of a constitutive model for materials with families of discontinuities (Ubiquitous-joint). To simplify the analysis of the problem and to examine some of the most sensitive variables, two more analyses are made, replacing the initial model by a Mohr's constitutive model, which considers the material as continuous. The results obtained from the Ubiquitous-joint model provide an acceptable representation of the field conditions, showing a failure mechanism type of rockfall from the face of the slope in the rhyolite, and the rupture surface of the breccia, without propagation of surface failure. In the analysis, when considering both materials as continuous, it is not possible to take account the fault conditions simultaneously, and this analysis also requires values of the mechanical parameters different from those recommended in literature.

Keywords:
Volcanic breccia; Serra Geral Formation; Ubiquitous-joint; numerical models

1. Introduction

In general, numerical studies of slope stability, besides requiring good characterization of the materials involved, need prior knowledge about the possible mechanisms and situations that could lead the system to rupture. Analysis of slope stability using the limit equilibrium method, even though it allows consideration of different layers in each case, does not take account of the effect of excessive mass deformations or of the structural control by the discontinuities that occur mainly in rocky layers. The level of fracture of a rocky mass is closely related to the failure system that it may develop, as discussed by Norrish and Wyllie (1996). In the same paper, these authors describe cases where the level of fracture of the rocky mass is very high, in which structural control by the discontinuities may be less important than the overall conditions of resistance, which are capable of causing a rotational rupture, as is well known in homogeneous slopes formed by cohesive soil.

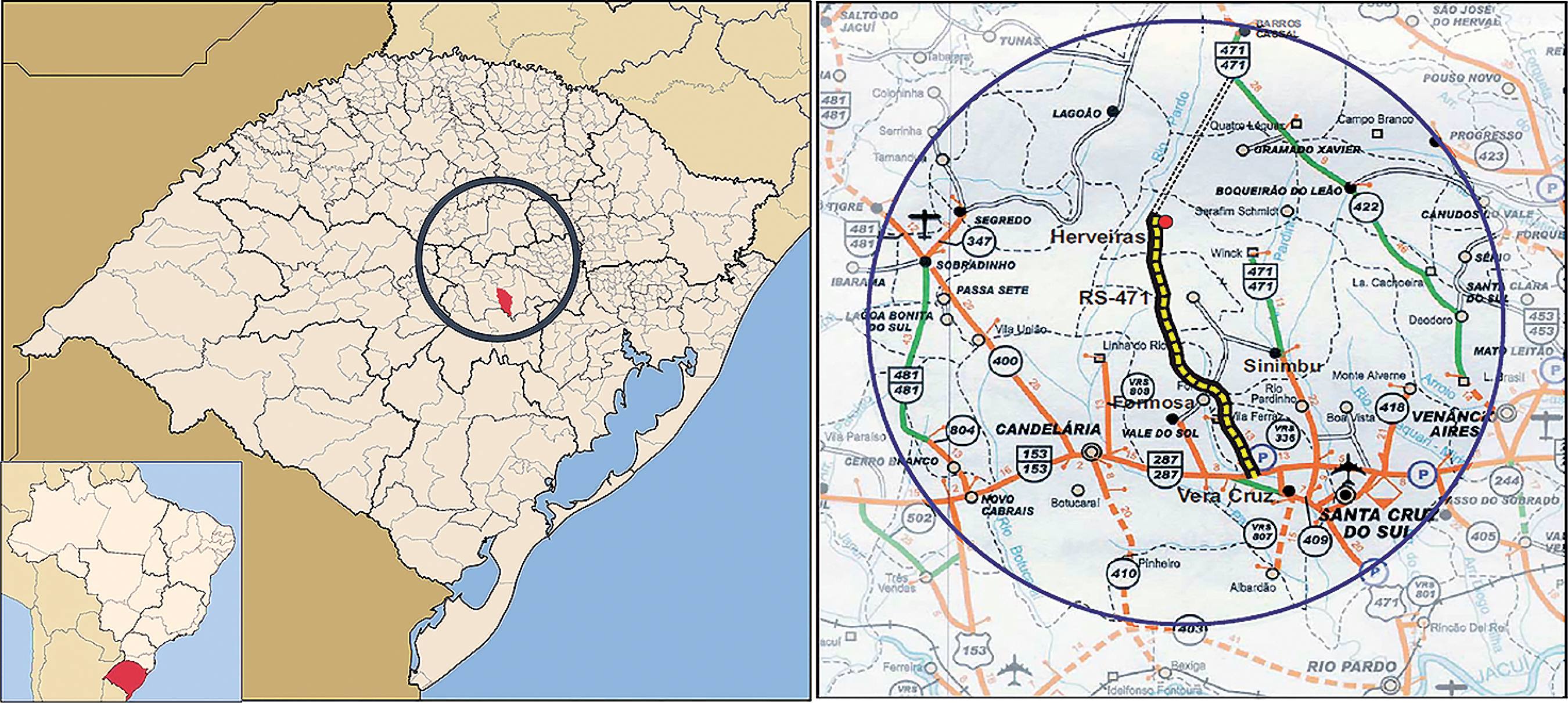
The present paper describes a study of a slope located in the state of Rio Grande do Sul, Southern Brazil, in a section of Highway RS-471/BR-153 between the cities of Barros Cassal and Vera Cruz (see Figure 1), inaugurated at the end of 2010. The slope analyzed has not generated global conditions for rupture since its opening during the course of this investigation. This work aims to obtain a single representative numerical model for the field conditions and those assumed in the study, through variations in the mechanical properties of the slope, as in the case of a continuous model.

Figure 1
Location of the area of study in the state of Rio Grande do Sul (modified from DAER, 2002).

2. Characterization of the area of study

The area of study is located in the acid sequence of the Serra Geral Formation (IBGE 1986), which is composed of rhyolites over a modified volcanic breccia layer. This breccia is not related to acid spill, and so it can be inferred that the arrangement is a result of contact between the basic sequence (with the volcanic breccia on the top) and the acid sequence (with the rhyolite as its base). The studied slope is at k55+340 of the construction project, between altitudes of 505 and 480 m, corresponding to a half-hillside and a homogeneous cut section. No regional faulting is found at this point (see Figure 2). The rhyolite layer has a low degree of weathering, but a high level of fracturing (5-50 fractures/m). This situation is currently causing constant rock falls (Varnes 1978; Cruden and Varnes 1996). No global rupture has been observed, at least in this slope.

Figure 2
(a) Overview of the studied slope. (b) Fracture condition on the rhyolite layer.

2.1 Geotechnical Parameters

The determination of physical characteristics and the resistance parameters for the volcanic breccia was done by the Laboratory of Soil Mechanics of the Federal University of Rio Grande do Sul, at the request of the design company for the project (ECOPLAN Engineering). The values of the angles of friction and the cohesion were estimated from the results of CIU triaxial tests, made in undisturbed test bodies (see Figure 3).

Figure 3
Deviatoric stress versus axial strain for k55+340 (LMS-UFRGS 2004).

Table 1 summarizes the values obtained in the laboratory for the volcanic breccia. The modulus of elasticity was calculated from linear elastic sections obtained from each of the triaxial compression tests. The value for the Poisson coefficient corresponds to a lower limit for this type of materials.

Table 1
Summary of the parameters of the volcanic breccia (LMS-UFRGS 2004).

Parameter		Value
Liquid limit	LL	51.4 %
Plastic limit	LP	38.1 %
Plasticity index	I p	13.3%
Density	d	28.84 kN/m3
Angle of friction (at peak)	φ'p	15.25°
Cohesion	c'	138.77 kPa
Modulus of elasticity	E	146.63 MPa
Poisson coefficient	μ	0.35*

• ^*
  Parameter obtained from the current literature

Owing to a lack of test results for the rhyolite, the mechanical properties of the particles were taken as estimated by Hoek and Brown (1997) for very good quality hard rock masses, listed in Table 2.

Table 2
Summary of the parameters of the broken rhyolite (Hoek and Brown 1997).

Parameter		Value
Density	d	26 kN/m3
Angle of friction (at peak)	φ'p	46°
Cohesion	c'p	13 MPa
Modulus of elasticity	E	42000 MPa
Poisson coefficient	μ	0.2

Table 3 summarizes the parameters for the discontinuities of the rhyolite. These discontinuities were considered to be plain and with no infillings, and therefore the values of cohesion, dilatability, and tension resistance were taken as zero. The results for the discontinuities were obtained through field and laboratory studies for a section located between sections 55+840 and 56+200; however, in geologic and geotechnical terms, they are considered parts of the same project unit. An interface was established between the two layers, which allowed neither relative slipping between the two layers nor their separation, but only elastic displacements. The tangential and normal rigidities were considered to be equal. Thus, the value taken for this interface was K_N = K_S = 253.33 MPa/m.

Table 3
Summary of the parameters for the discontinuities of the rhyolite (DAER 2010).

Parameter	Value
Dip	78°
Cohesion	0.0
Dilatancy	0.0
Angle of friction	36°
Tension resistance	0.0

2.2 Structural model and element mesh for numerical analysis

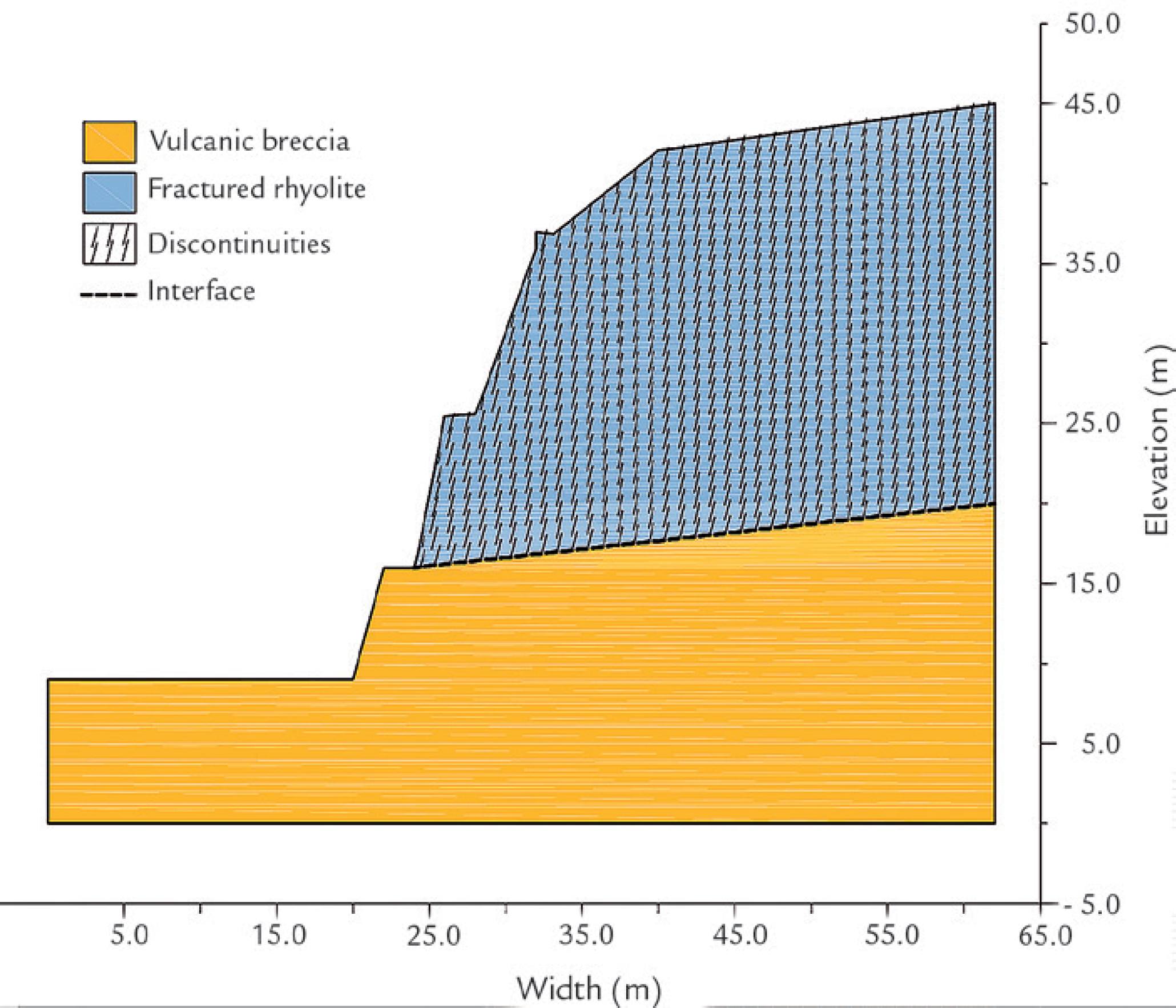
Figure 4 presents the model to be evaluated, including the system of discontinuities of the rhyolite. For the analyses ignoring the presence of discontinuities, the geometry of the section remains constant, with some of the material properties being modified in an attempt to reproduce the rupture mechanism from the first case. The material parameters for the mass without discontinuities are obtained as part of the results of the simulation process. Figure 5 presents the element mesh for this analysis, as well as the boundary conditions imposed on the model. The thick black line indicates the interface defined by the material change. The analysis of the model for each condition was performed using FLAC version 5.00 software developed by ITASCA.

Figure 4
Model of the evaluated section.

Figure 5
Mesh of elements with fixed areas.

3. Results

Results are presented for the three types of simulation conditions: a discontinuous rocky mass, a continuous mass with a flat rupture, and a continuous mass with a deep rupture.

3.1 Discontinuous rocky mass

To obtain a model that represents the current degree of fracture in the rocky mass, the Ubiquitous-joint model available in FLAC was applied. Since the simulation was carried out in two dimensions, only the discontinuities perpendicular to the model were taken into account. This type of constitutive model, besides allowing rupture surfaces for continuum materials according to the Mohr-Coulomb criterion, allows visualization of the effects of ruptures associated with sliding along different discontinuities. Figure 6 presents different states for the elements of which the model is composed, enabling visualization of the elements under instability, either for the curved surfaces of rupture (see the volcanic breccia) or for the sliding of the elements along the discontinuities. In the center of the rhyolite mass, it is also possible to observe the presence of consistent slide surfaces with the formation of alleviating tensions caused by the lateral expansion (in the lower part of the rhyolite layer).

Figure 6
States of the model (with Ubiquitous-joint).

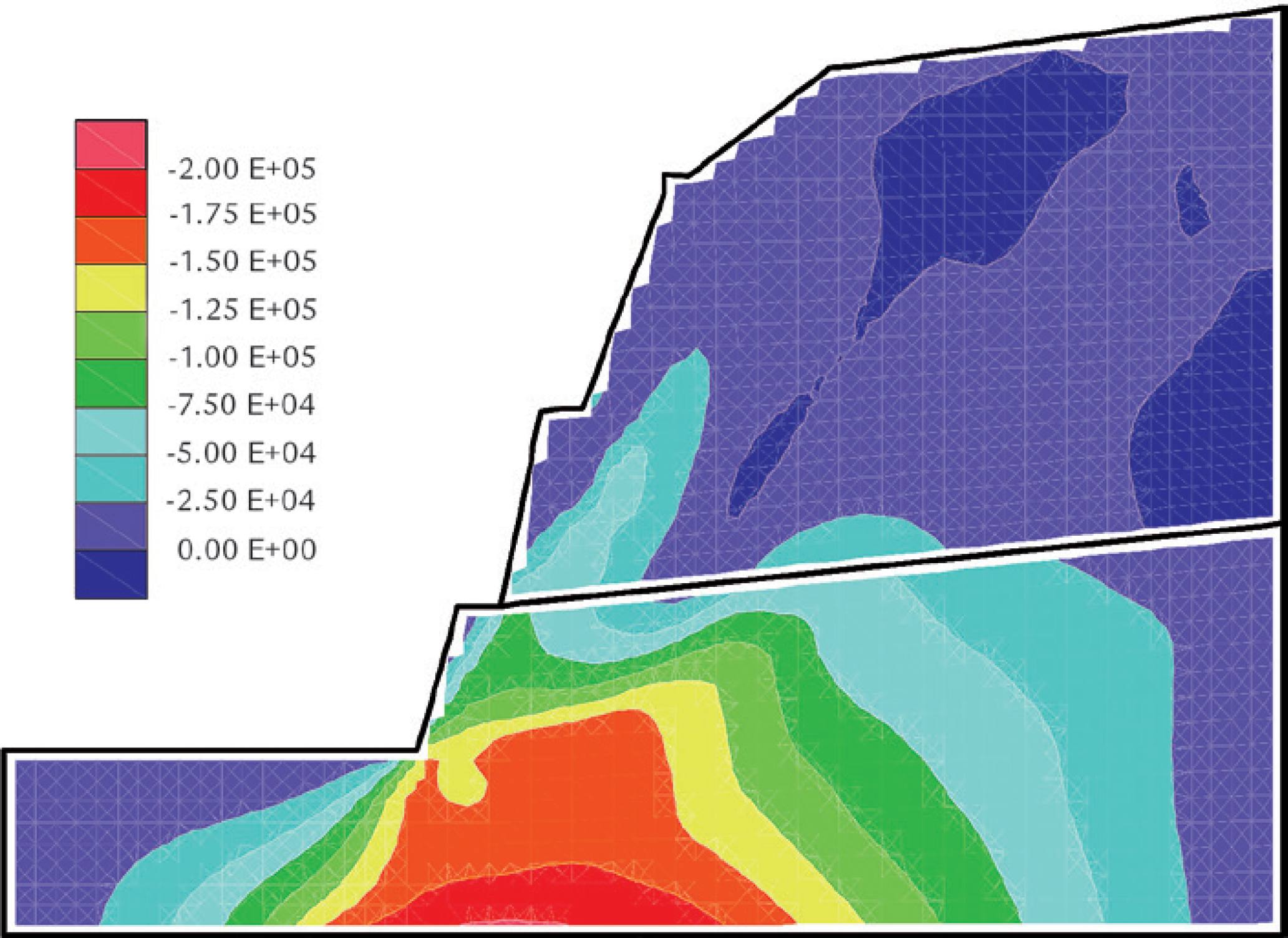
The distribution of displacement vectors presented in Figure 7 confirms the main source of rock particle falls, which are deposited on the lower part of the slope as well as on the highway (see Figure 2b). There exist a few points of origin of rock falls in the upper part of the layer, mainly caused by the slope declivity angle. The distribution of shear stress presented in Figure 8 is consistent with the condition imposed on the interface between the two layers, namely, continuity of stresses above and below it. The highest levels of tension arise at the foot of the slope, reaching yielding levels in the breccia and causing local rupture of the material (see Figure 2a).

Figure 7
Displacement vectors (with Ubiquitous-joint).

Figure 8
Shear stress S_xy (with Ubiquitous-joint).

3.2 Continuous mass with flat rupture

In this case, a flat rupture similar to those obtained using the Ubiquitous-joint model was made, but for a rocky mass with no fractures or systems of discontinuities. As such, some variations were necessary: considering the rhyolite layer as a continuum and modifying its properties of resistance to a flat rupture in the rock layer, rather than to a deep rupture controlled by the volcanic breccia. Hoek and Brown (1997) suggest a reduction in the properties of the rock if it is fractured, and when the mass is confined. Because of the geometry of the slope, it is not possible to consider this mass as confined, and also the value for the angle of declivity of the slope has a strong effect on the volume of the material in rupture. The geotechnical parameters applied in this analysis were constant for the breccia; for the rhyolite, after multiple iterations with small increases, the following final values were adopted:

• cohesion = 0.0,

• angle of friction = 69°.

Figure 9 shows the results of this simulation. The properties of the breccia were not decreased, since the existence of a rupture surface in the breccia influences its propagation along the rhyolite layer. For the given angle of declivity of the slope, the angle of friction for the rhyolite given by the simulation is not consistent with any values in literature: however, it does predict shallow failures (see Figure 10). These flat ruptures retain the form predicted by a Mohr-Coulomb model, exhibiting a rupture surface curve.

Figure 9
States of the model (continuous, flat rupture).

Figure 10
Displacement vectors (continuous, flat rupture).

The distribution of shear stress presented in Figure 11 suggests a reduction in the levels of shear stress in the areas next to the slope face, but the condition of maximum tension at the foot of the slope is maintained.

Figure 11

3.3 Continuous mass with deep rupture

In an attempt to simulate ruptures located at the foot of the slope, while retaining the properties of the interface, the rupture surface was propagated discontinuously along the rhyolite layer, this being the worst-case representation of conditions in the field. In this situation, the parameters of the rhyolite and the breccia were very different. The variations in the breccia were imposed by the necessity to generate the rupture surface in it, since the parameter values obtained from the triaxial tests could not cause rupture in this material. After several iterations, starting with the initial values for both materials, a qualitatively good representation was obtained with the following values: For the breccia, cohesion = 96.4 kPa, angle of friction = 18°; and for the rhyolite, cohesion = 13.0 kPa, angle of friction = 60°.

Figure 12 presents different states of the model. No surface rupture was observed in the slope. The value for the angle of friction of the rhyolite was adopted because of the sensitivity of this material to a rupture surface from the breccia. With this value of the angle of friction, the susceptibility of the rhyolite remained low, although it should be pointed out that it is a theoretical value, not necessarily representative of realistic situations. It can be seen from Figure 13 that it was not possible to obtain significant horizontal displacements along the slope face, confirming the absence of boulders in unstable condition, and therefore, denying the possibility of rockfalls.

Figure 12
States of the model (continuous, deep rupture).

Figure 13
Displacement vectors (continuous, deep rupture).

The distribution of shear stress presented in Figure 14 is similar to those obtained in the previous cases, but with a reduction in the stress concentration at the foot of the slope. Although the concentration of shear stress at the foot is reduced, there is a concentration of the mechanical response in the volcanic breccia layer, representing a minor mechanical contribution for the rhyolite, with an absence of ruptures in the slope face. The plastification zones inside the rhyolite mass are associated with a Mohr-Coulomb failure surface along the slope, initiated by the rupture in the breccia.

Figure 14
Shear stress S_xy (continuous, deep rupture).

4. Conclusions

Using the Ubiquitous-joint model, it has been possible to obtain a representation very close to the real conditions for the slope studied, defined by the following processes:

• superficial rupture of the rhyolite layer and falls of blocks, mainly on the first slope bed and on the shoulder of the road;

• superficial rupture of the volcanic breccia at the foot of the slope, without affecting elements away from the slope.

When the rhyolite layer was considered as continuous, it was not possible to simulate both processes simultaneously. It was therefore necessary to model each rupture separately and apply the resistance parameters through a mathematical model. It can thus be inferred that it is not possible to represent a discontinuous mass satisfactorily by using a continuous model, because of the high degree of uncertainty in the parameters involved in the rupture, in the geometry of the surface, and in the rupture surfaces.

The effect of the slope angle was important when determining the areas subject to loss of material by sliding. Thus, the losses were small in the upper part of the slope, where the declivities are less than the dip of the discontinuities, but high in the lower part of the rhyolite layer, in which the declivity is greater than the dip. In all the modeling cases, the need to reach a rupture state makes convergence of the system impossible, precluding the existence of a unique answer for each case. Therefore, further analysis and assessment of the results are necessary. Although the Ubiquitous-joint model allows analysis of a discontinuous mass, the analysis is limited by a number of important variables, including variations in ambient temperature, volumetric and temperature gradients along the fractured mass, and vibrations imposed during the construction of the highway, among others.

5. References

• AUTONOMOUS DEPARTMENT OF HIGHWAYS - DAER. Stabilization of rock slopes Project: topographic saddle - km 55+840 to km 56+200 - Cut 21. RS/471 Highway, section Barros Cassal - Santa Cruz do Sul (in portuguese). Porto Alegre (Brazil), 2010. 58p.
• AUTONOMOUS DEPARTMENT OF HIGHWAYS-DAER. Engineering final Project: RS/471 Highway, section Barros Cassal - Santa Cruz do Sul (in portuguese). v. 1. Porto Alegre (Brazil), 2002. 246p.
• BRAZILIAN INSTITUTE OF GEOGRAPHY AND STATISTICS - IBGE. SH.22 Sheet: Porto Alegre and part of SH.21 Uruguaiana and SI.22 Mirim Lagoon sheets. Natural Resources Survey (in portuguese). Rio de Janeiro (Brazil). v. 33, 1986. 794p.
• CRUDEN, D. M. & VARNES, D. J. Landslide types and processes. In: TURNER, A. K., SCHUSTER, R. L. (Eds.). Landslides: investigation and mitigation. Special Report 247 Washington, D. C.: Transportation Research Board, National Research Council. v. 247, p. 36-75, 1996.
• HOEK, E., BROWN, E. T. Practical estimates of rock mass strength. International Journal of Rock Mechanics and Mining Sciences v. 34, n. 8, p 1165-1186. 1997.
• ITASCA Consulting Group FLAC - Fast Lagrangian Analysis of Continua, Ver. 5.0 User's Guide. Minneapolis: Itasca. 2005.
• NORRISH, N. I., WYLLIE, D. C. Rock slope stability analysis. In: TURNER, A. K., SCHUSTER, R. L. (Eds.). Landslides: investigation and mitigation. Special Report 247. Washington, D. C.: Transportation Research Board, National Research Council. p. 391 - 425, 1996.
• SOIL MECHANICS LABORATORY (LMS) - UFRGS. RS 471 (Vera Cruz/RS) Test report (in portuguese). Porto Alegre (Brazil), 2004. 25p.
• VARNES, D. J. Slope movement types and processes. In: SCHUSTER, R. L., KRIZEK, R. J. (Ed.).Landslides: analysis and control. Special Report 176. Washington, D. C.: Transportation Research Board, National Research Council. p. 11 - 33. 1978.

Publication Dates

• Publication in this collection
  Apr-Jun 2016

History

• Received
  21 July 2015
• Accepted
  28 Jan 2016