Resumos
O desempenho de unidades de contato que operam em regime de fluxo contínuo depende, entre outros, do padrão de escoamento que se desenvolve no seu interior. Já o levantamento de dados experimentais, como a elevação da superfície d'água e do campo de velocidades, não é uma tarefa fácil. Por tais razões, o uso de modelos numéricos na obtenção de padrões de escoamento em unidades de contato tem se tornado uma boa alternativa. A falta de dados hidrodinâmicos para a calibração e verificação de modelos numéricos tem sido um dos principais fatores que vem limitando o uso mais extensivo dessa ferramenta. O presente trabalho propõe uma nova técnica de calibração de modelo numérico, baseada no ajuste de curvas de passagem obtidas pelo modelo numérico e as obtidas experimentalmente ao longo das unidades de contato. A metodologia proposta é parcialmente avaliada e os resultados indicam ser essa uma técnica bastante promissora.
Unidades de contato; modelagem numérica; hidrodinâmica; calibração de modelo; traçadores
The performance of continuous flow contact units relies, among other factors, on the flow pattern inside them, and that the measurement of flow patterns in this type of unit is not an easy task. For this reason, the use of numerical models to obtain flow patterns in contact units has become a good alternative. However, the lack of hydrodynamic data to calibrate the models has been one of the main factors limiting a more extensive use of numerical models for this purpose. This work proposes a new calibration technique for numerical models which is based on the best fitting of measured and simulated flow through curves throughout the unit. The proposed methodology is partially evaluated and the results indicate it to be very promising.
Contact units; numerical modeling; hydrodynamics; model calibration; tracers
ARTIGO TÉCNICO
Proposta de calibração de modelos hidrodinâmicos aplicados a unidades de contato utilizando uma função de distribuição de tempos de residência
A proposal of calibration of hydrodynamic models of contact units using a residence time distribution function
Edmilson Costa TeixeiraI; Julio Tomás Aquije ChacaltanaII; Renato do Nascimento SiqueiraIII; Camila Gomes PachecoIV
IEngenheiro Civil pela UFBA. Mestre em Engenharia Civil pela EESC-USP. Doutor em Engenharia Civil pela University of Bradford (Inglaterra). Professor do Departamento e do Programa de Pós-Graduação em Engenharia Ambiental da UFES
IIGraduação em Engenharia de Mecânica dos Fluidos pela Universidad Nacional Mayor de San Marcos, UNMSM, Lima-Perú. Mestre e Doutor em Engenharia Mecânica dos Fluidos pela Universidade Federal do Rio de Janeiro (PEM-COPPE/UFRJ). Professor do Departamento e do Programa de Pós-Graduação em Engenharia Ambiental da UFES
IIIEngenheiro Mecânico e Mestre em Engenharia Ambiental pela UFES. Doutor em Engenharia Civil pela Loughborough University of Technology (Inglaterra). Professor Colaborador do Programa de Pós-Graduação em Engenharia Ambiental da UFES
IVBióloga pela Universidade Federal do Espírito Santo (UFES). Mestre em Engenharia Ambiental pela UFES
Endereço para correspondência Endereço para correspondência: Edmilson Costa Teixeira Departamento de Engenharia Ambiental - Universidade Federal do Espírito Santos - UFES Av. Fernando Ferrari, s/nº - Goiabeiras 29060-970 Vitória - ES - Brasil Tel.: (27) 3335-2675 Email: edmilson@npd.ufes.br
RESUMO
O desempenho de unidades de contato que operam em regime de fluxo contínuo depende, entre outros, do padrão de escoamento que se desenvolve no seu interior. Já o levantamento de dados experimentais, como a elevação da superfície d'água e do campo de velocidades, não é uma tarefa fácil. Por tais razões, o uso de modelos numéricos na obtenção de padrões de escoamento em unidades de contato tem se tornado uma boa alternativa. A falta de dados hidrodinâmicos para a calibração e verificação de modelos numéricos tem sido um dos principais fatores que vem limitando o uso mais extensivo dessa ferramenta. O presente trabalho propõe uma nova técnica de calibração de modelo numérico, baseada no ajuste de curvas de passagem obtidas pelo modelo numérico e as obtidas experimentalmente ao longo das unidades de contato. A metodologia proposta é parcialmente avaliada e os resultados indicam ser essa uma técnica bastante promissora.
Palavras-chave: Unidades de contato, modelagem numérica, hidrodinâmica, calibração de modelo, traçadores.
ABSTRACT
The performance of continuous flow contact units relies, among other factors, on the flow pattern inside them, and that the measurement of flow patterns in this type of unit is not an easy task. For this reason, the use of numerical models to obtain flow patterns in contact units has become a good alternative. However, the lack of hydrodynamic data to calibrate the models has been one of the main factors limiting a more extensive use of numerical models for this purpose. This work proposes a new calibration technique for numerical models which is based on the best fitting of measured and simulated flow through curves throughout the unit. The proposed methodology is partially evaluated and the results indicate it to be very promising.
Keywords: Contact units, numerical modeling; hydrodynamics, model calibration, tracers.
INTRODUÇÃO
A eficiência do tratamento em uma unidade de contato está intimamente relacionada com os padrões de escoamento no seu interior. Entretanto, devido a dificuldades em medir escoamentos complexos (tridimensionais, reversos, turbulentos), as unidades de contato são tradicionalmente tratadas como "caixas pretas", considerando-se apenas informações em suas seções de entrada e de saída (Falconer e Liu, 1988; Teixeira; 1993).
A determinação dos padrões de escoamento nem sempre é uma tarefa fácil e normalmente necessita de mão de obra especializada e equipamentos sofisticados, o que implica em altos custos para a realização dos experimentos, inviabilizando na maioria das vezes a obtenção do campo de velocidades. Este fato justifica a adoção da abordagem do tipo "caixa preta" para se avaliar o desempenho das unidades.
A aplicação da modelagem numérica em estudos relacionados à desinfecção de água (hidrodinâmica e processo de tratamento) dá origem a uma nova forma de adquirir conhecimento a respeito de processos físicos, químicos e biológicos que ocorrem no interior das unidades. Entre as vantagens da modelagem numérica pode-se citar a simplicidade e o baixo custo, quando comparada com modelagem física ou medições diretas. Porém, entre os fatores que contribuem para o número reduzido de trabalhos nessa linha encontra-se a falta de dados de monitoramento que possam ser utilizados na validação dos modelos numéricos, devido às dificuladades citadas anteriormente.
Com objetivo de superar este problema, neste trabalho, o padrão de escoamento dentro de uma unidade de contato chicanada é obtido através da calibração de curvas de passagem obtidas pelo modelo. As curvas de passagem são comumente utilizadas para a avaliação hidrodinâmica de unidade de contato por serem de fácil obtenção e baixo custo quando comparado com a medição dos campos de velocidade. Esta nova proposta de calibração, baseada no ajuste das curvas de passagem medidas e simuladas pelo modelo, parte do princípio de que se várias curvas de passagem obtidas no interior da unidade, e não apenas a curva obtida na saída, forem reproduzidas pelo módulo de simulação de transporte de soluto do modelo numérico é porque o módulo hidrodinâmico também está calibrado.
Depois de calibrado e validado, o modelo pode ser utilidade tanto para o diagnóstico do desempenho de unidades existentes como para o desenvolvimento mais racional de novas unidades.
O MODELO DIVAST
O modelo numérico utilizado neste estudo, para a apresentação e avaliação parcial da metodologia proposta, é o DIVAST (Depth Integrated Velocity And Solute Transport). As equações governantes deste modelo são do tipo águas rasas; resultado da integração na vertical 2DH das equações tridimensionais de Reynolds para um fluido incompressível e das hipóteses de pressão hidrostática e onda longa. O código numérico deste modelo é escrito em linguagem FORTRAN 77 e foi desenvolvido por Falconer (1976) para estudar a circulação de jatos forçados em reservatórios e portos.
O modelo DIVAST tem sido tradicionalmente utilizado na área costeira. Gradativamente seu emprego na área de tratamento de águas tem sido ampliado. Kashefipour et al (2001) utilizaram este modelo para estudar a hidrodinâmica e a distribuição da concentração de coliformes fecais no sistema Estuarino de Ribble localizado na costa noroeste da Inglaterra. Wang (1995) utilizou este mesmo modelo num estudo do processo de desinfecção em uma unidade de contato. Nacionalmente, este modelo vem sendo utilizado no Programa de Pós-Graduação de Engenharia Ambiental da Universidade Federal do Espírito Santo (PPGEA/UFES) para determinar os padrões de escoamento e o transporte de poluentes no interior das baías do Espírito Santo e de Vitória (Rocha, 2000; Castro, 2001; Barros, 2002; Maciel, 2004) e, recentemente, para o estudo da hidrodinâmica do litoral do Espírito Santo (Viegas, 2006). Neste trabalho, o modelo é utilizado para avaliar a hidrodinâmica no interior de uma unidade de contato.
Equações governantes
As equações que representam os princípios físicos da conservação da massa, da quantidade de movimento, e da conservação da substância com médias de Reynolds são integradas na vertical, fazendo-se uso das hipóteses de fluido incompressível, pressão hidrostática, e onda longa. O resultado deste procedimento são as equações do tipo águas rasas. As equações que representam o movimento levam em consideração o efeito de Coriolis, as tensões provocadas pelo vento, o atrito com o fundo e as tensões turbulentas de Reynolds.
A equação da conservação da massa é a Equação 2.
Na Equação (1), o termo a representa a taxa de variação da elevação, e os termos b e c representam respectivamente as variações espaciais das vazões unitárias na direção X e na direção Y.
A equação da conservação da quantidade de movimento na direção X é a Equação 2.
Os termos da Equação (2) representam os seguintes efeitos: aceleração local (a), aceleração advectiva (b), rotação da Terra - aceleração de Coriolis (c), gradiente de pressão (d), tensões provocadas pelo vento (e), atrito com o fundo (f) e as tensões turbulentas (g).
A equação da conservação da quantidade de movimento na direção Y é dada pela Equação 3.
Analogamente, os termos da Equação (3) representam os mesmos efeitos que a Equação (2).
A equação tridimensional de transporte de soluto integrada sobre a coluna da água fornece a equação bidimensional de transporte de solutos, também conhecida como equação da advecção-difusão, apresentada na Equação 4.
As definições das variáveis físicas da Equação (4) são apresentadas na Tabela 1.
De acordo com Preston apud Falconer e Ismail (1997), os coeficientes de dispersão-difusão (m2/s) são definidos como:
Onde: kl e kt são, respectivamente, a constante adimensional de dispersão longitudinal e a constante adimensional de difusão turbulenta lateral, cujos valores sugeridos por Elder (1959) correspondem, respectivamente, a 5,93 e 0,23 para canal retilíneo.
Solução das equações governantes
As equações diferenciais parciais governantes dos processos hidrodinâmicos e de transporte de soluto não possuem solução analítica. Portanto, elas devem ser solucionadas numericamente. O método numérico usado para dar solução às equações é o método das diferenças finitas.
O tipo particular de esquema de diferenças finitas no modelo DIVAST é baseado no Método Implícito de Direção Alternada conhecido como ADI (Alternating Direction Implicit). O método envolve a subdivisão de cada passo de tempo em dois meio passos de tempo. Desta forma, um esquema implícito pode ser aplicado, porém considerando-se apenas uma direção implicitamente para cada meio passo de tempo. No primeiro meio passo de tempo, a elevação da água (h) e a componente da velocidade (U) são solucionadas na direção do eixo (X), e no segundo meio passo de tempo, a elevação da água (h) e a componente da velocidade (V) são solucionados na direção do eixo (Y). Incluídas as condições de contorno, as equações algébricas resultantes para cada passo de tempo são solucionadas usando-se o método direto de eliminação de Gauss.
A malha usada é do tipo deslocada com espaçamentos iguais nas direções X e Y; a célula é quadrada. As variáveis h (elevação) e S (concentração) estão localizadas no centro dos quadrados e as componentes da velocidade, U e V, estão localizadas na metade das faces do quadrado, com a componente da velocidade (U) ao longo do eixo (X) positivo e a componente da velocidade (V) ao longo do eixo (Y) positivo. Maiores detalhes sobre a discretização das equações da conservação da massa, conservação da quantidade de movimento, e de transporte de solutos do modelo DIVAST são encontrados em Falconer (1976).
METODOLOGIA
Modelagem física
Os dados utilizados para calibrar o modelo DIVAST são as curvas de passagem registradas experimentalmente por Siqueira (1998) em um estudo voltado para a avaliação do coeficiente de mistura da unidade, utilizando diversas metodologias existentes na literatura.
A unidade utilizada era do tipo chicanada, com 2,40m de comprimento, 1,81m de largura e 0,26m de profundidade. Foram introduzidas nesta unidade sete chicanas longitudinais com 0,03m de largura e 2,20m de comprimento, dividindo a unidade em oito compartimentos. O circuito hidráulico, as dimensões da unidade de contato e a localização dos pontos de monitoramento usados para registrar as curvas de passagem do traçador estão mostrados na Figura 1.
A vazão utilizada foi de 1,0 L/s e o traçador foi o Cloreto de Potássio (KCl). Este traçador era lançado através de um difusor localizado a 0,10m da extremidade do dissipador de energia, o qual ocupava toda a largura do compartimento (0,2m) e era posicionado a 0,13m do fundo da unidade (meia altura da lâmina dágua). O monitoramento da passagem do traçador foi realizado a 80% do comprimento útil de cada compartimento (pontos de A-G), com exceção do último compartimento em que o monitoramento foi realizado na saída da unidade (ponto H). O volume de traçador injetado foi de 54 ml a uma concentração de 40 mg/L.
O experimento teve duas repetições sob as mesmas condições, desta forma, foram obtidas duas curvas de passagem experimentais para cada ponto de monitoramento. A curva média entre as duas curvas experimentais é tomada como referência e usada para ajustar as curvas de passagem obtidas pelo modelo numérico. A curva média para cada ponto de monitoramento é mostrada na Figura 2. Nesta Figura as curvas para os dois primeiros compartimentos não são mostradas, pois nestas seções o traçador ainda não havia se misturado completamente na seção transversal.
Calibração do modelo DIVAST
A calibração consistiu em ajustar algumas variáveis físicas a fim de obter a melhor resposta do modelo computacional quando comparada aos dados experimentais. Os parâmetros utilizados no ajuste das curvas de passagem foram: a rugosidade do fundo (ks) e a vazão (Q) para a hidrodinâmica e a constante adimensional de dispersão longitudinal (kl) e a constante adimensional de difusão turbulenta lateral (kt) para a dispersão do soluto. A hidrodinâmica é afetada somente por ks e Q, enquanto que as curvas de passagem são afetadas por kl, kt, ks e Q. Além disso, a vazão normalmente não é utilizada como um parâmetro de calibração, mas devido a imprecisões no aparelho de medição de vazão (rotâmetro), resolveu-se permitir uma variação de até 4% neste parâmetro para um melhor ajuste entre os resultados experimentais e obtidos pelo modelo.
Ajuste da Constante Adimensional de Difusão Turbulenta Lateral (kt) e da Vazão (Q)
A princípio, foram ajustados somente os parâmetros kt e vazão, mantendo-se fixos os parâmetros ks e kl. A unidade de contato foi feita de aço revestido. A rugosidade (ks) para este tipo de material é de 0,0004m para material novo e está numa faixa de 0,0005 a 0,0012m para material usado (Netto e Alvarez, 1988). O valor fixado para a rugosidade do fundo foi ks = 0,0005m e o valor fixado para a constante adimensional de dispersão longitudinal (kl = 4,57) foi o obtido experimentalmente por Siqueira (1998).
Outros autores utilizaram o ks como parâmetro de calibração do modelo. Falconer e Ismail (1997), por exemplo, realizou simulações para vários valores de ks e encontrou um ks igual a 0,001m para uma unidade de contato feita de madeira compensada.
A constante adimensional de dispersão longitudinal (kl) influencia na dispersão do soluto. Elder (1959) propõe um kl = 5,93 em um estudo realizado num canal retilíneo. Falconer (1997) encontrou um kl = 13 para a calibração de um modelo numérico utilizado para estudar a dispersão do traçador em uma unidade de contato chicanada. Esta unidade também possuía oito compartimentos, contudo, o comprimento de cada compartimento era cerca de 4,5 vezes a largura, enquanto que no experimento de Siqueira (1998) a relação entre o comprimento e largura da unidade é igual a 12. Em unidades de tratamento de água e efluentes, o aumento da relação entre o comprimento e a largura da unidade tende a diminuir o valor de kl. Outro valor de kl foi encontrado por Teixeira (1993) para unidades chicanadas (kl = 7,12).
Elder (1959) apresenta em seu estudo um valor de kt igual a 0,23 para a dispersão de soluto num canal reto e um valor de kt igual a 1,00 foi obtido por Falconer (1997) para um canal chicanado. Desta forma, optou-se por utilizar valores de kt no intervalo 0,23 < kt < 1,0 para a calibração do modelo.
Como mencionado anteriormente, a vazão normalmente não é utilizada como parâmetro de calibração, mas a medida de vazão pelo rotâmetro utilizado por Siqueira (1998) foi de 1L/s, com uma incerteza relativa em torno de 5%. Para cada valor de kt variou-se a vazão até mais 4% em relação à vazão de operação, de forma a se obter a que melhor ajustasse os picos de concentração das curvas de passagem numérica e experimental.
Tendo vários valores de kt com sua respectiva vazão, identificou-se qual par kt - Q que melhor ajusta as curvas de passagem. Para a calibração do modelo, foi escolhido o par kt - Q que apresentou o menor valor do Erro Percentual de Área (EPA) médio da unidade chicanada (Rauen, 2001). O parâmetro EPA representa a porcentagem de área não-coincidente entre as duas curvas de passagem envolvidas em uma comparação. Sendo ele calculado com base em curvas normalizadas, de área unitária. O valor máximo para este parâmetro é 100%.
Ajuste da Constante Adimensional de Dispersão Longitudinal (kl)
Depois de ajustados os parâmetros kt e vazão, procedeu-se o ajuste da constante adimensional de dispersão longitudinal. Foram realizadas simulações para valores de kl entre 2,50 e 6,50. O valor de ks foi fixado em 0,5 mm. O EPA foi utilizado para verificar o ajuste entre as curvas medidas e estimadas pelo modelo.
Ajuste da rugosidade do fundo (ks)
Calibradas as constantes adimensionais de dispersão longitudinal, de difusão turbulenta lateral e a vazão, partiu-se para o ajuste da rugosidade do fundo. Os valores de ks utilizados na calibração foram 0,05; 0,1; 0,5; 2,5 e 5,0mm. O parâmetro EPA também foi utilizado para se quantificar o erro entre as curvas de passagem medidas e simuladas.
Este processo de calibração é do tipo iterativo, onde a calibração prossegue até que a diferença entre o valor do parâmetro EPA médio de uma iteração e o valor desse parâmetro para a iteração anterior seja inferior à diferença máxima admissível, cujo valor dependerá do problema a ser analisado. Se a diferença for superior à admissível, volta-se ao ajuste da constante adimensional de difusão turbulenta lateral e da vazão, fixando os valores da constante adimensional de dispersão longitudinal e da rugosidade do fundo encontrados na primeira iteração. A Figura 3 ilustra o procedimento de calibração.
RESULTADOS E DISCUSSÃO
Ajuste de kt e vazão
Para escolher qual a vazão para um determinado kt, foi escolhido o menor valor do erro percentual absoluto médio (MAPE: Mean Absolute Percentage Error) entre o tempo de pico simulado e o experimental para cada ponto de monitoramento. O valor de MAPE é dado por:
onde tpe e tps representam os tempos de pico experimental e simulado, respectivamente. O valor de MAPE calculado pela equação 8 representa uma média dos ajustes para os compartimentos 3 a 8.
Os valores do MAPE dos tempos de pico das curvas dentro da unidade para cada valor de vazão e para um mesmo valor de kt estão mostrados na Tabela 2. O menor valor do MAPE, entre parênteses, está associado ao par kt - Q que apresentou um melhor ajuste dos tempos de pico. Sendo assim, para cada valor de kt encontrou-se a vazão que melhor ajustou os tempos de pico das curvas.
O próximo passo é identificar qual par kt - Q que melhor ajustou as curvas de passagem. Para isto foi escolhido o par kt - Q que apresentou o menor valor do Erro Percentual de Área (EPA) médio da unidade chicanada. De acordo com a Tabela 2 percebe-se que o par kt - Q que apresentou menor valor médio de EPA (4,77%) foi encontrado para kt = 0,50 e Q = 1,02 L/s, representando uma maior proximidade dos resultados numéricos com os experimentais. Logo, estes serão os valores de kt e Q considerados como ajustados na primeira iteração.
As curvas simuladas e medidas ao longo de toda a unidade de contato para esta etapa do processo iterativo estão apresentadas na Figura 4.
Ajuste da Constante Adimensional de Dispersão Longitudinal (kl)
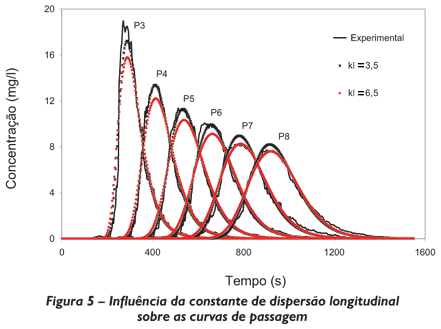
Fixados os valores de ks = 0,5mm, kt = 0,50 e Q = 1,02 L/s, partiu-se para o ajuste do parâmetro kl. O valor de referência utilizado para o parâmetro kl é o obtido através do experimento de Siqueira (1998), que é igual a 4,57. Simulações foram realizadas para diversos valores de kl maiores e menores do que o de referência. Os valores de kl utilizados nas simulações foram, 2,50; 3,50; 4,57; 5,50 e 6,50, porém, para facilitar a visualização dos resultados, somente as simulações para kl = 3,5 (menores desvios) e kl = 6,5 (maiores desvios) são mostradas na Figura 5.
Pode-se perceber na Figura 5 que quanto maior o valor de kl, menor é o pico de concentração da curva, ou seja, para o valor de kl igual a 6,5 a pluma de traçador está mais espalhada longitudinalmente do que para kl igual a 3,5; o que significa que o tempo de chegada é menor para o maior valor de kl.
O erro em cada ponto de monitoramento para os cinco valores de kl simulados é apresentado na Figura 6. Fazendo-se uma análise dos erros apresentados nesta figura é possível perceber a sensibilidade do modelo ao valor de kl. No ponto de monitoramento 3, por exemplo, houve uma variação de 3% entre o EPA máximo e mínimo, para os pontos 5 e 6 esta variação foi em torno de 2,3%, enquanto que para o ponto 8 esta variação foi de 1,1%. Observa-se também que para os compartimentos de 3 a 6, há uma tendência em aumentar o valor do erro com o aumento de kl; para os compartimentos 7 e 8 esta relação se inverte.
De acordo com a Tabela 4, percebe-se que o valor de kl que apresentou menor EPA médio (4,49%) para os valores de kt, 0,50 e vazão 1,02 L/s, foi o de 3,50. Por outro lado, um valor de kl que apresente valores menores de EPA médio pode estar entre 2,50 e 3,50 ou 3,50 a 4,57, pois não foi feito um refinamento maior entre os valores de kl testados.
Ajuste da rugosidade do fundo (ks)
Depois do ajuste de kl, foram realizados mais quatro simulações para a calibração de ks. Os demais parâmetros foram fixados em kt = 0,50, Q = 1,02 L/s e kl = 3,50. O resultado da simulação para a rugosidade de fundo ks = 0,05 é apresentado na Figura 7, onde são mostradas as curvas de passagem obtidas experimentalmente e as curvas obtidas numericamente
O aumento da rugosidade tende a frear o escoamento, proporcionando uma maior dispersão do traçador no interior da unidade, a maior diferença entre os picos de concentração para as curvas de passagem avaliadas neste trabalho foi de 0,4 mg/L (0,05 < ks < 5,00).
O erro calculado entre a curva numérica e a medida, para cada compartimento, e para cada valor de ks está mostrado na Figura 8. Através desta figura pode-se perceber que a sensibilidade ao efeito do ks variou ao longo da unidade de contato. O maior efeito pode ser observado no ponto 4, onde houve uma variação de 1,8% entre os valores máximo e mínimo do EPA médio. A sensibilidade a este parâmetro é menor à medida que se aproxima da saída da unidade.
A Tabela 4 indica os valores dos EPA médio para cada valor de rugosidade do fundo. Percebe-se que o menor valor de EPA médio é encontrado para ks igual a 0,5 mm.
Continuação do processo iterativo
Verificado que o valor de kl obtido na primeira interação (kl = 3,50) é diferente do valor originalmente proposto, kl = 4,57; inicia-se agora um novo processo de iteração. Mantendo agora fixos os valores de kl =3,50 e ks =0,5 mm, volta-se para a etapa de calibração da constante adimensional de difusão turbulenta lateral e da vazão (passo 3), a fim de se verificar se é possível obter um ajuste ainda melhor das curvas de passagem. Depois de realizado novamente todo o procedimento descrito nas seções anteriores, as curvas simuladas se aproximaram ainda mais das curvas experimentais, e os parâmetros que proporcionaram este melhor ajuste para a segunda iteração foram: kl = 2,50; kt = 0,40; Q = 1,00 L/s e ks = 0,1 mm. Novamente, foi realizado o mesmo procedimento para uma terceira iteração e os valores dos parâmetros que resultaram deste processo iterativo foram: kl = 2,50; kt = 0,50; Q = 1,00 L/s e ks = 0,1 mm. O EPA médio obtido para a primeira iteração foi de 4,49% enquanto que para a segunda iteração foi de 3,02% e para a terceira de 2,98%. Como pode ser observado, à medida que se aumenta o número de iterações os valores dos parâmetros tendem a convergir. O processo de calibração deve continuar até ocorrer convergência dos valores dos parâmetros de calibração. Neste trabalho considerou-se que o valor médio do parâmetro EPA menor que 3% já representa um bom ajuste entre as curvas medidas e estimadas.
A Figura 9 mostra as curvas experimentais e simuladas obtidas a partir da metodologia de calibração para a primeira iteração (a), segunda iteração (b) e terceira iteração (c).
Considerando os valores dos parâmetros resultantes da proposta de calibração, kl = 2,50; kt = 0,50; Q = 1,00 L/s e ks = 0,1 mm, pode-se dizer que estes valores estão de acordo com os valores encontrados na literatura. Entretanto, o valor de kl encontrado (2,50) é menor que aqueles encontrados por Elder (1959) e Siqueira (1998), 5,93 e 4,57, respectivamente.
Padrões de escoamento
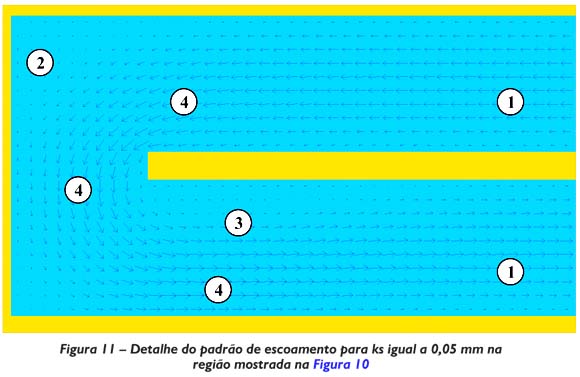
Como visto na seção anterior, o modelo foi capaz de simular as curvas de passagem (transporte de soluto) na unidade de tratamento. Isto indica que provavelmente o padrão de escoamento está bem representado pelo modelo. De fato, os resultados gerados (Figura 10) conseguiram captar vários aspectos esperados para o escoamento em uma unidade de contato chicanada. As principais características observadas nesta simulação são mais bem visualizadas na Figura 11, que representa uma ampliação da parte em destaque na Figura 10.
De acordo com a Figura 11, na região (1) o escoamento apresenta-se bem comportado, com um perfil de velocidade quase uniforme na região central do escoamento. A região (2) é uma região de baixas velocidades caracterizada como zona morta. O fluido que entra nesta região é aprisionado, sendo liberado aos poucos para o escoamento principal. A região (3) é caracterizada por uma zona de recirculação adjacente às chicanas, diminuindo a seção útil do escoamento e acelerando o escoamento na região (4) que pode ser caracterizada com uma região de curto-circuito (caminhos preferenciais). A presença de zonas mortas, recirculações e curto-circuitos podem diminuir o desempenho da unidade. Portanto, a identificação destas regiões é de suma importância para a proposição de melhorias em unidades de tratamento que já encontram-se em operação e para o projeto mais racionais de novas unidades
Com a aplicação desta proposta de calibração, modelos que ainda não foram validados, devido a falta de campos de velocidade para tal finalidade, poderão ser calibrados e utilizados como ferramenta para a obtenção do campo de escoamento.
CONCLUSÕES
A proposta de calibração apresentada neste estudo respondeu satisfatoriamente, levando a excelentes ajustes entre as curvas simuladas pelo modelo e medidas experimentalmente. O padrão de escoamento obtido com o modelo calibrado também apresentou as principais características esperadas para o escoamento neste tipo de unidade, como a presença de zonas mortas, recirculações e curto-circuito, o que indica que a metodologia proposta é bastante promissora como ferramenta para obtenção dos padrões de escoamento em unidades onde não é possível ou é inviável obter tais informações por medições diretas. Entretanto, o processo de calibração foi efetuado para curvas de passagem médias nas seções e não para pontos específicos no interior da unidade. Em tais casos, modelos hidrodinâmicos mais simples poderiam levar a bons resultados, quanto as distribuições de tempo de residência (curvas de passagem), sem necessariamente ser a melhor representação do escoamento. Recomenda-se que a proposta seja testada para escoamentos mais complexos com monitoramento pontual de curvas de passagem e para que esta metodologia possa ser aplicada de forma mais segura, dados de velocidade ainda fazem-se necessários para validação deste estudo.
AGRADECIMENTOS
Ao CNPq pela concessão da bolsa à aluna de mestrado Camila Gomes Pacheco. Os autores também agradecem ao Professor Roger Falconer, da Cardiff University Reino Unido, pela concessão do código fonte do modelo computacional DIVAST que foi aprimorado para o desenvolvimento deste estudo.
Recebido: 31/03/06
Aceito: 29/01/07
- BARROS FILHO, G. C. Identificação dos Processos Físicos na Hidrodinâmica das Águas do Entorno da Ilha de Vitória. 2002. Dissertação (Mestrado em Engenharia Ambiental) Programa de Pós-Graduação em Engenharia Ambiental, Universidade Federal do Espírito Santo, Vitória, 2002.
- CASTRO, M. S. M. Análise da influência das agues do canal da passagem sobre o padrão de escoamento na baía do Espírito Santo. 2001. p. 126. Dissertação (Mestrado em Engenharia Ambiental) Programa de Pós-Graduação em Engenharia Ambiental, Universidade Federal do Espírito Santo, Vitória, 2001.
- ELDER, J. W. The Dispersion of Marked Fluid in Turbulent Shear Flow Journal of Fluid Mechanics, v. 5, p. 560-644, 1959.
- FALCONER, R. A. Mathematical Modelling of Jet-Forced Circulation in Reservoirs and Harbours. 1976. p. 237. Thesis (Doctor of Philosophy), Imperial College, London, 1976.
- FALCONER, R. A.; ISMAIL, A. I. B. M. Numerical modeling of tracer transport in a contact tank. Environment International, v.23, n.6, p. 763-773, 1997.
- FALCONER R.A.; LIU, S.Q. Modelling solute transport using the QUICK scheme. Journal of Environmental Engineering, ASCE, vol. 114, No. 1, pp. 3-20. 1998.
- KASHEFIPOUR, S. M. et al. Hydro-environmental modelling for bathing water compliance of an estuarine basin Water Research, v.36, pp. 1854-1868, 2002.
- NETTO, J. M. A.; ALVAREZ, G.A. Solução geral para o problema do escoamento de fluidos nos encanamentos. In:______. Manual de Hidráulica. 7. ed. São Paulo: Edgard Blücher LTDA, cap. 15, v. 1, p. 197. 1998.
- MACIEL, M. A. Modelagem do Padrão de escoamento no canal da passagem (Vitória - ES). 2004. 166 f. Dissertação (Mestrado em Engenharia Ambiental) - Universidade Federal do Espírito Santo, Programa de Pós-Graduação em Engenharia Ambiental, Universidade Federal do Espírito Santo, Vitória, 2004.
- RAUEN, W. B. Influência da escala geométrica na semelhança dinâmica e na desinfecção de águas com cloro em modelos reduzidos de unidades de contato. 2001. 100 f. Dissertação (Mestrado em Engenharia Ambiental) Programa de Pós-Graduação em Engenharia Ambiental, Universidade Federal do Espírito Santo, Vitória, 2001.
- ROCHA, A. B. Estudo da hidrodinâmica e do transporte de solutos na baía do Espírito Santo através de modelagem computacional. 2000. 108 f. Dissertação (Mestrado em Engenharia Ambiental) Programa de Pós-Graduação em Engenharia Ambiental, Universidade Federal do Espírito Santo, Vitória, 2000.
- SIQUEIRA, R. N. Desenvolvimento e aperfeiçoamento de critérios de avaliação da eficiência hidráulica e do cálculo do coeficiente de mistura em unidade de tratamento de água e efluentes. 1998. 126 f. Dissertação (Mestrado em Engenharia Ambiental) Programa de Pós-Graduação em Engenharia Ambiental, Universidade Federal do Espírito Santo, Vitória, 1998.
- TEIXEIRA, E. C. Hydrodynamic processes and hydraulic efficiency of chlorine contact units. 1993. p. 260. Thesis (Doctor of Philosophy), University of Bradford, U.K., 1993.
- VIEGAS, N. J. Farias. Modelagem numérica das marés no litoral do espírito santo 2006. 90 f. Dissertação (Mestrado em Engenharia Ambiental) - Universidade Federal do Espírito Santo, Programa de Pós-Graduação em Engenharia Ambiental, Universidade Federal do Espírito Santo, Vitória, 2004.
- WANG, H. Numerical modeling of flow and disinfection processes in chlorine contact tanks. 1995. p. 285. Thesis (Doctor of Philosophy), University of Bradford, U.K., 1995.
Endereço para correspondência:
Datas de Publicação
-
Publicação nesta coleção
13 Jul 2007 -
Data do Fascículo
Mar 2007
Histórico
-
Aceito
29 Jan 2007 -
Recebido
31 Mar 2006