Resumos
Compreender e quantificar os mecanismos relacionados à perda de carga e à remoção de partículas em um meio filtrante granular é de importância fundamental para o estudo do processo da filtração. Este trabalho apresenta o desenvolvimento dos modelos de perda de carga na filtração em meios porosos e a proposição da modelação matemática semiempírica da perda de carga para meios filtrantes limpos e do desenvolvimento do perfil de perda de carga ao longo do tempo de filtração a partir da equação de Ergun. Objetivou-se a determinação dos valores das constantes da equação de Ergun para meio granular de areia grossa e pedregulho. Alguns exemplos de aplicação dessa modelação matemática são também apresentados e discutidos pelos autores com base em dados experimentais obtidos em uma estação piloto de dupla filtração.
modelos de perda de carga; filtração direta ascendente; água de abastecimento; regime de Forchheimer
To understand and to quantify the head loss due to the particles removal in a porous medium has primary importance to filtration process study. This paper presents the development of the models of head loss used in the filtration in porous media and proposes a mathematical semi-empiric model for head loss in clean beds and head loss increasing profile during the filtration run length, by means of the Ergun equation. The goal was the determination of Ergun’s equation coefficients for granular material constituted of coarse sand and gravel. Examples of application of these mathematical modeling are also presented and discussed by the authors based on experimental data obtained in a double filtration pilot plant.
head loss models; up flow direct filtration; drinking water; Forchheimer regime
ARTIGO TÉCNICO
Modelação da perda de carga na filtração direta ascendente em meio granular de areia grossa e pedregulho
Modeling of the head loss in up flow coarse sand and gravel direct filtration
Alexandre BotariI; Luiz Di BernardoII
IEngenheiro Civil. Licenciado em Ciências Exatas, com ênfase em Matemática pela Universidade de São Paulo (USP). Doutor em Engenharia Civil pela Escola de Engenharia de São Carlos (EESC) da USP. Professor Adjunto da Universidade Estadual de Maringá (UEM)
IIEngenheiro Civil. Doutor em Engenharia Civil pela EESC/USP. Professor Titular do Departamento de Hidráulica e Saneamento da EESC/USP
Endereço para correspondênciaEndereço para correspondência: Luiz Di Bernardo Avenida Trabalhador São-Carlense, 400 Centro 13566-590 São Carlos (SP), Brasil Tel.: (16) 273-9528 E-mail: bernardo@sc.usp.br
RESUMO
Compreender e quantificar os mecanismos relacionados à perda de carga e à remoção de partículas em um meio filtrante granular é de importância fundamental para o estudo do processo da filtração. Este trabalho apresenta o desenvolvimento dos modelos de perda de carga na filtração em meios porosos e a proposição da modelação matemática semiempírica da perda de carga para meios filtrantes limpos e do desenvolvimento do perfil de perda de carga ao longo do tempo de filtração a partir da equação de Ergun. Objetivou-se a determinação dos valores das constantes da equação de Ergun para meio granular de areia grossa e pedregulho. Alguns exemplos de aplicação dessa modelação matemática são também apresentados e discutidos pelos autores com base em dados experimentais obtidos em uma estação piloto de dupla filtração.
Palavras-chave: modelos de perda de carga; filtração direta ascendente; água de abastecimento; regime de Forchheimer.
ABSTRACT
To understand and to quantify the head loss due to the particles removal in a porous medium has primary importance to filtration process study. This paper presents the development of the models of head loss used in the filtration in porous media and proposes a mathematical semi-empiric model for head loss in clean beds and head loss increasing profile during the filtration run length, by means of the Ergun equation. The goal was the determination of Erguns equation coefficients for granular material constituted of coarse sand and gravel. Examples of application of these mathematical modeling are also presented and discussed by the authors based on experimental data obtained in a double filtration pilot plant.
Keywords: head loss models; up flow direct filtration; drinking water; Forchheimer regime.
Introdução
A quantificação da perda de carga em um meio filtrante tem importância primária na filtração de água. Modelos que descrevem o perfil da perda de carga e a remoção de impurezas em função do tempo de filtração constituem valiosos instrumentos para a previsão, operação e manutenção de estações de tratamento de água (ETA).
Este trabalho apresenta o desenvolvimento histórico dos modelos de perda de carga e a modelação semiempírica da remoção de partículas ou impurezas (em termos de sólidos suspensos totais SST) utilizadas na filtração em meios granulares. Adicionalmente, apresenta-se aqui a formulação utilizada para a modelação semiempírica da perda de carga em meios granulares de areia, conforme desenvolvida por Botari (2007) e validada a partir de dados experimentais obtidos em experimentos de dupla filtração em instalação piloto.
Alguns trabalhos históricos constituem um marco na modelação do crescimento da perda de carga ao longo do tempo de filtração em meios granulares. O trabalho publicado por Poiseuille, em 1841, é um desses importantes divisores de águas na história da modelação da perda de carga (BOTARI, 2007).
Modelação da perda de carga
Após 15 anos da publicação de Poiseuille, Darcy (em 1856) publicou seu trabalho sobre a perda de carga em meios porosos. Os dois trabalhos apresentavam paralelismos entre si. Em seu trabalho, Poiseuille observou que o escoamento em um tubo capilar era diretamente proporcional à carga hidráulica que agia no tubo e inversamente proporcional ao seu comprimento (BOTARI, 2007).
Entretanto, foi Darcy que equacionou essa relação entre a perda de carga e o comprimento (ou altura) aplicado ao escoamento através de um meio poroso (areia). Por esse motivo, essa relação recebe o nome de equação ou Lei de Darcy, conforme a equação 1 (TRUSSELL; CHANG, 1999):
Onde:
Q: a vazão que passa pelo meio poroso (m3. s-1);
Kh: coeficiente de proporcionalidade também chamado de condutividade hidráulica de Darcy, que depende do tipo de material filtrante ou meio poroso (m.s-1);
A: área em planta do meio filtrante (m2);
ΔL: altura do meio poroso (m);
h: altura da lâmina de água acima do leito filtrante (m) (afluente ao filtro);
h0: altura de água medida a partir da parte posterior do leito filtrante (m) (efluente ao filtro).
Na Equação 1, a condutividade hidráulica (Kh) também depende das propriedades do fluido, além das características do meio poroso. Os valores típicos de Kh para areia utilizada na filtração de águas para fins de abastecimento variam entre 10-6 e 10-2 m.s-1. Se a perda de carga (Δh) for definida como igual a h + ΔL - h0, tem-se a Lei de Darcy na forma mais usualmente encontrada, como representado pela Equação 2:
Onde:
U: velocidade superficial ou taxa de filtração (m.s-1).
Para uma aplicação em um único tubo capilar, partindo-se do conceito de que o meio poroso pode ser visto como uma coleção de inúmeros tubos capilares paralelos que atravessam toda a profundidade do meio filtrante (ΔL), a relação Δh/ΔL pode ser descrita conforme Equação 3:
Onde:
Lcapilar: altura de capilaridade (igual à altura ΔL da Equação 1) (m);
µ: viscosidade dinâmica da água (kg.m-1.s-1);
ρf: massa específica da água (kg.m-3);
g: aceleração da gravidade (m.s-2);
Vcapilar: velocidade do fluido no capilar (m.s-1);
dcapilar: diâmetro interno do capilar (m).
Entretanto, como a velocidade no meio poroso não pode ser comparada com a velocidade dentro do capilar, pode-se aproximar para uma velocidade média nos espaços vazios do meio poroso, conforme Equação 4. Posteriormente, foi definida a superfície específica para o meio filtrante como a relação entre a área da superfície do meio poroso e o volume ocupado por este, como pode ser observado na Equação 5:
Onde:
Acapilar: área em planta do capilar; f é a porosidade média do meio filtrante.
Onde:
Se: superfície específica (m-1);
Asuperficial: área do meio filtrante (m-2);
L: altura do meio filtrante (m);
A: área em planta do meio filtrante (m-2).
Dessa forma o raio hidráulico (Rh) do capilar pode então ser definido como:
Como, para um tubo circular,  , o diâmetro interno do capilar será igual à:
, o diâmetro interno do capilar será igual à:
Combinando-se as Equações 2, 3, 6 e 7, obtém-se a Equação 8 para a perda de carga:
Acrescentando-se um coeficiente que expressa a tortuosidade do escoamento no interior do meio filtrante (kt), ou fator de correção do escoamento (adimensional), e rearranjando-se a Equação 8, obtém-se a Equação 9 ou ainda a Equação 10 nas suas formas mais conhecidas, para expressar a perda de carga para meio filtrante:
A Equação 10 é conhecida como a equação de Carman-Kozeny, onde a condutividade hidráulica (Kh) é expressa em função das características do meio filtrante e do fluido e kt recebe o nome de constante de Kozeny, cujo valor para meios porosos de areia varia entre 2 e 3. O valor de 2,5 é frequentemente utilizado para a constante de Kozeny (kt), ou seja, a quantidade 2 kt assume o valor igual a 5 (Trussell; Chang, 1999). Para material poroso esférico uniforme, a superfície específica será:
Portanto, a condutividade hidráulica para material poroso esférico, substituindo-se a Equação 11 na Equação 10, será:
Ao passo que a equação para perda de carga (Equação 9) será igual a:
Trussell e Chang (1999), confirmaram que a formulação proposta por Kozeny, a partir da lei de Darcy (Equação 10) é válida para número de Reynolds menores que 1. Nesse regime, também conhecido como regime de arrasto, a perda de carga é dada, principalmente, pelo arrasto que ocorre na superfície do coletor (grão do meio filtrante).
Para número de Reynolds um pouco maior, entretanto, começam a ocorrer perdas em forma de turbilhões, o que traz abruptas mudanças nos perfis de velocidade nas seções transversais dos escoamentos. Em uma faixa do número de Reynolds entre 1 e 100, o regime de escoamento chama-se Regime de Forchheimer, que exige a adição de um termo não linear à Equação 8.
Números de Reynolds maiores que 100 caracterizam escoamentos na transição entre laminar e turbulento ou então regimes puramente turbulentos. Para a filtração, entretanto, o número de Reynolds se situa numa faixa entre 0,5 e 50, fato que insere o escoamento, quase que inteiramente, no regime de Forchheimer (TRUSSELL; CHANG, 1999).
Ergun e Orning (1949) propuseram uma equação a partir da formulação de Kozeny (Equação 8) para o Regime de Forchheimer. Nesse regime, ocorre o início da transição da predominância das forças viscosas para as forças cinéticas. Maiores detalhes serão abordados na metodologia proposta, com a apresentação do modelo matemático de perda de carga proposta neste trabalho.
Posteriormente, Ergun (1952) acrescentou o fator de forma, ou superfície específica, na formulação. Segundo Trussell e Chang (1999), a equação de Ergun (1952), relaciona a perda de carga e a taxa de filtração de forma "suave e contínua" na região do escoamento, conhecido como Regime de Forchheimer, conforme Equação 14:
Onde kh1 e kh2 são constantes de proporcionalidade, para as quais Ergun (1952) encontrou valores iguais a 150 e 1,75, respectivamente. Valores entre 110 e 245 para kh1 e entre 1,3 e 5,3 para kh2, também têm sido encontrados na literatura (TIEN, 1989; TRUSSELL; CHANG, 1999).
A equação de Ergun (1952) tem sido largamente utilizada para o cálculo da perda de carga em leito limpo, tendo sido modificada para utilização em meios granulares estratificados (para granulometria variável ao longo da profundidade da camada ou meio filtrante). Geralmente, essa modificação apresenta-se como na forma da Equação 15 (DI BERNARDO; DANTAS, 2005):
Onde:
ψ: coeficiente de esfericidade do grão coletor;
Xi: fração correspondente da camada i;
dgi: média geométrica entre os tamanhos das aberturas de duas peneiras consecutivas (ensaio de granulometria) da camada i.
Stevenson (1997) notou que a velocidade (taxa de filtração) e a porosidade têm grande influência na perda de carga, o que exige o uso do termo não linear para a filtração no Regime de Forchheimer. Outros trabalhos mostram claramente que a maior parte da perda de carga se dá nas primeiras camadas de filtração ou, ainda, na camada suporte para o caso da filtração direta ascendente, entretanto outros parâmetros afetam a perda de carga na filtração (HUNT; HWANG; McDOWELL-BOYER, 1993; KURODA, 2002; DI BERNARDO, 2004).
A maior parte da perda de carga observada no filtro ocorre em suas primeiras camadas, e isso permanece mesmo durante o restante do ciclo (ou carreira) de filtração. O mesmo ocorre com a deposição de partículas ou impurezas. Tobiason e Vigneswaran (1994) notaram que as partículas maiores depositam-se nos primeiros centímetros da primeira camada do leito filtrante ao passo que as partículas de tamanho inferiores a 1 µm penetram mais fundo, ou seja, nas camadas posteriores. Obviamente, fatores como a granulometria, o uso ou não de polímeros, o tipo e a dosagem de coagulante, a taxa de filtração, o tamanho e a distribuição do tamanho de partículas podem determinar o perfil da perda de carga durante o ciclo de filtração.
Embora as altas taxas de filtração tendam a produzir altos valores absolutos de perda de carga, geralmente conduzem a baixos valores de perda de carga relativa ou normalizada (h/h0) por unidade de massa retida no meio filtrante (HUNT; HWANG; McDOWELL-BOYER, 1993).
Segundo Botari (2007), duas explicações são plausíveis para esse fato:
primeiramente, em altas taxas de filtração, ocorre a redução da eficiência de remoção de partículas devido à penetração dessas partículas nas camadas mais profundas do leito filtrante, o que torna mais homogênea a distribuição de partículas ao seu longo, conduzindo a baixos valores de perda de carga relativa;
em segundo lugar, com o aumento da velocidade, o mecanismo preponderante na retenção de partículas é o impacto inercial. Além disso, comparativamente, a retenção de partículas pelo mecanismo de sedimentação predomina em relação ao mecanismo de difusão, consequentemente provocando um depósito de partículas no meio filtrante mais compacto.
OMelia e Ali (1978) já haviam observado que as partículas menores conduziam a maiores valores de perda de carga se comparado a partículas maiores, para uma mesma quantidade de massa retida. Darby e Lawler (1990) fizeram a mesma observação e atribuíram à maior área superficial de contato com o fluido a explicação para esse fato, o que conduziu à introdução do diâmetro das partículas na maior parte das formulações para a perda de carga na filtração.
Hunt, Hwang e McDowell-Boyer (1993) também verificaram que, embora o volume de massa retida no leito filtrante fosse constante, ocorria um aumento na perda de carga. A explicação pode residir na natureza dinâmica da retenção de partículas. O fluido modifica as características da massa depositada, uma vez que os mecanismos de aderência e desprendimento ocorrem simultaneamente no leito e podem proporcionar o rearranjo e a compactação do depósito de partículas (ou impurezas), embora a variação total de massa no volume de leito seja nula.
Para OMelia e Ali (1978), a superfície específica (Se) (da concepção de Carman-Kozeny Equações 9 e 10) que expressa a área superficial do coletor, teria a forma da Equação 16:
Onde:
Se: área superficial por unidade de volume (m-1);
Ac e Ap: respectivamente, a área superficial do coletor e da partícula coletada por ele (m2) e
Vc e Vp: seus respectivos volumes (m3).
A área superficial do coletor e da partícula será igual a  e
e  , respectivamente (dc e dp: diâmetro do coletor e da partícula, respectivamente). O volume do coletor e da partícula será, respectivamente,
, respectivamente (dc e dp: diâmetro do coletor e da partícula, respectivamente). O volume do coletor e da partícula será, respectivamente,  . Substituindo-se na Equação 16 e rearranjando-se convenientemente, teremos a Equação 17:
. Substituindo-se na Equação 16 e rearranjando-se convenientemente, teremos a Equação 17:
Nesse caso, obtém-se o número de partículas coletados no volume de controle em questão, ponderando-se as relações dp/dc pela relação Np/Nc (Np é o número de partículas coletadas por unidade de volume do leito; Nc é o número de coletores por unidade de volume de leito filtrante) na Equação 17, como se observa na Equação 18:
Observe que um fator de correção (β') correspondente à fração das superfícies das partículas que contribuem efetivamente com a perda de carga foi introduzido no cálculo da área superficial da Equação 18.
Segundo Botari e Di Bernardo (2007), se for considerado um coletor isoladamente, Npserá o número total de partículas retidas pelo grão. Para coletores e partículas esféricas, a Equação 13 será igual à Equação 19, considerando-se que o número de coletores por unidade de volume do leito filtrante (Nc) em função da porosidade inicial (f0) seja igual à Equação 20:
Observa-se que a Equação 13 é extensamente utilizada para o cálculo da perda de carga de meios filtrantes limpos e que sua forma modificada por OMelia e Ali (1978) (Equação 18) pode ser aplicada ao estágio de serviço (carreira) de filtração e a meios granulares estratificados (para granulometria variável ao longo da profundidade da camada ou meio filtrante). Similarmente, a Equação 21, para meios granulares estratificados, que ficou conhecida como equação de Fair e Hatch, é também largamente utilizada, mas apenas para o cálculo de perda de carga em leito limpo (FAIR; GEYER; OKUN, 1973):
onde:
ψ: coeficiente de esfericidade do grão coletor;
Xi: fração correspondente da camada i;
dgi: média geométrica entre os tamanhos das aberturas de duas peneiras consecutivas (ensaio de granulometria) da camada i.
Di Bernardo (2004) verificou que a Equação 21 não se adequou satisfatoriamente aos resultados para leito limpo obtidos experimentalmente no caso do uso de material granular de areia grossa e sobretudo pedregulho nos filtros ascendentes de sua instalação piloto, tendo obtido desvio superior a 10 e 20%, respectivamente.
As equações desenvolvidas por OMelia e Ali (1978) consideravam a porosidade constante ao longo da carreira (ciclo) de filtração. Obviamente, essa suposição não é verdadeira, o que levou Vigneswaran e Chang (1986) e, posteriormente, Tobiason e Vigneswaran (1994) a introduzirem a variação da porosidade em função da mudança nas características do depósito.
Segundo Vigneswaran e Chang (1986), o número total de partículas retidas pelo grão (Np) se relaciona com o número de partículas retidas por unidade de volume de leito filtrante (Nb) pela relação Np Nc = Nb. O número de coletores por unidade de volume (Nc) foi definido pela Equação 20. Destarte, pode-se considerar que a variação de porosidade no volume de controle ao longo do tempo de filtração e da altura ou profundidade do leito filtrante [f (z, t)] será obtida pela ponderação do número de partículas retidas por unidade de volume de leito filtrante (Nb) e pelo volume das partículas nesse volume de controle, assumindo-se uma porosidade para o depósito formado, conforme Equação 22 (BOTARI, 2007):
Considerando-se Nb = Nc Np e 1 - fo =  , a Equação 22 se torna igual a:
, a Equação 22 se torna igual a:
Sendo que fdé a porosidade do depósito, que é considerada constante para uma água bruta e suas respectivas partículas (ou impurezas) que mantenham suas características inalteradas ao longo do ciclo ou carreira de filtração. Obviamente, nem sempre isso é verdadeiro. A modelação completa para a remoção de partículas foi desenvolvida por Botari (2007).
Stevenson (1997) fez interessantes observações sobre a Equação 23, indicando que o fator 1 f0 que aparece no numerador representa um fator de correção entre a área específica e o volume de leito.
Note que f0 deve ter um valor constante, uma vez que o número de grãos por unidade de volume não muda ao longo do ciclo de filtração, ao passo que 1 fd do denominador faz a conversão entre a velocidade de aproximação e a velocidade intersticial (poros). Embora haja bastantes exceções, o modelo de Vigneswaran e Chang (1986) tem obtido razoável sucesso em caracterizar a perda de carga não linear em trabalhos experimentais (DARBY; ATTANASIO; LAWLER, 1992; TOBIASON; VIGNESWARAN, 1994; BOTARI; DI BERNARDO, 2007).
Aplicação da metodologia proposta
Para Trussell e Chang (1999), o escoamento em meios porosos, mesmo para números de Reynolds próximos ao valor da unidade, pode contar com linhas de corrente que apresentam alguma influência inercial. De fato, dois tipos de eventos que caracterizam a influência inercial ocorrem no escoamento em meios porosos:
expansão e contração das linhas de corrente do escoamento ao passo que "chegam" ou "saem" do volume do entorno do grão coletor;
diferentes linhas de corrente curvilíneas no escoamento ao passo que "chegam" ou "saem" do volume do entorno do grão coletor.
A Figura 1A apresenta uma microfotografia que mostra as linhas de corrente em torno dos grãos do material filtrante. Segundo Ergun (1952), a perda de carga em meios filtrantes granulares deve-se, simultaneamente, a perdas viscosas e cinéticas. A equação desenvolvida por Ergun (1952) pode ser aplicada a todos os tipos de escoamentos, fato observado no gráfico da Figura 1B. Note que a equação de Ergun (linha curva cheia da Figura 1B) não está apenas definida para as mesmas regiões definas pelas equações de Carman-Kozeny e de Burke-Plummer (linha tracejada e linha pontilhada da Figura 1B, respectivamente), mas também para a região entre os domínios dessas duas equações. Trussell e Chang (1999) mostraram que a filtração em meios porosos ocorre, em geral, no chamado Regime de Forchheimer (Escoamento laminar) em um intervalo do número de Reynolds que varia entre 0,5 e 50. O número de Reynolds para os grãos coletores utilizados neste trabalho também apoia a afirmação de Trussell e Chang (1999) a respeito do regime de Forchheimer.
As Tabelas 1 e 2 apresentam os valores do número de Reynolds para os diâmetros médios dos grãos coletores das camadas do Filtro Ascendente de Areia Grossa (FAAG) e do Filtro Ascendente de Pedregulho (FAP), respectivamente, bem como as taxas de filtração e a relação DF/dc médio utilizadas no trabalho de Botari (2007), onde DF é o diâmetro interno dos filtros e dc médio é o diâmetro médio dos grãos coletores.
A relação DF/dc médio é importante em virtude da influência do efeito da rugosidade da parede no desenvolvimento do perfil de velocidade e das linhas de fluxo em torno dos grãos coletores, mesmo no caso de escoamentos em regime laminar (LIMA; SILVA, 2002). Para Lang et al. (1996), essa relação deve ser superior a 50 para que o erro da perda de carga viscosa seja inferior a 5%, considerando-se apenas perdas viscosas. Entretanto, a formulação utilizada, a equação de Ergun (1952), não contempla apenas as perdas viscosas, mas também as perdas cinéticas ao considerar a parcela relativa ao incremento da velocidade que ocorre junto às paredes dos grãos, linhas de corrente de maiores velocidades e junto à parede do filtro (instalação piloto, nesse caso particular).
Portanto, Botari (2007) optou pela adoção da abordagem de Ergun (1952) no chamado Regime de Forchheimer para escoamentos laminares, uma vez que, para muitas camadas, a relação DF/dc médio é menor que 50, o que proporciona aumento nas perdas cinéticas pelo efeito das paredes. Assim, a modelação matemática da perda de carga apresentada considera a parcela cinética no cômputo da perda de carga total, compensando o acréscimo da perda de carga advinda do efeito das paredes na formação do perfil de velocidade do escoamento.
A equação para a perda de carga de Ergun (1952) para um coletor esférico (Equação 14), pode ser escrita considerando-se a variação no espaço e no tempo, conforme Equação 24.
onde Sc e Sp são o fator de forma do coletor e da partícula, respectivamente.
Observa-se na Equação 24 que tanto a parcela viscosa quanto a parcela inercial recebem a influência do fator de correção (β') correspondente à fração das superfícies das partículas que contribuem efetivamente com a perda de carga. No escoamento ascendente, a gradação granulométrica do respectivo valor do diâmetro é função da profundidade no leito filtrante [dc (z)], incrementado de baixo para cima, conforme Equação 25:
Sendo que L é a profundidade do filtro ou da camada em questão. O valor do diâmetro do coletor será o valor da média geométrica dc ( ) entre o valor do diâmetro em zi(na posição i da altura z) e zi+1 (na posição i+1 da altura z), conforme Equação 26:
) entre o valor do diâmetro em zi(na posição i da altura z) e zi+1 (na posição i+1 da altura z), conforme Equação 26:
onde:
dc ( i): diâmetro médio (geométrico) do coletor na posição i, entre o espaço zi e zi+1;
i): diâmetro médio (geométrico) do coletor na posição i, entre o espaço zi e zi+1;
dc (zi): diâmetro do coletor no espaço zi e dc(zi+1) é o diâmetro do coletor no espaço zi+1.
As condições iniciais (para tempo t = 0) para a modelação de perda de carga são:
Onde:
f0: porosidade inicial (de leito limpo).
As demais condições para o cálculo da perda de carga no leito limpo (t = 0) serão: NL0(z) = 0 e Np0(z) = 0. Demais elementos da modelação de remoção de partículas foram apresentados por Botari e Di Bernardo (2007).
As constantes da equação de Ergun (1952) kh1 e kh2 da Equação 14 se relacionam com as constantes kh1 e kh2 da Equação 27 conforme as Equações 28 e 29, respectivamente:
Os valores de kh1 e kh2 na forma da Equação 14 é a mais usualmente encontrada na literatura. Observe que os valores kh1 e kh2 da Equação 24 para o estágio de serviço durante a filtração deverá assumir valores diferentes daquele encontrado para a Equação 27 no estágio de leito limpo (t = 0). Evidentemente, isso se dá em função da deposição de partículas no leito que altera o volume e a forma dos vazios do leito filtrante ao longo do tempo de filtração.
Resultados
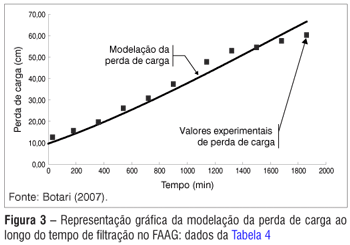
As Tabelas 3 e 4 e as Figuras 2 e 3 apresentam os resumos das simulações para perda de carga em função da remoção de impurezas (em termos de SST) e os gráficos da perda de carga ao longo de uma carreira de filtração, respectivamente, para o meio filtrante cujos dados experimentais foram obtidos no FAAG da instalação piloto de dupla filtração desenvolvida por Di Bernardo (2004), conforme características apresentadas na Tabela 1.
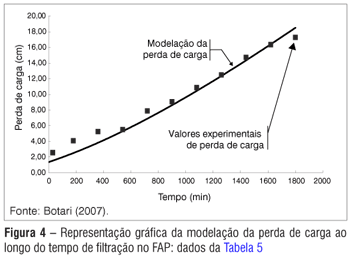
As Tabelas 5 e 6 e as Figuras 4 e 5 apresentam os resumos das simulações para perda de carga em função da remoção de impurezas (em termos de SST) e os gráficos da perda de carga ao longo de uma carreira de filtração, respectivamente, para o meio filtrante cujos dados experimentais foram obtidos no FAP da mesma instalação, conforme características apresentadas na Tabela 2.
Para a obtenção dos dados de meios filtrantes e efluentes apresentados nas Tabelas 3 a 6, foi empregada a microscopia ótica do Laboratório de Processos Biológicos (LPB) (SHS-EESC/USP) para a visualização do tamanho e forma das partículas de caulinita encontradas em suspensão na água de estudo. O tamanho médio encontrado para as partículas de caulinita do sobrenadante (água de estudo), tendo sido observadas opticamente cem imagens por contagem de campo visual, foi de 2,1 µm, ao passo que o coeficiente de esfericidade (ψp) foi da ordem de 0,58 valores próximos aos encontrados na literatura (SUGUIO, 1973). Para a caracterização do material filtrante, utilizou-se uma escala de comparação visual e metodologia preconizada por Suguio (1973), que consiste na contagem sobre retroprojetor de cem grãos de areia ou de pedregulho por camada especificada para os meios filtrantes.
O sistema de dupla filtração utilizado foi operado com água de estudo preparada com uma suspensão de caulinita, reservada em tanques dotados de agitadores para, posteriormente, alimentarem a caixa de mistura de água bruta, onde recebia mais uma agitação, sendo então bombeada para a caixa de nível constante. A caixa de nível constante garantia a vazão desejada para o sistema, extravasando a vazão excedente que era encaminhada, através do retorno, para a caixa de mistura de água bruta. A vazão desejada para o sistema, oriunda da caixa de nível constante, descia para a caixa de mistura rápida e recebia o coagulante. A solução de sulfato de alumínio (coagulante) era bombeada do tanque de preparação para posteriormente ser encaminhada aos sistemas de filtração. Foram realizadas análises das leituras piezométricas e coleta de amostras ao longo dos meios granulares e ao longo do tempo de filtração (frequência de leitura de três em três horas). Maiores detalhes sobre a instalação piloto, o programa computacional da modelação em linguagem Fortran e o modelo de remoção de partículas em termos de SST, bem como a relação entre esses dois parâmetros (partículas e SST) e entre Turbidez e SST, podem ser obtidos em Botari (2007) e em Botari e Di Bernardo (2007).
As constantes da equação de Ergun (1952) utilizadas nos resultados terão os mesmos valores para leito limpo e para o estágio de filtração (serviço) em virtude das características do modelo de remoção de partículas adotado por Botari e Di Bernardo (2007), sendo que serão os valores de kh1 e kh2, da Equação 14, que se relacionam com kh1 e kh2 da Equação 24, conforme as Equações 28 e 29.
Como se pode observar na Figura 2, a modelação da perda de carga para a carreira de filtração 1 obteve uma boa aderência aos resultados experimentais, conforme valor de R2 (98%) da Tabela 3. Os resultados apresentados na Tabela 4 e Figura 3 mostram que a modelação da carreira de filtração 2 expressa com razoável aderência os valores experimentais de perda de carga até cerca de metade do tempo da carreira de filtração. Observa-se na Figura 3 a ocorrência de oscilações nos valores experimentais de perda de carga a partir da metade final da carreira de filtração, oscilação não expressa na modelação.
A Tabela 5 e Figura 4 apresentam resultados experimentais e de modelação para a perda de carga na carreira de filtração 3 para o filtro ascendente de pedregulho (FAP). É interessante observar que nesse caso as oscilações nos dados experimentais ocorreram no primeiro terço da carreira de filtração e a modelação não pôde, igualmente, expressar essas variações, como mostra a Figura 4.
Ainda assim, o valor do coeficiente de correlação múltipla (R2) apresenta 97% de aderência aos dados experimentais.
Deve-se observar também o valor bem maior (185) da constante kh1 da equação de Ergun (1952), conforme Tabela 5. Na Figura 5, observa-se uma perda de carga inicial alta em relação ao perfil da Figura 4, em virtude da taxa de filtração 33% maior que a carreira de filtração observada nessa última. Outro fato digno de nota é o valor (271) da constante kh1 de da equação de Ergun (1952), como apresentado na Tabela 6.
Os demais resultados para a modelação das camadas do FAAG apresentados por Botari (2007) obtiveram um valor médio do coeficiente de correlação (R2) superior a 90%, com um desvio padrão menor que 10%, como pode ser visto na Tabela 7. Ao passo que os demais resultados para a modelação das camadas do FAP apresentados por Botari (2007) obtiveram um valor médio de R2 superior a 85%, com um desvio padrão menor que 20%, como mostra a Tabela 7.
O R2 é chamado de coeficiente de determinação, ou seja, um indicador do grau de correspondência entre os valores estimados pela regressão e os dados experimentais, definidos conforme as Equações 30 a 32:
Onde:
n: número de observações;
Yj: ordenada do valor experimental;
Yestj: valor de Yj estimado pela regressão;
 : média dos valores das ordenadas experimentais.
: média dos valores das ordenadas experimentais.
Quando R2 expressa uma regressão não linear é chamado de coeficiente de determinação múltipla (MENDENHALL; SINCICH, 1995). Quanto mais próximo do valor unitário for R2, mais confiável será a regressão ou linha de tendência.
Os valores para as constantes da equação de Ergun (1952) (kh1e kh2) obtidos neste trabalho situaram-se próximos das faixas de valores elencados por Trussell e Chang (1999). Deve-se atentar ao fato de que para a modelação das camadas com granulometria maior, os valores para a constante kh2 eram superiores aos valores obtidos nas camadas com granulometria menor.
Na média, os valores de kh1 variaram em uma faixa entre 90 e 180 para o meio filtrante de areia grossa ao passo que, para o meio filtrante de pedregulho, tais valores situaram-se entre 100 e 240. No caso da constante kh2, os valores para o meio filtrante de areia grossa variaram, em média, entre 0,7 a 1,2 ao passo que, para o meio filtrante de pedregulho, variaram, em média, entre 1,0 e 2,5 (em alguns casos o valor aproximou-se de 5).
Conclusões
A opção pela equação de Ergun no Regime de Forchheimer para a perda de carga mostrou-se adequada às condições hidráulicas da instalação piloto e ao modelo proposto tanto para o caso do FAAG como do FAP.
A modelação obteve melhores resultados expressos em termos do coeficiente de correlação múltipla (R2) para o caso do FAAG do que no caso do FAP.
A modelação matemática proposta apresentou boa aderência aos valores experimentais tanto na condição inicial (t = 0) como na condição de serviço ao longo do tempo de filtração.
As oscilações observadas nos valores das medidas experimentais de perda de carga não puderam ser modeladas pelo modelo proposto.
Os valores dos coeficientes da equação 24 variaram bastante. Na grande maioria dos casos, os valores encontrados foram superiores ou minimamente iguais aos valores adotados na literatura para a equação de ERGUN (1952) para leito limpo;
O valor da constante kh1 da equação de Ergun para meio filtrante de areia grossa variou, em média, entre 90 e 180; o valor da constante kh2 da equação de Ergun para meio filtrante de areia grossa variou, em média, entre 0,7 e 1,2; o valor da constante kh1 da equação de Ergun para meio filtrante de pedregulho variou, em média, entre 100 e 240; o valor da constante kh2 da equação de Ergun para meio filtrante de pedregulho variou, em média, entre 1,0 e 2,5.
Recomendações
Os autores verificaram que os coeficientes (150 e 1,75) da Equação15 não devem ser utilizados indiscriminadamente, tanto para meios filtrantes de areia grossa como para pedregulho.
Com base no presente trabalho, os autores recomendam a utilização dos valores 150 e 180, na ausência de valores experimentais, para as constantes kh1 da equação de Ergun para areia grossa e pedregulho, respectivamente, para o cálculo da perda de carga na situação inicial (leito limpo), uma vez que se aproximam mais daqueles observados neste trabalho.
Recomenda-se, ainda, a utilização dos valores 1,0 e 1,5 na ausência de valores experimentais, para as constantes kh2 da equação de Ergun para areia grossa e pedregulho, respectivamente, para o cálculo da perda de carga na situação inicial (leito limpo), pois, da mesma forma, aproximam-se mais daqueles observados neste trabalho.
Agradecimentos
Os autores agradecem à Fundação de Amparo à Pesquisa do Estado de São Paulo (Fapesp) pela bolsa de pós-doutorado do primeiro autor (processo 07/50723-8), ao Departamento de Hidráulica e Saneamento da Escola de Engenharia de São Carlos da Universidade de São Paulo, à Universidade Estadual de Maringá e ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) pela bolsa de Produtividade em Pesquisa do segundo autor.
Recebido: 21/08/07
Aceito: 06/03/09
- BOTARI, A. Modelação matemática da perda de carga e da remoção de turbidez e de partículas na filtração direta ascendente 402f. Tese (Doutorado) Escola de Engenharia de São Carlos da USP, São Carlos, 2007.
- BOTARI, A.; DI BERNARDO, L. Modelação matemática macroscópica da perda de carga e da remoção de sólidos suspensos totais na filtração direta ascendente. Engenharia Sanitária e Ambiental v. 12, n. 2, p. 149-159, 2007.
- DARBY, J.L.; ATTANASIO, R.E.; LAWLER, D.F. Filtration of heterodisperse suspensions: modeling of particle removal and head loss. Water Research, v. 26, n. 6, p. 711-736, 1992.
- DARBY, J.L; LAWLER, D.F. Ripening in depth filtration: effect of particle size on removal and head loss. Environmental Science and Technology, v. 24, n. 7, p. 1069-1078, 1990.
- DI BERNARDO, A. Desempenho de sistemas de dupla filtração no tratamento de água com turbidez elevada. 269f. Tese (Doutorado) Escola de Engenharia de São Carlos da USP, São Carlos, 2004.
- DI BERNARDO, L.; DANTAS, D.B.A. Métodos e técnicas de tratamento de água São Carlos: Rima, 2005. Volume I.
- ERGUN, S. Fluid flow trough packed columns. Chemical Engineering Progress, v. 42, n. 2, p. 89-94, 1952.
- ERGUN, S.; ORNING, A. Fluid flow trough randomly packed columns and fluidized beds. Industrial and Engineering Chemistry, v. 41, n. 6, p. 1179-1184, 1949.
- FAIR, G.M.; GEYER, J.C.; OKUN, D.A. Purificacion de aguas y tratamiento y remocion de aguas residuales México: Limusa, 1973.
- HUNT, J.R.; HWANG, B.; McDOWELL-BOYER, L.M. Solids accumulation during deep bed filtration. Environmental Science and Technology, v. 27, p. 1099-1107, 1993.
- KURODA, E.K. Avaliação da filtração direta ascendente em pedregulho como pré-tratamento em sistemas de dupla filtração 238f. Dissertação (Mestrado em Engenharia Hidráulica e Sanitária) Escola de Engenharia de São Carlos da USP, São Carlos, 2002.
- LANG, J.S. et al Investigating filter performance as a function of the ratio of filter size to media size. Journal AWWA, v. 8, n. 8, p. 122-130, 1996.
- LIMA E SILVA, A.L.F. Desenvolvimento e implementação de uma nova metodologia para modelagem de escoamentos sobre geometrias complexas: método da fronteira imersa com modelo físico virtual 142f. Tese (Doutorado) Universidade Federal de Uberlândia, Uberlândia, 2002.
- MENDENHALL, W.; SINCICH, T. Statistics for Engineering and the Sciences. 4. ed. New Jersey: Prentice-Hall International Inc.,1995.
- OMELIA, C.R.; ALI, W. The role of retained particles in deep bed filtration. Progress in Water Technology, v. 10, n. 5/6, p. 167-182, 1978.
- STEVENSON, D.G. Flow and filtration through granular media: the effect of grain and particle size dispersion. Water Research, v. 31, n. 2, p. 310-322, 1997.
- SUGUIO, K. Introdução à sedimentologia São Paulo: Edgard Blücher, 1973.
- TIEN, C.A. Granular filtration of aerosols and hydrosols London: Butterworth Publishers, 1989. Series in Chemical Engineering.
- TOBIASON, J.E.; VIGNESWARAN, B. Evaluation of a modified model for deep bed filtration. Water Research, v. 28, n. 2, p. 335-342, 1994.
- TRUSSELL, R.R.; CHANG, M. Review of flow through porous media as applied to headloss in water filters. Journal of Environmental Engineering, v. 125. n. 11, p. 998-1006, nov. 1999.
- VIGNESWARAN, S.; CHANG, J.S. Mathematical modeling of the entire cycle of deep bed filtration. Water, Air and Soil Pollution, v. 29, p. 155-164, 1986.
Endereço para correspondência:
Datas de Publicação
-
Publicação nesta coleção
17 Jul 2009 -
Data do Fascículo
Jun 2009
Histórico
-
Aceito
06 Mar 2009 -
Recebido
21 Ago 2007