Resumos
Nesta fase do trabalho objetivou-se estimar parâmetros para equações mensais de estimativas de precipitação de intensidade máxima em intervalos de 5, 10, 15, 20, 25, 30 e 60 minutos para 165 localidades do Estado de São Paulo. A partir de dados mensais de séries históricas de 31 anos de precipitação máxima de "um dia", utilizou-se da distribuição de probabilidade de Gumbel para os cálculos da probabilidade de ocorrência de valores extremos em cada mês. Utilizando-se da metodologia proposta por Occhipinti & Santos (1966), as chuvas máximas de "um dia" foram desagregadas para precipitações de intensidade máxima em 24 horas e nos sete intervalos de tempo acima descritos, para cada uma das 165 localidades e em cada mês. Os parâmetros alfa e beta foram calculados, para cada um dos sete intervalos de duração da chuva, com F(x)= 90% e em cada uma das 165 localidades propostas. As séries de precipitação máxima de "um dia" foram submetidas ao teste de Kolmogorov-Smirnov, confirmando bom ajuste com distribuição de Gumbel. A metodologia mostrou bom desempenho, considerando-se que as diferenças percentuais relativas dos resultados das precipitações máximas obtidas com os parâmetros alfa e beta, de 25 localidades, comparadas com os obtidos pela metodologia de Occhipinti, foram de modo geral menores que 0,5%.
Intensidade máxima; precipitação; distribuição de probabilidade
The objective of this phase of the work was to obtain parameters for monthly equations of maximum of estimations precipitation intensity in intervals of 5, 10, 15, 20, 25, 30 and 60 minutes covering 165 places of São Paulo State. Starting from the historical series of 31 years of maximum precipitation of "one day", it was used Gumbel probability distribution for calculating the probability of occurrence of extreme values in every month. Using the methodology proposed by Occhipinti & Santos (1966), the maximum rains of "one day" were dissociated in precipitation of maximum intensity in 24 hours in the seven intervals of time described above, for each one of the 165 places in every month. The parameters a and b were calculated, for each one of the seven rains intervals of durations with F(x) = 90% in each one of the 165 proposed places. The parameters and were calculated, for each one of the seven intervals of duration of the rain, with F(x) = 90% and in each one of the 165 proposed places. The series of maximum precipitation of "one day" were submitted to the test of Kolmogorov-Smirnov, witch results confirmed the good adjustment with distribution of Gumbel. The methodology showed good performance, considering that the relative percentile differences, of the results of the maximum precipitations obtained with the parameters and , of 25 places, compared with those obtained by the methodology of Occhipinti, they were in general smaller than 0,5%.
Maximum intensity; rain; probability distribution
CIÊNCIAS AGRÁRIAS
Parâmetros para equações mensais de estimativas de precipitação de intensidade máxima para o estado de São Paulo1 1 . Trabalho desenvolvido pelo NEPA - Núcleo de Estudos e Pesquisas Ambientais da Faculdade de Tecnologia de Sorocaba/SP - FATEC-SO - Fase I
Parameters for monthly equations of maximum intensity estimates of rain for the São Paulo state - Phase I
José Carlos FerreiraI; Luis Antonio DanielII; Mauro TomazelaIII
IProfessor Pleno, Doutor em Eng. Agrícola/Unicamp - Diretor Científico NEPA/FATEC-SO ferraro1@terra.com.br
IIProfessor Pleno, Livre Docente/Unicamp - Diretor Administrativo do NEPA/FATEC-SO daniel51@terra.com.br
IIIProfessor Pleno, MSc/USP - Membro do NEPA/FATEC-SO tomazela@zaz.com.br
RESUMO
Nesta fase do trabalho objetivou-se estimar parâmetros para equações mensais de estimativas de precipitação de intensidade máxima em intervalos de 5, 10, 15, 20, 25, 30 e 60 minutos para 165 localidades do Estado de São Paulo. A partir de dados mensais de séries históricas de 31 anos de precipitação máxima de "um dia", utilizou-se da distribuição de probabilidade de Gumbel para os cálculos da probabilidade de ocorrência de valores extremos em cada mês. Utilizando-se da metodologia proposta por Occhipinti & Santos (1966), as chuvas máximas de "um dia" foram desagregadas para precipitações de intensidade máxima em 24 horas e nos sete intervalos de tempo acima descritos, para cada uma das 165 localidades e em cada mês. Os parâmetros alfa e beta foram calculados, para cada um dos sete intervalos de duração da chuva, com F(x)= 90% e em cada uma das 165 localidades propostas. As séries de precipitação máxima de "um dia" foram submetidas ao teste de Kolmogorov-Smirnov, confirmando bom ajuste com distribuição de Gumbel. A metodologia mostrou bom desempenho, considerando-se que as diferenças percentuais relativas dos resultados das precipitações máximas obtidas com os parâmetros alfa e beta, de 25 localidades, comparadas com os obtidos pela metodologia de Occhipinti, foram de modo geral menores que 0,5%.
Termos para indexação: Intensidade máxima, precipitação, distribuição de probabilidade.
ABSTRACT
The objective of this phase of the work was to obtain parameters for monthly equations of maximum of estimations precipitation intensity in intervals of 5, 10, 15, 20, 25, 30 and 60 minutes covering 165 places of São Paulo State. Starting from the historical series of 31 years of maximum precipitation of "one day", it was used Gumbel probability distribution for calculating the probability of occurrence of extreme values in every month. Using the methodology proposed by Occhipinti & Santos (1966), the maximum rains of "one day" were dissociated in precipitation of maximum intensity in 24 hours in the seven intervals of time described above, for each one of the 165 places in every month. The parameters a and b were calculated, for each one of the seven rains intervals of durations with F(x) = 90% in each one of the 165 proposed places. The parameters and were calculated, for each one of the seven intervals of duration of the rain, with F(x) = 90% and in each one of the 165 proposed places. The series of maximum precipitation of "one day" were submitted to the test of Kolmogorov-Smirnov, witch results confirmed the good adjustment with distribution of Gumbel. The methodology showed good performance, considering that the relative percentile differences, of the results of the maximum precipitations obtained with the parameters and , of 25 places, compared with those obtained by the methodology of Occhipinti, they were in general smaller than 0,5%.
Index terms: Maximum intensity, rain, and probability distribution.
INTRODUÇÃO
A dificuldade de obter informações sobre os níveis de precipitação de intensidade máxima tem sido o principal obstáculo para o planejamento e trabalhos aplicados em terraceamento, construção de galerias e canais de escoamento, pontes, estradas e drenagem de áreas rurais e urbanas, bem como em atividades de orientação e combate as enchentes na zona urbana. Mesmo com uma razoável rede hidrológica, o Estado de São Paulo conta com poucos pluviógrafos, de modo a atender a demanda por informações sobre precipitações intensas. Além disso, dados de precipitação intensa, extraídos de pluviogramas exigem muita paciência e trabalho manual para serem obtidos. Os primeiros trabalhos realizados para obter estimativas de precipitações intensas no Brasil, foram realizados por Pfafstetter (1957), seguidos por Banzatto & Benincasa (1986) e Vieira et al. (1991), entre outros. Equações de precipitação de intensidade máxima têm sido desenvolvidas para algumas regiões do Brasil. Pinto et al. (1996) estabeleceram equações de chuvas intensas para algumas localidades do Estado de Minas Gerais e Pruski (1997) desenvolveu metodologia baseada no uso de sistemas de informações geográficas para obtenção de equações de chuvas intensas em qualquer localidade no Estado do Paraná. Os mesmos Vieira et al. (1991) desenvolveram mapeamento da chuva diária máxima provável para o Estado de São Paulo. Occhipinti & Santos (1966) propuseram metodologia prática para desagregar dados de precipitação de intensidade máxima de "um dia" em precipitação de intensidade máxima de 24 horas. Cardoso et al. (1998), realizaram a análise de chuvas intensas a partir da desagregação de chuvas diárias de Lages e de Campos Novos em Santa Catarina. A principal limitação na determinação das equações de precipitação máxima está na determinação dos parâmetros alfa e beta. Os quatro métodos mais conhecidos para estimativas desses parâmetros, são descritos em Assis et al. (1996). Neste estudo, optou-se pelo método de desagregação de chuva, visando estimar os parâmetros alfa e beta de equação de chuvas intensas mensais para o Estado de São Paulo, a partir de informações de chuva de "um dia" de 165 localidades, com fins de aplicações em obras de drenagem.
MATERIAL E MÉTODOS
Foram utilizados dados de precipitação de intensidade máxima de "um dia", com séries históricas de 31 anos, completas, com início em 1962 e término em 1992, de 165 postos pluviométricos do DAEE do Estado de São Paulo identificados pelo código do posto e pelas coordenadas geográficas em minutos. Em cada localidade e em cada ames, foram estudadas as séries de 31 anos de dados de precipitação máxima de "um dia". Como essas informações não continham as altitudes de todos os postos, completou-se com as altitudes médias do município de origem do posto. Os valores dos níveis máximos prováveis de intensidade de chuva máxima no mês, foram calculados pela função de distribuição de probabilidade proposta por Gumbel (1958), dada por:
Em que a e b são parâmetros a serem calculados pelos momentos da distribuição, nos quais o sinal negativo do expoente é aplicado para obter valores máximos, com
para T igual ao período de retorno em anos. As 165 séries dos valores de precipitação de intensidade máxima de "um dia" foram submetidas ao ajuste de modelo probabilístico de Gumbel e testadas pelo método de Kolmogorov-Smirnov, conforme recomendado em Assis et al. (1996). Todas as séries foram testadas, conforme descrito em Assis et al. (1996) e apresentaram diferenças máximas Dm abaixo do valor crítico (D cr) para a= 5% , mostrando bom ajuste das séries ao modelo de Gumbel. A opção pelo método dos momentos recaiu na sua praticidade, mesmo porque o método da verossimilhança além de apresentar resultados bem próximos, exige mais cálculos e o uso de estimativas. Para o teste Kolmogorov-Smirnov, utilizou-se o "software estatístico SPSS 7.5 for windows" nos laboratórios da FCM/Unicamp.
Os cálculos dos parâmetros a e b foram estimados pelas equações :
Nas equações 3 e 4, s e  são respectivamente as estimativas do desvio padrão e a média da série dos dados. Aplicando-se logaritmos em (1), a equação geral para estimativas de precipitações de intensidade máxima fica:
são respectivamente as estimativas do desvio padrão e a média da série dos dados. Aplicando-se logaritmos em (1), a equação geral para estimativas de precipitações de intensidade máxima fica:
Em que I é o valor máximo esperado da chuva no período de retorno T e {- ln[-ln[F(x)]] = lT uma variável reduzida, descritos em Assis et al. (1996) e Kite (1985). Na Tabela 1, proposta por Ferreira et al. (1999), mostra-se os valores da variável reduzida T = ln{-ln[F(x)]} com quatro algarismos significativos em função do período de retorno.
Os valores das estimativas de precipitação de intensidade máxima de "um dia" foram desagregadas em precipitação de intensidade máxima de 24 horas, conforme metodologia proposta por Occhipinti & Santos (1966). Na tabela 2, mostra-se os fatores multiplicativos para obter a desagregação das chuvas, nos intervalos de tempo propostos.
Deste modo, a partir dos dados de precipitação de intensidade máxima de 24 horas, foram desagregadas as chuvas de intensidade máxima para 1 hora, 30 minutos, 25 minutos, 20 minutos, 15 minutos, 10 minutos e 5 minutos, conforme Tabela 2, adaptada de Cardoso et al. (1998).
Para cada localidade, e para cada intervalo de tempo de duração da precipitação máxima, foram calculados, com base na equação de valores extremos (GUMBEL, 1958), os parâmetros e pelo método dos momentos de cada série dos dados originais, com base nas estimativas do desvio padrão e da média, conforme proposto em Assis et al. (1996).
Para testar o método, foram calculadas as estimativas de precipitação máxima por desagregação para o mês de janeiro, de 25 localidades, nos intervalos de 5, 15, 30 e 60 minutos, para comparar com os resultados estimados pelos parâmetros alfa e beta, obtidos para as respectivas localidades nos mesmos intervalos de tempo. As diferenças relativas percentuais dos resultados obtidos por ambos os métodos, foram calculadas pela relação:
Em que:
DD = dados estimados por desagregação a partir dos dados observados;
DE = dados estimados com os parâmetros alfa e beta.
RESULTADOS E DISCUSSÃO
Pela Tabela 3 são apresentados os valores de alfa e beta das 165 localidades estudadas e em 7 intervalos de duração da chuva no mês, bem como, as médias, os desvios padrões e os coeficientes de variação em cada intervalo de tempo. Devido ao grande número de informações, na Tabela 3 apresenta-se apenas os resultados para o mês de Janeiro. Escolheu-se o mês de janeiro, para a discussão dos resultados, visto que é neste mês que ocorrem os maiores níveis de precipitação de intensidade máxima no Estado de São Paulo, (FERREIRA et al., 1999). Vê-se, nos valores da Tabela 3, que em cada um dos 165 postos de chuva os valores de alfa e beta diminuem com o intervalo de tempo de duração da chuva.
Ainda na Tabela 3, observa-se que apesar dos altos valores dos coeficientes da variação para alfa (28%), estes, são praticamente iguais nos sete intervalos de duração da chuva. Para o parâmetro beta, os coeficientes de variação são menores, todos da ordem de 13%. Os altos valores para os coeficientes de variação de alfa são justificados pelos elevados desvios padrões da população dos dados.
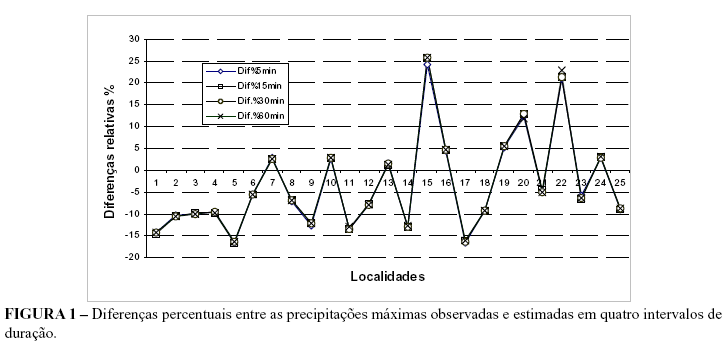
Na Tabela 4 mostra-se, para o mês de janeiro em 25 localidades, as diferenças relativas percentuais entre as chuvas intensas de 5, 15, 30 e 60 minutos, estimadas com os parâmetros, alfa e beta para um período de retorno de 10 anos, com as chuvas máximas nos mesmos intervalos de tempo, obtidas por desagregação, a partir dos dados observados de chuva máxima de 1 dia. As estatísticas dessa tabela mostram coeficientes de variação de cerca de 10% para os quatros intervalos de tempo de duração da chuva desagregada, enquanto que, para as precipitações estimadas com os parâmetros alfa e beta, os coeficientes de variação são praticamente o dobro nos respectivos intervalos de duração da chuva. As diferenças relativas entre as precipitações estimadas pelos parâmetros alfa e beta, com as chuvas estimadas por desagregação foram calculadas pela equação (6).
O gráfico da Figura 1 é apresentado para facilitar a observação. Verifica-se que, em 16 localidades as diferenças percentuais são negativas, sendo que em 6 localidades foram menores que 5%. De modo geral, em 64 % das localidades as diferenças absolutas são menores que 10.
Em todas as localidades, os pontos das curvas do gráfico se ajustam bem. Em 64% as diferenças são negativas, indicando que nessas localidades as estimativas de precipitação máximas, calculadas pelos parâmetros alfa e beta foram menores que as estimativas de precipitação obtidas por desagregação. As maiores diferenças positivas ocorreram em Pindamonhangaba, Santo Antonio do Pinhal e São Sebastião da Gama e a localidade onde as diferenças foram menores foi Pedregulho. Não foram identificados fatores relacionados às coordenadas geográficas e as altitudes das 25 localidades, que justificassem o comportamento da distribuição espacial das precipitações estudadas. Pinto et al. (1996), desenvolvendo equações para chuvas intensas em Minas Gerais para 29 localidades, relataram o mesmo comportamento para as chuvas intensas.
No gráfico da Figura 2, vê-se que as diferenças entre as chuvas estimadas com os parâmetros alfa e beta e as estimativas obtidas por desagregação, aumentaram com o tempo de duração da chuva. No gráfico são perceptíveis as acentuadas diferenças entre as chuvas estimadas para Pindamonhangaba, comparadas com as demais localidades.
Assim, para cada intervalo de duração de precipitação de intensidade máxima que se deseje obter, os parâmetros alfa e beta neste estudo podem ser aplicados para obter estimativas, no mês de interesse e no período de retorno desejado.
Por exemplo, para um período de retorno de 10 anos, em Sorocaba no mês de janeiro, a equação para precipitação de intensidade máxima com duração de 30 minutos, fica, com base na forma geral It = b + 2,250 a, descrita por:
I30+24,46+92,25009,01 (7)
Em que:
I30= chuva máxima esperada
b = 24,46 , a = 9,01 (Tabela 3) e
2,250 é a variável reduzida para T = 10 anos (Tabela 1)
As equações 8, 9 e 10, ilustram exemplos para outros intervalos de tempo de duração da chuva em outros períodos de retorno para Sorocaba.
* Os valores da variável reduzida, correspondentes ao período de retorno foram extraídos da Tabela 1.
CONCLUSÕES
No teste em 25 localidades, o método utilizado para obter os parâmetros alfa e beta, mensais, com base no desvio padrão e na média, mostrou bom desempenho, considerando que as variações entre as diferenças relativas de precipitação máxima de cada localidade em quatro intervalos de duração da chuva, ficaram abaixo de 0,5%.Além disso, sendo mensais os parâmetros estimados, as equações especificam o mês de interesse de aplicação, disponibilizando as estimativas máximas de precipitação, para tomadas de decisão em planejamento agrícola e em drenagem urbana.
Para fins de uso dos parâmetros alfa e beta, obtidos nesta metodologia no dimensionamento de obras em hidrologia recomenda-se, a inclusão de coeficientes de segurança nos projetos, visto que em 64% das localidades as diferenças relativas das precipitações máximas esperadas foram negativas.
(Recebido para publicação em 14 de janeiro de 2004 e aprovado em 16 de agosto de 2005)
- ASSIS, F. N.; ARRUDA, H. V.; PEREIRA, A. R. Aplicações de estatística à climatologia: teoria e prática. Pelotas: UFP, 1996. 161 p.
- BANZATTO, D. A.; BENINCASA, M. Estimativas de chuvas diárias máximas prováveis com duração de um dia, para o Estado de São Paulo Jaboticabal: UNESP, 1986. (Boletim técnico, 6).
- CARDOSO, C. O.; ULLMANN, M. N.; BERTO, I. Análise de chuvas intensas a partir de desagregação das chuvas diárias de Lajes e Campos Novos (SC). Revista Brasileira de Ciência do Solo, Campinas, v. 22, p. 131-140, 1998.
- FERREIRA, J. C.; DANIEL, L. A.; LOMBARDI NETO, F. Mapas mensais de precipitação máxima e erosividade para o Estado de São Paulo de interesse à Engenharia 1999. Tese (Doutorado) Universidade Estadual de Campinas, Campinas, 1999.
- GUMBEL, E. J. Statistics of extremes Columbia: Columbia University, 1958. 357 p.
- KITE, G. W. Frequency and risk analysis in hydrology water resourcers 3. ed. [S.l.: s.n.], 1985. 233 p.
- OCCHIPINTI, A. G.; SANTOS, P. M. Relações entre as precipitações máximas de ¨um dia¨ e de ¨24 horas¨ na cidade de São Paulo São Paulo: IAG/USP, 1966.
- PFAFSTETTER, O. Chuvas intensas no Brasil Rio de Janeiro: Ministério da Viação e Obras Públicas, 1957. 420 p.
- PINTO, F. F.; FERREIRA, P. A.; PRUSKI, F. F.; ALVES, A. R.; CECON, P. R. Equações de chuvas intensas para algumas localidades do Estado de Minas Gerais. Revista Brasileira de Engenharia Agrícola, Viçosa, v. 16, n. 1, p. 91-104, 1996.
- PRUSKI, F. F. Metodologia baseada no uso de sistema de informações geográficas para obtenção de equações de chuvas intensas em qualquer localidade do Estado de Paraná. Revista Brasileira de Engenharia Agrícola, Viçosa, v. 5, n. 3, p. 254-265, 1997.
- VIEIRA, S. R.; LOMBARDI NETO, F.; BURROWS, I. T. Mapeamento da chuva diária máxima provável para o Estado de São Paulo. Revista Brasileira de Ciência do Solo, Campinas, 1991.
Datas de Publicação
-
Publicação nesta coleção
18 Ago 2008 -
Data do Fascículo
Dez 2005
Histórico
-
Aceito
16 Ago 2005 -
Recebido
14 Jan 2004