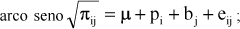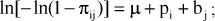Modelos de predição para sobrevivência de plantas de Eucalyptus grandis

Prediction models of Eucalyptus grandis plant survival

COMUNICAÇÃO

Modelos de predição para sobrevivência de plantas de Eucalyptus grandis

Prediction models of Eucalyptus grandis plant survival

Telde Natel Custódio^I; Décio Barbin^II

^IEngenheiro Agrícola, Doutor em Agronomia, Pesquisador - Departamento de Agricultura/DAG - Universidade Federal de Lavras/UFLA - Cx. P. 3037 - 37200-000 - Lavras, MG - [e-mail] ^IIEngenheiro Agrônomo, Doutor em Agronomia, Professor Titular - Departamento de Ciências Exatas/LCE - Escola Superior de Agricultura "Luiz de Queiroz"/ESALQ - Universidade de São Paulo/USP - Avenida Pádua Dias, 11 - Cx. P. 9 - 13418-900 - Piracicaba, SP - [e-mail]

RESUMO

Objetivou-se com este trabalho comparar modelos de predição de plantas sobreviventes de Eucalyptus grandis. Utilizaram-se os seguintes modelos: modelo linear misto com os dados transformados, utilizando-se as transformações angular e BOX-COX; modelo linear generalizado misto com distribuição binomial e funções de ligação logística, probit e complemento log-log; modelo linear generalizado misto com distribuição Poisson e função de ligação logarítmica. Os dados são provenientes de um experimento em blocos ao acaso, para avaliação de progênies maternas de Eucalyptus grandis, aos 5 anos de idade, em que a variável resposta são plantas sobreviventes. Para comparação dos efeitos entre os modelos foram estimadas as correlações de Spearman e aplicado o teste de permutação de Fisher. Foi possível concluir que, o modelo linear generalizado misto com distribuição Poisson e função de ligação logarítmica se ajustou mal aos dados e que as estimativas para os efeitos fixos e predição para os efeitos aleatórios, não se diferenciaram entre os demais modelos estudados.

Termos para indexação: Estatística aplicada, modelo linear misto, transformação de dados, modelo linear generalizado misto.

ABSTRACT

The objective of this work was to compare models for prediction of the survival of plants of Eucalyptus grandis. The following models were used: linear mixed model with the transformed data, by utilizing the angular transformations and BOX-COX; generalized linear mixed model with binomial distribution and logistic functions, probit and complement log-log links; generalized linear mixed model with Poisson distribution and logarithmic link function. The data came from a randomized block experiment for evaluation of Eucalyptus grandis maternal progenies at five years old, in which the variable response are surviving plants. For comparison of the effects among the models the correlations of Spearman were estimated and the test of permutation of Fisher was applied. It was possible to conclude that: the generalized linear mixed model with Poisson distribution and logarithmic link function misadjusted to the data; the estimates for the fixed effects and prediction for the random effects did not differ among the to other studied models.

Index terms: Applied statistics, linear mixed model, transformation of data, generalized linear mixed model.

O gênero Eucalyptus é amplamente cultivado no Brasil pela sua importância como espécie botânica de grande diversidade e boa adaptabilidade a vários tipos de ambiente. Assim, são crescentes as pesquisas no sentido de estabelecer florestas de usos múltiplos, voltados principalmente para atender a demanda de madeira para os mercados nacional e internacional, utilizados para diversos fins. Dentre as espécies do gênero Eucalyptus destaca-se a espécie E. grandis, de ampla diversidade de uso e potencialidade.

Uma vez reconhecida a sua importância, torna-se necessário considerar que o aumento da produção das florestas não depende somente de técnicas de manejo. Aliado a essas técnicas torna-se necessária a aplicação do melhoramento genético, com o intuito de tornar os povoamentos florestais mais produtivos, aumentando sua adaptabilidade não só ao tipo de utilização, mas também ao tipo de uso final. No melhoramento, uma característica avaliada de grande importância é o número de plantas sobreviventes ao final de um experimento.

A variável sobrevivência de plantas geralmente é estudada na forma de proporção, dividindo-se o número de plantas sobreviventes pelo total de plantas na parcela. Quando não se realiza um estudo adequado das características da distribuição de freqüências, esse tipo de dados são analisados, mediante a técnica da análise de variância ou de regressão, sem se ter a certeza de que todas as exigências necessárias para a aplicação dessas técnicas foram satisfeitas.

Mas, para que esses dados sejam analisados mediante essas técnicas é necessário que eles atendam às pressuposições nas quais as análises se baseiam. Em certos casos quando não é possível satisfazer as pressuposições para análise de variância ou de regressão na própria escala observada, transformações têm sido feitas para uma escala mais apropriada com o objetivo de se conseguir homogeneidade de variâncias e uma distribuição aproximadamente normal.

No caso de proporções de plantas sobreviventes, o arco seno da raiz quadrada dessas proporções, seria então utilizado em uma análise de variância ou regressão. Essa operação é conhecida como transformação angular, sendo uma das mais utilizadas (SNEDECOR & COCHRAN, 1989; STEEL & TORRIE, 1980). Portanto, essa transformação é feita admitindo-se que a variável resposta segue uma distribuição binomial. Uma outra opção de transformação seria a transformação de Box & Cox (1964). Assim, espera-se que a transformação homogeneizará a variância, o que é uma das exigências para a validade dos testes estatísticos. Porém, em muitas situações práticas, a transformação necessária para estabilizar a variância pode não ser a mesma para se obter uma resposta linear.

Outra abordagem seria a utilização das proporções sem o uso de transformação, assumindo-a como sendo proveniente de uma distribuição binomial, ou ainda, a utilização somente do número de plantas sobreviventes, admitindo-o como sendo de uma distribuição de Poisson, e proceder à análise pela metodologia dos modelos lineares generalizados.

Os modelos lineares generalizados foram desenvolvidos por Nelder & Wedderburn (1972), visando à análise de dados associados a distribuições pertencentes à família exponencial com um parâmetro. Segundo McCullagh & Nelder (1989), um modelo linear generalizado é composto por um componente aleatório associado à distribuição da variável resposta; um componente sistemático linear nos parâmetros, denominado preditor linear; uma função de ligação, que liga o componente aleatório ao componente sistemático, ou seja, relaciona a média ao preditor linear. Incorporando efeitos aleatórios no preditor linear, têm-se os modelos lineares generalizados mistos. Nesse sentido, a função de ligação deve ser incorporada aos estimadores dos efeitos fixos, preditores dos efeitos aleatórios e estimadores dos componentes de variância dos efeitos aleatórios, conforme Schall (1991).

Devido às abordagens citadas, objetivou-se com este trabalho comparar modelos de predição de plantas sobreviventes de Eucalyptus grandis, considerando-se as diferentes metodologias estatísticas, através dos seguintes modelos: modelo linear misto utilizando-se as transformações angular e BOX-COX; modelo linear generalizado misto com distribuição binomial e funções de ligação logística, probit e complemento log-log; modelo linear generalizado misto com distribuição Poisson e função de ligação logarítmica.

Foram utilizados dados provenientes de um experimento para avaliação de progênies de Eucalyptus grandis, aos 5 anos de idade, em que a variável resposta são plantas sobreviventes. O experimento foi instalado no delineamento em blocos casualizados, com 6 plantas por parcela, 10 repetições e 25 progênies maternas. Na avaliação da sobrevivência foram atribuídos os valores 1 para as plantas vivas e 0 para as mortas.

Para verificação da normalidade dos dados aplicou-se o teste de Shapiro-Wilk, através do PROC UNIVARIATE do SAS (SAS INSTITUTE, 2001), considerando os dados como proporções e contagem de plantas sobreviventes. Foram constatados que os mesmos não apresentaram normalidade, justificando assim a transformação dos dados ou a análise pela teoria de modelos lineares generalizados.

Assim, foram considerados os seguintes modelos para fins de comparação:

A - Modelo linear misto com transformação angular:

B - Modelo linear misto com transformação BOX-COX:

C - Modelo linear generalizado misto com distribuição binomial e função de ligação logística:

D - Modelo linear generalizado misto com distribuição binomial e função de ligação probit:

E - Modelo linear generalizado misto com distribuição binomial e função de ligação complemento log-log:

F - Modelo linear generalizado misto com distribuição Poisson e função de ligação logarítmica:

em que π_ij é a proporção de plantas sobreviventes para a progênie i no bloco j; y_ij é o número de plantas sobreviventes para a progênie i no bloco j; m é uma constante inerente a todas as observações (média geral); p_i é o efeito da i-ésima progênie (i = 1, 2, ...., 25), considerado aleatório; b_j é o efeito do j-ésimo bloco (j = 1, 2, ..., 10), considerado fixo; e_ij é o erro aleatório.

Os modelos foram ajustados utilizando-se o programa SAS (SAS INSTITUTE, 2001), através da PROC MIXED para os modelos A e B, e por meio da macro GLIMMIX para os modelos C, D, E e F.

Para comparação das estimativas dos efeitos fixos e efeitos aleatórios preditos, foram estimadas as correlações de Spearman entre os efeitos dos modelos, com o intuito de se verificar o grau de associação entre eles, e também aplicado o teste de permutação de Fisher, para se verificar se os modelos diferem estatisticamente entre si.

Para a verificação da qualidade do ajuste dos modelos C, D, E e F (presença de superdispersão (Φ < 1) ou subdispersão (Φ < 1 ), estimou-se o parâmetro de dispesão (f), baseado na estatística de Pearson X² generalizada (JFRGENSEN, 1987), dado por:

em que: é a função de variância estimada sob o modelo que está sendo ajustado, sendo: n igual ao número de observações; p igual ao número de parâmetros envolvidos no modelo; são as proporções observadas de plantas sobreviventes; são as proporções de plantas sobreviventes estimadas pelo modelo.

As estimativas para o parâmetro de dispersão , considerando os modelos C, D, E e F estão apresentadas na Tabela 1.

Verifica-se que os valores das estimativas do parâmetro de dispersão, para os modelos C, D e E estão bem próximos de um, valor admitido no modelo binomial, indicando que a variância está consistente com a distribuição assumida, isto é, os dados não fornecem evidências da presença de superdispersão ou subdispersão para os modelos assumidos. Para o modelo F, observa-se que este apresentou uma estimativa muito inferior a um, valor admitido no modelo Poisson, caracterizando a presença de subdispersão, ou seja, a variância não está consistente com a distribuição assumida para este modelo, indicando que o modelo está mal ajustado aos dados. Assim os modelos C, D e E, apresentaram um melhor ajuste em comparação ao modelo F.

Na Tabela 2 estão apresentadas as estimativas dos efeitos fixos considerando-se os diferentes modelos de ajuste.

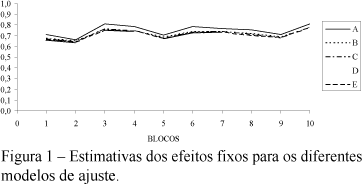
Pode-se constatar pelas estimativas dos efeitos fixos, que estas apresentaram valores bem próximos entre os diferentes modelos, indicando assim que estes apresentaram ajustes semelhantes, o que também pode ser verificado pela Figura 1, onde estão plotados os valores para as estimativas de efeitos fixos para os modelos ajustados.

A Tabela 3 apresenta os valores das correlações de Spearman dos efeitos fixos entre os modelos, onde pode-se verificar altas correlações, confirmando então que esses modelos apresentaram ajustes bastante coincidentes.

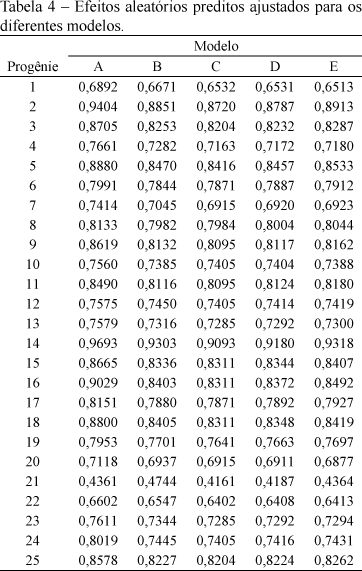
Observa-se através da Figura 1 uma ligeira diferença entre os valores do modelo A em relação aos demais modelos.Os efeitos aleatórios preditos, considerando os diferentes modelos de ajuste, estão apresentados na Tabela 4.

Constata-se pelos resultados dos efeitos aleatórios preditos, apresentados na Tabela 4, que estes, da mesma forma que para as estimativas dos efeitos fixos, apresentaram valores bem próximos, quando se ajustaram os modelos sob os diferentes enfoques, indicando que esses modelos apresentaram ajustes semelhantes.

Na Figura 2, estão plotados os valores dos efeitos aleatórios preditos considerando os diferentes modelos de ajuste, onde se pode observar que os modelos apresentaram ajustes bem semelhantes.

Verifica-se também que o modelo A se diferenciou um pouco mais dos demais modelos, apresentando valores ligeiramente maiores para os efeitos aleatórios preditos.

Apesar de o modelo A apresentar valores dos efeitos fixo e aleatório, um pouco maiores em relação aos demais modelos, há recomendações desaconselhando o uso da transformação angular quando as proporções se aproximam de um dos extremos, isto é, menor que 0,20 ou maior que 0,80 (STEEL & TORRIE, 1980). Em casos extremos, Bartlett (1947) sugere a substituição de 0 por 1/4 e n por n - 1/4, deixando os outros valores inalterados.

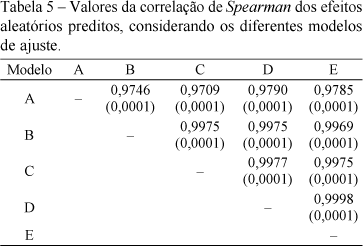
A Tabela 5 mostra os valores das correlações de Spearman dos efeitos aleatórios entre os diferentes modelos de ajuste, quando se observa que os modelos apresentaram altas correlações, indicando assim que os mesmos apresentaram ajustes bastante coincidentes.

O nível de significância (α) obtidos através do teste de Permutação de Fisher, para comparação das estimativas dos efeitos fixos e aleatórios entre os diferentes modelos de ajuste, estão apresentados nas Tabelas 6 e 7, respectivamente.

Verifica-se pelos resultados apresentados na Tabela 6 e 7, através do nível de significância (α) obtidos, que as estimativas dos efeitos fixos e aleatórios, ajustados para os diferentes modelos, não diferem estatisticamente entre si.

Recebido em 4 de agosto de 2006

Aprovado em 28 de setembro de 2007

• BARTLETT, M. S. The use of transformations. Biometrics, Washington, v. 3, n. 1, p. 39-52, 1947.
• BOX, G. E. P.; COX, D. R. An analysis of transformations. Journal of the Royal Statistical Society, B, [S.l.], v. 26, p. 211-252, 1964.
• JÆRGENSEN, B. Exponencial dispersion models: with discussion. Journal of the Royal Statistical Society, Series B, [S.l.], v. 49, n. 2, p. 127-162, 1987.
• McCULLAGH, P.; NELDER, J. Generalized linear models 2. ed. London: Chapman and Hall, 1989. 511 p.
• NELDER, J. A.; WEDDERBURN, R. W. M. Generalized linear models. Journal of the Royal Statistical Society, [S.l.], v. 135, p. 370-384, 1972.
• SAS INSTITUTE. Release 8.02 Cary, 2001.
• SCHALL, R. Estimation in generalized linear models with random effects. Biometrika, Washington, v. 78, p. 719 727, 1991.
• SNEDECOR, G. W.; COCHRAN, W. G. Statistical methods 8. ed. Iowa: Iowa State University, 1989. 503 p.
• STEEL, R. G. D.; TORRIE, J. H. Principles and procedures of statistics 2. ed. New York: McGraw-Hill, 1980. 633 p.

Datas de Publicação

• Publicação nesta coleção
  09 Mar 2010
• Data do Fascículo
  2009

Histórico

• Aceito
  28 Ago 2007
• Recebido
  04 Ago 2006