Resumos
Este trabalho investiga a relação entre a taxa de juros e a volatilidade da taxa de câmbio real efetiva no Brasil. Através de um modelo GARCH multivariado simultâneo, que permite estimar equações para a média e variância em um único estágio, observou-se que não é possível afirmar que a volatilidade da taxa de câmbio real efetiva e a taxa de juros (nominal ou real) sejam independentes. Adicionalmente, houve evidência de que a variância da taxa de câmbio real efetiva é afetada pelos choques defasados na média e na variância da taxa de juros. No contexto do regime de metas para a inflação, tais resultados sugerem que a elevada volatilidade cambial no Brasil pode estar de alguma forma relacionada com a regra de política monetária adotada.
Volatilidade cambial; Taxa de juros; Modelos GARCH multivariados simultâneos; Modelo BEKK
This paper discusses the relationship between interest rate and the real effective exchange rate volatility in Brazil. Using a multivariate simultaneous GARCH model, allowing estimate equations for the mean and the variance in a single stage, it was observed that the real effective exchange rate volatility and interest rate (nominal or real) are not independent. Furthermore, it was found that the real effective exchange rate variance is affected by lagged shocks in the interest rate mean and variance. Under the inflation targeting regime the former results suggest that the high exchange rate volatility in Brazil could be related to the monetary policy rule adopted.
Real exchange rate volatility; Interest rate; Multivariate simultaneous GARCH models; BEKK model
ARTIGOS
Volatilidade da taxa de câmbio real e taxa de juros no Brasil: evidências de um modelo VAR-GARCH-M para o período 1999-2010
Vinícius dos Santos Cerqueira
Técnico de planejamento e pesquisa do Instituto de Pesquisa Econômica Aplicada (IPEA). E-mail: vinicius.cerqueira@ipea.gov.br
RESUMO
Este trabalho investiga a relação entre a taxa de juros e a volatilidade da taxa de câmbio real efetiva no Brasil. Através de um modelo GARCH multivariado simultâneo, que permite estimar equações para a média e variância em um único estágio, observou-se que não é possível afirmar que a volatilidade da taxa de câmbio real efetiva e a taxa de juros (nominal ou real) sejam independentes. Adicionalmente, houve evidência de que a variância da taxa de câmbio real efetiva é afetada pelos choques defasados na média e na variância da taxa de juros. No contexto do regime de metas para a inflação, tais resultados sugerem que a elevada volatilidade cambial no Brasil pode estar de alguma forma relacionada com a regra de política monetária adotada.
Palavras-chave: Volatilidade cambial; Taxa de juros; Modelos GARCH multivariados simultâneos; Modelo BEKK.
ABSTRACT
This paper discusses the relationship between interest rate and the real effective exchange rate volatility in Brazil. Using a multivariate simultaneous GARCH model, allowing estimate equations for the mean and the variance in a single stage, it was observed that the real effective exchange rate volatility and interest rate (nominal or real) are not independent. Furthermore, it was found that the real effective exchange rate variance is affected by lagged shocks in the interest rate mean and variance. Under the inflation targeting regime the former results suggest that the high exchange rate volatility in Brazil could be related to the monetary policy rule adopted.
Keywords: Real exchange rate volatility; Interest rate; Multivariate simultaneous GARCH models; BEKK model.
JEL classification: E49
1 Introdução
A elevada instabilidade relacionada ao câmbio tem sido uma característica marcante da economia brasileira nos últimos anos. Considerando-se a média do coeficiente de variação da taxa de câmbio real efetiva, para diversas economias no período 1999-2009, nota-se que o Brasil possui a taxa de câmbio mais volátil de um conjunto importante de países (ver Figura 1). Um ponto relevante nesse debate é a investigação acerca das causas dessa volatilidade. O objeto de estudo deste trabalho consiste em testar a existência de uma relação significativa entre a taxa de juros do Sistema Especial de Liquidação e Custódia (SELIC) e a elevada volatilidade da taxa de câmbio real efetiva no Brasil. Tal preocupação se justifica pelos resultados teóricos da chamada "nova macroeconomia para economias abertas" que enfatiza importância da taxa de juros e da política monetária para as flutuações da taxa de câmbio. Adicionalmente, muitos trabalhos têm mostrado que a volatilidade cambial pode afetar negativamente variáveis reais como investimento, exportações e crescimento.
A literatura econômica apresenta algumas evidências de que uma instabilidade da taxa de câmbio pode afetar negativamente variáveis reais. Darby et al. (1999), ao analisar dados de países europeus, mostram que, a partir de certo ponto, a volatilidade da taxa de câmbio real efetiva afeta negativamente o investimento. Servén (2003) confirma esse resultado para países em desenvolvimento, enfatizando que o impacto é significativamente negativo, principalmente para volatilidades acima da mediana da amostra.
Com relação ao fluxo de comércio, Chowdhury (1993), ao analisar dados dos países do G7, mostra evidências de que a volatilidade da taxa de câmbio real prejudica as exportações. Essa relação é confirmada por Bitencourt et al. (2007), que utilizam dados do comércio setorial no MERCOSUL. Tenreyro (2007), no entanto, utiliza uma amostra mais ampla de países e mostra que a variabilidade de taxa da câmbio nominal não tem impacto significativo sobre o fluxo de comércio. Uma contribuição teórica ao debate pode ser vista em Bacchetta & Van Wencoop (2000), em que os autores argumentam que regimes de câmbio fixo, apesar de reduzirem a volatilidade da taxa de câmbio (real e nominal), podem não ser eficientes para aumentar o comércio externo. A argumentação é de que, em certas circunstâncias, essa variável não é afetada pelo câmbio, pois tal efeito dependeria de como os sistemas cambiais são implantados. Outra questão levantada pelos autores é que o regime cambial pode afetar de maneira diferente o comércio externo e o consumo doméstico. Assim, mesmo nas situações em que um regime menos flexível afeta positivamente o comércio exterior, pode haver efeitos negativos de bem-estar devido à redução do consumo interno.
A relação entre volatilidade cambial e crescimento econômico também é bastante controversa. Levy-Yeyati & Sturzenegger (2003) utilizam uma amostra de 183 países no período pós Bretton-Woods e tentam relacionar regime cambial1 1 Neste trabalho a classificação dos regimes cambiais é feita com base no comportamento de um conjunto de variáveis macroeconômicas. e crescimento. Os autores concluem que para os países em desenvolvimento, regimes cambiais menos flexíveis estão associados a períodos de menor crescimento. Os resultados para os países desenvolvidos apontampara a inexistência de efeito significativo dos regimes cambiais sobre o crescimento. Por outro lado, Bagella et al. (2006) mostram que o efeito positivo da maior flexibilidade do câmbio no crescimento não significa necessariamente que a volatilidade cambial não tenha impacto negativo sobre o mesmo. Isso seria válido apenas para as taxas bilaterais com o dólar. Para a volatilidade da taxa real efetiva os resultados mostramefeito significativo e negativo. Aghion et al. (2009) avançam ao demonstrar que o nível de desenvolvimento financeiro é importante para amagnitude e existência do impacto negativo da volatilidade da taxa de câmbio real efetiva sobre o crescimento. Em geral, nas economias com mercados financeiros com baixa capacidade de absorver choques macroeconômicos (o que evidênciaria umbaixo nível de desenvolvimento financeiro), a volatilidade cambial pode afetar negativamente o crescimento.
Diante das controvérsias apresentadas, parece que alguns aspectos são razoavelmente consensuais na literatura:
a) A partir de certo ponto, a volatilidade da taxa de câmbio real efetiva pode ter efeito negativo sobre variáveis como exportações, investimento e crescimento;
b) O efeito da volatilidade da taxa nominal de câmbio sobre essas variáveis é incerto;
c) Existe forte correlação entre a volatilidade da taxa nominal e a da taxa real efetiva de modo que regimes cambiais menos flexíveis reduzem a volatilidade da última. Contudo não é possível afirmar que tais regimes contribuam para o aumento das exportações, investimento e crescimento. Uma possível explicação estaria no dilema entre os custos de regimes cambiaismenos flexíveis e os possíveis benefícios de umamenor volatilidade cambial.
Verifica-se então que a volatilidade da taxa de câmbio real efetiva é um fenômeno que tem custos econômicos que não podem ser desconsiderados. Esta seria a justificativa para as investigações relacionadas às possíveis causas da instabilidade cambial. Um ponto frequentemente levantado na literatura é a possível relação entre a política monetária e volatilidade cambial. No caso brasileiro, a políticamonetária temcomo principal instrumento a fixação da taxa SELIC. Ao investigar a propagação dos efeitos defasados de choques nessa variável na variância da taxa de câmbio real efetiva, este trabalho tenta contribuir para a literatura empírica relacionada ao debate sobre as causas da elevada volatilidade da taxa de câmbio real no Brasil. Nessa perspectiva, foi utilizado um modelo GARCH multivariado simultâneo que permite modelar, ao mesmo tempo, médias e variâncias condicionais em um único estágio. Essa metodologia também permite a realização de testes de causalidade da média e/ou variância de uma variável para a média e/ou variância da outra.2 2 Neste trabalho, o termo causalidade é utilizado no sentido de "causalidade Granger". Uma apresentação detalhada de testes de causalidade em modelos GARCH multivariados pode ser vista em Comte & Lieberman (2000). Ver também Serletis & Shahmoradi (2006). Ressalta-se que não se trata de identificar "o quanto" a média e a variância da taxa de câmbio real efetiva respondem aos choques na SELIC, pois no modelo utilizado, a matriz de variância/covariância não é constante. O que o modelo VAR-GARCH-M permite testar é se a variância em t de uma variável é afetada por choques defasados na média e/ou pela variância defasada de outra variável. Assim, a questão central do trabalho é investigar se choques na taxa de juros e a variância da mesma afetam defasadamente a variância da taxa de câmbio real efetiva no Brasil no período 1999-2010.
O texto está dividido em sete seções além desta introdução: na primeira é apresentada uma sumária revisão da literatura sobre as possíveis causas da volatilidade cambial; na segunda é explicitada a metodologia empírica e os dados utilizados no trabalho; na terceira são apresentados os resultados; na quarta são apresentados os resultados de um teste de robustez dos estimadores; na quinta as considerações finais; na sexta as referências e na sétima, o ApêndiceApêndice.
2 Possíveis causas da volatilidade cambial
Alguns estudos têm apresentado resultados que visam contribuir para o entendimento das causas da variabilidade cambial. Divereux & Engel (2002) mostram que tanto no caso da taxa nominal como da taxa real de câmbio a volatilidade pode ser derivada de certa rigidez das variáveis macroeconômicas a choques cambiais. Um exemplo seria uma situação em que o conjunto de preços em moeda local elimina a passagem de mudanças na taxa de câmbio para os preços aos consumidores. Galí & Monacelli (2005) argumentam que, em certas situações, uma regra de política monetária segmentada que alcança simultaneamente a estabilização dos preços aos consumidores e do hiato do produto implica em volatilidade da taxa de câmbio nominal e dos termos de troca maiores em relação a uma regra que reage à inflação medida por índice geral de preços e ao hiato do produto (regra simples de Taylor).
Outra possível causa da volatilidade da taxa real efetiva seria o grau de abertura comercial. Evidências desse efeito são apresentadas por Hou (2002), que justifica tal relação argumentando que quanto menor a abertura comercial, maior o impacto de choques macroeconômicos sobre os movimentos da taxa de câmbio real efetiva. A questão central seria a elevada participação dos bens não transacionáveis na composição do índice geral de preços. Como os preços desses bens são, em geral, mais rígidos em relação aos choques cambiais e monetários, o ajustamento seria mais lento e incompleto o que seria uma potencial causa da volatilidade cambial.
Patereau (2007) enfatiza o papel da interação entre choques da política monetária e fricções no mercado de crédito para explicar a variabilidade da taxa real e nominal. É importante ressaltar que os resultados obtidos nesse trabalho são robustos a uma maior flexibilidade dos preços. Adicionalmente, o autor mostra que as fricções no mercado de crédito não estão relacionadas à completude dos mercados e sim a assimetrias de informação, que poderiam causar racionamento neste mercado.
Em síntese, os aspectos que aparecem com frequência na literatura como sendo potenciais causadores da volatilidade cambial são: rigidez de preços, baixo nível de desenvolvimento dos mercados financeiros domésticos (no que se refere à capacidade de absorver choques macroeconômicos) e grau de abertura comercial. Como foi visto, esses aspectos podem interagir e afetar simultaneamente a variabilidade cambial. Ressalta-se que esses fatores, além de impactarem diretamente, tenderiam a amplificar os eventuais efeitos da política monetária sobre a volatilidade da taxa de câmbio real.
Os modelos da chamada New open-economy macroeconomics (NOEM) geralmente apresentam soluções explicitas para a variância da taxa de câmbio e enfatizam a relação entre esta variável e a política monetária. Tal abordagem, apresentada em Obstfeld & Rogoff (1995) e Obstfeld (2000), utiliza modelos de equilíbrio geral com microfundamentos e rigidez nominal de preços e salários. Esses modelos também contemplam um conjunto importante de possíveis imperfeições demercado como: incompletude de mercados, concorrência monopolística, assimetria de informação etc. Nesse contexto, a NOEM tem buscado reavaliar os resultados convencionais sobre os canais de transmissão dos choques cambiais e monetários, bem como tem avançado na derivação de regras ótimas de política monetária. Obstfeld (2000), Divereux & Engel (2002), Galí & Monacelli (2005) e Patereau (2007) utilizam tal framework e, de maneira geral, apresentam evidências teóricas de que a política monetária pode ter uma relação de simultaneidade com o nível e a volatilidade da taxa de câmbio nominal e real.
Pelo exposto, consta-se que a literatura teórica temexplicitado possíveis canais através dos quais a volatilidade cambial poderia estar associada às regras monetárias e, por conseguinte, às flutuações da taxa de juros. Este trabalho pretende dialogar com esta literatura na medida em que propõe uma investigação empírica, para o caso brasileiro, sobre a relação entre as médias e as variâncias da taxa de juros e da taxa de câmbio real.
No Brasil, o regime de metas para inflação tem como principal instrumento as operações de mercado aberto, e a variável utilizada frequentemente para analisar os movimentos da política monetária é a taxa SELIC. Dessa forma, a investigação sobre a relação entre volatilidade da taxa de câmbio real efetiva e da taxa de juros é, para o caso brasileiro, um desenvolvimento empírico que se insere na lógica da NOEM, no que se refere aos impactos da política monetária sobre a dinâmica da taxa de câmbio real. Nessa perspectiva, este trabalho investiga duas relações: a primeira entre taxa SELIC e volatilidade da taxa de câmbio real efetiva, e a segunda entre taxa real de juros (SELIC descontada a inflação medida pelo IPCA) e volatilidade da taxa de câmbio real efetiva. No caso da taxa real de juros, trata-se de uma estratégia de incorporação, no modelo, dos efeitos da dinâmica dos preços internos e o consequente efeito sobre o retorno real dos títulos federais. Essa estratégia foi utilizada por conta da importância do comportamento dos preços internos nos modelos teóricos emquestão e da inviabilidade da inclusão da taxa de inflação como mais uma variável explícita no modelo (que acarretaria na estimação de muitos parâmetros e em crescentes dificuldades computacionais).
3 Estratégia de investigação empírica
Considerando os modelos multivariados para a análise de volatilidade, as duas principais classes são: os modelos multivariados de volatilidade estocástica (MVE)3 3 Uma apresentação sobre essa classe de modelos pode ser vista em Harvey (1994). e os modelos GARCH multivariados. Na primeira, a variância presente de uma variável é função de seus valores passados, dos valores passados da variância das outras variáveis que integram o sistema e de um termo estacionário gaussiano. Esses modelos são mais parcimoniosos em relação aos modelos GARCH e a estimação é, geralmente, menos complexa. A desvantagem dos modelos MVE é que eles adotam como premissa a ideia de que a variância é independente dos choques que afetam a média das variáveis do sistema. Ou seja, no caso deste trabalho, a utilização dos modelos MVE não permitiria avaliar se um choque na taxa de juros afeta, depois de algum tempo, a volatilidade cambial. Essa é a justificativa para a utilização do modelo GARCH multivariado, pois nele é possível modelar média e variância conjuntamente e testar as possíveis inter-relações. No caso específico da relação entre taxa de juros e taxa de câmbio real, nada garante, a priori, a independência entre a dinâmica da média e da variância.
Em relação aos GARCH multivariados duas classes de modelos muito utilizadas são: a) o modelo BEKK, apresentado por Engle & Kroner (1995); b) o modelo conhecido como Dynamic Conditional Correlation (DCC) introduzido por Engle (2002). O modelo DCC é uma generalização do modelo CCC (Constant Conditional Correlation) de Bollerslev (1990). Como demonstra Caporin (2012), os modelos BEKK e DCC são muito parecidos, sendo que o primeiro estima covariâncias condicionais e o segundo, correlações condicionais. As razões teóricas para a escolha do modelo BEKK foram:
Como demonstra Caporin & McAller (2008), Caporin (2012), o modelo BEKK pode ser utilizado para se obter estimativas consistentes para correlações condicionais dinâmicas;
Apesar de depender da existência de momentos que não podem ser parametricamente testados, como relatado em Caporin (2012), as condições para consistência e normalidade assintótica foram provadas para diversas especificações do modelo BEKK. O mesmo não acontece comos modelos DCC.
Além das razões teóricas e assintóticas mencionadas, considerando as hipóteses que se pretende testar neste trabalho, a estrutura do modelo BEKK parece adequada por sua relativa simplicidade de interpretação e por viabilizar a realização dos testes propostos.
3.1 O modelo VAR-GARCH-M
Para uma correta identificação do filtro GARCH, é necessária uma especificação adequada para a média. Nesse contexto, o modelo VARMA-GARCHM possibilita modelar simultaneamente média e variância. Nesse modelo, o componente VARMA visa eliminar a autocorrelação das séries e, ao mesmo tempo, viabilizar testes de causalidade entre as mesmas. O componente "M" corresponde aos termos defasados da variância na equação da média. Assim, a equação para a média é dada por:
onde:
yt = vetor formado por  (modelo 1) ou
(modelo 1) ou  (modelo 2) sendo VTRJ = variação da taxa real de juros, VSELIC = variação da taxa SELIC e VTCRE = variação percentual do índice da taxa de câmbio real efetiva;
(modelo 2) sendo VTRJ = variação da taxa real de juros, VSELIC = variação da taxa SELIC e VTCRE = variação percentual do índice da taxa de câmbio real efetiva;
a = vetor das constantes  , com "juros" = VTRJ , V SELIC;
, com "juros" = VTRJ , V SELIC;
et|Ωt−1 ∼ N (0, Ht) = vetor do resíduo condicional ao conjunto de informações Ω disponíveis em t−1, com média zero e matriz de variância/covariância dada por Ht =  . Assim, o vetor et é definido como
. Assim, o vetor et é definido como  , a correlação entre e(juros)t e e(vtcre)t igual a ρt =
, a correlação entre e(juros)t e e(vtcre)t igual a ρt =  e ul i.i.d (0,1) com l = juros,vtcre;
e ul i.i.d (0,1) com l = juros,vtcre;
Φi = matrizes relacionadas aos vetores autorregressivos yt−i, dada por  , com i = 1, . . . , p (defasagens);
, com i = 1, . . . , p (defasagens);
Γj = matrizes relacionadas aos vetores de média móvel et−j, dada por  , com j = 1, . . . , q (defasagens);
, com j = 1, . . . , q (defasagens);
Θk = matrizes relacionadas aos termos "M"  , dada por
, dada por  , com k = 1, . . . , z (defasagens);
, com k = 1, . . . , z (defasagens);
O componente utilizado para explicar a variância é um modelo multivariado simultâneo GARCH proposto por Engle & Kroner (1995), também conhecido como modelo BEKK, cuja estrutura é representada pela equação:
Onde C, Bg e Aq são matrizes 2×2, sendo que a matriz C é triangular, para garantir que Ht seja definida como positiva.4 4 Para uma prova de que, nessas circunstancias, Ht é definida positiva ver Engle & Kroner (1995).
Na equação 2, o primeiro termo é constante ao longo do tempo, o segundo representa o impacto da variância passada sobre a variância presente e o terceiromede o impacto das inovações defasadas, ocorridas na equação damédia, na variância presente. É por este último termo que umchoque na taxa de juros pode afetar a volatilidade cambial, por exemplo.
A análise de estabilidade domodelo VARMA(p,q)-GARCH(s,r)-M(z) é feita para cada componente. No caso da equação 1, que representa a equação para a média, é necessário garantir que as condições de estabilidade e invertibilidade sejam satisfeitas. Considerando os desenvolvimentos de Hallin & Paindaveine (2005), o componente VARMA(p,q) da equação 1 atende a tais condições, respectivamente, se em:
todos os autovalores λi e λj estiverem fora do circulo unitário complexo.
Segundo Engle & Kroner (1995), as condições de estacionariedade em modelos BEKK são dadas por:
Condição de estabilidade 1 A equação 2 será covariância estacionária se, e somente se, todos os autovalores de  estão dentro do círculo unitário complexo, onde
estão dentro do círculo unitário complexo, onde  denota o produto de Kronecker.
denota o produto de Kronecker.
Condição de estabilidade 2 Quando Bj e Ai forem matizes diagonais, o modelo é denominado BEKK diagonal será estacionário se, e somente se,  < 1 para todo i, ou seja, a soma do quadrado dos elementos da diagonal principal das matrizes Bj e Ai são menores que um.
< 1 para todo i, ou seja, a soma do quadrado dos elementos da diagonal principal das matrizes Bj e Ai são menores que um.
Engle & Kroner (1995) mostram que se o modelo BEKK não for diagonal é possível que este seja estável, mesmo que a Condição de Estabilidade 2 não seja ate dida. Nesse caso, a convergência da variância/covariância, frente a efeitos efasados de um choque na média, tende a ser mais lenta.
3.2 Teste de Hipóteses
O modelo formado pelas equações 1 e 2 possibilita avaliar relações de causalidade tanto namédia como na variância. Tal avaliação será feita, seguindo a estratégia utilizada por Serletis & Shahmoradi (2006), que consiste em realizar testes de hipóteses conjuntos em relação aos parâmetros do modelo. Foram realizados os seguintes testes de hipótese a esse propósito:
Diagonal VARMA: H0 :
Não causalidade de JUROS em VTCRE na média: H0 :
Não causalidade de VTCRE em JUROS na média: H0 :
Inexistência do termo "M": H0 :
Termo "M" diagonal: H0 :
Inexistência do componente GARCH: H0 :
Modelo BEKK é diagonal: H0 :
Não causalidade da variância e dos choques na média de JUROS na variância de VTCRE: H0 :
Não causalidade da variância e dos choques na média de VTCRE na variância de JUROS: H0 :
O teste relacionado à Condição de Estabilidade 2 é:
Diagonal BEKK é não estacionária: H0 :
= 1
Evidentemente, esse teste não exclui a possibilidade de se rejeitar a hipótese nula no caso de  > 1. Nests caso, foram descartados os modelos em que, a hipótese de que o modelo BEKK é diagonal não fora rejeitada e
> 1. Nests caso, foram descartados os modelos em que, a hipótese de que o modelo BEKK é diagonal não fora rejeitada e  −1 > 0, independentemente do resultado da Condição de Estabilidade 1. O mesmo ocorreu com os modelos em que
−1 > 0, independentemente do resultado da Condição de Estabilidade 1. O mesmo ocorreu com os modelos em que  − 1 < 0, a hipótese de diagonal não estacionária não foi rejeitada ao nível de 1% de significância ou a condição de estabilidade 1 não fora satisfeita. Esse procedimento teve como objetivo aumentar o grau de confiança em relação à estabilidade dos modelos selecionados. Como será visto a seguir esse ponto é crucial para as propriedades assintóticas dos estimadores obtidos.
− 1 < 0, a hipótese de diagonal não estacionária não foi rejeitada ao nível de 1% de significância ou a condição de estabilidade 1 não fora satisfeita. Esse procedimento teve como objetivo aumentar o grau de confiança em relação à estabilidade dos modelos selecionados. Como será visto a seguir esse ponto é crucial para as propriedades assintóticas dos estimadores obtidos.
A estimação domodelo foi executada utilizando ométodo de quase-máxima verossimilhança (QMV)5
5
Na estimação repetiu-se o processo com diferentes valores iniciais e ordenamentos distintos das variáveis, objetivando minimizar a possibilidade de seleção de máximos locais.
sob a hipótese de que  (com i = JUROS, VTCRE) tem distribuição normal. Esse método consiste em uma estimação por máxima verossimilhança robusta a erros de especificação da função de densidade de probabilidade. Ou seja, considerando a possibilidade de que a hipótese de não normalidade de
(com i = JUROS, VTCRE) tem distribuição normal. Esse método consiste em uma estimação por máxima verossimilhança robusta a erros de especificação da função de densidade de probabilidade. Ou seja, considerando a possibilidade de que a hipótese de não normalidade de  não seja rejeitada, haveria um erro de especificação na função de verossimilhança para o modelo VARMA-GARCHM. Nesse contexto, é importante verificar em que circunstâncias os estimadores de quase-máxima verossimilhança (EQMV) são consistentes e assintoticamente normais.
não seja rejeitada, haveria um erro de especificação na função de verossimilhança para o modelo VARMA-GARCHM. Nesse contexto, é importante verificar em que circunstâncias os estimadores de quase-máxima verossimilhança (EQMV) são consistentes e assintoticamente normais.
O conjunto de condições para a consistência e a normalidade assintótica dos EQMV para um modelo VARMA-GARCH-M BEKK ainda é uma questão em aberto na literatura. Três trabalhos, no entanto, apresentam alguns desenvolvimentos e resultados importantes a esse respeito. O primeiro é o de Comte (2003), que generaliza os resultados de Jeantheau (1998)6
6
Esse trabalho mostra as condições para consistência forte e normalidade assintótica dos EQMV para modelos multivariados ARCH e para um modelo multivariado GARCH com correlação constante.
e mostra que a consistência e a normalidade assintótica podem ser obtidas para os EQMV do modelo BEKK se a condição de estabilidade 1 for atendida,  for independente e se existir o segundo e o oitavo momento de et. O segundo trabalho é o de Ling & McAleer (2003), que avança ao demonstrar que os EQMV para um VARMA-GARCH são consistentes e assintoticamente normais desde que as condições de estabilidade para a média e variância/covariância sejam satisfeitas e que exista o sexto momento para et. O terceiro trabalho é de Hafner & Preminger (2009), que ao analisarem as propriedades assintóticas de um modelo multivariado GARCH na forma vetorial7
7
Ver Bollerslev et al. (1988) eEngle & Kroner (1995).
(conhecido como vec), verificam as dificuldades de se obter a normalidade assintótica no contexto um GARCH integrado.
for independente e se existir o segundo e o oitavo momento de et. O segundo trabalho é o de Ling & McAleer (2003), que avança ao demonstrar que os EQMV para um VARMA-GARCH são consistentes e assintoticamente normais desde que as condições de estabilidade para a média e variância/covariância sejam satisfeitas e que exista o sexto momento para et. O terceiro trabalho é de Hafner & Preminger (2009), que ao analisarem as propriedades assintóticas de um modelo multivariado GARCH na forma vetorial7
7
Ver Bollerslev et al. (1988) eEngle & Kroner (1995).
(conhecido como vec), verificam as dificuldades de se obter a normalidade assintótica no contexto um GARCH integrado.
As considerações acima demonstram a importância do rigor na avaliação dos resultados dos testes relativos à estabilidade do modelo e à independência do termo  . Para este último, foi utilizado o teste diagnóstico "Q" multivariado proposto por Hosking (1980), objetivando detectar a presença de autocorrelação e/ou heterocedasticidade condicional. O teste foi aplicado para os resíduos padronizados e para o quadrado dos mesmos definidos respectivamente como:
. Para este último, foi utilizado o teste diagnóstico "Q" multivariado proposto por Hosking (1980), objetivando detectar a presença de autocorrelação e/ou heterocedasticidade condicional. O teste foi aplicado para os resíduos padronizados e para o quadrado dos mesmos definidos respectivamente como:
O objetivo foi selecionar modelos em que  fosse aproximadamente ruído branco, o que, juntamente comas condições de estabilidade, constitui um conjunto importante de resultados, tendo em vista as propriedades assintóticas dos EQMV.
fosse aproximadamente ruído branco, o que, juntamente comas condições de estabilidade, constitui um conjunto importante de resultados, tendo em vista as propriedades assintóticas dos EQMV.
3.3 Dados utilizados nas estimações
O período de análise vai de junho de 1999 a maio de 2010,8
8
O início em junho de 1999 se justifica pela forte instabilidade decorrente da desvalorização da taxa de câmbio no início daquele ano. Assim, optou-se por utilizar as séries a partir do segundo semestre.
num total de 133 observações, e as séries utilizadas foram: taxa over Selic acumulada no mês anualizada (SELIC), Índice de Preços ao Consumidor Amplo (IPCA) e taxa de câmbio real efetiva (TCRE).9
9
Série disponibilizada pelo Instituto de Pesquisa Econômica Aplicada (IPEA) no site:
http://www.ipeadata.gov.br/ipeaweb.dll/ipeadata?1291100625. É calculada pela média ponderada do índice de paridade do poder de compra dos 16 maiores parceiros comerciais do Brasil. A paridade do poder de compra é definida pelo quociente entre a taxa de câmbio nominal (em R$ unidade de moeda estrangeira) e a relação entre o Índice de Preço por Atacado (IPA) do país em cada caso e o Índice de Preços por Atacado oferta global (IPA-OG/FGV) do Brasil. As ponderações utilizadas são as participações de cada parceiro no total das exportações brasileiras em 2001.
Todas as séries foram obtidas junto ao banco de dados do IPEADATA. A estimativa para a taxa de juros realmensal anualizada foi: TRJ =  −1, onde selict é a taxa over Selic acumulada no mês, πIPCAt é a inflação mensal medida pelo IPCA.
−1, onde selict é a taxa over Selic acumulada no mês, πIPCAt é a inflação mensal medida pelo IPCA.
Para garantir a estacionariedade das séries, aplicou-se a primeira diferença nas séries TRJ, SELIC over e no caso da taxa de câmbio real efetiva apurou-se a variação percentual mensal. Logo as séries utilizadas nas estimações foram:
VSELIC = variação da taxa over Selic acumulada no mês anualizada; VTRJ = variação da TRJ; VTCRE = variação percentual da taxa de câmbio real efetiva.
A Tabela 1 mostra os resultados dos testes de raiz unitária ADF (Dickey- Fuller aumentado), PP (Phillips-Perron) e KPSS (Kwiatkoski-Phillips-Schmidt- Shin) para as séries VSELIC, VTRJ e VTCRE come semefeito sazonal. Verificase que não há evidência de integração em ambos os casos.
Embora tenham sido testados modelos com as séries VSELIC, VTERJ e VTRE ajustadas sazonalmente,10 10 As séries foram dessazonalizadas através do software Eviews 6.0 pelo método de médias móveis. Este método apresentou melhores resultados em relação ao CENSUS X-12. os resultados reportados referem-se apenas aos modelos que atenderam aos critérios mencionados acima. Assim, a análise dos resultados se concentrou em dois modelos: um com VTRJ e VTCRE e outro com VSELIC e VTCRE.
3.4 Seleção dos modelos
O procedimento econométrico utilizado para a seleção dos modelos incluiu as seguintes etapas:
1. Verificar se o modelo é estável na média e na variância/covariância;
2. análise dos resultados do teste "Q" multivariado para os resíduos padronizados e para o quadrado dos mesmos;
3. Seleção dosmodelos através daminimização dos critérios de informação de Akaike (AIC), Baysiano Schwarz (BIC), Hannan e Quinn (HQ) e erro de previsão final (FPE).
Com relação ao teste Q, o critério de seleção utilizado foi descartar os modelos que apresentaram valores para Q(4), Q(8) ou Q(12) que rejeitassem a hipótese de inexistência de autocorrelação ou heterocedasticidade condicional ao nível de 10% de significância.
Em virtude do grande número de parâmetros e das dificuldades computacionais envolvidas no processo de estimação, adotou-se s = r = 1. Essa especificação, além de parcimoniosa, é consistente comevidências apresentadas por trabalhos empíricos sobre a superioridade dos modelos GARCH(1,1) no que se refere à previsão da volatilidade cambial.11 11 Ver, por exemplo, Hansen & Lunde (2005). Os trabalhos de Igesias & Phillips (2002) e Serletis & Shahmoradi (2006), apesar de não tratarem do tema, também utilizam r = s = 1 em modelos . Para a ordem da defasagem do termo "M", foram testadas as especificações z = 0 e z = 1. Isso significa testar se a variância tem efeito significativo sobre amédia do sistema contemporaneamente e após um mês. O processo de seleção de modelos revelou, no entanto, que o efeito da variância nosmodelos é basicamente contemporâneo, de modo que os modelos com melhor desempenho nas etapas 1, 2 e 3 tiveram o termo "M" com z = 0.
Por fim, foram aplicados os procedimentos de seleção para identificar p e q. As tabelas 2 e 3 mostram os resultados dos critérios de seleção das especificações testadas.12 12 Foram testados modelos com a VTRJ e VTCRE dessazonalizadas e modelos com VSELIC e VTCRE com sazonalidade. Todavia, nenhuma das especificações passou pelos critérios de seleção 1 e 2. Verifica-se que apenas o VAR(3)-GARCH(1,1)-M(1) para o modelo com VTRJ e VTCRE (modelo 1) e o VAR(5)-GARCH(1,1)-M(1) para o modelo com VSELIC e VTCRE com as séries dessazonalizadas (modelo 2) passaram pelas etapas 1 e 2.
4 Resultados
A Tabela A.1Apêndice, no ApêndiceApêndice, mostra o conjunto de parâmetros obtidos nas estimações. Com relação às condições de estabilidade, as Tabelas 4 e 5 mostram os resultados dos testes da restrição diagonal BEKK13 13 Como será visto, a hipótese de BEKK diagonal fora rejeitada nos dois modelos. Dessa forma, em um contexto em que a condição de estabilidade 1 é satisfeita, a única informação adicional desse teste é que a variância/covariância converge rapidamente em face de distúrbios defasados ocorridos na equação para a média. estacionária e as Tabelas 6 e 7 mostram os resultados dos testes de estabilidade para cada modelo. Nota-se que os modelos selecionados satisfazem tais condições. Quanto ao comportamento dos resíduos padronizados, os resultados do teste "Q" multivariado para os dois modelos (Tabelas 8 e 9) mostram que não há evidência de autocorrelação e heterocedasticidade condicional.
Os resultados dos testes de hipótese estão nas tabelas 10 e 11. Para o modelo 1, observa-se que existe evidência de simultaneidade na média e na variância. Por outro lado, a variância parece afetar contemporaneamente apenas a média da própria variável. Isso não implica, no entanto, que o impacto da variância de uma variável na média da outra não exista em termos defasados. Para o modelo 2, a hipótese de não simultaneidade entre as médias não foi rejeitada. Todavia, a hipótese de inexistência de impactos das variâncias nas médias foi rejeitada ao nível de 10%. Adicionalmente, ao nível de 6% de significância, não é possível afirmar que a média de uma variável seja independente da variância da outra. Os resultados mostram também que parece haver simultaneidade entre a variância da VSELIC e da VTCRE. Desse modo, os testes apontam para o fato de que a relação entre as médias de VSELIC e VTCRE se dá através da variância das mesmas. Apesar de não se rejeitar a inexistência de simultaneidade na média, um choque em uma variável pode afetar a média da outra através dos efeitos defasados desse choque sobre a variância e, por conseguinte, sua propagação para a equação da média condicional. Assim, o modelo VAR-GARCH-M-BEKK rejeitou nos dois casos a independência da variância da taxa de juros e da taxa de câmbio real efetiva. Ou seja, considerando o objetivo deste artigo, os dados para o período 1999- 2010 apresentam evidências de que choques na taxa de juros afetam, depois de algum tempo, a volatilidade da taxa de câmbio real efetiva no Brasil.
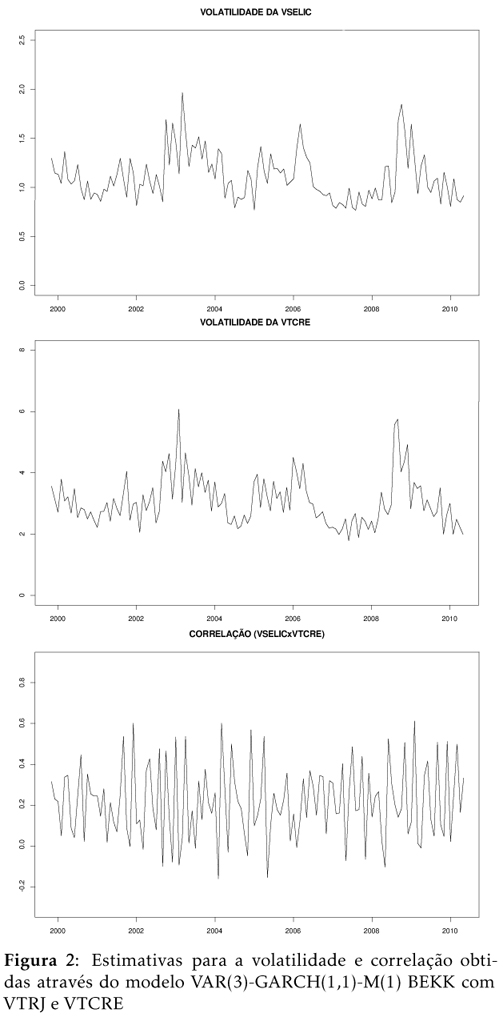
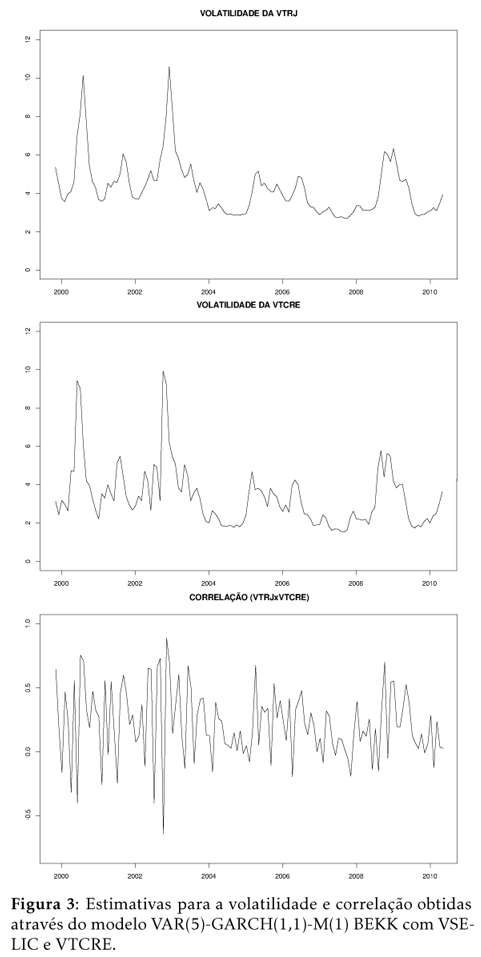
As Figuras 2 e 3 mostram as estimativas para a variância e para a correlação condicionais, obtidas para o período que vai de novembro de 1999 a maio de 2010.
Os gráficos mostram que a principal diferença entre as estimativas para a volatilidade da VTCRE é o pico observado no segundo semestre de 2000, gerado no modelo que utiliza a VTRJ. Uma possível explicação para esse pico é a instabilidade dos preços domésticos durante o ano de 2000, derivada de problemas de safra e choques de preços administrados.14 14 Ver Minella et al. (2002). Os dois momentos de forte volatilidade, identificados nosmodelos, são: o segundo semestre de 2002 e final de 2008. O primeiro pode ser atribuído às instabilidades relacionadas às eleições presidenciais de 2002 e o segundo possivelmente temrelação coma recente crise financeira nos EUA. As estimativas para a correlação condicional de VTRJ-VTCRE e VSELIC-VTCRE mostram que, em ambos os casos, apesar de serem predominantemente positivas, há uma acentuada oscilação ao longo do período de análise, sobretudo nos momentos de maior volatilidade.
5 Análise de Robustez
Apesar de as condições observáveis para a normalidade assintótica e consistência dos estimadores de QMV terem sido satisfeitas, é possível que o pequeno número de observações e a não normalidade dos erros possam ocasionar uma perda de eficiência destes estimadores. Para tentar verificar a robustez dos resultados apresentados na seção anterior foi estimada uma versão semiparamétrica do modelo. Para tanto, foi utilizada a abordagem proposta por Long et al. (2009) na estimação domodelo para amatriz de variâncias e covariâncias condicionais. O estimador combina um primeiro estágio de estimação paramétrica com um segundo estágio em que ocorre a correção não paramétrica. Adicionalmente, foi realizado um teste para correta especificação do modelo paramétrico.15 15 Long et al. (2009) apresenta detalhes sobre as propriedades assintóticas do teste para correta especificação do modelo, provas da normalidade assintótica dos estimadores semiparamétricos e uma análise do potencial preditivo destes estimadores em amostras finitas.
A abordagem semiparamétrica proposta por Long et al. (2009) trata apenas do componente GARCH do modelo. Ou seja, como é comum em análises de séries financeiras, não se modela a persistência das médias. As séries macroeconômicas, no entanto, costumam apresentar elevada persistência e este tratamento pode não ser adequado. Para obter estimativas compatíveis com as obtidas através dos estimadores de QMV foi adotado o seguinte procedimento:
a) O componente VAR(p) do modelo é estimado por máxima verossimilhança;
b) Com os resíduos do VAR(p), estima-se uma primeira aproximação do modelo BEKK semiparamétrico;
c) De posse das estimativas para as variâncias condicionais, estima-se o VAR(p) com as variâncias como variáveis explicativas (as especificações são análogas às dos modelos estimados por QMV);
d) Estima-se novamente o modelo BEKK com os resíduos do VAR(p) do passo "c";
e) Os passos "c" e "d" são repetidos B vezes ou até que ocorra a convergência dos parâmetros, de modo que interações adicionais não alterem os resíduos do componente VAR(p) do modelo.16 16 Utilizou-se B = 500. O critério de convergência adotado foi interromper o processo se nenhum elemento da matriz Gt = e't et apresentasse variação superior a 10−5 para uma interação ência foi obtida após 17 interações no modelo 1 e 08 interações no modelo 2.
Depois de estimados, os modelos passarampelo teste de correta especificação.17 17 Ver detalhes em Long et al. (2009). A hipótese nula do teste é que o modelo paramétrico está corretamente especificado. Os resultados do VAR(3)-GARCH(1,1)-M(1), para o modelo com VTRJ e VTCRE (modelo 1), e do VAR(5)-GARCH(1,1)-M(1) (modelo 2), para o modelo com VSELIC e VTCRE, não rejeitaram a hipótese nula de correta especificação para os níveis de 10%, 5% e 1% de significância. Todavia, Long et al. (2009) mostram que o poder do teste diminui significativamente com a redução da amostra.18 18 Os autores analisam o poder do teste para diversas amostras de 500 e 250 observações de dados gerados artificialmente. Dessa forma, mesmo que o teste não evidencie incorreta especificação, é possível que a estimação semiparamétrica possa gerar um ganho de eficiência em relação à abordagem paramétrica.
Uma dificuldade de se avaliar a eficiência dos estimadores é que a volatilidade não é uma variável observável. Awartani & Corradi (2005), ao compararem o potencial preditivo de modelos GARCH univariados para o S&P-500, concluem que, se o valor esperado da variável é zero, o quadrado dos retornos oferece uma boa proxy para volatilidade não observável da mesma. Uma alternativa então foi escolher como proxy para as variâncias não observáveis o quadrado dos resíduos do componente VAR de cada modelo, sem a inclusão das variâncias como variáveis explicativas. Como mostra a tabela 12, as médias dessas variáveis são próximas de zero. Assim, as estimativas paramétricas e semiparamétricas para a volatilidade da taxa de juros e da taxa de câmbio real efetiva foram comparadas com o quadrado dos resíduos de um VAR(3) para as séries do modelo 1 e com um VAR(5) para as séries do modelo 2. A tabela 13 mostra a comparação do erro quadrático médio (EQM) dos modelos paramétricos (QMV) e semiparamétricos.
Observa-se que as estimativas paramétricas por QMV, em geral, obtiveram um desempenho superior às estimativas semiparamétricas. Destaca-se o baixo EQM da estimativa da volatilidade da variável VSELIC (modelo 2). Considerando que os testes para a correta especificação do modelo semiparamétrico não rejeitaram a hipótese nula de que os modelos estão corretamente especificados, pode-se inferir que:
O poder de teste diminui rapidamente com a redução da amostra;
Os resultados de Long et al. (2009), que mostram um melhor desempenho preditivo dos estimadores semiparamétricos para o caso de modelos BEKK escalares19 19 No caso do modelo BEKK escalar, as matrizes A e B na equação 2 podem ser adequadamente representadas por escalares. Sendo k o numero de variáveis, o numero total de parâmetros estimados no modelo BEKK escalar é 0,5 k ( k + 1) + 2 e no modelo BEKK representado na equação (2) 0,5 k ( k + 1) + 2 k2. O modelo BEKK escalar não permite, contudo, testar separadamente se a variância de uma variável afeta defasadamente a da outra. podem não ser diretamente transportáveis para modelos BEKK na forma da equação 2 e com amostras inferiores a 250 observações;
Estimadores de QMV podem apresentar ganhos de eficiência preditiva em relação aos estimados por máxima verossimilhança.20 20 Em Long et al. (2009) os modelos paramétricos são estimados por máxima verossimilhança.
6 Considerações Finais
Este trabalho teve como objetivo investigar a relação entre a dinâmica da volatilidade da taxa de câmbio real efetiva e as variações taxa de juros no Brasil. Os resultados dos testes de hipótese realizados no modelo VAR-GARCH-M em geral rejeitam a hipótese de independência entre a volatilidade da taxa de câmbio real efetiva e as flutuações da taxa de juros real e nominal. Mais especificamente, houve evidência de que a variância da taxa de câmbio real efetiva é afetada pelos choques defasados na média e na variância da taxa de juros. Considerando que o regime demetas para a inflação no Brasil temcomo principal instrumento a fixação da taxa SELIC, os resultados deste trabalho sugerem que a volatilidade cambial no Brasil possivelmente teve sua dinâmica afetada pela regra de política monetária adotada no período analisado. Tal consideração confirma os resultados de trabalhos como os de Obstfeld (2000), Divereux & Engel (2002), Galí & Monacelli (2005) Patereau (2007). Esses autores enfatizam a relação entre política monetária e volatilidade cambial. Um ponto importante destacado por Galí & Monacelli (2005) é que as regras que visam estabilizar índices de preços ao consumidor tendem a provocar elevada volatilidade da taxa de juros e da taxa de câmbio real. A justificativa apresentada seria a potencial rigidez dos preços ao consumidor aos choques cambiais e monetários.
Recebido em 11 de maio de 2011
Aceito em 25 de abril de 2012
- Aghion, P., Bacchetta, P., Ranciere, R. & Rogoff, K. (2009), 'Exchange rate volatility and productivity growth: The role of financial development', Journal of Monetary Economics 56, 494513.
- Awartani, B.M. & Corradi, V. (2005), 'Predicting the volatility of the S&P-500 index via GARCH models: The role of asymmetries', International Journal of Forecasting 21(1), 167184.
- Bacchetta, P. & Van Wencoop, E. (2000), 'Does exchange-rate stability increase trade and welfare?', The American Economic Review 90(5), 10931109.
- Bagella, M., Bacchetti, L. & Hasan, I. (2006), 'Real effective exchange rate volatility and growth: A framework to measure advantages of flexibility vs. costs of volatility', Journal of Banking & Finance 30, 11491169.
- Bitencourt, M. V. L., Larson, D. W. & Thonpson, S. R. (2007), 'Impactos da volatilidade da taxa de câmbio no comércio setorial do mercosul', Estudos Econômicos 37(4), 791816.
- Bollerslev, T. (1990), 'Modelling the coherence in short-run nominal exchange rates: a multivariate generalized ARCH approach', Review of Economic and Statistics 72, 498505.
- Bollerslev, T., Engle, R. F. &Wooldridge, J. M. (1988), 'A capital asset pricing model with time varying covariances', Journal of Political Economy 96, 116131.
- Caporin, M. (2012), 'Do we really need both BEKK and DCC? A tale of two multivariate GARCH models', Journal of Economic Surveys 26(4), 736751.
- Caporin, M. & McAller, M. (2008), 'Scalar BEKK and indirect DCC', Journal of Forecasting 27, 537549.
- Chowdhury, A. R. (1993), 'Does exchange rate volatility depress trade flows? evidence from error-correction models', The Review of Economics and Statistics 75(4), 700706.
- Comte, F. (2003), 'Asymptotic theory for multivariate GARCH processes', Journal of Times Series Analysis 84, 6184.
- Comte, F. & Lieberman, O. (2000), 'Second-order noncausality in multivariate GARCH processes', Journal of Times Series Analysis 21(5), 535557.
- Darby, J., Hallett, A. H., Ireland, J. & Piscitelli, L. (1999), 'The impact of exchange rate uncertainty on level of investment', The Economic Journal 109(454), C55C67.
- Divereux, M. B. & Engel, C. (2002), 'Exchange rate pass-through, exchange rate volatility and exchange rate disconnect', Journal of Monetary Economics 49, 913940.
- Engle, R. (2002), 'Dynamic conditional correlation: a simple class of multivariate generalized autoregressive conditional heteroskedasticity models', Journal of Business and Economic Statistics 20, 339350.
- Engle, R, F. & Kroner, K, F. (1995), 'Multivariate Simultaneous Genaralized ARCH', Econometric Theory 11, 122150.
- Galí, J. & Monacelli, T. (2005), 'Monetary policy and exchange rate volatility in a small open economy', The Review of Economic Studies 72, 707734.
- Hafner, C.M. & Preminger, A. (2009), 'On asymptotic theory formultivariate GARCH models', Journal of Multivariate Analysis 100, 20442054.
- Hallin, M. & Paindaveine, D. (2005), 'Affine-invariant aligned rank tests for the multivariate general linear model with VARMA errors', Journal of Multivariate Analysis 93, 122163.
- Hansen, P. R. & Lunde, A. (2005), 'A forecast comparison of volatility models: does anything beat a GARCH(1,1)?', Journal of Applied Econometrics 10, 873889.
- Harvey, A. (1994), 'Multivariate stochastic variance models', The Review of Economic Studies 61(2), 247264.
- Hosking, J. R. M. (1980), 'The multivariate portmanteau statistic', Journal of the American Statistical Association 75(371), 602608.
- Hou, H. (2002), 'Real exchange rate volatility and economic openness: Theory and evidence', Journal of Money, Credit and Banking 34(3), 611630.
- Igesias, E. M. & Phillips, G. D. A. (2002), 'Another look about the evolution of the risk premium: a VAR-GARCH-M model', Economic Modelling 20, 777789.
- Jeantheau, T. (1998), 'Strong consistency of estimators for multivariate ARCH models', Econometric Theory 14, 7086.
- Levy-Yeyati, E. & Sturzenegger, F. (2003), 'To float or to fix: Evidence on the impact of exchange rate regimes on growth', The American Economic Review 93(4), 11731193.
- Ling, S. & McAleer, M. (2003), 'Asymptotic theory for a vector arma-garch model', Econometric Theory 19, 280310.
- Long, X., Sub, L. & Ullah, A. (2009), Estimation and forecasting of dynamic conditional covariance: A semiparametric multivariate model.
- Minella, A., De Freitas, P. S., Goldfajn, I. & Muinhos, M. K. (2002), Inflation targeting in brasil: lessons and challenges, Working paper series, Banco Central do Brasil.
- Obstfeld, M. (2000), 'New directions for stochastic open economy models', Journal of International Economics 50(1), 117153.
- Obstfeld, M. & Rogoff, K. (1995), 'Exchange rates dynamics redux', Journal of Political Economics 103(3), 624660.
- Patereau, L. (2007), 'Price-to-market limited participation and exchange rates dynamics', Journal of Economic Dynamics & Control 31, 32813320.
- Serletis, A. & Shahmoradi, A. (2006), 'Velocity and the variability of money growth: evidence from a VARMA, GARCH-M model', Macroeconomic Dynamics 10(5), 652666.
- Servén, L. (2003), 'Real-Exchange-Rate Uncertainty and Private Investment in LDCS', The Review of Economics and Statistics 85(1), 212218.
- Tenreyro, S. (2007), 'On the trade impact of nominal exchange rate volatility', Journal of Development Economics 82, 485508.
Apêndice

Datas de Publicação
-
Publicação nesta coleção
02 Dez 2013 -
Data do Fascículo
Set 2013
Histórico
-
Recebido
11 Maio 2011 -
Aceito
25 Abr 2012