Resumos
Regiões hidroclimaticamente homogêneas em relação à distribuição de freqüência de chuvas diárias foram caracterizadas na região hidrográfica do Atlântico, trecho Leste, no estado de Minas Gerais e delimitadas através das metodologias de análises estatísticas multivariadas (análises dos componentes principais rotacionados e de agrupamentos). O método de agrupamento proposto por Ward e adotado por proporcionar a melhor distribuição espacial dos grupos, indicou cinco e três grupos para os critérios de classificação, respectivamente, de meso e macroescala hidroclimática, na região de estudo.
precipitação pluvial; análise multivariada; regiões homogêneas
Hydroclimatically homogeneous areas in relation to the frequency distribution of daily rainfalls were characterized in the hydrographic area of the Atlântico eastern part, in the State of Minas Gerais, Brazil. The hydroclimatically homogeneous areas were delimited through the methodologies of multivariate statistical analyses (rotated principal components analyses and clustering analysis). The method of clustering analysis proposed by Ward was used, because it provided the best space distribution of the groups. The results indicated five and three groups for, respectively, the meso and macro scale hydro climatic classification criteria, in the studied area.
rainfall; multivariable analysis; homogeneous areas
METEOROLOGIA E CLIMATOLOGIA AGRÍCOLA
Determinação de regiões homogêneas quanto à distribuição de freqüência de chuvas no leste do Estado de Minas Gerais
Determination of homogeneous areas according to the frequency of rainfalls in the Eastern part of Minas Gerais, Brazil
Júlio C. F. de Melo JúniorI; Gilberto C. SediyamaII; Paulo A. FerreiraII; Brauliro G. LealII
ICENAMB, UNIVASF. CEP 56308-190, Petrolina, PE. Fone: (087) 3862-2817. E-mail: julio.melo@univasf.edu.br
IIDEA/UFV. Fone: (31) 3899 1905. E-mail: sediyama@ufv.br; pafonso@ufv.br; brauliro@ig.com.br
RESUMO
Regiões hidroclimaticamente homogêneas em relação à distribuição de freqüência de chuvas diárias foram caracterizadas na região hidrográfica do Atlântico, trecho Leste, no estado de Minas Gerais e delimitadas através das metodologias de análises estatísticas multivariadas (análises dos componentes principais rotacionados e de agrupamentos). O método de agrupamento proposto por Ward e adotado por proporcionar a melhor distribuição espacial dos grupos, indicou cinco e três grupos para os critérios de classificação, respectivamente, de meso e macroescala hidroclimática, na região de estudo.
Palavras-chave: precipitação pluvial, análise multivariada, regiões homogêneas
ABSTRACT
Hydroclimatically homogeneous areas in relation to the frequency distribution of daily rainfalls were characterized in the hydrographic area of the Atlântico eastern part, in the State of Minas Gerais, Brazil. The hydroclimatically homogeneous areas were delimited through the methodologies of multivariate statistical analyses (rotated principal components analyses and clustering analysis). The method of clustering analysis proposed by Ward was used, because it provided the best space distribution of the groups. The results indicated five and three groups for, respectively, the meso and macro scale hydro climatic classification criteria, in the studied area.
Key words: rainfall, multivariable analysis, homogeneous areas
INTRODUÇÃO
Devido ao processo natural de desenvolvimento do Brasil, torna-se cada vez maior a necessidade de se proceder ao uso racional de recursos hídricos. A utilização irracional desses recursos tem trazido conseqüências, não apenas ambientais, ligados ao solo, clima e água, mas também problemas sociais, econômicos e políticos.
Desta maneira, o estabelecimento de metodologias apropriadas para definir o comportamento pluvial em níveis regionais, é de suma importância para suprir as deficiências das informações hidroclimáticas como, por exemplo, nas tomadas de decisões para o planejamento do uso dos recursos hídricos sob o ponto de vista agrícola, urbano e energético.
A delimitação das regiões homogêneas de chuva, quando realizada de forma integrada, isto é, considerando-se as suas variações interanuais, pode revelar a forma de atuação dos sistemas geradores da chuva na região; assim, uma descrição e caracterização das distribuições pluviométricas implicam em uma convivência melhor com fenômenos adversos.
As regiões hidroclimaticamente homogêneas não só estabelecem os indicadores do potencial do meio físico e biológico para a região em estudo mas, também, registram e delimitam as áreas de padrões homogêneos de atividades agrícolas e dos recursos naturais nela existentes (Sediyama et al., 2001).
A utilização da informação local espacialmente disseminada por intermédio da delimitação das regiões homogêneas, atenua os erros de amostragem, incrementando a confiabilidade das inferências estatísticas locais, podendo oferecer, como exemplo, subsídios para regionalização hidrológica e para preenchimento de falhas, proporcionando uma densidade ótima da rede pluviométrica, visto que a falta de informações pelo interrompimento das observações tem sido evidenciada com grande freqüência, na maioria das séries pluviométricas.
Muitos trabalhos têm sido realizados estudando-se o regime de chuvas da região Sul do Brasil. Sansigolo & Nery (1998) aplicaram as metodologias de análise fatorial e de agrupamento aos dados de chuva nas regiões Sul e Sudeste do Brasil, visando à sua regionalização e melhor compreensão de seus padrões sazonais e interanuais.
Silva & Nery (2001) utilizaram a análise de componentes principais para determinar regiões homogêneas de chuva no estado do Paraná. Os autores concluíram que, desta forma, foi impossível separar dois grupos homogêneos de chuva, caso em que a visualização do grau de similaridade entre indivíduos não é clara.
Objetivando identificar regiões homogêneas de chuva para posterior análise periodográfica no estado do Ceará, Silva et al. (2001) procuraram reunir as estações disponíveis em grupos distintos, de acordo com o comportamento das chuvas trimestrais em cada uma das mesmas; para isto, utilizou-se a análise de agrupamento, empregando-se o método de classificação hierárquico aglomerativo de Ward, tendo como medida de similaridade a distância euclidiana ao quadrado e a inércia intra-classe como critério de agregação. Segundo o autor, o método proposto por Ward aplicado aos totais trimestrais levou à classificação das 20 estações em quatro grupos.
No presente trabalho realizou-se a análise espacial do regime de chuvas para a região hidrográfica do Atlântico, trecho Leste no estado de Minas Gerais, tendo em vista o seguinte objetivo: obter e espacializar grupos de estações pluviométricas que caracterizam regiões homogêneas de freqüência de chuva, por intermédio da análise espacial, utilizando-se os procedimentos da análise estatística multivariada: componentes principais rotacionados e agrupamentos para toda a região hidrográfica em estudo.
MATERIAL E MÉTODOS
Região de estudo
A área de estudo abrange a região hidrográfica do Atlântico, trecho Leste, no Estado de Minas Gerais e se compõe das bacias hidrográficas dos rios Doce, Jequitinhonha, Mucuri, Paraíba do Sul e Pardo e as denominadas Bacias do Leste (rios Itabapoana, Itapemirim, São Mateus, Itanhém, Jucuruçu e Buranhém); esta representa aproximadamente 21% da região Sudeste do País e está situada entre os paralelos 14º 58' 54" e 22º 22' 47" S e os meridianos de 39º 51' 31" e 44º 40' 2" W, com altitude média de 651,3 m e área de 193.733,00 km2, aproximadamente.
Base de dados e aplicativos
As séries de dados de chuva utilizadas neste estudo, foram obtidas junto à Agência Nacional de Águas - ANA, a partir do sistema de informações hidrológicas (Hidroweb, 2003).
As estações pluviométricas foram espacializadas obtendo-se, assim, a distribuição espacial das estações na região. Após a análise da distribuição espacial, foram selecionadas 163 estações pluviométricas, com 30 anos de dados, geograficamente distribuídas, cujo período de recorrência foi de 1944 a 2000, abrangendo toda a região em estudo e áreas vizinhas, obtidas por meio de um "buffer", a uma distância de 50 km do limite da região hidrográfica. Admitiu-se que os dados das séries de chuva foram consistidos, conforme ANA.
Utilizou-se a base vetorial de dados constituída pelos vetores da região hidrográfica e de hidrografia. Os vetores da região hidrográfica e de hidrografia foram obtidos junto ao Instituto Mineiro de Gestão das Águas (IGAM, 2003), em escalas de 1:100.000 e 1:50.000, respectivamente, cujo responsável pelo geoprocessamento foi o próprio IGAM.
As análises estatísticas multivariadas foram realizadas utilizando-se o aplicativo StatisticaÒ 6.0, desenvolvido pela "StatSoft".
Para a espacialização foi utilizado o Sistema de Informação Geográfica, ArcGIS® 8.1, desenvolvido pelo "Enviromental Systems Research Institute - ESRI", como ferramenta de representação espacial dos dados.
Análise espacial das freqüências de chuva
A análise espacial das freqüências de chuva na região hidrográfica foi desenvolvida com os métodos estatísticos de análise multivariada: análise de componentes principais e análises de agrupamento.
Estabeleceram-se 10 classes de freqüência absoluta, para as estações pluviométricas com 30 anos de dados diários. Para a obtenção das classes, sendo estas com amplitude variável, utilizou-se um aplicativo desenvolvido em linguagem pascal. Os intervalos das classes de freqüência absoluta dos valores de chuva diária utilizados e as amplitudes, estão dispostos na Tabela 1.
Análise dos componentes principais
A análise dos componentes principais consistiu no cálculo dos autovalores e correspondentes autovetores de uma matriz de correlações. Nesta matriz simétrica, os elementos da diagonal principal foram as variâncias das freqüências absolutas padronizadas de cada classe (variáveis padronizadas) e os demais elementos, os valores de covariâncias entre pares de variáveis padronizadas.
Seja uma matriz na qual se teve um conjunto de p variáveis observadas (classes de freqüências), X1, X2, ..., Xj, ..., Xp, para cada indivíduo i (estações pluviométricas), perfazendo o total de n indivíduos; esta matriz possui uma ordem n x p, em que n e p foram iguais a 163 e 10, respectivamente.
Do ponto de vista matemático-estatístico, a análise dos componentes principais busca transformar o conjunto original das variáveis observadas em um novo conjunto de variáveis, denominados componentes principais, que obedeçam às seguintes propriedades (Cruz, 1990):
a) seja Yi um componente principal, então Yi é uma combinação linear de Xj
Yi = ai1X1 + ai2X2 + ... + apiXip
(1)
de modo análogo para outro componente Yi'
Yi' = ai'1X1 + ai'2X2 + ... + ap'iXip
(2)
sujeitos a restrição:

(3)
b) os componentes são não-correlacionados, ou seja, são independentes entre si.
Cov(Yi, Yi') = 0
(4)
ou seja,

(5)
c) Dentre todos os componentes, Y1 é o que apresenta a maior variância, Y2 é o que indica a segunda maior e, assim, sucessivamente.
Var(Y1) > Var(Y2) > ... > Var(Yp)
(6)
d) O somatório das variâncias de cada componente principal (Yi) é igual ao somatório das variâncias de cada variável original (Xj)

(7)
Com base nessas propriedades, a solução do problema será apresentada a partir da matriz de correlação, denominada R, entre as variáveis, para que a análise não seja influenciada pelas diferentes escalas das classes de freqüência absolutas utilizadas.
Sendo R uma matriz simétrica de correlação, de dimensão p x p, da qual os autovalores (li) e os autovetores (ai) são extraídos, a solução é obtida resolvendo-se o sistema
(R - li I)ai = F
(8)
em que:
li - são as raízes características (ou autovalores) da matriz R. Existem p autovalores correspondentes às variâncias de cada um dos p componentes principais
I - é a matriz identidade de dimensão p x p
ai - autovetor ou vetor característico ou uma matriz p x 1, contendo os p coeficientes para cada autovalor li correspondente ao componente principal Yi
F - é um vetor nulo, de dimensão p x 1
A importância de cada componente principal pode ser avaliada pela sua correlação existente com cada variável Xj, ou seja,

(9)
Rotação em componentes principais - análise fatorial
Para rotação dos componentes principais selecionaram-se os três primeiros componentes e, após a rotação, visualizou-se o resultado de dispersão gráfica no espaço tridimensional. Na dispersão gráfica foram observados pontos mais próximos, que apresentaram maiores similaridades, separando-se grupos com características comuns. O procedimento de cálculo baseou-se no critério varimax de rotação, apresentado por Harman (1976).
Análises de agrupamento
Medidas de dissimilaridade ou de distância. A medida de dissimilaridade mais utilizada é a distância euclidiana, a qual é simplesmente a distância geométrica tomada em um espaço de p dimensões. Sendo Xij a observação da i-ésima estação pluviométrica (i = 1, 2, …, n), com referência a j-ésima variável ou freqüência absoluta em cada classe (j = 1, 2, …, p) estudada, define-se a distância euclidiana padronizada entre dois postos i e i', por meio da expressão

(10)
sendo

(11)
em que Zij, s(Xj) e  são, respectivamente, a variável padronizada, o desvio-padrão e a média da j-ésima variável original.
são, respectivamente, a variável padronizada, o desvio-padrão e a média da j-ésima variável original.
Métodos de agrupamentos
Utilizaram-se três métodos no desenvolvimento da análise de agrupamento: método do vizinho mais próximo, do vizinho mais distante e o proposto por Ward Júnior (1963), apresentados a seguir. Para o método do vizinho mais próximo e do vizinho mais distante utilizou-se, como medida de dissimilaridade, a distância euclidiana padronizada e, para o método proposto por Ward, a distância euclidiana padronizada ao quadrado, sendo esta uma premissa para aplicação deste método.
Vizinho mais próximo (Single Linkage)
Este método consiste, inicialmente, de uma matriz de distância (dissimilaridade) entre estações pluviométricas (indivíduos). São identificados os dois indivíduos mais similares (menor distância entre eles), os quais são reunidos em um grupo inicial. A seguir, é calculada a distância daquele primeiro grupo em relação aos demais indivíduos.
A distância entre um grupo e um indivíduo é fornecida pela expressão (Manly, 1994)
d(ab)c = min{dac; dbc}
(12)
ou seja, a distância entre o grupo constituído pelos indivíduos, a e b, e o indivíduo c, é fornecida pelo menor elemento do conjunto das distâncias dos pares de indivíduos (ac) e (bc).
Segundo Liberato (1995), constitui-se uma nova matriz de dissimilaridade, de dimensão menor que a inicial e se identificam os indivíduos e/ou grupos mais similares, incorporando-se outro indivíduo ao grupo inicial ou formando um segundo grupo, caso a menor distância da nova matriz de dissimilaridade seja visualizada entre dois outros indivíduos. Nas etapas seguintes trabalha-se com matrizes de dissimilaridade com dimensões cada vez menores, finalizando o agrupamento de todos os indivíduos em um único grupo, formando um dendrograma ou árvore.
Vizinho mais distante (Complete Linkage)
O método de agrupamento hierárquico do vizinho mais distante possui o procedimento semelhante àquele do vizinho mais próximo, com uma diferença importante: a cada estádio, a medida de distância é dada por aquela que proporcionará a maior distância entre dois indivíduos e/ou grupos, conforme Eq. 13.
A distância entre um grupo e um indivíduo é fornecida pela expressão (Manly, 1994)
d(ab)c = max{dac; dbc}
(13)
isto é, a distância entre o grupo constituído pelos indivíduos a e b e o indivíduo c, é fornecida pelo maior elemento do conjunto das distâncias dos pares de indivíduos (ac) e (bc).
Como o método do vizinho mais próximo se constitui uma nova matriz de dissimilaridade com dimensão menor que a inicial e se identificam os indivíduos e/ou grupos mais similares, incorporando-se outro indivíduo do grupo inicial ou formando um segundo grupo, caso a menor distância da nova matriz de dissimilaridade seja visualizada entre dois outros indivíduos trabalha-se, nas etapas seguintes com matrizes de dissimilaridade de dimensões cada vez menores, finalizando com o agrupamento de todos os indivíduos em um único grupo, formando um dendrograma.
Ward
Consideram-se neste método, para a formação inicial do grupo, aqueles indivíduos que proporcionam a menor soma de quadrados dos desvios.
O agrupamento é feito a partir das somas de quadrados dos desvios entre acessos ou a partir do quadrado da distância Euclidiana, uma vez que se verifica a relação

(14)

(15)
em que:
SQDj(ii') - a soma de quadrado dos desvios, para a j-ésima variável, considerando-se os postos i e i'
dii'2 - quadrado da distância euclidiana entre os postos i e i'
n - número de variáveis avaliadas
A soma de quadrados dos desvios total é dada por

(16)
em que:
g - número de estações pluviométricas a serem agrupadas.
Na análise de agrupamento identifica-se, na matriz D, cujos elementos são os quadrados das distâncias euclidianas, ou na matriz S, em que os elementos são as somas dos quadrados dos desvios, o par de acessos que proporciona a menor soma de quadrados dos desvios (Ward Júnior, 1963). Com esses acessos agrupados, uma nova matriz de dissimilaridade com dimensão inferior é recalculada, considerando-se que:

(17)

(18)
em que:
k - número de estações pluviométricas no grupo que, neste caso, é igual a 3 e assim, sucessivamente.
No procedimento realiza-se a análise de agrupamento seguindo-se os (g - 1) passos de agrupamento para que seja formado o dendrograma.
RESULTADOS E DISCUSSÃO
Análise espacial das freqüências de chuva
Para início da análise espacial da chuva na região hidrográfica, as freqüências absolutas foram obtidas para as classes com amplitudes variáveis e crescentes. O histograma das freqüências absolutas de chuva diária, considerando-se as freqüências de dias sem chuva, possui forte assimetria positiva, razão pela qual as primeiras classes de freqüências possuíram amplitudes inferiores em relação às últimas, proporcionando melhor discretização das informações do histograma onde as chuvas ocorrem com maiores freqüências. Desta forma, obtiveram-se as freqüências absolutas para as dez classes que forneceram melhores informações para os métodos estatísticos multivariados, sendo estes sensíveis a pequenas variações das amplitudes nas primeiras classes de freqüência.
Análise dos componentes principais
Com base nas dez classes de freqüência absoluta que foram padronizadas (variáveis) para cada estação pluviométrica, procedeu-se à análise de componentes principais. A variância total existente no conjunto de dados multivariados analisados é igual ao número de variáveis analisadas, visto que os dados foram padronizados com média e variância igual a 0 e 1, respectivamente.
Para a análise espacial das freqüências de chuva são considerados apenas os três primeiros componentes, que explicam 85,37% da variação total; os seis últimos componentes, que juntos explicam 14,63% da variação total, foram desconsiderados.
Rotação em componentes principais - análise fatorial
Com o propósito de melhor interpretar a estrutura multivariada das freqüências de classes de chuva, procede-se à rotação dos componentes principais, por intermédio da qual os fatores de carga são transformados de tal forma que os maiores valores são maximizados e os menores minimizados.
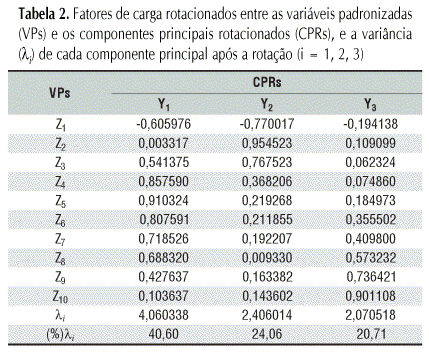
A Tabela 2 apresenta as correlações ou fatores de carga rotacionados entre as dez variáveis padronizadas e os três componentes principais rotacionados.
Observa-se que as variáveis padronizadas (freqüências das classes de chuva padronizadas) Z4, Z5, Z6, Z7 e Z8 apresentam maiores correlações com o primeiro componente principal (Y1), enquanto as variáveis Z1, Z2 e Z3 indicam maiores correlações com o segundo componente principal (Y2) e as variáveis Z9 e Z10 apresentam maiores correlações com o terceiro componente principal (Y3).
Observa-se que as variáveis padronizadas (freqüências das classes de chuva padronizadas) Z4, Z5, Z6, Z7 e Z8 apresentam maiores correlações com o primeiro componente principal (Y1), enquanto as variáveis Z1, Z2 e Z3 indicam maiores correlações com o segundo componente principal (Y2) e as variáveis Z9 e Z10 apresentam maiores correlações com o terceiro componente principal (Y3).
Associando o significado físico aos três primeiros componentes principais (Tabela 2), para que a análise dos componentes principais rotacionados seja de utilidade máxima, o componente principal Y1 representa as freqüências de classes com totais de chuva intermediários, o Y2 representa as freqüências de classes para dias sem chuva ou com baixos totais de chuva e o Y3 diz respeito às freqüências de classes com totais de chuva elevados ou extremos.
Por meio da análise visual da dispersão gráfica verifica-se a formação de 11 grupos com características homogêneas de freqüência de chuvas; a maioria dos grupos é constituída por poucos indivíduos, e um único grupo é formado por 124 indivíduos que correspondem a 76,07% das estações pluviométricas analisadas.
Na Figura 1A apresenta-se a espacialização dos 11 grupos com características homogêneas de freqüência de chuvas, obtidos por meio da análise dos componentes principais rotacionados. Constatou-se a presença de 11 grupos (regiões homogêneas) e se tem que sete estão situados dentro da região hidrográfica.
As delimitações das áreas nos mapas (Figura 1, A, B e C), por linhas tracejadas, foram colocadas apenas para permitir uma visualização melhor dos grupos sem nenhum critério objetivo não representando, portanto, isolinhas.
As considerações sobre a configuração do posicionamento espacial dos grupos obtidos por meio da análise dos componentes principais, serão suprimidas pelo fato de que esta serviu apenas para realizar um estudo preliminar da distribuição espacial das regiões homogêneas; esta análise será complementada pela análise multivariada de agrupamento, visto que são questionáveis a avaliação da divergência em análise gráfica e o estabelecimento de grupos de similaridade de maneira subjetiva, com base na simples inspeção visual da dispersão (Cruz, 1990).
Métodos de agrupamento
Vizinho mais próximo (Single linkage)
O método do vizinho mais próximo "Single linkage" apresentou agrupamento irregular e foi descartado. Braga et al. (1998) e Ribeiro et al. (1996) se depararam com situação semelhante, sendo também descartados os agrupamentos obtidos. Segundo Cruz (1990) e Manly (1994), não existe método de agrupamento aceito como o melhor, donde há necessidade de se testar vários, para se verificar qual deles apresentará melhores resultados.
Vizinho mais distante (Complete linkage)
A determinação do número de grupos para o dendrograma é feita de forma visual e pelo critério de inércia entre saltos, em que o maior salto, em relação aos anteriores, é definido como o ponto de corte. Para o método do vizinho mais distante adota-se o ponto de corte igual a 45% de dissimilaridade, obtendo-se a formação de cinco grupos com características homogêneas de freqüência de chuvas.
A Figura 1B mostra a espacialização dos cinco grupos com características homogêneas de freqüência de chuvas, obtidos com a análise de agrupamento na qual se utilizou o método do vizinho mais distante. Dos cinco grupos (regiões homogêneas) encontrados, quatro estão situados dentro da região hidrográfica, dos quais são feitas maiores considerações.
As considerações apresentadas nos próximos parágrafos, referem-se à Figura 1B e descrevem a configuração espacial dos grupos.
O primeiro grupo ocupa áreas distintas situadas ao Sul e ao extremo Sul na região hidrográfica. Este grupo é composto por quatro estações pluviométricas, consideradas pertencentes à região, em que três estão situadas em uma área próxima ao limite no extremo Sul, mas fora da região hidrográfica; o primeiro grupo se sobrepõe ao segundo, em uma área ao Sul na região hidrográfica. A sobreposição pela estação pluviométrica 02243202 (Fazenda São Gabriel, MG) apresenta-se como possível indício de diferenciação microclimática, em relação às regiões vizinhas; por outro lado o segundo grupo ocupa áreas distintas, situadas no extremo Sul, Sudoeste e Oeste, na região hidrográfica, e é composto por 12 estações pluviométricas, consideradas pertencentes à região, dentre as quais duas estão situadas em uma área próxima ao limite no Sudoeste, porém fora da região hidrográfica; este grupo se sobrepõe ao terceiro, em uma área a Oeste na região hidrográfica. A sobreposição pelas estações pluviométricas 01943002 (Conceição do Mato Dentro, MG) e 01943025 (Morro do Pilar, MG) apresenta-se como possível indício de diferenciação microclimática, em relação às regiões vizinhas; referente ao terceiro grupo, este ocupa áreas distintas situadas ao Sul, Sudeste, Sudoeste, Centro, Oeste e Leste na região hidrográfica, além de ser formado por 36 estações pluviométricas, tidas como pertencentes à região, sendo que cinco delas estão situadas em áreas próximas aos limites no Sudeste, Leste e Sudoeste fora, no entanto, da região hidrográfica. Este grupo se sobrepõe aos segundo e quarto, em áreas a Sudoeste e Leste da região hidrográfica, respectivamente. A sobreposição no segundo grupo pela estação pluviométrica 02143007 (Vargem do Engenho, MG) apresenta-se como região de transição situada no limite Sudoeste da região hidrográfica, que complementa uma área com características homogêneas de freqüência de chuvas no Estado de Minas Gerais; outrossim, a sobreposição no quarto grupo pela estação pluviométrica 01840004 (Barra de São Francisco, ES) também se apresenta como região de transição, mas situada no limite Leste da região hidrográfica e complementa uma pequena área com características homogêneas de freqüência de chuvas no estado do Espírito Santo; o penúltimo grupo ocupa áreas distintas, situadas no Sul, Centro, Leste, Oeste, Nordeste, Noroeste e Norte na região hidrográfica, e se compõe de 25 estações pluviométricas, tidas como pertencentes à região; ressalta-se que quatro delas estão situadas em áreas próximas aos limites no Leste e Sul, porém fora da região hidrográfica. Este grupo se sobrepõe ao terceiro, em áreas ao Sul e Centro da região hidrográfica. A sobreposição em áreas ao Sul, pelas estações pluviométricas 02142014 (Paquequer, RJ) e 02243015 (Moura Brasil, RJ), e em área ao centro, pela estação pluviométrica 02042016 (São Miguel do Anta, MG), apresenta-se como possíveis indícios de diferenciação microclimática, em relação às regiões vizinhas; enfim, tem-se o quinto grupo, que não é encontrado dentro da região hidrográfica mas em área situada fora, a uma distância máxima de 50 km do limite desta; ele ocupa uma pequena área isolada situada no Nordeste da região hidrográfica, no Estado da Bahia. Os outros quatro grupos são também encontrados fora da região hidrográfica em estudo.
Ward
Embora se tenha utilizado dois outros métodos referentes à análise estatística multivariada de agrupamento (vizinho mais próximo e vizinho mais distante), fez-se opção pelo método de classificação hierárquico aglomerativo, proposto por Ward, por ter apresentado melhores resultados que complementam os obtidos pela análise dos componentes principais rotacionados. Braga et al. (1998), apesar de terem utilizado três métodos de agrupamento para a delimitação das áreas homogêneas de chuva, no estado da Bahia, também optaram pelo método proposto por Ward, em razão de haver apresentado melhores resultados. Para este método, são adotados dois critérios de classificação: de meso e macroescala hidroclimática.
A determinação do número de grupos no dendrograma para o critério de mesoescala, é feita de forma visual, utilizando-se a técnica de inércia entre saltos, em que, para um salto maior em relação aos anteriores, é definido como o ponto de corte; para o critério de macroescala utiliza-se o próximo maior salto em relação aos anteriores, como definição do ponto de corte. Os pontos de corte adotados para os critérios de meso e macroescala hidroclimática, são iguais a 8,7% e 19,2% de dissimilaridade, obtendo-se a formação de cinco e três grupos com características homogêneas de freqüência de chuvas, respectivamente. Os primeiro e segundo grupos e os quarto e quinto grupos obtidos por meio do critério de mesoescala, são agrupados em dois novos grupos, denominados primeiro e terceiro grupos, respectivamente, gerando a classificação de macroescala. O terceiro grupo passa então a ser denominado simplesmente como segundo, sem nenhuma alteração de acordo com o critério de classificação de macroescala hidroclimática.
Na Figura 1C apresenta-se a espacialização dos cinco grupos com características homogêneas de freqüência de chuvas, obtidos por meio da análise de agrupamento, utilizando-se o método proposto por Ward, segundo o critério de classificação de mesoescala hidroclimática; todos os grupos (regiões homogêneas) estão situados dentro da região hidrográfica.
As considerações dos próximos parágrafos referem-se à Figura 1C e manifestam a configuração espacial dos grupos, obtidos por meio da análise de agrupamento, com o método proposto por Ward, segundo o critério de classificação de mesoescala hidroclimática.
O primeiro grupo ocupa áreas distintas situadas no Sul, Sudeste, Centro, Oeste e Noroeste na região hidrográfica e é formado por 21 estações pluviométricas, consideradas pertencentes à região, em que duas delas estão situadas em áreas próximas aos limites no Sul e Sudeste, porém fora da região hidrográfica. O primeiro grupo se sobrepõe ao quarto em áreas ao Sul e a Oeste, na região hidrográfica. A sobreposição pelas estações pluviométricas 02242028 (Anta, RJ), 02143013 (Estevão Pinto, MG) e 02142007 (Fazenda da Barra, MG) apresenta-se como sendo uma região de transição, situada no limite Sul da região hidrográfica, complementando uma pequena área com características homogêneas de freqüência de chuvas no estado do Rio de Janeiro. A sobreposição em área a Oeste pela estação pluviométrica 01943007 (Santa Bárbara, MG), apresenta-se como um possível indício de diferenciação microclimática, em relação às regiões vizinhas; o segundo grupo ocupa áreas situadas a Leste, Nordeste, Noroeste e Norte, na região hidrográfica, enquanto é composto de 20 estações pluviométricas, tidas como pertencentes à região e cinco estão situadas em áreas próximas aos limites no Sul e Leste, mas fora da região hidrográfica. Este grupo se sobrepõe ao primeiro, em áreas ao Sul e Centro da região hidrográfica. As sobreposições em áreas ao Sul pelas estações pluviométricas 02243015 (Moura Brasil, RJ) e 02142014 (Paquequer, RJ), e em área ao Centro pela estação pluviométrica 02042016 (São Miguel do Anta, MG) apresentam-se como possíveis indícios de diferenciações microclimáticas, em relação às regiões vizinhas; por sua vez o terceiro grupo ocupa pequenas áreas situadas no extremo Sul, na região hidrográfica; e é formado por cinco estações pluviométricas, consideradas pertencentes à região; ressalta-se que três estão situadas em área próxima ao limite no extremo Sul, fora, no entanto, da região hidrográfica. Trata-se de um grupo que se sobrepõe ao quarto, em uma pequena área no extremo Sul, na região hidrográfica, pela estação pluviométrica 02243202 (Fazenda São Gabriel, MG), que se apresenta como possível indício de diferenciação microclimática, em relação às regiões vizinhas, causada pela influência orográfica; além disso, é um grupo complementado por outras estações pluviométricas próximas, expandindo a região com características homogêneas de freqüência de chuvas nos estados do Rio de Janeiro e de Minas Gerais.
O quarto grupo ocupa áreas situadas no extremo Sul, Sul, Sudoeste e Oeste na região hidrográfica e 26 estações pluviométricas o constituem, além de consideradas pertencentes à região, sendo que uma delas se situa em área próxima ao limite no Sudoeste, porém fora da região hidrográfica. O quarto grupo não se sobrepõe a nenhum outro mas é sobreposto pelos primeiro, terceiro e quinto grupos.
O quinto grupo ocupa pequenas áreas isoladas, situadas no extremo Sul, Sul e Sudoeste, na região hidrográfica, que se sobrepõem ao quarto grupo, composto por cinco estações pluviométricas, consideradas pertencentes à região, três das quais estão situadas em áreas próximas aos limites no extremo Sul e Sudoeste, porém fora da região hidrográfica. As sobreposições pelas estações pluviométricas 02243008 (Manuel Duarte, RJ) e 02143016 (Torreões, MG), e 02143007 (Vargem do Engenho, MG) e 02043018 (Carandaí, MG), ocorrem em pequenas áreas isoladas, situadas no extremo Sul e Sudoeste da região hidrográfica, respectivamente. Essas áreas se apresentam como regiões de transição, situadas no limite da região hidrográfica, complementando uma pequena área com características homogêneas de freqüência de chuvas, nos estados do Rio de Janeiro e Minas Gerais, respectivamente. A sobreposição pela estação pluviométrica 02143001 (Guarani, MG) ocorre em uma pequena área isolada situada ao Sul da região hidrográfica e se apresenta como possível indício de diferenciação microclimática, em relação às regiões vizinhas.
Comparando-se os resultados obtidos com os encontrados por Catalunha (2000), verificou-se que o número de grupos de estações encontrados se assemelha aos obtidos pelo referido autor; este também evidencia a questão das sobreposições geográficas para a maioria dos grupos, o que se deve à capacidade do método de agrupamento em separar estações com pequenas diferenças de características. De acordo com o autor, a análise de agrupamento é uma ferramenta importante para se concluir que em uma mesma região podem existir estações pluviométricas, formando subgrupos diferentes. A metodologia fornece, também, informações sobre a influência de microclima na análise hidroclimatológica, evitando o conceito da generalização de informações por região.
Em relação aos possíveis indícios de diferenciação microclimática encontrados, Batista da Silva et al. (2001) também evidenciam o que pode ser explicado por possível microclima existente na região estudada no estado do Ceará, ocasionado por suas condições orográficas.
CONCLUSÕES
Como base nas metodologias empregadas e nos resultados obtidos, pôde-se concluir que:
1. A análise espacial do regime de chuvas utilizando-se os procedimentos da análise estatística multivariada permitiu se obter grupos que caracterizaram regiões homogêneas de freqüências de chuva, sendo estes geoespacializados, por intermédio de um Sistema de Informações Geográficas.
2. A análise estatística multivariada permitiu, por intermédio do método proposto por Ward, permitiu que se obtivessem grupos segundo os critérios de classificação de meso e macroescala hidroclimática, que caracterizaram as regiões homogêneas de freqüência de chuvas, apresentando coerência e boa representação espacial.
3. O método proposto por Ward apresentou a melhor representação espacial das regiões hidroclimaticamente homogêneas caracterizadas pelos grupos, em relação aos demais métodos empregados.
4. A análise de componentes principais rotacionados serviu apenas para se realizar uma análise preliminar da distribuição espacial das regiões hidroclimaticamente homogêneas, sendo questionável a avaliação da divergência em análise gráfica e o estabelecimento de grupos de similaridade de maneira subjetiva, com base na simples inspeção visual da dispersão.
AGRADECIMENTOS
Os autores agradecem à Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG), à Universidade Federal de Viçosa (UFV) e ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), pelo financiamento deste trabalho, à Agência Nacional de Águas (ANA) e ao Instituto Mineiro de Gestão das Águas (IGAM) pela cessão das séries de dados de chuva e da base de dados vetorial, respectivamente.
LITERATURA CITADA
Protocolo 051.04 - 22/04/2004 - Aprovado em 16/11/2005
- Braga, C. C.; Melo, M. L. D.; Melo, E. C. S. Análise de agrupamento aplicada a distribuição da precipitação no Estado da Bahia. In: Congresso Brasileiro de Meteorologia, 10, 1998, Brasília. Anais... Brasília: Sociedade Brasileira de Meteorologia, 1998. CD-Room.
- Catalunha, M. J. Avaliação do ajustamento de funções densidade de probabilidade a séries de precipitação pluvial no Estado de Minas Gerais. Viçosa: UFV, 2000. 72p. Dissertação Mestrado
- Cruz, C. D. Aplicações de algumas técnicas multivariadas no melhoramento de plantas. Piracicaba: ESALQ, 1990. 188p. Tese Doutorado
- Harman H. H. Modern factor analysis. Chicago: University of Chicago Press, 1976, 487p.
- Hidroweb Dados Hidrológicos, Séries Históricas; Sistema de Informações Hidrológicas. hidroweb.ana.gov.br/HidroWeb/ 05 jan. 2003.
- IGAM Geoprocessamento. Instituto Mineiro de Gestão das Águas. http://www.igam.mg.gov.br/geo.php 10 fev. 2003.
- Liberato, J. R. Aplicações de técnicas de análise multivariada em fitopatologia. Viçosa: UFV, 1995. 144p. Dissertação Mestrado
- Manly, B. F. J. Multivariate statistical methods. London: Chapman and Hall, 1994. 215p.
- Ribeiro, A.; Victoria, R. L.; Pereira, A. R.; Villa Nova, N. A.; Martinelli, L. A.; Mortatti, J. Análise do regime pluviométrico da região amazônica a partir de dados de onze localidades. Revista Brasileira de Meteorologia, Brasília, v.11, n.1/2, p.25-35, 1996.
- Sansigolo, C. A.; Nery, J. T. Análise de fatores comuns e agrupamentos das precipitações nas regiões sudeste e sul do Brasil. In: Congresso Brasileiro de Meteorologia, 10, 1998, Brasília. Anais... Brasília: Sociedade Brasileira de Meteorologia, 1998. CD-Room.
- Sediyama, G. C.; Melo Júnior, J. C. F.; Santos, A. R.; Ribeiro, A.; Hamakawa, P. J.; Costa, L. C.; Costa, J. M. N.; Costa, M. H. Zoneamento agroclimático do cafeeiro (Coffea arábica L.) para o Estado de Minas Gerais. Revista Brasileira de Agrometeorologia, Santa Maria, v.9, n.3 (Nº Especial: Zoneamento Agrícola), p.501-509, 2001.
- Silva, E. S.; Nery, J. T. Distribuição espacial e temporal da precipitação na região Centro-Sul do Paraná. In: Congresso Brasileiro de Agrometeorologia, 12, 2001, Fortaleza. Anais... Fortaleza: Sociedade Brasileira de Agrometeorologia, 2001. p.111-12.
- Silva, J. B. da; Cunha, F. B.; Gavião Neto, W. P. Modelagem das chuvas trimestrais por regiões homogêneas no Estado do Ceará. Revista Brasileira de Agrometeorologia, Santa Maria, v.9, n.2, p.317-24, 2001.
- Ward, Júnior H. Jr. Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association, Alexandria , v.58, n.301, p.236-244, 1963.
Datas de Publicação
-
Publicação nesta coleção
20 Out 2006 -
Data do Fascículo
Jun 2006
Histórico
-
Recebido
22 Abr 2004 -
Aceito
16 Nov 2005