Resumos
O conhecimento da distribuição granulométrica dos sedimentos em suspensão em cursos d'água é fundamental para a realização de estudos hidrossedimentológicos. As técnicas geralmente utilizadas para a avaliação da distribuição granulométrica de amostras de sedimentos resultam em valores pontuais, dependendo de posterior interpolação para o traçado da curva granulométrica e para a obtenção de diâmetros característicos específicos. A transformação de valores pontuais em funções contínuas pode ser realizada por meio de modelos matemáticos; entretanto, são poucos os estudos desenvolvidos com a finalidade de determinar o melhor modelo para o ajuste de curvas granulométricas. Neste trabalho, objetivou-se a seleção de modelos para o traçado de curvas granulométricas de sedimentos em suspensão em rios; utilizando-se 30 amostras contendo de 8 a 10 pontos medidos, testaram-se 14 diferentes modelos. A comparação entre os modelos foi baseada na diferença da soma do quadrado dos erros entre os valores observados e os ajustados, cujos resultados indicaram que os modelos Haverkamp & Parlange (1986) e Skaggs et al. (2001), ambos com 3 parâmetros de ajuste, são os melhores para o traçado das curvas granulométricas de amostras de sedimentos em suspensão em rios.
hidrossedimentologia; hidrossedimentometria; curvas de crescimento
The knowledge about particle-size distribution of suspended sediments in river is fundamental for some hydro-sedimentological studies. In general, the techniques used to determine the particle-size distribution of a sample results in pointwise values, demanding a subsequent interpolation to fit the complete particle-size distribution curve and to obtain specific characteristic diameters values. The transformation of discrete points into continuous functions can be made by mathematical models. However, few studies have been developed with the purpose of determining the best model for fitting particle-size distribution curves. The objective of this paper was to select models for fitting particle-size distribution curves of suspended sediments in river water. Using the particle-size distribution, results from 30 samples of suspended sediments of river with 8 to 10 measured points, with 14 different models were tested. The parameter used to compare the models was the sum of the square errors between the measured and calculated values obtained in the adjustment of each model. The results showed that the Haverkamp & Parlange (1986) and Skaggs et al. (2001) models, both with three fitting parameters, are the best for adjusting particle-size distribution curves of river suspended sediment samples.
hydro-sedimentology; hydro-sedimentometry; growth curves
GESTÃO E CONTROLE AMBIENTAL
Seleção de modelos para o traçado de curvas granulométricas de sedimentos em suspensão em rios
Selection of models for adjusting particle size distribution curves of suspended sediments in river
Jorge E. F. W. Lima; Euzebio M. da Silva
EMBRAPA Cerrados. BR 020, km 18, CP 08223, CEP 73301-970, Planaltina, DF. Fone: (61) 3388-9894. E-mail: jorge@cpac.embrapa.br; euzebio@cpac.embrapa.br
RESUMO
O conhecimento da distribuição granulométrica dos sedimentos em suspensão em cursos d'água é fundamental para a realização de estudos hidrossedimentológicos. As técnicas geralmente utilizadas para a avaliação da distribuição granulométrica de amostras de sedimentos resultam em valores pontuais, dependendo de posterior interpolação para o traçado da curva granulométrica e para a obtenção de diâmetros característicos específicos. A transformação de valores pontuais em funções contínuas pode ser realizada por meio de modelos matemáticos; entretanto, são poucos os estudos desenvolvidos com a finalidade de determinar o melhor modelo para o ajuste de curvas granulométricas. Neste trabalho, objetivou-se a seleção de modelos para o traçado de curvas granulométricas de sedimentos em suspensão em rios; utilizando-se 30 amostras contendo de 8 a 10 pontos medidos, testaram-se 14 diferentes modelos. A comparação entre os modelos foi baseada na diferença da soma do quadrado dos erros entre os valores observados e os ajustados, cujos resultados indicaram que os modelos Haverkamp & Parlange (1986) e Skaggs et al. (2001), ambos com 3 parâmetros de ajuste, são os melhores para o traçado das curvas granulométricas de amostras de sedimentos em suspensão em rios.
Palavras-chave: hidrossedimentologia, hidrossedimentometria, curvas de crescimento
ABSTRACT
The knowledge about particle-size distribution of suspended sediments in river is fundamental for some hydro-sedimentological studies. In general, the techniques used to determine the particle-size distribution of a sample results in pointwise values, demanding a subsequent interpolation to fit the complete particle-size distribution curve and to obtain specific characteristic diameters values. The transformation of discrete points into continuous functions can be made by mathematical models. However, few studies have been developed with the purpose of determining the best model for fitting particle-size distribution curves. The objective of this paper was to select models for fitting particle-size distribution curves of suspended sediments in river water. Using the particle-size distribution, results from 30 samples of suspended sediments of river with 8 to 10 measured points, with 14 different models were tested. The parameter used to compare the models was the sum of the square errors between the measured and calculated values obtained in the adjustment of each model. The results showed that the Haverkamp & Parlange (1986) and Skaggs et al. (2001) models, both with three fitting parameters, are the best for adjusting particle-size distribution curves of river suspended sediment samples.
Key words: hydro-sedimentology, hydro-sedimentometry, growth curves
INTRODUÇÃO
A presença de sedimentos nos cursos d'água é conseqüência dos processos erosivos ocorridos nas suas bacias de drenagem. A elevada concentração de sedimentos nos rios pode comprometer ou restringir o uso da água. Projetos de barragens, captações e estações de tratamento de água, por exemplo, são diretamente influenciados pela presença de sedimentos na fonte hídrica, bem como os organismos aquáticos e aqueles que consomem a água em seu estado bruto, diretamente do rio.
O transporte de sedimentos pela água é regido pela relação entre a capacidade de carreamento do escoamento e a força necessária para deslocar as partículas sólidas disponíveis em seu curso. As partículas mais finas e leves, como as argilas e siltes, precisam de menos energia que as partículas de areia para serem carreadas. Escoamentos muito velozes e turbulentos possuem grande capacidade de carreamento de sedimentos, sendo pouco seletivos, ou seja, deslocam sedimentos finos e grossos. À medida que a velocidade do escoamento diminui, o transporte de sedimentos se torna mais seletivo; assim, os processos de erosão, transporte e deposição de sedimentos são dependentes da granulometria do material particulado presente na bacia.
A descarga sólida total em uma seção transversal de um curso d'água é o somatório da descarga de sedimentos em suspensão e da descarga de sedimentos do leito. A separação da medição se deve ao fato das forças de resistência ao movimento envolvidas nos processos de transporte em suspensão e no leito serem diferentes (Carvalho et al., 2000). Existem métodos diretos e indiretos para a determinação da descarga sólida total de uma seção, porém, devido à dificuldade de obtenção de dados e aos custos envolvidos, os indiretos são os mais utilizados. Segundo Dinehart (1997), os dados comumente requeridos para o uso de métodos indiretos de cálculo da descarga sólida total são: a vazão líquida, a concentração de sedimentos em suspensão, a distribuição granulométrica dos sedimentos em suspensão, a distribuição granulométrica dos sedimentos do leito, a declividade da linha d'água e a temperatura da água. Os métodos apresentados por Einstein (1950), por Colby & Hembree (1955) e por Stevens & Yang (1989), que estão entre os mais utilizados, confirmam a colocação de Dinehart (1997).
Em geral, as técnicas utilizadas para a avaliação da distribuição granulométrica de amostras resultam em valores pontuais, dependendo de posterior interpolação para o traçado da curva granulométrica e a obtenção de diâmetros característicos específicos. Esta interpolação é feita, muitas vezes, de forma gráfica, podendo representar fonte de erro nas etapas de desenho da curva e de leitura da medida. Este procedimento, por sua vez, pode resultar na obtenção de diferentes respostas a partir de uma mesma base de dados, o que pode ser solucionado com a utilização de modelos matemáticos.
A transformação de valores pontuais em funções contínuas pode ser realizada utilizando modelos matemáticos; entretanto, poucos estudos têm sido desenvolvidos com a finalidade de se determinar o melhor modelo para o ajuste de curvas granulométricas. Hwang et al. (2002) destacaram as funções log-normais e as do tipo curvas de crescimento como as freqüentemente utilizadas para representar curvas granulométricas de partículas de solo. Ressalta-se que os modelos mais adequados à representação da curva granulométrica devem ser capazes de traçar uma função contínua em forma de "S", a exemplo dos modelos de curvas de crescimento descritos por Naime et al. (2001), Fredlund et al. (2000), Haverkamp & Parlange (1986), Lima & Silva (2002), entre outros.
Hwang et al. (2002) realizaram estudo comparando 7 modelos: 5 log normais, com 1, 2 e 3 parâmetros (Buchan et al., 1993); Gompertz (1825), com 4 parâmetros (Nemes et al., 1999); e Fredlund, com 4 parâmetros (Fredlund et al., 2000), utilizando 1.387 amostras de solos coreanos. Esses autores concluíram que: o modelo de Fredlund apresentou o melhor desempenho na maioria dos solos estudados, tendo sua performance melhorada com o incremento no teor de argila; e o modelo de Gompertz, mesmo com quatro parâmetros, foi apenas um pouco melhor que os demais, com 2 e 3 parâmetros. Observaram, ainda, variações no desempenho de ajuste dos modelos em função da classe de solo analisada, o que foi confirmado por Hwang (2004).
O trabalho realizado por Hwang et al. (2002) representa importante contribuição na comparação de modelos para o traçado da curva granulométrica, porém seu estudo é relativamente incompleto visto que outros modelos, potencialmente adaptáveis a esta finalidade, não foram contemplados; além disso, a comparação direta entre modelos com diferente número de parâmetros pode favorecer aos que os têm em maior quantidade, tornando duvidosas as suas conclusões em relação ao desempenho dos modelos testados. Hwang (2004) avaliou o efeito da textura na performance de 9 modelos; entretanto, mais uma vez comparou modelos com diferentes números de parâmetros, o de Fredlund et al. (2000) com 4 e os demais com 2 ou 3.
Silva et al. (2004), trabalhando com base de dados granulométricos de 130 solos brasileiros com apenas 4 pontos medidos, avaliaram 14 modelos diferentes para o ajuste de suas curvas e concluíram que, apesar da melhor classificação, o modelo de Skaggs et al. (2001), com dois parâmetros e modificações propostas por Silva et al. (2004), em alguns casos, falhou em reproduzir o traçado sigmoidal esperado, sendo o seu emprego recomendado com ressalvas; desta forma, foram indicados, como os mais recomendados para tal fim, os seguintes modelos: Skaggs et al. (2001), Lima & Silva (2002), Weibull (1951) e Morgan et al. (1975), todos com 3 parâmetros.
Silva et al. (2004) utilizaram amostras com apenas 4 frações granulométricas medidas e, normalmente, nos trabalhos laboratoriais com dados de sedimentos de rios, obtém-se um número maior de pontos da curva. Essa diferença no número de pontos utilizados para o traçado da curva pode resultar em uma nova classificação dos melhores modelos para tal finalidade.
Neste trabalho, objetivou-se a seleção de modelos para o traçado de curvas granulométricas de sedimentos suspensos em rios.
MATERIAL E MÉTODOS
Para confecção deste trabalho, utilizaram-se resultados de análises granulométricas de 30 amostras de sedimentos em suspensão, coletadas na Bacia Araguaia-Tocantins, no ano 2000, pela empresa Hidroesb, a serviço da Engevix. O método utilizado para determinação da distribuição granulométrica dessas amostras foi o do tubo de remoção pela base (Carvalho et al., 2000). A variabilidade granulométrica das amostras utilizadas pode ser observada na Figura 1.
Como se observa na Figura 1, há grande variabilidade na distribuição granulométrica das amostras, o que é favorável para o estudo pretendido, uma vez que os modelos serão testados para diferentes tipos de curvas; outra constatação advinda da análise da Figura 1 é que os diâmetros das partículas foram sempre inferiores a 0,2 mm, indicando que as amostras se compõem de partículas de argila, silte e areia fina.
Os dados apresentados na Figura 1 foram utilizados para o ajuste de 14 modelos matemáticos do tipo curva de crescimento (Tabela 1). A comparação entre os modelos foi baseada na diferença da soma de quadrado dos erros verificados entre os valores observados e os ajustados. Diferentemente de Silva et al. (2004), que trabalharam com amostras de solo que tiveram apenas 4 frações granulométricas levantadas, as amostras de sedimentos em suspensão em rios utilizadas neste estudo apresentam de 8 a 10 pontos observados.
Para determinação dos parâmetros de ajuste dos modelos aos pontos medidos da curva, utilizou-se a rotina "Solver" do programa Microsoft Excel. A função-objetivo do processo de otimização foi descrita de forma a minimizar a soma de quadrados dos erros (SQerro) entre os valores observados e os calculados das freqüências acumuladas. Tratando-se de uma otimização de modelos não-lineares, a escolha dos valores iniciais dos parâmetros a serem ajustados foi fundamental para a convergência do processo de otimização para o mínimo global. Desta forma, os valores iniciais dos parâmetros para a otimização foram estimados com auxílio gráfico, observando-se a proximidade entre a curva gerada e os pontos medidos. Para garantir que o resultado obtido era realmente o mínimo global, o procedimento de otimização foi repetido até a estabilização do resultado da SQerro; nos casos em que a curva ajustada divergia substancialmente dos pontos observados, a otimização foi refeita com outras estimativas iniciais na expectativa de melhoria do resultado.
Para permitir a comparação entre os modelos sob uma mesma base, os resultados de SQerro obtidos com cada modelo foram normalizados por meio da divisão do valor encontrado pela respectiva média geral dos SQerro dos trinta ajustes efetuados. Os valores normalizados foram ordenados e separados em 6 classes (Iman & Conover, 1983), as quais tiveram suas freqüências e probabilidades acumuladas de ocorrência determinadas. Os 6 intervalos de valores de SQerro normalizados e respectivas probabilidades acumuladas de ocorrência foram dispostos em gráfico, possibilitando a identificação do tipo de distribuição estatística que melhor representa essa relação. Analisando-se a disposição dos 84 pontos do gráfico, 6 pontos por modelo, definiu-se a provável distribuição capaz de representar a probabilidade de ocorrência dos valores de SQerro; em seguida, comprovou-se, estatisticamente, por meio da medida de correlação entre os valores observados da probabilidade acumulada e os calculados pelo modelo de distribuição, se a proposição era realmente válida; além disso, efetuou-se um teste qui-quadrado para a verificação da aderência do modelo aos pontos (Levin, 1987).
Uma vez definido o modelo que representa a distribuição da probabilidade de ocorrência dos valores de SQerro, para cada modelo, gerou-se uma curva de distribuição deste parâmetro. A disposição das curvas geradas em um mesmo gráfico possibilitou uma classificação preliminar dos modelos, pois, quanto mais à esquerda a curva, menor o valor de SQerro médio obtido pelo modelo, portanto, mais adequado é ele para o ajuste dos dados medidos. Destaca-se que o SQerro médio da distribuição estatística foi determinado pelo método dos mínimos quadrados, utilizando-se procedimentos de otimização não-linear disponíveis do programa Microsoft Excel. O teste da razão de verossimilhança (Silva & Azevedo, 2002) foi aplicado para verificar se os resultados dos modelos foram estatisticamente diferentes a 5% de probabilidade.
RESULTADOS E DISCUSSÃO
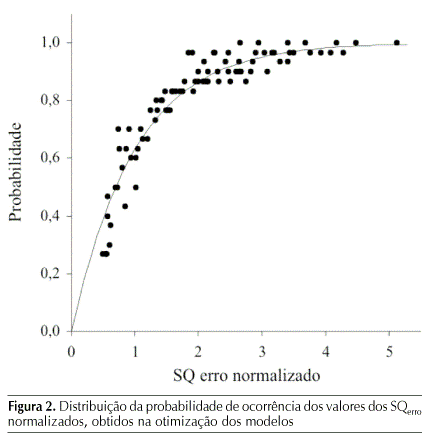
Apresenta-se, na Figura 2, a distribuição dos pontos correspondentes às probabilidades acumuladas de ocorrência dos valores dos SQerro normalizados, resultantes da otimização dos 14 modelos avaliados.
Analisando-se a disposição dos pontos apresentados na Figura 2, verificou-se que a distribuição exponencial é a que melhor os representa, fato este que pode ser comprovado estatisticamente por meio da medida da correlação entre os valores observados e os calculados da probabilidade acumulada, que foi de 95,61%; outrossim, o teste Qui-quadrado de aderência (Levin, 1987) confirmou que a distribuição exponencial representa, realmente, a população de dados observados.
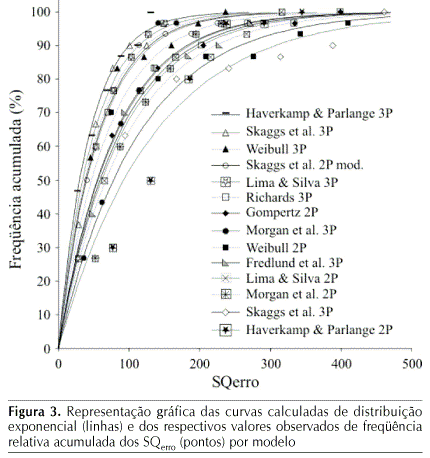
A distribuição exponencial correspondente a cada modelo ficou então estabelecida como: Freqüência acumulada de ocorrência de SQerro = 1 - EXP(-SQerro/SQerro médio). Os resultados obtidos no ajuste dos 14 modelos analisados encontram-se ilustrados na Figura 3, em que os pontos do gráfico representam os valores observados de freqüência relativa acumulada das 6 classes em que foram distribuídos os SQerro de cada modelo e as curvas, o ajuste dos pontos pelo modelo de distribuição exponencial.
Na Figura 3, quanto mais próxima está a curva do eixo das ordenadas, menor o valor do SQerro médio do modelo e, conseqüentemente, melhores são os seus resultados obtidos no ajuste das curvas granulométricas. Para permitir melhor interpretação da Figura 3, sua legenda foi disposta em ordem crescente de classificação dos modelos; assim, o modelo Haverkamp & Parlange 3P foi o que apresentou, em termos médios, o melhor ajuste das curvas granulométricas analisadas, sendo representado pela curva mais à esquerda da figura; por sua vez, o modelo Haverkamp & Parlange 2P foi o que mostrou os piores resultados, sendo representado pela curva que está mais distante do eixo das ordenadas.
Para verificar se os resultados dos modelos foram significativamente diferentes a 5% de probabilidade, utilizou-se o teste da razão de verossimilhança (Silva & Azevedo, 2002) entre as amostras, duas a duas, cujos resultados são apresentados na Tabela 2.
Pode-se observar, na Tabela 2, que os resultados dos modelos Haverkamp & Parlange 3P e Skaggs et al. 3P não diferem significativamente entre si a 5% de probabilidade; portanto, segundo os resultados obtidos, esses são os dois modelos mais recomendados para o traçado de curvas granulométricas de sedimentos em suspensão com o número de pontos medidos variando entre 8 e 10. Os modelos Weibull 3P, Skaggs et al. 2P (mod) e Lima & Silva 3P também apresentaram bons resultados, demonstrando potencial para execução da tarefa; no entanto, não foram tão bons quanto o melhor modelo.
Merece destaque o resultado obtido pelo modelo Skaggs et al. 2P (mod) que, com apenas 2 parâmetros de ajuste, foi capaz de se classificar entre os melhores modelos, superando, inclusive, modelos de 3 parâmetros, como o Morgan et al. 3P e o Fredlund et al. 3P. Utilizando curvas granulométricas com apenas 4 pontos medidos, Silva et al. (2004) também detectaram a grande flexibilidade do modelo Skaggs et al. 2P (mod) que, apesar de ter obtido os melhores resultados, teve seu uso recomendado com ressalvas visto que trabalhando com número reduzido de pontos medidos, algumas vezes, a curva ajustada não seguia o traçado sigmoidal esperado. No presente trabalho, utilizando maior número de pontos medidos para o ajuste, de 8 a 10, não se detectou esse tipo de problema. Hwang et al. (2002) também notaram que o maior número de parâmetros do modelo não é garantia de sucesso no ajuste de curvas granulométricas.
A classificação apresentada na Tabela 2 não confirma o resultado do trabalho de Hwang et al. (2002), de que o modelo de Fredlund et al. (2000) é o mais apropriado para o traçado de curvas granulométricas. Entre os modelos com 3 parâmetros de ajuste, ele foi o que apresentou os piores resultados, fato que confirma a hipótese levantada por Silva et al. (2004), de que Hwang et al. (2002) tenham deixado de considerar modelos potencialmente melhores que os utilizados em seu estudo; além disso, ao compararem modelos com diferentes números de parâmetros de ajuste, Hwang et al. (2002) e Hwang (2004) beneficiaram aqueles que tinham maior quantidade de parâmetros de ajuste como, no caso deles, o de Fredlund et al. (2000).
Os modelos recomendados por Silva et al. (2004) para o traçado de curvas granulométricas a partir de 4 pontos medidos foram: Skaggs et al. 3P, Lima & Silva 3P, Weibull 3P e Morgan et al. 3P.
Analisando-se conjuntamente os resultados obtidos neste trabalho e no de Silva et al. (2004), que avaliaram os mesmos modelos, observa-se que, apesar de ter alcançado excelente desempenho na presente avaliação, o modelo Haverkamp & Parlange 3P não está inserido entre os recomendados para o traçado de curvas granulométricas a partir de apenas 4 pontos medidos; o inverso ocorreu com o modelo Morgan et al. 3P, que apresentou melhor classificação com menor número de pontos medidos. Os modelos Skaggs et al. 3P, Lima & Silva 3P e Weibull 3P mostraram bons resultados em ambos os trabalhos, o que os torna passíveis de serem utilizados para o traçado de curvas granulométricas sem maiores restrições com relação ao número de pontos observados. Esses resultados indicam que, apesar do modelo Haverkamp & Parlange 3P ter obtido os melhores ajustes com o número de pontos medidos variando entre 8 e 10, com menor número de pontos, seu uso deve ser visto com restrições.
CONCLUSÕES
1. Os modelos Haverkamp & Parlange 3P e Skaggs et al. 3P são os melhores para o traçado de curvas granulométricas de amostras de sedimentos em suspensão em rios quando o número de pontos levantados varia entre 8 e 10.
2. Os modelos Weibull 3P, Skaggs et al. 2P (mod) e Lima & Silva 3P também apresentaram bons resultados, demonstrando potencial para a execução da tarefa proposta.
AGRADECIMENTOS
À empresa Engevix, pela disponibilização da base de dados granulométricos utilizados na confecção deste trabalho, e ao Dr. Newton de Oliveira Carvalho, pela estimada colaboração.
LITERATURA CITADA
Protocolo 139.05 - 30/09/2005 Aprovado em 31/08/2006
- Buchan, G. D.; Grewal, K. S.; Robson, A. B. Improved models of particle-size distribution: An illustration of model comparison techniques. Soil Science Society of America Journal, Madison, v.57, n.4, p.901-908, 1993.
- Carvalho, N. O.; Filizola Jr., N. P.; Santos, P. M. C.; Lima, J. E. F. W. Guia de práticas sedimentométricas. Brasília: ANEEL, 2000. 154p.
- Colby, B. R.; Hembree, D. W. Computations of total sediment discharge: Niobrara River near Cody, Nebraska. USGS water supply paper 1357. Washington: USGS, 1955. 187p.
- Dinehart, R. L. Sediment transport at gagging stations near Mount St. Helens, Washington, 1980-90, data collection and analysis: USGS professional paper 1573. Washington: USGS, 1997. http://vulcan.wr.usgs.gov/Projects/Sediment_Trans/ PP1573 /HTMLReport/PP1573.6.html 24 Fev. 2005.
- Einstein, H. A. The bed-load function for sediment transportation in open channel flows. USDA Soil Conservation Service technical bulletin 1026. Washington: USDA, 1950. 65p.
- Fredlund, M. D.; Fredlund, D. G.; Wilson, G. W. An equation to represent grain-size distribution. Canadian Geotechnical Journal, Ottawa, v.37, n.4, p.817-827, 2000.
- Gompertz, B. On the nature of the function expressive of the low of human mortality, and a new mode of determining the value of live contengencies. Philosophical Transactions of Royal Society, London, v.115, n.1, p.513-585, 1825.
- Haverkamp, R.; Parlange, J. Y. Predicting the water-retention curve from particle-size distribution: I. Sandy soils without organic matter. Soil Science Society of America Journal, Madison, v.142, n.6, p.325-339, 1986.
- Hwang, S. I. Effect of texture on the performance of soil particle-size distribution models. Geoderma, Amsterdan, v.123, n.3, p.363-371, 2004.
- Hwang, S. I.; Lee, K. P; Lee, D. S.; Powers, S. E. Models for estimating soil partilce-size distributions. Soil Science Society of America Journal, Madison, v.66, n.4, p.1143-1150, 2002.
- Iman, R. L.; Conover, W. J. A modern approach to statistics, New York: John Wiley & Sons, 1983. 497p.
- Levin, J. Estatística aplicada a ciências humanas. 2.ed. São Paulo: Harbra, 1987. 392p.
- Lima, J. E. F. W.; Silva, E. M. Utilização do modelo modificado de Genuchten para o traçado da curva granulométrica. In: Encontro Nacional de Engenharia de Sedimentos, 5, 2002, São Paulo. Anais... São Paulo: ABRH., 2002, p.121-125.
- Morgan, P. H.; Mercer, L. P.; Flodin, N. W. General model for nutritional responses of higher organisms. Proceedings of the National Academy of Sciences, Stanford, v.72, n.11, p.4327-4331, 1975.
- Naime, J. M.; Vaz, C. M. P; Macedo, A. Automated soil particle size analizer based on gamma-ray attenuation. Computer and Electronics in Agriculture, Amsterdam, v.31, n.3, p.295-304, 2001.
- Nemes, A.; Wösten, J. H. M.; Lilly, A.; Oude Voushaar, J. H. Evaluation of different procedures to interpolate particle-size distribuitions to achieve compatibility within soil databases. Geoderma, Amsterdan, v.90, n.3, p.187-202, 1999.
- Richards, F. J. A flexible growth function for empirical use. Journal of Experimental Botany. v.10. p.290-300, 1959.
- Silva, E. M.; Azevedo, J. A. Influência do período de centrifugação na curva de retenção de água em solos de Cerrado. Pesquisa Agropecuária Brasileira, Brasília, v.37, n.10, p.1487-1494, 2002.
- Silva, E. M.; Lima, J. E. F. W.; Rodrigues, L. N.; Azevedo, J. A. Comparação de modelos matemáticos para o traçado de curvas granulométricas. Pesquisa Agropecuária Brasileira, Brasília, v.39, n.4, p.363-370, 2004.
- Skaggs, T. H.; Arya, L. M.; Shouse, P. J.; Mohanty, B. P. Estimating particle-size distribution from limited soil texture data. Soil Science Society of America Journal, Madison, v.65, n.4, p.1038-1044, 2001.
- Stevens, H. H.; Yang, C. T. Summary and use of selected fluvial sediment-discharge formulas. USGS water resources investigations report 89-4026, Denver: USGS, 1989. 121p.
- Weibull, W. A statistical distribution function of wide applicability. ASME Journal of applied mechanics. p.293-297, 1951.
Datas de Publicação
-
Publicação nesta coleção
07 Mar 2007 -
Data do Fascículo
Fev 2007
Histórico
-
Aceito
31 Ago 2006 -
Recebido
30 Set 2005