Resumos
O presente trabalho propôs estudar a secagem de sálvia a diferentes temperaturas do ar e posterior ajuste dos dados experimentais obtidos com os diferentes modelos matemáticos. Para condução do experimento de secagem foram utilizados 6 secadores de bandeja, empregando-se as temperaturas de 40, 50, 60, 70, 80 e 90 °C. Utilizou-se o delineamento experimental de blocos ao acaso, com três repetições, colocando-se 800 g de folha fresca em cada bandeja. Para o ajuste dos modelos matemáticos aos dados experimentais, realizou-se análise de regressão não-linear, pelo método Quasi-Newton, através do programa computacional Statistica 6.0®, em que os valores dos parâmetros dos modelos foram estimados em função da temperatura do ar de secagem. Os resultados mostraram que pequenos incrementos no valor da temperatura do ar de secagem promovem redução significativa no tempo de secagem. O modelo de Henderson & Pabis (1961) modificado e o de Midilli et al. (2002) se mostraram adequados para descrever o processo de secagem de sálvia para a faixa de temperatura de 40 a 90 °C, enquanto os modelos da aproximação da difusão e o de dois termos, se mostraram adequados para descrever a cinética de secagem para a faixa de temperatura de 60 a 90 °C.
plantas medicinais; desidratação; modelos matemáticos; Salvia officinalis L
The aim of this work was to study the drying of sage at different air temperatures and to fit the experimental data with different mathematical models. The experiments were carried out using 6 tray dryers, for the temperatures of 40, 50, 60, 70, 80 and 90 °C. A randomized experimental design, with three replications, using 800 g of fresh leaves in each tray, was used. For the fitting of mathematical models to the experimental data the non-linear regression by the Quasi-Newton method was used. The values of the parameters of the models were estimated in terms of drying air temperature using the software Statistica 6.0®. The results showed that small increments in drying air temperature of drying results in a significant reduction in the drying time; the model of Henderson and Pabis (1961) modified model and the Midilli et al. model (2002) were adequate to describe the drying of sage in the temperature range of 40 to 90 °C; and the model of approximation of diffusion and the two terms model were adequate to describe the kinetics of drying in the range of temperature from 60 to 90 °C.
medicinal plants; dehydration; mathematical models; Salvia officinalis L
ARMAZENAMENTO E PROCESSAMENTO DE PRODUTOS AGRÍCOLAS
Análise da cinética de secagem de folhas de sálvia1 1 Projeto com apoio da FAPERGS, edital PROCOREDES III
Drying kinetics analysis of sage leaves
Lauri L. RadünzI; Altemir J. MossiI; Cláudio A. ZakrzevskiII; Antonio S. do AmaralII; Lucas GrassmannIII
IUFFS, Campus de Erechim, Av. Dom João Hoffmann, 313, CEP 99700-000, Erechim, RS, Fone: (54) 3522-6598; 3522-8115, E-mail: laurilr@uffs.edu.br; altemirmossi@pq.cnpq.br
IIURI, Campus de Erechim, CEP 99700-000, Erechim, RS, Fone: (54) 3520-9000, E-mail: amossi@uri.com.br; caz@uri.com.br; asamaral@uri.com.br
IIITécnico Agrícola, URI, Erechim, Fone: (54) 3321-1943, E-mail: grassmann@uri.com.br
RESUMO
O presente trabalho propôs estudar a secagem de sálvia a diferentes temperaturas do ar e posterior ajuste dos dados experimentais obtidos com os diferentes modelos matemáticos. Para condução do experimento de secagem foram utilizados 6 secadores de bandeja, empregando-se as temperaturas de 40, 50, 60, 70, 80 e 90 °C. Utilizou-se o delineamento experimental de blocos ao acaso, com três repetições, colocando-se 800 g de folha fresca em cada bandeja. Para o ajuste dos modelos matemáticos aos dados experimentais, realizou-se análise de regressão não-linear, pelo método Quasi-Newton, através do programa computacional Statistica 6.0®, em que os valores dos parâmetros dos modelos foram estimados em função da temperatura do ar de secagem. Os resultados mostraram que pequenos incrementos no valor da temperatura do ar de secagem promovem redução significativa no tempo de secagem. O modelo de Henderson & Pabis (1961) modificado e o de Midilli et al. (2002) se mostraram adequados para descrever o processo de secagem de sálvia para a faixa de temperatura de 40 a 90 °C, enquanto os modelos da aproximação da difusão e o de dois termos, se mostraram adequados para descrever a cinética de secagem para a faixa de temperatura de 60 a 90 °C.
Palavras-chave: plantas medicinais, desidratação, modelos matemáticos, Salvia officinalis L.
ABSTRACT
The aim of this work was to study the drying of sage at different air temperatures and to fit the experimental data with different mathematical models. The experiments were carried out using 6 tray dryers, for the temperatures of 40, 50, 60, 70, 80 and 90 °C. A randomized experimental design, with three replications, using 800 g of fresh leaves in each tray, was used. For the fitting of mathematical models to the experimental data the non-linear regression by the Quasi-Newton method was used. The values of the parameters of the models were estimated in terms of drying air temperature using the software Statistica 6.0®. The results showed that small increments in drying air temperature of drying results in a significant reduction in the drying time; the model of Henderson and Pabis (1961) modified model and the Midilli et al. model (2002) were adequate to describe the drying of sage in the temperature range of 40 to 90 °C; and the model of approximation of diffusion and the two terms model were adequate to describe the kinetics of drying in the range of temperature from 60 to 90 °C.
Key words: medicinal plants, dehydration, mathematical models, Salvia officinalis L.
INTRODUÇÃO
A sálvia (Salvia officinalis L) da família Lamiaceae, é originária do Mediterrâneo e se adapta à região sul do Brasil. É considerada aromática e com propriedades medicinais, possibilitando seu uso como condimento e na medicina doméstica (Martins et al., 1998). Trata-se de uma planta medicinal muito popular, que há décadas vem sendo estudada, em virtude dos componentes antioxidantes, além de amplamente usada para tratamento de vários grupos de doenças, preparação de alimentos, fabricação de cosméticos, perfumes e produtos de higiene (Cuvelier et al., 1996).
Conforme Di Stasi (1996), no Brasil, cerca de 20% da população consomem 63% dos medicamentos disponíveis e o restante encontra, nos produtos de origem natural, especialmente nas plantas medicinais, a única fonte de recurso terapêutico.
Simal et al. (2000) obtiveram as curvas de secagem de aloé (Aloe barbadensis Miller) com teor de água inicial de aproximadamente 98% e final de 33% b.s. e concluíram que o período de secagem a taxa constante não foi observado mas apenas o período difusional; apesar disto, importante influência da temperatura no aumento da taxa de secagem pode ser notada, com exceção para a secagem a 80 °C; esta redução na taxa de secagem foi atribuída ao fato de que a temperatura superior a 70 °C causa endurecimento da superfície do produto dificultando o fenômeno de difusão de umidade.
Para a secagem de cardamomo-gigante (Amomum subulatum Roxburgh), Rao et al. (2001) utilizaram um secador dotado de resistência elétrica para aquecimento do ar de secagem. As condições experimentais foram: ar aquecido a 70, 82 e 90 °C e vazão do ar de secagem de 0,46, 0,58 e 0,69 m3 min-1, sendo que o produto apresentava umidade inicial de aproximadamente 80% e final de 10% b.u.; eles observaram que a declividade da curva de secagem foi constante até determinado tempo de secagem e, então, decresceu, indicando duas regiões de secagem, ou seja, o período de taxa constante e o período de taxa decrescente de secagem.
As características da secagem de folhas de Cymbopogon citratus (D.C.) Stapf em camada delgada foram estudadas por Martinazzo et al. (2007) para a faixa de temperatura de 30 a 60 °C, utilizando modelos semiteóricos e empíricos. Os modelos avaliados foram: exponencial, Page, Page modificado, Thompson, difusão oito termos, Henderson & Pabis (1961), logarítmico, dois termos, exponencial de dois termos, Wang & Singh (1978), Henderson & Pabis (1961), Midilli et al. (2002) e aproximação da difusão; notaram, então, que o modelo de Midilli et al. (2002) foi o que melhor se ajustou aos dados experimentais, apresentando o maior coeficiente de determinação e menor erro médio estimado.
Com o objetivo de ajustar modelos matemáticos aos dados experimentais, Barbosa et al. (2007) utilizaram folhas de erva-cidreira-brasileira, colhidas com teor de água em torno de 85% b.u. as quais foram submetidas a secagem em secador de plantas medicinais, com ar em temperatura de 40, 50, 60, 70 e 80 °C e velocidade de 0,29 + 0,03 m s-1. Para cada teste de secagem foram utilizados 400 g de folhas em camada de 0,15 m de espessura, e realizados três testes para cada temperatura. Aos dados experimentais se ajustaram diversos modelos de cinética de secagem, dentre eles, Henderson & Pabis (1961), Henderson & Pabis modificado, Midilli et al. (2002), Page (1949) e Wang & Singh (1978), concluindo que os modelos de Page (1949) e Midilli et al. (2002) representaram melhor a secagem de erva-cidreira-brasileira.
Arslan & Özcan (2008) realizaram a secagem de folhas de alecrim (Rosmarinus officinalis L., Lamiaceae) ao sol, em forno (50 °C) e em micro-ondas (700 W, 2450 MHz); esses autores avaliaram diversos modelos matemáticos para ajustá-los aos dados experimentais de secagem, e concluíram que o modelo logarítmico de Midilli e de Küçük apresentou ajuste adequado aos dados experimentais de secagem de folhas de alecrim quando secado ao sol e na estufa; já para a secagem em forno de micro-ondas os modelos de Page, Page modificado, Midilli et al. (2002) apresentaram o melhor ajuste de dados experimentais.
Um experimento de secagem em camada delgada com capim limão foi realizado por Ibrahim et al. (2009), com o objetivo de verificarem o efeito da temperatura e da umidade do ar na cinética de secagem, em que os autores empregaram três temperaturas de secagem (35, 45 e 55 °C) e três valores de umidade relativa (30, 40 e 50%), com velocidade do ar em 1 m s-1, ajustaram 4 modelos matemáticos semiteóricos aos dados experimentais, sendo: Newton, Henderson & Pabis (1961), Page e Page modificado, e concluíram que todos os modelos apresentaram ajuste satisfatório; entretanto, o modelo Newton apresentou o melhor ajuste entre os modelos estudados.
Assim, o presente trabalho teve por objetivo estudar a secagem de sálvia a diferentes temperaturas do ar e posterior ajuste dos dados experimentais obtidos a diferentes modelos matemáticos.
MATERIAL E MÉTODOS
Utilizou-se, para realização do trabalho de secagem, a sálvia (Salvia officinalis L.). A espécie foi cultivada na área experimental da Universidade Regional Integrada do Alto Uruguai e das Missões, Campus II, de Erechim, RS.
A coleta foi realizada no início do florescimento, no horário das 7 às 8 h, cortando-se as plantas a aproximadamente 10 cm acima do solo. O material, após a coleta, era encaminhado ao laboratório de secagem para a seleção e a homogeneização. No processo de seleção eram retiradas partes doentes e danificadas, assim como qualquer material estranho presente e só então as plantas foram picadas em pedaços de no máximo 10 cm, sem se remover as folhas do caule; após esta etapa as plantas eram homogeneizadas.
O teor de água foi determinado imediatamente após a homogeneização do material e, também, ao final do processo de secagem, empregando-se o método gravimétrico. Utilizou-se a metodologia recomendada pela ASAE (2000), com aproximadamente 25 g de amostra para cada uma das três subamostras, mantendo-se o material em estufa com circulação forçada do ar a temperatura de 103 ± 2 °C, durante 24 h.
Com referência à condução do experimento de secagem, foram usados 6 secadores, todos constituídos de 1 bandeja na câmara de secagem, cuja fonte de aquecimento foi um conjunto de resistência elétrica. O ajuste do valor desejado para a temperatura foi realizado através de um controlador automático de temperatura. Para os tratamentos de secagem foram utilizadas as seguintes temperaturas: 40, 50, 60, 70, 80 e 90 °C, todas com variação de ± 2 °C.
A câmara de secagem de cada secador era composta de bandeja construída em aço inoxidável, com dimensões de 0,30 m de lado e 0,50 m de altura. As temperaturas do ar ambiente, de secagem e de exaustão, foram monitoradas através de termopares tipo "J", acopladas a um microcomputador via sistema de aquisição de dados field logger, em que os valores foram armazenados neste microcomputador.
Mediu-se a velocidade do ar com um anemômetro de fio quente, com intervalo de leitura de 0,05 m s-1, determinada acima da bandeja em que se encontrava o produto, a qual foi mantida em aproximadamente 0,5 m s-1, controlando-se o fluxo de entrada de ar na câmara de secagem.
Utilizou-se o delineamento experimental de blocos ao acaso, com três repetições, sendo que cada bloco foi constituído de uma data de coleta.
Para calcular a umidade de equilíbrio empregou-se o modelo ajustado por Kouhila et al. (2001) para esta espécie, conforme apresentado na Eq. 1.

(1)
sendo:
Ue - umidade de equilíbrio, %b.s.
T - temperatura do ar, °C
UR - umidade relativa do ar na câmara de secagem, decimal
k, c, n - parâmetros que dependem da natureza do produto
Calculou-se a razão de umidade (RU) do produto para o tempo t, conforme apresentado na Eq. 2.

(2)
sendo:
RU - razão de umidade, adimensional
Ux - teor de água do produto no tempo x, %b.s.
Ue - umidade de equilíbrio, %b.s.
U0 - teor de água inicial do produto, %b.s.
Os valores de RU observados para cada temperatura do ar de secagem foram avaliados por 12 diferentes modelos matemáticos de regressão não-linear, conforme a Tabela 1.
Para o ajuste dos modelos matemáticos aos dados experimentais, realizou-se análise de regressão não-linear, pelo método Quasi-Newton, empregando-se o programa computacional Statistica 6.0®, cujos valores dos parâmetros dos modelos foram estimados em função da temperatura do ar de secagem.
A escolha do modelo foi realizada em função do coeficiente de determinação ajustado (R2), do erro médio relativo (EMR), do erro médio estimado (EME) e pela análise dos resíduos.
O erro médio relativo e o erro médio estimado para cada modelo foram calculados conforme demonstrado nas Eqs. 3 e 4, respectivamente.

(3)

(4)
sendo:
n - número de observações
Y - valor observado
Y0 - valor estimado pelo modelo
GLM - graus de liberdade do modelo
RESULTADOS E DISCUSSÃO
Constatou-se que os valores da umidade de equilíbrio calculados através do modelo ajustado por Kouhila et al. (2001), foram de: 5,9; 4,3; 3,2; 2,6; 1,8 e 1,3% b.u., respectivamente, para a secagem com ar aquecido a 40, 50, 60, 70, 80 e 90 °C.
Na Tabela 2 são apresentados os valores dos coeficientes de determinação ajustados (R2), dos erros médios relativos (EMR) e dos erros médios estimados (EME), para cada um dos modelos matemáticos avaliados.
Dentre os 12 modelos avaliados e conforme os resultados obtidos para os coeficientes de determinação ajustados tanto para os erros médios relativos como para os erros médios estimados, demonstrados na Tabela 2, apenas o modelo de Henderson & Pabis modificado e o modelo de Midilli et al. (2002) apresentaram ajuste adequado para descrever o processo de secagem de sálvia para a faixa de temperatura estudada (desde 40 até 90 °C). Pode-se observar que o EMR, para ambos os modelos, variou entre 1,82 e 9,49%, e que segundo Aguerre et al. (1989), considera-se que resultados de erro médio relativo (EMR) abaixo de 10% indicam ajuste adequado dos valores observados em relação aos ajustados pelo modelo em questão. Em relação ao coeficiente de determinação (r2), ambos os modelos apresentaram valores elevados, acima de 99%, o que, segundo Madamba et al. (1996) significa um bom ajuste para representação do fenômeno de secagem; quanto aos resíduos, ambos os modelos apresentaram distribuição aleatório, o que é desejável que ocorra.
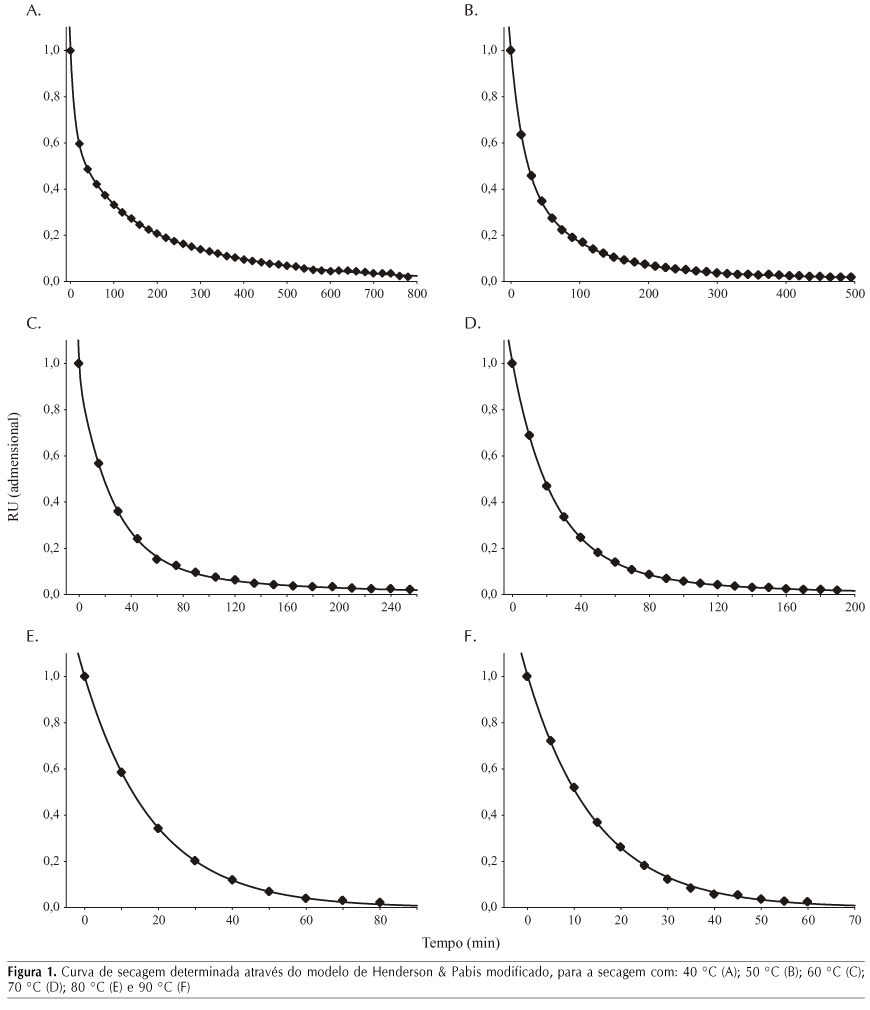
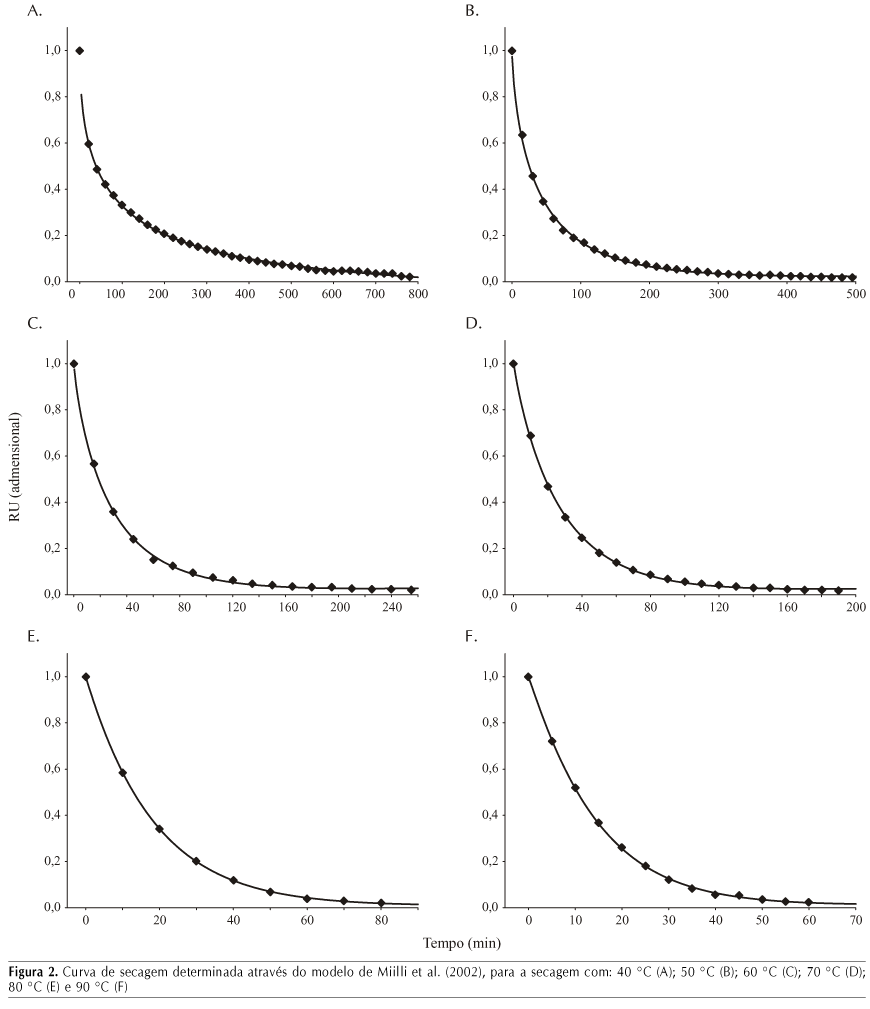
Nas Figuras 1 e 2 estão demonstradas as curvas de secagem observadas durante o processo de secagem, para as seis diferentes temperaturas avaliadas, juntamente com os valores ajustados pelos modelos matemáticos. Como previsto, o tempo de secagem decresce com o aumento da temperatura do ar. Os tempos médios necessários para completar o processo de secagem foram de 780, 495, 255, 190, 80 e 60 min para as temperaturas 40, 50, 60, 70, 80 e 90 °C, respectivamente, cujos resultados estão de acordo com estudos realizados anteriormente para a secagem de produtos vegetais (Mohapatra & Rao, 2005). Esses valores proporcionaram reduções de tempo, quando comparados com a secagem a 40 °C, de aproximadamente: 1,6; 3,1; 4,1; 9,8 e 13,0 vezes, respectivamente, para as temperaturas de secagem com 50, 60, 70, 80 e 90 °C.
Nota-se, porém, que os modelos da aproximação da difusão e o de dois termos, também apresentaram ajuste satisfatório, tanto para o coeficiente de determinação, que foi superior a 0,99, como para o erro médio relativo, exceto para a temperatura do ar de secagem de 50 °C, visto que o erro médio relativo foi superior a 10%. Quanto aos resíduos, os mesmos apresentaram dispersão tendenciosa para os tratamentos de secagem com ar aquecido a 40 e 50 °C e, para os demais tratamentos, dispersão aleatória; desta forma, esses modelos não podem descrever todo o intervalo de temperatura de secagem estudado (40 a 90 °C), mas apenas a faixa de 60 a 90 °C.
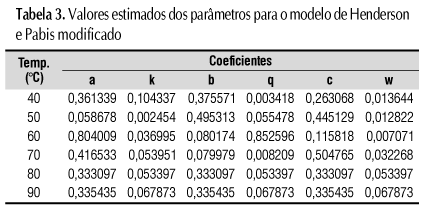
Tem-se nas Tabelas 3 e 4, os valores estimados dos parâmentos para o modelo de Henderson e Pabis modificado e para o modelo de Midilli et al. (2002), pois apenas estes apresentaram ajuste adequado para toda a faixa de temperatura avaliada.
Os resultados corroboram com os obtidos por Martinazzo et al. (2007), que avaliaram as características da secagem de folhas de Cymbopogon citratus (D.C.) Stapf em camada delgada, para a faixa de temperatura de 30 a 60 °C, e concluíram que o modelo de Midilli et al. (2002) foi o que melhor se ajustou aos dados experimentais; resultado semelhante foi constatado por Barbosa et al. (2007), que secaram folhas de erva-cidreira-brasileira com temperatura entre 40 e 80 °C e concluíram que os modelos de Page e Midilli et al. (2002) foram os que representaram a melhor cinética de secagem; já para a secagem de Mentha crispa L., em que usaram temperaturas do ar de 30, 40 e 50 °C, Park et al. (2002) obtiveram o melhor ajuste dos dados com o modelo de Page. Em estudos com chá preto, Temple & Boxtel (1999) e com capim-limão, Martins (2000), concluíram que o melhor ajuste foi obtido com o modelo exponencial de Lewis; portanto, a determinação do modelo matemático depende da espécie de planta, devendo-se realizar estudos individuais para as diversas espécies existentes.
CONCLUSÕES
1. Pequenos incrementos no valor da temperatura do ar de secagem promovem redução significativa no tempo de secagem.
2. O modelo de Henderson & Pabis (1961) modificado e o de Midilli et al. (2002), se mostraram adequados para descrever o processo de secagem de sálvia para a faixa de temperatura de 40 a 90 °C.
3. O modelo da aproximação da difusão e o de dois termos se mostraram adequados apenas para descrever a cinética de secagem para a faixa de temperatura de 60 a 90 °C.
AGRADECIMENTOS
Os autores agradecem à Secretaria de Ciência e Tecnologia do Estado do Rio Grande do Sul e à FAPERGS, pelo suporte financeiro.
LITERATURA CITADA
Protocolo 045.09 - 03/04/2009 - Aprovado em 26/03/2010
- Aguerre, R. J.; Suarez, C.; Viollaz, P. E. New BET type multi-layer sorption isotherms - Part II: Modelling water sorption in foods. Lebensmittel-Wissenschaft & Technologie, v.22, n.4, p.192-195, 1989.
- Akpinar, E. K.; Bicer, Y. Modelling of the drying of eggplants in thin-layers. International Journal of Food Science and Technology, v.40, n.3, p.1-9, 2005.
- Arslan, D.; Özcan, M. M. Evaluation of drying methods with respect to drying kinetics, mineral content and colour characteristics of rosemary leaves. Energy Conversion and Management, v.49, n.5, p.1258-1264, 2008.
- ASAE - American Society of Agricultural Engineers. Standards Engineering Practices Data: Moisture measurement-forages, ASAE S358.2 DEC99. St. Joseph: American Society of Agricultural Engineers, 2000. p.565-572.
- Barbosa, F. F.; Melo, E. C.; Santos, R. H. S.; Rocha, R. P.; Martinazzo, A. P.; Radünz, L. L.; Gracia, L. M. N. Evaluation of mathematical models for prediction of thin-layer drying of brazilian lemon-scented verbena leaves (Lippia alba (Mill) n.e. Brown). Revista Brasileira de Produtos Agroindustriais, v.9, n.1, p.73-82, 2007.
- Bruce, D. M. Exposed-layer barley drying, three models fitted to new data up to 150 şC. Journal of Agricultural Engineering Research, v.32, p.337-348, 1985.
- Cuvelier, M. E.; Richard, H.; Berset, C. Antioxidative activity and phenolic composition of pilot-plant and commercial extracts of sage and rosemary. Journal of the American Oil Chemists Society, v.73, n.5, p.645-652, 1996.
- Di Stasi, L. C. Plantas medicinas, arte a ciência: Um guia prático de estudo interdisciplinar. São Paulo: UNESP, 1996. 230p.
- Henderson, S. M. Progress in developing the thin layer drying equation. Transactions of the ASAE, v.17, n.6, p.1167-1172, 1974.
- Henderson, S. M.; Pabis, S. Grain drying theory I. Temperature effect on drying coefficient. Journal of Agriculture Engineering Research, v.6, n.3, p.169-174, 1961.
- Ibrahim, M.; Sopian, K.; Daud, W. R. W. Study of the drying kinetics of lemon grass. American Journal of Applied Sciences, v.6, n.6, p.1070-1075, 2009.
- Karathanos, V. T. Determination of water content of dried fruits by drying kinetics. Journal of Food Engineering, v.39, n.4, p.337-344, 1999.
- Kassen, A. S. Comparative studies on thin layer drying models for wheat. In: International Congress on Agricultural Engineering, 13., 1998, Marocco. Proceedings... Marocco, v.6, p.2-6, 1998.
- Kouhila, M.; Belghit, A.; Daguenet, M.; Boutaleb, B. C. Experimental determination of the sorption isotherms of mint (Mentha viridis), sage (Salvia officinalis) and verbena (Lippia citriodora). Journal of Food Engeneering, v.47, n.4, p.281-287, 2001.
- Lewis, W. K. The rate of drying of solids materials. The Journal of Industrial and Engineering Chemistry, v.13, n.5, p.427-432, 1921.
- Madamba, P. S.; Driscoll, R. H.; Buckle, K. A. Thin layer drying characteristics of garlic slices. Journal of Food Engineering, v.29, n.1, p.75-97, 1996.
- Martinazzo, A. P.; Corrêa, P. C.; Resende, O.; Melo, E. C. Análise e descrição matemática da cinética de secagem de folhas de capim-limão. Revista Brasileira de Engenharia Agrícola e Ambiental, v.11, n.3, p.301-306, 2007.
- Martins, E. R.; Castro, D. M.; Castellani, D. C.; Dias, J. E. Plantas medicinais. Viçosa: UFV, 1998. 220p.
- Martins, P. M. Influência da temperatura e da velocidade do ar de secagem no teor e na composição química do óleo essencial de capim-limão (Cymbopogon citratus (D. C.) Stapf). Viçosa: UFV, 2000. 77p. Dissertação Mestrado
- Midilli, A.; Kucuk, H.; Vapar, Z. A new model for single-layer drying. Drying Technology, v.20, n.7, p.1503-1513, 2002.
- Mohapatra, D.; Rao, P. S. A thin layer drying model of parboiled wheat. Journal of Food Engineering, v.66, n.4, p.513-518, 2005.
- O'Callaghan, J. R.; Menzies, D. J.; Bailey, P. H. Digital simulation of agricultural dryer performance. Journal of Agricultural Engineering Research, v.16, n.3, p. 223-244. 1971.
- Overhults, D. D.; White, G. M.; Hamilton, M. E.; Ross, I. J. Drying soybeans with heated air. Transactions of the ASAE, v.16, n.2, p.195-200, 1973.
- Page, G. E. Factors influencing the maximum rates of air drying shelled corn in thin layers. Indiana: Purdue University, 1949. M. Sc. Thesis
- Park, K. J.; Vohnikova, Z.; Brod, F. P. R. Evaluation of drying parameters and desorption isotherms of garden mint leaves (Mentha crispa L.). Journal of Food Engeneering, v.51, n.3, p.193-199, 2002.
- Rao, V. G.; Mande, S.; Kishore, V. V. N. Study of drying characteristics of large-cardamon. Biomass e Bioenergy, v.20, n.1, p.37-43, 2001.
- Sharaf-Elden, Y.I.; Blaisdell, J. L.; Hamdy, M. Y. A model for ear corn drying. Transactions of the ASAE, v.5, n.4, p.1261-1265, 1980.
- Simal, S.; Femenía, A.; Llull, P.; Roselló, C. Dehydration of aloe vera: simulation of drying curves and evaluation of functional properties. Journal of Food Engineering, v.43, n.2, p.109-114, 2000.
- Temple, S. J.; Boxtel, A. J. B. van. Thin layer drying of black tea. Journal Agricultural Engineering Research, v.74, n.2, p.167-176, 1999.
- Togrul, I. T.; Pehlivan, D. Modelling of drying kinetics of single apricot. Journal of Food Engineering, v.58, n.1, p.23-32, 2003.
- Wang, C. Y.; Singh, R. P. Use of variable equilibrium moisture content in modeling rice drying. Transactions of the ASAE, v.78, n.6, p.6505, 1978.
Datas de Publicação
-
Publicação nesta coleção
06 Out 2010 -
Data do Fascículo
Set 2010