Abstract
In this study, the breeding perspectives of 41 open-pollinated progenies of Eucalyptus grandis were evaluated based on their wood traits. The progenies were distributed in two experiments in a randomized complete block design, with three replicates and linear plots containing six plants each. The traits were assessed at eight years of age. Two trees from each plot were selected for this assessment based on better growth, stem form and phytosanity. Significant differences in basic density, sapwood/heartwood ratio, bowing, specific gravity, parallel compression and static bending were detected among the progenies. These traits were potentially promising for breeding programs, with heritability coefficients that varied from 0.34 to 0.61 on a progeny mean basis. There was no genetic variation in the moisture content, board end-splitting, log volume under bark, log eccentricity, bark content, crooking, and shear strength of the progenies. Intermediate to highly significant genetic correlations were detected among the physical and mechanical properties, as well as between pairs of traits such as basic density and log end-splitting, basic density and bowing, specific gravity and bowing, sapwood/heartwood ratio and bowing, log volume and bowing, and log volume and log end-splitting. These results show that the levels of growth stress in trees can be reduced by selection using indirect traits such as the sapwood/heartwood ratio and bowing.
breeding; eucalypt; genetic parameters; wood quality
PLANT GENETICS
RESEARCH ARTICLE
Estimates of genetic parameters of wood traits for sawn timber production in Eucalyptus grandis
Paulo Eduardo Telles dos SantosI; Isaias Olívio GeraldiII; José Nivaldo GarciaIII
IEmbrapa Florestas, Colombo, PR, Brazil
IIUniversidade de São Paulo, Escola Superior de Agricultura Luiz de Queiroz, Departamento de Genética, Piracicaba, SP, Brazil
IIIUniversidade de São Paulo, Escola Superior de Agricultura Luiz de Queiroz, Departamento de Ciências Florestais, Piracicaba, SP, Brazil
Correspondence Correspondence to Paulo Eduardo Telles dos Santos Embrapa Florestas Estrada da Ribeira km 111 Caixa Postal 319, 83411-000 Colombo, PR, Brazil E-mail: peduardo@cnpf.embrapa.br
ABSTRACT
In this study, the breeding perspectives of 41 open-pollinated progenies of Eucalyptus grandis were evaluated based on their wood traits. The progenies were distributed in two experiments in a randomized complete block design, with three replicates and linear plots containing six plants each. The traits were assessed at eight years of age. Two trees from each plot were selected for this assessment based on better growth, stem form and phytosanity. Significant differences in basic density, sapwood/heartwood ratio, bowing, specific gravity, parallel compression and static bending were detected among the progenies. These traits were potentially promising for breeding programs, with heritability coefficients that varied from 0.34 to 0.61 on a progeny mean basis. There was no genetic variation in the moisture content, board end-splitting, log volume under bark, log eccentricity, bark content, crooking, and shear strength of the progenies. Intermediate to highly significant genetic correlations were detected among the physical and mechanical properties, as well as between pairs of traits such as basic density and log end-splitting, basic density and bowing, specific gravity and bowing, sapwood/heartwood ratio and bowing, log volume and bowing, and log volume and log end-splitting. These results show that the levels of growth stress in trees can be reduced by selection using indirect traits such as the sapwood/heartwood ratio and bowing.
Key words: breeding, eucalypt, genetic parameters, wood quality.
Introduction
The genus Eucalyptus is one of the most widely cultivated hardwood genera in tropical and subtropical regions of the world, primarily because of its economic importance. This success largely reflects the adaptability of this genus to a variety of climatic and edaphic conditions, its fast growth, and the versatility and usefulness of its wood for industrial applications. Despite these advantages, eucalypts are prone to suffer strong stresses within the living trees, known as growth stresses (Kubler, 1987), that is reflected in the warping and splitting of logs and boards. Such defects reduce the general quality of the end product and limit the usefulness of the wood. Additional traits that can be important in determining the value of eucalypts wood include its basic density, mechanical properties, and juvenile wood content, all of which can be modified through breeding programs.
Various studies have shown that growth stress is genetically controlled, with considerable natural variability in this trait (Nicholson, 1973; Hillis, 1978; Chafe, 1979; Wilkins, 1986; Malan, 1984, 1988a,b, 1991; Yang and Fife, 2000). Thus, appropriate breeding programs can introduce important genetic gains to minimize the negative effects caused by high levels of growth stress. Quantification of the genetic control of this trait and an understanding of the relationships among the relevant wood properties are important for developing breeding strategies to improve the quality of wood and its usefulness.
Malan and Hoon (1992) found no relationship between growth stress and other traits in E. grandis. Thus, the diameter at breast height (DBH) and tree height showed no relationship with the level of growth stress. However, in wood samples taken from progeny tests, there was significant variation in log end-splitting, with the high heritabilities observed for this trait (up to 0.50) suggesting that this defect was sufficiently inherited to allow its reduction by genetic improvement. Since no relationship was found between the level of growth stress and wood properties, genetic progress may be obtained without any detrimental effects to other wood properties (Malan, 1995). Malan (1988c) reported estimates for the genetic parameters of several tree and wood characteristics in E. grandis grown in South Africa. Significant variation among progenies was found for DBH, total tree height and basic density. The heritability coefficient estimates were 0.30, 0.45 and 0.45, respectively. Genetic correlation estimates among these traits were negative and significant for DBH and basic density (rG = 1.035) and for tree height and basic density (rG = 0.673).
In this study, we estimated the heritability coefficients and examined the genetic and phenotypic correlations and the expected response to selection for selected traits of importance for sawn timber production in Eucalyptus grandis.
Material and Methods
The material used in this study was obtained from two open-pollinated progeny tests of Eucalyptus grandis (Hill ex Maiden), originally from Atherton, Queensland, Australia and of Luís Antônio, São Paulo, Brazil provenance, established at Altinópolis, in the State of São Paulo. The experiments were planted in 1992 and the evaluations were done at 8 years of age. The trials were established using two randomized complete block designs, with 20 and 21 treatments that resulted in a total of 41 progenies. Each trial consisted of three replicates and six-tree linear plots such that the initial stand of each progeny was represented by 18 plants. However, since only two plants from each plot were used in this study, in the end each progeny was evaluated using six-trees, corresponding to those with the best properties for sawn timber based on a combined phenotypic assessment of growth, stem form and phytosanity. The initial spacing was 3 m x 2 m and the survival rate was 70%. The geographic coordinates and the edaphic and climatic characterization of the field trial sites were as follows: latitude 21º04'42"S, longitude 47º22'02"W, altitude 703 m, mean annual rainfall (1994 to 2000) 1,276 mm, frost frequency (1994 to 2000) 2.4 per year, mean annual temperature (1994 to 2000) 23.8ºC, climate Cwa, according to the W. Köppen international classification system, soil quartz sand (Quartzpsament).
The logs were obtained using a chainsaw for tree felling and stem partitioning operations, and were converted into boards using an industrial sawmill. The primary mechanical processing was done with a twin band saw and the secondary processing was done with a two-shaft circular saw. Boards 260 cm long, 2.54 cm thick and 10-15 cm wide were obtained by regulating the twin band saw gauge, depending on the log diameter. One log and three disks per tree were used to characterize the experimental material (Figure 1).
Log evaluation
Log volume under the bark: The diameter under the bark was measured for each log end, and the corresponding areas under the bark for each end, as well as the average area of the ends, were estimated. The log volume was then obtained by multiplying the average area by the length of the log.
Sapwood/heartwood ratio: The heartwood area was calculated from the average diameter of the heartwood and the sapwood area was the difference between the area under the bark and heartwood area. The final ratio was the average of the estimates of heartwood/sapwood ratios based on the areas for the two ends.
Bark content: The bark content was calculated as the difference between the log volumes over and under the bark divided by the log volume over the bark.
Eccentricity: This was estimated as the quotient between the largest and the smallest radii obtained from the largest diameter for each log end. The final eccentricity was the average of the values for the two ends.
Log end-splitting index (LESI): The log end-splitting index was assessed in each log end using the method of Conradie (1980), within a maximum time interval of 6 h after felling. The final LESI was the average of the values for the two log ends.
Disk evaluation
Basic density: The basic density was determined in disks 2-3 cm thick that were free of bark. Two wedges were obtained from opposite each other in each disk and the basic density was determined using the water displacement method. The basic density of the disk was calculated as the average density of the two wedges.
Moisture content: The moisture content was estimated by weighing the two disk wedges remaining from the previous step packed in impermeable plastic bags. After weighing in a moist state, the wedges were oven-dried until a constant weight was reached. The difference between the wet and dry weights divided by dry weight corresponded to the moisture content in percentage.
Board evaluation
Bowing deflection and crooking deflection: The deflections were measured in each board using a section of aluminum (3.5 m x 2.5 cm x 5 cm) as a fixed reference. The deflection readings were obtained by placing the aluminum section an equal distance from the board ends. The average bowing and crooking deflections were obtained for each log as the sum of each type of deflection divided by the number of boards.
Board end-splitting index in green condition (BESI-G) and board end-splitting index in dried condition (BESI-D): The longest splits, parallel to the board axis, were measured at the top and bottom positions of each board obtained from the main block of every log (the number of boards ranged from 3 to 7, depending on the minimum diameter of the log). The indexes were calculated by dividing the length of splits altogether by the number of boards, in the green and dried conditions, respectively.
Physical and mechanical properties: Samples obtained from the outer board of each log were used to determine the physical and mechanical properties after the boards had been naturally dried during 5 months followed by a complementary drying process in an industrial kiln during 4 days in order to reach a final humidity of ~12%. The samples were prepared from the central part of the boards and were free of any defect. One sample with dimensions appropriate for each test was obtained from each log, as follows: specific gravity and parallel compression 3 cm x 2 cm x 2 cm, shear strength 3 cm x 2 cm x 2 cm (with an area to be ruptured of 4 cm2 and a protrusion of 0.5 cm from the main block), and static bending 20 cm x 2 cm x 2 cm. The mechanical tests were done in a universal testing device. The load speeds applied were: parallel compression 4,000 N/min, shear strength 1,000 N/min, and static bending 500 N/min. The rupture load readings were obtained and the tension values at the resistance limits were computed using the appropriate formulas for each situation, as described by Santos et al. (2003).
Statistical and genetic analysis
The statistical model for traits evaluated at a single position in trees was Yij(m) = µ + tm + pi(m) + rj(m) + eij(m), where Yij(m) is the value of progeny i in replicate j within the respective experiment m, µ is the general mean of the combined analysis, tm is the effect of experiment m (m1 = 1 and m2 = 2), assumed to be fixed, pi(m) is the effect of progeny i (i1 = 1,...,p1; i2 = 1,...,p2) within the respective experiment (m1 or m2), assumed to be random, rj(m) is the random effect of replication j (j = 1,...,r) within the experiment and eij(m) is the experimental error, with the assumption of eij ~ N (0; s 2).
The statistical model for traits evaluated at two or three positions in trees was Yijk(m) = µ + tm + pi(m) + rj(m) + eij + hk(m) + ejk + (ph)ik(m) + eijk(m) , where Yijk(m) is the value of progeny i in replicate j at position k within the respective experiment m,µ is the general mean of the combined analysis, tm is the effect of experiment m (m1 = 1 and m2 = 2), assumed to be fixed, pi(m) is the effect of progeny i (i1 = 1,...,p1; i2 = 1,...,p2) within the respective experiment (m1 or m2), assumed to be random, rj(m) is the random effect of replicate j (j = 1,...,r) within the experiment, eij = e(a) is the experimental error of the plot units, with the assumption of eij ~ N (0; s 2e(a)), hk(m) is the effect of position k (k = 1,...,h) within the experiment, assumed to be fixed, ejk = e(b) is the experimental error of the subplot units, with the assumption of ejk ~ N (0; s 2e(b)), (ph)ik(m) is the effect of interaction between progeny i (i1 = 1,...,p1; i2 = 1,...,p2) and position k (k = 1,...,h) within the respective experiment (m1 or m2), assumed to be random, and eijk(m) = e(c) is the experimental error of the combination of progeny and position effects, with the assumption of eijk ~ N (0; s 2e(c)).
The data were analyzed using the general linear model (GLM) procedure of SAS® software. Variance component estimates were obtained by applying the MIXED procedure, followed by the option REML (restricted maximum likelihood variance components estimation procedure).
The genetic coefficient of variation was estimated by the expression  where
where  is the genetic variance estimate among progenies and
is the genetic variance estimate among progenies and  is the general mean. The heritability coefficient among progeny means was estimated by the expression
is the general mean. The heritability coefficient among progeny means was estimated by the expression  where
where  is the genetic variance among progenies and
is the genetic variance among progenies and  is the phenotypic variance among progeny means. The confidence intervals at the 95% probability level associated with the heritability coefficient estimates were determined according to the method of Knapp et al. (1985). The genetic gain for each trait was estimated as
is the phenotypic variance among progeny means. The confidence intervals at the 95% probability level associated with the heritability coefficient estimates were determined according to the method of Knapp et al. (1985). The genetic gain for each trait was estimated as  and
and  where ds is the differential of selection,
where ds is the differential of selection,  is the heritability coefficient among progeny means and
is the heritability coefficient among progeny means and  is the general mean.
is the general mean.
The analysis of covariance for pairs of traits was based on the same model used for univariate analysis of variance, following the basic methodology proposed by Vencovsky and Barriga (1992), but excluding the fixed effect "position". The genetic correlation among progenies was estimated as  where Côvp(x,y) is the genetic covariance among progenies for the traits "x" and "y",
where Côvp(x,y) is the genetic covariance among progenies for the traits "x" and "y",  (x) is the genetic standard deviation among progenies for the trait "x" and
(x) is the genetic standard deviation among progenies for the trait "x" and  is the genetic standard deviation among progenies for the trait "y". The phenotypic correlation among progeny means was estimated as
is the genetic standard deviation among progenies for the trait "y". The phenotypic correlation among progeny means was estimated as  where
where  is the phenotypic covariance among progeny means for the traits "x" and "y",
is the phenotypic covariance among progeny means for the traits "x" and "y",  (x) is the phenotypic standard deviation among progeny means for the trait "x" and
(x) is the phenotypic standard deviation among progeny means for the trait "x" and  (y) is the phenotypic standard deviation among progeny means for the trait "y".
(y) is the phenotypic standard deviation among progeny means for the trait "y".
Results and Discussion
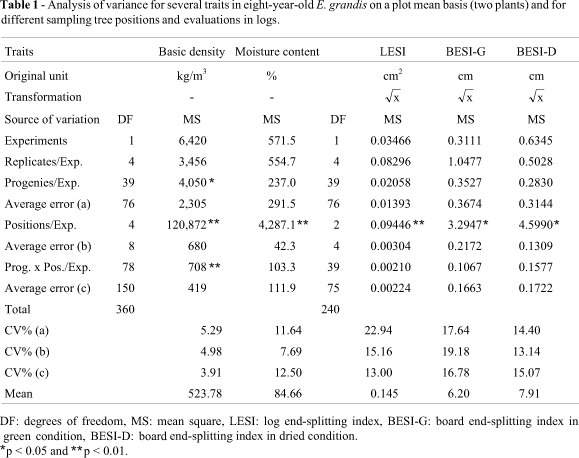
No significant differences were detected for most of the traits among the progenies of E. grandis studied here (Tables 1 and 2). However, significant differences were detected for basic density, sapwood/heartwood ratio, bowing, specific gravity, parallel compression and static bending. Therefore, for breeding purpose, these were the traits that initially were most promising for selection.
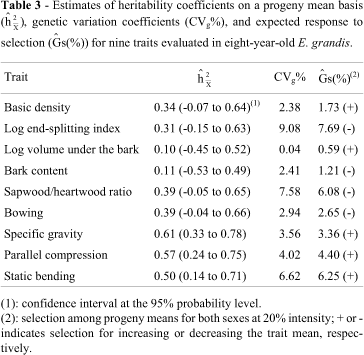
The estimated heritability coefficients on a progeny mean basis are shown in Table 3 for the traits basic density (h2 = 0.34), LESI (h2 = 0.31), sapwood/heartwood ratio (h2 = 0.39), bowing (h2 = 0.39), specific gravity (h2 = 0.61), parallel compression (h2 = 0.57) and static bending (h2 = 0.50). For the other traits, the estimates were very low and non-significant. In general, the estimated genetic coefficients of variation were also very low. This could have been caused by the preliminary selection of trees within the experimental plots prior to evaluation. The traits LESI, sapwood/heartwood ratio and static bending showed the highest estimated coefficients of genetic variation (9.08%, 7.58% and 6.62%, respectively).
The expected genetic gains from the selection for each trait based on progeny means and at a selection intensity of 20% ranged from 0.59% to 7.69% (Table 3). These values were compatible with the genetic variation found in this population and corresponded to selection in both sexes, with the intercrossing of only selected trees. This finding indicates that a clonal seed orchard would be appropriate to capture the expected gains. Based on an analysis of isoenzyme variability, Morán and Bell (1983) and Mori (1993) reported outcrossing rates of 84% and 88% for E. grandis, indicating the presence of a certain degree of endogamy. According to Resende et al. (1995), these genetic responses to selection correspond to immediate gains that are valid only for the first generation of recombination since a new equilibrium would be reached only after a few generations of outcrossing because of the relatively low inbreeding rate of this species.
The BESI-G and BESI-D were unable to discriminate the progenies under the two conditions of humidity (Table 1), and it was impossible to obtain valid heritability estimates for these parameters, thus indicating that these variables could be seriously affected by uncontrolled factors attributable mainly to imperfections in mechanical processing, drying effects and physical shocks. These traits are therefore not recommended as useful parameters for selection in breeding programs.
Garcia et al. (2001) reported that lowering the distribution gradient of the tension and compression stresses and producing more uniform wood properties along the longitudinal axis of the tree are also essential for reducing splitting and bowing.
The genetic correlations among progenies and the phenotypic correlations among progeny means (Table 4) were estimated only for pairs of traits of interest for breeding purposes. The genetic and phenotypic correlations between log volume under the bark and basic density were practically null (r = 0.008 and 0.030, respectively), indicating that these traits could be selected independently. In contrast, the genetic and phenotypic correlations between basic density and specific gravity were highly positive (r = 0.750 and 0.682, respectively), which explains the similar pattern of association of these two parameters in relation to parallel compression and static bending, two mechanical properties that are strongly influenced by the former parameters. These relationships are easily explained by the fact that fiber and vessel wall thicknesses, as well as lumen diameter, change according to the wood density or specific gravity. Thus, wood samples with a higher density or specific gravity contain fewer empty intracellular spaces and a more compact arrangement of the structural anatomical elements (fibers and vessels). This results in greater resistance to mechanical force, whereas wood of lower density tends to be less resistant to such force.
The genetic correlation between basic density and LESI was positive and intermediate (r = 0.439), while the phenotypic correlation was positive but low (r = 0.206). The genetic correlation between log volume under the bark and LESI was positive and intermediate (r = 0.405), whereas the phenotypic correlation between these two parameters was slightly higher (r = 0.332). Hence, selecting for an increase in wood density and tree volume may negatively affect log end-splitting since a reduction in this trait is desirable.
The genetic correlation between log volume under the bark and bowing was negative and intermediate (r = 0.623), and the phenotypic correlation was also negative and low (r = 0.144). From the point of view of an increase in tree diameter, greater dimensions may decrease the growth stress gradient between the tension and compression zones within the bole, thereby reducing the internal strength that causes board bowing. This approach should be considered as a plausible explanation for the existence of a highly positive genetic correlation between the sapwood/heartwood ratio and bowing (r = 0.924) and also for the positive phenotypic correlation between these traits (r = 0.326). Since bowing is an indicator of the original level of stress within the tree, it is desirable to select genotypes with lower values for this trait. The sapwood/heartwood ratio should be used as an indirect trait to facilitate the selection procedures. This trait provides an indication of the amount of wood recently formed during secondary growth of the stem relative to that formed in the early stages of the tree life cycle. Heartwood generally has more stable physical and mechanical properties that represent important advantages when selecting trees for sawn timber production. Selecting trees with a lower sapwood/heartwood ratio is particularly important since growing trees soon leave the juvenile stage and begin to form adult wood of better quality at an earlier stage.
The genetic correlation between the LESI and bowing was negative and low (r = 0.252) and the phenotypic correlation was virtually null (r = 0.054). The genetic and phenotypic correlations between specific gravity and bowing were positive and of intermediate and low magnitude (r = 0.518 and 0.237, respectively). Finally, the genetic correlation between basic density and bowing was highly positive (r = 1.053), while the phenotypic correlation was positive and intermediate (r = 0.359). Whereas the correlation between basic density and LESI was positive and intermediate, that between basic density and bowing was more pronounced. These findings showed that both the LESI and bowing were good indicators of the level of growth stress in these trees. In this regard, bowing is a more appropriate trait for an indirect assessment of growth stress, primarily because of its lower vulnerability to errors during evaluation. Since the population showed an adequate basic density for sawn timber, there is little need to modify this parameter. By not interfering with this parameter, one also avoids a negative effect on the LESI and bowing.
The intermediate to highly positive genetic correlations seen between basic density and bowing and between specific gravity and bowing suggested that a mutual dependence between these traits. Since board bowing is an indirect indicator of growth stress, we concluded that the magnitude of growth stress was influenced by wood density. The same pattern of variation was seen for the correlation between basic density and the LESI, although of lower magnitude. This correlation reinforced the supposition that wood density was genetically closely related to the level of growth stress in this population.
In general, the main aspects considered in eucalypts breeding programs designed to improve the production of sawn timber are an increase in wood volume per tree and refinement of the physical and mechanical properties of the wood to enhance its final use. Several studies have shown that growth rate and the main properties of wood (most of them directly dependent on the basic density) have no phenotypic and/or genetic relationship to the levels of growth stress in the tree (Malan, 1979, 1988b, 1991; Malan and Hoon, 1992; Schacht et al., 1998). In the present study, the phenotypic correlations generally showed the same pattern, particularly when the LESI was used as an indirect variable to assess growth stress. This finding was supported by the correlations between the log volume under the bark and the LESI and between basic density and the LESI, both of which were non-significant (Table 4). Although growth rate and wood density can be negatively correlated (Malan, 1988b, 1991), several studies in eucalypts have shown that this relationship is sometimes weak (Greaves et al., 1997; Tibbits and Hodge, 1998) or that the traits are unrelated to each other (Malan, 1993; DeBell et al., 2001). As already mentioned, the genetic and phenotypic correlations between the log volume under the bark and basic density were practically null. In a coetaneous population of trees such as studied here, the individual volume of each tree represents its rate of growth, and this allows direct comparisons with the results of other studies.
For the population investigated here, joint selection for a high growth rate, a wood density adjusted for the final intended use, and a low level of growth stress would be difficult because of the correlations among these parameters. Ideally, during selection, an appropriate balance between the basic density, bowing and the LESI should be reached in order to provide wood with the desired properties. One possible strategy would be to increase the basic density a little without causing significant losses to bowing and the LESI, both of which are closely related to sawn timber production. The negative genetic correlation seen between log volume under the bark and bowing tends to favor an increase in wood production and a decrease in the level of growth stress.
Based on the strength of the correlations for several of the heritability coefficients estimated here, some of the traits examined have good prospects for use in breeding programs designed to improve the quality of wood for mechanical processing, especially considering the ease with which they can be measured. This was particularly the case for the sapwood/heartwood ratio, bowing and specific gravity. Although the use of genetic correlations as a tool for selecting appropriate traits can create some problems, overall this approach generally facilitates the selection procedure. The strategy chosen may involve an increase in the volumetric production of wood and a decrease in the sapwood/heartwood ratio, in association with the low selection intensity of basic density or specific gravity. Such an approach would be expected to result in significant gains in wood productivity and timber quality.
In summary, the ideotype of eucalyptus trees studied here can be described as highly vigorous, with good stem formation, a high growth rate, a low sapwood/heartwood ratio, intermediate wood density (or specific gravity), minimal log end-splitting and low board bowing. Appropriate selection for these traits should help to improve the final quality of timber obtained from eucalypt trees.
Acknowledgements
The authors thank Celina Ferraz do Valle, César Augusto V. Bonine, Marcelo Onuki, Votorantim Celulose e Papel and Eucatex S/A Indústria e Comércio for the technical and operational support they provided during this work.
Received: October 8, 2003; Accepted: May 25, 2004
Associate Editor: Marcio de Castro Silva Filho
- Chafe SC (1979) Growth stress in trees. Aust For Res 9:203-223.
- Conradie WE (1980) Utilization of South African grown Eucalyptus grandis (W. Hill ex Maiden) as veneer logs. Part 1: Control of end splitting in veneer logs. Special Report n. 206, National Timber Research Institute/CSIR, Pretoria, 27 pp.
- DeBell DS, Keyes CR and Gartner BL (2001) Wood density of Eucalyptus saligna grown in Hawaiian plantations: Effects of silvicultural practices and relation to growth rate. Aust For 64:106-110.
- Garcia JN, Crêspo EA and Baillères H (2001) Influence of log characteristics and machines performance on Eucalyptus board end splitting and board deflections. In: Szymani R (ed) Proceedings of The 15th International Wood Machining Seminar, Los Angeles, USA, pp 163-171.
- Greaves BL, Borralho NMG, Raymond CA, Evans R and Whiteman P (1997) Age-age correlations in, and relationships between basic density and growth in Eucalyptus nitens Silvae Genet 46:264-270.
- Hillis WE (1978) Wood quality and utilization. In: Hillis WE and Brown AG (eds) Eucalypts for Wood Production. 2nd edition. CSIRO, Adelaide, pp 259-289.
- Knapp SJ, Stroup WW and Ross WM (1985) Exact confidence intervals for heritability on a progeny mean basis. Crop Sci 25:192-194.
- Kubler H (1987) Growth stresses in trees and related wood properties. For Abst 48:131-189.
- Malan FS (1979) The control of end splitting in sawlogs: A short literature review. S Afr For J 109:14-18.
- Malan FS (1984) Studies on the phenotypic variation in growth stress intensity and its association with tree and wood properties of South African grown Eucalyptus grandis (Hill ex Maiden). PhD thesis, University of Stellenbosch, Stellenbosch.
- Malan FS (1988a) Wood density variation in four trees of South African grown Eucalyptus grandis (Hill ex Maiden). S Afr For J 144:36-42.
- Malan FS (1988b) Relationships between growth stress and some tree characteristics in South African grown Eucalyptus grandis S Afr For J 144:43-46.
- Malan FS (1988c) Genetic variation in some growth and wood properties among 18 full-sib families of South African grown Eucalyptus grandis: A preliminary investigation. S Afr For J 146:38-43.
- Malan FS (1991) Variation, association and inheritance of juvenile wood properties of Eucalyptus grandis Hill ex Maiden with special reference to the effect of rate of growth. S Afr For J 157:16-23.
- Malan FS (1993) The wood properties and qualities of three South African-grown eucalypt hybrids. S Afr For J 167:35-44.
- Malan FS (1995) Eucalyptus improvement for lumber production. In: IPEF, IPT, IUFRO and ESALQ (eds) Anais do Seminário Internacional de Utilização da Madeira de Eucalipto para Serraria, São Paulo, Brazil, pp 1-19.
- Malan FS and Hoon M (1992) Effect of initial spacing and thinning on some wood properties of Eucalyptus grandis S Afr For J 163:13-20.
- Morán GF and Bell JC (1983) Eucalyptus. In: Tanksley DS and Orton TJ (eds) Isozymes in Plant Genetics and Breeding - Part B, Elsevier, Amsterdam, pp 423-441.
- Mori ES (1993) Variabilidade genética isoenzimática em uma população de Eucalyptus grandis Hill ex Maiden submetida a diferentes intensidades de seleção. Doctoral thesis, Universidade de São Paulo, Piracicaba, SP.
- Nicholson JE (1973) Growth stress differences in eucalypts. For Sci 19:169-174.
- Resende MDV, Vencovsky R and Fernandes JSC (1995) Selection and genetic in populations of Eucalyptus with mixed mating system. In: Proceedings of the IUFRO Conference on Eucalypt Plantations: Improving Fibre Yield and Quality. Hobart, Australia, pp 191-193.
- Santos PET, Geraldi IO and Garcia JN (2003) Estimates of genetic parameters for physical and mechanical properties of wood in Eucalyptus grandis Sci For 63:54-64.
- Schacht L, Garcia JN and Vencovsky R (1998) Genetic variation of growth stress indicators in clones of Eucalyptus urophylla Sci For 54:55-68.
- Tibbits W and Hodge G (1998) Genetic parameters and breeding value predictions for Eucalyptus nitens wood fiber production traits. For Sci 44:587-598.
- Vencovsky R and Barriga P (1992) Genética Biométrica no Fitomelhoramento. Sociedade Brasileira de Genética, Ribeirão Preto, 486 pp.
- Wilkins AP (1986) Nature and origin of growth stresses in trees. Aust For 49:56-62.
- Yang JL and Fife D (2000) Wood properties of three provenances of plantation-grown Eucalyptus globulus Labill. I. Growth strain. In: Proceedings of the IUFRO Conference on The Future of Eucalypts for Wood Products, Launceston, Australia, pp 301-309.
Publication Dates
-
Publication in this collection
14 Jan 2005 -
Date of issue
2004
History
-
Accepted
25 May 2004 -
Received
08 Oct 2003