Abstract
Conservation genetics has been focused on the ecological and evolutionary persistence of targets (species or other intraspecific units), especially when dealing with narrow-ranged species, and no generalized solution regarding the problem of where to concentrate conservation efforts for multiple genetic targets has yet been achieved. Broadly distributed and abundant species allow the identification of evolutionary significant units, management units, phylogeographical units or other spatial patterns in genetic variability, including those generated by effects of habitat fragmentation caused by human activities. However, these genetic units are rarely considered as priority conservation targets in regional conservation planning procedures. In this paper, we discuss a theoretical framework in which target persistence and genetic representation of targets defined using multiple genetic criteria can be explicitly incorporated into the broad-scale reserve network models used to optimize biodiversity conservation based on multiple species data. When genetic variation can be considered discrete in geographical space, the solution is straightforward, and each spatial unit must be considered as a distinct target. But methods for dealing with continuous genetic variation in space are not trivial and optimization procedures must still be developed. We present a simple heuristic and sequential algorithm to deal with this problem by combining multiple networks of local populations of multiple species in which minimum separation distance between conserved populations is a function of spatial autocorrelation patterns of genetic variability within each species.
biodiversity conservation; population structure; geographic genetics
ANIMAL GENETICS
RESEARCH ARTICLE
Optimization procedures for establishing reserve networks for biodiversity conservation taking into account population genetic structure
José Alexandre Felizola Diniz FilhoI, II; Mariana Pires de Campos TellesIII
IUniversidade Federal do Goiânia, Instituto de Ciências Biológicas, Departamento de Biologia Geral, Goiânia, GO, Brazil
IIUniversidade Católica de Goiás, Departamento de Biologia, Goiânia, GO, Brazil
IIIUniversidade Católica de Goiás, Departamento de Zootecnia e Instituto do Trópico Subúmido, Goiânia, GO, Brazil
Send correspondence to Send correspondence to José Alexandre Felizola Diniz Filho Universidade Federal do Goiânia, Instituto de Ciências Biológicas, Departamento de Biologia Geral Caixa Postal 131 74001-970 Goiânia, GO, Brazil E-mail: diniz@icb.ufg.br
ABSTRACT
Conservation genetics has been focused on the ecological and evolutionary persistence of targets (species or other intraspecific units), especially when dealing with narrow-ranged species, and no generalized solution regarding the problem of where to concentrate conservation efforts for multiple genetic targets has yet been achieved. Broadly distributed and abundant species allow the identification of evolutionary significant units, management units, phylogeographical units or other spatial patterns in genetic variability, including those generated by effects of habitat fragmentation caused by human activities. However, these genetic units are rarely considered as priority conservation targets in regional conservation planning procedures. In this paper, we discuss a theoretical framework in which target persistence and genetic representation of targets defined using multiple genetic criteria can be explicitly incorporated into the broad-scale reserve network models used to optimize biodiversity conservation based on multiple species data. When genetic variation can be considered discrete in geographical space, the solution is straightforward, and each spatial unit must be considered as a distinct target. But methods for dealing with continuous genetic variation in space are not trivial and optimization procedures must still be developed. We present a simple heuristic and sequential algorithm to deal with this problem by combining multiple networks of local populations of multiple species in which minimum separation distance between conserved populations is a function of spatial autocorrelation patterns of genetic variability within each species.
Key words: biodiversity conservation, population structure, geographic genetics.
Introduction
One of the fundamental challenges in conservation biology involves the development of theoretical principles and methods for the design of nature reserves (Williams et al., 2004). This is very important because the establishment of reserves is the main strategy adopted by governments to preserve biodiversity, despite many criticisms and potential conflicts with other human activities (Margules and Pressey, 2000; Aaron et al., 2001; Balmford et al., 2001).
The most important criterion to define the reserve system should be to achieve maximum representation of biodiversity but, unfortunately, political and economic interests are usually more important than scientific criteria (Margules and Pressey, 2000). However, since the early 1980s quantitative methods to establish reserve networks that preserves maximum biodiversity at the smallest possible cost have been available (Church et al., 1996; Pressey et al., 1997; Margules and Pressey, 2000; Cabeza and Moilanen, 2001; Williams et al., 2004). In most practical applications, conservation targets are defined as the occurrence of species or, when distributional data are not available, as vegetation types obtained by remote sensing techniques. As recently discussed by Brooks et al. (2004), there is considerable discussion on how hierarchical level biodiversity should be factored into such reserve network models, although there seems to be a consensus that biodiversity patterns are surrogates for population processes and so, when possible, both ecological (abundance, growth rates, demographic stochasticity) and genetic (estimates of inbreeding, gene flow and fitness) data should be incorporate into modeling to ensure the viability of conservation targets (Pressey, 2004).
Despite these theoretical discussions, it is difficult to add complex patterns of biodiversity at multiple hierarchical levels to quantitative models for conservation planning. Under the risk of introducing a false dichotomy, we believe that conservation genetics has been focused on two slightly different, but not mutually exclusive, approaches (for general definitions see Frankham et al., 2002). On the one hand, rare, endemic or endangered species with narrow current geographic ranges have usually been studied to assess population viability, principally by measuring endogamy and trying to link this estimate with other demographic characteristics such as fecundity and mortality and, consequently, to help minimizing their extinction risks. Due to their narrow ranges and conservation status, such species are usually considered priority conservation targets and will be certainly represented in optimally defined reserve designs. On the other hand, for broadly-distributed and abundant species, genetic data is usually used to analyze population structure to allow the identification of evolutionary significant units (ESUs) and management units (MUs) or other phylogeographic patterns, including those that can be associated with habitat loss or fragmentation by human activities (and, of course, viability analysis of specific populations of these species can also be conducted). Although these species are useful in allowing an explicit understanding of evolutionary and ecological processes driving genetic diversity (including those magnified by human actions), they are usually only marginally considered in reserve design processes. Such populations will, of course, be part of optimum designs by default and will be randomly selected in systems due to the broad overall distribution of the species. However, local populations or genetic variants of non-threatened species are usually not explicitly considered as priority targets, even though genetic analyses can show that they could be treated as independent and unique targets in reserve selection models and subjected, as genetic units, to the same persistence problems of narrow-ranged species. So, if population genetic structure is not explicitly incorporated into regional conservation planning, it is not difficult to imagine that endangered species will have more of their (current) genetic diversity preserved than non-threatened species, which will suffer from loss of genetic variability that may be concentrated into a few populations that were not incorporated (by chance alone) into conservation units.
These two views are usually not considered simultaneously in the context of establishing broad-scale, regional conservation planning, despite the large amount of current literature discussing the conservation implications of population and metapopulation genetic structure (see Hanski and Gilpin 1997). Conservation genetics have been focused on the ecological and evolutionary persistence of targets (species or other intraspecific units), especially when dealing with narrow-ranged species and their representation, but no generalized solution for where to concentrate conservation efforts for multiple targets with different genetic characteristics have yet been achieved.
In this paper, we outline a theoretical framework in which these two approaches to conservation genetics could be explicitly incorporated into the broad-scale reserve network models used to optimize biodiversity conservation based on multiple species data.
Principles of reserve network design
Methods to find reserve networks by optimization usually start by asking what is the minimum cost necessary to represent all targets (Williams et al., 2004). One general principle underlying this process is complementarity, which states that different units in the conservation system must try to deal with different targets such that that there is minimum of overlap of targets and minimum redundancy in the system.
In the simplest form, the cost of a reserve network or system may be defined by its total area or simply by the number of reserves (usually of equal size). However, it is not uncommon to include as costs more complex variables that express the difficulty of incorporating a spatial unit into the network, such complex variables including the human population living in the region, price of land, agricultural potential of the area, probability of habitat loss, and even the spatial aggregation of reserves (which minimize transport and other management costs) (Briers, 2002; Chown et al., 2003). On the other hand, conservation targets usually include a list of different species or vegetation types, but can also include other ecological processes or can weight species differentially depending on their endangered status, potential impact on humans or their evolutionary history (Seal et al., 1998; Secherest et al., 2003; Diniz-Filho, 2004).
In a simple example (Figure 1A), if one wants to find the minimum number of sites that represent all four species (targets) in a region to generate an optimum reserve network, two sites must be preserved in order to get at least one population of each species (the minimum representation problem). Although this is a simple example with an intuitive solution, mathematically, this is a problem of integer linear programming (ILP) and can be very complicated when dealing with large matrices and several costs and weights, or when multiple objectives for each target are desired such as the conserve of at least two or three populations of each species.
Mathematically, the information as to whether a species (or any other conservation target) is present or not in a set of sites is contained in a species-by-sites (m x n) matrix A, whose elements (Aij) are unity if a species is present and zero if it is absent. Also, a vector X of dimension n determines whether or not a site is included (also coded as 1 or 0) in the reserve network. Based on these elements, the minimum representation is:
The objective function (1) minimizes the number of sites, whereas inequalities (2) ensure that each species will be represented at least once in the final set of sites. The integral in (3) ensures that each state variable xj is either zero or one, making the problem an integer one (Rodrigues et al., 2000). This problem is NP-complete, so that the difficulty of guaranteeing an optimum solution increases exponentially with the number of targets m. However, different computational algorithms based on heuristic or meta-heuristic procedures can be used to solve this problem. A very simple approach is to use a sequential and heuristic search, the so-called greedy approach (Church et al., 1996; Pressey et al., 1997) which consists of first finding the site with the largest overlap of species (i.e. the site with maximum richness) and choosing it as the first selected site in the network and then assuming that all species present in this site are already preserved. The next step is to choose the site that has maximum richness for species not present in the first site (maximum complementarity), and select it as the next one to be added to the network. The search continues until all species are added to the system. Although this approach is quite simple and can easily be applied to large matrices, it does not produce optimal solutions (Pressey et al., 1997) and standard ILP techniques such as branch-and-bound, or computational techniques such as simulated annealing (Possingham et al., 2000; Cabeza and Moilanen, 2001; Rodrigues et al., 2002a), need to be used to find these optimum solutions. The modeling process can also be improved by adding more elements, such as differential weighting of both conservation targets and sites (for more complex models see Rodrigues et al., 2000). For example, when all targets (species) need to be represented at least b times the inequality (2) becomes
In terms of types of targets, the general idea is to include species as targets (but see Pressey, 2004) based on their distribution maps. However, population level processes can make this decision much more difficult because of issues related both to persistence and representation. For example, Gaston et al. (2001) and Araújo and Williams (2001) both showed that if only distributional data (occurrence of multiple species in a region) is considered optimization procedures based on the complementarity described above tend to find networks whose units are located at the periphery of the range of most species if bounded ecological communities occur in the region concerned (for a more recent approach see also McCarthy et al., 2005). Under classic central-periphery demographic models, the persistence of such species and populations may be problematic, although other models do exist. Alternative models of population structure under other historical scenarios were discussed by Hampe and Petit (2005).
In terms of representation, does defining species as coherent and unique evolutionary units ensure biodiversity representation? In other words, is it enough to conserve one or a few randomly chosen populations of many species, even if they are above the minimum viable population sizes needed for their persistence. We believe that it is not only possible, but better, to define targets within each species taking into account their internal ecological and evolutionary genetic structure and to consider this structure in the reserve design process.
There have been long discussions in conservation genetics about this issue, but centered on the concept of evolutionary significant units (ESUs) and management units (MUs) for intraspecific conservation (for reviews see Crandall et al., 2000; Fraser and Bernatchez, 2001). Also, the population genetic structure of a species is strongly dependent on its breeding system and demographic parameters (Loveless and Hamrick 1984) as well as regional events of historical partition (vicariance) which simultaneously affect multiple species with similar life-history parameters (Avise 2000; Lapointe and Rissler 2005). Thus, our basic aim in this paper is to define how the outcome of these debates can be incorporated into the previously discussed models for reserve network that have been designed to simultaneously conserve multiple species. We suggest two possible solutions, one assuming discrete patterns (the discrete concept) and the other assuming continuous patterns of population structure processes in geographical space (the continuous variation in geographic space concept).
The discrete concept of population genetic structure
The discrete concept refers to the situation when it is possible to clearly allocate the genetic variability of a species distributed in geographic space in such a way that different groups of local populations can be distinguished from each other based on various different criteria. In this case, the solution is straightforward: each of these spatial units must be used as a target in optimization routines so that a species whose range is divided into ki units will have a target equal to at least ki samples spatially structured for species i (Fig. 1B). However, note that this is different from simply increasing the conservation goals for each species as expressed in inequality (2a) because such choices within the ranges of the species are not a simple function of minimum overlap between ranges but instead depend on genetic structure.
A simple variation of conservation goals among species (by creating a parameter b for each species, bi), generated under a linear (or any other function) relationship between the number of population conserved and the intraspecific genetic diversity (say, by increasing the number of conserved populations for species with more genetic variability) would, of course, increase the chance of selecting populations representing different evolutionary units within species. In this case, inequality (2) would be
However, since this model is not spatially explicit about the intraspecific genetic units, it would fail in many situations, depending on the spatial covariation of population genetic structure among units of different species.
The division of the geographic range of a species into multiple units can appear under distinct criteria and by many evolutionary processes but, in general, depends on isolation caused by long-term historical processes such a barrier to gene flow. This will result in relatively high FST values and a clear geographic structure of populations, which could be clearly visualized by clustering and ordination techniques. Distinct phylogeographic units, as defined by Avise (2000), based on mtDNA could be used as conservation targets in the same way as the classical concept of evolutionary significant units based on reciprocal monophyly of mitochondrial haplotypes. Crandall et al. (2000) and Fraser and Bernatchez (2001) discussed the validity of defining ESUs based on only mtDNA.
Under a purely stochastic process of population differentiation by historical isolation, the number of units within a species will increase monotonically with the size of the geographic range to form a broken-stick distribution of fragmented ranges (MacArthur, 1972) in which species with wide geographic ranges are divided more into subunits whereas narrowly distributed species are more genetically homogeneous. As a consequence, there will appear a relationship between the geographic-range size-frequency distribution (RSFD) of targets and the number of reserves in the network designed to conserve the population genetic structure of multiple species.
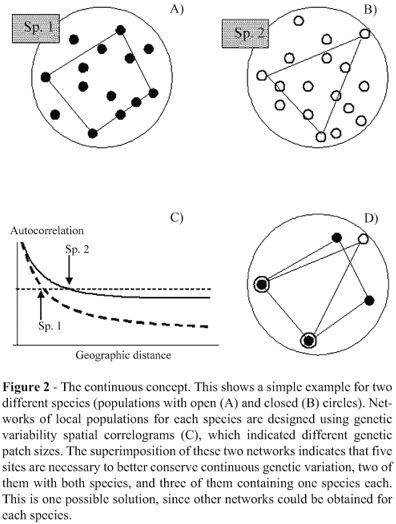
However, the situation is often more complex because barriers can simultaneously affect, or not affect, various species in the system. If the barrier affects gene flow simultaneously in multiple species the subunits for different species will be spatially congruent in such a way that the overall number of reserves in the system will slowly increase in relation to the number of species in the system, this relationship being even more accentuated if the range of the species are more or less of the same size (Figure 2). This increase will be slower than if barriers randomly affect different species because intraspecific spatial units will not be spatially congruent so that the final number of reserves necessary to conserve all species will increase faster in relation to the number of species. This variation in historical effects tends to occur when one is dealing with species with very different life histories and ecological characteristics in such a way that variable population structures within species will be found in the same area.
In some sense, this process is already happening for some taxonomic groups for which the biological species concept is being replaced by phylogenetic concepts to define species, in a process that has recently been called taxonomic inflation (Isaac et al., 2004). For this reason, many recent papers have suggested that conservation targets must be better defined by measurements of phylogenetic diversity and not necessarily by discrete, and often arbitrary, units such as species (Faith, 1992; Crozier, 1997; Rodrigues et al., 2002b; Sechrest et al., 2003; Onal, 2003, Tôrres and Diniz-Filho, 2004; Bickford et al., 2004).
The continuous variation in geographic space of genetic variation
In many situations, genetic variability cannot be partitioned into discrete groups of populations but is a continuous function of geographic space in such a way that statistical and mathematical procedures, including those designed to establish ESUs, used to establish evolutionary units based on discrete structures will not work, generating a recent debate on theory and methods for intraspecific conservation (see Paetkaeu, 1999).
We have previously suggested that statistical analysis of genetic variation by spatial autocorrelation could be useful to define operational units for conservation (Diniz-Filho and Telles, 2002). Spatial autocorrelation measures the similarity between samples for a given variable as a function of spatial distance (Sokal and Oden, 1978a,b; Griffith, 1987; Legendre and Legendre, 1998; Diniz-Filho et al., 2003; Epperson, 2003). For quantitative or continuous variables such as allele frequencies, abundance and species richness Morans coefficient (I) is the most commonly used coefficient in univariate autocorrelation analyses and is given as
where n is the number of samples (local populations), yi and yj are the values of the allele frequencies in populations i and j,  is the average of y and wij is an element of the matrix W. In this matrix, wij = 1 if the pair i, j of local populations is within a given distance class interval (indicating populations that are connected in this class) and wij = 0 when the converse is true. The value of S is the number of entries (connections) in the W matrix. The value expected under the null hypothesis of the absence of spatial autocorrelation is -1/(n - 1). Detailed computations of the standard error of this coefficient are given in Griffith (1987) and Legendre and Legendre (1998).
is the average of y and wij is an element of the matrix W. In this matrix, wij = 1 if the pair i, j of local populations is within a given distance class interval (indicating populations that are connected in this class) and wij = 0 when the converse is true. The value of S is the number of entries (connections) in the W matrix. The value expected under the null hypothesis of the absence of spatial autocorrelation is -1/(n - 1). Detailed computations of the standard error of this coefficient are given in Griffith (1987) and Legendre and Legendre (1998).
Morans I usually varies between -1 for maximum negative autocorrelation and +1 for maximum positive autocorrelation. Non-zero I values indicate that allele frequencies in local populations connected at a given geographic distance are more similar (positive autocorrelation) or less similar (negative autocorrelation) than expected for randomly associated pairs of populations. The geographic distances can be partitioned into discrete classes to create successive W matrices which result in different I values for the same variable and allows autocorrelation to be evaluated as a function of spatial distance using a graph called a spatial correlogram which furnishes a descriptor of the spatial pattern in the data. When multiple allele frequencies are analyzed, average correlograms can be calculated. Alternatively, analogous multivariate correlograms can be computed based on pair-wise genetic distance matrices such as Neis genetic distances, or any other appropriated form, using Mantel tests (Diniz-Filho and Telles, 2002; Telles et al., 2003). A similar reasoning can be based on the procedure proposed by Wagner et al. (2005), who recently generalized variograms based on Analyses of Molecular Variance (AMOVA) to describe continuous genetic structure in microsatellite data.
The basic idea of the procedure devised by us (Diniz-Filho and Telles, 2002) is that the intercept of the spatial correlogram (or the average intercept calculated for many variables), which is the spatial distance at which the autocorrelation statistics become non-significant (hereafter called DC), furnishes a distance at which local populations become statistically independent from each other (see also Diniz-Filho, 2001). Sampling populations separated by this distance will minimize redundancy while at the same time ensuring that a high level of genetic variability is included with less effort. As recently pointed out by Manel et al. (2003) in the context of the new field of landscape genetics, although this procedure still need to be tested and evaluated it can furnish an initial basis for working with the continuous distribution of genetic variability and evolutionary processes in geographic space.
To apply the concept of operational units developed by us in the context of multiple species it would be necessary to use an algorithm that finds the minimum number of overlapping sites that are, for each species, situated at a given distance DC defined by the intercept of the correlogram. In a first approximation, if all species have the same DC value as consequence of similar life-histories and ecology affecting the dynamic of genes among local populations in similar ways and if the spatial process is stationary and forms no strong clinal structures (for a discussion of the impact of non-stationary in the method see Telles et al., 2003) the problem is reduced to finding the minimum number of sites (reserves) that conserve all species for a given time and in which all reserves are situated at least at a distance DC from each other. In this case the number of local populations to be conserved within each species will be a function of the size range, since larger ranges can be covered with more populations situated at a distance DC apart. Again, if the RSFD is constant (i.e. all species have approximately the same range), the number of populations to be conserved within each species is given by the ratio between DC and the range extent (defining the parameter b in inequality 2b). The overall problem is also reduced to finding the minimum number of reserves that conserve all species a given time when all reserves are situated at least at a distance DC from each other. This could be easily implemented in standard conservation planning programs such as SITES by defining the minimum separation distance based on the DC value established by autocorrelation analysis.
However, in empirical situations, none of these three assumptions of the initial approximation will hold (i.e., DC -values are not the same for all species, genetic variability is not stationary for all species and RSFD is not a constant) so much more complex optimization models with explicit spatial structure should be developed to deal with these three cases.
Explicit spatial models for reserve design are still in their infancy and have usually focused on the problem of the spatial aggregation of reserves because of the need to minimize management costs (Briers, 2002; Williams et al., 2004). For the working problem we proposed, it would be necessary to find explicit combinations of populations of all species in such a way that distances between reserves are situated at a given distance that respect DC values for each species within the reserve. The number of populations to be conserved for each species vary and are given by a complex function of the species DC value and the extent of occurrence when all species are considered simultaneously. Mathematically, the objective function (1) could be rewritten as
were pi can assume values of 0 or 1 indicating if, for species i , the site j is important or not, in the sense of obeying the minimum distance DC(i) from other sites previously established for the species i. Of course, this function must work under an explicit spatial configurations and, in certain conditions, it may fail to achieve a minimum representation because the result will tend to zero if there is little spatial congruence between the genetic structures of different species. Probably it would be necessary to relax the minimum distance DC i iteratively to obtain a solution.
Despite the complexity of this explicit spatial model, we can suggest a simple sequential heuristic algorithm to deal with this situation, as follows:
1. Calculate the spatial correlogram for each species of interest and establish its DC -values by averaging correlograms of different allele frequencies, intercepts or by combining multiple variables into genetic distances and then calculating a multivariate correlogram;
2. Based on DC -values and species distribution, calculate all (or many) possible networks for each species, defining multiple possible population of each species as conservation targets;
3. Superimpose the multiple solutions for all species, trying to find best overlap of networks of target populations of all species and then defining the sites for reserves;
A statistical approach could also be adopted to choose between combination of networks, by incorporating a confidence interval of distances among populations, that could be established based on multiple errors of DC. However, the entire procedure can be very complex if multiple networks exist for each species (once again, a function of DC in relation to range extent) and if many species and many local populations are analyzed. A small hypothetical example is shown in Figure 2 showing one network for each of the two species in a system. This sequential and heuristic algorithm will almost certainly produce a sub-optimal solution, but computational procedures such as simulated annealing and genetic algorithms could be adapted to search multiple combinations of networks among species and tentatively find the best combinations of sites by avoiding local minimums.
Concluding Remarks
In this paper we discussed some procedures that can be used to take into account genetic population structure in the modern methods used for the spatial design of conservation reserves. The methods discussed focus mainly on the improved representation of biodiversity, since a single population cannot fully represent a broadly-distributed species. If we consider also that overall genetic variability and a more balanced overall heterozygosity can diminish the risk of the extinction of a species, then the approaches proposed here are also important for species persistence.
Methods based on discrete genetic units are relatively simple and can easily be implemented in the standard software for conservation planning based on meta-heuristic procedures, such as SITES, SPOTand C-PLAN, or on linear optimization solutions such as CPLEX. However, methods for dealing with continuous genetic variation within populations are not trivial and optimization procedures must still be developed.
More importantly, the data necessary to incorporate population genetic structure into models is not generally available at present because for any given region the population genetic structure of all species defined as conservation targets should be known based on multiple samples well distributed in geographic space. We hope that a better understanding of the methods and the urgent need for these data to improve conservation planning can furnish guidelines for future research programs in molecular and population genetics. Of course, even if a few species among the targets have been studied, their genetic structure could be taken into account. Genetic data could then play a more explicit and integrating role in conservation, focused not only on the survival of a few flagship populations or species but as a part of general programs to improve the representation and persistence of the entire regional biodiversity.
Acknowledgments
This work was supported by a PRONEX program of the Brazilian agency CNPq / SECTEC-GO (proc. 23234156) for establishing conservation priorities in the Brazilian Cerrado. We thank L. M. Bini and one anonymous reviewer for many suggestions that improved the ideas presented in this paper. Work by JAFDF has been continuously supported by CNPq productivity fellowships and by the Brazilian agency Fundação de Amparo à Pesquisa da Universidade Federal de Goiás (FUNAPE/UFG).
Received: February 14, 2005; Accepted: September 21, 2005.
Associate Editor: Sergio Furtado dos Reis
- Aaron GB, Gullison RE, Rice RE and Fonseca GAB (2001) Effectiveness of parks in protecting tropical biodiversity. Science 291:125-128.
- Araújo MB and Williams PH (2001) The bias of complementarity hotspots toward marginal populations. Conservation Biology 15:1710-1720.
- Avise J. (2000) Phylogeography. Harvard University Press, Cambridge, 447 pp.
- Balmford A, Moore JL, Brooks T, Burgess N, Hansen LA, Williams P and Rahbek C (2001) Conservation conflicts across Africa. Science 291:2616-2619.
- Bickford SA, Laffan SW, de Kok RPJ and Orthia LA (2004) Spatial analysis of taxonomic and genetic patterns and their potential for understanding evolutionary histories. Journal of Biogeography 31:1715-1733.
- Briers RA (2002) Incorporating connectivity into reserve selection procedures. Biological Conservation 103:77-83.
- Brooks T, Fonseca GAB and Rodrigues ASL (2004). Species, data, and conservation planning. Conservation Biology 18:1682-1688.
- Cabeza M and Moilanen A (2001) Design of reserve network and the persistence of biodiversity. Trends in Ecology and Evolution 16:242-248.
- Chown SL, van Rensburg BJ, Gaston KJ, Rodrigues ASL and van Jaarsveld AS (2003) Energy, species richness, and human population size: Conservation implications at a national scale. Ecological Applications 13:1233-1241.
- Church RL, Stoms DM and Davis FW (1996) Reserve selection as a maximal covering location problem. Biological Conservation 76:105-112.
- Crandall KA, Bininda-Emonds ORP, Mace GM and Wayne RK (2000) Considering evolutionary processes in conservation biology. Trends Ecol Evol 15: 290-295.
- Crozier RH (1997) Preserving the information content of species: Genetic diversity, phylogeny and conservation worth. Annu Rev Ecol Syst 28:243-268.
- Diniz-Filho JAF (2001) Phylogenetic autocorrelation under distinct evolutionary processes. Evolution 55:1104-1109.
- Diniz-Filho JAF (2004). Phylogenetic diversity and conservation priorities under distinct models of phenotypic evolution. Conservation Biology 18:698-704.
- Diniz-Filho, JAF and Telles MPC (2002) Spatial autocorrelation analysis and the identification of operational units for conservation in continuous populations. Conservation Biology 16:924-935.
- Diniz-Filho JAF, Bini LM and Hawkins BA (2003) Spatial autocorrelation and red herrings in geographical ecology. Global Ecology & Biogeography 12:53-64.
- Epperson, BK (2003) Geographical Genetics. Princeton University Press, Princeton, 356 pp.
- Faith DP (1992) Conservation evaluation and phylogenetic diversity. Biol Conserv 61:1-10.
- Frankham R, Ballou DJ and Briscoe DA (2003). Introduction to Conservation Genetics. Cambridge University Press, Cambridge, 617 pp.
- Fraser DJ and Bernatchez L (2001) Adaptive evolutionary conservation: Towards a unified concept for defining conservation units. Molecular Ecology 10:2741-2752.
- Gaston KJ, Rodrigues ASL, van Rensburg BJ, Koleff P and Chown SL (2001) Complementary representation and zones of ecological transition. Ecology Letters 4:4-9.
- Griffith DA (1987) Spatial Autocorrelation: A primer. Resource publications in Geography. Association of American Geographers, Washington DC, 92 pp.
- Hampe A and Petit RJ (2005) Conserving biodiversity under climatic change: The rear edge matters. Ecology Letters 8:461-467.
- Hanski IA and Gilpin ME (1997) Metapopulation Biology: Ecology, Genetics and Evolution. Academic Press, Orlando, 453 pp.
- Isaac NJB, Mallet J and Mace GM (2004) Taxonomic inflation: Its influence on macroecology and conservation. Trends in Ecology and Evolution 19:464-469.
- Lapointe F-J and Rissler LJ (2005) Congruence, consensus and the comparative phylogeography of codistributed species in California. Evolution 166:290-299.
- Legendre P and Legendre L (1998) Numerical Ecology. Elsevier, Amsterdan, 853 pp.
- Loveless MD and Hamrick JL (1984) Ecological determinants of genetic structure in plant populations. Annu Rev Ecol Syst 15:65-95.
- MacArthur R (1972) Geographical Ecology. Princeton University Press, Princeton, 269 pp.
- Margules CR and Pressey RL (2000) Systematic conservation planning. Nature 405:243-253.
- McCarthy MA, Thompson CJ and Possingham HP (2005) Theory for designing nature reserves for single species. American Naturalist 165:250-257.
- Manel S, Schwartz MK, Luikart G and Taberlet P (2003) Landscape genetics: Combining landscape ecology and population genetics. Trends in Ecology and Evolution 15:189-197.
- Onal H (2003) Preservation of species and genetic diversity. Amer J Agr Econ 85:437-447.
- Paetkau D (1999) Using genetic to identify intraspecific conservation units: A critique of current proposals. Conservation Biology 13:1507-1509.
- Possingham H, Ball I and Andelman S 2000. Mathematical methods for identifying representative reserve networks. In: Ferson S and Burgman M (eds) Quantitative Methods for Conservation Biology. Springer-Verlag, New York, pp 291-306.
- Pressey RL (2004) Conservation planning and biodiversity: Assembling the best data for the job. Conservation Biology 18:1677-1681.
- Pressey RL, Possingham HP and Day JR (1997) Effectiveness of alternative heuristic algorithms for identifying indicative minimum requirements for conservation reserves. Biological Conservation 80:207-219.
- Rodrigues ASL, Cerdeira JO and Gaston KJ (2000) Flexibility, efficiency, and accountability: Adaptive reserve selection algorithms to more complex conservation problems. Ecography 23:565-574.
- Rodrigues ASL and Gaston KJ (2002a) Optimisation in reserve selection procedures - Why not? Biological Conservation 107:123-129.
- Rodrigues ASL and Gaston KJ (2002b) Maximizing phylogenetic diversity in the selection of networks of conservation areas. Biological Conservation 105:103-111.
- Sechrest W, Brooks TM, Fonseca GAB, Konstant WR, Mittermeier RA, Purvis A, Rylands AB and Gittleman JL (2002) Hotspots and the conservation of evolutionary history. P Natl Acad Sci USA 99:2067-2071.
- Sokal RR and Oden NL (1978a) Spatial autocorrelation in biology. 1. Methodology. Biological Journal of Linnean Society 10:199-228.
- Sokal RR and Oden NL (1978b) Spatial autocorrelation in biology. 2. Some biological implications and four applications of evolutionary and ecological interest. Biological Journal of Linnean Society 10:229-249.
- Telles MPC, Coelho ASG, Chaves LJ, Diniz-Filho JAF and Valva FD (2003) Genetic diversity and population structure of Eugenia dysenterica DC (cagaiteira - Myrtacea) in Central Brazil: Implications for conservation and management. Conservation Genetics 4:685-595.
- Tôrres NM and Diniz-Filho JAF (2004) Phylogenetic autocorrelation and evolutionary diversity of Carnivora (Mammalia) in conservation units of the New World. Genetics & Molecular Biology 27:511-516.
- Wagner HH, Holderegger R, Werth S, Gugerli F, Hoebbe SE and Scheidegger C (2005) Variogram analysis of the spatial genetic structure of continuous populations using multilocus microsatellite data. Genetics 169:1739-1752.
- Williams JC, ReVelle CS and Levin SA (2004) Using mathematical optimization models to design nature reserves. Front Ecol Environ 2:98-105.
Send correspondence to
Publication Dates
-
Publication in this collection
12 June 2006 -
Date of issue
2006
History
-
Accepted
21 Sept 2005 -
Received
14 Feb 2005