Abstract
Comparisons of covariance patterns are becoming more common as interest in the evolution of relationships between traits and in the evolutionary phenotypic diversification of clades have grown. We present parallel analyses of covariance matrix similarity for cranial traits in 14 New World Monkey genera using the Random Skewers (RS), T-statistics, and Common Principal Components (CPC) approaches. We find that the CPC approach is very powerful in that with adequate sample sizes, it can be used to detect significant differences in matrix structure, even between matrices that are virtually identical in their evolutionary properties, as indicated by the RS results. We suggest that in many instances the assumption that population covariance matrices are identical be rejected out of hand. The more interesting and relevant question is, How similar are two covariance matrices with respect to their predicted evolutionary responses? This issue is addressed by the random skewers method described here.
covariance matrix; common principal components; random skewers; New World monkeys; quantitative genetics
EVOLUTIONARY GENETICS
RESEARCH ARTICLE
Research Article Comparing covariance matrices: Random Skewers method compared to the common principal components model
James M. CheverudI; Gabriel MarroigII
IDepartment of Anatomy and Neurobiology, Washington University School of Medicine, Saint Louis, MO, USA
IIDepartamento de Genética e Biologia Evolutiva, Instituto de Biociências, Universidade de São Paulo, São Paulo, SP, Brazil
Send correspondence to Send correspondence to James M. Cheverud Department of Anatomy and Neurobiology Washington University School of Medicine 660 S. Euclid Ave. Campus Box 8108 Saint Louis, MO, 63110, USA E-mail: cheverud@pcg.wustl.edu
ABSTRACT
Comparisons of covariance patterns are becoming more common as interest in the evolution of relationships between traits and in the evolutionary phenotypic diversification of clades have grown. We present parallel analyses of covariance matrix similarity for cranial traits in 14 New World Monkey genera using the Random Skewers (RS), T-statistics, and Common Principal Components (CPC) approaches. We find that the CPC approach is very powerful in that with adequate sample sizes, it can be used to detect significant differences in matrix structure, even between matrices that are virtually identical in their evolutionary properties, as indicated by the RS results. We suggest that in many instances the assumption that population covariance matrices are identical be rejected out of hand. The more interesting and relevant question is, How similar are two covariance matrices with respect to their predicted evolutionary responses? This issue is addressed by the random skewers method described here.
Key words: covariance matrix, common principal components, random skewers, New World monkeys, quantitative genetics.
Introduction
The evolution of phenotypic and genetic variance/ covariance matrices, referred to as simply covariance matrices throughout this paper, is a crucial subject in evolutionary biology (Steppan et al. 2002). In a pivotal paper Lande (1979) showed that, under certain assumptions, estimation of the additive genetic variance-covariance matrix (G) enables us to predict how a set of quantitative traits will evolve under conjoint operation of mutation and genetic drift or in response to natural selection (Lande and Arnold 1983; Turelli 1988). The pattern and level of additive inheritance described by G-matrices is also crucial to the "evolutionary constraints" approach, which seeks to understand the existing diversity of life forms from comparisons of patterns of phenotypic, and ideally genetic, interrelationships among continuous distributed traits (Cheverud 1984, 1996; Steppan 1997; Arnold and Phillips 1999). Both, phenotypic (P) and genetic (G) matrices are important for understanding the evolution of complex morphologies for several reasons. First, genetic correlations and variance/covariance parameters are estimated from phenotypic attributes, properly weighted by genealogical information. Second, although the G matrix helps determine the rate and direction of evolutionary response to natural selection, phenotypic covariance patterns give us direct information about the pattern and level of variation available for selection and are the ultimate target of selection. Phenotypic matrices also play a role in the multivariate evolutionary response equation for natural selection
(Dz = Gb)
because the gradient selection vector b, which summarizes the directional selection force operating on each individual character independently of other traits, is calculated as the inverse of the phenotypic matrix times the selection differential (S) (b = P -1 S), where Dz is the evolutionary change in a vector of trait means. Third, there is increasing evidence that phenotypic and genetic variance/covariance matrices are quite similar, especially for morphological traits, in many diverse organisms (Cheverud 1988, 1995, 1996; Roff 1995, 1996; Steppan 1997; Waitt and Levin 1998; Arnold and Phillips 1999; Marroig and Cheverud 2001), allowing P matrices to be substituted for G matrices in evolutionary studies.
The comparison of P and G matrices within and across taxa, while crucial for evolutionary biology, is dependent on reliable statistical methods, a research area that has been growing during the last two decades. Several methods have been proposed and used for comparing covariance and correlation matrices (Lovsfold 1986; Shaw et al., 1995; Cheverud 1988, 1995, 1996), from vector correlation among principal components to matrix correlation and a maximum-likelihood test for matrix equality. Recently, Roff and colleagues (Begin and Roff 2001, 2003, 2004; Roff 2002; Begin et al. 2004) have introduced a series of new matrix comparison methods, including the T-method, an element by element approach, using percent reduction in Mean Square Error, and the Jackknife-MANOVA method. The T-method (Roff et al. 1999) involves the calculation of the overall sum of the absolute values of differences between the elements of two symmetrical matrices, in other words:
where Aij is the covariance between traits i and j in matrix A and Bij is the corresponding covariance in matrix B, the summation being extended to all diagonal and off diagonal elements in the two matrices (sum of the number of diagonal elements plus the number above or below the diagonal). Similarly, T2 statistics can be calculated which are basically the sum of the squared differences between corresponding matrix elements (instead of the module). Both statistics can be extended to three or more populations by computing all pairwise comparisons. To test the null hypothesis that the elements in one matrix from one population do not differ from the corresponding elements in the other population matrix, we estimate the probability associated with each T value observed via randomizations. Hypothesis testing is conducted by permuting individuals between data arrays and calculating pseudovalues of T or T2 from the randomization procedure (Tr and T2r). Significance is evaluated as the fraction of times Tobs > Tr (or T2obs > T2r). Steppan et al. (2002) have recently reviewed many of these methods.
Common principal component analysis (CPC) has been suggested as a potentially useful tool for simultaneously comparing covariance matrices among two or more taxa (Flury 1988; Steppan 1997; Phillips and Arnold 1999; Arnold and Phillips 1999). CPC analysis is particularly well suited for covariance matrix comparisons because it allows a diversity of hypotheses of relationships among matrices (from unrelated structure to proportionality and equality) to be tested in a hierarchical fashion using any number of matrices (Flury 1988; Phillips and Arnold 1999; Arnold and Phillips 1999). This analysis is based on the description and comparisons of matrices using their decomposition into eigenvalues and eigenvectors (principal components). Flurys model (1988) allows covariance matrices to share more complex relationships than just being equal or unequal, providing a test of several other hypotheses (proportionality, common principal components, partial common principal components) besides matrix equality or unrelated structure (Phillips and Arnold 1999). In this way, CPC analysis builds and tests a hierarchy of relationships among two or more covariance matrices, from unrelated structure to PCPC1, sharing the first PC, PCPC2, sharing the first two PCs,and so on until CPC, sharing all PCs, proportionality and finally equality, each step up in the hierarchy being more inclusive and only being true if the lower levels also holds (see Phillips and Arnold 1999). For each hypothesis in the hierarchy a new set of matrices based on the sample (original) matrices is constructed by maximum-likelihood methods that are constrained so that the hypothesis in question is true. The relative degree of difference between the original and constrained matrices determines the likelihood that the particular hypothesis is true. The difference between the likelihood function values of two steps in the hierarchy is distributed as a chi-square and therefore a standard c2 test could be used to detect significant differences in matrix structure. The CPC test does not have an associated parameter designating the strength of similarity among matrices, relying only on significance testing. We propose a metric described below based on the extent of shared PC structure.
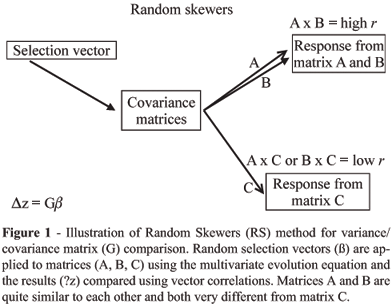
Alternatively, Cheverud (1996) compared the correlation of selection response between two matrices using a series of random selection vectors as a measure of matrix similarity. This "Random Skewers" procedure was derived from ecological methods (Manly 1991) and is a direct application of Landes (1979) multivariate response to selection equation (equation 1). Some number of random selection vectors (~1,000 to 10,000) are applied to both matrices and their responses compared using the vector correlation. Elements of the selection vectors are drawn from a uniform distribution of values between 0.0 and 1.0 and randomly assigned positive or negative signs at 50% probability. The total length of the vector is then standardized to 1.0 (sum of the squared vector elements equals 1.0). This random selection vector (or skewer) is applied to each of the covariance matrices of interest and the response vectors recorded. Since the selection vector is always of unit length, the length of a response vector is given as the sum of the squared response vector elements and can be compared between two matrices by taking their ratio. This is a measure of the relative levels of variance in the two matrices along this dimension of multivariate space. However, when comparing covariance matrices we are often primarily concerned with the pattern of response, rather than its magnitude. The vector correlation measures the co-linearity of the selection responses in multivariate morphometric space. It is equal to the cosine of the angle between the vectors (Figure 1). Of course, the same random selection vector is applied to each matrix so that their simulated evolutionary responses can be compared. The results of these vector comparisons will differ depending on the specific multivariate dimension tested, so we use the average vector correlation between matrix responses to as many as 10,000 random selection vectors as an overall measure of matrix similarity. If two matrices are equal, the average response to random selection vectors is expected to be co-linear or equals one and contrarily, if two matrices are completely unrelated with no shared structure, the average response is expected to be perpendicular or equal to zero (Figure 1).
The statistical significance of a random skewers set can be evaluated against the null hypothesis of no shared structure by using the distribution of vector correlations among k element random, unit-length vectors, where k is the number of traits in the analysis. If the observed vector correlation exceeds 95% of the vector correlations found among the random vectors, there is significant structural similarity between the covariance matrices. In practice, the null hypothesis of no structural similarity is nearly always rejected. Alternatively, a bootstrap approach can be used to measure variation in matrices drawn from population samples. Cheverud et al. (1989; Cheverud, 1996) used a bootstrap test of self-matrix correlation to evaluate matrix repeatability. A bootstrap sample of N individuals is produced by randomly sampling N individuals, with replacement, from the population. A covariance matrix is generated from this sample and compared to the original observed covariance matrix using the random skewers procedure. Covariance matrix repeatability is given by the average squared vector correlation between predicted selection responses of the observed and bootstrap matrices. This approach can also be used to test the null hypothesis of no difference between two covariance matrices by comparing the bootstrap sample matrices from one species with the observed covariance matrix of the other species (see below).
This paper has three goals: first, present a distribution free method for comparing pairs of covariance matrices based on the expected similarity among responses to random selection vectors; second, evaluate these results in relation to Roffs T-test; third, discuss some possible problems in interpreting results from the CPC analysis associated with sample sizes of the matrices compared, problems that one should be aware of in order for the full potential of CPC as a tool in evolutionary studies to be realized.
Materials and Methods
Thirty-nine skull measurements were taken on 5,222 Neotropical primate specimens deposited in several natural history museums (a complete list of material with specimen numbers, museum and taxonomy used can be obtained upon request from the authors). This data set is the same as used by Marroig and Cheverud (2001). Of the sixteen Platyrrhine (Strepserrhini, Primates) genera, two (Brachyteles and Callimico) were excluded because their small sample sizes preclude the proper application of the CPC program (Phillips 1998). Pooled within-groups phenotypic variance/covariance matrices were obtained for each genus following procedures outlined in Marroig and Cheverud (2001) by correcting for sex and taxonomic variation within genus (specific or sub-specific rank depending on the taxonomic arrangement employed for each genus).
Both, T- and T2 statistics (Roff et al. 1999) were applied to test whether or not each pair of NWM covariance matrices were statistically different. The software to implement both T- statistics was kindly provided by L.J. Revell (http://iguana.wustl.edu/~liam/programs/index.htm). Because the T-method relies on bootstrapping the data, recalculating each covariance matrix in every step of the 1,000 samplings, specimen values should be used as a input for the program, not the covariance matrices. Because nearly all of our matrices are pooled-within groups matrices already accounting for other sources of variation (such as sex, species, or sex by species interaction), we used the residuals of the appropriate general linear model for each genus as the data input for the T-method. Variance/ covariance matrices were also analyzed using the CPC software (Phillips 1998) in a pairwise fashion for each possible combination of the 14 South American primate genera. We use both the step-up and the model building approaches (Arnold and Phillips 1999; Phillips and Arnold 1999) to interpret CPC results. The number of partial common principal components analyzed was limited to seven, since for this data set few loadings beyond the fifth principal component are significantly different from zero. The results from CPC analyses were transformed into scores in order to be able to correlate those results with the harmonic or geometric mean of the sample sizes of the matrices involved in each comparison. The full CPC hierarchy comprises 10 categories, from unrelated structure to equality and therefore equality was considered as one and unrelated as zero. Any result between these extreme possibilities was considered as a proportion of the total number of categories. For example, if two matrices had 7 principal components in common, the similarity between those 2 matrices is 0.7 (7 common components divided by total number of categories 10). After this transformation of the CPC results to a "similarity matrix", this matrix was correlated with the matrix of harmonic and geometric means of the sample sizes using matrix correlation and the Mantels test. The significance of the observed matrix correlation was calculated using 10,000 permutations of the columns and associated rows and by comparing the observed matrix correlation to the distribution of randomized matrix correlations.
Phillips and Arnold (1999) suggested that when considering CPC results and differences in the results among the approaches used to build the CPC hierarchy (Step-up, Jump-up and Model-Building approaches) the biological reality of the situation can be gleaned by looking at how well the matrices constructed using the constrained model match the actual matrices from the populations. Therefore, we select four cases to further examine the possible influence of the sample sizes upon the CPC results. These four cases correspond to the following situations: full CPC result with low average sample size; full CPC result with high average sample size; unrelated structure with high average sample size; and unrelated structure with low average sample size. For each of these four examples the original matrices were compared to several reconstructed matrices constrained by the PCPC or CPC models, from PCPC1 to proportionality. The comparisons were made using the Random Skewers procedure with the VCVCOMP program, which is available from the authors upon request. Although matrix correlation followed by Mantels test between paired matrices has been used for comparing variance/covariance matrices matrix (Lovsfold 1986; Arnold and Phillips 1999) this approach is not suitable for comparing this kind of matrix. Columns and rows of variance/covariance matrices usually differ in scale because larger measurements tend to have larger variances and the reverse is true for smaller measurements. This scaling problem means that the randomized columns and associated rows of the variance/covariance matrix are not strictly comparable to one another.
The Random Skewers (RS) procedure does not have this scale problem because the columns and rows of both matrices are not randomized. Instead, the randomization is obtained by repeatedly varying the selection vector applied to both matrices in each round. We compare the same 14 variance/covariance matrices used in the T-method and CPC analyses using the RS method (for a complete analyses of this data set see Marroig and Cheverud 2001). The resulting similarity matrix among the 14 Neotropical primate genera was also compared to CPC results and sample sizes using matrix correlation followed by Mantels test. In order to better understand the properties of the RS method, we use a Monte Carlo approach to look at pairwise similarity between any two matrices. Since samples used to estimate pooled-within groups covariance matrices have a structure, which controls for variation associated with sex and taxonomic differences, a bootstrap procedure is difficult to apply. Instead we used a Monte Carlo approach by generating m data sets, each composed of n individuals with 39 measurements randomly drawn from a population having the observed covariance structure, where n stands for the number of specimens in the original sample. This is performed using the Cholesky decomposition. The covariance matrix specified by each of these m data sets is calculated and then compared to the observed matrix of the other genus involved in the pairwise comparison using the average vector correlation between simulated selection responses. In this way, the distribution of correlations around the observed random skewer can be observed.
Results
Table 1 presents the CPC results for each pairwise comparison among the 14 New World Monkey generic covariance matrices and their sample sizes. Table 1 also presents the Random Skewers results above the diagonal. There is a negative and significant correlation between the CPC results transformed to a similarity matrix and both the harmonic (r = -0.374, p = 0.0065) and geometric means (r = -0.410, p = 0.0012) of the sample sizes. This indicates that increasing the average sample sizes of the matrices decreases the apparent similarity of the matrices. It is more difficult to reject the hypothesis of common structure with smaller samples. This is reinforced by the comparison of the observed matrices of the four selected cases (with combinations of high or low sample sizes and unrelated or CPC structure) to the matrices constructed using the constrained models of the CPC hierarchy (Table 2). All pairwise comparisons show high similarity between the reconstructed matrices and the original ones at all levels in Flurys hierarchy, except for a few matrices in the Cacajao x Cebuella comparison (a combination of low sample sizes and unrelated structure in the CPC result). In this comparison at all steps in the hierarchy one of the original matrices presents a stronger fit to the reconstructed matrices than the other, resulting in an overall lower fit than the other comparisons. Even so, most of these correlations are above 0.9, a value usually associated with quite strong similarity (see Table 2). The comparison between tamarins (Saguinus) and marmosets (Callithrix) is particularly interesting because the two matrices are based on the highest sample sizes in our data set (N = 1135 and 504 respectively). For both genera, the similarity between the original matrix and the reconstructed ones is nearly one at all steps in the hierarchy, from unrelated to equality, a result that suggest that the original matrices are in fact nearly identical to one another. However, all three approaches (Step-up, Jump-up and Model building) suggested by Flury (1988) and Phillips and Arnold (1999) indicate that the hypothesis of shared structure between these two genera should be rejected quite confidently (see Table 3). Perhaps the structures are significantly different but that difference is extremely small. Moreover, if the same two matrices (Callithrix and Saguinus) are compared again using the CPC, but using a 10 times smaller sample size as input, the result for all 3 approaches indicate a full proportional relationship between them.
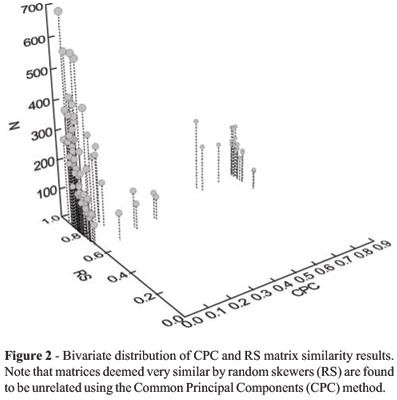
There is a low, non-significant correlation between RS results and CPC results (r = 0.163, p = 0.18) indicating that the techniques are giving different answers to the question of matrix similarity. This is because RS uses a quantitative measure of association, not based on sample sizes, while CPC results are largely determined, in our data set, by sample size considerations. There is also a positive and significant correlation between the RS results and both, harmonic mean (r = 0.453, p = 0.0198) and geometric mean (r = 0.413, p = 0.0286) of the matrix sample sizes. This result indicates that matrices with higher sample sizes appear to be more similar than matrices with lower sample sizes. This probably results from the fact that matrices with high sample sizes are estimated with more confidence than matrices with lower sample sizes. Note that this is in opposition to the association between CPC interpretations and sample sizes.
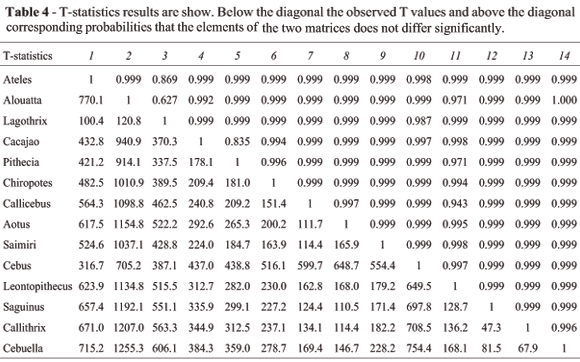
Tables 4 and 5 present the results of the T- and T2-statistics, with observed values below the diagonal and associated probabilities above the diagonal. Notice that among all 91 pairwise comparisons of covariance matrices none present significant differences among them.
Discussion
Results of the two T-statistics and the random skewers are basically in agreement. Random Skewers results indicate that covariance matrices are basically very similar in NWM, while not strictly constant or equal. The T-method results do not reject the null hypothesis that the elements in one covariance matrix are the same as the corresponding elements in the second matrix. This congruence of results between RS and T-statistics is in marked contrast to the CPC results.
Matrix sample sizes affect the RS and the CPC methods in opposite ways (Figure 2). Pairwise matrix comparisons estimated with low sample sizes are generally less similar to one another than matrices estimated with high sample sizes using the RS method. This relationship is a result of the sampling error associated with any matrix estimation and results in greater random error in the estimates of matrix elements in comparisons made using smaller samples. This is the same pattern was found by Steppan (1997) in his rarefaction analysis of the matrix correlation using Mantels test and also discussed by Cheverud (1996) in the context of matrix estimation reliability.
Conversely, for the CPC method, matrices estimated with higher sample sizes reject the null hypothesis of similarity more frequently than matrices with relatively lower sample sizes. Because the CPC model takes into account sample size in deriving the c2 probabilities, the main effect of increasing sample size is to increase the power of the method to reject common structure. This is apparent in the Saguinus x Callithrix case analyzed in detail here. In this case, even if the maximum likelihood matrices reconstructed under the equality and all steps below in Flurys hierarchy are nearly identical to the original matrices, all three approaches for choosing an appropriate model in CPC analysis indicate that those matrices are unrelated in their structure. Conversely, the RS method indicates that covariance structure is really quite similar. With large sample sizes even small differences in the variance/covariance structure of the matrices leads to statistically significant CPC tests, even when the differences are biologically trivial. Unlike the usual null hypothesis of no structure, CPC procedure has as its null, identical structure. The surest way to avoid obtaining significant structural diversity is to use inadequate sample sizes. With large sample sizes, it is quite possible for matrices that are indeed very similar, to be found significantly different from each other. Both methods behave as expected statistically, but it is clear that a CPC result of "unrelated" matrix structures can be obtained even in situations in which the matrices are nearly identical (r > 0.9). A similar conclusion concerning CPC was reached by Houle et al. (2002) on the basis of simulation results.
The above discussion suggests that future applications of CPC to studies of matrix evolution face something of a dilemma. To what extent are statistically significant differences between the matrices compared biologically meaningful? For example, at first sight the comparison using the CPC technique suggests that in general there is very little shared covariance structure among Neotropical primate genera. This result indicates that attempts to reconstruct past evolutionary forces operating to differentiate phenotypic means of populations will be questionable given the violation of the basic assumption of constant or proportional within-group variance/covariance structures. However, while statistically significant differences among Platyrrhine covariance matrices are detected by CPC, a closer examination suggests that those differences are trivial or insignificant from a biological point of view as demonstrated by the Saguinus-Callithrix comparison. In two previous studies comparing variance/covariance and correlation patterns using CPC and matrix correlation this conflict between statistical and biological significance was apparent (Steppan 1997, Ackermann and Cheverud 2000). Steppan (1997) found that while matrix correlation results indicate a high similarity among covariance structures for skull traits of several populations and species of the rodent genus Phyllotys, CPC analyses indicates that there is very little shared structure. Ackermann and Cheverud (2000) also employed matrix correlation and CPC for comparing tamarin (Saguinus) species and found discrepancies between the results of both techniques.
We stress here that researchers should follow Phillips and Arnolds (1999) suggestion to inspect closely the CPC model reconstructed matrices at each step in the hierarchy to confirm how well those matrices fit the original ones. This seems to be particularly material if the sample sizes and number of traits of the matrices compared is high. Otherwise, one could be misled into thinking that rejection of a common covariance structure among populations using CPC means that the covariance patterns are indeed unrelated. While significantly different statistically, this difference may not be biologically meaningful in the evolutionary context. The influence of sample size and number of traits on hypothesis testing in CPC analysis should be addressed by a power analysis (Patrick Phillips personal communication). Power is the probability of rejecting the null hypothesis when it is false and the alternative hypothesis is correct (Sokal and Rohlf 1995). However, even when power curves become available for CPC tests (Phillips 1998) the careful inspection of original and reconstructed matrices seems to be prudent in judging CPC results.
The Random Skewers method presented here could be a useful method for comparing variance/covariance matrices. First, the RS method, like matrix correlation, gave an easily interpretable statistic that is also continuously distributed and approximately normal and reflects the overall similarity in covariance structure (Figure 3). While in theory the value of the vector correlation ranges from zero (orthogonality) to one (collinearity) in practice matrix elements are estimated with some degree of error because they are only estimates, not population values. This limits the maximum observable correlation between estimated matrices. Matrix repeatability, which is the proportion of the variance in the observed elements due to variation in the true population values, can be used to set upper limits for the maximum average correlation which can be expected between estimated matrices (see Cheverud 1996). Second, the RS method is a direct extension of the multivariate evolutionary response equation for natural selection and therefore is particularly attractive for evaluating whether or not two variance/covariance matrices are similar enough to allow selection gradients to be reconstructed. This is because given any fixed selection vector, if two matrices are similar, the direction of evolution specified by each matrix in response to this vector should also be similar. Third, unlike CPC, which is strongly influenced by the number of traits in the matrices, the RS method like matrix correlation is not. The only influence is that, as already noted, with more traits included the accuracy of the matrix, as an overall structure description should also increase, which is a biologically attractive perspective.
Finally, RS is appropriate for comparing variance/covariance matrices, where matrix correlations followed by Mantels test is not. Although matrix correlation has been used for comparing variance/covariance matrices (Lovsfold 1986, Arnold and Phillips 1999) they are not suited for randomization tests where the matrix elements are shuffled because patterns of covariance are measured on a different scale for each row (and associated column). Usually larger traits will also present larger variances where the reverse is true for traits with smaller absolute values. This scale dependency of variances and consequently the associated covariances mean that variance/covariance matrix elements are not interchangeable. While RS still has the advantage of being a distribution free method, based on extensive re-sampling, matrix elements are not exchanged. Instead, re-sampling is accomplished by applying random selection vectors upon the matrices compared and then measuring their expected evolutionary responses.
Acknowledgements
This research was supported by grants from the Conselho Nacional de Pesquisas (CNPq), Fundação de Amparo à Pesquisas do Estado do Rio de Janeiro (FAPERJ), Fundação de Amparo a Pesquisa do Estado de São Paulo Biota São Paulo (FAPESP), Fundação José Bonifácio (FUJB), Projeto de Conservação e Utilização Sustentável da Diversidade Biológica (PROBIO), an American Museum of Natural History Collections Study Grant, a fellowship from the Conselho Nacional de Pesquisas (CNPq) and NSF grant SBR-9632163. We also thank Liam Revell for access to his programs for matrix compasrison analysis. We are grateful also for the two anonymous reviewers for their helpful comments and suggestions.
Received: July 11, 2006; Accepted: January 31, 2007.
Associate Editor: Louis Bernard Klaczko
- Ackermann RG and Cheverud JM (2000) Phenotypic covariance structure in tamarins (Genus Saguinus): A comparison of variation patterns using matrix correlation and common principal component analysis. Am J Phys Anthropol 111:489-501.
- Arnold SJ and Phillips PC (1999) Hierarchical comparison of genetic variance-covariance matrices. II. Coastal-island divergence in the garter snake, Thamnophis elegans Evolution 53:1516-1527.
- Begin M and Roff DA (2001) An analysis of G matrix variation in two closely related cricket species, Gryllus firmus and G. pennsylvanicus J Evol Biol 14:1-13.
- Begin M and Roff DA (2003) The constancy of the G matrix through species divergence and the effects of quantitative genetic constraints on phenotypic evolution: A case study in crickets. Evolution 57:1107-1120.
- Begin M and Roff DA (2004) From micro- to macroevolution through quantitative genetic variation: Positive evidence from field crickets. Evolution 58:2287-2304.
- Begin M, Roff DA and Debat V (2004) The effect of temperature and wing morphology on quantitative genetic variation in the cricket, Gryllus firmus, with an appendix examining the statistical properties of the Jackknife-MANOVA method of matrix comparison. J Evol Biol 17:1255-1267.
- Cheverud JM (1984) Quantitative genetics and developmental constraints on evolution by selection. J Theor Biol 110:155-171.
- Cheverud JM (1988) A comparison of genetic and phenotypic correlations. Evolution 42:958-968.
- Cheverud JM (1995) Morphological integration in the saddle-back tamarin (Saguinus fuscicollis) cranium. Am Nat 145:63-89.
- Cheverud JM (1996) Quantitative genetic analysis of cranial morphology in the cotton-top (Saguinus oedipus) and saddle-back (S. fuscicollis) tamarins. J Evol Biol 9:5-42.
- Flury B (1988) Common Principal Components and Related Multivariate Models. Wiley, New York, 258 pp.
- Houle D, Mezey J and Galpern P (2002). Interpretation of the results of common principal components analyses. Evolution 56:433-440.
- Lande R (1979) Quantitative genetic analysis of multivariate evolution, applied to brain: Body size allometry. Evolution 33:402-416.
- Lande R and Arnold SJ (1983). The measurement of selection on correlated characters. Evolution 37:1210-1226.
- Lovsfold D (1986) Quantitative genetics of morphological differentiation in Peromyscus I. Tests of the homogeneity of genetic covariance structure among species and subspecies. Evolution 40:559-573.
- Manly BFJ (1991) Randomization and Monte Carlo Methods in Biology. Chapman and Hall, New York, 281 pp.
- Marroig G and Cheverud JM (2001) A comparison of phenotypic variation and covariation patterns and the role of phylogeny, ecology and ontogeny during cranial evolution of New World Monkeys. Evolution 55:2576-2600.
- Phillips PC (1998) CPC: Common Principal Components Analysis. University of Oregon, Eugene, OR. Software available at: dawrkwing.oregon.edu/~pphil/software.html.
- Phillips PC and Arnold SJ (1999) Hierarchical comparison of genetic variance-covariance matrices. I. using the Flury hierarchy. Evolution 53:1506-1515.
- Roff DA (1995) The estimation of genetic correlations from phenotypic correlations: A test of Cheveruds conjecture. Heredity 74:481-490.
- Roff DA (1996) The evolution of genetic correlations: An analysis of patterns. Evolution 50:1392-1403.
- Roff DA (2002) Comparing G matrices: A MANOVA approach. Evolution 56:1286-1291.
- Roff DA, Mousseau TA and Howard DJ (1999) Variation in genetic architecture of calling song among populations of Allonemobius socius, A. fasciatus, and a hybrid population: Drift or selection? Evolution 53:216-224.
- Shaw FH, Shaw RG, Wilkinson GS and Turelli M (1995) Changes in genetic variances and covariances: G whiz! Evolution 49:1260-1267.
- Sokal RR and Rohlf FJ (1995). Biometry. Freeman Press, San Francisco, 850 pp.
- Steppan SJ (1997) Phylogenetic analysis of phenotypic covariance structure. I. Contrasting results from matrix correlation and common principal component analyses. Evolution 51:571-586.
- Steppan SJ, Phillips PC and Houle D (2002) Comparative quantitative genetics: Evolution of the G matrix. TREE 17:320-327.
- Turelli M (1988) Phenotypic evolution, constant covariances and the maintenance of additive variance. Evolution 43:1342-1347.
- Waitt DE and Levin DA (1998) Genetic and phenotypic correlations in plants: A botanical test of Cheveruds conjecture. Heredity 80:310-319.
Publication Dates
-
Publication in this collection
04 June 2007 -
Date of issue
Mar 2007
History
-
Received
11 July 2006 -
Accepted
31 Jan 2007