Abstract
Though introduced recently, complex networks research has grown steadily because of its potential to represent, characterize and model a wide range of intricate natural systems and phenomena. Because of the intrinsic complexity and systemic organization of life, complex networks provide a specially promising framework for systems biology investigation. The current article is an up-to-date review of the major developments related to the application of complex networks in biology, with special attention focused on the more recent literature. The main concepts and models of complex networks are presented and illustrated in an accessible fashion. Three main types of networks are covered: transcriptional regulatory networks, protein-protein interaction networks and metabolic networks. The key role of complex networks for systems biology is extensively illustrated by several of the papers reviewed.
bioinformatics; complex networks; metabolic networks; protein-protein networks; systems biology; transcription networks
REVIEW ARTICLE
Complex networks: the key to systems biology
Luciano da F. Costa; Francisco A. Rodrigues; Alexandre S. Cristino
Instituto de Física de São Carlos, Universidade de São Paulo, São Carlos, SP, Brazil
Send correspondence to Send correspondence to: Luciano da F. Costa Instituto de Física de São Carlos, Universidade de São Paulo Caixa Postal 369 13560-970 São Carlos, SP, Brazil E-mail: luciano@if.sc.usp.br
ABSTRACT
Though introduced recently, complex networks research has grown steadily because of its potential to represent, characterize and model a wide range of intricate natural systems and phenomena. Because of the intrinsic complexity and systemic organization of life, complex networks provide a specially promising framework for systems biology investigation. The current article is an up-to-date review of the major developments related to the application of complex networks in biology, with special attention focused on the more recent literature. The main concepts and models of complex networks are presented and illustrated in an accessible fashion. Three main types of networks are covered: transcriptional regulatory networks, protein-protein interaction networks and metabolic networks. The key role of complex networks for systems biology is extensively illustrated by several of the papers reviewed.
Key words: bioinformatics, complex networks, metabolic networks, protein-protein networks, systems biology, transcription networks.
Introduction
While a great deal of the advances in physics and chemistry have stemmed from reductionist approaches where the subject of interest, such as an atom or particle, is systematically isolated from the rest of the world in a strictly controlled environment, biology defies such a paradigm by encompassing the whole range of spatial and temporal scales present in nature: ranging from the molecules being observed to the observer built from molecules. Having mapped the basic secrets of the genome - that big reference book for protein and RNA synthesis - biology now progresses to the more integrative and dynamic aspects of life along the road of development and evolution. How is the synthesis of proteins affected by the surrounding anatomy, and vice-versa? How does the environment interfere with the control of gene expression? How do species, products of genetic programs, interact with the environment? How do cells, initially with identical molecular composition, ultimately differentiate to produce the myriad of tissues and functions in an organism? To answer such questions will correspond to ultimately unveiling the final secrets of life.
However, while impressive experimental results have been continuously obtained in biology, the challenge of integrating all such results into a coherent whole remains. The integrative attempts at solving such a problem are now part of the new area of systems biology. Three main problems to be addressed are: (i) to organize the ever increasing experimental results from complex biological systems (e.g. protein-protein interaction, gene expression profiles, metabolic pathways) into suitable respective representations and models; (ii) to be able to simulate the dynamics of such models under varying conditions, so as to unveil important biological patterns and structures; and (iii) to find the means for effectively connecting such models at the several spatial and time scales involved.
While the study of genes and proteins continues to be important, looking at isolated components is not enough to understand most biological processes. For instance, as discussed by Vogelstein et al. (2000), the analysis of the signaling pathway involving the p53 tumor-suppressor gene is more important than looking at this gene only. Indeed, a combined attack on genes connected to p53 caused more severe effects than the removal of the gene itself (Franklin et al., 2000). Thus, the characterization of biological networks should be similar to that for other types of complex systems, such as the Internet, the World Wide Web (WWW) and society. The recent theory of complex networks constitutes a particularly promising possibility to characterize and model the intricate structures and dynamics that govern the biological process.
The beginning of complex network theory can be traced back to the first work on graph theory, developed by Leonhard Euler in 1736 but, stimulated by works such as those by Barabási and Albert (1999), research on complex networks has only recently been applied to areas such as biology, economics, linguistics, medicine, social sciences, technology and transport. Though formalized recently complex networks research (Boccaletti et al., 2006; Newman, 2003; Costa et al., 2007) has progressed steadily to become one of the most promising and dynamic scientific areas. Representing an extension of graph theory (see, for example, Chartrand and Lesniak, 1986), complex networks research focuses on the characterization, analysis, modeling and simulation of complex systems involving many elements and connections, examples being the internet, gene regulatory networks, protein-protein networks, social relationships and the WWW. In complex networks research special attention is given not only to trying to identify special patterns of connectivity, such as the shortest average path between pairs of nodes (Newman, 2003), but also to considering the evolution of connectivity and the growth of networks, an example from biology being the evolution of protein-protein interaction networks in different species (Vázquez et al., 2003b).
More recently, growing attention has also been focused on the investigation of dynamic unfolding in systems underlain by specific types of networks, an example being how neuronal activity depends on specific types of connectivity between neurons (Costa and Sporns, 2005). Ultimately, efforts will converge on the consideration of the interplay between such dynamics and the dynamics of the evolution of the networks. One of the reasons for the impressive advance and popularization of complex networks research in the brief period since the application of this methodology to science and technology consists of their intrinsic potential to represent virtually any system composed of discrete elements. Fortunately, most natural and biological systems are indeed discrete in nature and can be represented as networks. For instance, in a protein-protein interaction network, each protein is represented as a node, or vertex, while the possible interactions between proteins are expressed as links, or edges, between respective nodes. Similarly, metabolic pathways can be represented as networks formed by metabolites, reactions and enzymes connected by two types of relationship, mass flow and catalytic regulation (Jeong et al., 2000), while transcriptional regulations can be naturally represented by complex networks where vertices represent genes and directed edges denote regulatory effects on the target genes (Balazsi et al., 2005).
In order to understand complex biological systems, the three following key concepts need to be considered (Aderem, 2005): (i) emergence, the discovery of links between elements of a system because the study of individual elements such as genes, proteins and metabolites is insufficient to explain the behavior of whole systems; (ii) robustness, biological systems maintain their main functions even under perturbations imposed by the environment; and (iii) modularity, vertices sharing similar functions are highly connected. All these three features have been widely studied in complex networks research, as, for instance, in the case of the Internet (Albert et al., 2000) and protein-protein interaction networks (Jeong et al., 2001). Therefore, complex networks theory can be largely applied for developing systems biology research because many tools for network characterization, modeling and simulation are already available.
This review will start by presenting an accessible introduction to the basic concepts of complex networks, including their definition, measurement and traditional models, and will go on to review the main developments in the application of complex networks to systems biology, with special attention given to more recent and comprehensive articles, thereby complementing and extending previous reviews of this area such as that by Barabási and Oltvai (2004).
Basic Concepts of Complex Networks
The structure of complex networks can be represented as a graph, which is an ordered pair G = (V, E) formed by a set V ≡ {1, 2, i, , N} of vertices, or nodes, connected by a set E ≡ {e1, e2, , eM} of edges, or links, (Bollobás, 1998; Diestel, 2000; West, 2001) (Figure 1). Each edge represents a link between two vertices, i.e., ep = (i, j) indicates the connection between the vertices i and j. If the edges have direction, the graph is said to be a directed graph and G is an ordered pair G = (V, E→), where V is the set of vertices and E→ is the set of ordered pairs of arcs, or arrows. In this case, each arc ep = (i, j) is a directed edge extending from node i, called the head, to j, called the tail.
Figure 1 shows an undirected and a directed network and their respective adjacency matrices. A network can be represented by its adjacency matrix A (Figure 1a). The elements aij are equal to 1 whenever there is an edge connecting the vertices i and j, and equal to 0 otherwise. When the graph is undirected, the adjacency matrix is symmetric, i.e., the elements aij = aji for any i and j.
The networks studied some decades ago included a few dozen vertices and could even be drawn on a piece of paper. However, real networks can now be composed of thousands or millions of vertices and their quantitative analysis cannot be performed using drawings and visual analysis. In order to characterize such complex networks, it is necessary to take topological measurements into account, which can provide valuable insights about the structure of networks (Costa et al., 2007). Basic network measurements are related to vertex connectivity, occurrence of cycles and the distances between pairs of nodes, among other possibilities. The most elementary characterization of a node i can be obtained in terms of the degree of vertices (Figure 1). Although the vertex degree is a very simple measurement, it is particularly meaningful for network characterization. For instance, in protein-protein interaction networks, highly connected proteins tend to be essential for the survival of the organism (Jeong et al., 2001). The average degree, corresponding to the average of the degrees of all vertices, is a global measurement of the connectivity of the network. The most highly connected nodes are called hubs, which are fundamental for several important properties of networks, such as resilience against random failures (Albert et al., 2000). Note that the concept of resilience in complex network theory cannot be immediately extended to biological networks, since, compared to other types of networks, organisms can be much more sensitive to small changes such as a missing gene or a defective protein.
The degree distribution of a network, P(k), gives the probability that a chosen vertex has degree k. It is obtained by counting the number of nodes with a given connectivity and dividing by N. This measurement provides an easy way to infer the overall connectivity and can be used for network classification. If most vertices have a similar degree, P(k) will be a peak distribution (Figure 2a). However, most biological networks are scale-free, implying that their distribution of connections is uneven and approximating a power-law P(k) ≈ k-γ, where γ is a constant. In this case, while most vertices are little connected, a huge number of edges is concentrated in a small number of nodes. It can also be shown that scale free networks have higher probability of exhibiting hubs (Barabási and Albert, 1999).
In most complex networks, it is important to quantify how vertices with different degrees are connected. The determination of the degree correlation can be achieved by considering the Pearson correlation coefficient (r) between the degrees at both ends of the edges (-1< r < 1). Such a measurement is called assortativity (Newman, 2002). If r > 0 then vertices with similar degrees tend to be connected and the network is assortative but if r < 0 highly connected vertices tend to connect to vertices with few connections and the network is disassortative, while if r = 0 there is no pairwise correlation between vertex degrees and the networks is non-assortative. Disassortative networks are known to be resilient to simple target attack, in other words when some hubs are removed the network does not instantly fragment into many disconnected components (Vázquez and Moreno, 2003). Most biological networks are disassortative, examples being neural networks (r = -0.226; Watts and Strogatz, 1998), metabolic networks (r = -0.24; Jeong et al., 2000) and protein-protein interaction networks (r = -0.156; Jeong et al., 2001).
Another important property of networks relates to the distances between pairs of vertices, which is measured by the path length, i.e., the number of edges needed to be crossed while going from one vertex to another in such a way that each node is visited only once. The shortest path length (ℓ) between two vertices i and j is given by the length of the shortest path that connects i and j. For instance, in Figure 1, the shortest path length between vertices 1 and 6 is ℓ16 = 3. The average shortest path length is computed by considering the distance matrix L, in which the entry ℓij represents the length of the shortest paths between the nodes i and j. A general feature of biological networks is their small-world property in which any two nodes in the system can be connected by relatively short paths along existing edges. For example, the value of the average shortest path length in the protein-protein interaction network of Saccharomyces cerevisiae is ℓ ≈ 7 (Jeong et al., 2001) and in metabolic networks is ℓ ≈ 3 (Jeong et al., 2000). In metabolic networks, the paths correspond to the biochemical pathways connecting two substrates. A more formal definition of small-worldness, considering the increase of the shortest paths with the size of the network, can be found in Newman (2001).
Biological networks can also be characterized in terms of the subgraphs and cycles present in their topology (Figure 3). Some subgraphs are called motifs, corresponding to patterns of connectivity which are statistically more abundant in real networks than in their respectively random versions (Milo et al., 2002). Motifs are associated with specific functions in different networks (Wuchty et al., 2003). The simplest motif is composed of three fully connected vertices (triangles).
The clustering coefficient of a node i (cci) is given by the following ratio,
Examples of three configurations resulting in different respective clustering coefficient values are given in Figure 4. The average clustering coefficient is computed by adding the values of the clustering coefficient of all nodes and dividing by N. Some biological networks tend to present high clustering coefficient values. For instance, in the protein-protein interaction network of S. cerevisiae, <cc> ≈ 0.18 (Costa et al., 2007).
The characterization and classification of complex networks (Costa et al., 2007) can also be achieved by considering measurements related to community structure, hierarchies, centrality and motifs.
Complex Networks Models
The simplest complex network model was proposed by Paul Erdös and Alfred Rényi in 1959 (see also Flory, 1941). This model is called the random graph of Erdös and Rényi and is constructed in the following way. Starting with a set of N disconnected vertices (nodes), edges (links) are added according to a fixed probability p (Erdös and Rényi, 1959; Erdös and Rényi, 1960). The distribution of connections of networks generated by this model follows a Poisson distribution for large N (Figure 2a). An intrinsic feature of such a model is the highly homogeneous number of connections at each vertex, which results in networks which can be well characterized by their average node degree.
Because its simplicity, the random model is not suitable to represent most real networks. In 1998, Watts and Strogatz observed that, unlike random networks, real-world networks tended to present many third-order cycles. Watts and Strogatz (1998) therefore proposed a model called the small-world network model, which starts with a fully regular network of N vertices in which each vertex is connected to its k nearest neighbors. Next, each edge is randomly rewired with probability p. This model lies between regularity and randomness. When p = 0, the structure is ordered with high number third-order cycles (high average clustering coefficient) but large average shortest path length. Otherwise, when p → 1, the network becomes a kind of random graph. However, this model produces networks whose degree distribution is still homogeneous.
It has been shown that the connectivity of the World Wide Web is far from regular because a few vertices tended to concentrate a large fraction of the network connections (Barabási and Albert, 1999) and the same structure has been found in the Internet (Faloutsos et al., 1999), metabolic networks (Jeong et al., 2000), protein-protein interaction networks (Jeong et al., 2001) and in networks of scientific collaboration (Barabási et al., 2002). The presence of hubs is directly related to the scale-free distribution of node degrees, where a straight line is obtained in log-log plots of the node distribution (Figure 2b).
To explain the uneven distribution of connectivity in several real networks, the so-called scale-free network model has been developed (Barabási and Albert, 1999), which is based on two basic rules: (i) growth, in which the network evolving process starts with a set of m0 vertices and grows at each subsequent step by the addition of a new vertex with m links; and (ii) preferential attachment, in which the vertices receiving the new edges are chosen following a linear preferential attachment rule, where the probability of the new vertex i connecting with an existing vertex j is proportional to the degree of j. In this model, the most connected vertices have a greater probability of receiving new links. Despite the success in reproducing the scale-free degree distribution, the scale-free network model generates non-assortative networks with small average clustering coefficients. Thus, this model is not suitable for representing some real networks (Costa et al., 2007). Other complex network models have been developed for specific applications (Boccaletti et al., 2006).
Biological Networks
The availability of completely sequenced genomes and the development in molecular biology of high-throughput techniques such as microarray technology (Schena et al., 1995; Ren et al., 2000) and two-hybrid systems (Fields and Song, 1989) have allowed genome-wide studies of biological processes that arise from complex interaction between genetic entities, such as proteins, RNAs and DNA (Lockhart and Winzeler, 2000; Uetz and Hughes, 2000). These cellular entities interact with one another according to their functional roles. For instance, protein-protein interactions, related to cellular communication by signal transduction, activate or repress the transcription of genes, changing the molecular composition of the cell. These separate modules are 'building blocks' of the biological systems, working together to shape the phenotypic pattern of the cells and organisms (Hartwell et al., 1999). Mapping out all these interconnected modules helps to understand and model their topological and dynamical properties (Barabási, 2007).
The most critical networks for controlling cellular systems are those related to transcription, protein-protein interaction and metabolism (Barabási and Oltvai, 2004). Despite the great diversity of networks in cell biology, they share several global properties. For instance, most networks within the cell are characterized by (i) a scale-free degree distribution (also called power-law), (ii) a small average shortest path length between any two nodes (small-world), (iii) a disassortative nature, (iv) a modular organization and (v) a structural and dynamical robustness (Barabási and Oltvai, 2004; Albert, 2005).
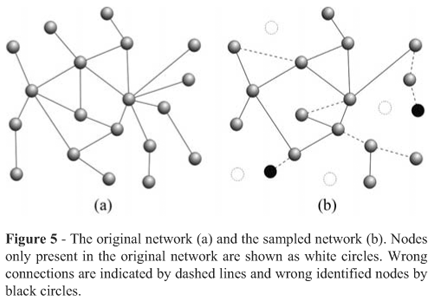
One limitation in biological networks analysis is the incomplete/noisy data sampling characterized by missing edges and/or vertices or the presence of links and nodes that do not exist in a real system (Figure 5). These errors usually constitute experimental artifacts or noise, caused by human error or technical limitations. A typical example of sampling limitations is found in methods for the detection of protein-protein interaction. The most commonly used methods are co-affinity purification followed by mass spectrometry (co-AP/MS; Gavin et al., 2002) and the yeast two-hybrid assay (Y2H; Fields and Song, 1989). Both methods have limitations that can influence the definition of network structures. Currently, such maps should be viewed as hypotheses pending validations by an appropriate biological assay. Even so, they can be useful as a partial description of protein-protein interactions (Walhout et al., 2000). Therefore, in the meantime as the databases get more complete, it is important to develop methods to quantify the completeness of networks and study the implications of errors resulting from data sampling. Novel and relevant information and insights can be obtained by applying complex networks concepts to model biological systems despite some incompleteness. Although sampling remains an important issue, current databases offer an unprecedented opportunity to study regulatory organization of the cell from the perspective of complex networks.
Transcriptional Regulatory Networks
The great complexity of organisms arises more as a consequence of elaborated regulation of gene expression than from differences in genetic content in terms of the number of genes (Carroll, 2000; Levine and Tjian, 2003). The transcription network is a critical system that regulates gene expression in a cell. Transcription factors (TFs) respond to changes in the cellular environment, regulating the transcription of target genes (TGs) and connecting functional protein interactions to the genetic information encoded in inherited genomic DNA in order to control the timing and sites of gene expression during biological development. These regulators bind as complexes to specific cis-elements near the start of the transcription site to increase or decrease the rate of mRNA production via RNA polymerase stabilization (Davidson et al., 2002; Wray et al., 2003; Alon, 2007).
Transcription regulation maps have been constructed for Escherichia coli (Huerta et al., 1998; Thieffry et al., 1998; Shen-Orr et al., 2002; Gama-Castro et al., 2008) and S. cerevisiae (Lee et al., 2002; Harbison et al., 2004; MacIsaac et al., 2006). The interactions between TFs and TGs can be represented as a directed graph. The two types of nodes (TF and TG) are connected by arcs (Figure 6a, arrows) when regulatory interaction occurs between regulators and targets (Babu et al., 2004; Alon, 2007). Transcriptional regulatory networks display interesting properties that can be interpreted in a biological context to better understand the complex behavior of gene regulatory networks. At a global network level, when the out-degree distribution of TFs is considered scale-free distribution is observed while the in-degree distribution of TGs shows exponential distribution (Guelzim et al., 2002) (Figure 1b). The scale-free network indicates that most TFs regulate a few TGs but a few TFs interact with many TGs, however in the exponential network most TGs are regulated by the same TF (Barabási and Oltvai, 2004; Albert, 2005).
At a local network level, these networks are organized in substructures such as motifs and modules. In this case, motifs represent the simplest units of the network architecture required to create specific patterns of inter-regulation between TFs and TGs. Three most common types of motifs can be found in gene regulatory networks: (1) single input, (2) multiple input and (3) feed-forward loop (Babu et al., 2004; Shen-Orr et al., 2002) (Figure 7). Target genes belonging to the same single and multiple input motifs tend to be co-expressed, and the level of co-expression is higher when multiple transcription factors are involved (Yu et al., 2003). Modularity in the regulatory networks arises from groups of highly connected motifs that are hierarchically organized, in which modules are divided into smaller ones (Babu et al., 2004; Albert, 2005). Some modules can be assigned to particular biological processes, but there is no consensus on the precise groups of genes and interactions that form modular structure (Ihmels et al., 2002; Bar-Joseph et al., 2003, Babu et al., 2004).
The evolution of gene regulatory networks mainly occurs through extensive duplication of transcription factors and target genes with inheritance of regulatory interactions from ancestral genes (Teichmann and Babu, 2004; Babu et al., 2004), while the evolution of motifs does not show common ancestry but is a result of convergent evolution (Conant and Wagner, 2003).
Protein-Protein Interaction Networks
The interactions between proteins are essential to keep the molecular systems of living cells working properly. Protein-protein interaction is important for various biological processes such as cell-cell communication, the perception of environmental changes and protein transportation and modification. Complex network theory is suitable to study protein-protein interaction maps because of its universality and integration in representing complex systems. In complex network analysis each protein is represented as a node and the physical interactions between proteins are indicated by the edges in the network (Figure 6b).
Jeong et al. (2001) showed that the structure of the protein-protein interaction network of the yeast S. cerevisae is completely heterogenous, questioning the previous belief that protein interactions were generated at random. In this way, while few proteins have a huge number of connections, most proteins have just one or two links. As observed for yeast, the same type of topology was found in the bacterium Helicobacter pylori (Rain et al., 2001) and in the insect Drosophila melanogaster (Giot et al., 2003). Such discoveries suggest that the scale-free nature of protein-protein interaction networks is a common property of all organisms. A good review about the protein-protein network characterization can be found in Colizza et al. (2005).
In addition to the scale-free structure, protein-protein interaction networks also present the small-world effect, modular organization (Barabási and Oltvai, 2004) and motifs (Milo et al., 2002). For the latter, not only individual proteins should be conserved during evolution, but also modules and specific motifs (Hartwell et al., 1999; Poyatos and Hurst, 2004). Indeed, Wuchty et al. (2003) analyzed the conservation of 678 yeast proteins with orthologs from another five eukaryote species and showed that motifs can be conserved from the simplest organisms to the most complex ones. Although conservation of network motifs is seen during evolution, it has been shown by Hormozdiari et al. (2007) that the duplication model, based on Ohno's model of genome growth (Ohno, 1970), can explain the emergence of the most common properties as small-world effect and power-law degree distribution, with a frequency comparable to that seen in real networks.
One of the greatest challenges in the post-genomic era is the prediction of protein functions. Proteins that share connections in a protein-protein interaction network tend to have similar functions (Hishigaki et al., 2001). Empirical observations have indicated that 70% to 80% of protein interaction partners share at least one function (Schwikowski et al., 2000). In this way, by analyzing the neighborhood of known proteins, it is possible to infer some of the functional roles of their direct neighbors. Such an approach, called majority rule assignment, has been greatly improved by considering higher neighborhood levels (Hishigaki et al., 2001) and by minimizing the number of physical interactions between different functional categories of proteins and considering the connections between unknown proteins (Vázquez et al., 2003a).
The importance of proteins can be inferred by analysis of their local topological properties. For instance, because of the importance of hubs, Jeong et al. (2001) investigated the relationship between lethality and connectivity and found a positive correlation between the fraction of lethal protein with a given degree k and the respective protein degree, which seems to imply that proteins with high degree, such as hubs, would tend to be essential. In this way, the analysis of network structure can be useful to determine the importance of proteins and to predict their functions.
The models constructed to explain the evolution of protein interaction networks are based on the hypothesis that all proteins of a family evolved from a common ancestor (Ohno, 1970). Based on this concept, Vázquez et al. (2003b) suggested a model in which each node in a network represents a protein that is expressed by a gene, with the network evolving by duplication and divergence. In the duplication step, a protein, i, in the network is randomly duplicated and a new protein, i', is created with links to each neighbor j of i and an interaction between i and i' is established with probability p. In the divergence step, a node j connected to i and i' loses the connection (i, j) or (i, j) according to a probability q. It is interesting to note that this model does not consider preferential attachment, even though it generates networks with power-law degree distribution. This model was later improved considering other linking dynamics (Sole and Fernandez, 2003; Berg et al., 2004) and empirical observations (Wagner, 2001; Wagner, 2003).
The interaction between proteins can also be analyzed at the domain level. Protein domains are the basic structures within a protein that are self-stabilizing and often self-folding (Phillips, 1966). Such compact structures (Richardson, 1981) are related to the evolution and folding of proteins (Bork, 1991). Domains join to form multi-functional proteins (Chothia, 1992), where each domain can perform a defined function either independently or with their neighboring domains (George and Heringa, 2002). The functionality of proteins is defined by their specific domains.
Networks of domain interactions can be constructed considering protein complexes, Rosetta Stone sequences or protein-protein interaction networks, or all three of these approaches (Wuchty, 2001; Wuchty, 2002; Ng et al, 2003). Wuchty (2001) considered the first two approaches and showed that protein domain interactions follow a power-law distribution and present both small-world behavior and a high average clustering coefficient. Costa et al. (2006) studied the relationship between connectivity and lethality at the domain level, but, since there are no databases on domain lethality, the criteria considered were domain lethality in a weak sense, where a domain is lethal if it appears in a lethal protein, and domain lethality in a strong sense, where a domain is lethal if it only appears in a single-domain lethal protein. In this case, Costa et al. showed that the correlations between connectivity and essentiality for domains, in both the weak and strong sense, are significantly higher than the correlations obtained for proteins. Therefore, domains seem to be particularly important in defining protein interactions and protein lethality.
Metabolic Networks
Metabolism is primarily determined by genes, environment and nutrition. It consists of chemical reactions catalyzed by enzymes to produce essential components such as amino acids, sugars and lipids, and also the energy necessary to synthesize and use them in constructing cellular components. Since the chemical reactions are organized into metabolic pathways, in which one chemical is transformed into another by enzymes and co-factors, such a structure can be naturally modeled as a complex network. In this way, metabolic networks are directed and weighted graphs, whose vertices can be metabolites, reactions and enzymes, and two types of edges that represent mass flow and catalytic reactions (Figure 6c). One widely considered catalogue of metabolic pathways available on-line is the Kyoto Encyclopedia of Genes and Genomes (KEGG, see Internet Resources Section).
Jeong et al. (2000) characterized the metabolic networks of 43 organisms from all three domains of life, and found that metabolic organization is not random, but follows the scale-free degree distribution. In this way, the probability that a given substrate participates in k reactions followed a power-law, P(k) ≈ k-γ, with γ ≈ 2.2 in all 43 organisms. Additionally, metabolic networks are small-world (ℓ ≈ 3), where two metabolites can be connected by a small path - paths correspond to the biochemical pathway connecting two substrates. For example, Wagner and Fell (2001) showed that the center of the E. coli metabolism map is glutamate and pyruvate, with a mean shortest path length equals to 2.46 and 2.59, respectively. An interesting finding by Jeong et al. (2000) is that the diameter of metabolic networks is the same for all the 43 organisms analyzed, contrasting with the results obtained for other types of networks where the diameter increases logarithmically with the addition of new vertices. Indeed, as the complexity of organisms grows, individual substrates tend to form more connections in order to maintain a relatively constant network diameter.
Since metabolic networks are scale-free, a few hubs concentrate a high number of connections (Wagner and Fell, 2001). This property makes such a type of network tolerant to random failures, but vulnerable to directed attacks. So, the sequential removal of nodes in decreasing order of degree increases the network diameter and quickly separates the network into disconnected components. For instance, in-silico and in-vivo mutagenesis studies of E. coli has shown a metabolic network highly tolerant to removal of a considerable number of enzymes (Edwards and Palsson, 2000). Another important discovery is that only 4% of all substrates encountered in the 43 organisms were present in all species and that such substrates are hubs (Jeong et al., 2000).
The structure of metabolic networks is organized in a modular and hierarchical fashion, and, indeed, many investigations involving metabolic networks functionality have suggested the existence of modular organization (Schuster et al., 2000). These modules are discrete entities composed of several metabolic substrates densely connected by biochemical reactions. Ravasz et al. (2002) have shown that the average clustering coefficient of metabolic networks of the 43 organisms studied by Jeong et al. (2000) is independent of the network size. Also, this value tended to be higher than those of scale-free networks of the same size. Furthermore, the average clustering coefficient followed a scaling law with the number of links, c(k) ≈ k-1, indicating hierarchical organization. This suggests that metabolic networks are characterized by a scale-free degree distribution and have an average clustering coefficient independent of network size and hierarchical and modular organization. Ravasz et al. (2002) suggested a model of metabolic organization that reproduces these properties.
Other Biological Networks
Many other biological systems, at varying space and time scales, can be represented and studied using complex networks. For instance, food webs provide an example of biological organization at the largest scale, namely that of ecology. In this case, species are represented by vertices and edges are directed from predator to prey (Cohen et al., 1970), indicating energy flow. Differently from cellular networks, food webs are not scale-free and do not present a high average clustering coefficient, which is an indication of absence of modularity (Garlaschelli et al., 2003; Garlaschelli, 2004). The importance of food webs is related to species extinction and ecological disasters with potential applications to environmental management. Other biological networks include neural networks and society. Neural networks are composed of neuronal cells connected by synapses (Watts and Strogatz, 1998) or functional areas connected by pathways (Costa and Sporns, 2005; Costa and Sporns, 2006) while societies can be organized in terms of interpersonal relationships such as collaborative work, e-mails exchanges, friendship, sexual relations. etc. (Newman, 2003; Boccaletti et al., 2006). Barabási recently suggested that the spread of diseases can be studied in social networks by looking at different complexity levels (Barabási, 2007). In this case, the top level represents society, the middle level represents the networks of diseases where two diseases are connected if they have a common genetic or functional origin and the lowest level consists of the complex network connecting cellular components such as metabolism, protein interaction and gene regulatory networks. For instance, some genes or metabolic dysfunctions can be of fundamental importance in obesity, which itself is related to diseases such as asthma, insulin resistance and diabetes. Furthermore, social interactions can be related to the spreading of dietary habits and exercise patterns. Thus, the understanding of the interactions between cellular, disease and social networks can help in quantifying which factors contribute the most to individual diseases.
Conclusion and Perspectives
Major changes have occurred in biological research during the last few decades, progressing all the way from genome sequencing to functional genomics, animal development and even medicine and ecology. Such an evolution has been largely characterized by not only increasing complexity but also the need to integrate the dynamics of processes over wider time and space scales. One of the principal challenges in biological research concerns the integration of the different systems in an ordered and effective manner, therefore increasing the chances of discovering how important biological properties emerge. Although introduced into the biological sciences only recently, complex networks research provides a powerful tool not only for organizing the complexity of biological data but also for integrating the different subsystems involved and has been wide and effectively applied to the representation, characterization and modeling of several biological systems.
The current article provided an up-to-date review of the major developments, while focusing on the most recent advances. Continuing advances in the application of complex networks in biology should be expected over the forthcoming decades, representing one of the keys to a more complete understanding of life. However, such perspectives are still subjected to a few limitations. It would be interesting to have larger databases with higher quality and confidence (Aderem, 2005). Furthermore, the wide application of complex networks concepts and methods by biologists and physicians could largely benefit not only from the development of database libraries and software applications but also from systematic collaboration between researchers with complementary backgrounds. An important related issue concerns the standardization of data formats, which would allow smoother integration of the results in the literature and the existing databases. Finally, because of the intense multidisciplinary approach implied by the application of complex networks to biology, it would be interesting to invest in enhancing the multidisciplinary nature of research teams. Provided such aspects are properly addressed, the perspectives are almost unlimited.
One of the most exciting prospects would be the comprehensive integration of the several biological subsystems so that more realistic models and simulations could be obtained. For instance, it would be possible to consider the evolution of gene families under diverse environmental changes and phylogenetic constraints, with possible implications for the development of new therapies. One particularly interesting problem which may benefit from complex networks research is the study of the gene regulatory networks of stem cells while trying to identify interactions conserved throughout different species which can pinpoint the basic framework of cell fate determination. All in all, complex networks are poised to provide one of the most important keys to systems biology.
Acknowledgments
Luciano da F. Costa is grateful to the Brazilian agencies FAPESP (05/00587-5) and CNPq (proc. 301303/06-1) for financial support. Francisco A. Rodrigues acknowledges sponsorship by FAPESP (07/50633-9) and Alexandre S. Cristino is grateful to FAPESP (06/61232-2).
Internet Rescources
Received: October 16, 2007; Accepted: January 22, 2008.
Associate Editor: Sandro José de Souza
- Aderem A (2005) Systems biology: Its practice and challenges. Cell 121:511-513.
- Albert R (2005) Scale-free networks in cell biology. J Cell Sci 118:4947-57.
- Albert R, Jeong H and Barabási AL (2000) Error and attack tolerance of complex networks. Nature 406:378-382.
- Alon U (2007) An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman and Hall, Boca Raton, 320 pp.
- Babu MM, Luscombe NM, Aravind L, Gerstein M and Teichmann SA (2004) Structure and evolution of transcriptional regulatory networks. Curr Opin Struct Biol 14:283-91.
- Balazsi G, Barabási AL and Oltvai ZN (2005) Functional organization of transcriptional-regulatory networks. FEBS J 272:103-103.
- Bar-Joseph Z, Gerber GK, Lee TI, Rinaldi NJ, Yoo JY, Robert F, Gordon DB, Fraenkel E, Jaakkola TS, Young RA, et al. (2003) Computational discovery of gene modules and regulatory networks. Nat Biotechnol 21:1337-42.
- Barabási AL (2007) Network medicine - From obesity to the "diseasome". N Engl J Med 357:404-407.
- Barabási AL and Albert R (1999) Emergence of scaling in random networks. Science 286:509-512.
- Barabási AL and Oltvai ZN (2004) Network biology: Understanding the cell's functional organization. Nat Rev Genet 5:101-113.
- Barabási AL, Jeong H, Ravasz R, Néda Z, Vicsek T and Schubert A (2002) On the topology of the scientific collaboration networks. Physica A 311:590-614.
- Berg J, Lässig M and Wagner A (2004) Structure and evolution of protein interaction networks: A statistical model for link dynamics and gene duplications. BMC Evol Biol 4:51.
- Boccaletti S, Latora V, Moreno Y, Chaves M and Hwang DU (2006) Complex networks: Structure and dynamics. Physics Rep 424:175-308.
- Bollobás B (1998) Modern Graph Theory, Graduate Texts in Mathematics. Springer, New York, 184 pp.
- Bork P (1991) Shuffled domains in extracellular proteins. FEBS Lett 286:47-54.
- Carroll SB (2000) Endless forms: The evolution of gene regulation and morphological diversity. Cell 101:577-580.
- Chartrand G and Lesniak L (1986) Graphs & Digraphs, Wadsworth Publ. Co., Belmont, 359 pp.
- Chothia C (1992) One thousand families for the molecular biologist. Nature 357:543-544.
- Cohen J, Briand F, Newman C and Palka Z (1970) Community Food Webs: Data and Theory Bio-Mathematics. Springer-Verlag, Berlin, 220 pp.
- Colizza V, Flammini A, Maritan A and Vespignani A (2005) Characterization and modeling of protein-protein interaction networks. Physica A 352:1-27.
- Conant GC and Wagner A (2003) Convergent evolution of gene circuits. Nat Genet 34:264-266.
- Costa LF and Sporns O (2005) Hierarchical features of large-scale cortical connectivity. Eur Phys J B Condensed Matter 48:567-573.
- Costa LF and Sporns O (2006) Correlating thalamocortical connectivity and activity. Appl Phys Lett 89:013903.
- Costa LF, Rodrigues FA and Travieso G (2006) Protein domain connectivity and essentiality. Appl Phys Lett 89:174101-1-174101-3.
- Costa LF, Rodrigues FA, Travieso G and Boas PRV (2007) Characterization of complex networks: A survey of measurements. Adv Physics 56:167-242.
- Davidson EH, Rast JP, Oliveri P, Ransick A, Calestani C, Yuh CH, Minokawa T, Amore G, Hinman V, Arenas-Mena C, et al. (2002) A genomic regulatory network for development. Science 295:1669-1678.
- Diestel R (2000) Graph Theory. Springer-Verlag, Heidelberg, 431 pp.
- Edwards J and Palsson B (2000) The Escherichia coli MG1655 in silico metabolic genotype: Its definition, characteristics, and capabilities. Proc Natl Acad Sci USA 97:5528-5523.
- Erdös P and Rényi A (1959) On random graphs. Publ Math 6:290-297.
- Erdös P and Rényi A (1960) On the evolution of random graphs. Publ Math Inst Hung Acad Sci 5:17-61.
- Faloutsos M, Faloutsos P and Faloutsos C (1999) On power-law relationships of the Internet topology. Comp Commun Rev 29:251-262.
- Fields S and Song O (1989) A novel genetic system to detect protein-protein interactions. Nature 340:245-246.
- Flory PJ (1941) Molecular size distribution in three dimensional polymers. II. Trifunctional branching units. J Amer Chem Soc 63:3091-3096.
- Franklin D, Godfrey V, O'Brien D, Deng C and Xiong Y (2000) Functional collaboration between different cyclin-dependent kinase inhibitors suppresses tumor growth with distinct tissue specificity. Mol Cell Biol 20:6147-6158.
- Garlaschelli D (2004) Universality in food webs. Eur Phys J B 38:277-285.
- Garlaschelli D, Caldarelli G and Pietronero L (2003) Universal scaling relations in food webs. Nature 423:165-168.
- Gavin A, Boesche M, Krause R, Grandi P, Marzioch M, Bauer A, Schultz J, Rick J, Michon A, Cruciat C, et al. (2002) Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature 415:141-147.
- Gama-Castro S, Jiménez-Jacinto V, Peralta-Gil M, Santos-Zavaleta A, Peñaloza-Spinola MI, Contreras-Moreira B, Segura-Salazar J, Muniz-Rascado L, Martinez-Flores I, Salgado H, et al. (2008) RegulonDB (version 6.0): Gene regulation model of Escherichia coli K-12 beyond transcription, active (experimental) annotated promoters and textpresso navigation. Nucleic Acids Res. 36:D120-D124.
- George RA and Heringa J (2002) An analysis of protein domain linkers: Their classification and role in protein folding. Protein Eng 15:871-879.
- Giot L, Bader J, Brouwer C, Chaudhuri A, Kuang, B, Li Y, Hao Y, Ooi C, Godwin B, Vitols E, et al. (2003) A protein interaction map of Drosophila melanogaster. Science 302:1727-1736.
- Guelzim N, Bottani S, Bourgine P and Kepes F (2002) Topological and causal structure of the yeast transcriptional regulatory network. Nat Genet 31:60-63.
- Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, MacIsaac KD, Danford TW, Hannett NM, Tagne JB, Reynolds DB, Yoo J, et al. (2004) Transcriptional regulatory code of a eukaryotic genome. Nature 431:99-104.
- Hartwell LH, Hopfield JJ, Leibler S and Murray AW (1999) From molecular to modular cell biology. Nature 402:C47-52.
- Hishigaki H, Nakai K, Ono T, Tanigami A and Takagi T (2001) Assessment of prediction accuracy of protein function from protein-protein interaction data. Yeast 18:523-531.
- Hormozdiari F, Berenbrink P, Prulj N and Sahinalp SC (2007) Not all scale-free networks are born equal: The role of the seed graph in PPI network evolution. PLoS Comput Biol 3:e118.
- Huerta AM, Salgado H, Thieffry D and Collado-Vides J (1998) RegulonDB: A database on transcriptional regulation in Escherichia coli Nucleic Acids Res 26:55-59.
- Ihmels J, Friedlander G, Bergmann S, Sarig O, Ziv Y and Barkai N (2002) Revealing modular organization in the yeast transcriptional network. Nat Genet 31:370-377.
- Jeong H, Tombor B, Albert R, Oltvai ZN and Barabási AL (2000) The large-scale organization of metabolic networks. Nature 407:651-654.
- Jeong H, Mason SP, Barabási AL and Oltvai ZN (2001) Lethality and centrality in protein networks. Nature 411:41-42.
- Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, et al. (2002) Transcriptional regulatory networks in Saccharomyces cerevisiae Science 298:799-804.
- Levine M and Tjian R (2003) Transcription regulation and animal diversity. Nature 424:147-51.
- Lockhart DJ and Winzeler EA (2000) Genomics, gene expression and DNA arrays. Nature 405:27-36.
- MacIsaac KD, Wang T, Gordon DB, Gifford DK, Stormo GD and Fraenkel E (2006) An improved map of conserved regulatory sites for Saccharomyces cerevisiae BMC Bioinformatics 7:113.
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D and Alon U (2002) Network motifs: Simple building blocks of complex networks. Science 298:824-827.
- Newman MEJ (2001) Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys Rev E Stat Nonlin Soft Matter Phys 64:016132.
- Newman MEJ (2002) Assortative mixing in networks. Phys Rev Lett 89:208701.
- Newman MEJ (2003) Structure and function of complex networks. SIAM Review 45:167-256.
- Ng S, Zhang Z and Tan S (2003) Integrative approach for computationally inferring protein domain interactions. Bioinformatics 19:923-929.
- Ohno S (1970) Evolution by Gene Duplication. Springer-Verlag, New York, 160 pp.
- Phillips DC (1966) The three-dimensional structure of an enzyme molecule. Sci Am 215:78-90.
- Poyatos J and Hurst L (2004) How biologically relevant are interaction-based modules in protein networks? Genome Biol 5:R93.
- Rain J, Selig L, De Reuse H, Battaglia V, Reverdy C, Simon S, Lenzen G, Petel F, Wojcik J, Schaechter V, et al. (2001) The protein-protein interaction map of Helicobacter pylori Nature 409:211-215.
- Ravasz E, Somera A, Mongru D, Oltvai Z and Barabási A (2002) Hierarchical organization of modularity in metabolic networks. Science 297:1551-1555.
- Ren B, Robert F, Wyrick JJ, Aparicio O, Jennings EG, Simon I, Zeitlinger J, Schreiber J, Hannett N, Kanin E, et al. (2000) Genome-wide location and function of DNA binding proteins. Science 290:2306-2309.
- Richardson JS (1981) The anatomy and taxonomy of protein structure. Adv Prot Chem 34:167-339.
- Schena M, Shalon D, Davis RW and Brown PO (1995) Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science 270:467-470.
- Schuster S, Fell D and Dandekar T (2000) A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat Biotechnol 18:326-332.
- Schwikowski B, Uetz P and Fields S (2000) A network of protein-protein interactions in yeast. Nat Biotechnol 18:1257-1261.
- Shen-Orr SS, Milo R, Mangan S and Alon U (2002) Network motifs in the transcriptional regulation network of Escherichia coli Nat Genet 31:64-68.
- Sole R and Fernandez P (2003) Modularity "for free" in genome architecture? Arxiv preprint q-bio/0312032.
- Teichmann SA and Babu MM (2004) Gene regulatory network growth by duplication. Nat Genet 36:492-496.
- Thieffry D, Huerta AM, Perez-Rueda E and Collado-Vides J (1998) From specific gene regulation to genomic networks: A global analysis of transcriptional regulation in Escherichia coli Bioessays 20:433-440.
- Uetz P and Hughes RE (2000) Systematic and large-scale two-hybrid screens. Curr Opin Microbiol 3:303-308.
- Vázquez A and Moreno Y (2003) Resilience to damage of graphs with degree correlations. Phys Rev E Stat Nonlin Soft Matter Phys 67:015101.
- Vázquez A, Flammini A, Maritan A and Vespignani A (2003a) Global protein function prediction from protein-protein interaction networks. Nat Biotechnol 21:697-700.
- Vázquez A, Flammini A, Maritan A and Vespignani A (2003b) Modeling of protein interaction networks. Complexus 1:38-44.
- Vogelstein B, Lane D and Levine AJ (2000) Surfing the p53 network. Nature 408:307-310.
- Wagner A (2001) The yeast protein interaction network evolves rapidly and contains few redundant duplicate genes. Mol Biol Evol 18:1283-1292.
- Wagner A (2003) How the global structure of protein interaction networks evolves. Proc Biol Sci 270:457-466.
- Wagner A and Fell DA (2001) The small world inside large metabolic networks. Proc Biol Sci 268:1803-1810.
- Walhout A, Boulton S and Vidal M (2000) Yeast two-hybrid systems and protein interaction mapping projects for yeast and worm. Yeast 17:88-94.
- Watts DJ and Strogatz SH (1998) Collective dynamics of small-world networks. Nature 393:440-442.
- West DB (2001) Introduction to Graph Theory. Prentice Hall, Upper Saddle River, 588 pp.
- Wray GA, Hahn MW, Abouheif E, Balhoff JP, Pizer M, Rockman MV and Romano LA (2003) The evolution of transcriptional regulation in eukaryotes. Mol Biol Evol 20:1377-419.
- Wuchty S (2001) Scale-free behavior in protein domain networks. Mol Biol Evol 18:1694-1702.
- Wuchty S (2002) Interaction and domain networks of yeast. Proteomics 2:1715-1723.
- Wuchty S, Oltvai ZN and Barabási AL (2003) Evolutionary conservation of motif constituents in the yeast protein interaction network. Nat Genet 35:176-179.
- Yu H, Luscombe NM, Qian J and Gerstein M (2003) Genomic analysis of gene expression relationships in transcriptional regulatory networks. Trends Genet 19:422-427.
- KEGG: www.genome.jp/kegg
Send correspondence to:
Publication Dates
-
Publication in this collection
18 Aug 2008 -
Date of issue
2008
History
-
Accepted
22 Jan 2008 -
Received
16 Oct 2007