Abstract
Evaluation of performance stability and high yield is essential for yield trials conducted in different environments. We determined the stability of 10 bread wheat (Triticum aestivum L.) genotypes (5 cultivars and 5 advanced lines) using nonparametric stability measures and compared nonparametric stability statistics across 19 environments in the Central Anatolian Region of Turkey. Experiments were setup in a randomized complete block design with four replications. Nonparametric stability measures revealed that AL-2, Karahan-99 and Altay-2000 were the most stable and well adapted genotypes across the 19 environments. In addition, it was concluded that graphs of mean grain yield (t ha-1) vs. nonparametric measures (Si(¹), Si(²), S(³), Si(6) and σgy) values and kr vs. σr values could enhance visual efficiency of genotype selection based on genotype by environment interaction. Furthermore, high TOP values, Si(³) and Si(6) were associated with high grain yield, but the other nonparametric stability measures were not positively correlated with grain yield and instead characterized a static concept of stability. Choice of genotype for increased grain yield in bread wheat would, therefore, be expected to change yield stability by increasing the values of the Si(³), Si(6) and TOP nonparametric stability statistics.
bread wheat (Triticum aestivum L.); nonparametric stability analysis; yield
Nonparametric stability methods for interpreting genotype by environment interaction of bread wheat genotypes (Triticum aestivum L.)
Mevlut Akcura; Yuksel Kaya
Bahri Dagdas International Agricultural Research Institute, Konya, Turkey
Send correspondence to Send correspondence to: Mevlut Akcura Bahri Dagdas International Agricultural Research Institute P.O. Box 125 Konya, Turkey E-mail: mevlut_akcura@yahoo.com.
ABSTRACT
Evaluation of performance stability and high yield is essential for yield trials conducted in different environments. We determined the stability of 10 bread wheat (Triticum aestivum L.) genotypes (5 cultivars and 5 advanced lines) using nonparametric stability measures and compared nonparametric stability statistics across 19 environments in the Central Anatolian Region of Turkey. Experiments were setup in a randomized complete block design with four replications. Nonparametric stability measures revealed that AL-2, Karahan-99 and Altay-2000 were the most stable and well adapted genotypes across the 19 environments. In addition, it was concluded that graphs of mean grain yield (t ha-1) vs. nonparametric measures (Si(1), Si(2), S(3), Si(6) and σgy) values and kr vs. σr values could enhance visual efficiency of genotype selection based on genotype by environment interaction. Furthermore, high TOP values, Si(3) and Si(6) were associated with high grain yield, but the other nonparametric stability measures were not positively correlated with grain yield and instead characterized a static concept of stability. Choice of genotype for increased grain yield in bread wheat would, therefore, be expected to change yield stability by increasing the values of the Si(3), Si(6) and TOP nonparametric stability statistics.
Key words: bread wheat (Triticum aestivum L.), nonparametric stability analysis, yield.
Introduction
The study of genotype by environment interaction (GEI) has assumed great importance in genotype testing programs because yield performance of a genotype is a result of the interaction between the genotype and environment. Environmental factors, such as rainfall, temperature and soil structure play an important role in genotype performance, grain yield and quality. Increase of genetic potential for yield is an important objective of bread wheat breeding programs in Turkey.
Genotype by environment interactions are important sources of variation in any crop, and the term stability is sometimes used to characterize a genotype, which shows a relatively constant yield, independent of changing environmental conditions. On the basis of this idea, genotypes with a minimal variance for yield across different environments are considered stable. This idea of stability may be considered as a biological or static concept of stability (Becker and Leon, 1988). This concept of stability is not acceptable to most breeders and agronomists, who prefer genotypes with high mean yields and the potential to respond to agronomic inputs or better environmental conditions (Becker, 1981). The high yield performance of released varieties is one of the most important targets of breeders, which explains why they prefer a dynamic concept of stability (Becker and Leon, 1988).
Bread wheat genotypes are generally evaluated in multi-environment trials (MET) to test their performance across environments and to select the best genotypes for specific environments. In most cases, GEI is significant, complicating yield improvement studies, but the release of a genotype with consistent performance over a wide range of environments should lead to stability in production. However, a measure of the relative yield stability of bread wheat genotypes under a wide range of environmental conditions is needed for determining the efficiency of a genotype evaluation program. In light of these considerations a number of statistical procedures have been applied to estimate the stability of genotypes and related interactions.
The statistical techniques applied to this type of data can be as follows: linear formulations, like joint-regression (Yates and Cochran, 1938; Eberhart and Russell, 1966); multivariate clustering techniques (Lin and Butler, 1990); multiplicative methods based on additive main effects and multiplicative interaction (AMMI; Zobel et al., 1988; Gauch, 1992); or nonparametric methods (Huehn, 1979). Genotype by environment interaction modeled using multi-environment trials can be used to assess phenotypic stability of genotypes, although phenotypic stability is often defined in a variety of ways, with increasing numbers of stability statistics having been developed (Gauch and Zobel, 1996; Sabaghnia et al., 2006).
There are two major approaches to studying genotype by environment interactions and determining the adaptation of genotypes (Huehn, 1996). The most common approach is parametric analyses, which are based on statistical assumptions about the distribution of genotypic, environmental and GEI effects. Another approach is nonparametric or analytical clustering, which makes no specific modeling assumptions when relating environments and phenotypes relative to biotic and abiotic environmental factors. Parametric measures of phenotypic stability are mostly related to variance components or related statistics. These stability estimates have good properties under certain statistical assumptions, based on the normal distribution of errors and interaction effects, but may not perform well if these assumptions are violated by factors such as the presence of outliners (Huehn, 1990a). Due to the fact that parametric tests for the significance of variances and variancerelated measures can be very sensitive to the underlying statistical assumptions an alternative approach is to use techniques such as non-parametric measures that are more robust to departures from the assumptions used in parametric analysis (Adugna and Labuschagne, 2003).
The other approach is to use nonparametric techniques, and several procedures have been proposed based on comparing ranks of genotypes in each environment, with genotypes with similar ranking across environments being considered stable (Huehn, 1979; Nassar and Huehn, 1987; Kang, 1988; Ketata et al., 1989; Fox et al., 1990). The following four nonparametric measures of phenotypic stability have been proposed by Huehn (1979) and Nassar and Huehn (1987): Si(1), the genotype absolute rank difference mean as tested over n environments; Si(2), the between-ranks variance over the n environments; Si(3), the sum of the absolute deviations of the squares of ranks for each genotype; and Si(6), the sum of the squares of ranks for each genotype relative to the mean of ranks. See also Sabaghnia et al. (2006). It is possible to not only assign mean yield ranks, with the genotype with the highest yield being ranked 1, but also ranks for the Shukla stability variance (Shukla, 1972) in which the lowest estimated yield value is ranked 1 (Kang 1988), with the sum of these two sets of ranks resulting in an index in which the genotype with lowest rank-sum is considered to be the most desirable. In addition, a nonparametric superiority measure for general adaptability has been suggested based on stratified ranking of the cultivars in each separate environment, with the proportion of sites at which a specific cultivar occurred in the top third of the ranks (the TOP value), the middle third of the ranks (the MID value) and the lower third of the ranks (the LOW value) being calculated, a genotype with a high TOP value (i.e., occurring principally in the top third of the ranks) being considered as a widely adapted genotype (Fox et al., 1990). Nonparametric statistical procedures have several advantages over parametric stability statistics in that they are easy to use and interpret, no assumptions are needed regarding the distribution of the observed values, removal or addition of one or several genotypes cause little variation in the results and outlier bias is reduced (Huehn, 1990a).
The objectives of this study were to identify bread wheat genotypes that have both high grain yield and stable performance across different environments for semiarid areas of Turkey and study the relationships between different nonparametric stability statistics.
Materials and Methods
Data source
Ten bread wheat (Triticum aestivum L.) genotypes (Table 1) were evaluated at different sites in Turkey during the 2002/2003 and 2003/2004 growing seasons (Table 2). For both growing seasons the sowing dates ranged from 20 September to 15 October depending on the soil moisture. The total number of environments (site x growing season) was 19, each location in a given year being considered as a separate environment.
Experimental layout was a randomized complete block design with four replications. Sowing was done by an experimental drill in 1.2 m x 7 m plots, consisting of six rows with 20 cm left between the rows. Seeding rate was 550 seeds m-2 for all environments. Fertilizer application was 27 kg N ha-1 and 69 kg P2O5 ha-1 at planting and 40 kg N ha-1 at the stem elongation stage. Harvesting was done in 1.2 m x 5 m plots by experimental combine. Grain yield (t ha-1) was obtained by converting plot yield to yield per hectare.
Statistical analysis
We used four sets of nonparametric statistics to estimate stability in this study. One of them (Huehn, 1979; Nassar and Huehn, 1987) consisted of four nonparametric stability statistics (Si(1), Si(2), Si(3) and Si(6)) combining mean yield and stability (see also Becker and Leon, 1988). Two-way data with k genotypes and q environments used rij as the rank of the ith genotype in the jth environment and  i as the mean rank across all environments for the ith genotype, the equations used being as follows:
i as the mean rank across all environments for the ith genotype, the equations used being as follows:
Si(1), genotype absolute rank difference mean as tested over n environments (Huehn, 1990a)
Si(2), between-ranks variance over n environments (Huehn, 1990a)
Si(3), sum of the absolute deviations of the squares of ranks for each genotype (Nassar and Huehn, 1987)
Si(6), sum of the squares of ranks for each genotype relative to the mean of ranks (Nassar and Huehn, 1987)
where ◊ rij are ranks of genotypes in each environment based on Xij - (Xi - X ), rij* are ranks of genotypes in each environment based on the mean yields Xij,  =
= 
 /q and
/q and  i• =
i• =  rij/q.
rij/q.
The significance tests for the Si(1) and Si(2) statistics were determined as suggested by Nassar and Huehn (1987). The chi-square (χ2) values associated with Si(1) and Si(2) were obtained using the expression χ2 = S Zi(m), where m = 1, 2, Zi(m) = [Si(m) - E (Sim)]2 / V(Sim), E(Si(m)) = expected value (= mean) of Si(m), and V(Si(m)) = Si(m) variance. The significance test for the null hypothesis that all the genotypes are equally stable was done using a chi-square distribution with k degrees of freedom.
Another set of nonparametric stability statistic was Kang's (1988) rank-sum (RS), where both yield and Shukla's stability variance are the selection criteria, that assigns a weight of one to both yield and stability, which allows identification of high-yielding and stable varieties. In this method, both the highest yielding genotype and the genotype with the lowest stability variance are ranked 1 and after ranking all the genotypes the ranks by yield and by stability variance are added for each genotype and the genotype with the lowest RS value is considered the most desirable.
We also used the methodology described by Fox et al. (1990), who proposed a nonparametric superiority measure for general adaptability using stratified ranking of cultivars. Ranking was done at each location separately and the number of sites at which the cultivar occurred in the TOP, MID, and LOW third of the ranks was computed. Genotypes mostly within the top third were considered as widely adapted cultivars.
The last set of nonparametric stability statistic used in this study included the rank (kr) method, plotting mean rank across environments against standard deviation (σr) of ranks for all genotypes, and grain yield (gy), plotting mean grain yield across environments against standard deviation (σgy) of yields for all genotypes Ketata et al. (1989). A genotype is considered stable if its kr or gy value is relatively consistent in all the environments. i.e., showing low kr or high gy and having a low σr (Flores et al., 1998). The σr, calculated from the yield rank of genotypes in each environment (rij) based on the uncorrected mean yield values (Xij), is expressed as
The σgy, calculated from the grain yield of genotypes in each environment (gyij) based on the uncorrected mean yield values (Xij), is expressed as
All the stability statistics were compared using Spearman's rank correlation (Steel and Torrie, 1980). The SAS software (SAS Institute, 1999) was used to analyze the results of the nonparametric stability analysis based on the mean values of yield (t ha-1) obtained over environments. Lu (1995) developed a SAS-based computer program that computes the nonparametric Si(1) and Si(2) statistics and a comprehensive SAS program (SASG x ESTAB) became available which calculates different parametric and nonparametric stability statistics (Hussein et al., 2000). Both of these programs were used to calculate different nonparametric stability statistics described in our paper.
Results and Discussion
The overall mean grain yield for all the genotypes varied between environments ranged from 1.55 t ha-1 for environment 4 to 4.36 t ha-1 for environment 11 (Table 2). Variance analysis for grain yield showed that, genotypes, environments and GEI were significant (data not shown). The significant GEI indicated that the responses of the genotypes changed depending on environmental conditions.
Nine stability measures and the mean yield for each genotype over all environments are given in Table 3. The Si(1) and Si(2) (Nassar and Huehn, 1987) statistics are two rank stability measures, the Si(1) statistic measuring the mean absolute rank difference of a genotype over environments, with Si(1) = 0 for a genotype with maximum stability, while Si(2) gives the variance between the ranks over environments, with zero variance being an indication of maximum stability. The exact variance and expectation of Si(1) and Si(2) were given by Huehn (1990a). The nonparametric Si(1) and Si(2) statistics are measures of stability alone and are strongly correlation with each other even when using the uncorrected yield data, being nearly perfectly correlated with each other if the uncorrected yield data is adjusted for genotypic effects using the corrected values. However, the values of the Si(1) and Si(2) statistics obtained using the uncorrected yield data and the corrected data are often considerably different and show only medium or low correlation (Huehn, 1990b). The Si(1) statistic is preferred for practical applications because it is very easy to calculate and allows a clear and objective interpretation it represents the mean absolute rank difference between the environments. Furthermore, an efficient test of significance is available for this statistic (Huehn, 1990a).
The Zi(1) and Zi(2) values for each genotype were calculated based on the ranks of the corrected data and summed over genotypes to obtain Z values (Table 3), with the Z1 sum of 4.98 and the Z2 sum of 4.57 both being less than the critical χ2 value (18.31 for n - 1 = 10 environments and p = 0.05) and thus indicating no significant differences in rank stability among the nine genotypes grown in the eleven environments. No genotype was significantly unstable relative any of the other genotypes because they all showed small Z values compared with the critical χ2 value (6.63 for n - 1 = 1 genotypes and p = 0.01), a significance level of p = 0.01 corresponding to a comparison-wise error rate of about 0.05 (Lu, 1995).
Plots of mean yield (t ha-1) against the Si(1) and Si(2) values are given in Figures 1 and 2 respectively. Mean Si(1) and Si(2) values and grand mean yield divide both figures into four sections, with section 1 containing that high-yielding genotypes with small Si(1) and Si(2) values, section 2 containing high-yielding genotypes with large Si(1) and Si(2) values, section 3 containing low-yielding genotypes with large Si(1) and Si(2) values, and section 4 containing low-yield genotypes with small Si(1) and Si(2) values. The genotypes were distributed in the different sections of Figures 1 and 2 as follows: section 1 contained the Karahan-99, Altay-2000 and AL-2 genotypes, which can be considered to be the most stable and well adapted genotypes in all environments (i.e., had general adaptation ability); section 2 contained the Gerek-79 and AL-3 genotypes, which were assumed to be sensitive to environmental changes and to be more specific with regard to their adaptability to high-yielding environments; section 3 contained the Bagci-2002, AL-1 and AL-5 genotypes, which appeared to be poorly adapted in all the environments; and section 4 contained the Yakar-99 and AL-4 genotypes, which showed greater resistance to environmental fluctuation and therefore increasing specificity of adaptability to low-yielding environments. Regarding the choice between the Si(1) and Si(2) statistic, Nassar and Huehn (1987) suggest that the S1(1) statistic should be used in any case in which a genotype shows unusual fluctuations between sections. Prior to any decision to use a genotype in a specific environment it is crucial to be aware of the ranking of the genotypes in each environment, with Figure 1 [mean yield (t ha-1) against Si(1)] and Figure 2 [mean yield (t ha-1) against Si(2)], which show high concordance, providing a means to achieve this. For example, the Karahan-99, AL-2 and Altay-2000 genotypes were most stable and well adapted across environments (Figure 1 and 2) but Karahan-99 had the higher mean rank and AL-2 the lower, so Karahan-99 should be selected in preference to AL-2 on account of the fact that Karahan-99 has higher yield across environments than AL-2.
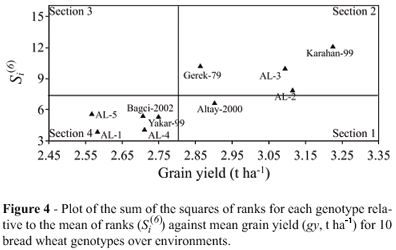
Two other nonparametric statistics, described by Huehn (1979), Si(3) and Si(6) (Figures 3 and 4) combine yield and stability based on the yield ranks of genotypes in each environment. These statistics measure stability in units of the mean rank of each genotype, described in more detail in the original paper by Huehn (1979), with the lowest value for each of these statistics indicating maximum stability for a certain genotype. For example, the Si(1) and Si(2) statistics showed that AL-2 was the most stable genotype, although this was supported by the Si(3) statistic, but the Si(6) statistic indicated that Altay-2000 was the most stable genotype. The mean yield of the AL-2 genotype was relatively high, but the mean yield of Altay-2000 was relatively low (Table 3).
Kang's (1988) nonparametric stability statistic (RS) uses both yield and stability variance (Shukla, 1972), with the genotype having the lowest rank-sum being the most favorable. In our study, the AL-2 genotype had the minimum RS value and was, therefore, the most stable genotype, followed by the Altay-2000, Yakar-99 and AL-4 genotypes (Table 3). The RS statistic also indicated AL-1, AL-5 and Gerek-79 were the most undesirable genotypes (Table 3).
According to Fox et al. (1990) a genotype usually found in the top third of entries across environments can be considered relatively well adapted and stable. Thus, in our study, the most stable genotype was Karahan-99 because it ranked in the top third of genotypes in a high percentage of environments (i.e., had a high TOP value), followed by the AL-2 and AL-3 genotypes, with the least-desirable genotypes being AL-4, Yakar-99, AL-5 and AL-1 (Table 3).
Ketata et al. (1989) proposed using two nonparametric methods, one based on ranking and the other on grain yield. In the ranking method the rank (kr) and the standard deviation of ranks (σr) is used, with the high yielding (3.12 t ha-1) and stable AL-2 genotype being in section 1 while the low yielding (2.57 t ha-1 to 2.75 t ha-1) and stable Altay-2000, Bagci-2002, Yakar-99, AL-1 and AL-4 genotypes are in section 2 (Figure 5). In contrast to the general adaptability of genotypes in sections 1 and 2, the genotypes in sections 3 and 4 lacked stable yield performance but, their average yield was not low and when single environments were considered even extremely high. These genotypes (Karahan-99, Gerek-79 and AL-3) had rank values lower than the mean kr value and had σr greater than the mean (Table 3) and appeared to be sensitive to environmental changes. In fact, the Karahan-99 and AL-3 genotypes gave higher grain yields than the overall mean and could be recommended for cultivation in favorable environments, whereas Gerek-79, which also produced almost average grain yield, had kr and σr values close to the mean and exhibited less sensitivity to environmental changes based on these nonparametric stability statistics (Figure 5). Genotype AL-5 in section 4 of Figure 5 showed a kr value greater than the mean kr and gy below the overall mean (Table 3), and was relatively better adapted to poor environments and insensitive to environmental changes. The results for the grain yield gy and grain yield standard deviation (σgy) method are presented in Figure 6, from which it can be seen that Karahan-99 (3.13 t ha-1), Altay-2000 (2.90 t ha-1) and Gerek-79 (2.86 t ha-1) were all high yielding genotypes with stability appearing section 2. In section 4 genotypes AL-2 (3.12 t ha-1) and AL-3 (3.10 t ha-1) had higher gy than the mean and their σgy values were close to the mean (0.96), with the high gy and low σgy values indicating that these genotypes could be considered stable.
The relationship between the four different sets of stability statistics
We found significant positive rank correlations between gy and the nonparametric Si(3), Si(6) and TOP statistics (Table 4), supporting the findings of Becker and Leon (1988) who also reported high rank correlations between gy and the Si(3) and Si(6) statistics. Selection for increased grain yield in bread wheat would, therefore, be expected to change grain yield stability by increasing the Si(3), Si(6) and TOP stability statistics. This would lead to the development of genotypes specifically adapted to environments with optimal growing conditions. Such genotypes would be less than optimal in yield performance when cultivated in poor environments though they could give maximum yields when cultivated in optimal environments. On the other hand, a significantly negative rank correlation between gy and kr was found. Furthermore, there were significant positive correlation between Si(2) and RS between Si(3) and Si(6) TOP with σr and also between the Si(6) and TOP and σr nonparametric stability statistics. In addition, there were significant negative rank correlations between kr and gy, Si(3), Si(6) and TOP (Table 4).
The Si(1), Si(2) and RS stability statistics were positively and significantly correlated and, indicated that the three measures were similar in classifying the genotypes according to their stability under different environmental conditions. Scapim et al. (2000) also found significantly positive correlations between the Si(1), Si(2) and Si(3) nonparametric statistics. Similarly, Flores et al. (1998) reported high rank correlations between Si(1) and Si(2) in faba bean (Vicia faba L.) and pea (Pisum sativum L.). Consequently, only one of these statistics would be sufficient to select the stable genotypes in a breeding program.
Nonparametric stability measurements seem to be useful alternatives to parametric measurements (Yue et al., 1997), although they do not supply information about genotype adaptability. In fact, there are several reasons to prefer nonparametric stability models, one being that outlier bias is avoided and no assumptions are needed about the distribution of the data and the second is that nonparametric statistics are easy to use and to interpret. Based on these considerations, it appears that the estimation of stability is an appropriate approach for GEI analysis, this view being supported by the fact that a variety of parametric and nonparametric stability measures have been compared in the literature (Lin et al, 1986; Flores et al., 1998; Sabaghnia et al., 2006).
Our study indicates that the nonparametric statistics Si(1), Si(2), Si(3), Si(6) plus kr, σr and σgy values together with ranks can be recommended for estimating the nonparametric stability statistics of genotypes grown in different environments. These statistics can be used by breeders and agronomists who need to make selection based upon genotype x environment interactions. In addition, there were significant positive rank correlations between gy and TOP, Si(3) and Si(6), indicating that selection for increased grain yield in bread wheat would therefore be expected to change grain yield stability by increasing the Si(3), Si(6) and TOP nonparametric stability statistics. Furthermore, the plots relating mean grain yield (gy, t ha-1) against the nonparametric Si(1), Si(2), Si(3), Si(6) and σgy statistics and kr against σr values could enhance the visual efficiency of selection based on GEI.
Received: October 5, 2007; Accepted: March 13, 2008.
Senior Editor: Ernesto Paterniani
- Adugna W and Labuschagne MT (2003) Parametric and nonparametric measures of phenotypic stability in linseed (Linum usitatissimum L.). Euphytica 129:211-218.
- Becker HC (1981) Correlations among some statistical measures of phenotypic stability. Euphytica 30:835-840.
- Becker HC and Leon J (1988) Stability analysis in plant breeding. Plant Breed 101:1-23.
- Eberhart SA and Russell WA (1966) Stability parameters for comparing varieties. Crop Sci 6:36-40.
- Flores E, Moreno MT and Cubero JI (1998) A comparison of univariate and multivariate methods to analyze environments. Field Crops Res 56:271-286.
- Fox PN, Skovmand B, Thompson BK, Braun HJ and Cormier R (1990) Yield and adaptation of hexaploid spring triticale. Euphytica 47:57-64.
- Gauch HG (1992) Statistical Analysis of Regional Yield Trials. Elsevier, Amsterdam, 278 pp.
- Gauch HG and Zobel RW (1996) AMMI analysis of yield trials. In: Kang MS and Gauch HG (eds) Genotype by Environment Interaction. CRC Press, Boca Raton, pp 85-122.
- Hildebrand PE (1990) Modified stability analysis and on-farm research to breed specific adaptability for ecological diversity. In: Kang MS (ed) Genotype-By-Environment Interaction and Plant Breeding. Louisana State, Baton Rouge, pp 169-180.
- Huehn M (1990a) Nonparametric measures of phenotypic stability: I. Theory. Euphytica 47:189-194.
- Huehn M (1990b) Nonparametric measures of phenotypic stability: II. Applications. Euphytica 47:195-201.
- Huehn M (1996) Non-parametric analysis of genotype x environment interactions by ranks. In: Kang MS and Gauch HG (eds) Genotype by Environment Interaction. CRC Press, Boca Raton, pp 213-228.
- Huehn VM (1979) Beiträge zur Erfassung der phänotypischen Stabilität. EDV Med Biol 10:112-117.
- Hussein MA, Bjornstad A and Aastveit AH (2000) SASG x ESTAB: A SAS program for computing genotype x environment stability statistics. Agron J 92:454-459.
- Kang MS (1988) A rank-sum method for selecting high-yielding, stable corn genotypes. Cereal Res Comm 16:113-115.
- Ketata HY and Yau SK Nachit M (1989) Relative consistency performance across environments. International Symposium on Physiology and Breeding of Winter Cereals for stressed Mediterranean Environments, Montpellier, pp 391-400.
- Lin CS and Butler G (1990) Cluster analyses for analyzing two-way classification data. Agron J 82:344-348.
- Lin CS, Binns MR and Lefkovitch LP (1986) Stability analysis. where do we stand? Crop Sci 26:894-900.
- Lu HS (1995) PC-SAS Program for estimating Huhn's nonparametric stability statistics. Agron J 87:888-891.
- Nassar R and Huehn M (1987) Studies on estimation of phenotypic stability: Tests of significance for nonparametric measures of phenotypic stability. Biometrics 43:45-53.
- Sabaghnia N, Dehghani H and Sabaghpour SH (2006) Nonparametric methods for interpreting genotype x environment interaction of lentil genotypes. Crop Sci 46:1100-1106.
- SAS Institute (1999) SAS/STAT User's Guide. 2nd edition. SAS Institute Inc., Cary.
- Scapim CA, Oliveira VR, Braccinil AL, Cruz CD, Andrade CAB and Vidigal MCG (2000) Yield stability in maize (Zea mays L.) and correlations among the parameters of the Eberhart and Russell, Lin and Binns and Huehn models. Genet Mol Biol 23:387-393.
- Shukla GK (1972) Some aspects of partitioning genotype-environmental components of variability. Heredity 28:237-245.
- Steel RGD and Torrie JH (1980) Principles and Procedures of Statistics, a Biometrical Approach. 2nd edition. McGraw-Hill, New York, 633 pp.
- Yates E and Cochran WG (1938) The analysis of groups of experiments. J Agric Sci 28:556-580.
- Yue GL, Roozeboom KL, Schapaugh WT and Liang GH (1997) Evaluation of soybean cultivars using parametric and non-parametric stability estimates. Plant Breed 116:271-275.
- Zobel RW, Wright MJ and Gauch HG (1988) Statistical analysis of a yield trial. Agron J 80:388-393.
Send correspondence to:
Publication Dates
-
Publication in this collection
01 Sept 2008 -
Date of issue
Dec 2008
History
-
Accepted
13 Mar 2008 -
Received
05 Oct 2007