Alguns aspectos da mecânica das alças de retração ortodôntica

Some aspects of the mechanics of the orthodontic retraction springs

ARTIGO INÉDITO

Alguns aspectos da mecânica das alças de retração ortodôntica

Some aspects of the mechanics of the orthodontic retraction springs

Marcelo do Amaral Ferreira^I; Paulo César Borges^II; Marco Antônio Luersen^II

^IEspecialista em Ortodontia, Mestre em Ciências e Doutorando em Ciências pelo CPGEI – Programa de Pós-Graduação em Engenharia Elétrica e Informática Industrial - UTFPR (Universidade Tecnológica Federal do Paraná)

^IIDoutor em Engenharia pelo PPGEM – Programa de Pós-Graduação em Engenharia Mecânica e de Materiais - UTFPR

^{Endereço para correspondência}

RESUMO

As alças de retração ortodôntica são comumente empregadas em sistema Edgewise por meio de uma abordagem seccional (ex.: retração de caninos) ou por meio de uma abordagem segmentada (ex.: retração dos dentes anteriores em conjunto). Estas alças podem modular a demanda de ancoragem, dependendo dos objetivos impostos pelo plano de tratamento. Neste trabalho são discutidas as propriedades mecânicas relacionadas ao projeto de alças de retração ortodôntica, o sistema de forças decorrente de sua conformação geométrica e ativação, e os métodos empregados para testá-las. Dentre as técnicas utilizadas na análise de uma alça, o Método dos Elementos Finitos (MEF) merece destaque. Embora seja baseado em modelos matemáticos, é uma ferramenta eficaz e não onerosa para a simulação computacional de um protótipo, podendo-se assim avaliá-lo antes de sua construção física. Já os métodos experimentais se aproximam mais da condição real, porém com custo mais elevado. A utilização em diferentes estágios de ambos os métodos é aconselhável para um melhor desenvolvimento e caracterização dos protótipos.

Palavras-chave: Alças ortodônticas. Propriedades mecânicas. Testes mecânicos. Unidade de ancoragem.

ABSTRACT

Retraction springs are commonly used in Edgewise mechanics in a sectional (e.g. canine retraction) or in a segmental approach (e.g. "en masse" anterior retraction). These springs can modulate the anchorage needs depending on the treatment plan objectives. In this work it is discussed the mechanical properties related to the spring’s design, the force system originated by their geometric shape and activation, and the methods used to test them. Among the techniques used to analyze a retraction spring, it can be pointed out the Finite Element Method (FEM). Nevertheless the FEM is based on mathematical models, it is an efficient non-onerous way for computational simulation of a prototype, so it can be evaluated before its physical construction. On the other hand, the experimental methods are closer to real conditions, but they are more costly. The use of both methods in different stages is recommended for a better development and characterization of prototypes.

Key words: Orthodontic springs. Mechanical properties. Mechanical experiments. Anchorage unit.

INTRODUÇÃO

As alças de retração ortodôntica vêm sendo estudadas há cerca de cinqüenta anos, por meio de procedimentos experimentais^{4,5,7-10,12,13,14,23,25}, analíticos^{15,18,21,22,27,29} e numéricos como o Método dos Elementos Finitos (MEF)^1,11,24. Uma vez ativadas, as alças exercem carregamento sobre um ou mais dentes e esses o transmitem para o ligamento periodontal, produzindo movimentação dentária. Conforme o plano de tratamento delineado, pode-se obter a retração isolada de caninos, com o intuito de "aliviar" uma situação de desalinhamento dentário, por falta de espaço (discrepância dentoalveolar), na região anterior e também de obter relação de caninos de Classe I. Podem ser utilizadas como componentes dos arcos segmentados para a retração do bloco anterior (caninos e incisivos), protração dos blocos posteriores (pré-molares e molares), ou ambos os movimentos. A protração de um lado do arco dentário e retração de outro podem ser planejadas em casos onde ocorra assimetria^2,19.

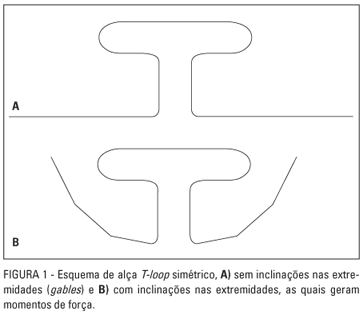
Um complexo sistema de forças torna-se presente quando da inserção dessas alças nas canaletas verticais dos braquetes dos caninos e nas canaletas horizontais dos tubos auxiliares das bandas dos molares. Esse sistema de forças é constituído de componentes de forças verticais, horizontais, momentos de força e de binários (momentos que ocorrem no interior do tubo molar após inserção da alça previamente conformada, provenientes de duas forças paralelas de mesma intensidade, mas de sentidos opostos). Os efeitos indesejáveis no posicionamento dos dentes podem ser controlados por: (A) adequada conformação geométrica das alças, com angulações em suas extremidades (efeito de momento de força ou efeito gable, ver Fig. 1), no plano sagital e vestibulolingual (neste caso, para evitar deslocamento da coroa do canino para vestibular, durante a distalização do mesmo); (B) por meio de ancoragem intra-arco (ex. barra palatalina); e (C) por meio de ancoragem extra-bucal².

A Mecânica Segmentada de Arcos (MSA) emprega alças, porém difere das demais técnicas pelo fato de apresentar três segmentos de arcos unidos entre si, por alças e/ou por dispositivos auxiliares, como a barra palatalina e o arco lingual. Arcos de titânio-molibdênio (TMA) com o objetivo de intrusão ou de extrusão podem ser também utilizados, adaptados em tubos auxiliares para produzir os movimentos desejados. Na MSA as alças são conformadas geometricamente e, em seguida, fixadas por dois extremos: um localizado anteriormente em um braquete (apoio engastado) e outro localizado posteriormente, na forma de um tubo (engaste deslizante)^{16, 26}.

O sistema de forças atuantes nos pontos de fixação (extremos da alça) é função da conformação geométrica inicial e da posição da circunvolução (loop). Ao fixar uma alça pelas extremidades, uma deformação inicial é aplicada sobre ela e, devido às propriedades elásticas do metal, ela tenderá a retornar para a sua posição original, provocando, assim, forças e momentos sobre os pontos de apoio. A conformação geométrica da alça pode ser obtida por meio de um template (um desenho padrão da alça para diversas situações de ativação, sobre o qual se conforma a geometria da alça). Os valores decorrentes do sistema de forças podem ser tabelados, onde estariam dispostos os níveis de força, a magnitude da ativação correspondente, os momentos produzidos pelas extremidades anterior e posterior da alça, denominados momentos alfa (a) e beta (b), respectivamente, a constante elástica e as relações momento-força (M/F)^5,7. Uma maneira fácil de obter um template é por meio de programas de CAD (Computer Aided Design, ou Projeto Auxiliado por Computador), como pode ser visto na figura 2.

O tipo de movimentação resultante dependerá do plano de tratamento estabelecido, estando diretamente relacionado com a geometria da alça utilizada, a forma e as dimensões da secção transversal do fio, a liga metálica, bem como o uso de forças auxiliares, como a de elásticos intermaxilares. Uma vez ativada, a alça tende a voltar ao seu estado inicial, liberando a energia elástica que foi armazenada durante a sua abertura (ativação), provocando o deslocamento dos dentes. Após serem conformadas geometricamente (exemplo da alça em T-loop (Fig. 3), as alças devem apresentar inclinações em suas extremidades, as quais geram momentos de força. Poucas alças têm seus momentos determinados de acordo com as inclinações de suas extremidades, ou seja, poucas possuem um template para auxílio da conformação geométrica, onde uma dada conformação em graus corresponderia a uma magnitude de momento de força.

Assim, de forma a contribuir no estudo, entendimento e melhor utilização das alças ortodônticas, o objetivo deste trabalho é discutir a mecânica associada à sua função de movimentação dentária, as suas principais propriedades mecânicas (a resistência à deflexão, a força elástica máxima e a relação momento-força), bem como os métodos comumente utilizados para avaliá-las.

REVISÃO DA LITERATURA

Diversas alças de retração ortodôntica, com finalidade de fechar espaços de maneira sistemática e controlada, vêm sendo estudadas e desenvolvidas ao longo dos anos. Como exemplo, as clássicas alças retangulares verticais, com loop fechado, desenvolvidas por Bull³, as alças verticais helicoidais estudadas por Fryar¹², e depois modificadas por Burstone, Baldwin e Lawless⁴, as alças verticais estudadas por meio de métodos analíticos e experimentais²⁹, e as alças em T-loop⁶. Inicialmente as alças foram testadas experimentalmente, considerando a força armazenada por unidade de ativação (constante elástica). Com a evolução desses dispositivos^20,29, foi necessário considerar suas componentes verticais, os momentos alfa (região anterior) e beta (região posterior) e a relação momento-força (M/F). Em 1933, Peyton e Moore²⁰ estudaram alças do tipo cantilever "reflexas" para a inclinação vestibular de incisivos, as quais eram soldadas a um arco lingual. As alças eram feitas de ouro com secção transversal de 0,018" (0,457mm) de diâmetro e eram testadas em termos de força-deflexão, fixando uma de suas extremidades por meio de um tubo e aplicando "pesos mortos" no lado livre da alça em diferentes posições. Fryar¹² estudou experimentalmente, em 1960, na Universidade de Indiana, alças helicoidais verticais para retração de caninos e também alças para a retração dos dentes anteriores, confeccionadas em aço inox e com secção transversal de 0,008" x 0,020" (0,203mm x 0,508mm). O método consistia em testes de tração onde segmentos de fios de secção transversal de 0,021" x 0,025’’ (0,533mm x 0,635mm) se uniam às alças por meio de um tubo. Um desses segmentos de fio permitia prender uma extremidade da alça de maneira fixa, enquanto a outra era dobrada em ângulo reto para que essa fosse inserida perpendicularmente em um transdutor, o que evitaria que a alça se inclinasse e, ao mesmo tempo, simularia sua posição em boca. Teasley, Penley e Morrison²⁷, da Universidade do Texas, desenvolveram um instrumento capaz de resolver complexos sistemas de força em seis componentes (vestibulolingual, distomesial e apico-oclusal). O instrumento foi construído com seis extensômetros de deslocamento, com acurácia de 2% e precisão considerada alta, segundo análise estatística. Em 1974, Yang e Baldwin²⁹ compararam, experimentalmente, variações de alça "vertical" e da alça Bull-loop feitas de aço inox de 0,017" x 0,022’’ (0,432mm x 0,558mm), por meio de um dispositivo mecânico-eletrônico para a medição da constante de mola, das forças aplicadas e das deflexões resultantes. As alças foram também estudadas por meio de simulação numérico-computacional, utilizando o método dos elementos finitos. As alças com geometria Bull-loop produziram constante de mola de 57gf/mm, enquanto as alças verticais produziram 114gf/mm. Em 1982, Burstone⁶ avaliou, experimentalmente, alças em titânio-molibdênio (TMA) do tipo T-loop com secção transversal de 0,017" x 0,025’’ (0,432mm x 0,635mm), por meio de um transdutor especialmente desenvolvido para testar o desempenho de alças para retração anterior, protração posterior e ambos os movimentos simultaneamente. Essas alças foram capazes de produzir momentos de força necessários para os movimentos desejados, além de permitirem a retração isolada de caninos, quando construídas de maneira híbrida, com fios 0,018-0,017" x 0,025’’ (0,457-0,432mm x 0,635mm).

Em 1997, Siatkowski²⁴ realizou um criterioso estudo sobre arcos contínuos com alças chamadas Opus loop, construídos com liga de titânio-molibdênio (TMA) de secção transversal de 0,017" x 0,025" (0,432mm x 0,635mm) e de aço inox 0,016" x 0,022" e 0,018" x 0,025" (0,406mm x 0,558mm e 0,457mm x 0,635mm, respectivamente) onde inicialmente foi feita uma abordagem analítica, seguida de um estudo experimental, utilizando uma célula de carga para medir forças e momentos. Segundo o autor, esses arcos são capazes de produzir um sistema de forças mais eficiente, por meio de relações M/F que variam em um pequeno espectro (8 a 9,1mm), e sem contar com a introdução de momentos residuais, o que permite um verdadeiro período de repouso quando desativados.

Ferreira⁹ testou o comportamento mecânico de alças de retração, com geometria "duplo delta" (Ricketts), de aço inox, cromo-cobalto e titânio-molibdênio (TMA), com diferentes secções transversais, por meio de testes de tração. Os testes foram realizados por meio de um transdutor de deslocamento linear e de extensômetros de resistência elétrica, onde uma das extremidades da alça era presa, enquanto a outra permitia o deslocamento. A calibração do transdutor foi feita através da utilização de "pesos mortos". As alças feitas de titânio-molibdênio mostraram a menor constante de mola (84,9gf/mm), enquanto as alças de aço inox com secção transversal 0,019" x 0,025" (0,483mm x 0,635mm) mostraram as maiores (275gf/mm). Constatou-se que as alças de aço inox de secções transversais 0,019" x 0,025" (0,483mm x 0,635mm) e 0,018" x 0,025" (0,457mm x 0,635mm) não mostraram diferenças significativas, o mesmo se verificando com as alças de cromo-cobalto 0,016" x 0,022" (0,406mm x 0,558mm) e aquelas de aço inox 0,017" x 0,022" (0,432mm x 0,558mm). Também o mesmo ocorrendo para as alças de titânio-molibdênio 0,019" x 0,025" (0,483mm x 0,635mm) e 0,016" x 0,016" (0,406mm x 0,406mm) de cromo-cobalto.

Ferreira et al.¹⁰ estudaram o desempenho de um protótipo de alça de retração ortodôntica, desenvolvido na Universidade Tecnológica Federal do Paraná (UTFPR), por meio de um novo dispositivo de medição de forças⁸, o qual continha doze extensômetros de resistência elétrica que transformavam solicitações mecânicas em sinais elétricos. As alças estudadas foram confeccionadas em titânio-molibdênio com secções transversais de 0,016" x 0,022" (0,406mm x 0,558mm) e 0,017" x 0,025" (0,432mm x 0,635mm). Neste estudo obtiveram-se as interações entre as variáveis geométricas e o sistema de forças resultantes das ativações.

Também simulações computacionais utilizando o Método dos Elementos Finitos (MEF)^1,11,24 podem constituir uma ferramenta útil para avaliar um determinado protótipo. Em uma simulação podem-se estimar as forças, momentos e tensões em função da ativação, antes de construir o protótipo físico. Desta forma, caso seja necessário, pode-se redefinir a geometria da alça, objetivando melhorar seu desempenho. A figura 4 apresenta um protótipo de alça que foi analisada pelos autores do presente artigo utilizando o MEF.

CONCEITOS DA BIOMECÂNICA APLICADOS AO MOVIMENTO DENTÁRIO

Centro de resistência e centro de rotação

Para que se possa entender a biomecânica do movimento dentário é necessário conhecer os conceitos de centro de resistência e centro de rotação.

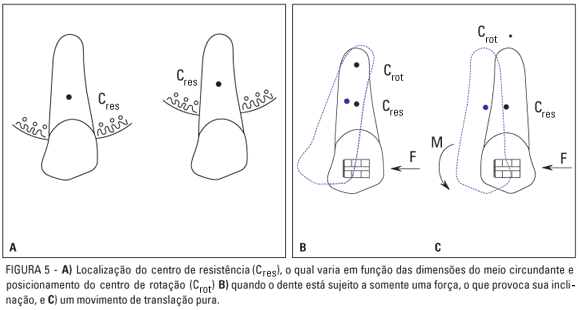
O centro de resistência (Cres) é definido como o ponto onde a aplicação de uma força pura produzirá apenas movimento de translação, sendo que se deve imaginar o dente imerso em seu meio de suporte, denominado periodonto, o que compreende o osso alveolar, o ligamento periodontal e o cemento. Conforme a altura do osso alveolar, tem-se uma distinta localização do centro de resistência. Segundo Burstone et al.⁵ esse ponto estaria situado aproximadamente no terço radicular a partir da crista óssea alveolar dos dentes com uma só raiz (Fig. 5A), e ao nível da região de furca (local onde as raízes começam a se separar) nos dentes com mais de uma raiz²⁸. Ainda segundo Burstone et al.⁵, o centro de resistência de dentes unirradiculares estaria situado a, aproximadamente, 66% do comprimento da raiz do ápice em direção à crista óssea alveolar.

O centro de rotação (Crot) é definido como o ponto em torno do qual o dente gira (Fig. 5B). Sua posição pode variar conforme o sistema de forças atuantes, sendo determinada pela relação momento-força (M/F) medida no nível do braquete. A magnitude desta relação também caracterizará o tipo de movimento dentário.

Relação momento-força (m/f)

Uma força simples aplicada a um dente, no nível do seu braquete, gera um momento de força que é proporcional à força multiplicada pela distância do braquete até o centro de resistência. Este momento é responsável pelo movimento da raiz para um lado e da coroa para outro. Logo, para que se possa obter apenas movimento coronal, ou apenas radicular, ou até mesmo a translação, é necessária a incorporação de um momento de binário, também aplicado ao braquete. O movimento dentário pode ser descrito como uma combinação de translação e rotação¹⁹, e o tipo de movimento produzido será definido pela relação momento-força (M/F)^1,19,24. A relação momento-força (M/F) permite estabelecer se haverá predomínio de rotação ou translação, o que dependerá da intensidade da força e dos momentos aplicados. Nos estudos envolvendo alças ortodônticas, geralmente as forças são expressas em gramas-força (gf) ou Newtons (N) e os momentos correspondentes em gramas-força-milímetro (gf.mm) ou Newtons-milímetro (N.mm), respectivamente. Desta forma, a unidade da relação M/F será milímetros (mm).

Burstone et al.⁵ propõem que, na movimentação de incisivos centrais superiores, quando da aplicação de uma relação M/F de 10mm, o centro de rotação estará localizado no infinito e ocorrerá um movimento de translação. Quando a relação M/F for de 12mm, o movimento predominante será de inclinação radicular. Caso seja aplicada uma força simples sobre a coroa, na altura do braquete, tem-se que M = 0 então M/F = 0, e o centro de rotação estará localizado próximo ao centro de resistência, então o movimento será de inclinação de raiz e coroa para lados opostos (uncontrolled tipping). Finalmente, para a relação M/F de 5mm ter-se-á o centro de rotação próximo ao ápice radicular, com conseqüente movimento de coroa (controlled tipping)⁵. A relação momento-força (M/F) relativamente constante é necessária para que se tenha controle do centro de rotação da unidade ativa, e para isso é preciso um sistema de forças com baixa resistência à deflexão¹⁹.

Segundo Raboud et al.²¹, para caninos superiores, quando a relação M/F for de 8,5mm ocorrerá translação, ao passo que para relações menores que esta ocorrerá inclinação em torno do ápice radicular (Crot), e para relações maiores haverá inclinação em torno da coroa dentária (Crot). Segundo Siatkowski²⁴, obtém-se translação de caninos superiores quando a relação momento-força é de aproximadamente 9,4mm. Note que, na realidade, o movimento de translação não existe sem que haja a participação de pequenos movimentos de rotação, os quais são corrigidos à medida que a força se dissipa sobre o dente.

Existem dois tipos de momento: o momento de uma força e o momento de um binário. Um binário é um par de forças iguais e em sentidos opostos e paralelas, capaz de girar um dente em torno de seu centro de rotação, o qual coincide com o centro de resistência. O binário não é capaz de alterar o centro de resistência. O momento de um binário tende a produzir rotação de forma diferente do movimento circunlinear produzido por um momento de força²⁸ (Fig. 6).

A descrição de um sistema complexo de forças e momentos aplicados sobre um braquete deve ser relacionada ao centro de resistência. Uma força pura horizontal sobre o braquete resulta em inclinação do dente, então o movimento de translação será obtido por ação de um momento adicional a essa força puramente horizontal sobre o braquete. Assim, a relação M/F é igual à distância do braquete ao centro de rotação⁷.

Em outros termos, uma força simples, horizontal, aplicada ao braquete, gera um momento em relação ao centro de resistência de um dente. Logo, para contrabalançar esse efeito, seria necessária a aplicação de um momento contrário, cuja intensidade é estimada multiplicando a força simples, horizontal, pela distância do braquete ao centro de resistência do dente, obtendo-se assim um movimento de translação. Se a relação momento/força for maior do que esta distância ter-se-á inclinação de raiz.

Relação carga-deflexão

A relação carga-deflexão indica a carga que será requerida por unidade de deflexão. Esta relação depende dos seguintes fatores:

1) Forma e dimensões da geometria da alça (T-loop, Vertical-loop, Duplo ovóide, Duplo delta, Bull loop, etc.)

2) Secção transversal do fio metálico (circular ou retangular e suas dimensões);

3) Propriedades mecânicas do fio (tipo de liga metálica).

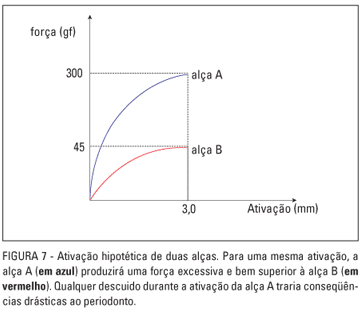
Tendo-se informações sobre a relação carga-deflexão pode-se ter um melhor controle da magnitude das forças e momentos que estão sendo empregados. A constante elástica é a propriedade que determina a relação carga-deflexão. Desde que as magnitudes das forças no aparelho ortodôntico sejam tais que o limite elástico do material do fio não seja ultrapassado, a relação carga-deflexão varia direta e linearmente com esta constante¹⁷. No entanto, dependendo da geometria, e do tipo de liga, a lei de Hooke pode não ser verificada para a alça. Uma alça cuja relação carga-deflexão seja alta armazenará uma carga muito grande por unidade de ativação, o que implicará em uma ativação muito pequena. Por outro lado, uma alça cuja relação carga-deflexão seja adequada permitirá uma ativação de 2 ou 3mm, sem, contudo, chegar a uma carga excessiva. Ressalta-se, ainda, que em alças com alta relação carga-deflexão, o operador teoricamente teria que fazer uma ativação muito pequena (décimo de milímetro) para chegar a uma carga aceitável, sendo que na clínica é praticamente impossível obter este alto grau de precisão, tornando a margem de erro muito ampla (Fig. 7).

Força elástica máxima

A força elástica máxima é a maior força que se pode aplicar a um fio metálico sem produzir deformação permanente⁴. É a propriedade que limita a manipulação dos fatores responsáveis pela resistência à deflexão, pois, caso as forças ultrapassarem a força elástica máxima, a tensão mecânica no fio ultrapassa a tensão de escoamento, e este sofre deformações permanentes (também chamadas de deformações plásticas), modificando suas propriedades elásticas e, conseqüentemente, o desempenho da alça. Caso a alça apresente uma força elástica máxima muito baixa, facilmente sofrerá deformação plástica pelas forças da mastigação⁴, ou mesmo pelas forças geradas durante sua ativação. Essa propriedade responde proporcionalmente à terceira potência do diâmetro da liga de secção circular, à largura multiplicada pelo quadrado da altura da secção transversal em fios de secção retangular, e à tensão limite de escoamento da liga metálica do fio (característica intrínseca do material). O aumento de comprimento do fio para a realização de circunvoluções, com o intuito de baixar a resistência à deflexão, não altera a força elástica máxima, desde que a dimensão ântero-posterior da alça permaneça inalterada¹⁷.

Variação da constante elástica com a geometria da alça

A constante elástica é dependente do módulo de elasticidade (E) dos materiais da liga metálica e da geometria da alça. O módulo de elasticidade é um índice de rigidez do material. Assim sendo, quanto maior é esse módulo maior é a resistência à deflexão, ou seja, maior a carga acumulada por milímetro de ativação da alça. Portanto, a geometria da alça e o tipo de liga metálica utilizada para sua construção são de fundamental importância no que se refere ao sistema de forças resultante. Assim, uma maneira de se modificar a constante elástica, e conseqüentemente modificar também a resistência à deflexão e o sistema de forças atuantes, é através da alteração do módulo de elasticidade (E) da liga metálica empregada, ou seja, utilização de um material de outra natureza metálica. Assim, escolhendo materiais como o titânio-molibdênio (b-titânio), cujo módulo de elasticidade é menor que o do aço inoxidável, pode-se diminuir a constante elástica e a resistência à deflexão.

As ligas de titânio-molibdênio (TMA) apresentam ampla flexibilidade e conformabilidade, o que as torna eletivas para a confecção de alças. Essas ligas apresentam tensão de escoamento de aproximadamente 1.280MPa e módulo de elasticidade (E) de 69GPa, o que corresponde a 33% do módulo de elasticidade do aço inoxidável e cerca de 35% das ligas de cromo-cobalto.

A SEGMENTAÇÃO DA MECÂNICA

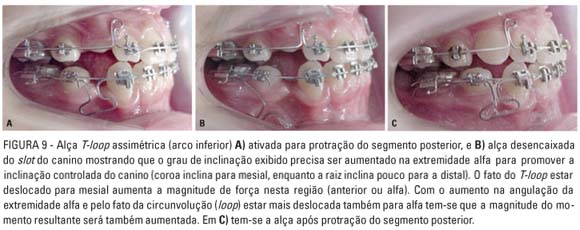
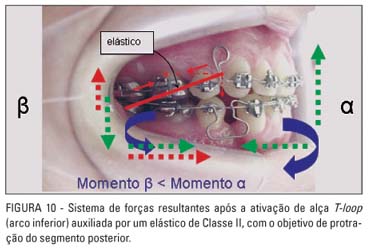
Com a evolução da técnica do arco de canto (Edgewise), surgiram os sistemas conhecidos como tracks (nome dado ao conjunto de arcos segmentados que permite deslizamento dos grupos de dentes), característicos da técnica segmentada dos arcos, descrita por Braun e Marcotte¹. Neles os arcos metálicos são constituídos de vários segmentos, unidos entre si indiretamente por meio dos braquetes e tubos (acessórios que suportam e permitem deslizamento dos arcos metálicos), onde um dente, ou um grupo de dentes, se aproxima entre si por meio de alças de fechamento de espaço. Com isso, é possível aplicar forças pré-determinadas e precisas, bem como obter melhor controle dos momentos gerados pela alça de retração, a qual une os segmentos posteriores e o anterior. A figura 8 mostra um exemplo de alça T-loop assimétrica para retração isolada do canino. Na figura 8A a alça não está ativada, enquanto na figura 8B a alça está ativada. A figura 9 apresenta a alça em um contexto segmentado, onde o arco inferior mostra que a região anterior da alça está inserida na canaleta vertical do braquete do canino, enquanto a porção posterior insere-se no tubo auxiliar da banda molar. Observe a presença de arco contínuo como um eixo de deslizamento utilizado por alguns autores¹. A presença deste eixo certamente introduz mais atrito durante a movimentação e restringe até certo ponto (dependendo da secção transversal utilizada) o sistema de forças resultante. Parece ser um recurso utilizado para evitar alteração do plano de oclusão durante o deslocamento, porém não há referência na literatura quanto às vantagens e desvantagens do uso deste arco. Na MSA, alguns autores⁵ não o utilizam, enquanto outros o fazem¹. Neste caso particular, o objetivo é promover a protração do segmento posterior e menor retração do anterior. A figura 9A mostra a alça engastada (adaptada) no tubo vertical do canino e no tubo molar, e a figura 9B exibe o aspecto da alça desencaixada no arco inferior, em situação pré-contornada, evidenciando o grau de inclinação nas extremidades. Note que o T-loop está mais deslocado para o lado anterior (alfa), existindo algum grau de inclinação na extremidade posterior (beta), o que produz um momento nas extremidades do sistema após o encaixe do segmento anterior da alça. O fato do T-loop estar deslocado para mesial aumenta a magnitude do momento nesta região (alfa). A inserção de uma pré-ativação na extremidade alfa produzirá um aumento dos momentos em alfa (a) e também em beta (b). O momento a é utilizado para que se obtenha inclinação controlada no segmento anterior. Como o T-loop está deslocado para a, tem-se que a magnitude do momento resultante neste lado será superior ao encontrado em b. Caso o grau de inclinação em um dos extremos seja aumentado, o efeito do momento também será intensificado. O tipo de movimento resultante será definido pelo grau de inclinação das extremidades da alça e da posição do T-loop em relação ao espaço inter-braquetes. À medida que se desloca o T-loop em relação a um dos extremos da alça, aumenta-se o momento exercido pelo lado deslocado. Isto não significa, porém, que o momento do lado oposto será inferior, o que dependerá também do grau de inclinação das extremidades⁵. A figura 9C mostra o deslocamento ocorrido. É importante ressaltar que se façam compensações (20° a 40°) no plano vestibulolingual (Fig. 3), nas extremidades alfa (anterior) e beta (posterior), para que se evite movimentação dos caninos para vestibular durante o deslocamento²¹. Na prática, é de boa norma estar atento e verificar a posição das coroas desses dentes a cada consulta e, se for necessário, corrigir a compensação, seja para aumentar o efeito de momento vestibulolingual, seja para diminuí-lo. A figura 10 exemplifica o sistema de forças resultante após ativação da alça, quando se deseja a protração do segmento posterior. A ativação da alça gera forças de sentido contrário na direção horizontal, o que leva ao fechamento do espaço (flechas horizontais verdes). Os momentos de binário (flechas arredondadas azuis) mostram que existe um diferencial de magnitudes, que na região anterior é maior que na posterior, o que gera uma força extrusiva no segmento anterior, em virtude da proximidade da dobra em "V", e intrusiva no segmento posterior (maior), devido ao seu maior distanciamento da dobra em "V". Note que o T-loop está deslocado para a região anterior, o que ajuda a aumentar o momento nessa região. Um meio auxiliar no fechamento do espaço está exemplificado pelo elástico intra-arco (linha oblíqua vermelha). A componente horizontal (linha vermelha tracejada horizontal) da força exercida pelo elástico está diretamente relacionada com o fechamento do espaço auxiliando a força exercida pela alça. Já a componente vertical (linha vermelha tracejada vertical) gera uma força extrusiva indesejável sobre os molares inferiores e incisivos superiores.

Deve-se também sempre estar atento às variabilidades biológicas, pois diferentes anatomias dentárias provocam diferentes respostas biológicas para as mesmas magnitudes de forças e momentos. Além disso, na clínica, a limitada exatidão em aplicar determinada ativação em uma alça e a variação das forças da mastigação podem causar regiões de deformação plástica, alterando a direção e magnitude da força empregada pela alça.

CONCLUSÕES

Nesse artigo foram abordados aspectos sobre a mecânica das alças de retração ortodôntica e suas propriedades mecânicas. Essas alças desempenham um papel relevante para a movimentação dentária, seja utilizando-as em um contexto seccional, atuando em um ou mais quadrantes do arco dentário de maneira isolada, seja fazendo parte de um arco segmentado. O conhecimento da biomecânica é de fundamental importância para o entendimento do sistema de forças envolvido e, conseqüentemente, para a escolha adequada da alça e das magnitudes de ativações e pré-ativações. A construção de templates para a conformação dessas alças, baseada nas forças e momentos desejados, permite ao clínico seu uso racional, promovendo movimentação dentária adequada, dentro de níveis biológicos compatíveis e de forma sistematizada, controlando de forma mais acurada o tipo de movimento desejado. A modelagem computacional através do Método dos Elementos Finitos é um meio eficiente, com custo relativamente baixo, e serve para estudar o comportamento de um corpo. Assim, pode-se simular diferentes configurações de alças sem a construção de protótipos físicos. Entretanto, deve-se lembrar que o Método dos Elementos Finitos baseia-se em modelos matemáticos, onde são feitas hipóteses simplificadoras, as quais devem ser conhecidas e verificado seu campo de validade, para que os resultados finais obtidos sejam próximos da realidade. Já os métodos experimentais se aproximam mais da condição real, porém com custo mais elevado, requerendo dispositivos ou máquinas apropriadas. A utilização em diferentes estágios de ambos os métodos é aconselhável para um melhor desenvolvimento e caracterização dos protótipos de alças.

Enviado em: setembro de 2006

Revisado e aceito: abril de 2007

• ¹
  BRAUN, S.; MARCOTTE, M. R. Rationale of the segmented approach to orthodontic treatment. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 108, no. 1, p. 1-8, 1995.
• ²
  BRAUN, S.; SJURSEN, R. C.; LEGAN, H. L. On the management of extraction sites. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 112, no. 6, p. 645-655, 1997.
• ³
  BULL, H. L. Obtaining facial balance in the treatment of Class II, division 1. Angle Orthod., Appleton, v. 21, no. 3, p. 139-149, 1951.
• ⁴
  BURSTONE, C. J.; BALDWIN, J. J; LAWLESS, D. T. The application of continuous forces to Orthodontics. Angle Orthod., Appleton, v. 31, no. 1, p. 1-14, 1961.
• ⁵
  BURSTONE C. J.; STEENBERGEN, E. V.; HANLEY, K. J. Modern Edgewise mechanics and the segmented arch technique. Farmington: Ormco Corporation, 1995.
• ⁶
  BURSTONE, C. J. The segmented arch approach. Am. J. Orthod., St. Louis, v. 82, no. 5, p. 361-378, 1982.
• ⁷
  BURSTONE, C. J.; KUHLBERG, A. T-loop position and anchorage control. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 112, no. 1, p. 12-18, 1997.
• ⁸
  DILLENBURG, J. A.; SCHNEIDER, A.; LUSA, I. Projeto de construção de medição de forças e de momentos produzidos por uma mola ortodôntica Porto Alegre: UFRGS, 2001.
• ⁹
  FERREIRA, M. A. The wire material and cross-section effect on double delta closing loops regarding load and spring rate magnitude: an in vitro study. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 115, no. 3, p. 275-282, 1999.
• ¹⁰
  FERREIRA, M. A.; OLIVEIRA, F. T.; IGNÁCIO, S. A.; BORGES, P. C. Experimental force definition system of a new orthodontic retraction spring. Angle Orthod., Appleton, v. 75, p. 334-343, 2005.
• ¹¹
  FERREIRA, M. A.; ORLOWSKI, R.; LUERSEN, M. A.; BORGES, P. C. Análise do desempenho de alças de retração ortodôntica via método dos elementos finitos. In: CONGRESSO BRASILEIRO DE ENGENHARIA BIOMÉDICA, 17. 2000, Florianópolis. Anais... Florianópolis: [s.l.], 2000. p. 178-183.
• ¹²
  FRYAR, G. M. Load deflection determinations of specific wire configurations. 1960. 75 f. Master (Thesis)-Indiana University, Indiana, 1960.
• ¹³
  GJESSING, P. Biomechanical design and clinical evaluation of a new canine retraction spring. Am. J. Orthod., St. Louis, v. 87, no. 5, p. 353-362, 1985.
• ¹⁴
  HASKELL, B. S.; SPENCER; W. A.; DAY, M. Auxiliary springs in continuous arch treatment: part I: an analytical study employing the finite element method. Part I. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 98, no. 5, p. 387-397, 1990.
• ¹⁵
  _____. Auxiliary springs in continuous arch treatment: part II: appliance use and case reports. Part II. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 98, no. 6, p. 488-498, 1990.
• ¹⁶
  JARABAK, J. R.; FIZZEL, J. A. Technique and treatment with light wire Edgewise appliances 2nd ed. St. Louis. C. V. Mosby, 1972.
• ¹⁷
  KUSY, R. P.; GREENBERG, A. R. Effects of composition and cross section on the elastic properties of orthodontic archwires. Angle Orthod., Appleton, v. 51, p. 325-341, 1981.
• ¹⁸
  MAZZA, D.; MAZZA, M. Specialized spring design in segmented Edgewise Orthodontics. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 112, no. 6, p. 684-693, 1997.
• ¹⁹
  NANDA, R.; BURSTONE, C. J. Biomechanics in clinical Orthodontics. [USA]: W. B. Saunders, 1997.
• ²⁰
  PEYTON, F. A.; MOORE, G. R. Flexibility studies on gold alloy wires and orthodontic appliance. Int. J. Orthod., Milwaukee, v. 19, p. 903-919, 1933.
• ²¹
  RABOUD, D. W.; FAULKNER, M. G.; LIPSETT, A. W.; HABERSTOCK, D. W. Three-dimensional effects in retraction appliance design. Am. J. Orthod. Dentofacial Orthop, St. Louis, v. 112, no. 4, p. 378-403, 1997.
• ²²
  RINALDI, T. C.; JOHNSON, B. E. An analytical evaluation of a new spring design for segmented space closure. Angle Orthod., Appleton, v. 65, no. 3, p. 187-198, 1995.
• ²³
  SCELZA NETO, S. P.; MUCHA, J. N.; CHEVITARESE, O. Mola de fechamento de espaços em Ortodontia em forma de lágrima: desempenho em tração. Rev. Bras. Odontol., Rio de Janeiro, n. 5, p. 10-14, 1984.
• ²⁴
  SIATKOWSKI, R. E. Continuous archwire closing loop design, optimization and verification. Part I. Am. J. Orthod. Dentofacial Orthop., St. Louis, v. 112, no. 4, p. 393-402, 1997.
• ²⁵
  SOLONCHE, D. J.; BURSTONE, C. J.; VANDERBY, R. JR. A device for determining the mechanical behavior of orthodontic appliances. IEEE Trans. Biomed. Eng., New York, v. 24, no. 6, p. 538-539, 1977.
• ²⁶
  SOUZA, S. A. Ensaios mecânicos de materiais metálicos: fundamentos teóricos e práticos. 5. ed. São Paulo: E. Blücher, 1987.
• ²⁷
  TEASLEY, G. H.; PENLEY, W.; MORRISON, E. The design and fabrication of an electro-mechanical instrument utilized to analyze orthodontic forces. Am. J. Orthod., St. Louis, v. 49, no. 11, p. 868, 1963. Abstracts.
• ²⁸
  VALET, R.; PAGIN, J. Le centre de résistance. Rev. Orthop. Dento Faciale, Paris, v. 21, p. 115- 129, 1987.
• ²⁹
  YANG, T. Y.; BALDWIN, J. J. Analysis of space closing springs in Orthodontics. J. Biomech., New York, v. 7, no. 5, p. 21-28, 1974.

Datas de Publicação

• Publicação nesta coleção
  02 Jun 2008
• Data do Fascículo
  Jun 2008

Histórico

• Recebido
  Set 2006
• Aceito
  Abr 2007