Abstracts
INTRODUCTION:
In epidemiological studies, misclassification error, especially differential misclassification, has serious implications.
OBJECTIVE:
To illustrate how differential misclassification error (DME) and non-differential misclassification error (NDME) occur in a case-control design and to describe the trends in DME and NDME.
METHODS:
Different sensitivity levels, specificity levels, prevalence rates and odds ratios were simulated. Interaction graphics were constructed to study bias in the different settings, and the effect of the different factors on bias was described using linear models.
RESULTS:
One hundred per cent of the biases caused by NDME were negative. DME biased the association positively more often than it did negatively (70 versus 30%), increasing or decreasing the OR estimate towards the null hypothesis.
CONCLUSIONS:
The effect of the sensitivity and specificity in classifying exposure, the prevalence of exposure in controls and true OR differed between positive and negative biases. The use of valid exposure classification instruments with high sensitivity and high specificity is recommended to mitigate this type of bias.
Classification; Bias; Case-control studies; Odds ratios; Sensitivity and specificity; Computer Simulation
INTRODUÇÃO:
Em estudos epidemiológicos, o erro de classificação, especialmente o diferencial tem sérias implicações.
OBJETIVO:
Explicar como se expressa o erro de classificação diferencial (ECD) e não diferencial (ECND) em um estudo de caso-controle e descrever padrões de comportamento.
MÉTODOS:
Simularam-se diferentes níveis de sensibilidade, especificidade, prevalência e odds ratio (OR). Construíram-se gráficos de interação para estudar o comportamento do viés nos diferentes cenários e mediante modelos lineares se descreveu o efeito dos diferentes fatores sobre esse viés.
RESULTADOS:
O 100% dos vieses apresentados ante um ECND foram negativos, enquanto que no caso do ECD observou-se que este enviesa a associação positivamente em maior proporção que negativamente (30 versus 70%), aproximando ou afastando a estimação da OR para a hipótese nula.
CONCLUSÕES:
O efeito da sensibilidade e a especificidade na classificação da exposição, da prevalência da exposição nos controles e da OR verdadeira sobre o viés relativo difere entre os vieses negativos e positivos. O uso de instrumentos de classificação da exposição validados, com altos níveis de sensibilidade e especificidade, se recomendam para mitigar esse tipo de viés.
Classificação; Viés; Estudo de casos e controles; Razão de Chances; Sensibilidade e especificidade; Simulação por computador
INTRODUCTION
Case-control studies are commonly utilized, especially for studying rare diseases11. Kleinbaum D, Kupper L, Morgenstern H. Epidemiologic Research:
Principles and Quantitative Methods New York: Van Nostrand Reinhood Company,
1982.
2. Rothman K, Greenland S. Modern Epidemiology. 3th ed. Philadelphia:
Lippincott Raven Publishers, 2012.
-
33. dos-Santos I. Cancer Epidemiology: Principles and Methods. Lyon,
Francia: IARC Library Cataloguing in Publication Data, 1999.. Both case identification and control selection
should be carried out with the greatest possible rigor. Lack of rigor could lead to
systematic errors and consequently to invalid results33. dos-Santos I. Cancer Epidemiology: Principles and Methods. Lyon,
Francia: IARC Library Cataloguing in Publication Data, 1999.. Similarly, if the exposure, the disease or both are misclassified, the
association measures, the odds ratio (OR) and the conclusions will be biased11. Kleinbaum D, Kupper L, Morgenstern H. Epidemiologic Research:
Principles and Quantitative Methods New York: Van Nostrand Reinhood Company,
1982.. In any epidemiological study, the inappropriate
classification of the exposure or of the disease is known as misclassification error,
which can be divided into two types: non-differential misclassification error (NDME) or
differential misclassification error (DME). This type of error is usually found in
studies that investigate socially unacceptable behaviour or behaviours considered
private that can generate shame or stigma44. Sanders SA, Hill BJ, Yarber WL, Graham CA, Crosby RA, Milhausen RR.
Misclassification bias: diversity in conceptualisations about having 'had sex'. Sex
Health 2010; 7: 31-4., such
as sexual behaviour or the use of psychoactive substances55. Rikala M, Hartikainen S, Saastamoinen LK, Korhonen MJ. Measuring
psychotropic drug exposures in register-based studies - validity of a dosage
assumption of one unit per day in older Finns. Int J Methods Psychiatr Res 2013;
22(2): 155-65.. It is known that NDME biases the risk estimate (typically represented by
an odds ratio in case-control studies) towards the null hypothesis22. Rothman K, Greenland S. Modern Epidemiology. 3th ed. Philadelphia:
Lippincott Raven Publishers, 2012.
,
66. Bross I. Misclassification in 2x2 tables. Biometrics. 1954; 10:
478-86.
7. Newell D. Errors in the interpretation of errors in epidemiology. Am
J Public Health Nations Health 1962; 52: 1925-8.
8. Keys A, Kihlberg J. Effect of misclassification on estimated relative
prevalence of a characteristic: Part I. Two populations infallibly distinguished:
Part II. Errors in two variables. Am J Public Health Nations Health 1963; 53:
1656-65.
9. Gullen WH, Bearman JE, Johnson EA. Effects of misclassification in
epidemiologic studies. Public Health Rep 1968; 83: 914-8.
10. Goldberg J. Effects of misclassification on bias in difference
between 2 proportions and relative odds in fourfold table. J Am Stat Assoc 1975; 70:
7.
-
1111. Weinberg C, Umbach D, Greenland S. When will nondifferential
misclassification of an exposure preserve the direction of a trend. Am J Epidemiol
1994; 140(6): 565-71.. The behavioural trends of NDME have been
extensively described, but DME trends are not yet clear1212. Szklo M, Nieto F. Epidemiología intermedia. Conceptos y
aplicaciones. España: Díaz de Santos, 2003.. Consider a 2 x 2 contingency table in any type of epidemiological study
that represents the results observed among non-diseased and diseased individuals as a
function of the exposure variable, where a and b
represent, respectively, the number of diseased and non-diseased exposed
individuals and c and d represent the number of
diseased and non-diseased unexposed individuals, respectively. Exposure
misclassification error occurs when the diseased group and the non-diseased group are
considered to be exposed although they were not and unexposed although they were66. Bross I. Misclassification in 2x2 tables. Biometrics. 1954; 10:
478-86.
,
1212. Szklo M, Nieto F. Epidemiología intermedia. Conceptos y
aplicaciones. España: Díaz de Santos, 2003.. A similar situation would occur if error
arose in the classification of the disease. Equations 1 to 4 show how misclassification
error affects the frequencies in the 2 x 2 table. These equations have been derived by
us using equation 9 from the Vogel and Geffeller paper131. Kleinbaum D, Kupper L, Morgenstern H. Epidemiologic Research:
Principles and Quantitative Methods New York: Van Nostrand Reinhood Company,
1982..
a' = aSeD + c(1 - SpD) Eq. (1)
b' = aSeN + c(1 - SpN) Eq. (2)
c' = (1-SeD)+cSpD Eq. (3)
d' = b(1 - SeN) + dSpN Eq. (4)
In these equations, a and a' indicate, respectively, the true and observed numbers of diseased persons exposed, b and b' the true and observed numbers of non-diseased exposed, c and c' the true and observed numbers of diseased unexposed, and d and d' the true and observed numbers of non-diseased unexposed. Se D and Se N represent the sensitivity of classifying those truly exposed among the diseased (Se D ) and non-diseased (Se N), and Sp D and Sp N are the specificities for classifying those truly unexposed among the diseased (Sp D) and non-diseased (Sp N). The reasoning behind these equations is that the group of diseased individuals will include a percentage of truly exposed subjects (a) who will be classified as such by a certain instrument (laboratory test, survey, etc.). This percentage corresponds to the sensitivity of the instrument for classifying subjects as exposed (Se D). In addition, some of the individuals who were truly not exposed (c) will be classified by the instrument as exposed. This percentage represents the instrument's false positive rate (1 - Sp D). Therefore, among diseased individuals, the number of subjects classified by the instrument as exposed (1- Sp D) will be equal to the fraction of individuals correctly classified, aSe D, in addition to the fraction of individuals incorrectly classified, c(1 - Sp D). Similarly, the number of diseased subjects classified by the instrument as unexposed (c') is equal to the fraction of individuals correctly classified as such, cSp D , plus the fraction of individuals incorrectly classified, a(1 - Se D). Likewise, the number of subjects classified as exposed and unexposed by an instrument in a non-diseased population (b' and d') is determined by the sensitivity and specificity of the instrument in that population (Se N and Sp D). The subjects classified as exposed (b') will correspond to the fraction of individuals correctly classified, bSe N, plus the fraction of individuals incorrectly classified d(1 - Sp N). Similarly, the subjects classified as unexposed (d') will equal the fraction of individuals correctly classified, dSp N, added to the fraction of individuals incorrectly classified, b(1 - Se N).
Non-differential misclassification error occurs when Se D = Se N and Sp D = Sp N , otherwise, the bias is considered a differential misclassification error1212. Szklo M, Nieto F. Epidemiología intermedia. Conceptos y aplicaciones. España: Díaz de Santos, 2003.. The true odds ratio is OR= ad/cb, and the observed or estimated odds ratio is OR' = a'd'/c'b'. If the sensitivities and specificities in non-diseased and diseased individuals are equal to 100%, the true odds ratio is equal to the observed (OR = OR'), and if they are equal to 50%, the observed odds ratio will be equal to (OR' = 1). A similar situation would occur with other risk measures employed in different epidemiological designs. Using equations 5 to 8, it is possible to use the true table frequencies to replace the corresponding sensitivities and specificities for the following formulas derived (also by the authors) from the equations described above:
If the sensitivities and specificities of the instrument employed for classifying exposed/unexposed individuals (non-diseased as well as diseased) are known, then researchers can correct this type of error. However, this is not always possible. Therefore, in this article, the effect of misclassification error (differential and non-differential) on odds ratio estimates is simulated using a case-control design. This effect is simulated as a function of the sensitivity and specificity of the exposure classification given different prevalence rates of the exposure among the controls and different true ORs to describe how misclassification error occurs and to identify possible trends. These trends may guide the discussion of results in this type of studies when there are deficiencies in the classification instruments.
MATERIALS AND METHODS
OUTCOME
The OR was utilized as the measure of risk in our case-control study, and the observed value was calculated using a 2×2 table. To study the effect of misclassification error on the estimation of the OR, we used different scenarios with variations in the sensitivity and specificity of the exposure classification for cases and controls, the prevalence of the exposure among the controls and the OR. The effect was measured according to the bias produced by varying these parameters. By definition, bias is the difference between the estimated OR and the true OR1414. Daniel W, Cross C. Biostatistics: A Foundation for Analysis in the Health Sciences. USA: Wiley, 2013.. Relative bias (expressed as a percentage) is the quotient between this difference and the true OR (expressed in hundreds). Negative bias values indicate underestimates of the OR, and positive bias values indicate overestimates. Likewise, bias values close to zero indicate the absence of bias.
STUDY DESIGN
Simulation studies employed in various areas of research are very useful to understand the behaviour of certain phenomena under different virtual scenarios prompted by researchers through some specialized software. In statistical robustness studies these are very common to observe the behaviour of an estimator under different scenarios that could occur in reality. Given the similarity between the simulation studies and experimental studies, this last approach is used to quantify the effect of misclassification in case-control studies1515. Salazar JC, Baena A. Análisis y diseño de experimentos aplicados a estudios de simulación. Dyna revfacnacminas. 2009; 159: 249-57.. For this, we have considered six factors:
-
the sensitivity of the exposure classification among the cases;
-
the specificity of the exposure classification among the cases;
-
the sensitivity of the exposure classification among the controls;
-
the specificity of the exposure classification among the controls;
-
the prevalence of the exposure among the controls; and
-
the odds ratio.
There were five levels for factors 1 - 4 (0, 25, 50, 75 and 100%) and two levels for factors 5 - 6 (5 and 30% for the prevalence and 2 and 7 for the OR). A total of 2,500 scenarios were generated (45 x 22). One hundred of these scenarios comprised the NDME analysis because the factors 1 and 3 levels as well as the factors 2 and 4 levels were the same. Therefore, the number of factors considered in this analysis was reduced to four. The remainder of scenarios (n = 2,400) made up the DME analysis, conserving the six initially stated factors.
STATISTICAL ANALYSIS
Interaction graphics were used to study relative bias as a function of the factors that varied, estimating the median bias for each group of combinations. Using linear models, the effect of the varying factors (i.e., the explanatory variables) on relative bias (i.e., the outcome variable) was studied, using a 0.05 level of statistical significance. Because positive relative bias occurred only with DME, which presented a high level of variability, the DME analyses were stratified according to the sign of the bias. Because of the high variability, a natural logarithmic transformation was used for the DME outcome in the linear models. Given the complexity of the DME results, in a subsequent analysis of this type of misclassification error, we considered OR estimates with absolute relative bias less than 15% as having no bias or moderate bias. This cut-off was the minimum value close to 0% which yielded an adequate sample size to do comparisons. For this analysis, we created a categorical variable with three levels:
-
Negative bias or underestimation of the OR (relative bias values smaller than -15%);
-
Bias absent (bias values greater than -15% but less than 15%); and
-
Positive bias or overestimation of the OR (bias values greater than 15%).
Spearman's correlation coefficient was used to assess the relationships between the different levels of the DME analysis factors and positive, absent or negative bias. P-values less than or equal to 0.05 were considered significant. The R statistical package (R CoreTeam (2013). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/) was utilized for generating the scenarios, producing the results of the simulation and conducting the data analyses. R scripts are available on request from the corresponding author.
RESULTS
NON-DIFFERENTIAL MISCLASSIFICATION ERROR
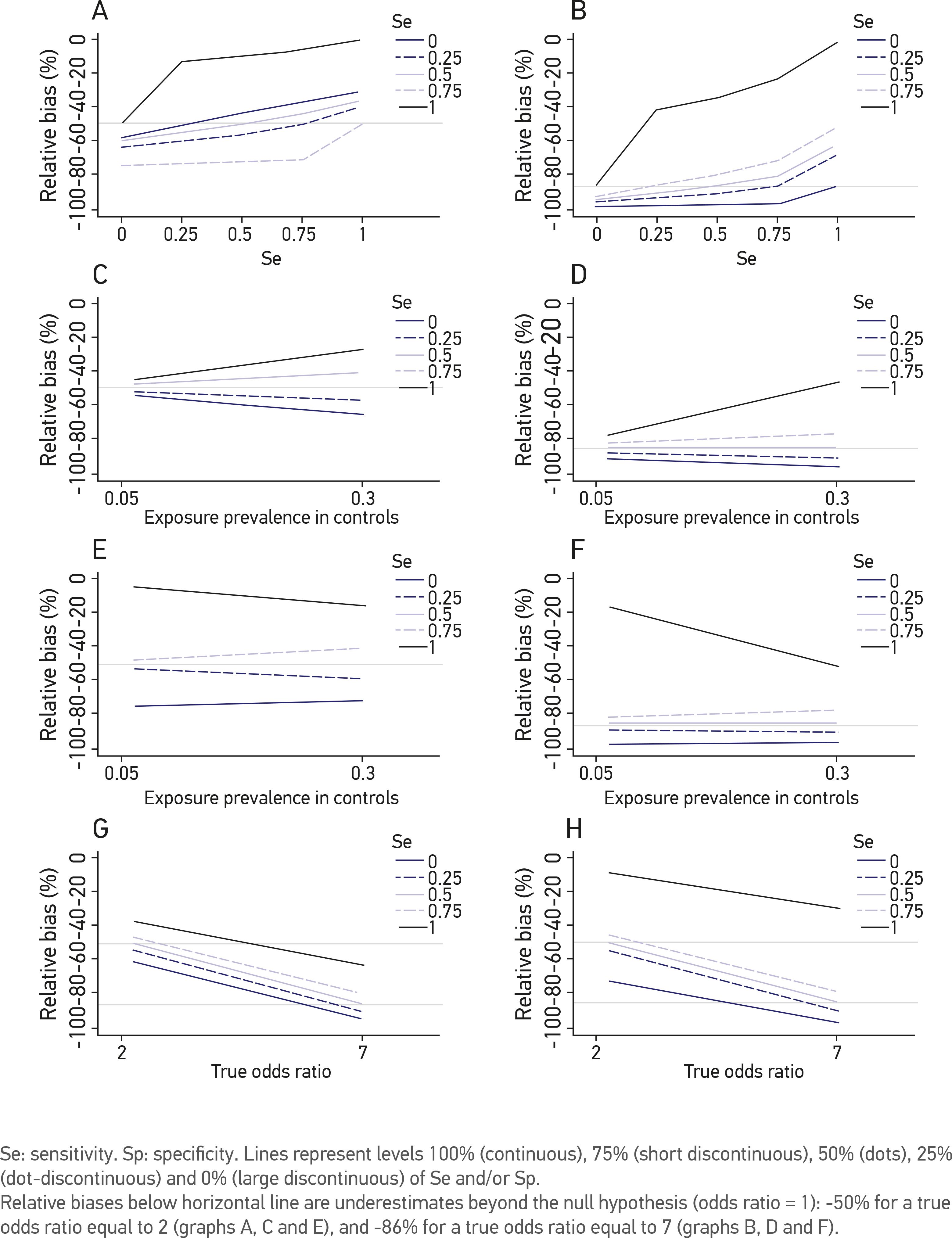
The bias attributable to NDME was negative in the whole 100 scenarios and very negative in many cases, indicating that in the presence of NDME in a case-control study, the risk is always underestimated, even beyond the null hypothesis (OR = 1). In extreme cases of NDME, the OR becomes the inverse of the true odds ratio if the sensitivity and specificity of the exposure classification tend towards 0%, it approaches one if the sensitivity and specificity of the exposure classification tend towards 50% and it tends towards the true OR if the sensitivity and specificity of the exposure classification tend towards 100% (Figures 1A and 1B). On the other hand, when the specificity of the exposure classification is 100% and the sensitivity is 0%, the OR is underestimated, but never drops below the value that corresponds with the null hypothesis (OR = 1). If the specificity tends towards 0%, even if the sensitivity is high, the OR is underestimated below the level of the null hypothesis (Figures 1A and 1B). According to the simulations we conducted, when the specificity level is higher than the sensitivity level, an unbiased estimate of the OR is produced (p-value for the interaction between sensitivity and specificity = 0.014).
Relative bias of the risk estimation (Odds Ratio) in a case-control study under the effect of non-differential misclassification error according to different levels of sensitivity and specificity of exposure classification, exposure prevalence in controls and true odds ratio. (A, C and E) correspond to the median of relative bias of a true odds ratio = 2; and (B, D and F) of a true OR = 7.
When the exposure prevalence among the controls was high and the sensitivity of the exposure classification was 100%, the OR estimate tended to be unbiased in the presence of NDME. When the sensitivity was lower, the exposure prevalence showed no effect (p-value for the interaction between sensitivity and prevalence = 0.20) (Figures 1C and 1D). The opposite effect was observed when we evaluated the relative bias by combining the specificity of the exposure classification with the prevalence of the exposure among the controls (p-value for interaction between specificity and prevalence = 0.52) (Figures 1E and 1F). Finally, we observed less bias in the estimates of moderate odds ratios. The relative bias increased when the true OR was greater, independent of the sensitivity and specificity (p-values for interaction between sensitivity versus OR and specificity versus OR = 0.88 and 0.13, respectively) (Figures 1G and 1H).
DIFFERENTIAL MISCLASSIFICATION ERROR
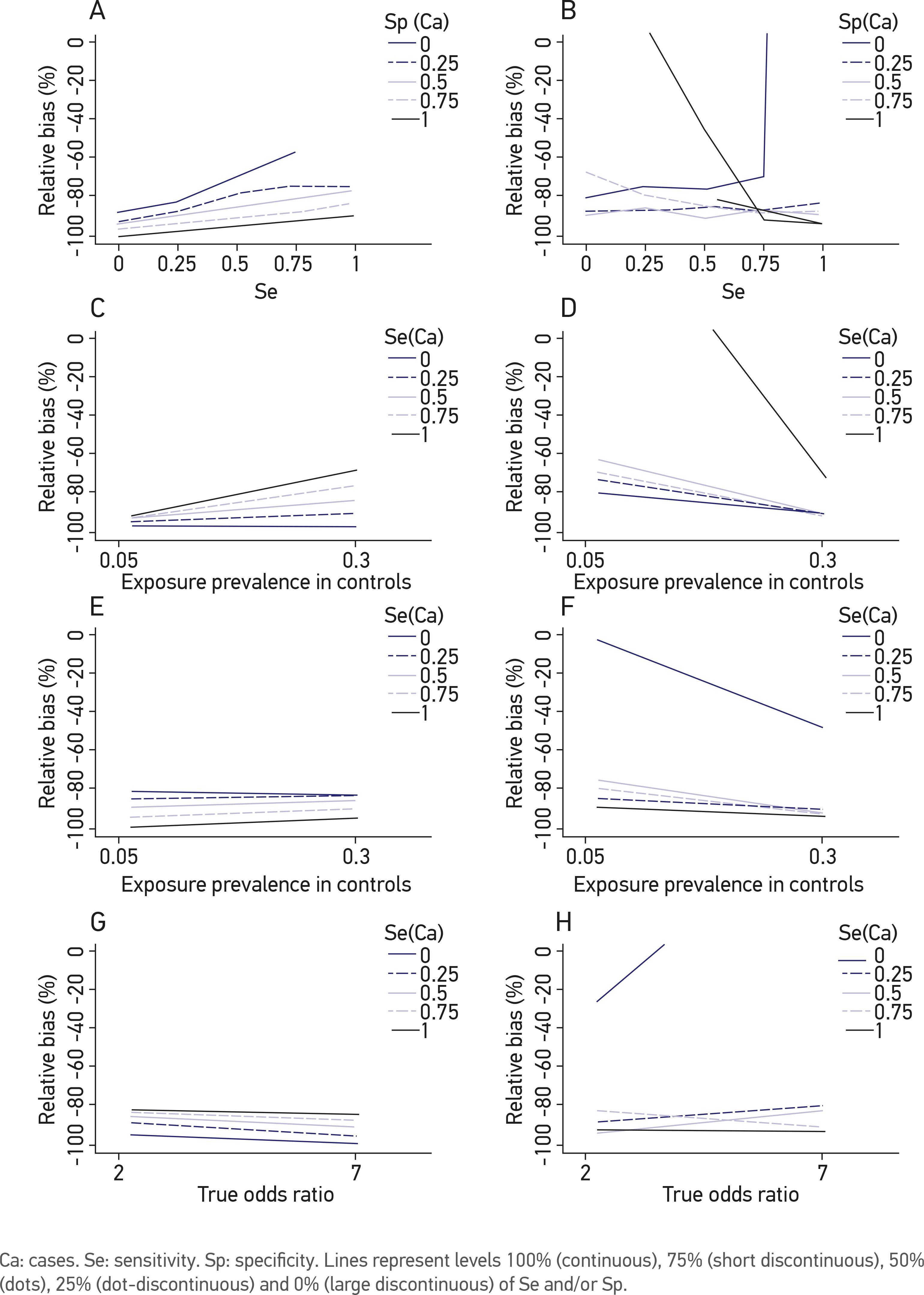
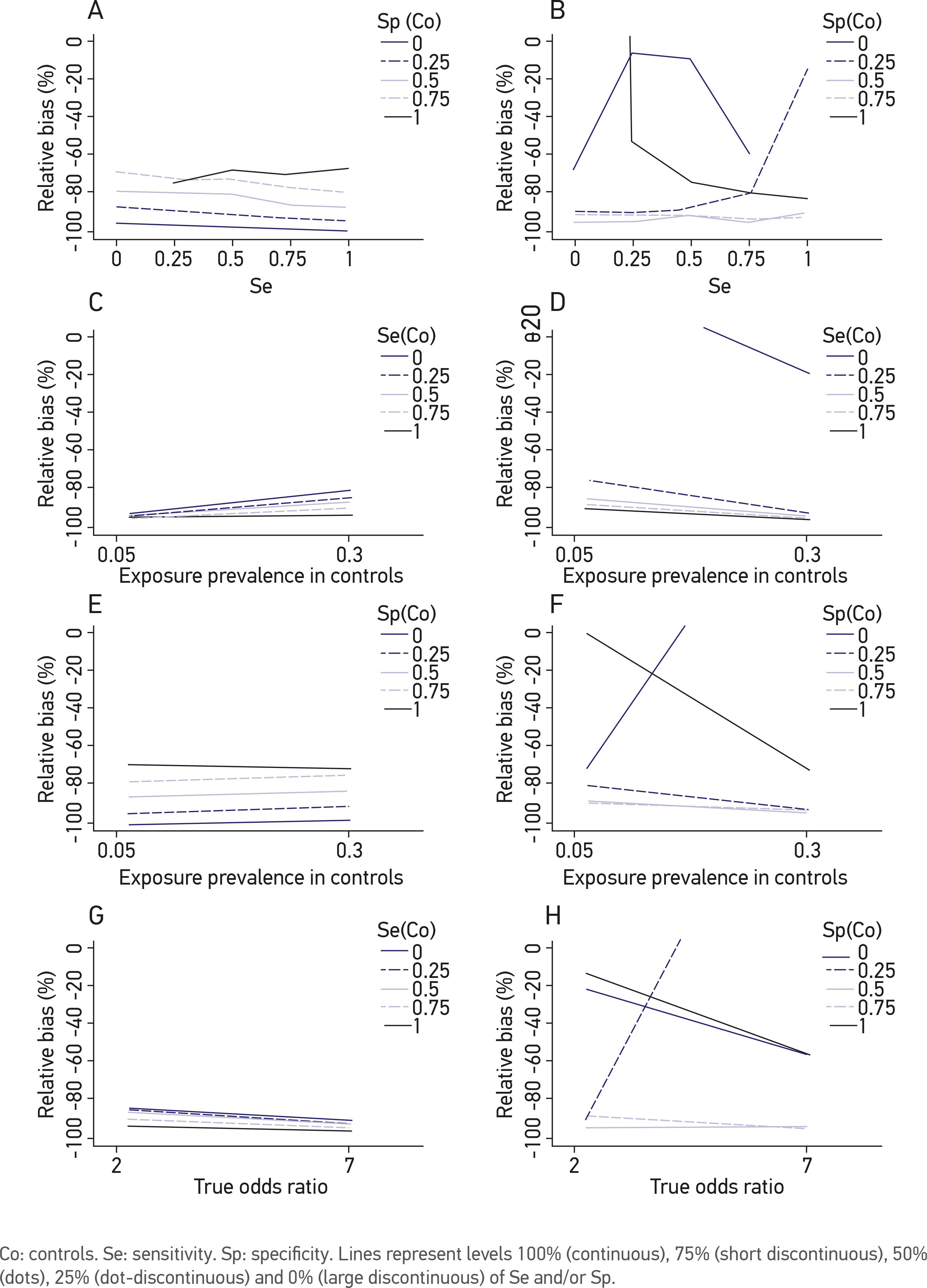
Of the 2,400 scenarios in the ECD analysis, 767 (32%) overestimated (i.e., positive bias) and 1,633 (68%) underestimated (i.e., negative bias) the true odds ratio. As opposed to the NDME analysis, the results of the DME are complex, not only because of the number of factors involved in the simulations but also because they do not produce a trend that clearly describes the effect of DME in relation to the combinations of factors. Therefore, the DME analysis is presented in a discriminatory manner according to the type of bias: negative or positive. Figures 2 to 4 correspond to the medians of the relative biases for different combinations of the six factors included in this analysis. High levels of sensitivity and specificity of the exposure classification among the cases (Se Ca and Sp Ca, respectively) reduce the bias, but they reduce positive bias more than negative bias (Figures 2A and 2B). A similar effect is observed for the sensitivity and specificity of the exposure classification among the controls (Se Co and Sp Co, respectively), although the effect is less clear for Se Co (Figures 3A and 3B). With regard to the prevalence of the exposure among the controls, the bias is lower when the exposure prevalence is high, independent of the sensitivity or specificity of the exposure classification, both for the cases and for the controls (Figures 2C to 2F and 3C to 3F). Regarding the specificity, the effect was the opposite of that observed for NDME. When the levels of sensitivity and specificity were combined with the levels of the true ORs for the cases and the controls, no clear pattern of bias was observed (Figures 2G, 2H, 3G and 3H). After combining Se Ca, Sp Ca, Se Co and Sp Co, we observed that the bias decreased with high levels of specificity more than with sensitivity in both the cases and the controls. However, these trends were not very clear (Figures 4A to 4H).
Relative bias of the risk estimation (odds ratio) in a case-control study under the effect of differential misclassification error according to different levels of sensitivity and specificity of exposure classification in cases, exposure prevalence in controls and true odds ratio. (A, C and E) correspond to negative biases (B, D and F) to positive biases.
Relative bias of the risk estimation (Odds ratio) in a case-control study under the effect of differential misclassification error according to different levels of sensitivity and specificity of exposure classification in controls, exposure prevalence in controls and true OR. (A, C and E) negative biases; (B, D and F) positive biases.
Relative bias of the risk estimation (Odds ratio) in a case-control study under the effect of differential misclassification error according to different levels of sensitivity and specificity of exposure classification defined for both cases and controls, exposure prevalence in controls and true odds ratio. (A, C and E) negative biases; (B, D and F) positive biases.
Table 1 presents the negative, absent or positive bias associated with DME according to each factor. Negative bias percentages decreased with high levels of Se Ca and Sp Co (Spearman's p-values = 0.017). In the other cases, the negative bias percentage increased. The complete opposite occurred with positive bias. The absence of bias was invariably observed for varying levels of sensitivity and specificity of the exposure classification among the cases and the controls (Spearman's p-values > 0.05). A high exposure prevalence among the controls was correlated with increased percentages of absent and negative bias and with a decreased percentage of positive bias, but these were not significant (Spearman's p-values = 1). High ORs were associated with an increase in negative bias and a decrease in positive and absent bias, but these results were not significant (Spearman's p-values = 1).
DISCUSSION
In research in general and in epidemiological research in particular, different forms of bias are frequently present and lead to findings that do not reflect precisely what is occurring. Biases are the result of deficiencies in the determination of the sample size, representativeness, data collection, definitions of relevant variables or design. The best-known biases in epidemiological research are selection, survival, loss to follow-up, detection, recall, inclusion/exclusion, confounding and misclassification1616. MacMahon B, Yen S, Trichopoulos D, Warren K, Nardi G. Coffee and cancer of the pancreas. N Engl J Med 1981; 304(11): 630-3..
Misclassification bias refers to errors made when classifying an individual into a
certain group, such as diseased individuals or individuals exposed to a certain factor.
It occurs when non-validated instruments are used and the sensitivity and specificity of
the classification method is unknown. Misclassification errors act in a particular
direction, positive or negative1717. Fox MP, Lash TL, Greenland S. A method to automate probabilistic
sensitivity analyses of misclassified binary variables. Int J Epidemiol 2005; 34:
1370-6.,
underestimating or overestimating the true value of the association measure, such as the
relative risk (RR) in cohort studies, the hazard ratio (HR) in longitudinal studies and
the odds ratio (OR) in case-control studies. Misclassification error can be differential
or non-differential. When DME occurs, the sensitivity and/or the specificity of the
classification of the subjects are different among comparison groups33. dos-Santos I. Cancer Epidemiology: Principles and Methods. Lyon,
Francia: IARC Library Cataloguing in Publication Data, 1999.. NDME results in a decrease in statistical power
(i.e., the ability of a test to show an association when one really exists), biasing the
value of the OR towards the null22. Rothman K, Greenland S. Modern Epidemiology. 3th ed. Philadelphia:
Lippincott Raven Publishers, 2012.
,
66. Bross I. Misclassification in 2x2 tables. Biometrics. 1954; 10:
478-86.
7. Newell D. Errors in the interpretation of errors in epidemiology. Am
J Public Health Nations Health 1962; 52: 1925-8.
8. Keys A, Kihlberg J. Effect of misclassification on estimated relative
prevalence of a characteristic: Part I. Two populations infallibly distinguished:
Part II. Errors in two variables. Am J Public Health Nations Health 1963; 53:
1656-65.
9. Gullen WH, Bearman JE, Johnson EA. Effects of misclassification in
epidemiologic studies. Public Health Rep 1968; 83: 914-8.
10. Goldberg J. Effects of misclassification on bias in difference
between 2 proportions and relative odds in fourfold table. J Am Stat Assoc 1975; 70:
7.
-
1111. Weinberg C, Umbach D, Greenland S. When will nondifferential
misclassification of an exposure preserve the direction of a trend. Am J Epidemiol
1994; 140(6): 565-71.. DME biases the association either towards or
away from the null hypothesis1212. Szklo M, Nieto F. Epidemiología intermedia. Conceptos y
aplicaciones. España: Díaz de Santos, 2003.. The majority of
the time, it is impossible to predict the direction of the bias because of the complex
framework involving differences in sensitivity, specificity and exposure prevalence
between the cases and the controls. Although Chyou1818. Chyou PH. Patterns of bias due to differential misclassification by
case-control status in a case-control study. Eur J Epidemiol 2007; 22:
7-17. claims to have found patterns of the effect of DME, such patterns are
described only for certain pre-established scenarios and not for a general scenario as
our study intended to. In fact it is one of the limitations Chyou refers in his
paper1818. Chyou PH. Patterns of bias due to differential misclassification by
case-control status in a case-control study. Eur J Epidemiol 2007; 22:
7-17.. Of course, one aspect to highlight in
the description of DME is that there is a strong influence of the prevalence of exposure
as well as the estimated effect size. In practice, DME often arises when surveys are
administered because it is possible that cases have better memory of the exposure than
the controls, which have less motivation to remember. These surveys do not always prompt
completely true responses, not because an individual intended to lie but because the
individual cannot recall their exposure history33. dos-Santos I. Cancer Epidemiology: Principles and Methods. Lyon,
Francia: IARC Library Cataloguing in Publication Data, 1999..
The immediate consequence is that when the exposure classification is determined, false
positives or false negatives arise1919. Hrubá D. [Smoking and breast cancer]. Klin Onkol. 2013; 26:
389-93..
This simulation study analyzed the bias in an odds ratio estimate generated in the presence of DME and NDME in a case-control design for different levels of sensitivity (Se) and specificity (Sp) of the exposure classification (in the cases and the controls), the exposure prevalence among the controls and the true OR. The NDME analysis was simpler than the DME analysis because it was possible to observe easily interpretable trends. In the simulation, we found that 100% of the bias produced by the NDME in estimating the OR is negative, weakening the association and driving the estimation of the risk measure towards the null hypothesis. In addition, we found that the unbiased OR estimates in the presence of NDME are achieved faster at higher levels of specificity compared with sensitivity. This could be a consequence in the selection of strategies to classify individuals, preferring those with a greater chance of exclude the presence of the studied event (i.e. more specific). DME biases the association positively or negatively, driving the OR estimate towards or away from the null hypothesis with great uncertainty. This situation, in which the magnitude of the association is under- or overestimated, leads researchers to affirm associations that do not truly exist or, on the contrary, to affirm their non-existence when they are actually present. This could have serious implications for the generation of new knowledge to reporting opposite effects devoid of plausibility. In fact, to give an example, this could be a plausible explanation for the protective effect of cigarette use in breast cancer in certain studies1919. Hrubá D. [Smoking and breast cancer]. Klin Onkol. 2013; 26: 389-93.. Therefore it should be ideal that researchers question how cigarette use has been measured and then implement better approaches such as measurements of metabolites in blood or hair, avoiding then self-report2020. Joya X, Manzano C, Álvarez AT, Mercadal M, Torres F, Salat-Batlle J, et al. Transgenerational exposure to environmental tobacco smoke. Int J Environ Res Public Health 2014; 11: 7261-74..
In this simulation, it was determined that the DME of the exposure in a case-control study produces positive bias, which is lower compared with the quantity of negative bias (30 versus 70%). However, the positive bias is highly variable and reaches unexpected sizes (as high as 50,000%). Another important finding of this study is that the effect of the factors (sensitivity and specificity of the exposure classification, the exposure prevalence among the controls, true OR) on relative bias is completely different for positive bias than for negative bias. There were no similarities between the two types of bias, and the bias seemed to be affected by all of the factors at the same time and not independently, which would indicate a high degree of interaction between them. These interactions are difficult to interpret using graphics because they only describe two-order interactions. However, the linear models revealed second-, third-, fourth-, and fifth-order significant interactions (data not shown). Of the 57 possible interactions in the DME analysis, 22 (39%) were significant for negative bias and 27 (47%) for positive bias, showing the degree of complexity in this analysis in comparison to the NDME analysis, which only revealed two significant interactions among the 11 possible interactions (18%).
Our analyses were based on the variation of the sensitivity and specificity of the classification of an event of interest. However, we recognize that there are other approaches which additionally include the predictive value of the classification methods such as the one Marshall2121. Marshall RJ. Misclassification of exposure in case-control studies: assessment by quality indices. Epidemiology 1994; 5: 309-14. proposed. Even so, we believe that the approach presented by us is useful for understanding the effects of the limitations in terms of sensitivity and specificity and even more useful because researchers could easily find explanations for the lack of associations or implausible findings through systematic reviews about the limitations of the instruments used by them. Although knowledge of prior information such as sensitivity and specificity of the exposure classification could allow researchers to detected misclassification bias2222. Marshall RJ. An empirical investigation of exposure measurement bias and its components in case-control studies. J Clin Epidemiol 1999; 52(6): 547-50. and correct it2323. Gustafson P, Le ND, Saskin R. Case-control analysis with partial knowledge of exposure misclassification probabilities. Biometrics 2001; 57: 598-609. , 2424. Marshall RJ. Assessment of exposure misclassification bias in case-control studies using validation data. J Clin Epidemiol 1997; 50(1): 15-9., we insist that is very useful to be aware about the effects of misclassification and how these could be avoided if researchers validate the methods of classification. As with any other type bias, it will always be best avoid bias rather than having to correct it.
CONCLUSION
It is likely that a misclassification error will occur if the sensitivity and specificity of any instruments used to compare groups are not exactly 100%. If this type of error occurs, it is preferable if it is non-differential. In cases of NDME, there is equilibrium in the bias, and the explanation of the study results is easier. In a case-control study, it is important to pay close attention not only to the identification of cases and to the appropriate selection of controls but also to the classification of the exposure. Thus, the use of validated classification instruments is emphasized so that instruments with high sensitivity and high specificity are selected. The design of the instrument and the appropriate formulation of the questions on a questionnaire are key components for avoiding DME. It is therefore important that epidemiologists and researchers are close not only to the elaboration and design of surveys, but also to the monitoring of the quality with which these are applied as well as the quality control of other classification procedures and tests laboratory and/or diagnostic tests.
SOFTWARE
Scripts in the form of R code are available on request from the corresponding author.
ACKNOWLEDGMENTS
This work was supported by Estrategia de Sostenibilidad 2013-2014, Universidad de Antioquia. AB is a recipient of a doctoral fellowship grant from Colombian Institute for Scientific and Technological Development (COLCIENCIAS 2010)
REFERENCES
-
1Kleinbaum D, Kupper L, Morgenstern H. Epidemiologic Research: Principles and Quantitative Methods New York: Van Nostrand Reinhood Company, 1982.
-
2Rothman K, Greenland S. Modern Epidemiology. 3th ed. Philadelphia: Lippincott Raven Publishers, 2012.
-
3dos-Santos I. Cancer Epidemiology: Principles and Methods. Lyon, Francia: IARC Library Cataloguing in Publication Data, 1999.
-
4Sanders SA, Hill BJ, Yarber WL, Graham CA, Crosby RA, Milhausen RR. Misclassification bias: diversity in conceptualisations about having 'had sex'. Sex Health 2010; 7: 31-4.
-
5Rikala M, Hartikainen S, Saastamoinen LK, Korhonen MJ. Measuring psychotropic drug exposures in register-based studies - validity of a dosage assumption of one unit per day in older Finns. Int J Methods Psychiatr Res 2013; 22(2): 155-65.
-
6Bross I. Misclassification in 2x2 tables. Biometrics. 1954; 10: 478-86.
-
7Newell D. Errors in the interpretation of errors in epidemiology. Am J Public Health Nations Health 1962; 52: 1925-8.
-
8Keys A, Kihlberg J. Effect of misclassification on estimated relative prevalence of a characteristic: Part I. Two populations infallibly distinguished: Part II. Errors in two variables. Am J Public Health Nations Health 1963; 53: 1656-65.
-
9Gullen WH, Bearman JE, Johnson EA. Effects of misclassification in epidemiologic studies. Public Health Rep 1968; 83: 914-8.
-
10Goldberg J. Effects of misclassification on bias in difference between 2 proportions and relative odds in fourfold table. J Am Stat Assoc 1975; 70: 7.
-
11Weinberg C, Umbach D, Greenland S. When will nondifferential misclassification of an exposure preserve the direction of a trend. Am J Epidemiol 1994; 140(6): 565-71.
-
12Szklo M, Nieto F. Epidemiología intermedia. Conceptos y aplicaciones. España: Díaz de Santos, 2003.
-
13Vogel C, Gefeller O. Implications of nondifferential misclassification on estimates of attributable risk. Methods Inf Med 2002; 41: 342-8.
-
14Daniel W, Cross C. Biostatistics: A Foundation for Analysis in the Health Sciences. USA: Wiley, 2013.
-
15Salazar JC, Baena A. Análisis y diseño de experimentos aplicados a estudios de simulación. Dyna revfacnacminas. 2009; 159: 249-57.
-
16MacMahon B, Yen S, Trichopoulos D, Warren K, Nardi G. Coffee and cancer of the pancreas. N Engl J Med 1981; 304(11): 630-3.
-
17Fox MP, Lash TL, Greenland S. A method to automate probabilistic sensitivity analyses of misclassified binary variables. Int J Epidemiol 2005; 34: 1370-6.
-
18Chyou PH. Patterns of bias due to differential misclassification by case-control status in a case-control study. Eur J Epidemiol 2007; 22: 7-17.
-
19Hrubá D. [Smoking and breast cancer]. Klin Onkol. 2013; 26: 389-93.
-
20Joya X, Manzano C, Álvarez AT, Mercadal M, Torres F, Salat-Batlle J, et al. Transgenerational exposure to environmental tobacco smoke. Int J Environ Res Public Health 2014; 11: 7261-74.
-
21Marshall RJ. Misclassification of exposure in case-control studies: assessment by quality indices. Epidemiology 1994; 5: 309-14.
-
22Marshall RJ. An empirical investigation of exposure measurement bias and its components in case-control studies. J Clin Epidemiol 1999; 52(6): 547-50.
-
23Gustafson P, Le ND, Saskin R. Case-control analysis with partial knowledge of exposure misclassification probabilities. Biometrics 2001; 57: 598-609.
-
24Marshall RJ. Assessment of exposure misclassification bias in case-control studies using validation data. J Clin Epidemiol 1997; 50(1): 15-9.
-
Financial support: Estrategia de Sostenibilidad 2013-2014, Universidad de Antioquia
Publication Dates
-
Publication in this collection
Apr-Jun 2015
History
-
Received
28 Apr 2014 -
Reviewed
10 Sept 2014 -
Accepted
08 Oct 2014