Resumen
Commercially available cordierite and mullite powders were used to obtain cordierite and cordierite-30wt% mullite materials by attrition milling, uniaxial pressing and sintering. Cordierite powders were the coarse (D50 = 1.82 mum), medium (D50 = 0.9 mum) and fine (D50 = 0.45 mum) single granulometric fractions and binary mixtures of them. Mullite powder employed in composites was the 7 h-attrition milled one (D50 = 1.3 mum). Hardness (H V) and fracture toughness (K IC) were measured by Vickers indentation techniques. Composites showed higher H V and K IC than cordierite matrices. In both materials, H V and K IC diminish with the increasing porosity. Dielectric constant (epsilon) and losses (tan delta) were determined at 1 MHz. An increase in epsilon and tan delta values was registered when mullite was present in composites with respect to cordierite material. Higher the porosity, epsilon was lower and tan delta increased. The thermal expansion coefficients (alpha) were determined up to 1000 °C resulting the alpha of the composite close to that of the silicon.
cordierita; mullita; sustratos en electrónica
Evaluacion Termica, Mecanica Y Electrica de Materiales Compuestos Cordierita-Mullita
M.A. Camerucci a , G. Urretavizcaya b , A.L. Cavalieri a
aInstituto de Investigaciones en Ciencia y Tecnología de Materiales (INTEMA),
Av. Juan B. Justo 4302 (7600), Mar del Plata, Argentina
bCentro Atómico Bariloche, Av. Bustillo km 9,5, Bariloche, Argentina
e-mail: andcamer@fi.mdp.edu.ar
Received: July 5, 2000; Revised: October 13, 2000
Commercially available cordierite and mullite powders were used to obtain cordierite and cordierite-30wt% mullite materials by attrition milling, uniaxial pressing and sintering. Cordierite powders were the coarse (D50 = 1.82 mm), medium (D50 = 0.9 mm) and fine (D50 = 0.45 mm) single granulometric fractions and binary mixtures of them. Mullite powder employed in composites was the 7 h-attrition milled one (D50 = 1.3 mm). Hardness (HV) and fracture toughness (KIC) were measured by Vickers indentation techniques. Composites showed higher HV and KIC than cordierite matrices. In both materials, HV and KIC diminish with the increasing porosity. Dielectric constant (e) and losses (tan d) were determined at 1 MHz. An increase in e and tan d values was registered when mullite was present in composites with respect to cordierite material. Higher the porosity, e was lower and tan d increased. The thermal expansion coefficients (a) were determined up to 1000 °C resulting the a of the composite close to that of the silicon.
Keywords: cordierita, mullita, sustratos en electrónica
1. Introduccion
La cordierita (2Al2O3.5SiO2.2MgO) y la mullita (3Al2O3.2SiO2) constituyen una clase de materiales cerámicos técnicamente importante aplicable a una gran variedad de áreas.
En la industria microelectrónica, una de las diez tecnologías más críticas de los 90, la baja constante dieléctrica, alta resistividad, elevada estabilidad térmica y química y muy bajo coeficiente de expansión térmica de la cordierita son propiedades adecuadas que junto a los menores costos de procesamiento lo hacen un material potencialmente utilizable como sustrato en reemplazo de la alúmina empleada tradicionalmente, cuya efectividad se ve limitada por su constante dieléctrica relativamente alta y su pobre conductividad térmica. Adicionalmente, su alta temperatura de sinterización restringe el material conductor a aquéllos con elevado punto de fusión, alto costo y generalmente alta resistividad como tugsteno, molibdeno o platino1-3.
Sin embargo, la cordierita presenta la desventaja de poseer propiedades mecánicas no muy buenas4 y un coeficiente de expansión térmica muy inferior al del chip de silicio.
Por otro lado, la mullita se emplea como material estructural debido a sus excelentes propiedades mecánicas aún a altas temperaturas y se considera un material adecuado para su uso en electrónica. El agregado de mullita a materiales de cordierita5-8 permite ajustar el coeficiente de expansión térmica del material compuesto al del chip de silicio sin ocasionar un gran deterioro en sus propiedades eléctricas. Adicionalmente, permite alcanzar los valores de media y baja respuesta mecánica requeridos para aplicaciones en electrónica de alta y baja perfomance.
Para obtener materiales que reúnan las propiedades adecuadas2 deberá realizarse un procesamiento que conduzca a materiales densos con tamaño de grano fino a partir del control de las distribuciones de tamaño de partícula y de su empaquetamiento y de las condiciones de sinterizado. Además, deberán minimizarse aquellos defectos que surjan del procesamiento de manera de obtener materiales con buena respuesta mecánica.
El objetivo de este trabajo es evaluar la respuesta mecánica y eléctrica y los coeficientes de expansión térmica de materiales de cordierita y compuestos cordierita-mullita en relación con sus características microestructurales (fases cristalinas y vítreas, porosidad) para seleccionar un material que cumpla los requerimientos para su empleo como sustrato en microelectrónica.
2. Materiales y Metodos
2.1. Materias primas y procesamiento
Se trabajó con materiales de cordierita y mullita comerciales (Baikowski) de 1,82 y 2,35 mm de tamaño medio de partícula (Deo); 3,4 y 2,3 m2/g de superficie específica BET (SE) y 2,6 y 3,05 g/cm3 de densidad picnométrica (dpic.), respectivamente. El acondicionamiento granulométrico de los polvos de cordierita y mullita originales se realizó por molienda por atrición9. Los polvos de cordierita comercial con su granulometría original y molidos a 1045 rpm durante 8 y 32 h se emplearon como fracciones de gruesos G, medios M (D50 = 0,9 mm; SE = 6,5 m2/g) y finos F (D50 = 0,45 mm; SE = 11,2 m2/g) y para la preparación de mezclas granulométricas binarias F/G, F/M y M/G en relaciones 30/70, 50/50 y 70/30 en peso.
Por cálculo del coeficiente de expansión térmica empleando los modelos de Turner y de Kerner10 se realizó una estimación del porcentaje de mullita que seria necesario agregar para ajustar el coeficiente de expansión del material compuesto al del chip de silicio (a = 3-3,5 x 10-6 °C-1). Así, los materiales compuestos se formularon por agregado de 30% en peso de mullita molida por atrición a 880 rpm durante 7 h (D50 = 1,3 mm; SE = 6,4 m2/g) con un acalculado = 3,1 x 10-6 °C-1.
Los polvos utilizados para obtener las mezclas granulométricas binarias de cordierita y los materiales compuestos, se homogeneizaron en molino de atrición con alcohol isopropílico durante 10 min, se secaron y tamizaron por malla N° 400 (37 mm).
Los polvos se compactaron en forma de pastillas por prensado uniaxial a 20 MPa sin agregado de aditivos y se sinterizaron en un horno eléctrico con elementos calefactores de MoSi2 a 1450 °C, 2 h con un ciclo de calentamiento/enfriamiento específico11. Las densidades de los materiales sinterizados (dS) se determinaron por el método de Arquímedes en agua a temperatura ambiente.
2.2. Determinación de dureza y tenacidad a la fractura
La dureza (HV) y el factor crítico de intensidad de tensiones (KIC) se determinaron por la técnica de indentación12-16 a partir de la medición de las dimensiones de las huellas y fisuras generadas por la aplicación de un indenter Vickers con una carga de 3,5 kg (microdurómetro Tukon modelo 300) sobre las muestras sinterizadas y pulidas sucesivamente con pastas de diamante de 6, 3 y 1 mm. Para el cálculo de HV en GPa se utilizó la expresión HV = 470 L/a2 donde L: carga [N] y a: semidiagonal de la huella [mm]. Para el cálculo de KIC se empleó la relación propuesta por Miranzo y col.17. El error en la determinación de los valores de H es de 5%, mientras que en KIC es superior. Los valores se obtuvieron para un módulo de Young máximo (Emáx) calculado empleando la ecuación empírica propuesta por Knudsen y Spriggs18 E = E°exp(-bP)19-21 con b = 3 para ambos materiales5 y E°máx obtenido considerando un modelo en paralelo10 con E°mullita = 210 GPa, E°cordierita = 134 GPa y E°vidrio = 73 GPa5, 22.
2.3. Determinación de propiedades eléctricas y coeficiente de expansión térmica
La constante dieléctrica (e) y el ángulo de pérdida (tg d) se determinaron a 1 MHz, a temperatura ambiente (impedancímetro Hewlett Packard 4284A LSR meter). e se calculó a través de medidas de capacidad (e = Cl/ e0A donde C: capacidad [F], e0: permitividad del vacío = 8,85 x 10-14 [F/cm], l: espesor de la muestra [cm] y A: área [cm2]) y la tg d se midió directamente. Las muestras sinterizadas (diámetro = 1,2 cm y espesor = 0,3 cm) se pulieron en sus caras planas con papeles de SiC de grados abrasivos 320 y 600, sucesivamente, para lograr el planoparalelismo y se recubrieron con pintura de plata como electrodos. El error es de 3-5% para e y 10-12% para tg d.
Para estimar los valores de la constante dieléctrica de los materiales compuestos a partir de la regla de las mezclas, se midieron a 1 MHz los valores de e de la cordierita y la mullita originales sinterizadas a 1450 y 1700 °C, 2 h, respectivamente y se normalizaron a porosidad cero empleando el factor (1-P), donde P: fracción de porosidad6,23. Los valores obtenidos fueron e0cordierita = 6,2 y e0mullita = 8,4. El valor de e0 obtenido para la mullita molida es más alto que los reportados5-6,23 que son del orden del determinado para el polvo de mullita original (e0mullitaoriginal = 6,8). Esto se podría asociar al mayor porcentaje de hierro determinado por análisis químico (<1%) en el polvo molido por atrición.
Los coeficientes de expansión térmica (a) se determinaron a una velocidad de calentamiento de 2 °C/min hasta 1000 °C (dilatómetro Adamel Lhomargy) sobre probetas prismáticas de longitud = 15 mm y sección = 0,6 x 0,3 mm2, compactadas por prensado uniaxial a 20 MPa y sinterizadas a 1450 °C, 2 h.
2.4. Cálculo de las densidades reales
Las densidades reales (dR) del polvo de cordierita y del material compuesto de cordierita-30% mullita tratados a 1450 °C, 2 h resultaron 2,57 y 2,70 g/cm3, respectivamente.
Para su cálculo se empleó la regla de las mezclas y se determinaron las fases presentes (confirmadas por DRX y FTIR) y sus porcentajes a partir de la correspondiente sección isotermal a 1450 °C del sistema SiO2-Al2O3-MgO24.
Las composiciones de ambos materiales se localizaron en el triángulo de compatibilidad cordierita-mullita-líquido y los porcentajes calculados fueron: 84, 10 y 6%, respectivamente en la cordierita y 50, 35 y 15% en el material compuesto cordierita-30% mullita. Se emplearon las densidades teóricas de la cordierita y mullita (2,52 y 3,16 g/cm3, respectivamente) y la densidad picnométrica del vidrio (2,51 g/cm3) formulado con la composición y porcentajes de equilibrio calculados a partir de la sección isotermal a 1450 °C (SiO2 = 63%, Al2O3 = 25%, MgO = 12%) y obtenido por 'quenching' en agua del fundido a 1600 °C, 2 h.
3. Resultados y Discusion
3.1. Efecto de la porosidad
Se estudió la influencia de la porosidad (% P = 100 - %dS/dR) de los materiales de cordierita y cordierita-30% mullita sobre los parámetros de fractura y los eléctricos. Los diferentes empaquetamientos en verde, obtenidos con las fracciones simples y mezclas granulométricas binarias formuladas, condicionaron los valores de porosidad alcanzados. Para ambos materiales, la dureza (HV) disminuye con el aumento de la porosidad (Fig. 1) debido al mayor aporte de la componente plástica de la deformación: de 8,1 a 6,4 GPa para los materiales de cordierita y de 9 a 7,4 GPa para los materiales compuestos en los rangos de porosidad de 2 a 7,5% y de 1,5 a 5%, respectivamente.
Tanto los valores de dureza de los materiales de cordierita G, M y F como los de los mismos con 30% de mullita siguen el orden HV (G) < HV (M) < HV (F) con la disminución de la porosidad. Los valores máximos y mínimos de dureza para los materiales de cordierita y cordierita-30% mullita corresponden a las materiales de cordierita F/M 70/30 (8,1 y 9 GPa) y M/G 30/70 (6,4 y 7,4 GPa), respectivamente. Para el ajuste de los valores experimentales, se consideró una variación exponencial de H con la porosidad, H = H0(exp - cP)5,25 donde H0: dureza del material totalmente denso, P: fracción de porosidad y c: constante, determinándose valores de la constante: c = 3,3 para cordierita y c = 5,4 para los compuestos. Mussler5 consideró un valor de c = 6 para ambos tipos de materiales.
La tenacidad a la fractura (KIC)disminuye con el aumento de la porosidad de 1,90 a 1,67 y de 2,03 a 1,83 MPam1/2 para los materiales de cordierita y cordierita-30% mullita, respectivamente (Fig. 2).
Tanto los valores de tenacidad obtenidos para las fracciones simples como los de estas fracciones con 30% de mullita siguen el mismo orden de variación que los de dureza KIC (G) < KIC (M) < KIC (F) con el incremento en la porosidad de estos materiales. Asimismo, los valores extremos corresponden a las matrices de cordierita F/M 70/30 que presentó la menor porosidad (1,90 y 2,03 MPam1/2) y M/G 30/70 (1,67 y 1,83 MPam1/2), matriz con la porosidad más alta. Considerando que en estos materiales el tamaño de poro es del orden del tamaño de grano (D50» 0,5 mm), el efecto de las grietas (defecto crítico mayor que el tamaño del poro) a lo largo del borde de grano será dominante. A mayor porosidad, el aumento de la cantidad de poros actuando como concentradores de esfuerzos explicaría la disminución en el valor de KIC por un efecto combinado del poro y la grieta cuando esta propaga.
La expresión de ajuste utilizada fue KIC = K0IC(exp-tP) resultando t = 2,0 para cordierita y t = 2,4 para cordierita-30% mullita, valores similares al reportado por Mussler5 (t = 3) para este tipo de materiales.
Para evaluar la variación de la constante dieléctrica (e) con la porosidad se consideraron un modelo en paralelo: e = e1V1 + e2V2 y un modelo en serie: 1/ e = V1 / e1 + V2 / e2 donde e: constante dieléctrica del compuesto; V1 y V2: fracciones en volumen de las fases 1 y 2 y e1 y e2: constantes dieléctricas10,26. Si una de las fases presentes es la porosidad (e1 = 1 y V1 = P), resulta: e = em -P(em - 1) en paralelo y e = em/[P(em - 1) + 1] en serie. Tanto en los materiales de cordierita (Fig. 3 a) como en los compuestos (Fig. 3 b) la disminución lineal de la constante dieléctrica con el aumento de la porosidad se atribuyó a la contribución del aire presente en los poros, de constante dieléctrica (e = 1) menor que la de la matriz sólida. Este es otro factor que contribuye a explicar los valores más altos de las constantes dieléctricas determinados en los materiales compuestos respecto de los materiales de cordierita en todo el rango de porosidades estudiadas (ecordierita = 6,1 a 5,85 y ecordierita-30% mullita = 6,8 a 6,51).
El mejor ajuste de los valores experimentales se logró empleando el modelo en paralelo. De este ajuste se puede asociar la estructura de los materiales a un arreglo de capacitores en paralelo de acuerdo a lo encontrado por Anderson 6, en discrepancia con Mussler 5 quien reporta un arreglo en serie.
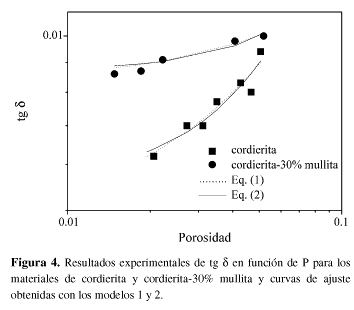
En lo referente al ángulo de pérdida (Fig. 4), se registraron valores de tg d más altos para los materiales compuestos y un aumento de la tg d con la porosidad. El incremento resultó menor para el material compuesto (0,0086 a 0,0098) que para el material de cordierita (0,0062 a 0,0094) en los rangos de porosidad estudiados. La diversidad de factores, además de la porosidad, que influyen en la variación de este parámetro no nos permiten dar una explicación simple para la disminución de la eficiencia eléctrica de los materiales compuestos frente a la de cordierita.
Algunos modelos simples que indican una dependencia lineal de la tg d con la porosidad fallan al predecir un valor nulo de tg d para materiales totalmente densos en los cuales existen fuentes de pérdidas como la orientación al azar de los granos y los bordes de granos. Se han propuesto diversas expresiones matemáticas que consideran en un término adicional las pérdidas debidas a la porosidad26:
tg d = (1-P) tg d0 + bPn (1)
tg d = (1-P) tg d0 + jP [P/(1-P)]2/3 (2)
donde tg d0: ángulo de pérdida para el material totalmente denso y b y j: constantes. La ecuación (2) se obtiene a partir de la expresión (1) asumiendo que la potencia de P resulta aproximadamente igual a 2/3. Este valor del exponente que tiene dimensiones de área, sugiere que las pérdidas se pueden asociar con el área superficial de los poros.
En la Fig. 4 se muestram, además de la dependencia de la tg d con la porosidad para ambos materiales estudiados, las correspondientes curvas de ajuste usando los modelos de las ecuaciones (1) y (2). Para ambos materiales, el mejor ajuste se obtuvo empleando el modelo 1 con los siguientes valores de los parámetros: n =1 - 1,5; tg d0 = 0,0049 - 0,0056 y b = 0,16 - 0,45 para la cordierita y con n = 1,1; tg d0 = 0,0084 y b = 0,055 para el material compuesto.
3.2. Efecto del agregado de 30% de mullita
Se estudió la variación de HV, KIC, e, tg d y a de los materiales de cordierita-30% mullita respecto de los valores determinados en las matrices de cordierita: G, M, F, F/G, M/G y F/M 50/50 y 70/30 (no se consideraron las mezclas binarias 30/70 que presentaron una menor densificación).
Los valores experimentales de los parámetros mecánicos se corrigieron a porosidad cero a partir de las relaciones, HV0 = H exp(cP) y KIC0 = KIC exp(tP) con c = 3,3 y t = 2 para cordierita y c = 5,4 y t = 2,4 para cordierita-30 % mullita (Tabla 1).
El aumento de la dureza (HV) de los materiales con 30% mullita respecto de los de cordierita (desde 7,2-8,1 a 7,4-9 GPa) se atribuyó a la influencia de la disminución de la porosidad y presencia de una mayor cantidad de mullita, factores que prevalecen frente al efecto adverso del incremento en la cantidad de vidrio.
Al eliminar el efecto de la porosidad, tanto en los materiales de cordierita como en los compuestos se observó un aumento de la dureza (HV0) (de 8,1 a 8,8 GPa para los materiales de cordierita y de 9,2 a 9,9 GPa para los compuestos con 30% de mullita). Esto puede asociarse con el incremento de los contenidos de mullita y de vidrio, aunque no pueden separarse los efectos de ambas fases para su análisis.
Se registró un incremento de la tenacidad a la fractura, KIC en los materiales formulados con un agregado de 30% de mullita (desde 1,67 a 1,90 MPam1/2 para los materiales de cordierita desde 1,86 a 2,03 MPam1/2 para los compuestos con 30% de mullita). Al eliminar el efecto de la porosidad los valores resultaron próximos a 2,00 MPam1/2 de acuerdo con los reportados en la literatura5,6, siendo ligeramente superiores para los materiales compuestos (KIC0 desde 1,83 a 2,00 para cordierita y desde 2,03 a 2,10 MPam1/2 para cordierita-30% mullita).
En la Tabla 2 se muestran los valores obtenidos de e, tg d y e0 para los materiales de cordierita y cordierita-30% mullita considerados. Los valores de e se corrigieron a porosidad cero: e0 = e/(1 P) donde P: fracción de poros y e: valores calculados por la regla de las mezclas empleando el modelo en paralelo.
En los materiales compuestos se determinó un aumento de la constante dieléctrica respecto del material de cordierita desde 5,85-6,10 a 6,59-6,80 y de 6,10-6,23 a 6,74-6,90 al restar el efecto de la porosidad. Esta variación se puede atribuir al efecto combinado del incremento de las cantidades de mullita (fase con e mayor) y de la fase vítrea (los óxidos alcalinotérreos como CaO y MgO aumentan la conductividad eléctrica de los vidrios de silicatos aunque en menor medida que los alcalinos y la incorporación de Al2O3 y otros óxidos tienen efectos no muy pronunciados22, 27) y de una disminución de porosidad al aumentar el contenido de mullita.
En cuanto al ángulo de pérdida, se determinó un incremento (0,0062-0,0094 a 0,0086-0,0098) con el agregado de 30% en peso de mullita. Ni el aumento de la cantidad de fase vítrea formada ni la disminución de la porosidad con el aumento en el contenido de mullita en los materiales compuestos permiten dar una explicación directa del resultado obtenido.
Los valores medidos de los coeficientes de expansión térmica de los materiales de cordierita (acordierita = 2,4 x 10-6 °C-1) y cordierita-30% mullita (acompuesto = 3,6 x 10-6 °C-1) confirman que con el agregado de este porcentaje de mullita, se logra ajustar el coeficiente de expansión del material compuesto al del silicio (asilicio = 3 - 3,5 x 10-6 °C-1) según se había obtenido por cálculo.
4. Conclusiones
Se obtuvieron materiales compuestos con propiedades mecánicas y eléctricas que cumplen los requerimientos para su empleo como sustratos en microelectrónica en reemplazo de la alúmina.
Los materiales compuestos presentaron valores de H y KIC más altos que los materiales de cordierita, mientras que en ambos tipos de materiales se registró una disminución de los parámetros con el incremento de la porosidad.
En los compuestos, tanto e como tg d resultaron más altos que para los materiales de cordierita.
Con el material compuesto, mezcla granulométrica binaria de finos y medios F/M en la proporción 70/30 como matriz y con 30% mullita como fase secundaria, se logró el mejor comportamiento mecánico (H = 9 GPa y KIC = 1,98 MPam1/2) sin producirse un importante deterioro de las propiedades eléctricas (e = 6,80 y tg d = 0,0086) y con un coeficiente de expansión térmica (3,6 x 10-6 °C-1) que se ajusta al del silicio.
- 1. Tumala, R.R J. Am. Ceram. Soc., v. 74 n. 5, p. 895-908, 1991.
- 2. Subramanian, M.A.; Corbin, D.R.; Chowdhry, U. Bull. Mat. Science, v. 16, n. 6, p. 665-678, 1993.
- 3. Knickerbocker, S.H.; Kumar, A.H.; Herron, L.W. Am. Ceram. Soc. Bull., v. 72, n. 1, p. 90-95, 1993.
- 4. Suzuki, H.; Ota, K.; Saito, H. J. Mater. Sci., v. 23, p. 1534-1538, 1988.
- 5. Mussler, B.H.; Shafer, M.W. Bull. Am. Ceram. Soc., v. 63, n. 5, p. 705- 710, 1984.
- 6. Anderson, R.M.; Gerhardt, R.; Wachtman, J.B.; Onn Jr., D.; Beecher, S. Advances in Ceramics, v. 26, p. 265-277, 1989.
- 7. Hodge J.D. Advances in Ceramics, v. 19, p. 117-129, 1986.
- 8. Monroe, D.L.; Wachtman, J.B. Jr. Proc. 1st Europ. Ceram. Soc. Conf. The Netherlands Elsevier Applied Science, London, p. 3.394-3.408, 1989.
- 9. Camerucci, M.A.; Cavalieri, A.L. J. Mater. Synthesis and Processing, v. 6, n. 2, p. 117-123, 1998.
- 10. Kingery, W.D. Introduction to Ceramics, Ed. John Wiley & Sons, New York, Cap. 15, p. 768-777, 1960.
- 11. Camerucci, M.A. Thesis Doctoral, Universidad Nacional de Mar del Plata, Dic. 1999.
- 12. Lawn, B.; Wilshaw, R. J. Mater. Sci., v. 10, p. 1049-1081, 1975.
- 13. Lawn, B.R.; Evans, A.G.; Marshal, D.B. J. Am. Ceram. Soc., v. 63, n. 9-10, p. 574-581, 1980.
- 14. Lawn, B.R.; Marshall, D.B. J. Am. Ceram. Soc., v. 62, n. 7-8, p. 347-350, 1979.
- 15. Liang, K.M.; Orange, G.; Fantozzi, G. J. Mater. Sci., v. 25, p. 207-214, 1990.
- 16. Li, Z.; Ghosh, A.; Kobayashi, A.S.; Bradt, R.C. J. Am. Ceram. Soc., v. 72, n. 6, p. 904-911, 1989.
- 17. Miranzo, P.; Moya, J.S. Ceramics International, v. 10, n. 4, p. 147-152, 1984.
- 18. Knudsen, F.P. J. Am. Ceram. Soc., v. 42, n. 8, p. 376-387, 1959.
- 19. Passmore, E.M.; Spriggs, R.M.; Vasilos, T. J. Am. Ceram. Soc., v. 48, n. 1, p. 1-7, 1965.
- 20. Dutta, S.K.; Mukhopadhyay, A.K.; Chakraborty, D. J. Am. Ceram. Soc., v. 71, n. 11, p. 942-947, 1988.
- 21. Torrecillas, R.; Moya, J.S. Bol. Soc. Esp. Ceram. Soc., v. 27, n. 3, p. 123-135, 1988.
- 22. Mari, E. Los Vidrios, Ed. Américalle, Argentina, p. 72-76, 1982.
- 23. Ebadzadeh, T.; Lee, W.E. J. European Ceram. Soc., v. 18, p. 837-848, 1998.
- 24. Smart, R.M.; Glasser, F.P. Ceramics International, v. 7, n. 3, p. 90-97, 1981.
- 25. Lee, W.E.; Rainforth, W.M. Ceramic Microstructures, Ed. Chapman & Hall, London p. 85-97, 1994.
- 26. Penn, S.J.; Alford, N.M.; Templeton, A.; Wang, X.; Xu, M.; Reece, M.; Schrapel, K. J. Am. Ceram. Soc., v. 80, n. 7, p. 1885-1888, 1997.
- 27. Fernandez, Navarro J.M. El Vidrio, C.S.I.C. Instituto de Cerámica y Vidrio, Madrid, p. 570-580, 1985.
Fechas de Publicación
-
Publicación en esta colección
04 Abr 2001 -
Fecha del número
Oct 2000
Histórico
-
Recibido
05 Jul 2000 -
Revisado
13 Oct 2000