Abstract
Wood is generally considered an anisotropic material. In terms of engineering elastic models, wood is usually treated as an orthotropic material. This paper presents an analysis of two principal anisotropic elastic models that are usually applied to wood. The first one, the linear orthotropic model, where the material axes L (Longitudinal), R( radial) and T(tangential) are coincident with the Cartesian axes (x, y, z), is more accepted as wood elastic model. The other one, the cylindrical orthotropic model is more adequate of the growth caracteristics of wood but more mathematically complex to be adopted in practical terms. Specifically due to its importance in wood elastic parameters, this paper deals with the fiber orientation influence in these models through adequate transformation of coordinates. As a final result, some examples of the linear model, which show the variation of elastic moduli, i.e., Young´s modulus and shear modulus, with fiber orientation are presented.
anisotropic material; orthotropic elastic models; wood elastic constants; fiber orientation; compression test
REGULAR ARTICLES
Remarks on orthotropic elastic models applied to wood
Nilson Tadeu MasciaI, * * e-mail: nilson@fec.unicamp.br ; Francisco Antônio Rocco LahrII
IFEC, State University of Campinas
IIEESC, State University of São Paulo
ABSTRACT
Wood is generally considered an anisotropic material. In terms of engineering elastic models, wood is usually treated as an orthotropic material. This paper presents an analysis of two principal anisotropic elastic models that are usually applied to wood. The first one, the linear orthotropic model, where the material axes L (Longitudinal), R( radial) and T(tangential) are coincident with the Cartesian axes (x, y, z), is more accepted as wood elastic model. The other one, the cylindrical orthotropic model is more adequate of the growth caracteristics of wood but more mathematically complex to be adopted in practical terms. Specifically due to its importance in wood elastic parameters, this paper deals with the fiber orientation influence in these models through adequate transformation of coordinates. As a final result, some examples of the linear model, which show the variation of elastic moduli, i.e., Young´s modulus and shear modulus, with fiber orientation are presented.
Keywords: anisotropic material, orthotropic elastic models, wood elastic constants, fiber orientation, compression test
1. Introduction
On the whole, in order to solve a solid mechanics problem some conditions must be satisfied. These conditions are related to equations of equilibrium, strain-displacement relations and material constitutive laws. The first and second conditions do not depend on the characteristics of the material of which the solid is composed. Whereas the third, which relates stress to strain components at any point in the solid, is a function of the material. These laws may be simple or complex, depending on the material of the body. In fact, the behavior of the real material is not easy to be comprehended. When trying to model mathematically that behavior, it is necessary to construct idealizations and perform simplifications, using a convincing theory and adequate experimental tests. The final result of modeling is to get an expression that can be used to predict a specific property, with an acceptable degree of reliability.
The most general elastic constitutive model formulated to describe the mechanical behavior of material is the anisotropic model. This kind of model implies that there is no material symmetry, and mechanical properties in certain directions are different. On the other hand, if there is material symmetry, the material can be denominated, for example, orthotropic or isotropic. In this context, the adequacy of a determined material for a certain elastic model is based on the existence of elastic symmetry axes. In these axes, denominated elastic principal axes, there is invariance of the constitutive relations under a group of transformations of coordinate axes.
In fact, the study of anisotropy implies knowing the constitutive law that governs the elastic behavior of the material and consequently, determining the constitutive tensor, Sijkl, and its components. In a completely elastic and anisotropic model this tensor has 81 unknown constants. By using adequate simplifications, this number can be reduced to 9 constants, which is denominated orthotopric model, or to 3 constants, the isotropic model.
Among the construction materials, wood, because of its internal structure with axes of elastic symmetry longitudinal, tangential and radial, reveals an orthotropic pattern. Thus, there are 9 constants to be determined. Besides this,due to nature of wood, the variation of grain angle constitutes the fundamental cause of wood anisotropy. It is responsible for the greatest changes in the values of the constitutive tensor components, i.e., in these wood elastic constants.
In this way, the goal of this paper is to examine the orthotropic models for wood, the linear and cylindrical ones, some elastic constitutive tensor components (Young's modulus and shear modulus), using an adequate transformation coordinate and also to present some examples showing the effect of grain orientation in these elastic parameters.
2. Theoretical Analysis of the Elastic Properties of Anisotropic Materials
2.1. Elastic models
According to Love1, Chen and Saleeb2 among others, the laws and equations that govern engineering problems are related to the stored energy in a solid. So, an elastic solid is capable of storing the energy developed by the external work and transforms it into potential elastic energy that is denoted as strain energy. During this process the body is deformed, but recovers its original shape and size.
In this condition, if no energy is dissipated during the process of deformation, under adiabatic and isothermal conditions, the derived equations from this supposition are termed elastic models of Green and the material that makes the body as hyperelastic material. Thus, a hyperelastic material is the one that has a strain energy function, denoted by Uo.
The elastic material of Green is, in fact, a special case of the most general elastic material called elastic material of Cauchy, but considering the existence of the Uo, in order to maintain unaltered the laws of thermodynamics. These laws say that no work is produced by an elastic material in a closed loading cycle.
For an elastic body, the current state of stress depends only on the current state of strain. Mathematically, the constitutive laws can be written as:
in which: sij is the stress tensor; ekl is the strain tensor, and Fij is the response function. Notice that only small strains given by  are considered in the strain tensor. The term ui,j represents the partial derivative of displacement.
are considered in the strain tensor. The term ui,j represents the partial derivative of displacement.
As has already been emphasized, the elastic models described by Equation 1 is both reversible and path independent since that strains are uniquely determined from the current state of stress or vice versa.
We can set the response function as polynomial relations of n-degree, relating stress and strain, by:
where: f0, f1... are elastic response parameters3.
One can observe that the first term in Equation 2 is related to the scalar state of stress or strain, the second term represents the first order model or linear model, the third term represents the second order or nonlinear model and so on.
Consider now an elastic solid in equilibrium, with conditions of respected compatibility. The Principle of Virtual Work relates a series of equilibrium Fi, Ti, sij,ui to a series of the virtual compatibility dui,deij via the following equation:
where: Ti is the surface force; Fi is the external body force; ui is the displacement; A is the area; V is the volume and d denotes variation. Figure 1 shows these parameters.
The left side of Equation 3 represents the variation of external work dW, while the right side represents the variation of the strain energy delta dU. From Equation 3 we can obtain that:
where:
Thus the relationship among sij, ekl and Uo can form the constitutive laws of the material. In general, these laws describe the behavior of the usual construction material.
Using the strain energy function and considering the Green elastic model, formulations of the constitutive laws for different classes of elastic materials can be established. So, consider a strain energy function given by:
where C0,dij,bijkl, aij are constants. In view of the strain energy formulation where the strain energy has a stationary value in relation to the strain tensor, it is possible to set C0 = 0. From Equation 5, the stresses can be expressed by:
It may also be taken into the account the fact that aij = 0, since that the initial strain field corresponds to an initial stress free state, and (bijkl + bklij) can be taken as Cijkl, we have:
The Cijkl is the tensor of material elastic constants.
Agreeing that | Cijkl | ¹ 0 Equation 7 can be expressed as:
where: Sijkl is the compliance tensor.
The Cijkl has 81 constants to be determined and must be symmetrical due to Cauchy's second law of motion. In addition, since both sij and ekl are symmetrical, the number of elastic constants is reduced to 21, with 18 independent ones4. This implies that in an anisotropic material with the principal stress directions do not coincide with the principal strain directions.
The constitutive laws may also be written in matrix form as:
Similarly for Sijkl, we obtain:
In this case, we used the contracted notation for stresses, strains and, consequently, for the constitutive tensor. It can be found in Ting5, where the indices 1, 2 and 3 correspond, for example, to the axes x, y and z. So the stresses are given by:
and the strains are written as:
The constitutive tensor becomes, then, a 6 x 6 symmetric matrix and the constitutive relationship is reduced to:
2.2. Elastic symmetry
According to Lekhnitskii6 all bodies, on the whole, can be divided into homogeneous and non-homogeneous bodies, and isotropic and anisotropic as well.
When a body is considered to be homogeneous, its physical properties, such as density, remain invariant in all directions, in any of its points. For non-homogeneous body its properties are not constants.
Wood, as was presented by Perkins7, might be classified as a material that possesses some levels of inhomogeneity from the macroscopic structure to microscopic structure. Dinwoodie8 noticed that there are four levels: macroscopic, microscopic, ultrastructural and molecular (See Figure 2). These levels could explain the adequacy of wood to the theory of Continuum Mechanics or certain features of it. For example, the wood crushing and the wood tensile strength could be related to the strength of the tracheids. Besides that, the components of stress, strain and elastic constants in different levels can be considered and the elastic properties would depend on the position in the tree. Moreover, the macroscopic constants Cijkl are not necessarily equal to the microscopic constant cijkl or, equal to the average values. However, when the medium is macroscopically homogeneous and when the strains are small and relatively homogeneous, one could consider the material response as homogeneous and Cijkl is approximately equal to cijkl.
If the elastic properties of the material are the same in certain directions at a point, then the material exhibits symmetry with respect to these directions. If symmetry exists, the material is generally said to be isotropic. Otherwise, if there is no symmetry at all, the material is said to be anisotropic.
Another interesting issue to be pointed out is that when a body presents certain kinds of symmetry, the constitutive relations are simplified. These simplifications can be done in different ways just as those used by Love1, where the strain energy function remains unaltered by all symmetrical coordinate system substitutions. Thus, for example, a corresponding substitution given by three axes of elastic symmetry,  , with i = 1,2,3 or also
, with i = 1,2,3 or also  , does not change Uo. Lekhnitskii6, on the other hand, performs these simplifications by developing in two different coordinate systems, symmetrical one to other. He compares the obtained constitutive relations, identifying, in this way, the existence of the elastic symmetry.
, does not change Uo. Lekhnitskii6, on the other hand, performs these simplifications by developing in two different coordinate systems, symmetrical one to other. He compares the obtained constitutive relations, identifying, in this way, the existence of the elastic symmetry.
A material with elastic symmetry under the linear transformation  , with
, with 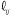 being the transformation tensor, requires that the constitutive tensor, either Crspq or Srspq, be submitted to the following condition:
being the transformation tensor, requires that the constitutive tensor, either Crspq or Srspq, be submitted to the following condition:
2.3. Classification of materials regarding as the number of elastic symmetrical planes
There are four cases of elastic symmetry that are considered most important. They are: one plane of elastic symmetry, three planes of elastic symmetry (orthotropic material), transversely isotropy material and isotropic m aterial. Since the purpose of this paper is to consider wood as an orthotropic body, we only analyzed this kind of elastic symmetry.
Thus, a body referred to a coordinate system xi is defined as orthotropic material if through each point there are three mutually perpendicular axes of elastic symmetry. Then, using the coordinate system x1, x2 and x3 (or x, y, and z), perpendicular to the three planes of material symmetry and considering the elastic properties to be invariant under counterclockwise rotation 180° of about three axes, and using one at time as showed in Figure 3.
Consequently, we obtain that:
And we find, either Crspq or Srspq,even in contracted notation, that:
Now, the engineering notation may be used for elastic constants and it can be written by:
where: Ei is the Young's modulus related to i direction, Gij is the shear modulus related to ij - plane and nij is the Poisson's ratio in ij - plane.
It could be interesting to apply to wood the theory of transversely isotropic material, since that would be possible to consider some simplifications to wood. This sort of material possesses a rotational elastic symmetry about one of the coordinate axes. In other words, if one takes, for example, the x-y plane as the plane of symmetry, in this plane, at any point having any direction, the elastic properties are the same, and the elastic constants are E, G and v in the following relationship:  . In addition to these constants in this model there are only two more to be determined.
. In addition to these constants in this model there are only two more to be determined.
For wood, the plane of isotropy could be the R-T plane. But, unfortunately, the results from experimental tests show that the elastic constant in R-direction is, in general, greater than in T-direction and the relationship among the E, G and v is not valid either.
2.4. Some considerations about the orthotropic model applied to wood
The theory of elasticity applied to wood is based on the hypothesis that wood has three mutually planes of elastic symmetry according to its internal structure. Bodig and Jayne9, in addition to this hypothesis, consider the material homogeneous. Therefore, the longitudinal- tangential surface is not a plane, but roughly cylindrical. The other two surfaces, the longitudinal-radial and radial-tangential are, truthfully, more straight. Thus, wood may be treated as a cylindrical orthotropic body.
There are many procedures in literature that treat wood as the cylindrical anisotropic body. Carrier10 described a mathematical analysis about thin wooden plates applying to the Airy's function in terms of cylindrical coordinates. Foschi11, Gopu and Goodman12 and Noack and Roth13, for example, presented a formulation of plane problems using this model in cylindrical coordinates for plane orthotropic curved beams. Hsu14 applied this model when studying the shrinkage in wood logs.
The cylindrical orthotropic elastic model can be regarded as:
in a cylindrical coordinate system r, z and q, considering the elastic tensor in contracted notation.
According to Lekhnitskii6, a body with cylindrical anisotropy must necessarily have the axis of anisotropy with the following property:
-
all directions parallel to the axis of anisotropy (for example
Laxis, that coincides with the axis of the core), passing through different points are equivalents;
-
all directions intersecting this axis at right angles (for example
R-direction, are also equivalent), and
-
all directions orthogonal to the first two are equivalent (in this case,
T-direction).
Furthermore, for a homogeneous body there is no difference between r and q. This implies that:
or:
Although it seems to be interestingly associated to wood as a cylindrical anisotropic model, as previously described to material with transversely plane of isotropy some results available in the literature indicate that, in general form, Eq ¹ Er and Gqz¹ Grz.
Another subject that might be arisen when analyzing the macroscopic structure of wood, following some ideas that can be found in Chung15, is concerned with adopting two different coordinate systems to wood. Firstly, considering a cylindrical axes: z-direction parallel to axis of the tree, q-axis parallel to annual growth rings and raxis perpendicular to o direction. Secondly, considering Cartesian coordinate system, L, R and T, as has been mentioned, to describe small parts, as a specimen. Figure 4 shows these axes.
This description corresponds to the Lekhnitskii's description, in which a body may have both curvilinear anisotropy and rectilinear anisotropy.
So, let x1 = r; x 2 = z; x3 = q be a global coordinate system (G) and x+1 = r = R; x+2 = T e x+3 = L be a local coordinate system (L). The coordinate transformation is given by:
Now it is possible to write stress and strain in terms of these systems as:
and:
where K is the following matrix:
and:
and [K-1]T is the transpose of the inverse of K.
One can consider certain coordinate transformations in order to analyze specific features of wood. For example, if the fibers are inclined of the angle a in relation the L - direction, we have:
When the fibers are inclined to R or T directions or both directions the equation be comes more complicated. This may happen when the log presents a spiral grain pattern.
Considering an axisymmetric body with the z-axis being the generator, the stress leads to:
and the strain:
Finally, the constitutive relations can be written in terms of matrices by:
and more simply:
And, using Equation 29 one can obtain the elastic parameters of wood in these coordinate systems.
If the generator were inclined in relation to z-axis, Equation 25 must appropriately be changed to mathematically express this fact.
Now, after presenting the general ideas of the cylindrical anisotropy applied to wood, we may make some reasons about choosing the rectilinear anisotropy only. The present work is concerned with the analysis of the orthotropic model applied to wood dealing with small specimens or small pieces, generally removed at some distance from the center of the trees. Here, we may admit wood as a rectilinear orthotropic body, avoiding the mathematical complication and experimental difficult as well, that may result from the assumption of the cylindrical orthotropic model.
In this way, arbitrating for wood the rectilinear ortrotropic model, with the three elastic principal axes denoted L, R and T the components of the compliance tensor Sijkl are given by Equation 17, replacing the indices 1,2 and 3 by L, T and R (See Figure 5).
However, we must to notice that if a different coordinate system is considered, other components of Sijkl will be nonzero and the constitutive laws will become more complicated to use.
Table 1, which uses data from Hearmon16, presents some values of elastic constants of 3 species of wood in order to show the wood anisotropy.
Next topic we will present some factors that influence the elastic properties for wood.
3. The Effect of Grain Angle
Many researchers, in the theoretical and experimental point of view have long studied the effect of grain angle. One of the most important procedures was formulated by Hearmon16, who reported the effect of grain angles in all the components of Sijkl, showing that for wood it is possible to obtain negative values of Poisson's ratio, which emphasized the wood anisotropy.
Goodman and Bodig17, presented the following coordinate transformation matrix:
in order to determine the wood elastic properties with respect to rotation q about the L axis and f about R - axis. The material axes and the board axes are: R, T,and L xi (x, y, z), respectly.
Equation 30 can be found using two coordinate transformations that can be written by:
in terms of tensor notation, where 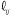 represent the set of direction cosines and the superscripts 1 and 2 are, respectively, the first and the second rotations. Since no rotation about T was considered, this coordinate transformation is limited to cases where the L material axis lies in the x1- x3 plane.
represent the set of direction cosines and the superscripts 1 and 2 are, respectively, the first and the second rotations. Since no rotation about T was considered, this coordinate transformation is limited to cases where the L material axis lies in the x1- x3 plane.
Bindzi and Samson18 carried out the following coordinate transformation relation:
with rotation f about L-axis and y about R-axis. It can be noticed that the R-axis lies in the x-y plane. This equation can be got as Equation 30 using Equation 31.
Both this and Goodman and Bodig's transformations are considered limited since it is not possible to obtain all relations between the board and material axes.
Hermanson19, studying the transformation of elastic properties for lumber to align these axes xi (x, y, z) with the material axes x'i (L, R, T), used three rotations l, r and f (denoted Euler's angles) about x, y and z axes, as can be seen in this Figure 6.
Thus, we can write that:
or in terms of matrix, by:
with A equals to:
where c and s indicate cos and sin, respectively.
The final relation between these systems is given by:
or:
where A is written by:
After that, the three Euler's angles were related to the surface angles a, b and g, through the following relations:
These angles can be seen in Figure 7.
In this way, it was possible to find the Euler's angles by knowing the surface angles and evaluating all wood elastic constants by using the complete coordinate transformation to elastic properties, given by:
where: 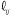 and S are function of components of the matrix A.
and S are function of components of the matrix A.
Now, by means of Equation (38), we can determine, for example, S1111,S2222,S3333 or, simply, the board elastic moduli, by:
where i = x,y,z. And the components: S4444,S5555,S6666 or, the board shear modulus, by:
where: ij = xy, yz, xz.
4. Examples
4.1. Theoretical examples
In order to present some examples of the use of the present theory, firstly we constructed tri-dimensional diagrams using Equation 39 and Equation 40, where it is showed the variation of Young´s modulus and shear modulus in function of the two Euler's angles, as we can see in Figures 8, 9, 10 and 11. Secondly, we constructed bi-dimensional diagrams with the objective of showing the relationship between shear modulus with the Euler´s angle l (see Figure 6), which expresses the variation of theses wood elastic parameters in the LT and LR planes, whose planes usually considered in practical cases. Figures 12 and 13 show this variation. For this analysis we used a hardwood species, Ipê (Tabebuia sp) and a softwood species, Pinus caribaea var. bahamensis.
The elastic parameters were determined by Mascia20 and are presented in Table 2.
We can observe that both the values and the relations among the elastic constants (see Table 2) have influence on the shapes of the last figures and also depend on the wood species considered in the analysis (softwood or hardwood).
4.2. Experimental example
Finally, we used some results of Young´s modulus, of Jatobá (Hymenaea stilbocarpa), to verify the agreement between theoretical and experimental data, from Furlani21. The goal of this procedure was to determine the modulus of elasticity in some fiber orientations determined with respect to the R-T, the R-L and the T-L plane.
These parameters were estimated from the experimental data or better (See Table 3).
To achieve this, lumbers were cut according to Figure 7 in L-direction varying the angle b on the R-T plane of the following angles: 0°, 15°, 30°, 45°, 60°, 70° and 90°. After this, blocks were obtained from these lumbers but varying the angle a over the lumber axis on the R-T plane by 0°, 3°and 5° and finally considering the angle g of 0°, 45° and 90°. In this way, 21 specimens of 5 cm x 5 cm x 15 cm were obtained for the compression tests. Table 4 shows Young´s modulus (the modulus of elasticity) data.
5. Two Sample t-Test and Confidence Interval
It was considered the 21-data set to establish relations between theoretical and experimental data, through the statistical analysis (See AnnexAnnex). Table 5 shows the experimental and theoretical values of Young´s modulus.
From the Two sample t-Test22 for C1 vs C2, we obtain the -Table 6.
With 95% CI (Confidence Interval) for mean C1: b1 mean C2:b2: ( - 2963; 4530) and t-Test mean C1 equal mean C2 (versus not equal): t = 0.42 P = 0.67 DF = 39 and tf (P%) around 1.69.
From this statistical analysis we can conclude that the hypothesis H0: b1 = b2 can be accepted with a high level of significance. In other words: the agreement among the theoretical values in z-direction and the experimental values described by Equation 39 is satisfactory.
To better illustrate this argument we present Figures 14 and 15 showing the agreement between the experimental and theoretical results as a function of grain angles.
These presented diagrams evidenced the strong relation between the analyzed wood elastic parameters and the fiber orientation and consequently the wood anisotropy.
6. Conclusions
In this paper, the general concepts of the orthotropic elastic model, particularly the rectilinear and cylindrical models, were described. Taking into account both to consider practical considerations and to avoid mathematical complications, the linear model is considered more usual.
In order to present some applications of this model, it was developed some examples for softwood and hardwood species, by analyzing theoretical data from a specific expression resulted from this model and checking experimental data obtained from compression tests in Jatobá (Hymenaea stilbocarpa).
We have already commented that the variation of grain angle, which constitutes the main reason for wood anisotropy, is responsible for the greatest changes in the values of the constitutive tensor components.
In general, the most important conclusion from this study can be summarized as follows:
-
the agreement between the rectilinear orthotropic model, described by the theoretical values and the experimental values, can be considered satisfactory.
The present statistical analyses indicated that only some results of the data did not adequately fit in the model especially because wood to be a non-homogeneous and an anisotropic material.
It is important to notice that this conclusion is restricted to the current experimental data. In order to make generalizations about these results, it is necessary to perform more tests taking into account other species of wood, and in other fiber orientations.
Received: January 11, 2006; Revised: May 12, 2006
Notation
indices
strain tensor, strain
stress tensor, stress
coordinate system
strain energy function
tensor of material elastic constants
compliance tensor
modulus of elasticity related to i direction
shear modulus related to ijplane
Poisson's ratio in ij-plane
modulus of elasticity from the experimental data
modulus of elasticity from theoretical data
matrix
elements of tensor or matrix
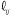
coordinate transformation tensor, coordinate
material axes
Longitudinal direction
Tangential l direction
Radial direction
Euler's angles
Sample mean
degrees of freedom
the value from a t-distribution where a is 1 - confidence level/100
number of specimens
probability
standard deviation
1. Two Sample t- Test Description from Minitab Program
1.1. Confidence interval
where ta/2 is the value from a t-distribution table where a is 1 - confidence level/100. The sample standard deviation, s, of (b1 - b2) and the degrees of freedom depend upon the variance assumption.
You can specify a confidence level of any number between 1 and 100 in Confidence level. The confidence level is 95% by default.
1.2. Hypothesis test
Minitab calculates the test statistic, t, by
and we compare with tf (P%), obtained from table of t-Student distribution with level of significance P%.
The sample standard deviation, s, of (b1 - b2) depends upon the variance assumption.
1.3. Standard deviations
When you assume unequal variances, the sample standard deviation of (b1 - b2) is 
The test statistic degrees of freedom are
where  .
.
When you assume equal variances, the common variance is estimated by the pooled variance
The standard deviation of (b1 - b2) is estimated by 
The test statistic degrees of freedom are (n1 + n2 - 2).
- 1. Love AE. A Treatise On The Theory Of Elasticity. New York: Dover Publications; 1944.
- 2. Chen EF, Saleeb A. Constitutive Equations For Engineering Materials New York: John Wiley & Sons, Inc; 1982.
- 3. Desai CS, Siriwardane HJ. Constitutive Laws for Engineering Materials -with Emphasis on Geologic Materials New Jersey: Prentice-Hall; 1984.
- 4. Novozhilov VV. Theory of Elasticity. London: Pergamon Press; 1961.
- 5. Ting TCT. Anisotropic Elasticity. Theory and Applications. New York: Oxford University Press; 1996.
- 6. Lekhnitskii SG. Theory of Elasticity of an Anisotropic Body Moscow: Mir; 1981
- 7. Perkins RW. Concerning the Mechanics of Wood Deformation. Forest Products Journal. 1967; 17(3):55-67.
- 8. Dinwoodie JM. Timber- Its Nature And Behavior New York: Van Nostrand Reinhold Company; 1981.
- 9. Bodig J, Jayne, BA. Mechanics of Wood and Wood Composites. New York: Van Nostrand; 1982.
- 10. Carrier GF. Stress Distributions in Cylindrical Aelotropic Plates. Journal Of Applied Mechanics 1943; 10(1):117-22.
- 11. Foschi RO. Plane- Stress Problem in a Body with Cylindrical Anisotropy, with Special Reference to Curved Douglas-Fir Beams. Forestry Branch Departmental Publication. 1968; 1244(1):1-21.
- 12. Gopu VKA, Goodman JR. Analysis of Double-Tapered Pitched and Curved Laminated Beam Section. Wood Science. 1974; 7(1):52-60.
- 13. Noack D, Rooth VW. On the Theory of Elasticity of Orthotropic Material." Wood Science and Technology. 1976; 10(1):97-110.
- 14. Hsu NN, Tang RC. Internal Stresses in Wood Logs Due to Anisotropic Shrinkage. Wood Science 1974; 7(1):43-51.
- 15. Chung TJ. Applied Continuum Mechanics. Cambridge: Cambridge University Press; 1996.
- 16. Hearmon RFS. The Elasticity of Wood and Plywood. Forest Products Research Special Report. 1948; 7(1):1-87.
- 17. Goodman JR., Bodig J. Orthotopic Elastic Properties of Wood. Journal of Structural Division. 1970; 96(11):2301-19.
- 18. Bindzi I, Samson M. New Formula for Influence of Spiral Grain on Bending Stiffness of Wooden Beams. Journal of Structural Division 1995; 121(11):1541-46.
- 19. Hearmonson JC. The Triaxial Behavior Of Redwood Using A New Confined Compression Device. [D. Phil thesis], Madison:University of Wisconsin;1996.
- 20. Mascia NT. Considerações a respeito da anisotropia na madeira [Tese de Doutorado] São Carlos: EESC-USP; 1991.
- 21. Furlani JE. Um Estudo Sobre A Variação Numérica Do Coeficiente De Poisson Na Madeira, Considerando A Anisotropia Do Material. [Dissertação de Mestrado].Campinas: UNICAMP; 1995.
- 22. Ryan BF, Joiner BL. Minitab Handbook. Belmont: Duxbury Press; 1994.
Annex
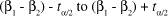
Publication Dates
-
Publication in this collection
19 Oct 2006 -
Date of issue
Sept 2006
History
-
Reviewed
12 May 2006 -
Received
11 Jan 2006





































































