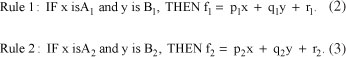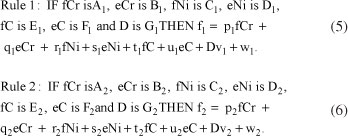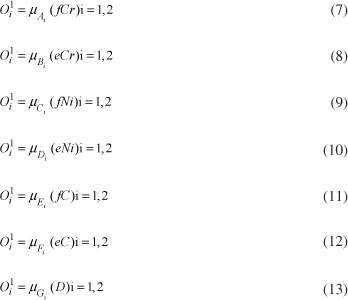Abstract
In the present study, the tensile strength of ferritic and austenitic functionally graded steels produced by electroslag remelting has been modeled. To produce functionally graded steels, two slices of plain carbon steel and austenitic stainless steels were spot welded and used as electroslag remelting electrode. Functionally graded steel containing graded layers of ferrite and austenite may be fabricated via diffusion of alloying elements during remelting stage. Vickers microhardness profile of the specimen has been obtained experimentally and modeled with adaptive network-based fuzzy inference systems (ANFIS). To build the model for graded ferritic and austenitic steels, training, testing and validation using respectively 174 and 120 experimental data were conducted. According to the input parameters, in the ANFIS model, the Vickers microhardness of each layer was predicted. A good fit equation which correlates the Vickers microhardness of each layer to its corresponding chemical composition was achieved by the optimized network for both ferritic and austenitic graded steels. Afterwards; the Vickers microhardness of each layer in functionally graded steels was related to the yield stress of the corresponding layer and by assuming Holloman relation for stress-strain curve of each layer, they were acquired. Finally, by applying the rule of mixtures, tensile strength of functionally graded steels configuration was found through a numerical method. The obtained results from the proposed model are in good agreement with those acquired from the experiments.
chemical concentration profile; microhardness; tensile strength; ANFIS; ESR; ferritic FGS; austenitic FGS
Application of ANFIS for analytical modeling of tensile strength of functionally graded steels
Ali Nazari* * e-mail: alinazari84@aut.ac.ir
Department of Materials Engineering, Savhe Branch, Islamic Azad University, Saveh, Iran
ABSTRACT
In the present study, the tensile strength of ferritic and austenitic functionally graded steels produced by electroslag remelting has been modeled. To produce functionally graded steels, two slices of plain carbon steel and austenitic stainless steels were spot welded and used as electroslag remelting electrode. Functionally graded steel containing graded layers of ferrite and austenite may be fabricated via diffusion of alloying elements during remelting stage. Vickers microhardness profile of the specimen has been obtained experimentally and modeled with adaptive network-based fuzzy inference systems (ANFIS). To build the model for graded ferritic and austenitic steels, training, testing and validation using respectively 174 and 120 experimental data were conducted. According to the input parameters, in the ANFIS model, the Vickers microhardness of each layer was predicted. A good fit equation which correlates the Vickers microhardness of each layer to its corresponding chemical composition was achieved by the optimized network for both ferritic and austenitic graded steels. Afterwards; the Vickers microhardness of each layer in functionally graded steels was related to the yield stress of the corresponding layer and by assuming Holloman relation for stress-strain curve of each layer, they were acquired. Finally, by applying the rule of mixtures, tensile strength of functionally graded steels configuration was found through a numerical method. The obtained results from the proposed model are in good agreement with those acquired from the experiments.
Keywords: chemical concentration profile, microhardness, tensile strength, ANFIS, ESR, ferritic FGS, austenitic FGS
1. Introduction
Functionally graded materials (FGM) possess properties that vary gradually with location within the material1. An FGM comprises a multi-phase material with volume fractions of the constituents varying gradually in a pre-determined (designed) profile, thus yielding a nonuniform microstructure in the material with continuously graded properties2. There are not enough studies on the plastic behavior of FGMs. Among these few works, most of the researchers have been modeled their work with the aid of conventional flow theories which are the one of the best tools that has ever proposed. For example, some of them have tried to use J2 flow theory3-5 but the empirical investigations haven't been linked to the obtained results because of the difficulty of FGMs fabrication. Okolednik6 although has used J integral concept to model several materials with yield stress gradient, but his studies was not confirmed by the experimental results. One of the FGMs with elastic-plastic behavior is functionally graded steel (FGS) which have recently been produced from austenitic stainless steel and carbon steel using electro slag refining (ESR) method7,8. In these composites, by selecting the appropriate arrangement and thickness of the primary ferritic and austenitic steels as electrodes, it is possible to obtain composites with several layers consist of ferrite, austenite, bainite and martensite. The resultant composites using two slices of original ferrite (α0) and original austenite (γ0) is as below:
where α, β and γ are ferrite, bainite and austenite phase in the final composite respectively; el is electrode; com is composite; and R is remelting.
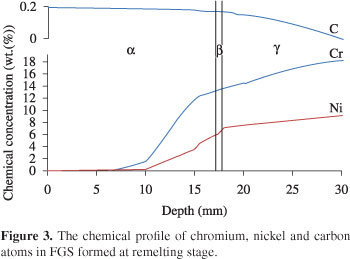
Diffusion of chromium, nickel and carbon atoms which taking place at the remelting stage in the liquid phase controls the chemical distribution of chromium, nickel and carbon atoms in the produced composites. The transformation characteristics of FGSs have previously been investigated, in that the diffusion coefficients of chromium, nickel, and carbon atoms at temperatures just above the melting point of iron were estimated. Also, the thicknesses of the emerging bainite and martensite phases were determined7.
Furthermore it has been shown that the tensile strength of the FGS composites depends on the composition and number of layers and those has been modeled based on the tensile behavior of individual phases8; to do so the yield stress of each element in the composites was related to the microhardness value of that element.
In the previous studies, Chary impact energy of functionally graded steels in both crack divider9-12 and crack arrester12,13 configurations was experimentally examined and modeled by different methods. In addition, the ductile to brittle transition of the specimens was studied in a series of works14-18. Fracture toughness of these specimens in terms of JIC in both crack divider19-21 and crack arrester21,22 configurations was also investigated. The tensile behavior of oblique layer functionally graded steels was the other property which studied in the previous studies23,24. Prediction Vickers hardness25 and tensile strength26 of functionally graded steels by the mechanism-based strain gradient plasticity theory was the other works done in this area. In a series of works, Charpy impact energy27-34 and fracture toughness35,36 of functionally graded steels was modeled based on strain gradient plasticity theory.
Several works have addressed utilizing of computer-aided prediction of engineering properties including those done by the authors14,18,37-40. Adaptive network-based fuzzy inference systems (ANFIS) is the famous hybrid neuro-fuzzy network for modeling the complex systems41. ANFIS incorporates the human-like reasoning style of fuzzy systems through the use of fuzzy sets and a linguistic model consisting of a set of IF-THEN fuzzy rules. The main strength of ANFIS models is that they are universal approximators41 with the ability to solicit interpretable IF-THEN rules. Nowadays, the artificial intelligence-based techniques like ANFIS42 have been successfully applied in the engineering applications. However, there is a lack of investigations on metallurgical aspects of materials.
In the present work, microhardness profile of functionally graded ferritic and austenitic steels has been modeled by ANFIS and then tensile strength of FGSs has been modeled analytically by means the ANFIS results. To build the model for graded ferritic and austenitic steels, training, testing and validation using respectively 174 and 120 experimental data were conducted. The obtained results have been compared by experimental ones to evaluate the software power for predicting the microhardness profile of functionally graded ferritic and austenitic steels. Two equations were presented by the ANFIS results which correlate the Vickers microhardness profile of both ferritic and austenitic steels to their corresponding chemical composition profile. Afterwards; by supposing suitable relationship between Vickers microhardness and the yield stress of the corresponding layer and by assuming Holloman relation for stress-strain curve of each layer, they were obtained. Finally, by applying the rule of mixtures, tensile strength of FGSs was found. There was a good agreement between the predicted results and those obtained from the experiments.
2. Experimental Procedure
To make FGSs, a miniature ESR apparatus was used. The consumed slag was a mixture of 20% CaO, 20% Al2O3 and 60% CaF2. The original ferritic and austenitic steels (α0 and γ0) which used as electrodes were commercial type AISI 1020 and AISI 316 steels respectively. The chemical composition of the as-received ferritic and austenitic steels is given in Table 1.
Ferritic and austenitic steel slices were spot welded in form of 2-piece electrode for remelting. The thickness of each slice in the primary electrode was 150 mm.
Remelting processes were carried out under a constant power supply of 16 KVA. After remelting, the composite ingots were hot-pressed down to the thickness of 30 mm. Forging and rolling operations were carried out at 980 °C and then specimens were air-cooled.
To investigate the variation of hardness in composites, Vickers microhardness test was employed using 100 gf weight.
The concentration of chromium, nickel and carbon in functionally graded steels was determined by data-equipped linear analyzer.
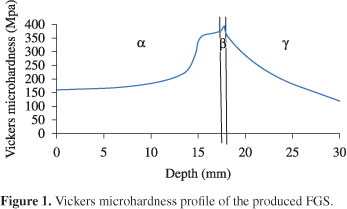
As the previous work8 indicate, a bainite layer is produced during remelting stage approximately in the middle of the forged specimen. Therefore, two series of tensile specimens were produced (one from the ferritic and the other from the austenitic graded region) in which bainite layer was not placed in the produced specimens as shown in Figure 1. Tensile specimens from the FGS specimens were made. Tensile tests were carried out under extension rate of 0.1 mm/s. Specimens dimension was in accordance to the ASTM E8 standard and it is shown in Figure 2. The as received rod was annealed at 980 °C and then air-cooled.
Tensile strength of as-received ferritic and austenitic steels which were annealed at 980 °C and then air-cooled was also measured.
For metallographic examinations, the plates were sliced, ground, polished, and etched in a "Kalling" solution and 1 pct Nital.
3. Experimental Results
Vickers microhardness profile of the ferritic and austenitic regions of the functionally graded steel is illustrated in Figure 1. The concentration profile of chromium, nickel and carbon atoms has been illustrated in Figure 3. All of the results show a good compatibility with the initial work done by Aghazadeh and Shahosseinie7. The mechanism of diffusion of chromium, nickel and carbon atoms has been discussed in that work7. In addition, metallographic studies from the cross section of the produced FGS show that the new stabilized phase (bainite layer) in the FGS produced is similar to those acquired in the previous works7-36 as shown in Figure 4; the thickness of bainite layer is 0.6 mm which was verified by Vickers microhardness examination as it is shown in Figure 1. Finally the stress-strain curves of original ferrite and original austenite specimens have been illustrated in Figure 5.
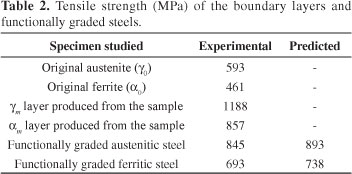
Tensile strength of FGSs has been illustrated in Table 2. For comparison, tensile strength of the specimens' edge (γ0, γm, α0 and αm layers) has been shown in Figure 5. Electron-probe microanalysis studies illustrate that the chemical composition of the α edge layer is pct C = 0.2, pct Cr = trace, and pct Ni = trace, and that of the γ edge layer is pct C = 0.07, pct Cr = 18.1, and pct Ni = 9.1, which is similar to those of original alpha and gamma steels; this is in accordance to the previous results7,8. Thus, the first boundary condition may be determined using the predicted Vickers hardness value and tensile strength of edge layers (i.e. original austenite, γ0 for γ region and original ferrite, α0 for α region). To achieve the tensile strength of γm and αm layers, tensile specimens of the same composition and same mechanical properties to γm and αm layers were prepared similar to the previous studies7,8. Initially, the average chemical composition of γm and αm layers was obtained (Table 3). Afterwards, samples with composition in accordance to the average chemical composition of γm and αm layers were produced by means of a vacuum induction furnace. Similar to the primary composites, the hot-pressing process was carried out at 980 °C, followed by air cooling. Through trial and error (i.e., conforming the chemical composition and changing the cooling rate), the sample with the nearest hardness to γm and αm layers was selected to make tensile test specimens. Tensile test results of (γ0, γm, α0 and αm layers are shown in Figure 5.
4. Architecture of ANFIS
The architecture of an ANFIS model with two input variables is shown in Figure 6. Suppose that the rule base of ANFIS contains two fuzzy IF-THEN rules of Takagi and Sugeno's type as follows:
The basic learning rule of ANFIS is the back-propagation gradient descent, which calculates error signals recursively from the output layer backward to the input nodes. This learning rule is exactly the same as the back-propagation learning rule used in the common feed-forward neural networks43,44. Recently, ANFIS adopted a rapid learning method named as hybrid-learning method which utilizes the gradient descent and the least-squares method to find a feasible set of antecedent and consequent parameters43,44. Thus in this paper, the later method is used for constructing the proposed models.
4.1. ANFIS structure and parameters
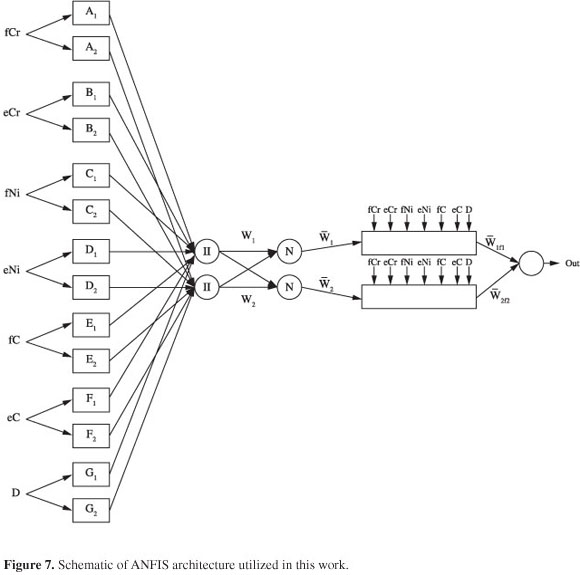
The structure of proposed ANFIS networks was consisted of the chromium concentration at the first of each layer (fCr), the chromium concentration at the end of each layer (eCr), the nickel concentration at the first of each layer (fNi), the nickel concentration at the end of each layer (eNi), the carbon concentration at the first of each layer (fC), the carbon concentration at the end of each layer (eC) and the distance of the middle of each layer from the specimen edge (D). To achieve a more accurate model, the concentration of chromium, nickel and carbon atoms in the first and the end sides of each layer were considered as inputs of the network to increase the total inputs to seven. It should be noted that the specimen edge was that side of the specimens with similar chemical composition to the original ferritic and austenitic steels respectively for graded ferritic and graded austenitic steels. The value for output layer was the average Vickers microhardness of each layer which was obtained from Equation 4:
where: Hv(x) is the Vickers microhardness profile of functionally graded steels, and xi+1-xi represents the thickness of each layer which was considered equal to 100 µm in this study.
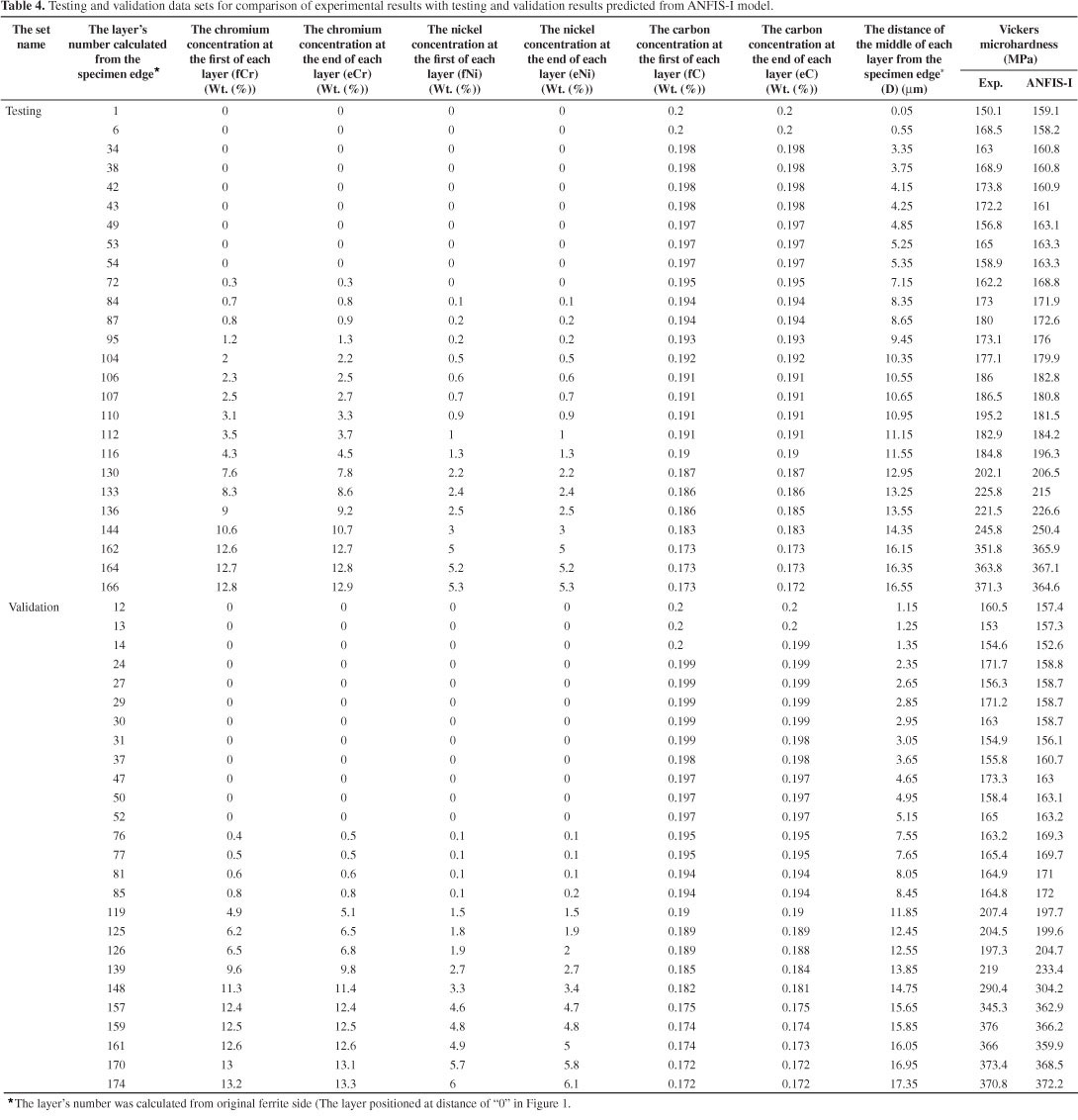
The input space is decomposed by three fuzzy labels. In this paper, for comparison purposes, two types of membership functions (MFs) including the triangular (ANFIS-I) and Gaussian (ANFIS-II) were utilized to construct the suggested models. To build the models, the thickness of the ferritic and austenitic regions was divided into 100 µm thick layers. Therefore, 174 and 120 layers were achieved for ferritic and austenitic regions, respectively. For graded ferritic region, from 174 collected data, 122 data (70%) were randomly chosen for training set, 26 (15%) data for testing set and the other 26 (15%) data for validation set (ANFIS-I model). For graded austenitic region, from 120 collected data, 84 data (70%) were randomly chosen for training set, 18 (15%) data for testing set and the other 18 (15%) data for validation set (ANFIS-II model). Moreover, up to 1000 epochs were specified for training process to assure the gaining of the minimum error tolerance.
One of the most difficult tasks in ANFIS studies is to find this optimal network architecture, which is based on the determination of numbers of optimal results. The assignment of initial weights and other related parameters may also influence the performance of the ANFIS to a great extent. However, there is no well defined rule or procedure to have an optimal network architecture and parameter settings where the trial and error method still remains valid. This process is very time consuming45-48.
In this study the Matlab NN toolbox is used for NN applications. To overcome optimization difficulty, a program has been developed in Matlab which handles the trial and error process automatically45-48. The program tries various functions and when the highest RMSE (Root Mean Squared Error) of the testing set, as the training of the testing set is achieved, it was reported45-48.
The IF-THEN rules in this study were achieved as follows. Suppose that the rule base of ANFIS contains two fuzzy IF-THEN rules of Takagi and Sugeno's type:
The corresponding equivalent ANFIS architecture is shown in Figure 7. The functions of each layer are described as follows41,42,49,50:
Layer 1 - Every node i in this layer is a square node with a node function:
where fCr, eCr, fNi, eNi, fC, eC and D are inputs to node i, and Ai, Bi, Ci, Di, Ei, Fi and Gi are the linguistic label (fuzzy sets: small, large, ...) associated with this node function.
Layer 2 - Every node in this layer is a circle node labeled П which multiplies the incoming signals and sends the product out. For instance,
Each node output represents the firing weight of a rule.
Layer 3 - Every node in this layer is a circle node labeled N. The ith node calculates the ratio of the ith rule's firing weight to the sum of all rule's firing weights:
Layer 4 - Every node in this layer is a square node with a node function:
where  is the output of layer 3, and {pi, qi, ri, si, ti, ui, vi, wi} is the parameter set.
is the output of layer 3, and {pi, qi, ri, si, ti, ui, vi, wi} is the parameter set.
Layer 5 - The signal node in this layer is a circle node labeled R that computes the overall output as the summation of all incoming signals, i.e.,
4.2. ANFIS results and discussion
In this study, the error arose during the training and testing in ANFIS-I and ANFIS-II models can be expressed as absolute fraction of variance (R2) which is calculated by Equation 1851:
where t is the target value and o is the output value.
All of the results obtained from experimental studies and predicted by using the training, testing and validation results of ANFIS-I and ANFIS-II models are given in Figures 8a and c; and Figures 9a and c, respectively. The linear least square fit line, its equation and R2 values were shown in these figures for the training, testing and validation data. Also, inputs values and experimental results with testing and validation results obtained from ANFIS-I and ANFIS-II models were given in Tables 4 and 5, respectively. As it is visible in Figures 8 and 9, the values obtained from the training, testing and validation sets in ANFIS-I and ANFIS-II models are very close to the experimental results. The results of testing and validation phases in Figures 8 and 9 show that the ANFIS-I and ANFIS-II models are capable of generalizing between input and output variables with reasonably good predictions.
The performance of the ANFIS-I and ANFIS-II models is shown in Figures 8 and 9. The best value of R2 is 99.75% for training set in the ANFIS-I model. The minimum values of R2 are 98.34% for testing set in the ANFIS-II model. All of R2 values show that the proposed ANFIS-I and ANFIS-II models are suitable and can predict microhardness profile of FGSs values very close to the experimental values.
From the optimized network, the best fit equation to predict Vickers microhardness values by the specific inputs was obtained. These relationships for ferritic and austenitic regions are expressed by Equations 19 and 20, respectively:
where: HV(α) and HV(γ) are the Vickers microhardness of each layer in ferritic and austenitic regions, respectively. The R2 values are between experimental results and those obtained by Equations 19 and 20 for ferritic and austenitic regions, respectively.
5. Modeling Tensile Strength
To model tensile strength of functionally graded steels it has been assumed that the austenitic functionally graded steel consists of mγ layers and ferritic functionally graded steel consists of mα layers. According to the previous work10, it has been assumed that tensile strength of each layer is related to its corresponding stress-strain curve.
According to the previous works9-12 it is assumed that the yield stress of each element is proportional to the Vickers microhardness of that element. Therefore, the yield stress of each layer in α and γ regions should also obey the hardness pattern. The yield stress of each layer may be related to the Vickers microhardness of that layer as:
where:
σy(γ0), σy(γm), σy(α0) and σy(αm) are the yield stress of γ0, γm, α0 and αm layers, respectively; and HV(γ0), HV(γm), HV(α0) and HV(αm) are the yield stress of γ0, γm, α0 and αm layers, respectively.
If it is assumed that the stress-strain curve of each layer obeys the Holloman relation, the imposed stress to each layer at yield strain of αm and γm layers may be given as;
where:
σ' and σ" are the imposed stress to each layer in α and γ regions at yield strain of αm and γm layer, respectively; Εαm and Εγm are the yield strain of αm and γm layers, respectively; and n(α) and n(γ) are the strain-hardening coefficient of each element in α and γ regions, respectively. It is assumed that the strain hardening coefficient of each element in the studied
where n(γ0), n(γm), n(α0) and n(αm) are the work-hardening exponent of γ0, γm, α0 and and αm layers, respectively and xγ0, xγm, xα0 and xαm are the positions of γ0, γm, α0 and αm layers, respectively.
Ε(α) and Ε(γ) in Equations 23 and 24 are defined as the yield strain of each layer in α and γ regions, respectively. By considering the suitable boundary conditions:
where: E is the Young modulus.
Therefore the stress-strain curve of each element could be determined. By applying tension loading, all of layers will fail at the ultimate tensile strain of the strongest layer (i.e. γm in austenitic FGS and αm in ferritic FGS). Therefore, tensile strength of each composite could be obtained as:
where: σts(α - FGS) and σts (γ - FGS) are the tensile strength of ferritic FGS and austenitic FGS, respectively.
The obtained results from the mathematical model are given in Table 2; there is a good agreement between the experimental and theoretical results.
6. Conclusions
In this work, tensile strength of FGSs produced by ESR process was examined experimentally and predicted by means of ANFIS. Variation of tensile strength in FGSs is due to variation of alloying elements such as chromium, nickel and carbon during the remelting stage. As alloying elements diffuses, FGSs with ferritic and austenitic graded layers together with bainite intermediate layer are created. A model based on ANFIS was introduced to predict the Vickers microhardness of ferritic and austenitic regions. The performance of the acquired optimized network was examined by R2 values. All of the obtained R2 values showed that ANFIS are capable to predict the Vickers microhardness of FGSs very close to the experimental data. It has been found that ANFIS models will be valid within the ranges of variables. Finally, two empirical equations obtained from optimized ANFIS-I and ANFIS-II networks was presented with an excellent accuracy to predict the Vickers microhardness of each layer by means of its input data. The Vickers microhardness of each layer in functionally graded steels was related to the yield stress of the corresponding layer and by assuming Holloman relation for stress-strain curve of each layer, the area under each stress-strain curve was acquired. Tensile strength of FGSs was obtained by means of the rule of mixtures. A good agreement was obtained between the predicted results and those obtained from the experiments.
Received: October 15, 2011
Revised: February 7, 2012
- 1. Sankar BV. An elasticity solution for functionally graded beams. Composites Science and Technology 2001; 61:689-696. http://dx.doi.org/10.1016/S0266-3538(01)00007-0
- 2. Jin ZH, Paulino GH and Dodds Junior RH. Cohesive fracture modeling of elastic-plastic crack growth in functionally graded materials. Engineering Fracture Mechanics 2003; 70:1885-1912. http://dx.doi.org/10.1016/S0013-7944(03)00130-9
- 3. Carpenter RD, Liang WW, Paulino GH, Gibeling JC and Munir ZA. Fracture Testing and Analysis of a Layered Functionally Graded Ti/TiB Beam in 3-Point Bending. Materials Science Forum. 1999; 308-311:837-842. http://dx.doi.org/10.4028/www.scientific.net/MSF.308-311.837
- 4. Williamson RL, Rabin BH and Drake JT. Finite element analysis of thermal residual stresses at graded ceramic-metal interfaces. Part I. Model description and geometrical effects. Journal of Applied Physics. 1993; 74:1310-1320. http://dx.doi.org/10.1063/1.354910
- 5. Giannakopoulos AE, Suresh S, Finot M and Olsson M. Elastoplastic analysis of thermal cycling: layered materials with compositional gradientes. Acta Metallurgica et Materialia. 1995; 43:1335-1354. http://dx.doi.org/10.1016/0956-7151(94)00360-T
- 6. Kolednik O. The yield stress gradient effect in inhomogeneous materials. International Journal of Solids and Structures. 2000; 37(5):781-808. http://dx.doi.org/10.1016/S0020-7683(99)00060-8
- 7. Aghazadeh Mohandesi J and Shahosseinie MH. Transformation Characteristics of Functionally Graded Steels Produced by Electroslag Remelting. Metallurgical and Materials Transactions A. 2005; 36A:3471-3476.
- 8. Aghazadeh Mohandesi J, Shahosseinie MH. and Parastar Namin R. Tensile Behavior of Functionally Graded Steels Produced by Electroslag Remelting. Metallurgical and Materials Transactions A. 2006; 37A:2125-2132.
- 9. Nazari A and Aghazadeh Mohandesi J. Modelling impact resistance of functionally graded steels with crack divider configuration. Materials Science and Technology 2010; 26:1377-1383. http://dx.doi.org/10.1179/174328409X405652
- 10. Nazari A and Aghazadeh Mohandesi J. Impact Energy of Functionally Graded Steels with Crack Divider Conûguration. Materials Science and Technology 2009; 25(6):847-852.
- 11. Nazari A, Aghazadeh Mohandesi J and Riahi S. Modeling Impact Energy of Functionally Graded Steels in Crack Divider Configuration Using Modified Stress-Strain Curve Data. International Journal of Damage Mechanics 2010; 21(1):27-50. http://dx.doi.org/10.1177/1056789510397073
- 12. Nazari A, Aghazadeh Mohandesi J, Hamid Vishkasogheh M and Abedi M. Simulation of impact energy in functionally graded steels. Computational Materials Science 2011; 50:1187-1196. http://dx.doi.org/10.1016/j.commatsci.2010.11.019
- 13. Nazari A and Aghazadeh Mohandesi J. Impact Energy of Functionally Graded Steels in Crack Arrester Configuration. Journal of Materials Engineering and Performance 2010; 19:1058-1064. http://dx.doi.org/10.1007/s11665-009-9578-4
- 14. Nazari A and Milani AA. Modeling ductile to brittle transition temperature of functionally graded steels by artificial neural networks. Computational Materials Science. 2011; 50:2028-2037. http://dx.doi.org/10.1016/j.commatsci.2011.02.003
- 15. Nazari A and Milani AA. Ductile to Brittle Transition Temperature of Functionally Graded Steels. International Journal of Damage Mechanics 2010; 21(1). http://dx.doi.org/10.1177/1056789511398270
- 16. Nazari A and Milani AA. Modeling Ductile - to - Brittle Transition Temperature of Functionally Graded Steels by Gene Expression Programming. International Journal of Damage Mechanics 2011; 22. http://dx.doi.org/10.1177/1056789511406561
- 17. Nazari A and Milani AA. Ductile to brittle transition temperature of functionally graded steels with crack arrester configuration. Materials Science and Engineering A. 2011; 528:3854-3859. http://dx.doi.org/10.1016/j.msea.2011.01.105
- 18. Nazari A and Milani AA. Modeling ductile to brittle transition temperature of functionally graded steels by fuzzy logic. Journal of Materials Science 2011; 46:6007-6017. http://dx.doi.org/10.1007/s10853-011-5563-z
- 19. Nazari A, Aghazadeh Mohandesi J and Riahi S. Modified Modeling Fracture Toughness of Functionally Graded Steels in Crack Divider Configuration. International Journal of Damage Mechanics 2011; 20:811-831. http://dx.doi.org/10.1177/1056789510382851
- 20. Aghazadeh Mohandesi J, Nazari A, Hamid Vishkasogheh M and Abedi M. Modelling Simul. Materials Science and Engineering 2010; 18:075007.
- 21. Nazari A, Aghazadeh Mohandesi J and Riahi S. Fracture Toughness of Functionally Graded Steels. Journal of Materials Engineering and Performance 2011. http://dx.doi.org/10.1007/s11665-011-9945-9
- 22. Nazari A, Aghazadeh Mohandesi J and Riahi S. Modeling fracture toughness of functionally graded steels in crack arrester configuration. Computational Materials Science 2011; 50:1578-1586. http://dx.doi.org/10.1016/j.commatsci.2010.12.019
- 23. Nazari A and Aghazadeh Mohandesi J. Modeling tensile strength of oblique layer functionally graded austenitic steel. Computational Materials Science 2011; 50:1425-1431. http://dx.doi.org/10.1016/j.commatsci.2010.11.029
- 24. Nazari A and Riahi S. Effect of layer angle on tensile behavior of oblique layer functionally graded steels. Turkish Journal of Engineering & Environmental Sciences 2010; 34:17-24.
- 25. Nazari A, Aghazadeh Mohandesi J and Tavareh S. Microhardness profile prediction of a graded steel by strain gradient plasticity theory. Computational Materials Science 2011; 50:1781-1784. http://dx.doi.org/10.1016/j.commatsci.2011.01.014
- 26. Nazari A, Aghazadeh Mohandesi J and Tavareh S. Modeling tensile strength of austenitic graded steel based on the strain gradient plasticity theory Computational Materials Science 2011; 50:1791-1794. http://dx.doi.org/10.1016/j.commatsci.2011.01.016
- 27. Nazari A and Mojtahed Najafi SM. Prediction Charpy impact energy of bcc and fcc functionally graded steels in crack divider configuration by strain gradient plasticity theory. Computational Materials Science 2011; 50:3178-3183. http://dx.doi.org/10.1016/j.commatsci.2011.05.047
- 28. Nazari A and Mojtahed Najafi SM. Prediction impact behavior of functionally graded steel by strain gradient plasticity theory. Computational Materials Science 2011; 50:3218-3223. http://dx.doi.org/10.1016/j.commatsci.2011.06.004
- 29. Nazari A. Modeling Charpy impact energy of functionally graded steel based on the strain gradient plasticity theory and modified stress-strain curve data. Computational Materials Science 2011; 50(12):3350-3357. http://dx.doi.org/10.1016/j.commatsci.2011.06.029
- 30. Nazari A. Application of strain gradient plasticity theory to model Charpy impact energy of functionally graded steels. Computational Materials Science 2011; 50(12):3410-3416. http://dx.doi.org/10.1016/j.commatsci.2011.06.039
- 31. Nazari A. Strain gradient plasticity theory to predict the input data for modeling Charpy impact energy in functionally graded steels. Computational Materials Science 2011; 50(12): 3442-3449. http://dx.doi.org/10.1016/j.commatsci.2011.07.007
- 32. Nazari A. Simulation of impact energy in functionally graded steels by mechanism-based strain gradient plasticity theory. Computational Materials Science 2012; 51(1):13-19. http://dx.doi.org/10.1016/j.commatsci.2011.07.010
- 33. Nazari A. Simulation Charpy impact energy of functionally graded steels by modified stress-strain curve through mechanism-based strain gradient plasticity theory. Computational Materials Science 2012; 51(1): 225-232. http://dx.doi.org/10.1016/j.commatsci.2011.07.027
- 34. Nazari A. Application of strain gradient plasticity theory to model Charpy impact energy of functionally graded steels using modified stress-strain curve data. Computational Materials Science 2012; 51(1):281-289. http://dx.doi.org/10.1016/j.commatsci.2011.07.057
- 35. Nazari A. Modeling fracture toughness of ferritic and austenitic functionally graded steel based on the strain gradient plasticity theory. Computational Materials Science 2011; 50:3238-3244. http://dx.doi.org/10.1016/j.commatsci.2011.06.008
- 36. Nazari A. Strain gradient plasticity theory for modeling JIC of functionally graded steels. Computational Materials Science 2011; 50(12): 3403-3409. http://dx.doi.org/10.1016/j.commatsci.2011.06.038
- 37. Nazari A and Riahi S. Computer-aided prediction of physical and mechanical properties of high strength cementitious composite containing Cr2O3 nanoparticles. Nano 2010; 5(5):301-318. http://dx.doi.org/10.1142/S1793292010002219
- 38. Nazari A and Riahi S. Prediction split tensile strength and water permeability of high strength concrete containing TiO2 nanoparticles by artificial neural network and genetic programming. Composites Part B: Engineering. 2011; 42:473-488. http://dx.doi.org/10.1016/j.compositesb.2010.12.004
- 39. Nazari A and Riahi S. Computer-aided design of the effects of Fe2O3 nanoparticles on split tensile strength and water permeability of high strength concrete. Materials and Design. 2011; 32:3966-3979. http://dx.doi.org/10.1016/j.matdes.2011.01.064
- 40. Nazari A and Didehvar N. Modeling impact resistance of aluminum-epoxy laminated composites. ANFIS 2011; 42:1912-1919.
- 41. Jang JSR. ANFIS: adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man and Cybernetics. 1993; 23(3):665-85. http://dx.doi.org/10.1109/21.256541
- 42. Sar1demir M. Predicting the compressive strength of mortars containing metakaolin by artificial neural networks and fuzzy logic. Advances in Engineering Software. 2009; 40(9):920-7. http://dx.doi.org/10.1016/j.advengsoft.2008.12.008
- 43. Topcu IB and Sar1demir M. Prediction of mechanical properties of recycled aggregate concretes containing silica fume using artificial neural networks and fuzzy logic. Computational Materials Science 2008; 42(1):74-82. http://dx.doi.org/10.1016/j.commatsci.2007.06.011
- 44. Jang JSR and Sun CT. Nuro-fuzzy modeling and control. Proceedings IEEE. 1995;83(3). http://dx.doi.org/10.1109/5.364486
- 45. Guzelbey IH, Cevik A and Erklig A. Prediction of web crippling strength of cold-formed steel sheetings using neural Networks. Journal of Constructional Steel Research 2006; 62:962-973. http://dx.doi.org/10.1016/j.jcsr.2006.01.008
- 46. Guzelbey IH, Cevik A and Gögüs MT. Prediction of rotation capacity of wide flange beams using neural Networks. Journal of Constructional Steel Research 2006; 62:950-961. http://dx.doi.org/10.1016/j.jcsr.2006.01.003
- 47. Cevik A and Guzelbey IH. Neural Network Modeling Of Strength Enhancement For Cfrp Confined Concrete Cylinders. Building & Environment. 2008; 43:751-763. http://dx.doi.org/10.1016/j.buildenv.2007.01.036
- 48. Cevik A and Guzelbey IH. A Soft computing based approach for the prediction of ultimate strength of metal plates in compression. Engineering Structures 2007; 29(3):383-394. http://dx.doi.org/10.1016/j.engstruct.2006.05.005
- 49. Ramezanianpour AA, Sobhani M and Sobhani J. Application of network based neuro-fuzzy system for prediction of the strength of high strength concrete. Amirkabir Journal of Science and Technology. 2004; 5(59-C):78-93.
- 50. Ramezanianpour AA, Sobhani J and Sobhani M. Application of an adaptive neurofuzzy system in the prediction of HPC compressive strength. In: Proceedings of the 4th international conference on engineering computational technology; 2004; Lisbon. Lisbon: Civil-Comp Press; 2004.
- 51. Topcu IB and Sar1demir M. Prediction of compressive strength of concrete containing fly ash using artificial neural network and fuzzy logic. Computational Materials Science. 2008; 41(3):305-11. http://dx.doi.org/10.1016/j.commatsci.2007.04.009
Publication Dates
-
Publication in this collection
05 Apr 2012 -
Date of issue
June 2012
History
-
Received
15 Oct 2011 -
Reviewed
07 Feb 2012