Avaliação de Métodos de Padronização dos Pesos Corporais às Idades de 205, 365 e 550 Dias

Evaluation of Body Weight Standardization Methods for 205, 365 and 550 Days of Age

Resumos

Foram comparados métodos de padronização dos pesos corporais às idades de 205, 365 e 550 dias. Utilizaram-se informações de animais da raça Nelore, criados na região Nordeste e controlados pela Associação Brasileira dos Criadores de Zebu (ABCZ). Compararam-se os métodos: MET1 - utilizado pela ABCZ; MET2 - curvas individuais de regressão linear para cada animal; MET3 - curvas individuais de regressão quadrática; MET4 - curvas individuais de Brody; MET5 - utilizado pelo Programa de Melhoramento Genético da Raça Nelore (PMGRN); e MET6 -- curvas individuais de Richards. Houve diferenças entre as médias dos pesos corporais calculadas pelos diferentes métodos. Foram verificadas altas correlações entre os métodos. As estimativas de variâncias e de parâmetros genéticos foram diferentes entre os métodos. Os métodos em execução no Brasil apresentam diferenças quanto à sua aproximação em representar a curva de crescimento dos animais. Apesar das altas correlações genéticas e de classificação dos animais por seus valores genéticos, as diferenças nesta classificação podem influenciar o processo de seleção e a resposta esperada à esta seleção.

bovinos de corte; curva de crescimento; métodos de padronização; modelos não lineares; pesos corporais

Methods of standardization of body weight for 205, 365 and 550 days of age were compared. It was used information of animals of the Nellore breed, raised in the Northeast Brazil, and controlled by the Brazilian Zebu Breeders Association (ABCZ). The following methods were compared: MET1 - used by ABCZ; MET2 - individual curves of linear regression for each animal; MET3 - individual curves of quadratic regression; MET4 - individual Brody curve; MET5 - used by the Program of Genetic Improvement of the Nellore breed (PMGRN); and MET6 -- individual Richards curves. There were differences among the means of the body weights calculated by the different methods. High correlations were verified among the methods. The variance and genetic parameters estimates were different among the methods. There were differences among methods used in Brazil with respect to their approach with the growth curve of the animals. In spite of the high genetic correlations and classification of the animals by their breeding values, the differences in this classification may influence the selection process and the expected response to it.

beef cattle; body weights; growth curves; non linear models; standardization methods

Avaliação de Métodos de Padronização dos Pesos Corporais às Idades de 205, 365 e 550 Dias

Raimundo Nonato Braga Lôbo¹, Raimundo Martins Filho²

RESUMO - Foram comparados métodos de padronização dos pesos corporais às idades de 205, 365 e 550 dias. Utilizaram-se informações de animais da raça Nelore, criados na região Nordeste e controlados pela Associação Brasileira dos Criadores de Zebu (ABCZ). Compararam-se os métodos: MET1 - utilizado pela ABCZ; MET2 - curvas individuais de regressão linear para cada animal; MET3 - curvas individuais de regressão quadrática; MET4 - curvas individuais de Brody; MET5 - utilizado pelo Programa de Melhoramento Genético da Raça Nelore (PMGRN); e MET6 ¾ curvas individuais de Richards. Houve diferenças entre as médias dos pesos corporais calculadas pelos diferentes métodos. Foram verificadas altas correlações entre os métodos. As estimativas de variâncias e de parâmetros genéticos foram diferentes entre os métodos. Os métodos em execução no Brasil apresentam diferenças quanto à sua aproximação em representar a curva de crescimento dos animais. Apesar das altas correlações genéticas e de classificação dos animais por seus valores genéticos, as diferenças nesta classificação podem influenciar o processo de seleção e a resposta esperada à esta seleção.

Palavras-chave: bovinos de corte, curva de crescimento, métodos de padronização, modelos não lineares, pesos corporais

Evaluation of Body Weight Standardization Methods for 205, 365 and 550 Days of Age

ABSTRACT - Methods of standardization of body weight for 205, 365 and 550 days of age were compared. It was used information of animals of the Nellore breed, raised in the Northeast Brazil, and controlled by the Brazilian Zebu Breeders Association (ABCZ). The following methods were compared: MET1 - used by ABCZ; MET2 - individual curves of linear regression for each animal; MET3 - individual curves of quadratic regression; MET4 - individual Brody curve; MET5 - used by the Program of Genetic Improvement of the Nellore breed (PMGRN); and MET6 ¾ individual Richards curves. There were differences among the means of the body weights calculated by the different methods. High correlations were verified among the methods. The variance and genetic parameters estimates were different among the methods. There were differences among methods used in Brazil with respect to their approach with the growth curve of the animals. In spite of the high genetic correlations and classification of the animals by their breeding values, the differences in this classification may influence the selection process and the expected response to it.

Key Words: beef cattle, body weights, growth curves, non linear models, standardization methods

Introdução

Sabe-se que o crescimento dos bovinos não se apresenta de forma linear. Esta não linearidade dificulta a padronização dos pesos corporais a determinadas idades, uma vez que nas criações comerciais os animais são pesados em idades distintas por imposições de ordem prática. A padronização é necessária para que se torne possível a comparação dos desempenhos dos animais. Em bovinos de corte, principalmente zebuínos, são utilizadas as idades padrão de 205, 365 e 550 dias.

Os métodos de padronização em uso no Brasil utilizam fórmulas que apresentam em sua estrutura o ganho de peso em determinado período. Entretanto, esse ganho de peso é considerado como sendo constante dentro do período, admitindo-se crescimento linear.

As principais experiências sobre o crescimento e o desenvolvimento ponderal começaram com as pesquisas de Hammond (1932) e dos membros da Escola de Cambridge, prosseguindo com os trabalhos de Brody (1945) e Palsson (1955). Por meio de vários estudos, esses autores conseguiram descrever graficamente o crescimento do animal, mediante uma curva chamada de curva de crescimento, que apresenta em todos os animais comportamento sigmoidal. Esse tipo de curva tanto pode ser aplicado ao animal como um todo, como a qualquer tecido ou região corporal. Analisando a curva de crescimento, podem ser estabelecidas quatro fases:

1) fase progressiva: nessa fase, a taxa de crescimento é muito elevada e positiva, chegando ao máximo no ponto de inflexão da curva;

2) fase regressiva: a partir do ponto de inflexão a taxa do crescimento começa a diminuir em virtude de uma serie de fatores que inibem progressivamente o crescimento, embora o animal não deixe de crescer. Graficamente o ponto de inflexão marca essa inversão na taxa do crescimento;

3) fase estacionária, quando o animal deixa de crescer e o crescimento pode ser considerado apenas uma renovação dos tecidos; e

4) morte: o crescimento para totalmente, os tecidos não são renovados e o animal morre (Craplet, 1966).

Assim, o ideal para a padronização dos pesos corporais seria a utilização de equações não-lineares aplicadas à sequência de pontos que relacionam o peso com a idade dos animais. Dentre as equações não-lineares utilizadas para descrever a curva de crescimento em animais estão a de Brody (Brody, 1945) e a de Richards (Richards, 1959). A primeira não apresenta ponto de inflexão, ao contrário da segunda. Estudos indicam ser a equação de Richards a melhor para descrever a curva de crescimento de bovinos e outros animais (Brown et al., 1976; Perotto et al., 1992). Sua principal vantagem está em não fixar o ponto de inflexão da curva.

O objetivo deste trabalho foi comparar alguns métodos de padronização (lineares e não-lineares) dos pesos corporais às idades de 205, 365 e 550 dias, utilizando como amostra dados da raça Nelore.

Material e Métodos

Utilizaram-se neste estudo, 34.558 informações de animais da raça Nelore criados na região Nordeste entre os anos de 1976 e 1999. Estas informações foram provenientes do controle de desenvolvimento ponderal realizado pela Associação Brasileira dos Criadores de Zebu (ABCZ). Neste banco de dados, 28.386 animais tinham registros de produção.

Os animais controlados pela ABCZ são pesados trimestralmente. Assim, a partir dessas pesagens, foi estimado para cada animal, de acordo com o método de padronização, seus pesos aos 205 (P205), 365 (P365) e 550 dias de idade (P550). Do total de informações disponíveis, apenas 18.196 animais tiveram seus pesos estimados para todos os métodos, por causa de falhas entre as pesagens e do atendimento do critério de convergência para os modelos não-lineares. Utilizaram-se nove pares (peso e idade) de observações por animal, sendo que a primeira pesagem ocorreu ao nascimento e a última em média aos 2 anos de idade (alguns animais chegaram a ser pesados aos 974 dias de idade).

Foram avaliados seis métodos de padronização:

1) Método utilizado pela ABCZ (MET1), cuja metodologia é apresentada a seguir (ABCZ, 2002):

Para P205 calcula-se o GMDd - ganho médio diário do animal do nascimento à desmama (GMDd = [peso à desmama - peso ao nascer] / idade do animal em dias na pesagem à desmama). Obtido o GMDd , realizam-se quatro ajustes: ajusta-se o GMDd para a época do ano da desmama, a idade do bezerro na pesagem, a idade da mãe e o sexo do animal. Obtido o GMDd ajustado calcula-se o P205 (P205 = [ GMDd ajustado x 205 dias ] + peso ao nascer).

Para P365 e P550 calcula-se o GMDpa - ganho médio diário pós-desmama acumulado, que é a média do GMDd e do GMDp - ganho médio diário pós-desmama (GMDp = [pesagem atual - P205] / idade do animal em dias na pesagem pós-desmama - 205). Uma vez obtido o GMDpa calcula-se os P365 e P550 por meio das seguintes fórmulas:

P365 = P205 + ( GMDpa x 160 dias )

P550 = P205 + ( GMDpa x 345 dias )

2) Método utilizando uma equação de regressão linear do peso sobre a idade, obtida para cada animal individualmente (MET2).

3) Método utilizando uma equação de regressão quadrática do peso sobre a idade, obtida para cada animal individualmente (MET3).

4) Método utilizando o modelo não-linear de Brody (MET4):

Wt = A (1 - be^-kt)

em que: Wt é o peso e t a idade; A, a assíntota, valor da função quando t tende ao infinito; b, uma constante de integração que se ajusta para situações, em que W0 e, ou, t0 são diferentes de zero; e k, a taxa na qual uma função logarítmica do peso, muda linearmente por unidade do tempo. É referida, comumente, como índice de maturidade, pois estima a taxa de maturação da curva, ou seja, a taxa relativa na qual A é alcançado. No aspecto biológico, k é interpretado como medida de crescimento ou velocidade de ganho. Graficamente pode ser interpretado como declividade da curva.

5) Método (MET5) utilizado pelo Programa de Melhoramento Genético da Raça Nelore (PMGRN) que utiliza as fórmulas descritas por Lôbo (1992):

Pp = Pa + GMD x da, quando da < ds, ou

Pp = Ps - GMD x ds, quando da > ds,

em que: Pp é o peso calculado às idades padrão (P205, P365 ou P550); GMD é a razão da diferença entre os pesos posterior e anterior, pelo número de dias contido no período compreendido entre as duas pesagens; Ps é o peso seguinte à idade-padrão; Pa é o peso anterior à idade-padrão; da são os dias compreendidos entre a pesagem anterior e a idade-padrão; e ds são os dias compreendidos entre a pesagem posterior e a idade-padrão.

6) Método utilizando o modelo não-linear de Richards (MET6):

Wt = A (1 - be^-kt)^M

em que: Wt, t, A, b e k já foram definidos anteriormente para a curva de Brody (MET4) e M é o parâmetro de generalização do modelo que permite que a localização do ponto de inflexão seja variável. Biologicamente pode ser interpretado como índice de maturação e serve como medida da taxa de mudança na velocidade de ganho de peso.

Os métodos que utilizam um modelo de predição (MET2, MET3, MET4 e MET6) permitem, uma vez estimada a curva para cada animal, predizer o peso em qualquer idade dentro do intervalo considerado para o ajuste. Entretanto, para a comparação entre os métodos, somente foram utilizados os pesos padronizados que correspondessem àqueles também calculados pelos MET1 e MET5, de maneira que o número de informações fosse igual para todos.

Os modelos de regressão linear e quadrático foram utilizados apenas para realizar comparações entre os métodos, pois, sabe-se que o crescimento dos bovinos não deve ser representado por uma reta ou uma parábola.

Para criação, avaliação e manutenção do banco de dados, estimação das curvas de crescimento para cada animal e dos pesos às idades padrão, utilizaram-se os procedimentos contidos no programa SAS (SAS, 1996). As equações de Brody e Richards foram ajustadas utilizando-se o procedimento NLIN (SAS, 1996).

Posteriormente, foi verificado a consistência das informações e estabelecimento do modelo matemático. Foram eliminados animais com informações incompletas ou duvidosas, com peso padronizado exageradamente reduzido ou elevado para a idade em questão. Após esta fase, restaram então 10.751 observações. Deve-se ressaltar que a grande redução no número de informações ocorreu de maneira geral para todos os métodos, não havendo favorecimento de um em detrimento dos outros. Os critérios de eliminação dos dados são importantes fatores que contribuem para a escolha de um melhor método de padronização, entretanto, neste estudo, não houve diferenças significativas entre os métodos em relação à redução no número de informações.

Para escolha da equação (MET2, MET3, MET4 e MET6) que melhor descrevesse os dados foram utilizados os critérios de coeficiente de determinação (R²), quadrado médio residual (QMR) e o erro de predição médio (EPM) proposto por Goonewardene et al. (1981).

Uma análise de correlação de Pearson foi realizada entre os pesos estimados pelos diferentes métodos, por meio do PROC CORR (SAS, 1996). As médias de peso estimadas para cada método foram comparadas pelo teste t (LSD), utilizando modelo matemático que incluiu os efeitos fixos de propriedade, sexo, mês e ano de nascimento e regime alimentar.

As estimativas dos componentes de variância e herdabilidade foram obtidas pelo método da Máxima Verossimilhança Restrita (REML), por meio de modelos animais uni-característica, utilizando-se o programa MTDFREML (Boldman et al., 1993), aplicando-se um modelo com o efeito fixo de grupo de contemporâneos, a idade da mãe como covariável e os efeitos aleatórios genético aditivo direto, genético aditivo materno e de ambiente permanente, além dos resíduos aleatórios, não observáveis. A variável grupo de contemporâneos foi definida pela concatenação das seguintes variáveis: mês e ano de nascimento, propriedade, sexo e grupo de regime alimentar.

A covariância entre os efeitos genéticos direto e materno foi considerada como sendo igual a zero, segundo recomendação de Schaeffer (1996), citado por Fries & Albuquerque (1998) e Lôbo et al. (2000).

Foi realizada análise de correlação entre os valores genéticos aditivos estimados pelos diferentes métodos de padronização, utilizando-se a correlação de Pearson do PROC CORR (SAS, 1996), pois de acordo com Van Vleck et al. (1987), a correlação entre os valores genéticos é a própria definição de correlação genética.

Para a comparação da classificação dos animais entre os métodos de padronização, com base no valor genético aditivo direto, foi realizada análise de correlação de classificação ou "rank", utilizando-se a correlação de Spearman do PROC CORR (SAS, 1996).

Resultados e Discussão

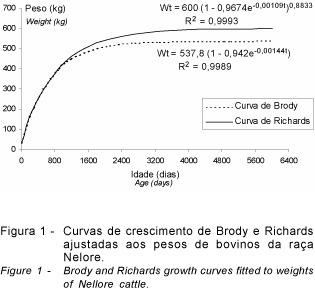
A Figura 1 ilustra o ajustamento das curvas de crescimento de Brody e Richards para todos os animais em conjunto. Ambas as curvas ajustaram muito bem os dados, entretanto a curva de Richards apresentou ajuste (R²=0,9993, QMR= 8,7848 e EPM=-0,43%) um pouco melhor do que a curva de Brody (R²=0,9989, QMR=12,7860 e EPM=-0,43%). As regressões linear (peso = 53,84 + 0,459idade; R² = 0,9792; QMR=260,5166; EPM=-7,74%) e quadrática (peso = 33,49 + 0,674idade - 0,0003idade²; R² = 0,9981; QMR=24,1617; EPM=-1,04%) também apresentaram bom ajustamento, mas de forma um pouco inferior. Os maiores R² foram associados com menores quadrados médios residuais (QMR), o que é esperado, uma vez que este faz parte do denominador da equação do R². Com base no erro de predição médio (EPM) todas as equações superestimaram os pesos observados, pois apresentaram sinal negativo, entretanto, as curvas de Brody e Richards apresentaram melhor qualidade de ajuste com valor inferior a 1%.

Deve-se salientar que todas estas curvas devem ser usadas apenas em idades dentro dos limites utilizados para sua estimativa. As curvas de regressão, em idades elevadas, fora deste limite, apresentam problemas do ponto de vista biológico, uma vez que a linear estima pesos muito acima dos parâmetros fisiológicos e a quadrática pesos muito abaixo destes e até negativos.

Perotto et al. (1992), comparando as funções de Richards, Gompertz, Monomolecular e Logística na descrição das curvas de crescimento de fêmeas leiteiras, observaram que a função de Richards descreveu melhor as curvas individuais dos animais. Detorre et al. (1992) identificaram ser a função de Von Bertalanffy, em comparação com a de Brody e a de Richards, a melhor para descrever as curvas de crescimento de vacas Retinta no Sudoeste da Espanha. Oliveira et al. (1994) também usaram a equação de Von Bertalanffy para descrever a curva de crescimento de vacas Guzerá. Para aves de postura, Braccini Neto et al. (1996) estudaram as equações de Richards, Brody, Von Bertalanffy, Gompertz e Logística, verificando serem melhores as curvas de Brody e Von Bertalanffy.

Considerando-se a não linearidade do crescimento e a melhor representação deste realizada pela curva de Richards (MET6), as discussões neste estudo serão tomadas assumindo-se este método, entre os estudados, como o mais adequado.

Na Tabela 1 estão apresentados o número de observações, as médias, os desvios padrão e os coeficientes de variação para os pesos aos 205 (P205), aos 365 (P365) e aos 550 dias de idade (P550) de acordo com os métodos de padronização estudados. O coeficiente de variação das médias não diferiu muito entre os métodos para todos os pesos estudados.

Houve diferenças estatísticas (P<0,05) entre todos os métodos para P205, exceção entre os MET2 e MET6. Estas diferenças alcançaram cerca de 7% entre a maior (MET5) e a menor (MET3) média. As maiores médias foram verificadas para os métodos em execução no Brasil, indicando provável superestimativa dessas. Nesta fase, a regressão linear (MET2) aproximou-se à curva de Richards (MET6).

Para P365 também verificou-se diferença estatística (P<0,05), exceção entre os MET1 e MET5 e entre os MET2 e MET6. As diferenças nas médias chegaram a 4% (entre as maiores, MET2 e MET6, e a menor, MET3). Para este peso, houve tendência de subestimativa das médias por todos os métodos (exceto MET2) em relação à curva de Richards.

As diferenças para P550 foram pequenas, menos de 4% entre a maior (MET3) e a menor (MET4) média. Houve maior semelhança entre os métodos, com igualdade entre os MET1, MET2 e MET5, e entre o MET1 e MET5 com o MET6. Verifica-se que apenas os métodos em execução no Brasil (MET1 e MET5) conseguem aproximar-se da estimativa considerada mais adequada. O MET2, que se igualava ao MET6 nos pesos anteriores, tendeu a superestimar a média aos 550 dias. O MET3 que subestimava às idades anteriores, superestimou aos 550 dias de idade.

As diferenças entre as médias estimadas pelos diferentes métodos podem ser explicadas pela forma e inclinação da curva que cada um assume e, pelo número de pontos considerados para realizar a estimativa.

Na fase inicial (P205), os métodos em execução no Brasil (MET1 e MET5), consideram apenas dois pontos (os mais próximos de 205 dias), assumindo constante o ganho de peso entre estes pontos. Dentre as fases estudadas, este período é o mais longo (205 dias) em relação às demais etapas (160 dias entre P205 e P365; 185 dias entre P365 e P550). Esta maior distância pode não estimar corretamente o peso aos 205 dias de idade, principalmente quando se utiliza o peso ao nascimento como no caso do MET1. Este método pode corrigir, pelo menos parcialmente, esta distância, por ajustar o GMDd para a idade à pesagem. No caso do MET5 o período entre as pesagens é mais curto o que reduz os problemas em considerar constante o ganho em peso entres as pesagens. Os métodos de regressão (linear e quadrática) e as curvas de Brody e Richards estimam este peso com base em todos os pontos disponíveis, inclusive aqueles entre o nascimento e a desmama, não considerados pelos MET1 e MET5. Esta consideração permite melhor estimativa do P205, pois os pontos intermediários auxiliam na determinação da inclinação da curva. Isto alerta para uma situação prática: Para que os criadores devem pesar seus animais periodicamente entre o nascimento e a desmama, se estes pesos não serão utilizados? Assim, bastaria pesar ao desmame, o que não é interessante, pois deve-se utilizar toda a informação disponível.

As diferenças aos 365 e 550 dias também devem ocorrer em virtude da representação das curvas. Os métodos em execução, da mesma maneira, consideram apenas dois pontos. Apesar do curto período entre 205 e 365 dias, estes métodos podem não ser sensíveis o bastante para distinguir as diferentes taxas de crescimento entre os animais. Assim, as estimativas para os MET6 e MET2 foram maiores para P365. Após os 550 dias ocorre redução na taxa de crescimento dos animais em relação ao período anterior (Figura 1). A semelhança entre os métodos é maior e aqueles em execução (MET1 e MET5) se igualam à curva de Richards. O método de regressão linear (MET2) se afasta do MET6, superestimando os pesos. Isto é de se esperar, uma vez que este método representa uma reta ascendente. A média do valor de A (valor assintótico) das curvas de Richards de todos os animais foi de aproximadamente 440 kg, entretanto, na curva de ajuste com todos os animais este parâmetro foi de 600 kg (Figura 1), indicando que na idade de 550 dias o peso estimado correspondeu a cerca de 50% do valor assintótico.

Na Tabela 2 estão apresentados os coeficientes de correlação de Pearson entre os pesos obtidos pelos vários métodos de padronização dos P205, P365 e P550. As correlações entre os métodos são todas altas, entre 0,89 e 0,99, para todos os pesos. Para P205 e P365, as maiores correlações ocorreram entre os MET1 e MET5 e entre os MET2 e MET6, reforçando o observado em relação às médias.

Os métodos em uso no Brasil (MET1 e MET5) foram muito semelhantes. Por outro lado, as maiores correlações entre a regressão linear (MET2) e a curva de Richards (MET6) indicam que a primeira pode ser usada como uma aproximação alternativa nesta etapa inicial do crescimento dos animais. De maneira geral, o MET5 foi o que se apresentou mais distante do MET6.

É interessante observar que o método não linear da curva de Brody (MET4) se aproximou bem à curva de Richards (MET6). A curva que representa o MET4 (Brody) não apresenta ponto de inflexão, não considerando a mudança na velocidade de crescimento na fase inicial. Por outro lado, aproximadamente metade das curvas de Richards dos animais deste estudo, apresentou o ponto de inflexão na idade zero. Isto significa, na prática, que estas curvas não apresentaram ponto de inflexão, o que torna as curvas dos dois métodos muito semelhantes. Este é um dos motivos que faz com que a curva de Brody possa ser utilizada na representação do crescimento dos bovinos.

Nas Tabelas 3, 4 e 5 estão apresentadas as variâncias e parâmetros genéticos de acordo com os métodos de padronização para os pesos aos 205 (P205), 365 (P365) e 550 dias de idade (P550). Para os três pesos considerados, percebem-se variações nos parâmetros genéticos estimados de acordo com o método de padronização avaliado, o que é preocupante, pois indica insegurança em relação aos métodos em execução. Se para uma mesma estrutura de dados, mesmos animais, há estimação de parâmetros diferentes com diferentes métodos de ajustes, algo precisa ser revisto.

A minimização do logaritmo da função de verossimilhança restrita (-2LogL) foi maior para o MET6 em todos os pesos estudados (Tabelas 3, 4 e 5).

Para P205 as diferenças não foram tão grandes. As estimativas de herdabilidade direta variaram de 0,11 a 0,13 (Tabela 3). Esta variação foi de 0,16 a 0,21 para P365 e de 0,22 a 0,29 para P550, variações consideráveis. O mais notável é que a diferença entre as herdabilidades para os MET1 e MET5, métodos muito semelhantes e em execução, são muito distintas, tanto para P365 (0,19 vs. 0,16; Tabela 4) quanto para P550 (0,26 vs. 0,22; Tabela 5).

Entre os métodos em execução, o método da ABCZ (MET1) apresentou maior semelhança com o MET6, apesar de ter apresentado menores estimativas de herdabilidade direta (0,11 vs. 0,12 para P205; 0,19 vs. 0,21 para P365 e 0,26 vs. 0,29 para P550). O método utilizado pelo PMGRN (MET5) se distanciou mais, à medida que aumentou a idade. O método de regressão linear foi o que apresentou maior similaridade ao MET6.

Comparando-se as variâncias genéticas diretas e as variâncias fenotípicas obtidas pelos métodos MET1 e MET5 com as obtidas pelo método MET6, percebe-se que a utilização da curva de Richards consegue captar melhor as diferenças genéticas entre os animais, uma vez que apresentou maiores estimativas de herdabilidade direta.

As estimativas de herdabilidade materna não diferiram muito, entretanto estes valores foram tão reduzidos em todos os pesos que não se esperaria muito esta variação. Por outro lado, as estimativas de variância materna para o MET6 no P205 é reduzida (Tabela 3) em relação aos demais métodos (exceto MET3) e muito superior aos MET1, MET4 e MET5 no P550 (Tabela 5).

Estes resultados indicam alguma distância entre os métodos em execução e o método teoricamente ideal (MET6). Isto demonstra que, além das diferenças nas estruturas dos dados e no número de observações que causam grandes variações entre os parâmetros estimados nos diferentes estudos verificados na literatura, o método de padronização do peso também influencia os resultados.

Na Tabela 6 estão apresentadas as correlações entre os valores genéticos obtidos pelos diferentes métodos e entre os pesos estudados. As correlações são todas altas e significativas (P<0,01). Em geral, os resultados são semelhantes aos verificados para as correlações simples (Tabela 2), ocorrendo as maiores correlações entre os MET1 e MET5 e entre os MET2 e MET6. Independente do método, as correlações genéticas entre os pesos nas várias idades situam-se em torno da média de 0,74, 0,63 e 0,75 entre os P205 e P365, P205 e P550, P365 e P550, respectivamente.

Na Tabela 7 estão apresentados os coeficientes de correlação de Spearman, de classificação ou "rank", da classificação dos animais pelos valores genéticos obtidos pelos diferentes métodos de padronização para P205, P365 e P550. Os valores da tabela são menores do que as correlações genéticas, ou seja, apesar da semelhança entre os valores genéticos estimados para os animais de acordo com o método de padronização, a ordem de classificação destes não é feita com a mesma semelhança. Os valores estão entre 0,86 e 0,98. Novamente, percebe-se maior semelhança entre os MET1 e MET5 e entre os MET2 e MET6. Maior distância também foi verificada entre o MET5 e o MET6, com coeficientes mais baixos (0,89 a 0,92; Tabela 7). Esta maior distância foi verificada principalmente no P205, fase de grandes alterações na velocidade de crescimento dos animais.

Esta ordem de classificação dos animais também é muito importante. Apesar das correlações de classificação serem altas, indicam ainda diferenças entre os métodos que devem ser consideradas.

Nas Tabelas 8, 9 e 10 estão apresentadas as classificações dos dez primeiros touros, ordenados por seus valores genéticos para P205, P365 e P550, respectivamente, de acordo com o método de padronização. Para todos os pesos, a ordem de classificação diferiu entre os métodos, não havendo nenhuma igualdade absoluta entre os mesmos. Há diferenças entre os touros classificados e inversões de classificação.

Para P205 os dois primeiros touros são os mesmos em todos os métodos, exceção ao MET5, em que o segundo melhor touro não foi nem classificado pelo MET6. Este animal também foi bem classificado (terceiro) pelo outro método em execução (MET1). O terceiro touro no MET6 é o quarto para o MET2, recebe a mesma classificação no MET3, não sendo classificado entre os dez para os demais métodos.

Para P550 os três primeiros animais são os mesmos para todos os métodos, apenas com inversões na posição. O touro 28673 que foi primeiro para o MET6, também foi o primeiro para os MET2, MET3 e MET4, sendo o terceiro para os MET1 e MET5. Isto é relevante pois os métodos em execução não conseguiram selecionar o melhor touro para a característica, quando comparados com os modelos de predição.

As correlações de Spearman considerando apenas os 726 touros são menores do que as correlações com todos os animais. Para P205 estas correlações caem entre 1 e 7 pontos percentuais. Para P365 e P550 esta queda foi de ordem semelhante. Considerando-se apenas os touros presentes nas listas dos dez primeiros dos diferentes métodos, as correlações caem mais ainda, entretanto permanecem altas e significativas para P550, confirmando a maior semelhança entre os métodos para este peso. Por outro lado, para P205 e P365, as correlações entre o MET6 e os MET1 e MET5 (em execução) não foram significativas (P>0,05). Isto se torna importante, pois considerando-se todos os animais, a correlação entre a ordem de classificação deveria ser próxima a um, caso os métodos fossem equivalentes, ainda mais em relação aos touros que devem sofrer maior pressão de seleção, sendo os maiores responsáveis pelo melhoramento genético dos animais.

Estas diferenças entre os métodos em relação aos parâmetros genéticos estimados e a ordem de classificação podem causar diferenças na resposta esperada à seleção. Os métodos em execução no Brasil (MET1 e MET5) apresentam diferenças entre si e principalmente em relação ao MET6, que, teoricamente, seria o método ideal, por descrever a curva de crescimento de bovinos. Estes métodos que utilizam fórmulas são práticos e de fácil execução, entretanto consideram poucos pontos de pesagem. Os criadores pesam seus animais periodicamente, muitas vezes aumentando custos e estresse aos animais, já sacrificados com disponibilidade alimentar, principalmente no Nordeste, e estas pesagens são pouco aproveitadas. Assim, de acordo com os resultados deste estudo esta aproximação não é suficiente, o que poderia comprometer os achados das pesquisas científicas e, principalmente, as respostas à seleção.

As diferenças verificadas entre os métodos provavelmente não influenciariam um processo de seleção massal, uma vez que são pequenas as diferenças entre os parâmetros genéticos e são altas as correlações estudadas, entretanto, na avaliação genética para identificação de animais superiores estas diferenças são consideráveis, uma vez que causam alterações na ordem de classificação dos touros. Por outro lado, estas diferenças provavelmente não causariam alteração na tendência genética, mas, se teoricamente for possível conseguir ganho genético superior por que deve satisfazer-se com ganho inferior.

Conclusões

Entre os métodos de padronização dos pesos corporais às idades padrão estudados, as curvas de Richards e de Brody foram as que melhor representaram o crescimento dos animais, com alguma superioridade da primeira em relação à segunda.

As respostas obtidas para os métodos em execução no Brasil apresentaram grandes semelhanças com os métodos não lineares (Brody e Richards), entretanto as pequenas diferenças verificadas entres eles podem não ser satisfatórias, dependendo do ponto de vista abordado, como a identificação de animais elite. Por outro lado, as pesagens intermediárias que são desprezadas nestes métodos podem fornecer informações importantes.

Dependendo do método utilizado haverá pequenas diferenças nos valores das médias dos pesos corporais, variâncias e parâmetros genéticos, mas que podem mascarar o conhecimento da natureza real destas respostas.

Provavelmente, as diferenças expressas na ordem de classificação dos animais tenham influência sobre o processo de seleção e a resposta esperada.

Literatura Citada

Recebido em: 24/05/01

Aceito em: 07/05/02

² D.S., Professor do Departamento de Zootecnia - Universidade Federal do Ceará. E.mail: [e-mail]

• ASSOCIAÇÃO BRASILEIRA DOS CRIADORES DE ZEBU - ABCZ. Disponível em: <http://www.abcz.org.br/tecnica/mge/novocdp.htm>. Acesso em: 03 jan. 2002.
• BOLDMAN, K.G.; KRIESE, L.A.; Van VLECK, L.D. et al. A manual for use MTDFREML USDA-ARS. Clay Center, NE. 1993. 120p.
• BRACCINI NETO, J.; DIONELLO, N.J.L.; SILVEIRA Jr., P et al. Análise de curvas de crescimento de aves de postura. Revista da Sociedade Brasileira de Zootecnia, v.25, n.6, p.1062-1073, 1996.
• BRODY, S. Bioenergetics and growth New York: Reinhhold Publ. Co. 1945. 1023p.
• BROWN, J.E.; FITZHUGH, H.A., Jr.; CARTWRIGHT, T.C. A comparison of nonlinear models for describing weight-age relationships in cattle. Journal of Animal Science, v.42, n.3, p.810-818, 1976.
• CRAPLET, C. Traité D'Elevage Moderne Tome III, La Viande de Bovins. Livre I. Paris: Vigot Frères Editeurs. 1966. 545p.
• DETORRE, G.L.; CANDOTTI, J.J.; REVERTER, A. et al. Effects of growth curve parameters on cow efficiency. Journal of Animal Science, v.70, n.9, p.2668-2672, 1992.
• FRIES, L.A.; ALBUQUERQUE, L.G. Pressuposições e restrições dos modelos animais com efeitos maternos em gado de corte. In: COSTA, M.J.; CROMBERG, V.U. (Eds.) Comportamento materno em mamíferos Bases teóricas e aplicações aos ruminantes domésticos. SP: SBEt-ETCO. 1998. p.179-36.
• GOONEWARDENE, L.A.; BERG, R.T.; HARDIN, R.T. A growth study of beef cattle. Canadian Journal of Animal Science, v. 61, p.1041-1048, 1981.
• HAMMOND, J. Farm Animals. 2.ed. London: Edward Arnold, 1932. 322p.
• LÔBO, R.B. Programa de melhoramento genético da raça Nelore. 2.ed. Ribeirão Preto: Universidade de São Paulo. 1992. 54p.
• LÔBO, R.N.B.; MARTINS FILHO, R.; PENNA, V.M. et al. Genetic parameters for growth traits of zebu cattle in the semi-arid region of Brazil. Ciência Animal, v.10, n.1, p.7-12, 2000.
• OLIVEIRA, H.N.; LÔBO, R.B.; PEREIRA, C.S. Relationships among growth curve parameters, weights and reproductive traits in Guzerá beef cows. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 5., 1994, Guelph. Proceedings... Guelph: University of Guelph, 1994. v.19. p.189-192.
• PALSSON, H. Conformation and Body Composition. In: HAMMOND, J. (Ed.) Progress in the physiology of farm animals London: Butterworths, 1955. 575p.
• PEROTTO, D.; CUE, R.I.; LEE, A.J. Comparison of nonlinear functions for describing the growth curve of three genotypes of dairy cattle. Canadian Journal of Animal Science, v.72, n.4, p.773-782, 1992.
• RICHARDS, F.F. A flexible growth function for empirical use. Journal of Experimental Botany, v.10, n.29, p.290-300, 1959.
• SAS INSTITUTE. User's Guide. version 6.11., 4.ed. v.2. Cary: 1996. 842p.
• Van VLECK, L.D.; POLLAK, E.J.; BRANFORD OLTENACU, E.A. Genetics for the animal sciences. New York: W.H. Freeman and Company, 1987. 391p.

Datas de Publicação

• Publicação nesta coleção
  09 Set 2005
• Data do Fascículo
  Jul 2002

Histórico

• Aceito
  07 Maio 2002
• Recebido
  24 Maio 2001