Resumos
Analisaram-se 335 dados de partos e leitegadas, pertencentes a 102 fêmeas Large White, nascidos entre 1985 e 1996, nas estações de setembro a fevereiro e março a agosto, na cidade do Recife, Estado de Pernambuco. O objetivo foi comparar equações de regressão para predição da natimortalidade. Utilizaram-se os modelos com transformação angular (TA), modelo linear generalizado (MLG) com distribuição binomial e ligação logit (BL), MLG com distribuição Poisson e ligação log (PL), MLG misto com distribuição binomial e ligação logit (BLM) e MLG misto com distribuição Poisson e ligação log (PLM). Foram considerados nos modelos os seguintes fatores: peso médio dos leitões ao nascimento em quilos (P), idade da mãe ao parto em anos (I), número de machos nascidos (M) e fêmeas nascidas (F). Os critérios para a seleção do melhor modelo foram a capacidade de predição e a análise de resíduos. O melhor modelo foi o MLG com distribuição binomial e função de ligação logit com as variáveis idade da mãe em anos, número de machos nascidos e número de fêmeas nascidas.
equação de regressão; modelo linear generalizado; natimortalidade; suínos
A total of 335 records of swine litters from 102 Large White females that farrowed between 1985 and 1996, born in the seasons of september to february and march to august, in the Recife city, in Pernambuco state (Brazil), were analysed. The objective was to compare regression equations to predict stillborn rates. Angular transformation (TA), a generalized linear model (GLM) with binomial distribution and logit link (BL), a Poisson GLM with log link (PL), a mixed GLM (GLMM) with binomial distribution and logit link (BLM) and a Poisson GLMM with log link were compared. Were considered the following sources of variation: average weight of piglets at birth in kilograms (P), age of the mother at birth in years (I), number of males (M) and females (F) born. Selection criteria for best model were prediction capacity and residual analysis. The best model was the GLM with binomial distribution with logit link with de variables age of the mother, number of males, and number of females.
generalized linear model; regression equation; sow; stillborn
MELHORAMENTO, GENÉTICA E REPRODUÇÃO
Modelos de predição da natimortalidade em suínos
A study on models for sow stillborn
Kleber Régis SantoroI; Severino Benone Paes BarbosaII; Mônica Calixto Ribeiro de HolandaIII
IBolsista CNPq, Pós-graduando Doutorado Integrado em Zootecnia, Univ. Fed. Rural de Pernambuco (UFRPE) - Departamento de Zootecnia - Rua Dom Manoel de Medeiros, s/n CEP 52171-900 Bairro Dois Irmãos Fone/Fax: (081) 3302-1550. E.mail: krsantoro@hotmail.com
IIProfessor Univ. Fed. Rural de Pernambuco (UFRPE) - Departamento de Zootecnia - Rua Dom Manoel de Medeiros, s/n. CEP: 52171-900 Bairro Dois Irmãos Fone/Fax: (081) 3302-1550. E-mail: sbarbosa@ufrpe.br
IIIPós-graduanda Doutorado Integrado em Zootecnia, Univ. Fed. Rural de Pernambuco (UFRPE) - Departamento de Zootecnia - Rua Dom Manoel de Medeiros, s/n CEP: 52171-900 Bairro Dois Irmãos Fone/Fax: (081) 3302-1550
RESUMO
Analisaram-se 335 dados de partos e leitegadas, pertencentes a 102 fêmeas Large White, nascidos entre 1985 e 1996, nas estações de setembro a fevereiro e março a agosto, na cidade do Recife, Estado de Pernambuco. O objetivo foi comparar equações de regressão para predição da natimortalidade. Utilizaram-se os modelos com transformação angular (TA), modelo linear generalizado (MLG) com distribuição binomial e ligação logit (BL), MLG com distribuição Poisson e ligação log (PL), MLG misto com distribuição binomial e ligação logit (BLM) e MLG misto com distribuição Poisson e ligação log (PLM). Foram considerados nos modelos os seguintes fatores: peso médio dos leitões ao nascimento em quilos (P), idade da mãe ao parto em anos (I), número de machos nascidos (M) e fêmeas nascidas (F). Os critérios para a seleção do melhor modelo foram a capacidade de predição e a análise de resíduos. O melhor modelo foi o MLG com distribuição binomial e função de ligação logit com as variáveis idade da mãe em anos, número de machos nascidos e número de fêmeas nascidas.
Palavras-chave: equação de regressão, modelo linear generalizado, natimortalidade, suínos
ABSTRACT
A total of 335 records of swine litters from 102 Large White females that farrowed between 1985 and 1996, born in the seasons of september to february and march to august, in the Recife city, in Pernambuco state (Brazil), were analysed. The objective was to compare regression equations to predict stillborn rates. Angular transformation (TA), a generalized linear model (GLM) with binomial distribution and logit link (BL), a Poisson GLM with log link (PL), a mixed GLM (GLMM) with binomial distribution and logit link (BLM) and a Poisson GLMM with log link were compared. Were considered the following sources of variation: average weight of piglets at birth in kilograms (P), age of the mother at birth in years (I), number of males (M) and females (F) born. Selection criteria for best model were prediction capacity and residual analysis. The best model was the GLM with binomial distribution with logit link with de variables age of the mother, number of males, and number of females.
Key Words: generalized linear model, regression equation, sow, stillborn
Introdução
A natimortalidade representa ao produtor, uma não realização de produção, a partir do momento em que um determinado número de animais não é terminado e comercializado.
A representatividade econômica total desta não comercialização pode ser calculada multiplicando-se o número total de animais natimortos pelo valor de um animal terminado e comercializado; além disso, podem ocorrer transtornos no planejamento da utilização dos recursos destinados à produção, tais como insumos e instalações, que deveriam ser contabilizados.
As perdas por natimortalidade, segundo Alba (1964), estariam entre 3,2 e 9,6%, o qual recomendou não ultrapassar 3,0% para que uma exploração seja considerada excelente e entre 3,1 e 5,0% para se considerar boa.
Segundo Nascimento & Santos (1997), várias patologias do útero gestante poderiam influenciar ou causar a natimortalidade, sendo muitas delas próprias de determinados animais, devido à especificidade entre espécies no que se refere aos mecanismos que envolvem o reconhecimento materno da gestação e também à estrutura e à função placentária. Daí a grande importância do conhecimento da fisiologia reprodutiva da espécie e de correto manejo reprodutivo (Dunne, 1975).
Kaneko (1988) salientou que as novas técnicas laboratoriais de análise bioquímica, aliadas a novas abordagens estatísticas seriam de grande auxílio na escolha de modelos e testes corretos na análise de dados complexos, como os hormonais envolvidos no período gestacional.
Os aspectos nutricionais da mãe e dos embriões também estariam envolvidos (Hughes & Varley, 1980), não somente aqueles presentes durante a gestação, mas também deficiências adquiridas ao longo do tempo, sendo destacadas as influências do iodo, cálcio, proteínas, vitamina A e riboflavina (Dunne, 1975).
A adaptabilidade dos animais ao meio seria outro fator influente, sendo que Alba (1964) apresentou resultados em que raças nativas tiveram menor natimortalidade que as importadas.
Há que se considerar ainda os aspectos genéticos (Dunne, 1975); e o estágio de desenvolvimento da mãe, pois animais mais velhos estariam mais propensos à natimortalidade (Alba, 1964; Dunne, 1975).
A condução de experimentos com o intuito de levantar dados sobre níveis hormonais durante a gestação seria relativamente complexa e muito estressante para os animais, além de economicamente dispendiosa devido ao número de animais e análises laboratoriais necessárias. Desta forma, a maioria dos dados disponíveis são aqueles provenientes das empresas ou criações comerciais, os quais limitam-se geralmente ao resultado final do processo, ou seja, aos dados sobre a mãe, reprodutor e leitegada, limitando muito o estudo a poucas variáveis explicativas.
A variável natimortalidade geralmente é estudada na forma de proporção, dividindo-se o número de leitões natimortos pelo total de leitões natimortos mais o número de leitões nascidos vivos. O arcoseno do valor resultante seria então utilizado em uma análise de variância ou regressão. Esta operação é denominada transformação angular, sendo uma das mais utilizadas (Cochran, 1940; Bartllet, 1947; Anscombe, 1948; Box & Cox, 1964; Pimentel Gomes, 1985; Sampaio, 1998; Steel et al., 1997).
Outra abordagem seria a utilização da proporção sem transformação, assumindo-a como sendo proveniente de uma distribuição binomial, ou ainda, a utilização somente do número de natimortos, aceitando-o como sendo de uma distribuição de Poisson, e proceder à análise pela metodologia dos modelos lineares generalizados, desenvolvidos por Nelder & Wedderburn (1972).
Devido às três diferentes abordagens citadas, objetivou-se com este trabalho comparar modelos de regressão na predição da natimortalidade em suínos, empregando-se as diferentes metodologias estatísticas, através dos seguintes modelos: transformação angular, modelo linear generalizado (MLG) com distribuição binomial e ligação logit, MLG com distribuição Poisson e ligação log, MLG misto (MLGM) com distribuição binomial e ligação logit e MLGM com distribuição Poisson e ligação log; utilizando-se dados sobre a mãe e a leitegada.
Material e Métodos
Selecionaram-se 335 dados de partos e leitegadas, provenientes de 102 fêmeas de raça Large White, pertencentes a uma granja comercial da cidade do Recife (PE), levantados entre julho de 1985 a dezembro de 1996, em duas estações de nascimento distintas, de setembro a fevereiro, para os meses secos, e março a agosto, para os meses chuvosos.
Utilizaram-se os modelos de regressão:
Transformação angular (TA):
MLG binomial com ligação logit (BL):
MLG Poisson com ligação log (PL):
MLGM binomial com ligação logit (BLM):
MLGM Poisson com ligação log:
em que µ é uma constante; os bi são os coeficientes de regressão para os efeitos considerados; Pi é o peso médio, em quilos, dos animais ao nascimento; Ij é a idade da mãe, em anos, ao parto; Mk é o número de machos nascidos; Fl é o número de fêmeas nascidas; am é o efeito da época de nascimento, sendo formado pelo ano e época, assumindo-se sendo independentemente e identicamente distribuído com am ~ N(0, ); e ~ N(0,
); e ~ N(0, ); e natimortos e vivos corresponde ao número de animais natimortos e ao número de nascidos vivos para o m-ésimo ou n-ésimo parto, conforme o modelo empregado.
); e natimortos e vivos corresponde ao número de animais natimortos e ao número de nascidos vivos para o m-ésimo ou n-ésimo parto, conforme o modelo empregado.
Considerou-se 1 para a estação seca e 2 para a estação chuvosa, na composição da época de nascimento.
A abordagem de um MLG é basicamente a que segue. Assumindo-se o modelo linear clássico  , com n observações; em que
, com n observações; em que  é o vetor de n respostas,
é o vetor de n respostas,  é o vetor de médias, e são p variáveis explicativas, e
é o vetor de médias, e são p variáveis explicativas, e  ,
,  K,
K,  os erros são normais e independentemente distribuídos. Os MLG generalizam o modelo linear clássico por meio da atribuição de uma distribuição para
os erros são normais e independentemente distribuídos. Os MLG generalizam o modelo linear clássico por meio da atribuição de uma distribuição para  pertencente à família exponencial, e supõe também
pertencente à família exponencial, e supõe também  , em que g ( × ) é chamada de função de ligação, ligando o vetor média
, em que g ( × ) é chamada de função de ligação, ligando o vetor média  ao preditor linear
ao preditor linear  . Estimativas de máxima verossimilhança são, então, obtidas pelo método dos mínimos quadrados ponderados iterativamente (Nelder & Wedderburn, 1972; McCullagh & Nelder, 1989).
. Estimativas de máxima verossimilhança são, então, obtidas pelo método dos mínimos quadrados ponderados iterativamente (Nelder & Wedderburn, 1972; McCullagh & Nelder, 1989).
A análise de um MLG é feita por meio de ajustes sucessivos, pela comparação de diferentes modelos. A diferença entre "deviances" - as medidas usadas para verificação de ajuste do modelo - possui distribuição aproximada de uma c² , sendo que o número de graus de liberdade corresponde à diferença no número de variáveis do modelo. Assim, ao se incluir ou excluir uma única variável, pode-se verificar a significância da mesma, comparando-se as diferenças entre "deviances" com uma c², com p-q graus de liberdade, em que p é o número de níveis das variáveis do modelo 2 e q do modelo 1, com p > q. Vários modelos, começando com um simples, que contém somente a média e indo até aquele com todas as variáveis de interesse, são então dispostos sucessivamente em uma tabela para a análise das "deviances" dos modelos, a qual recebe o nome de ANODEV, para verificar-se qual o mais apropriado (Nelder & Wedderburn, 1972; Cordeiro, 1986; Cox et al., 1987; McCullagh & Nelder, 1989; Dobson, 1990). As tabelas ANODEV para os modelos foram omitidas neste trabalho devido ao elevado número de modelos estudados e este não ser o objetivo do trabalho, mas sim comparar os modelos mais adequados. No entanto, providenciou-se a apresentação dos dados referentes aos modelos somente com a média, com todas as variáveis e com as variáveis significativas, representando os melhores modelos.
O ajuste dos modelos foi realizado com o programa SAS (SAS, 1996), pelas PROC REG, PROC GENMOD e macro GLIMMIX, para o modelo TA; BL e PL; e BLM e PLM, repectivamente.
Não é incomum que dados amostrais provenientes das distribuições binomial e Poisson apresentem variância superior à teórica esperada para a distribuição, o que é denominado sobredispersão. No caso da binomial var(Y) = nµ(1-µ)f, e para Poisson var(Y)= µf, em que f é o fator constante de sobredispersão, que poderia ser calculado aproximadamente dividindo-se o valor de c² de Pearson, do modelo completo, pelo número de graus de liberdade residual; quando o resultado for maior que um, então f > 1, e têm-se sobredispersão (Aitkin et al., 1989; McCullagh & Nelder, 1989), a estimativa de f seria aproximadamente não viesada e consistente para n grande, independentemente dos dados serem esparsos e ainda seria aproximadamente independente dos bi estimados. A matriz de covariâncias seria então inflacionada por f, o que poderia mudar a significância dos termos. Outra forma de estimar f é a proposta por Williams (1982), no entanto ela não foi utilizada neste trabalho, para o ajuste dos modelos, por não ser recomendada por McCullagh & Nelder (1989), pois altera os valores dos bi e não é aplicada à distribuição Poisson.
A sobredispersão da amostra foi estimada através das metodologias descritas por Williams (1982) e McCullagh & Nelder (1989), através das PROC LOGISTIC e PROC GENMOD, do SAS (SAS, 1996), para os modelos BL e PL, respectivamente.
Além das metodologias mencionadas, outras abordagens têm merecido atenção, na tentativa de identificar e modelar causas de variação extra e efeitos aleatórios nos MLGs, como o modelo beta-binomial, o modelo logístico-normal truncado, regressão de Poisson em modelo misto, MLGM com abordagem bayesiana, e métodos de Monte Carlo (Crowder, 1978; Zeger & Karim, 1991; Breslow & Clayton, 1993; Clayton, 1995; Wang et al., 1996; van der Tuow et al., 1997).
Entre as principais causas da sobredispersão podem ser citados os agrupamentos não identificados ("clusters"), modelo mal formado ou com variáveis importantes não incluídas, pontos extremos e expúrios ("outliers"), grande variação no denominador para a distribuição binomial e tabelas de contingência com grande número de variáveis (McCullagh & Nelder, 1989). Testes para a sobredispersão foram desenvolvidos por Dean (1992), Hines (1997) e Smith & Heitjan (1993), entre outros, mas nenhum destes foi empregado neste estudo, pois se assumiu a metodologia descrita em McCullagh & Nelder (1989), descrita anteriormente. Os modelos BLM e PLM foram construídos na tentativa de abranger a possível sobredispersão presente na amostra causada por "clusters", devido à época de nascimento; considerou-se a, então, de efeito aleatório e empregou-se a metodologia descrita por Wolfinger & O'Connel (1993), na estimação dos parâmetros.
Além da análise visual do comportamento preditivo dos modelos, a análise de resíduos seria outra ferramenta útil para se verificar qual o mais adequado. Existem vários tipos de resíduos para os MLGs disponíveis para serem trabalhados, como os de c², de Pearson, podendo ser ponderados ou não, entre outros (Pregibon, 1981; Williams, 1987; McCullagh & Nelder, 1989). Optou-se por trabalhar com os resíduos dados pela diferença entre os números de natimortos observado e o predito pelo modelo, por se entender que seriam de interpretação mais direta. Procedeu-se então à análise de variância dos resíduos e, posteriormente, a um teste de comparação de médias para os modelos estudados, supondo-se normalidade.
Deve-se salientar que dados fisiológicos, nutricionais e econômicos não foram analisados por não estarem disponíveis, além de estarem fora do escopo e do objetivo deste trabalho.
Resultados e Discussão
Estimativas de f pelas metodologias propostas por Williams (1982) e McCullagh & Nelder (1989) estão apresentadas na Tabela 1. Estas estimativas demonstraram que ocorreu sobredispersão na amostra para os modelos BL e PL, segundo o método de McCullagh & Nelder (1989), e no modelo PL segundo Williams (1982), justificando o estudo dos modelos PLM e BLM.
Estão apresentados nas Tabelas 2, 3 e 4 os dados referentes aos modelos somente com a média, com todas as variáveis e somente com os termos significativos, respectivamente.
Pode-se observar na Tabela 3 para b2, no modelo BL, e na Tabela 4 para m e b1, no modelo PLA, que houve mudanças na significância dos termos quando se utilizou a sobredispersão no modelo.
Constatou-se pelos resultados apresentados na Tabela 4, que os termos geralmente comuns para os modelos foram b3 e b4, sendo que b1 teve expressão somente nos modelos PLA e PLMA, e o termo b2 nos modelos BL, PLA e PLMA.
Os modelos PLA e PLB são provenientes do modelo PL, e PLMA e PLMB são provenientes do modelo PLM. Para ambos, PL e PLM, após a inserção de b4 na equação b1, b2 e b3 tornaram-se não significativos, igualmente as suas combinações com b4, mas sozinhos os três eram significativos. Isto não é incomum devido à metodologia de verificação da adequação de MLGs.
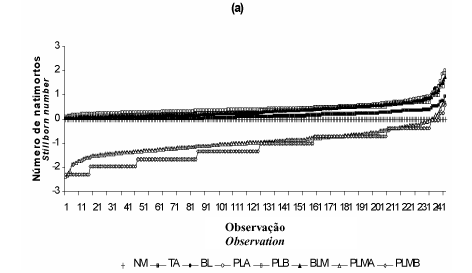
A predição de cada modelo, para o número de natimortos foi colocada nos gráficos da Figura 1, onde os valores estimados foram ordenados do menor para o maior. A natimortalidade foi separada nas categorias 0, 1, 2 e 3 a 10, nas Figura 1(a), 1(b), 1(c) e 1(d), respectivamente, para facilitar a visualização e a compreensão do comportamento dos valores preditos pelos modelos.
Visualmente, pela Figura 1, os modelos PLMA e PLMB foram os piores na predição de todas as categorias de natimortos. O modelo TA foi o melhor na categoria de zero natimortos, havendo uma grande proximidade entre os demais modelos. Para a categoria de um natimorto os melhores modelos foram BL, PLA, PLB e BLM, entretanto com um comportamento de superestimação em pelos menos três observações, o que não ocorreu com o modelo TA, apesar deste subestimar a maioria das observações. Em tratando-se da categoria de dois natimortos os modelos BL, PLA, PLB e BLM foram equivalentes na maioria das observações, mas o modelo PLA subestimou três observações em relação aos outros modelos. Para quatro natimortos os modelos BL, PLB e BLM se apresentaram como os melhores, sendo o BL melhor que os outros dois em uma observação. Nas categorias de quatro e cinco natimortos, com exceção dos modelos PLMA e PLMB, todos os demais tiveram comportamento semelhante. Os modelos BL, PLA, PLB e BLM foram os melhores ara a categoria de 10 natimortos. Considerando-se todas as categorias, os modelos BL, PLA, PLB e BLM estiveram muito próximos e foram os melhores, por vezes se confundindo, o que prejudicou a indicação de qual entre eles seria o melhor.
Assim sendo, lançou-se mão do recurso da análise de resíduos no julgamento dos modelos, como apresentado nas Tabelas 5 e 6; supondo-se normalidade para os mesmos.
Observou-se, Tabela 5 e Figura 1(a), que a maior variabilidade nos resíduos ocorreu na categoria de zero natimortos, e a menor na categoria de cinco natimortos, sendo que o coeficiente de determinação foi maior na categoria zero e menor na categoria de três natimortos. Estes resultados demonstraram que independentemente do coeficiente de variação dos resíduos, a equivalência entre os modelos aumentou o coeficiente de determinação, por haver vários resíduos com valores muito próximos.
Em uma visão geral, apesar de muitas vezes equivalentes (Tabela 6), o modelo PLB foi superior ao PLA, e o PLMB superior ao PLMA, com exceção da categoria zero (0), onde estas posições se inverteram para os dois últimos modelos. Segundo a Tabela 6 os melhores modelos, para as respectivas faixas de natimortalidade, foram: 0 - TA; 1 - BL, BLM, PLB e PLA; 2 - BL, BLM, PLB, PLA e TA; 3 - PLB, BLM, BL, TA, PLA e PLMB; 4 - BL, PLB, BLM, PLA e TA; 5 - BL, PLB, BLM, PLA e TA. A ordenação dos modelos foi feita pelo módulo da diferença, o que representou menores distâncias para as diferenças. Assim, de forma geral, o modelo BL foi o melhor.
A equivalência entre os modelos para a interpretação da natimortalidade como proporção ou contagem, Tabela 6, indicou que ambas abordagens seriam possíveis, apesar da distribuição binomial ter apresentado, geralmente, melhores ajustes.
O MLGM binomial foi superior ao MLGM Poisson, demonstrando uma melhor adequação e abordagem da sobredispersão dos dados, apesar da metodologia não ser recomendada quando os erros têm distribuição não normal, como por exemplo em dados binários (McCulloch, 2001).
Há recomendações desaconselhando o uso da transformação angular quando a proporção se aproxima de um dos extremos, ou seja, menor que 0,20 ou maior que 0,80 (Cochran, 1940; Bartlett, 1947; Steel et al., 1997). Nos casos extremos, Bartlett (1947) sugeriu a substituição de 0 por ¼ e n por n - ¼ , empiricamente, deixando os outros valores inalterados, enquanto que Cochran (1940) propôs um ajuste através de um processo iterativo. A transformação, entretanto, ainda seria menos vantajosa que o modelo binomial (Finney, 1978), que apresentaria melhores qualidades estatísticas na aproximação dos casos extremos (Berkson, 1944).
As estimativas negativas para b1, nos modelos PLA e PLMA (Tabela 4), indicaram influência na diminuição da natimortalidade com o aumento do peso médio ao nascimento, sendo evidente que existem limites biológicos para esta característica. O oposto ocorreu com b2, de estimativas positivas nos modelos BL, PLA e PLMA, que demonstrou um aumento da natimortalidade com o aumento da idade da mãe ao parto, entretanto, devido às características da amostra, apresentados na Tabela 7, as idades estudadas não apresentaram idade limite.
A proporção entre b3 e b4 , nos modelos TA, BL e BLM (Tabela 4), não é -1, o que indicaria igual predisposição em sentido oposto, ou seja, tanto machos como fêmeas teriam mesmo potencial, mas com sentidos opostos, para natimortalidade, o que levou a considerações sobre uma maior influência das fêmeas sobre a natimortalidade.
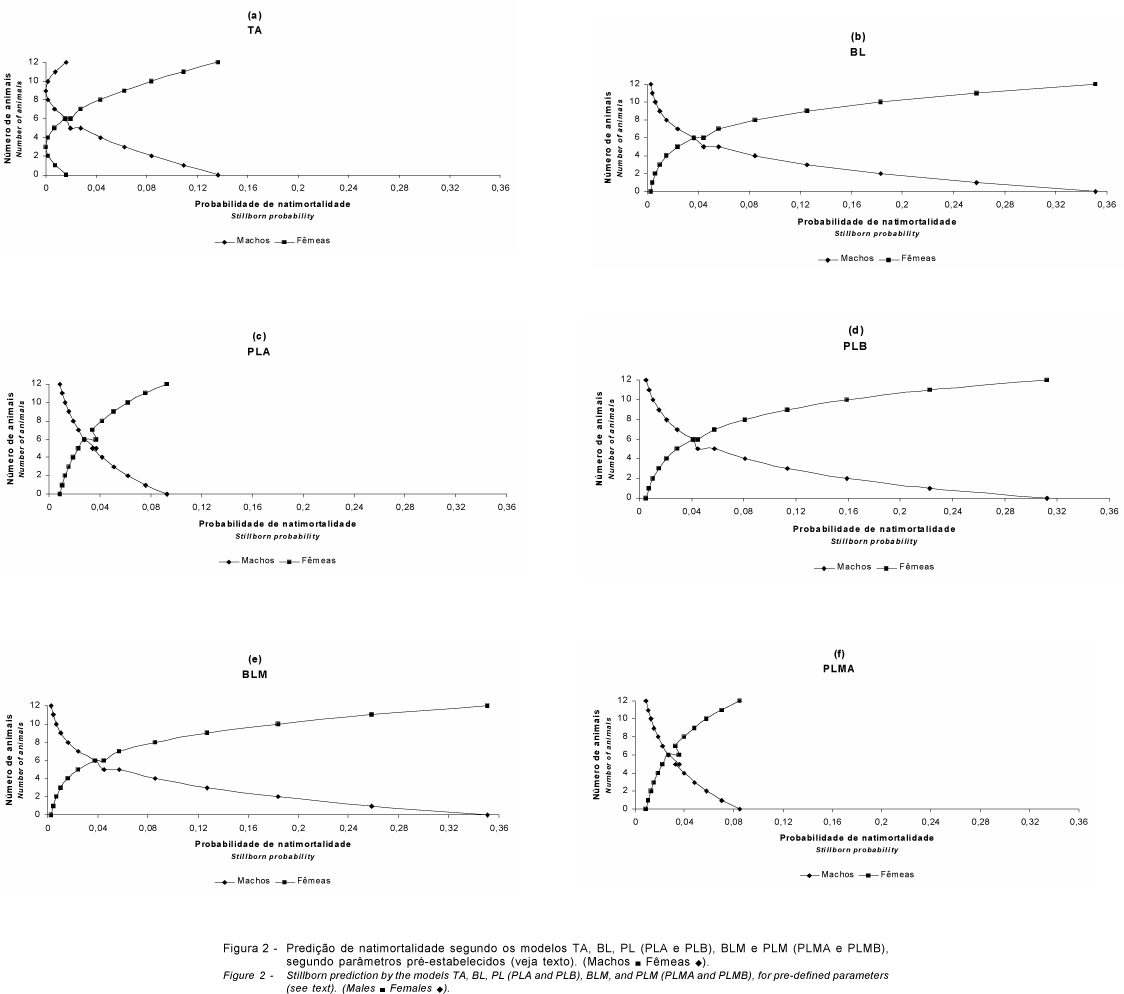
A partir do valores médios para idade em anos da mãe ao parto e peso médio ao nascimento dos leitões (Tabela 7), e variando-se o número de machos e fêmeas nascidos, obtiveram-se os gráficos da Figura 2, que representam a predição de cada modelo. Ficou demonstrado que a cada unidade macho substituída por fêmea, obteve-se um aumento na proporção de natimortalidade. O modelo TA (Figura 2a) teve comportamento de "reversão", de difícil interpretação biológica, o que foi creditado, em parte, aos problemas anteriormente citados com a transformação angular, desaconselhando-se o seu uso.
Devido aos resultados encontrados, Tabela 4 e Figura 2, deduziu-se que, além dos fatores ambientais, reprodutivos e genéticos normalmente avaliados, a consideração de fatores hormonais, nutricionais, fisiológicos e infecciosos, quando disponíveis, seriam deveras favoráveis à explicação do porquê da baixa natimortalidade, quando o número de machos é maior que o número de fêmeas. Talvez ocorra até mesmo uma predisposição do sexo à natimortalidade.
O conhecimento do controle genético do número de animais nascidos e outras variáveis relacionadas a ele ainda são deficientes, do ponto de vista dos locus que controlam a característica (Linville et al., 2001), cuja descoberta poderia levar a grandes avanços no melhoramento genético.
Conclusões
A partir dos resultados obtidos foi possível concluir que a modelagem da natimortalidade por um MLG, com distribuição binomial e função de ligação logit foi a mais adequada aos dados estudados.
A relação entre o sexo das crias e a natimortalidade indica a necessidade de estudos hormonais durante a gestação, na tentativa de detecção de algum fator influente.
Incentivam-se novos estudos nos quais informações como matriz de parentesco, mães com idades mais avançadas, peso e escore corporal da mãe antes do parto, nutrição, fisiologia e outros estejam disponíveis, para compor-se um modelo mais abrangente e detalhado.
Literatura Citada
Recebido em: 26/12/01
Aceito em: 11/02/03
- AITKIN, M.; ANDERSON, D.; FRANCIS, B. et al. Statistical modeling in GLIM Oxford: Oxford Science Publications, 1989. 374p.
- ALBA, J. Reproducción y Genética Animal Turrialba: Editorial SIC, 1964. 446p.
- ANSCOMBE, F.J. The transformation of poisson, binomial and negative-binomial data. Biometrika, v.35, p.246-254, 1948.
- BARTLETT, M.S. The use of transformations. Biometrics, v.3, n.1, p.39-52, 1947.
- BERKSON, J. Application of the logistic function to bio-assay. Journal American Statistical Association, v.39, n.227, p.357-365, 1944.
- BOX, G.E.P.; COX, D.R. An analysis of transformations. Journal Royal Statistical Society, Series B, v.26, n.2, p.211-243, 1964.
- BRESLOW, N.; CLAYTON, D. Approximate inference in generalized linear models. Journal American Statistical Association, v.88, p.9-25, 1993.
- CLAYTON, D.G. Generalized linear mixed models. In: GILKS, W.R.; RICHARDSON, S.; SPIEGELHALTER, D.J. (Eds.). Markov Chain Monte Carlo in Practice London: Chapman & Hall, 1995. p.275-301.
- COCHRAN, W.G. The analysis of variance when experimental errors follow the Poisson or Binomial laws. Annals of Mathematical Statistics, v.11, p.335-347, 1940.
- CORDEIRO, G.M. Modelos lineares generalizados. In: SIMPÓSIO NACIONAL DE PROBABILIDADE E ESTATÍTICA, 7., 1986, Campinas. Anais... Campinas: 1986. 286p.
- COX, D.R.; DAVISON, A.C.; FIRTH, D. et al. Generalized linear models and beyond London: Department of Mathematics - Imperial College, 1987. 120p.
- CROWDER, M.J. Beta-binomial Anova for proportions. Applied Statistics, v.27, p.34-37, 1978.
- DEAN, C.B. Testing overdispersion in Poisson and binomial regression models. Journal American Statistical Association, v.87, p.451-457, 1992.
- DOBSON, J.A. An introduction to generalized linear models London: Chapman & Hall, 1990. 174p.
- DUNNE, H.W. Abortion, stillbirth, fetal death, and infectious infertility. In: LEMAN, A.D. (Ed.). Diseases of swine 4.ed. Ames: Iowa State University Press, 1975. p.918-952.
- FINNEY, D.J. Statistical method in biological assay 3.ed. London: Charles Griffin & Company Ltd., 1978. 508p.
- HINES, R.J.O. A comparison of tests for overdispersion in generalized linear models. Journal Statistical Computation and Simulation, v.58, p.323-342, 1997.
- HUGHES, P.E.; VARLEY, M.A. Reproduction in pig Toronto: Butterworth, 1980. 241p.
- KANEKO, J.J. New concepts of test selection and utilization in veterinary clinical biochemistry. In: BLACKMORE, D.J. (Ed). Animal clinical biochemistry the future Cambridge: Cambridge University Press, 1988. p.105-112.
- LINVILLE, R.C.; POMP, D.; JOHNSON, R.K. et al. Candidate gene analysis for loci affecting litter size and ovulation rate in swine. Journal of Animal Science, v.79, p.60-67, 2001.
- McCULLAGH, P.; NELDER, J A. Generalized linear models 2.ed. London: Chapman & Hall, 1989. 511p.
- McCULLOCH, C.E. An introduction to generalized linear mixed models Piracicaba: 46 RBRAS/9 SEAGRO, 2001. 108p.
- NASCIMENTO, E.F.; SANTOS, R.L. Patologia da reprodução dos animais domésticos Rio de Janeiro: Guanabara-Koogan, 1997. 108p.
- NELDER, J.A.; WEDDERBURN, R.W.;M. Generalized linear models. Journal Royal Statistical Society, v.135, n.3, p.370-384, 1972. (Series A, Part 3)
- PIMENTEL GOMES, F. Estatística moderna na pesquisa agropecuária 2.ed. São Paulo: POTAFOS, 1985. 162p.
- PREGIBON, D. Logistic regression diagnostics. Annals of Statistics, v.9, n.4, p.705-724, 1981.
- SAMPAIO, I.B.M. Estatística alicada à experimentação animal Belo Horizonte:Universidade Federal de Minas Gerais, 1998. 221p.
- SAS INSTITUTE. SAS/STAT User's Guide: statistics 6.ed., v.1. Cary: SAS Institute, Inc., 1996.
- SMITH, P.J.; HEITJAN, D.F. Testing and adjusting for departures from nominal dispersion in generalized linear models. Applied Statistic, v.42, p.31-41, 1993.
- STEEL, G.D.; TORRIE, J.H.; DICKEY, D.A. Principles and procedures of statistics: a biometrical approach 3.ed. New York: McGraw-Hill, 1997. 666p.
- Van der TUOW, J.W.; GALBRAITH, R.F.; LASLETT, G.M. A logistic truncated normal mixture model for overdispersed binomial data. Journal Statistical Computation and Simulation, v.59, p.349-373, 1987.
- WANG, P.; PUTERMAN, M.L.; COCKBURN, I. et al. Mixed Poisson regression models with covariate dependent rates. Biometrics, v.52, p.381-400, 1996.
- WILLIAMS, D.A. Extra-binomial variation in logistic linear models. Applied Statistic, v.31, n.2, p.144-148, 1982.
- WILLIAMS, D.A. Generalized linear model diagnostics using the deviance and single case deletions. Applied Statistic, v.36, n.2, p.181-191, 1987.
- WOLFINGER, R.; O'CONNELL, M. Generalized linear mixed models: a pseudo-likelihood approach. Journal Statistical Computation and Simulation, v.48, 1993.
- ZEGER, S.L.; KARIM, M.R. Generalized linear models with random effects: a gibbs sampling approach. Journal American Statistical Association, v.86, n.413, p.79-86, 1991.
Datas de Publicação
-
Publicação nesta coleção
12 Dez 2003 -
Data do Fascículo
Out 2003
Histórico
-
Aceito
11 Fev 2003 -
Recebido
26 Dez 2001