Resumos
Foram realizados quatro estudos de simulação para verificar a distribuição de inversas de variáveis com distribuição normal, em função de diferentes variâncias, médias, pontos de truncamentos e tamanhos amostrais. As variáveis simuladas foram GMD, com distribuição normal, representando o ganho médio diário e DIAS, obtido a partir da inversa de GMD, representando dias para se obter determinado peso. Em todos os estudos, foi utilizado o sistema SAS® (1990) para simulação dos dados e para posterior análise dos resultados. As médias amostrais de DIAS foram dependentes dos desvios-padrão utilizados na simulação. As análises de regressão mostraram redução da média e do desvio-padrão de DIAS em função do aumento na média de GMD. A inclusão de um ponto de truncamento entre 10 e 25% do valor da média de GMD reduziu a média de GMD e aumentou a de DIAS, quando o coeficiente de variação de GMD foi superior a 25%. O efeito do tamanho dos grupos nas médias de GMD e DIAS não foi significativo, mas o desvio-padrão e CV amostrais médios de GMD aumentaram com o tamanho do grupo. Em virtude da dependência entre a média e o desvio-padrão e da variação observada nos desvios-padrão de DIAS em função do tamanho do grupo, a utilização de DIAS como critério de seleção pode diminuir a acurácia da variação. Portanto, para a substituição de GMD por DIAS, é necessária a utilização de um método de análise robusto o suficiente para a eliminação da heterogeneidade de variância.
bovinos de corte; critérios de seleção; inferência bayesiana; ganho de peso médio diário
Four simulation studies were conducted to verify the distribution of the inverse of variables with normal distribution, relatively to variances, averages, truncation points and sample sizes. The variables simulated were GMD, with normal distribution and representing average daily gain, and DIAS defined as a multiple of the inverse of GMD and representing days to reach a fixed body weight. The SAS® (1990) system was used, for simulation of the data, and for subsequent analysis of the results in all studies. The standard deviations simulated for GMD significantly affected DIAS sampling averages. The regression analyses showed a reduction on the mean and in the standard deviation of DIAS as a function of the increase in the average of GMD. Including a truncation point at about 10 to 25% of the mean value reduced the mean of GMD and increased the mean of DIAS when the coefficient of variation of GMD was above 25%. Size of the groups did not significantly affect averages of GMD or DIAS. Standard deviation and CV of GMD increased with the increase on group size. Due to the dependence between the average and the standard deviation and the variation observed in the standard deviations of DIAS as a function of group size, the use of DIAS as selection criteria may reduce the accuracy of the genetic evaluation. Therefore, in order to substitute GMD by DIAS, it is necessary the use of a method of analysis robust enough to eliminate the heterogeneity of variance.
beef cattle; selection criteria; bayesian inference; average daily gain
MELHORAMENTO, GENÉTICA E REPRODUÇÃO
Efeitos da transformação de uma variável com distribuição normal em sua inversa sobre os parâmetros de sua distribuição usando técnicas de Monte Carlo1 1 Projeto financiado pela FAPESP. Processo n. 01/10673-5.
Effects of transforming a normally distributed variable into its inverse on parameters of the distribution using Monte Carlo techniques
Mirella Leme Franco Geraldini SirolI; Janaina Conte HadlichII; Liliane SuguisawaII; André Rodrigues AbrahãoI; Sâmia Ramos HaddadIII; Henrique Nunes de OliveiraIV
IDoutoranda em Zootecnia, FMVZ/UNESP, bolsista da Capes
IIDoutoranda em Zootecnia, FMVZ/UNESP, bolsista da FAPESP
IIIMestranda em Zootecnia, FMVZ/UNESP, bolsista do CNPq
IVDepartamento de Melhoramento e Nutrição Animal - FMVZ /UNESP. Bolsista do CNPq
RESUMO
Foram realizados quatro estudos de simulação para verificar a distribuição de inversas de variáveis com distribuição normal, em função de diferentes variâncias, médias, pontos de truncamentos e tamanhos amostrais. As variáveis simuladas foram GMD, com distribuição normal, representando o ganho médio diário e DIAS, obtido a partir da inversa de GMD, representando dias para se obter determinado peso. Em todos os estudos, foi utilizado o sistema SAS® (1990) para simulação dos dados e para posterior análise dos resultados. As médias amostrais de DIAS foram dependentes dos desvios-padrão utilizados na simulação. As análises de regressão mostraram redução da média e do desvio-padrão de DIAS em função do aumento na média de GMD. A inclusão de um ponto de truncamento entre 10 e 25% do valor da média de GMD reduziu a média de GMD e aumentou a de DIAS, quando o coeficiente de variação de GMD foi superior a 25%. O efeito do tamanho dos grupos nas médias de GMD e DIAS não foi significativo, mas o desvio-padrão e CV amostrais médios de GMD aumentaram com o tamanho do grupo. Em virtude da dependência entre a média e o desvio-padrão e da variação observada nos desvios-padrão de DIAS em função do tamanho do grupo, a utilização de DIAS como critério de seleção pode diminuir a acurácia da variação. Portanto, para a substituição de GMD por DIAS, é necessária a utilização de um método de análise robusto o suficiente para a eliminação da heterogeneidade de variância.
Palavras-chave: bovinos de corte, critérios de seleção, inferência bayesiana, ganho de peso médio diário
ABSTRACT
Four simulation studies were conducted to verify the distribution of the inverse of variables with normal distribution, relatively to variances, averages, truncation points and sample sizes. The variables simulated were GMD, with normal distribution and representing average daily gain, and DIAS defined as a multiple of the inverse of GMD and representing days to reach a fixed body weight. The SAS® (1990) system was used, for simulation of the data, and for subsequent analysis of the results in all studies. The standard deviations simulated for GMD significantly affected DIAS sampling averages. The regression analyses showed a reduction on the mean and in the standard deviation of DIAS as a function of the increase in the average of GMD. Including a truncation point at about 10 to 25% of the mean value reduced the mean of GMD and increased the mean of DIAS when the coefficient of variation of GMD was above 25%. Size of the groups did not significantly affect averages of GMD or DIAS. Standard deviation and CV of GMD increased with the increase on group size. Due to the dependence between the average and the standard deviation and the variation observed in the standard deviations of DIAS as a function of group size, the use of DIAS as selection criteria may reduce the accuracy of the genetic evaluation. Therefore, in order to substitute GMD by DIAS, it is necessary the use of a method of analysis robust enough to eliminate the heterogeneity of variance.
Key Words: beef cattle, selection criteria, bayesian inference, average daily gain
Introdução
A maioria dos programas de melhoramento genético animal avalia dados de pesos em idades padrão ou ganhos de peso em determinado período, por serem características de fácil obtenção e análise. No entanto, a seleção com base nestas características pode resultar em aumento no peso dos animais adultos (Cartwright, 1970; Oliveira et al., 1994) e, conseqüentemente, em aumento no custo de manutenção do rebanho de vacas, reduzindo os lucros decorrentes da mudança genética obtida nos pesos e nos ganhos de peso.
Sobre estes aspectos, Fries (1996) propôs como critério alternativo de seleção para bovinos de corte o número de dias necessário para alcançar determinado peso em determinado estágio da vida do animal (DIAS). Segundo o autor, este critério mudaria a ênfase da seleção do numerador para o denominador do ganho de peso médio diário (GMD). Assim, seriam selecionados animais que atingissem mais rápido o ponto de abate.
A característica DIAS é calculada a partir do produto de uma constante pelo inverso do ganho de peso médio diário (GMD) em determinado estágio da vida do animal. Portanto, DIAS é, em última análise, uma transformação de uma variável com distribuição normal, o GMD, em sua inversa.
Uma vez que é possível haver animais com valor observado de GMD muito próximo ou até inferior a zero, torna-se necessário estabelecer, arbitrariamente, um ponto de truncamento no limite inferior da curva. Os indivíduos com valor de GMD inferior a este ponto são eliminados da análise. O efeito da fixação deste ponto de truncamento sobre a distribuição da variável normal é bem conhecido (Sorensen et al. 1998). Contudo, não se tem informação do efeito deste ponto de truncamento sobre a distribuição da variável inversa. Também é interessante conhecer o efeito do tamanho da amostra sobre os parâmetros da distribuição, uma vez que as inferências sobre os parâmetros dos grupos de progênie determinam o valor genético dos touros.
Fries & Albuquerque (1996) foram os primeiros a comparar o tempo para conseguir determinado ganho com o ganho de peso médio diário como critério de seleção. A única diferença observada foi a herdabilidade pouco mais elevada para a variável transformada, que, segundo os autores, proporcionaria ganho 54% superior em relação ao ganho médio diário no rebanho utilizado. Esta informação não se repetiu em outros trabalhos. Fries & Albuquerque (1996) observaram também que, quando as duas características eram submetidas à avaliação genética utilizando-se a metodologia dos modelos mistos, a ordem de classificação dos animais não era coincidente.
Mais recentemente, alguns trabalhos foram realizados para comparar ganho de peso com o número de dias para conseguir determinado peso como critério de seleção. Geralmente, os estudos têm demonstrado que a herdabilidade do ganho de peso é maior que a herdabilidade da característica alternativa. Tem-se observado também, que existem mudanças na classificação dos animais, embora nenhum trabalho tenha evidenciado a causa destas mudanças (Muniz et al., 2001). Alguns estudos apontam que a seleção para DIAS favoreceria touros que produzem progênies mais uniformes (Carvalheiro et al., 2001; Ortiz Peña et al., 2004), ponto ressaltado como vantagem, pois, em rebanhos comerciais, a uniformidade das progênies seria um grande benefício. Não foi encontrada nenhuma outra vantagem que justificasse o uso de DIAS como critério de seleção em substituição ao peso ou ao ganho de peso.
Os estudos indicam que, em geral, o ganho de peso tem distribuição aproximadamente normal e que dias para atingir determinado peso não tem distribuição normal. Tem-se observado ainda que a variância do ganho de peso é homogênea entre os diversos grupos de contemporâneos, apesar de haver grandes diferenças entre as médias dos grupos. DIAS tem distribuição desconhecida, claramente assimétrica e não apresenta variância homogênea entre os diversos grupos de contemporâneos. A variância, em geral, depende da média, sendo mais alta nos grupos com médias de dias maiores, ou seja, com médias de ganho de peso menores (Ortiz Peña et al., 2000; Garnero et al., 2001).
O objetivo neste trabalho foi, utilizando simulação, verificar o efeito de mudanças em alguns parâmetros de uma variável com distribuição normal (GMD) sobre a distribuição de sua inversa (DIAS) e a distribuição dos momentos amostrais desta população, quando subdividida em estratos.
Material e Métodos
Foram realizados quatro estudos de simulação com o objetivo de verificar a distribuição de inversas de variáveis com distribuição normal, em função de diferentes variâncias, médias, pontos de truncamentos e tamanhos amostrais. Em todos os estudos, foi utilizado o sistema SAS® (1990) para simulação dos dados e posterior análise dos resultados.
Inicialmente, foram simuladas cinco replicações de uma variável denominada GMD, com distribuição normal padrão (GMD~N(0,1)) e 400.000 observações cada uma. A seguir, cada replicação foi dividida em dez grupos de 40.000 observações. Foi, então, obtida uma nova variável (GMD1) multiplicando-se GMD por constantes 2, 4, ...20), de acordo com o grupo ao qual a observação estava alocada, e somando-se outra constante com valor de 200 em todos os grupos. Dessa forma, a variável GMD1 tinha distribuição normal com média 200 e variância entre 4 e 400, de acordo com o grupo. Outra variável (DIAS1) foi criada, obtida da transformação de GMD1 em sua inversa e multiplicada por 200 (DIAS1=200/GMD1). Esta variável teria média teórica de 1,00 unidade caso não houvesse variação dentro dos grupos. Foram, então, calculados as médias, os desvios-padrão, as variâncias de cada grupo para GMD1 e DIAS1 e a regressão da média de DIAS1 em cada grupo no desvio-padrão de GMD1 no mesmo grupo. Como o coeficiente de variação de GMD1 em cada grupo não foi alto, não houve possibilidade real de serem geradas observações próximas de zero, não havendo necessidade de truncar a variável GMD1. Como o número de observações em cada grupo foi muito grande, as mudanças observadas na média de DIAS1 puderam ser atribuídas às mudanças na variância de GMD1. Foram também estudadas as associações entre as médias, os desvios-padrão e os coeficientes de variação (CV) das duas características utilizando-se análise de correlação.
Procedimento semelhante foi realizado no estudo do efeito da média de uma variável com distribuição normal (GMD2) sobre a distribuição de sua inversa (DIAS2). Neste caso, as inversas foram geradas a partir de distribuições normais com mesma variância (100) e médias variando de 100 a 300. Foram calculadas as médias, os desvios-padrão e os coeficientes de variação (CV) das duas variáveis e as regressões da média e do desvio-padrão de DIAS2 na média simulada da variável normal (GMD2) e do desvio-padrão de DIAS2 na média de DIAS2, como forma de se constatar a heterogeneidade de variância.
Para o estudo do ponto de truncamento, foram geradas populações de uma variável normal (GMD3) com a mesma média (100) e diferentes variâncias (entre 100 e 900) e, em cada uma delas, a variável inversa (DIAS3) foi obtida após eliminação das observações cujos valores de GMD3 fossem inferiores aos pontos de truncamento, os quais variaram de 0 a 22,5. Novamente, foram obtidos as médias, os desvios-padrão e os coeficientes de variação para as duas variáveis em cada situação e as regressões das médias e dos desvios-padrão no ponto de truncamento.
No último estudo, foram simuladas seis populações, cada uma com 20.000 grupos de observações com distribuição normal, com média 100 e variância 20. Em cada população, o tamanho do grupo era fixo, assumindo os valores 2, 4, 8, 16, 32 ou 64 para cada população. Além da variável (GMD4), gerada com distribuição normal, foi obtida, da mesma forma que nos estudos anteriores, uma variável (DIAS4) gerada pelo produto de uma constante (K = 100) pela inversa de GMD4 (DIAS4 =100/GMD4). Para cada população foram calculados média, variância e coeficiente de variação de toda população e de cada grupo. Foi ainda aplicado o teste de Levene, citado por Wechsler (1998), para verificação da heterogeneidade de variância entre os grupos. Adicionalmente, nos grupos com 64 elementos, foi realizada uma análise de regressão para verificar se a variância e a média da variância de cada estrato é dependente da média, do desvio-padrão, do mínimo ou do máximo valor observado de GMD4 naquele grupo.
Resultados e Discussão
Na Tabela 1 constam as médias das médias, dos desvios-padrão e dos coeficientes de variação dos grupos, para a variável GMD1, gerada com distribuição normal e média 200 e de sua inversa (DIAS1= 200/GMD1), de acordo com o desvio-padrão utilizado na simulação de GMD1.
Houve grande proximidade entre a média real simulada e as médias amostrais e entre o desvio-padrão utilizado na simulação e o desvio-padrão amostral de cada um deles, como esperado, em razão do grande número de amostras geradas. A média de DIAS1 foi próxima de 1,00 em todos os grupos. A análise de regressão linear mostrou dependência significativa (P<0,01) entre as médias amostrais e os desvios-padrão simulados para esta característica, sendo o coeficiente de determinação (R2) superior a 91% em todas as amostras analisadas. Entretanto, a variação na média amostral foi muito pequena, de modo que os coeficientes de regressão linear variaram entre 0,000547 e 0,000595 nas cinco replicações.
Este resultado indicou que, quando foi realizada a transformação de uma variável normal em sua inversa, a média da última (DIAS1), embora dependente da variação na primeira, não apresentou mudança importante em função desta variação, ao menos no escopo coberto por este trabalho.
As correlações entre as médias amostrais das duas variáveis (GMD1 e DIAS1) foram não significativas e ficaram entre -0,61 e 0,03, o que era esperado, visto que a variação das médias amostrais de GMD1 era muito pequena. As correlações entre os desvios-padrão e entre os coeficientes de variação das duas variáveis por grupo foram significativas e maiores que 0,99, nas cinco replicações. Os coeficientes de variação das duas variáveis foram muito próximos e não dependeram do valor da constante utilizada no numerador quando da transformação de GMD1 para DIAS1.
A regressão da média de DIAS1 no desvio-padrão de GMD1, incluindo o efeito quadrático, elevou o coeficiente de determinação para mais de 99% em todos os conjuntos, sendo altamente significativo (P<0,01). Na Figura 1 consta a curva da regressão estimada, incluindo o efeito quadrático.
Verificou-se que a tendência de aumento ficou maior à medida que o desvio-padrão de GMD1 aumentou. A parte final do gráfico (extrapolação) indicou que, se o desvio-padrão fosse superior a 70, o que representa um coeficiente de variação de 35%, a mudança na média poderia atingir valores mais significativos. Passando-se o coeficiente de variação de 1 para 35%, o aumento na média de DIAS1 pode atingir 18%. O aumento do coeficiente de variação até estes níveis leva à necessidade de truncamento das distribuições, o que impediria o isolamento do efeito do desvio-padrão sobre a média. Por este motivo, preferiu-se utilizar a extrapolação.
Muniz et al. (2001) apresentaram um estudo em que a diferença entre as médias harmônicas e as médias aritméticas do ganho de peso das progênies de diversos touros foram dependentes dos desvios-padrão do ganho de peso nestes grupos. Os desvios-padrão não foram apresentados naquele estudo, mas foi possível verificar pelo gráfico, que existe variabilidade muito grande entre os desvios-padrão do GMD das progênies. O desvio-padrão variou, aproximadamente, entre 10 e 230 g, o que representaria coeficientes de variação de 2,5 até 57,5% em relação à média geral. Estes valores estão muito acima dos utilizados neste trabalho (entre um e 20%) e é possível que, nestes extremos de variação, o efeito do desvio-padrão de GMD sobre a média de DIAS seja mais importante.
Não há nenhum estudo mostrando que a variação entre os desvios-padrão das progênies de touros tenha origem genética intrínseca e, menos ainda, que possa ser herdada. Sabe-se que a variância genética aditiva dos filhos de um indivíduo poderia ser reduzida pela consangüinidade em até 1/4 da variância genética aditiva, se o indivíduo tivesse consangüinidade igual a um. Touros com consangüinidade de 0,5 poderiam reduzir a variância de seus filhos em até 1/8 da variância genética da característica. Supondo-se que, se a mudança na variação genética entre as progênies dos diversos touros seja realmente de origem genética intrínseca, ela não poderia ser muito maior que isso. Então, se o GMD tiver herdabilidade de 0,40, média de 200 e desvio-padrão fenotípico de 40 g, 1/8 da variância genética aditiva representaria 80 g2 ou 8,9 g em desvio-padrão. Mesmo considerando a região onde as mudanças provocam maior efeito, esta alteração no desvio-padrão não provocaria mudanças maiores que 5% na média de DIAS. Assim, ainda que a utilização de DIAS em vez de GMD possa favorecer touros consangüíneos, as mudanças provocadas devem ser muito pequenas em relação à variação que ocorre ao acaso.
Constam na Tabela 2 as médias das cinco replicações da variável GMD2, simulada com distribuição normal, com a mesma variância e com diferentes médias, e da variável DIAS2 obtida pela transformação de GMD2 (DIAS2=200/GMD2), de acordo com a média simulada do grupo para a variável GMD2.
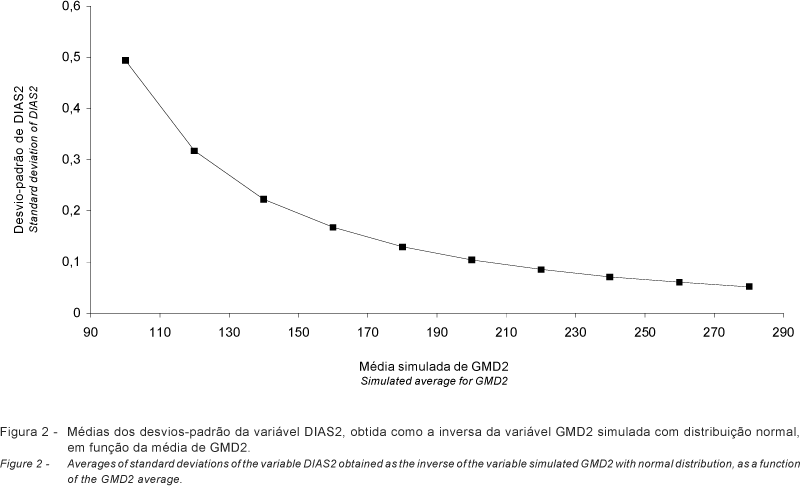
Para a variável com distribuição normal, o desvio-padrão foi constante e a média, próxima à média simulada. Assim, o coeficiente de variação (CV) diminuiu em função do aumento na média de GMD2. Para a variável DIAS2, a média foi inversamente proporcional à de GMD2, como esperado, e o desvio-padrão de DIAS2 diminuiu em função do aumento no valor simulado para a média de GMD2. A redução no desvio-padrão de DIAS2 em função do aumento na média de GMD2 foi, relativamente, maior que a redução na própria média de DIAS2. Desta forma, o coeficiente de variação de DIAS2 diminuiu bastante, apesar da redução na média de DIAS2, e manteve relação mais próxima com o coeficiente de variação de GMD2, a qual tem desvio-padrão constante. As análises de regressão mostraram redução significativa (P<0,01) da média e do desvio-padrão de DIAS2 em função do aumento na média de GMD2. O coeficiente de determinação da regressão foi maior que 90% em todas as replicações. A inclusão do efeito quadrático da média de GMD2 na equação de regressão aumentou o coeficiente de determinação para mais de 96% também em todas as replicações. A Figura 2 apresenta a distribuição da média das médias dos desvios-padrão de DIAS2 em função da média simulada de GMD2.
Na Figura 3 observa-se a curva de regressão do desvio-padrão de DIAS2 na média de DIAS2, incluindo um efeito quadrático, e que tem coeficiente de determinação de 99,9%.
O aumento do desvio-padrão de DIAS2 em função de sua média acelerou com o aumento na média. Considerando os extremos utilizados neste estudo, enquanto a média de DIAS2 elevou aproximadamente 2,9 vezes, o desvio-padrão de DIAS2 aumentou 9,5 vezes.
A dependência entre o desvio-padrão de DIAS e a média de GMD ou de DIAS foi bastante evidente e, como Fries & Albuquerque (1996) ressaltaram, nos grupos de contemporâneos em que a média de ganho médio diário é baixa, a variação de DIAS é muito maior, sendo mais fácil discriminar animais com base em suas diferenças em DIAS nestes grupos que naqueles em que a média de ganho médio diário é maior. Espera-se que nestes grupos haja aumento proporcional das variâncias genética e de ambiente. A heterogeneidade de variância de ambiente é sempre prejudicial quando se busca discriminar animais. A conseqüência é a redução da acurácia das predições dos valores genéticos e, portanto, do ganho genético (Hill, 1983; Vison, 1987). Se a heterogeneidade de variância de origem genética não for acompanhada por mudanças proporcionais na variância de ambiente poderá ser interessante, desde que a variância genética seja maior naqueles grupos em que deverão ser encontrados os indivíduos de maior valor para as características que se deseja selecionar (Garrick & Van Vleck, 1987; De Veer & Van Vleck, 1987).
No caso da transformação de ganho médio diário para dias, os dois tipos de heterogeneidade de variância devem ocorrer proporcionalmente, de modo que a herdabilidade não seja diferente entre os grupos. De qualquer forma, a variância genética será maior quando o ganho de peso for menor e, portanto, onde menos interessa discriminar os indivíduos em função do seu valor genético. Assim, a conseqüência esperada desta heterogeneidade de variância entre os grupos foi que, nos grupos com menor média de ganho médio diário, houve maior proporção de indivíduos com valores genéticos preditos mais extremos (mais altos ou mais baixos) que nos grupos com média alta para GMD, conforme salientado por Garnero et al. (2001) e por Ortiz Peña et al. (2000).
O número de observações truncadas cresceu com o aumento no valor adotado como ponto de truncamento e com o aumento no desvio-padrão da variável gerada.
Como é possível observar na Figura 4, a média da variável GMD3 aumentou significativamente (P<0,05) em função do aumento no ponto de truncamento apenas quando o desvio-padrão foi igual a 30 (CV=30%).
Embora significativo, o efeito sobre a média foi muito reduzido, cerca de 0,015 unidade (ou pontos percentuais) para cada unidade (1%) de aumento no ponto de truncamento. No caso de GMD3, estes valores puderam ser pensados como valores percentuais uma vez que a média simulada de GMD3 é igual a 100 unidades.
Consta na Figura 5 o efeito do ponto de truncamento sobre a média de DIAS3.
Foi verificado efeito significativo (P<0,01) com redução de 0,16% na média de DIAS3 em função do aumento de 1% no ponto de truncamento de GMD3, quando o desvio-padrão de GMD3 foi igual a 30 unidades (CV=30%). Quando o desvio-padrão simulado para GMD3 foi igual a 25 unidades, o efeito do ponto de truncamento sobre a média de DIAS3 foi muito pequeno (0,04%), apesar de significativo. Para os demais desvios simulados, não houve efeito significativo. No caso de DIAS3, os valores percentuais foram apresentados em relação à média teórica de DIAS3 (1,0 quando o desvio-padrão de GMD3 fosse igual a zero, Carvalheiro et al., 2001).
Não houve efeito do ponto de truncamento sobre o desvio-padrão de GMD3 em cada situação. O desvio de DIAS3, entretanto, é bastante afetado pelo ponto de truncamento quando o desvio-padrão simulado de GMD3 é mais alto. Na Figura 6 são apresentados os desvios-padrão de DIAS3 em função dos pontos de truncamento e dos desvios-padrão simulados para GMD3.
O efeito do ponto de truncamento sobre o desvio de DIAS3 foi bastante evidente no caso dos desvios-padrão simulados em 25 e 30 para GMD3. Estes resultados indicaram que a característica DIAS pode ser bastante influenciada pelo valor arbitrário atribuído ao ponto de truncamento do GMD, mas é claro que os limites fisiológicos determinam, em parte, os pontos de truncamento nos trabalhos deste tipo. Aparentemente, dentro da faixa dos coeficientes de variação utilizados neste trabalho, que englobaram os padrões normais de GMD, os pontos de truncamento acima de 10% do valor da média da característica quase não tiveram influência na distribuição da característica com distribuição normal, ou de sua inversa. Assim, foi adotado este valor como limite para as próximas simulações. Normalmente 10% do valor da média está abaixo dos limites fisiológicos aceitos para a característica, de forma que o ponto de truncamento deve ter pouca interferência sobre os resultados de avaliações genéticas envolvendo as características DIAS e GMD.
Constam na Tabela 3 as médias das médias, os desvios-padrão e os coeficientes de variação dos grupos de acordo com o número de indivíduos por grupo, para a variável simulada com distribuição normal, com média 100 e desvio-padrão 20 (GMD4) e a variável transformada (DIAS4=100/GMD4).
O aumento no número de observações abaixo do limite em função do aumento do número de observações geradas era esperado em função da distribuição de densidade do mínimo amostral (Mood et al., 1974). Não houve efeito significativo do tamanho dos grupos sobre as médias de GMD4 ou de DIAS4. As médias foram muito parecidas em todos os conjuntos. Os desvios-padrão e os coeficientes de variação amostrais médios de GMD4 aumentaram com o incremento no tamanho do grupo. Em DIAS4 estes aumentos foram ainda mais acentuados, o que era esperado, pois, conforme observado anteriormente, o aumento do desvio-padrão da variável inversa é sempre mais acentuado que o aumento do desvio na variável com distribuição normal. O aumento no desvio-padrão médio de GMD4 não foi acompanhado por mudança na média de DIAS4, quando consideradas as médias das médias dos grupos. Entretanto, quando se fez a regressão da média de DIAS4 no desvio-padrão de GMD4, dentro de cada tamanho de grupo, observou-se que a média foi significativa em todos os tamanhos de grupo.
Na Tabela 4 são apresentados os erros-padrão das médias e dos desvios-padrão de GMD4 e de DIAS4, de acordo com o tamanho do grupo.
Notou-se, conforme esperado, redução nos erros-padrão da média e dos desvios-padrão em função do aumento no tamanho do grupo.
O número de filhos de cada touro envolvido em programas de melhoramento é variável e a variação dos desvios padrão amostrais das médias das progênies dos touros é dependente do número de indivíduos nestas progênies. Na Tabela 5 são descritos os percentis 1, 10, 25, 50, 75, 90 e 99 para o desvio-padrão dos grupos de indivíduos, de acordo com o número de indivíduos nestes grupos, para uma variável com desvio-padrão de 20.
Observou-se que a variação dos desvios-padrão dos grupos foi muito maior nos mais numerosos que nos menos numerosos. Considerando-se que o tamanho do grupo representa o número de progênies de um touro, então, como o número de filhos de cada touro envolvido na análise é variável e a variação dos desvios-padrão amostrais das médias das progênies dos touros depende do número de indivíduos nestas progênies, a variação nos desvios-padrão é tão maior quanto menor a progênie do touro. Por outro lado, a mediana do desvio-padrão em grupos menores é menor que em grupos maiores. Aplicando-se estes resultados aos dados de grupo de progênies e confrontando-se com os resultados de funções da média aritmética e média harmônica (Muniz et al., 2001), verifica-se que a maior parte dos touros com poucos filhos iria beneficiar-se no processo de avaliação genética quando DIAS fosse a variável utilizada. Por outro lado, uma parcela importante dos touros com poucos filhos seria penalizada por apresentar, ao acaso, variação amostral bem maior que a variação média dos grupos. Por exemplo, pode-se dizer que cerca de 10% dos touros com dois filhos apresentarão desvios-padrão do GMD de suas progênies superiores a 99% daquelas progênies com oito elementos. O mesmo quadro pode ser observado nos touros com quatro e 16 filhos, com oito e 32 e com 16 e 64 filhos. Dessa forma, para os animais com menos filhos, a utilização de DIAS levará à penalização de uma parte e beneficiará outra, dependendo do desvio-padrão do GMD.
Considerando-se apenas o aspecto da relação entre o desvio-padrão do GMD e a média de DIAS, o uso de DIAS em substituição a GMD teria como conseqüência a inclusão de mais um fator de imprecisão na determinação dos valores genéticos dos animais. Assim, haveria redução da acurácia e, conseqüentemente, menor resposta à seleção em longo prazo.
Utilizando-se apenas os grupos de 64 animais, foi realizado um estudo para verificar os efeitos do desvio-padrão de GMD4 e do mínimo de GMD4 sobre a média de DIAS4. De acordo com a regressão do desvio-padrão de GMD4, na média de DIAS4, os efeitos linear e quadrático foram significativos e o R2 da equação mostrou que pouco menos de 9,18% da variação na média de DIAS4 foi explicada pelo desvio-padrão de GMD4 no grupo. Para a regressão e a distribuição da média de DIAS4, em função do valor mínimo de GMD4 observado no grupo, os efeitos também foram significativos e o R2 da equação foi de 23,82%, indicando que a média de DIAS4 foi muito mais dependente do valor mínimo observado na média de GMD4 que do desvio-padrão de GMD4. Quando os efeitos lineares do mínimo e do desvio-padrão de GMD4 foram incluídos na mesma regressão da média de DIAS4, verificou-se que, embora o efeito do desvio-padrão continue significativo, o aumento do R2 atribuído à inclusão do desvio-padrão foi menor que 0,001, reafirmando-se que as mudanças na média de DIAS4 foram muito mais conseqüência das variações no valor do mínimo de GMD4 que no desvio-padrão de GMD4.
Conclusões
Pontos de truncamento arbitrários, considerando-se os limites fisiológicos para GMD em animais com desenvolvimento normal, não devem afetar significativamente a distribuição das características estudadas.
A utilização de DIAS como critério de seleção pode diminuir a acurácia da avaliação, em razão da dependência entre a média e o desvio-padrão e da variação observada nos desvios-padrão de DIAS em função do tamanho do grupo. Portanto, para a substituição de GMD por DIAS, é necessário o uso de um método de análise robusto o suficiente para a eliminação da heterogeneidade de variância.
Agradecimento
Ao CNPq, à Capes e à FAPESP, pela concessão das bolsas de pesquisa e pelo financiamento do projeto.
Literatura Citada
Recebido: 26/04/05
Aprovado: 08/12/05
Correspondências devem ser enviadas para: mirellasirol@ig.com.br
- CARTWRIGHT, T.C. Selection criteria for beef cattle for the future. Journal of Animal Science, v.30, p.706-711, 1970.
- CARVALHEIRO, R; MUNIZ, C.A.S.D.; QUEIROZ, S.A. et al. Estudo da simulação das relações entre a média aritmética, a média harmônica e o desvio-padrão. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 38., 2001, Piracicaba. Anais Piracicaba: Sociedade Brasileira de Zootecnia, 2001. p.626-627.
- DE VEER, J.C.; Van VLECK, L.D. Genetic parameters for first lactation yields at three levels of herd production. Journal of Dairy Science, v.70, p.1434-1441, 1987.
- FRIES, L.A. Precocidade, precocidade e precocidade. In: REVISÃO DE CRITÉRIOS DE JULGAMRNTO E SELEÇÃO EM GADO DE CORTE, 1996, Uberaba. Anais... Uberaba: Associação Brasileira de Criadores de Zebu, 1996. p.15-21.
- FRIES, L.A.; ALBUQUERQUE, L.G. Avaliação genética de duas alternativas para medir precocidade de crescimento. In: SIMPÓSIO NACIONAL DE MELHORAMENTO ANIMAL, 1., 1996, Ribeirão Preto. Anais... Ribeirão Preto: Sociedade Brasileira de Melhoramento Animal, 1996. p.237-238.
- GARNERO, A.; LOBO, R.B.; BEZERRA, L.A.F. et al. Comparação entre alguns critérios de seleção para crescimento da raça Nelore. Revista Brasileira de Zootecnia, v.30, n.3, p.714-718, 2001.
- GARRICK, D.J.; Van VLECK, L.D. Aspects of selection for performance in several environments with heterogeneous variance. Journal of Animal Science, v.65, p.409-418, 1987.
- HILL, W.G. On selection among group with heterogeneous variance. Animal Production, v.36, p.59-68, 1983.
- MOOD, A.M.; GRAYBILL, F.A.; BOES, D.C. Introduction to the theory of statistics 3.ed. New York: McGraw-Hill, 1974. 512p.
- MUNIZ, C.A.S.D.; CARVALHEIRO, R.; QUEIROZ, S.A. et al. Critérios de seleção baseado em médias aritméticas e médias harmônicas. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 38., 2001, Piracicaba. Anais... Piracicaba: Sociedade Brasileira de Zootecnia, 2001. p.629-631.
- OLIVEIRA, H.N.; LOBO, R.B.; PEREIRA, C.S. et al. Relationship among growth curve paramaters, weights and reproductive traits in Guzera beef cows. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 5., 1994, Guelph. Proceedings... Guelph: 1994. p.182-192.
- ORTIZ PEÑA, C.D.; CARVALHEIRO, R.;QUEIROZ, S.A. et al. Comparison of selection criteria for pre-weaning growth traits of Nelore cattle. Livestock Production Science, v.86, p.163-167, 2004.
- ORTIZ PEÑA, C.D.; QUEIROZ, S.A.; FRIES, L.A. Análise comparativa de critérios de seleção para precocidade de crescimento pós-desmama em bovinos nelore no Paraguai. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 37., 2000, Viçosa, MG. Anais... Viçosa, MG: Sociedade Brasileira de Zootecnia/Gnosis, [2000] 18par. CD-ROM. Melhoramento Animal. Oral. 0043.
- STATISTICAL ANALYSES SYSTEM - SAS. User's guide: statistics. Versão 6.03. Cary: 1990. 584p.
- SORENSEN D.A.; GIANOLA, D.; KORSGAARD, I.R. Bayesian mixed-effects model analysis of a censored normal distribution with animal breeding applications. Acta Agricturae Scandinavica, v.48, p.222-229,1998.
- VISON, W.E. Potencial bias in genetic evaluation from differences in variation within herds. Journal of Dairy Science, v.70, p.2450-2455, 1987.
- WECHSLER, F.C. Fatoriais fixos desbalanceados: uma análise mal compreendida. Pesquisa Agropecuária Brasileira, v.3, n.33, p.231-262, 1998.
Datas de Publicação
-
Publicação nesta coleção
01 Set 2006 -
Data do Fascículo
Jun 2006
Histórico
-
Aceito
08 Dez 2005 -
Recebido
26 Abr 2005