Resumos
Foram utilizados 21.762 registros de peso do nascimento aos 550 dias de idade de 4.221 animais para estimativa das funções de covariância empregando modelos de regressão aleatória. Os modelos incluíram, como aleatórios, os efeitos genéticos aditivo direto e materno, de ambiente permanente de animal e de ambiente permanente materno e, como fixos, os efeitos de grupo contemporâneo, a idade da vaca ao parto (linear e quadrático) e o polinômio ortogonal de Legendre da idade do animal (regressão cúbica), como covariáveis. As variâncias residuais foram modeladas por uma função de variâncias com ordens de 2 a 6. Análises com polinômios ortogonais de diversas ordens foram realizadas para os efeitos genético aditivo direto, genético aditivo materno, de ambiente permanente de animal e de ambiente permanente materno. Os modelos foram comparados pelos critérios de informação Bayesiano de Schwarz (BIC) e Akaike (AIC). O melhor modelo indicado por todos os critérios foi o que considerou o efeito genético aditivo direto ajustado por um polinômio cúbico, o efeito genético materno ajustado por um polinômio quadrático, o efeito de ambiente permanente de animal ajustado por polinômio quártico e o efeito de ambiente permanente materno ajustado por polinômio linear. As estimativas de herdabilidade para o efeito direto foram maiores no início e no final do período estudado, com valores de 0,28 ao nascimento, 0,21 aos 240 dias e 0,24 aos 550 dias de idade. As estimativas de herdabilidade materna foram maiores aos 160 dias de idade (0,10) que nas demais fases do crescimento. As correlações genéticas variaram de moderadas a altas, diminuindo conforme o aumento da distância entre as idades. Maior eficiência na seleção para peso pode ser obtida considerando os pesos pós-desmama, período em que as estimativas de variância genética e herdabilidade foram superiores.
curva de crescimento; dados longitudinais; funções de covariância; gado de corte
Data provided by the Brazilian Zebu Breeders Association (ABCZ), consisting of 21,762 records from 4,221 animals of Tabapuã cattle, weighted from birth to 550 days of age, were used to estimate covariance functions by random regression models using Legendre polynomials of order two to five. Models included the direct and maternal genetic, animal and maternal permanent environmental random effects and compared by Schwarz´s Bayesian information criteria (BIC) and Akaike´s information criteria (AIC). Both criterions suggested the model including direct genetic, maternal genetic, animal permanent and maternal permanent environmental effects respectively adjusted by cubic, quadratic, fourth order and linear polynomials, and residual variances adjusted by fifth order variance function as the best one to describe the covariance structure of the used database. Direct heritability estimates were higher at the beginning and at the end of the growth trajectory. Maternal heritability estimates increased from birth to 160 days of age and decreased thereafter. In general, genetic correlation estimates decreased as age between weights increased. Efficiency of selection may be improved by using weights of the post weaning period because of their higher genetic variance and heritability estimates.
beef cattle; covariance function; growth curve; longitudinal data
MELHORAMENTO, GENÉTICA E REPRODUÇÃO
Estimação de parâmetros genéticos para peso do nascimento aos 550 dias de idade para animais da raça Tabapuã utilizando-se modelos de regressão aleatória1 1 Parte da tese de Doutorado do primeiro autor em Zootecnia na área de Produção Animal, UNESP/Jaboticabal, financiada pela CAPES.
Genetic parameters for weights from birth to 550 days of age of Tabapuã cattle using random regression models
Laila Talarico DiasI; Lucia Galvão de AlbuquerqueII; Humberto TonhatiII; Rodrigo de Almeida TeixeiraIII
IUniversidade Estadual de Londrina
IIDepartamento de Zootecnia da UNESP/Jaboticabal
IIIUniversidade de Brasília
RESUMO
Foram utilizados 21.762 registros de peso do nascimento aos 550 dias de idade de 4.221 animais para estimativa das funções de covariância empregando modelos de regressão aleatória. Os modelos incluíram, como aleatórios, os efeitos genéticos aditivo direto e materno, de ambiente permanente de animal e de ambiente permanente materno e, como fixos, os efeitos de grupo contemporâneo, a idade da vaca ao parto (linear e quadrático) e o polinômio ortogonal de Legendre da idade do animal (regressão cúbica), como covariáveis. As variâncias residuais foram modeladas por uma função de variâncias com ordens de 2 a 6. Análises com polinômios ortogonais de diversas ordens foram realizadas para os efeitos genético aditivo direto, genético aditivo materno, de ambiente permanente de animal e de ambiente permanente materno. Os modelos foram comparados pelos critérios de informação Bayesiano de Schwarz (BIC) e Akaike (AIC). O melhor modelo indicado por todos os critérios foi o que considerou o efeito genético aditivo direto ajustado por um polinômio cúbico, o efeito genético materno ajustado por um polinômio quadrático, o efeito de ambiente permanente de animal ajustado por polinômio quártico e o efeito de ambiente permanente materno ajustado por polinômio linear. As estimativas de herdabilidade para o efeito direto foram maiores no início e no final do período estudado, com valores de 0,28 ao nascimento, 0,21 aos 240 dias e 0,24 aos 550 dias de idade. As estimativas de herdabilidade materna foram maiores aos 160 dias de idade (0,10) que nas demais fases do crescimento. As correlações genéticas variaram de moderadas a altas, diminuindo conforme o aumento da distância entre as idades. Maior eficiência na seleção para peso pode ser obtida considerando os pesos pós-desmama, período em que as estimativas de variância genética e herdabilidade foram superiores.
Palavras-chave: curva de crescimento, dados longitudinais, funções de covariância, gado de corte
ABSTRACT
Data provided by the Brazilian Zebu Breeders Association (ABCZ), consisting of 21,762 records from 4,221 animals of Tabapuã cattle, weighted from birth to 550 days of age, were used to estimate covariance functions by random regression models using Legendre polynomials of order two to five. Models included the direct and maternal genetic, animal and maternal permanent environmental random effects and compared by Schwarz´s Bayesian information criteria (BIC) and Akaike´s information criteria (AIC). Both criterions suggested the model including direct genetic, maternal genetic, animal permanent and maternal permanent environmental effects respectively adjusted by cubic, quadratic, fourth order and linear polynomials, and residual variances adjusted by fifth order variance function as the best one to describe the covariance structure of the used database. Direct heritability estimates were higher at the beginning and at the end of the growth trajectory. Maternal heritability estimates increased from birth to 160 days of age and decreased thereafter. In general, genetic correlation estimates decreased as age between weights increased. Efficiency of selection may be improved by using weights of the post weaning period because of their higher genetic variance and heritability estimates.
Key Words: beef cattle, covariance function, growth curve, longitudinal data
Introdução
Entre as características de interesse para o melhoramento animal, algumas podem ser mensuradas repetidamente ao longo da vida do indivíduo como a produção mensal de leite e as características de crescimento como peso e altura, entre outras. Estas características são denominadas características repetidas ou longitudinais.
Uma das formas de se analisar essas características é tratar cada medida como se fosse uma característica diferente em modelos multicaracterísticas que consideram covariâncias não estruturadas. Entretanto, medidas registradas continuamente têm covariâncias estruturadas e devem ter tratamento estatístico diferenciado (Van der Werf & Schaeffer, 1997).
As funções de covariância (FC) são consideradas alternativa para se trabalhar com dados longitudinais por permitirem a descrição da mudança gradual das covariâncias em função do tempo e a predição de variâncias e covariâncias para pontos ao longo da curva de crescimento, ainda que haja pouca informação entre os pontos (Kirkpatrick et al., 1990, 1994; Meyer, 1998a, 1999a), e podem ser obtidas por matrizes de (co)variância entre os coeficientes de regressão estimados por meio de modelos de regressão aleatória (Meyer, 1998a).
Os modelos de regressão aleatória, denominados modelos de "dimensão infinita", possibilitam trabalhar com medidas tomadas inúmeras vezes durante a vida de um indivíduo e estão mais fortemente correlacionadas quanto mais próximas forem tomadas. Esses modelos são considerados casos especiais de funções de covariância e permitem estimar diretamente os coeficientes das funções de covariância pelo método da máxima verossimilhança restrita (Meyer & Hill, 1997; Meyer, 1998b).
No Brasil, alguns trabalhos utilizando modelos de regressão aleatória têm sido realizados com a finalidade de estudar características de crescimento de bovinos de corte. Para a raça Tabapuã, Sakaguti et al. (2003) aplicaram modelos de regressão aleatória para estimar funções de covariância para pesos tomados entre 365 e 650 dias de idade, entretanto, em virtude das limitações computacionais, ajustaram modelos linear e quadrático apenas para os efeitos de animal, não considerando os efeitos maternos. Os autores concluíram que os modelos de regressão aleatória permitiram estimar componentes de variância em qualquer idade, além de fornecerem parâmetros adicionais úteis às avaliações genéticas de bovinos de corte. Para animais da raça Nelore, Albuquerque & Meyer (2001) estimaram funções de covariância utilizando esses modelos para registros de pesos do nascimento aos 630 dias de idade e concluíram que as regressões aleatórias descreveram adequadamente as mudanças das covariâncias com a idade. Entretanto, Nobre et al. (2003) analisaram a curva de crescimento de bovinos Nelore do nascimento aos 683 dias de idade empregando modelos multicaracterísticas e regressão aleatória e observaram que os modelos de regressão aleatória foram mais sensíveis a problemas amostrais que os multicaracterísticas.
Os objetivos neste trabalho foram estimar funções de covariância genética direta e materna utilizando modelos de regressão aleatória a fim de verificar se essa metodologia descreve adequadamente as mudanças nas (co)variâncias dos pesos do nascimento aos 550 dias de idade e estimar parâmetros genéticos dos pesos nesse período, em animais da raça Tabapuã.
Material e Métodos
Foram utilizadas 21.762 informações de pesagens do arquivo zootécnico da Associação Brasileira dos Criadores de Zebu (ABCZ), de 4.221 animais da raça Tabapuã nascidos entre 1975 e 2000, mensurados ao nascimento e, em média, a cada 90 dias até 550 dias de idade.
Para as análises, foram considerados animais com pai e mãe conhecidos (peso ao nascer maior que 15 kg ou menor que 50 kg), nascidos de parto simples, pertencentes a grupos de contemporâneos com mais de oito animais, filhos de vacas com mais de dois anos de idade e intervalos de partos superiores a nove meses, criados em pastagens, cuja condição de criação era mamando sem ordenha ou desmamado e com informações de, no mínimo, cinco pesagens. No arquivo de pedigree, foram incluídas até três gerações de ancestrais.
O grupo de contemporâneos (GC) foi definido pelas variáveis proprietário, rebanho do proprietário, criador, rebanho do criador, sexo, condição de criação (mamando ou desmamado), ano e mês de nascimento e ano e mês da pesagem, como demonstrado na Tabela 1.
Para aumentar o número de animais em cada idade, foram criadas classes de idade, sendo a primeira para o nascimento (clid=0), as seguintes agrupadas a cada dois dias de idade até 240 dias (época da desmama) e, após esta idade, as classes de idade foram formadas a cada cinco dias até os 550 dias de idade (em torno de 18 meses de idade), formando 185 classes de idade.
O modelo utilizado neste trabalho considerou como fixos os efeitos de grupo de contemporâneos, os efeitos linear e quadrático de idade do bezerro à pesagem e idade da vaca como covariáveis e, como aleatórios, os efeitos genéticos aditivos direto e materno, o efeito de ambiente permanente materno e o efeito aleatório de ambiente permanente de animal (entre medidas repetidas do animal). Além disso, um polinômio ortogonal de Legendre, de ordem cúbica, sobre a idade à pesagem foi considerado no modelo como efeito fixo, para modelar a curva média da população.
O modelo geral pode ser representado por:
em que: yij = jésimo registro referente ao iésimo animal; Fij = conjunto de efeitos fixos; bm = coeficientes de regressão fixos para modelar a média da população; aij* = idade padronizada (-1 a +1) à pesagem; fm = mésimo polinômio de Legendre; aim, gim, dim, rim = coeficientes de regressão aleatórios para os efeitos genético direto, materno, de ambiente permanente de animal e materno; kA, kM, kC, kQ = ordem de ajuste dos polinômios correspondentes; e eij = efeito de ambiente temporário.
Em notação matricial, o modelo utilizado pode ser representado por:
em que: y = vetor de observações; b = vetor de efeitos fixos (incluindo Fij e bm); a = vetor aleatório dos coeficientes de regressão genéticos aditivos diretos; g = vetor aleatório dos coeficientes de regressão genéticos maternos; d = vetor aleatório dos coeficientes de regressão de ambiente permanente de animal; r = vetor aleatório dos coeficientes de regressão de ambiente permanente materno; X, Z1, Z2, W1, W2 = matrizes de incidência correspondentes; KA, KM, KC, KQ = matrizes dos coeficientes das funções de covariância para os efeitos genético aditivo direto, materno, de ambiente permanente de animal e de ambiente permanente materno, respectivamente; A = matriz de parentesco; I = matriz identidade; Na, Nm = número de animais com dados e número de mães, respectivamente; R = matriz diagonal contendo as variâncias residuais; e e = efeito de ambiente temporário.
As funções de covariância foram estimadas por máxima verossimilhança restrita (REML) utilizando-se o módulo DxMRR do pacote computacional DFREML (Meyer, 1998c).
O resíduo foi modelado como homogêneo ou considerando-se heterogeneidade de variâncias. Para modelar a heterogeneidade de variâncias residuais, foram utilizadas funções de variância (linear, quadrática, cúbica, quártica ou quíntica) assumindo-se um modelo log-linear, como descrito por Meyer (2001), representadas por:
em que: sj2 é a variância na jésima idade; s02, a variância do erro na média de idade; br e v, o coeficiente de regressão e o número de parâmetros da função de variância residual, respectivamente.
No total, foram testados dez modelos com ordens dos polinômios de cinco a dois. A ordem do polinômio para cada efeito aleatório foi diminuída de acordo com as estimativas de variância dos coeficientes de regressão aleatória e os autovalores relacionados.
As variâncias residuais foram consideradas homogêneas ou heterogêneas. Neste caso, foram utilizadas funções de variância residual linear (FV1), quadrática (FV2), cúbica (FV3), quártica (FV4) e quíntica (FV5), mantendo-se a ordem das funções de covariância para os efeitos genético direto (kA), de ambiente permanente de animal (kC) e de ambiente permanente materno (kQ) iguais a 4 (função de covariância cúbica).
A comparação entre os modelos foi realizada por meio dos critérios de informação Akaike (AIC) e Bayesiano de Schwarz (BIC), que permitem a comparação de modelos não-aninhados e penalizam modelos mais parametrizados, sendo o BIC o mais rigoroso, ou seja, o critério que favorece modelos mais parcimoniosos (Wolfinger, 1993; Nunez-Antón & Zimmerman, 2000):
Os critérios de informação foram determinados por:
em que: p = número de parâmetros do modelo; N = total de observações; e r = posto da matriz X (matriz de incidência para os efeitos fixos). Valores menores de AIC e BIC indicam melhor ajuste do modelo.
Resultados e Discussão
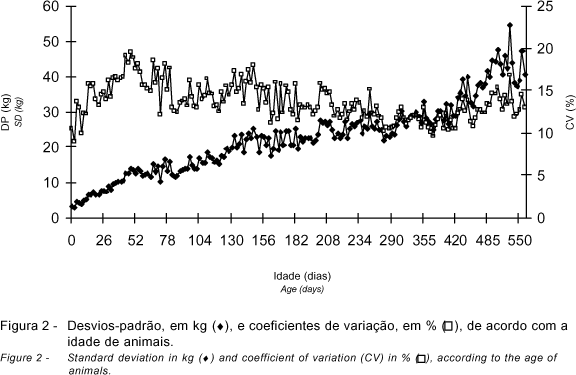
O número de registros, as médias de peso, os desvios-padrão e os coeficientes de variação relativos a cada idade são apresentados nas Figuras 1 e 2. Todos os animais foram pesados ao nascimento (4.221), mas, para não causar problemas de escala, a média de peso e o número de registros para esta idade não foram apresentados. Observou-se maior concentração de registros entre a desmama (240 dias de idade) e 340 dias de idade. As médias de peso aumentaram linearmente do nascimento aos 550 dias de idade, variando de 31,40 a 324,23 kg, respectivamente (Figura 1). Assim como as médias de peso, os desvios-padrão também apresentaram tendência de aumento com a idade. Os coeficientes de variação aumentaram do nascimento até cerca de 50 dias e, após esta idade, houve pequena diminuição do coeficiente de variação (Figura 2).
Os critérios de informação AIC e BIC indicaram a necessidade de se considerar a heterogeneidade de variâncias, sendo indicado como mais adequado o modelo com função de variância de ordem quíntica (Tabela 2).
A inclusão do efeito genético materno no modelo e o aumento da ordem da função de variância residual de cúbica para quíntica resultaram em aumento significativo do Log L e diminuição do AIC e BIC. Todos os critérios indicaram como mais adequado o modelo com ordens 4, 3, 5, 2 para os efeitos genéticos direto e materno, de ambiente permanente de animal e de ambiente permanente materno, respectivamente (Tabela 2). Entre os modelos que incluíram o efeito genético materno, o modelo com ordens 4, 3, 5, 2 foi o mais parcimonioso. Em geral, espera-se que modelos mais parametrizados tenham maiores valores de Log L, entretanto, isso nem sempre ocorreu, provavelmente por problemas de convergência.
Para todos os efeitos aleatórios estudados, o intercepto sempre apresentou a maior estimativa de variância associada. As correlações entre o intercepto e o coeficiente de regressão linear foram altas e positivas para todos os efeitos e variaram de 0,99 (efeito de ambiente permanente materno) a 0,76 (efeito de ambiente permanente de animal) (Tabela 3). Meyer (2002) encontrou resultados semelhantes para dados de peso do nascimento aos 820 dias de idade para animais da raça Polled Hereford.
As correlações entre o intercepto e o coeficiente de regressão quadrático foram baixa e positiva para o efeito direto (0,22), alta e negativa para o efeito materno (-0,81) e, praticamente, zero para o efeito de ambiente permanente de animal (-0,04) (Tabela 3). Estes resultados foram semelhantes aos descritos por Albuquerque & Meyer (2001) para dados de pesos de animais Nelore do nascimento aos 630 dias de idade.
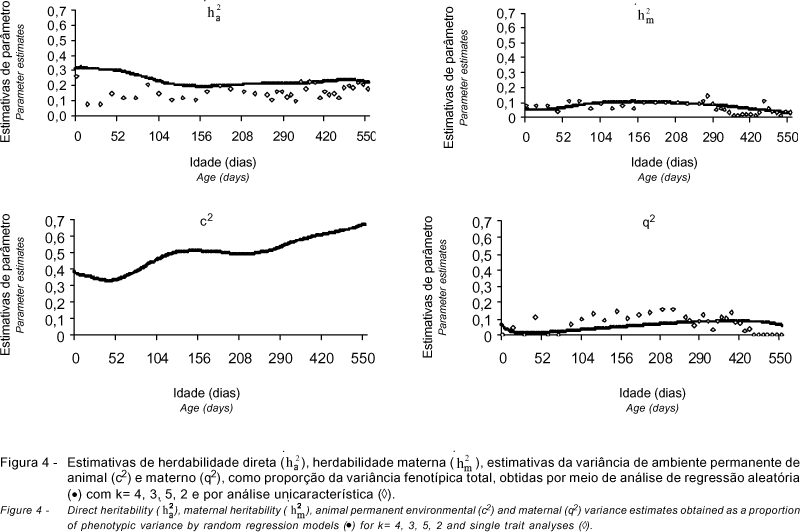
As estimativas dos componentes de variância encontradas para o modelo indicado pelos critérios de informação BIC e AIC (k = 4, 3, 5, 2) e as obtidas por meio de análises unicaracterísticas (Dias et al., 2005) são apresentadas nas Figuras 3 e 4.
De modo geral, as estimativas obtidas por regressão aleatória e por análises unicaracterísticas foram semelhantes. As variâncias residuais aumentaram gradativamente com a idade até 230 dias, aproximadamente. Após este período, verificou-se diminuição das estimativas até 500 dias, voltando a aumentar com a idade.
As estimativas de variância genética aditiva direta obtidas por análises de regressão aleatória (RA) e unicaracterística (UNI) apresentaram a mesma tendência em todo o período estudado. Os valores aumentaram com a idade de 2,58 e 2,23 kg2 ao nascimento a 224,41 e 166,13 kg2 aos 550 dias de idade para RA e UNI, respectivamente (Figura 3). Esta mesma tendência foi descrita na literatura para animais da raça Nelore (Albuquerque & Meyer, 2001; Cyrillo, 2003; Nobre et al., 2003).
Para o efeito de ambiente permanente de animal, observou-se aumento nas estimativas de variância em função da idade, sendo mais acentuado após 420 dias de idade. Tendências semelhantes foram relatadas por Albuquerque & Meyer, (2001) e Cyrillo (2003) para animais da raça Nelore. O rápido aumento observado na variância de ambiente permanente de animal após 420 dias de idade refletiu nas estimativas de variância fenotípica (Figura 3). A partição do efeito direto em genético e de ambiente permanente de animal nas análises de regressão aleatória, em geral, exige ordens maiores dos polinômios para o efeito de ambiente permanente de animal, o que pode resultar em problemas de modelagem. Diversos trabalhos na literatura têm mostrado que, para modelagem das mudanças nas variâncias de ambiente permanente de animal com a idade, são necessários polinômios de altas ordens, levando ao aumento do número de parâmetros do modelo e dos requerimentos computacionais (Brotherstone et al., 2000; Meyer, 2001).
As herdabilidades para o efeito aditivo direto estimadas por regressão aleatória e as análises unicaracterística foram semelhantes, em tendência, durante todo o período estudado, mas as obtidas por regressão aleatória foram, em geral, superiores. As estimativas decresceram do nascimento (0,28) até próximo à desmama (0,21), por volta de 240 dias de idade e, após esta idade, apresentaram tendência de aumento, atingindo 0,24 aos 550 dias de idade (Figura 4). Meyer (1999b; 2001) descreveu diminuição das estimativas de herdabilidade direta após o nascimento e aumento das estimativas após o período da desmama para pesos de gado de corte na Austrália. Os resultados deste trabalho também foram semelhantes aos observados por Albuquerque & Meyer (2001) para peso do nascimento aos 630 dias de idade de animais da raça Nelore. Entretanto, as estimativas de herdabilidade para o efeito direto obtidas neste trabalho foram inferiores às relatadas para bovinos da raça Tabapuã por Sakaguti et al. (2003), que obtiveram 0,34 para peso aos 365 e 536 dias de idade, entretanto, esses autores não consideraram os efeitos maternos no modelo de análise.
Também utilizando modelos de regressão aleatória, Cyrillo (2003) encontrou baixos valores de herdabilidade para peso ao nascimento (0,09) e observou diminuição nas estimativas de herdabilidade direta dos 35 dias (0,44) aos 210 dias de idade (0,22), voltando a aumentar até 378 dias de idade (0,40), para animais da raça Nelore. Nobre et al. (2003) estimaram menores herdabilidades para o efeito direto que as encontradas na literatura variando de 0,14 (nascimento) a 0,27 (683 dias de idade) para bovinos Nelore.
Os resultados obtidos para o efeito genético direto indicam que a seleção para peso pode ser mais efetiva se realizada após a desmama, período em que as estimativas da variância genética aditiva e da herdabilidade foram maiores possibilitando a melhor identificação de animais geneticamente superiores. Entretanto, quanto mais tarde a seleção for realizada, maior a correlação com o peso adulto (Barbosa, 1991; Oliveira, 1995), porém animais com pesos adultos maiores geralmente não são desejados.
As estimativas de variância de ambiente permanente de animal como proporção da variância fenotípica total, obtidas por regressão aleatória, diminuíram suavemente do nascimento (0,38) até os 50 dias de idade (0,33), aproximadamente, e, após esta idade, apresentaram tendência de aumento com a idade (Figura 4). Meyer (2001) verificou tendência de aumento com a idade nas estimativas de variância de ambiente permanente de animal, como proporção da variância fenotípica total, para animais da raça Polled Hereford. No mesmo trabalho, para animais da raça Wokalup, esse autor observou comportamento diferente das estimativas, que aumentaram rapidamente do nascimento à desmama, tendendo a diminuir com a idade. Os resultados obtidos neste estudo diferem dos relatados por Albuquerque & Meyer (2001), que observaram rápido aumento da variância de ambiente permanente de animal do nascimento aos 50 dias de idade e leve tendência de diminuição nas demais idades.
As estimativas de variância genética materna obtidas por regressão aleatória e análises unicaracterísticas foram similares durante praticamente todo o período. As estimativas aumentaram do nascimento (0,48 kg2) até próximo à época da desmama (29,43 kg2), diminuindo após este período e atingindo 24,48 kg2 aos 550 dias de idade (Figura 3). Comportamento semelhante foi descrito na literatura por Albuquerque & Meyer (2001) e Nobre et al. (2003) para bovinos da raça Nelore.
As estimativas da variância de ambiente permanente materno aumentaram progressivamente do nascimento (0,51 kg2) até 550 dias de idade (61,75 kg2), sendo que, no final do período estudado, as estimativas obtidas por regressão aleatória foram superiores às das análises unicaracterísticas (Figura 3).
As herdabilidades maternas estimadas pelos dois métodos de análise também foram semelhantes em todo o período (Figura 4). Pode-se notar aumento das estimativas do nascimento (0,05 e 0,08) até em torno de 160 dias de idade (0,10 e 0,11), decrescendo nas idades posteriores (0,08 e 0,09 aos 240 dias e 0,02 e 0,03 aos 550 dias de idade) nas análises de regressão aleatória e nas unicaracterísticas, respectivamente. Os maiores valores coincidiram com o período no qual as herdabilidades do efeito direto foram inferiores (Figura 4), concordando com os resultados relatados por Meyer (1999b). No Brasil, tendência semelhante foi obtida por Albuquerque & Meyer (2001) e Nobre et al. (2003) para as estimativas de herdabilidade materna do nascimento aos 630 e 683 dias de idade para animais da raça Nelore, respectivamente. Em uma revisão para animais Zebu, Mercadante et al. (1995) descreveram médias de estimativas de herdabilidade para efeito materno superiores às deste trabalho para peso ao nascer, à desmama, aos 365 e aos 550 dias de idade de 0,12; 0,18; 0,16 e 0,05, respectivamente.
Os resultados observados neste estudo comprovaram que os efeitos maternos começam a diminuir antes do período da desmama. Tendência semelhante foi relatada por Albuquerque & Meyer (2001) para animais da raça Nelore. Maior resposta à seleção para habilidade materna pode ser esperada se a seleção for realizada com base nos pesos do período pré-desmama, pois, neste período, as estimativas de variância genética materna e herdabilidade são maiores. Vale ressaltar que a seleção para habilidade materna deve resultar em fêmeas com maior potencial genético para produção leite, pois esta característica é o principal componente dos efeitos maternos (Hohenboken, 1985).
As estimativas de variância de ambiente permanente materno, como proporção da variância fenotípica total, obtidas por regressão aleatória e por análise unicaracterística, apresentaram mesma tendência durante todo o período estudado, entretanto, as estimativas obtidas por análise unicaracterística foram superiores às estimadas por meio de regressão aleatória (Figura 4). Segundo Meyer (1992), a separação dos efeitos maternos em genético e de ambiente permanente não é simples, principalmente com dados não-experimentais, existindo a possibilidade de se considerar apenas um dos efeitos maternos nos procedimentos de análise. As estimativas obtidas por regressão aleatória diminuíram no início do período, de 0,06 ao nascimento para 0,01 aos 70 dias de idade e, após este período, aumentaram até por volta de 450 dias de idade, diminuindo nas idades posteriores. Albuquerque & Meyer (2001), para animais da raça Nelore, relataram que as estimativas de ambiente permanente materno praticamente não mudaram com a idade e que as obtidas por análise unicaracterística foram maiores que as obtidas por regressão aleatória.
As estimativas de correlação fenotípica, genética direta, genética materna, de ambiente permanente de animal e de ambiente permanente materno entre os pesos nas idades estudadas para o modelo com k = 4, 3, 5, 2 são apresentadas na Figura 5.
De modo geral, as correlações fenotípicas diminuíram conforme as idades se distanciavam. As correlações entre peso ao nascimento e nas demais idades foram baixas (0,27; 0,26 e 0,13 entre o peso ao nascer e aos 240 dias, aos 365 dias e aos 550 dias, respectivamente). As correlações estimadas entre os pesos nas idades-padrão (240, 365 e 550 dias de idade) foram maiores, chegando a 0,94 no período de 240 e 365 dias de idade, a 0,61 entre 240 e 550 dias de idade e a 0,74 entre 365 e 550 dias de idade. Resultados similares foram reportados por Albuquerque & Meyer (2001) e Cyrillo (2003) para animais da raça Nelore.
As estimativas de correlação genética aditiva direta entre o peso ao nascimento e às demais idades foram, em geral, moderadas (0,58; 0,50 e 0,32 entre o peso ao nascer e aos 240, 365 e 550 dias de idade, respectivamente). Entre os pesos aos 240 e 365 dias, aos 240 e 550 dias e aos 365 e 550 dias, as estimativas foram altas 0,98; 0,78 e 0,88, respectivamente. Meyer (1994) e Robinson (1996) encontraram correlações moderadas entre o peso ao nascer e os pesos nas idades mais tardias, variando de 0,52 a 0,59 e 0,44 a 0,67, respectivamente. Os resultados deste trabalho estão de acordo com os obtidos no Brasil para animais da raça Nelore (Albuquerque & Meyer, 2001; Nobre et al., 2003). Em trabalho de revisão, Mercadante et al. (1995) relataram correlação genética moderada para animais Zebu entre o peso ao nascer e aos 240, 365 e 550 dias de idade, de 0,63; 0,41; 0,40, respectivamente, e entre o peso aos 240 e 365 dias, 240 e 550 e 365 e 550 dias de idade, de 0,78; 0,71 e 0,77, respectivamente, resultados ligeiramente inferiores aos obtidos neste estudo.
As estimativas de correlação genética materna entre o peso ao nascer e as idades-padrão foram moderadas: 0,38, 0,44 e 0,56 entre o peso ao nascimento e aos 240, 365 e 550 dias de idade, respectivamente. Essas correlações foram maiores com o aumento da distância entre as idades, o que não era esperado. Entre o peso aos 240 dias e aos 365 e 550 dias, as estimativas foram altas 0,99 e 0,89, respectivamente, e, entre os pesos aos 365 e 550 dias de idade, a correlação foi de 0,94 (Figura 5). Estes resultados sugerem que os efeitos maternos nestas idades sejam controlados pelos mesmos genes. Eler et al. (1995) obtiveram baixas estimativas de correlações genéticas maternas entre o peso ao nascer e à desmama e entre o peso à desmama e ao sobreano (0,21 e 0,18, respectivamente) e estimativas mais altas 0,84 entre a desmama e um ano de idade, para animais da raça Nelore. Albuquerque & Meyer (2001) relataram baixos valores de correlação genética materna entre o peso ao nascimento e aos 240, 360 e 550 dias de idade (0,14; 0,05 e 0,05, respectivamente) e correlações próximas à unidade entre as demais idades. Nobre et al. (2003) estimaram baixas correlações genética materna entre o peso ao nascer e os pesos próximos aos 60 dias de idade (0,20). Entretanto, os autores obtiveram maiores estimativas de correlação (acima de 0,70) entre os pesos aos 243 e 601 dias de idade.
As correlações de ambiente permanente de animal foram baixas, principalmente entre o peso ao nascimento e às idades-padrão (240, 365 e 550 dias de idade), sendo 0,25; 0,26 e 0,09, respectivamente. Resultados semelhantes foram apresentados por Albuquerque & Meyer (2001), que estimaram baixa correlação de ambiente permanente de animal entre o peso ao nascer e o peso aos 630 dias de idade (0,10). Por outro lado, Cyrillo (2003) encontrou alta correlação de ambiente permanente de animal entre o peso ao nascer e o peso aos 378 dias de idade (0,99) para animais da raça Nelore. Quanto às idades-padrão, as estimativas foram altas, chegando a 0,92 entre 240 e 365 dias, e moderadas, entre 240 e 550 dias (0,48) e entre 365 e 550 dias de idade (0,66).
As correlações de ambiente permanente materno foram moderadas entre os pesos do início e do final do período estudado. As correlações estimadas entre o peso ao nascer e aos 240, 365 e 550 foram, respectivamente, de 0,32; 0,34 e 0,36. Após o período da desmama, observaram-se valores altos de correlação, próximos à unidade, entre as idades subseqüentes. As estimativas de correlação entre o peso ao nascer e as demais idades foram inferiores às encontradas por Albuquerque & Meyer (2001), que relataram altas correlações de ambiente permanente materno entre o peso ao nascimento e aos 240, 360 e 550 dias de idade, de 0,84; 0,85 e 0,95, respectivamente, para animais da raça Nelore. Os resultados deste trabalho também diferiram dos encontrados por Cyrillo (2003), que estimou correlação de ambiente permanente materno igual à unidade para todas as idades entre o nascimento e 378 dias de idade para peso de machos da raça Nelore.
A partição dos efeitos aleatórios, separando os efeitos genéticos e de ambiente em direto e materno, é essencial para modelar adequadamente as mudanças nas variâncias. A modelagem do resíduo e as ordens de ajuste dos polinômios podem interferir na estimação dos componentes de variância. Na literatura, já foi demonstrado que considerar estrutura heterogênea de variância residual é mais adequado para ajustar dados longitudinais. Assumir homogeneidade da variância residual significa que o ambiente temporário afeta igualmente todas as idades, o que nem sempre ocorre. Além disso, grande parte da variação residual pode contaminar a variância de ambiente permanente de animal (Huisman et al., 2002). Quanto às ordens de ajuste dos polinômios, alguns estudos comprovaram que considerar altas ordens de ajuste aumenta a flexibilidade da curva, mas também eleva os requerimentos computacionais, a dificuldade de convergência e os problemas amostrais (Kirkpatrick et al., 1994; Meyer, 1998a).
Neste trabalho, o modelo definido como mais adequado pelos dois critérios de informação foi o que considerou os efeitos genético aditivo direto, genético materno, de ambiente permanente de animal e de ambiente permanente materno ajustados por polinômios cúbico, quadrático, quártico e linear, respectivamente, sendo o resíduo modelado por função de variância de ordem quíntica.
Conclusões
Os modelos de regressão aleatória mostraram-se adequados para descrever as mudanças nas variâncias dos pesos do nascimento aos 550 dias de idade de animais da raça Tabapuã.
De acordo com as mudanças ocorridas nas (co)variâncias genéticas do peso com a idade, a seleção baseada nos pesos pré-desmama pode resultar em maior resposta para habilidade materna. No entanto, se realizada após a desmama, maior eficiência na seleção para peso poderá ser obtida no período em que as estimativas de variância genética aditiva e de herdabilidade foram maiores, permitindo melhor identificação dos animais geneticamente superiores para esta característica para animais da raça Tabapuã.
Literatura Citada
Recebido: 10/05/05
Aprovado: 12/05/06
Correspondências devem ser enviadas para: laila@uepg.br
- ALBUQUERQUE, L.G.; MEYER, K. Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle. Journal of Animal Science, v.79, n.11, p.2776-2789, 2001.
- BARBOSA, P.F. Análise genético-quantitativa de características de crescimento e reprodução em fêmeas da raça Canchim Ribeirão Preto: Universidade de São Paulo, 1991. 237p. Tese (Doutorado em Genética) - Universidade de São Paulo, 1991.
- BROTHERSTONE, S.; WHITE, I.M.S.; MEYER, K. Genetic modeling of daily milk yield using orthogonal polynomials and parametric curves. Journal of Animal Science, v.70, n.2, p.407-416, 2000.
- CYRILLO, J.N.S.G. Estimativas de funções de covariância para o crescimento de machos Nelore utilizando modelos de regressão aleatória Jaboticabal: Universidade Estadual Paulista, 2003. 72p. Tese (Doutorado em Produção Animal) - Universidade Estadual Paulista, 2003.
- DIAS, L.T.; ALBUQUERQUE, L.G.; TONHATI, H. et al. Estimação de parâmetros genéticos para peso em diferentes idades para animais da raça Tabapuã. Revista Brasileira de Zootecnia, v.34, n.6, p.1914-1919, 2005.
- ELER, J.P.; van VLECK, L.D.; FERRAZ, J.B.S. et al. Estimation of variances due to direct and maternal effects for growth traits in Nelore cattle. Journal of Animal Science, v.73, n.11, p.3253-3258, 1995.
- HOHENBOKEN, W.D. Genetic structure of population. 7. Maternal Effects. In: CHAPMAN, A.B. (Ed.) General and quantitative genetics World Animal Science, 1998. p.135-1465.
- HUISMAN, A.E.; VEERKAMP, R.F.; ARENDONK, J.A.M. Genetics parameters for various random regression models to describe the weight data of pigs. Journal of Animal Science, v.80, n.3, p.575-582, 2002.
- KIRKPATRICK, M.; LOFSVOLD, D.; BULMER, M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics, v.124, p.979-993, 1990.
- KIRKPATRICK, M.; HILL, W.G.; THOMPSON, R. Estimating the covariance structure of traits during growth and aging, illustrated with lactations in dairy cattle. Genetics Research, v.64, p.57-69, 1994.
- MERCADANTE, M.E.Z.; LÔBO, R.B.; REYES, A. de los. Parámetros genéticos para características de crecimiento en cebuínos de carne. Archivos Latinoamericanos Producción Animal, v.3, p.45-89, 1995.
- MEYER, K. Bias and sampling covariances of estimates of variances components due to maternal effects. Genetics Selection Evolution, v.24, p.487-509, 1992.
- MEYER, K. Estimates of direct and maternal correlations among growth traits in Australian beef cattle. Livestock Production Science, v.38, n.2, p.91-105, 1994.
- MEYER, K. Estimating covariances functions for longitudinal data using a random regression model. Genetics Selection Evolution, v.30, p.221-240, 1998a.
- MEYER, K. Modeling 'repeated' records: covariance functions and random regression models to analyze animal breeding data. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUTION, 25., 1998, Armidale. Proceedings Armidale: 1998b. p.517.
- MEYER, K. DxMrr - A program to estimate covariance functions for longitudinal data by restrict maximum likelihood. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUTION, 27., 1998, Armidale. Proceedings Armidale: 1998c. p.465.
- MEYER, K. Estimates of genetic and phenotypic covariance functions for postweaning growth and mature weight of beef cows. Journal of Animal Breeding and Genetics, v.116, p.181-203, 1999a.
- MEYER, K. Estimates of direct and maternal genetic covariance functions for early growth of Australian beef cattle. In: ANNUAL MEETING OF THE EUROPEAN ASSOCIATION FOR ANIMAL PRODUCTION, 1999, Zurich. Proceedings Zurich: 1999b. p.4. (Mimeo)
- MEYER, K. Estimates of direct and maternal covariance functions for growth of Australian beef calves from birth to weaning. Genetics Selection Evolution, v.33, p.1-28, 2001.
- MEYER, K. Estimates of covariance functions for growth of Australian beef cattle from a large set of data. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 7., 2002, Montpellier. Proccedings Montpellier: [s.n.], 2002. (CD-ROM)
- MEYER, K.; HILL, W.G. Estimation of genetic and phenotypic covariance functions for longitudinal 'repeated' records by restrict maximum likelihood. Livestock Production Science, v.47, n.3, p.85-200, 1997.
- NOBRE, P.R.C.; MISZTAL, I.; TSURUTA, S. et al. Analyses of growth curves of Nellore cattle by multiple-trait and random regression models. Journal of Animal Science, v.81, n.4, p.918-926, 2003.
- NUÑEZ-ANTON, V.; ZIMMERMAN, D.L. Modeling nonstationary longitudinal data. Biometrics, v. 56, 699-705, 2000.
- OLIVEIRA, H.N. Análise genético-quantitativa da curva de crescimento de fêmeas da raça Guzerá Ribeirão Preto: Universidade de São Paulo, 1995. 73p. Tese (Doutorado em Genética) - Universidade de São Paulo, 1995.
- ROBINSON, D.L. Estimation and interpretation of direct and maternal genetic parameters for weights of Australian Angus cattle. Livestock Production Science, v.45, n.1, p.1-11, 1996.
- SAKAGUTI, E.S.; SILVA, M.A.; QUAAS, R.L. et al. Avaliação do crescimento de bovinos jovens da raça Tabapuã, por meio de análises de funções de covariâncias. Revista Brasileira de Zootecnia, v.32, n.4, p.864-874, 2003.
- Van der WERF, J.H.J.; SCHAEFFER, L.R. Random regression in animal breeding Ontario: University of Guelph, 1997. 70p. (Course notes).
- WOLFINGER, R.D. Covariance structure in general mixed models. Communications in Statistics, v.22B, p.1079-1106, 1993.
Datas de Publicação
-
Publicação nesta coleção
13 Dez 2006 -
Data do Fascículo
Out 2006
Histórico
-
Aceito
12 Maio 2006 -
Recebido
10 Maio 2005