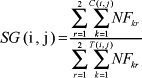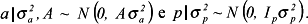Resumos
Foram estimados os componentes de variância para produção de leite e avaliado o impacto do aumento do número de animais na matriz de parentesco sobre os componentes de variância usando os métodos de Máxima Verossimilhança Restrita (REML) e Bayesiano via amostragem de Gibbs (GS). Utilizaram-se registros de produção de leite de vacas da raça Holandesa dos estados de Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul. Para cada estado, foram analisados dois conjuntos de dados: no primeiro, pedigree restrito, a matriz de parentesco foi constituída dos animais do respectivo estado; e, no segundo, pedigree completo, foram incluídos na matriz de parentesco os animais de todos os estados. Utilizou-se um modelo animal que incluiu os efeitos da estação de parto, rebanho-ano, grupo genético, ordem de parto e os efeitos genéticos aditivos e de ambiente permanente. As estimativas REML dos componentes de variância e de herdabilidade em todos os estados, obtidas com o pedigree restrito e com pedigree completo, foram similares. As estimativas REML de herdabilidade em Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul foram 0,19; 0,18; 0,26; 0,43 e 0,48, respectivamente. Houve fortes evidências de que as estimativas Bayesianas da variância genética com o PEDA foram superiores àquelas obtidas utilizando o PEDR. As herdabilidades e os desvios-padrão obtidos pelo método Bayesiano em Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul utilizando os pedigrees restrito e completo foram 0,21 ± 0,032 e 0,40 ± 0,025; 0,20 ± 0,017 e 0,27 ± 0,017; 0,28 ± 0,014 e 0,31 ± 0,014; 0,42 ± 0,041 e 0,56 ± 0,021; e 0,43 ± 0,039 e 0,55 ± 0,019, respectivamente. A variância genética aumentou significativamente em cada estado quando os animais dos outros estados foram incorporados na matriz de parentesco. Os menores desvios-padrão e intervalos de credibilidade dos componentes de variância foram estimados nos estados com maior número de lactações e sugerem que a precisão dos componentes de variância foi maior para esses estados.
amostragem de Gibbs; bovinos; convergência; herdabilidade; parentesco
Variance components (VC) for milk yield of Holstein cows were estimated and the effects of increasing of the number of animals in the numerator relationship matrix (NRM) were evaluated on VC estimates obtained by REML and Bayesian inference via Gibbs sampling (GS). Data were obtained from herds in the states of Minas Gerais, São Paulo, Paraná, Santa Catarina, and Rio Grande do Sul. Two data sets were created for each state. In the first set, the NRM included only the pedigree of the animals of the state under consideration (PEDR). In the second, the NRM included animals from the five states (PEDA). An animal model including the effects of herd-year, parity, season, genetic group, effects of additive genetic and permanent environment was used. The REML estimates of VC and heritability in each state obtained from PEDR and PEDA were similar. The heritability in Minas Gerais, São Paulo, Paraná, Santa Catarina, and Rio Grande do Sul was 0.19, 0.18, 0.26, 0.43, and 0.48, respectively. There was evidence that the posterior means of the genetic variance of PEDA analyses were significantly greater than PEDR. Heritability and standard deviations estimated by GS in Minas Gerais, São Paulo, Paraná, Santa Catarina, and Rio Grande do Sul, using PEDR (PEDA), were 0.21 ± 0.032 (0.40 ± 0.025), 0.20 ± 0.017 (0.27 ± 0.017), 0.28 ± 0.014 (0.31 ± 0.014), 0.42 ± 0.041 (0.56 ± 0.021) and 0.43 ± 0.039 (0.55 ± 0.019), respectively. The genetic variance of each state increased significantly when animals from the other states were incorporated in its NRM. The smallest standard deviations and VC credibility intervals were estimated in the states with more records, which suggested that the precision of the VC estimates was higher in those states.
convergence; dairy cattle; Gibbs sampling; heritability; relationship
MELHORAMENTO, GENÉTICA E REPRODUÇÃO
Alencariano José da Silva FalcãoI; Elias Nunes MartinsII; Claudio Napolis CostaIII; Josmar MazucheliIV
IIIDepartamento de Zootecnia da UEM, Maringá, PR
IIIEMBRAPA Gado de Leite
IVDepartamento de Estatística da UEM
RESUMO
Foram estimados os componentes de variância para produção de leite e avaliado o impacto do aumento do número de animais na matriz de parentesco sobre os componentes de variância usando os métodos de Máxima Verossimilhança Restrita (REML) e Bayesiano via amostragem de Gibbs (GS). Utilizaram-se registros de produção de leite de vacas da raça Holandesa dos estados de Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul. Para cada estado, foram analisados dois conjuntos de dados: no primeiro, pedigree restrito, a matriz de parentesco foi constituída dos animais do respectivo estado; e, no segundo, pedigree completo, foram incluídos na matriz de parentesco os animais de todos os estados. Utilizou-se um modelo animal que incluiu os efeitos da estação de parto, rebanho-ano, grupo genético, ordem de parto e os efeitos genéticos aditivos e de ambiente permanente. As estimativas REML dos componentes de variância e de herdabilidade em todos os estados, obtidas com o pedigree restrito e com pedigree completo, foram similares. As estimativas REML de herdabilidade em Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul foram 0,19; 0,18; 0,26; 0,43 e 0,48, respectivamente. Houve fortes evidências de que as estimativas Bayesianas da variância genética com o PEDA foram superiores àquelas obtidas utilizando o PEDR. As herdabilidades e os desvios-padrão obtidos pelo método Bayesiano em Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul utilizando os pedigrees restrito e completo foram 0,21 ± 0,032 e 0,40 ± 0,025; 0,20 ± 0,017 e 0,27 ± 0,017; 0,28 ± 0,014 e 0,31 ± 0,014; 0,42 ± 0,041 e 0,56 ± 0,021; e 0,43 ± 0,039 e 0,55 ± 0,019, respectivamente. A variância genética aumentou significativamente em cada estado quando os animais dos outros estados foram incorporados na matriz de parentesco. Os menores desvios-padrão e intervalos de credibilidade dos componentes de variância foram estimados nos estados com maior número de lactações e sugerem que a precisão dos componentes de variância foi maior para esses estados.
Palavras-chave: amostragem de Gibbs, bovinos, convergência, herdabilidade, parentesco
ABSTRACT
Variance components (VC) for milk yield of Holstein cows were estimated and the effects of increasing of the number of animals in the numerator relationship matrix (NRM) were evaluated on VC estimates obtained by REML and Bayesian inference via Gibbs sampling (GS). Data were obtained from herds in the states of Minas Gerais, São Paulo, Paraná, Santa Catarina, and Rio Grande do Sul. Two data sets were created for each state. In the first set, the NRM included only the pedigree of the animals of the state under consideration (PEDR). In the second, the NRM included animals from the five states (PEDA). An animal model including the effects of herd-year, parity, season, genetic group, effects of additive genetic and permanent environment was used. The REML estimates of VC and heritability in each state obtained from PEDR and PEDA were similar. The heritability in Minas Gerais, São Paulo, Paraná, Santa Catarina, and Rio Grande do Sul was 0.19, 0.18, 0.26, 0.43, and 0.48, respectively. There was evidence that the posterior means of the genetic variance of PEDA analyses were significantly greater than PEDR. Heritability and standard deviations estimated by GS in Minas Gerais, São Paulo, Paraná, Santa Catarina, and Rio Grande do Sul, using PEDR (PEDA), were 0.21 ± 0.032 (0.40 ± 0.025), 0.20 ± 0.017 (0.27 ± 0.017), 0.28 ± 0.014 (0.31 ± 0.014), 0.42 ± 0.041 (0.56 ± 0.021) and 0.43 ± 0.039 (0.55 ± 0.019), respectively. The genetic variance of each state increased significantly when animals from the other states were incorporated in its NRM. The smallest standard deviations and VC credibility intervals were estimated in the states with more records, which suggested that the precision of the VC estimates was higher in those states.
Key Words: convergence, dairy cattle, Gibbs sampling, heritability, relationship
Introdução
Na década de 80, o método da Máxima Verossimilhança começou a ser empregado na estimação de componentes de variância (CV) em conjunto de dados desbalanceados, pois apresentava ótimas propriedades e não compartilhava das limitações inerentes aos métodos até então utilizados. No entanto, os estimadores de Máxima Verossimilhança de componentes de variância não incluíram a perda de graus de liberdade resultante da estimação dos efeitos fixos do modelo de análise. Esse problema foi contornado por Patterson & Thompson (1971), que realizaram modificações no método de Máxima Verossimilhança, resultando na metodologia conhecida como máxima verossimilhança restrita (REML). Outras vantagens do REML são a propriedade de reduzir o viés, em decorrência da seleção, e a capacidade de utilizar toda informação disponível. Essas vantagens levaram o método REML a ser largamente utilizado no melhoramento animal.
No entanto, nas duas últimas décadas, o paradigma Bayesiano associado ao método MCMC (Monte Carlo Markov Chains) tem propiciado novas perspectivas a questões relacionadas à estimação de componentes de variância e parâmetros genéticos (Gianola & Fernando, 1986; Van Tassell, 1994; Weigel & Rekaya, 2000; Martins et al., 2002). A crescente demanda pelos procedimentos Bayesianos via MCMC no melhoramento animal deve-se principalmente à facilidade de implementação para grande conjuntos de dados, decorrente da menor exigência de memória computacional e do uso de distribuições a priori acerca dos parâmetros.
Um problema relevante, no contexto de cadeias de Markov, é o estudo do comportamento assimptótico da densidade a posteriori de interesse. Para aplicar os métodos MCMC em problemas práticos, é necessário saber se o algoritmo convergiu e quando convergiu. Portanto, é fundamental decidir em que ponto é razoável crer que as amostras são de fato representativas da distribuição estacionária de interesse da cadeia de Markov. Outro entrave dos métodos MCMC relaciona-se à lentidão na convergência dos algoritmos, em virtude da correlação entre os valores amostrais gerados, e constitui outro desafio ainda maior na implementação do método (Cowles & Carlin, 1994; Gamerman, 1996).
Uma das maiores conquistas no melhoramento animal foi a possibilidade de incorporação da inversa da matriz de parentesco (Henderson, 1976) nas equações de modelos mistos. O uso da matriz de parentesco deve melhorar a precisão das estimativas dos valores genéticos e quase sempre aumenta a correlação entre os valores genéticos dos indivíduos aparentados (Henderson, 1976; Dempfle, 1990). Segundo Schenkel (1999), a robustez dos métodos de estimação de componentes de variância, baseados na verossimilhança, apóia-se, até certo ponto, na especificação completa e correta da matriz de parentesco.
Diversos trabalhos comprovam que a inclusão da matriz de parentesco aditivo aumenta a acurácia das avaliações genéticas (Kennedy & Moxley, 1975; Pollak et al., 1977; Carlson et al., 1984). Van Vleck & Hudson (1982), aplicando o método 3 de Henderson a um modelo de touro, demonstraram que a inclusão do parentesco entre os touros aumenta os valores das estimativas de herdabilidade.
Este trabalho foi realizado com os objetivos de estimar os componentes de variância e herdabilidade para produção de leite e investigar o impacto causado pelo aumento no número de animais na matriz de parentesco sobre os componentes de variância, por meio do método de máxima verossimilhança restrita (REML) e de procedimentos Bayesianos via amostrador de Gibbs.
Material e Métodos
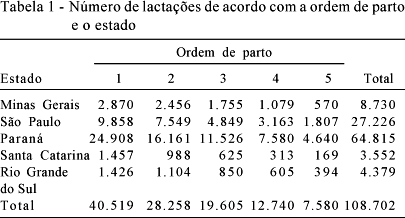
Foram analisados 108.702 registros de produção de leite de vacas, cujas parições ocorreram entre os anos de 1980 e 1993, distribuídas em 1.626 rebanhos. Essas informações foram geradas dentro do programa oficial de controle leiteiro da raça Holandesa, conduzido por associações e núcleos de criadores dos estados de Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul, integrantes do Arquivo Zootécnico Nacional gerenciado pela EMBRAPA Gado de Leite, em Juiz de Fora, Minas Gerais. As edições e restrições impostas ao conjunto de dados (Tabela 1), realizadas no sistema SAS® (SAS, 2001), foram descritas por Falcão et al. (2006).
Para analisar o impacto causado pelo aumento do número de animais na matriz de parentesco nas estimativas dos componentes de variância e nos parâmetros genéticos, foram criados dois arquivos de dados para cada estado. Os dois arquivos continham registros de produção apenas dos animais do estado, porém, o primeiro contemplava em sua matriz de parentesco só os animais desse estado e foi denominado arquivo com pedigree restrito (PEDR), enquanto o segundo arquivo incluiu na sua matriz de parentesco todos os animais do arquivo final, ou seja, os animais do estado mais os animais dos demais estados, denominado arquivo com pedigree aumentado (PEDA) (Tabela 2).
A seguinte medida de similaridade genética (SG), proposta por Rekaya et al. (1999), foi usada para avaliar a magnitude dos laços genéticos entre duas regiões:
em que C (i,j) = número de touros usados em comum nas regiões i e j; T (i,j) = número total de touros usados nas duas regiões; e NFkr = número de filhas do touro k na região r (r=1, 2). Neste trabalho, foi calculada a similaridade genética entre o estado i (i = Minas Gerais, São Paulo, Paraná, Santa Catarina, Rio Grande do Sul) e o agrupamento dos demais estados j (j = agrupamento 1 ...., agrupamento 5), em que o agrupamento 1 reúne os de São Paulo, Paraná, Santa Catarina e Rio Grande do Sul, o agrupamento 2 os estados de Minas Gerais, Paraná, Santa Catarina e Rio Grande do Sul e assim por diante. Desta forma, no arquivo de dados do estado i, foram considerados somente os animais desse estado, enquanto, no arquivo dos outros estados agrupados, incluiu-se o pedigree de todos os animais, exceto os do estado i.
As análises para cada estado, com pedigree restrito ou completo, foram realizadas com um modelo animal que incluiu os efeitos fixos da subclasse rebanho-ano de parição, grupo genético, estação de parição e ordem de parto e os efeitos aleatórios genético aditivos, de ambiente permanente e residual, conforme descrito em [1]:
em que: Y = vetor das produções de leite ajustadas para 305 dias de lactação (PL305) em cada estado; X = matriz de incidência dos efeitos fixos; β = vetor dos efeitos fixos da subclasse rebanho-ano de parição, grupo genético, estação de parição e ordem de parto; Z = matriz de incidência dos efeitos genéticos aditivos; = vetor dos efeitos aleatórios genéticos aditivos do animal; W = matriz de incidência dos efeitos permanentes de ambiente; p = vetor das contribuições de ambiente permanente; e e = vetor de erros aleatórios associados a cada observação. Admitiu-se que y, a, p e e possuem distribuição conjunta normal multivariada, como segue abaixo:
em que G = A  , P = Ip
, P = Ip  e, R = In
e, R = In  em que A = matriz de coeficientes de parentesco entre os animais, de ordem m quando nesta matriz foram incluídos exclusivamente os animais de um estado analisado e, de ordem q, quando as análises da PL305 desse estado incluíram em sua matriz de parentesco todos os animais do arquivo final de dados; Z = matriz de incidência dos valores genéticos, de ordem n x m para Am e, de ordem n x q para Aq; W = uma matriz de incidência dos efeitos permanentes de ambiente, de ordem m x p; In = uma matriz identidade de ordem n; Ip = uma matriz identidade de ordem p;
em que A = matriz de coeficientes de parentesco entre os animais, de ordem m quando nesta matriz foram incluídos exclusivamente os animais de um estado analisado e, de ordem q, quando as análises da PL305 desse estado incluíram em sua matriz de parentesco todos os animais do arquivo final de dados; Z = matriz de incidência dos valores genéticos, de ordem n x m para Am e, de ordem n x q para Aq; W = uma matriz de incidência dos efeitos permanentes de ambiente, de ordem m x p; In = uma matriz identidade de ordem n; Ip = uma matriz identidade de ordem p;  = variância genética aditiva;
= variância genética aditiva;  = variância de efeito permanente de ambiente, associado às vacas;
= variância de efeito permanente de ambiente, associado às vacas;  = variância do efeito temporário de ambiente; n = número total de lactações em cada estado; p = número de vacas com registro de lactação; m = número de indivíduos no pedigree restrito; e q = número de indivíduos pedigree completo.
= variância do efeito temporário de ambiente; n = número total de lactações em cada estado; p = número de vacas com registro de lactação; m = número de indivíduos no pedigree restrito; e q = número de indivíduos pedigree completo.
Os componentes de variância estimados pelo método REML foram obtidos por meio dos programas do sistema MTDFREML, descrito por Boldman et al. (1995), enquanto a implementação dos princípios Bayesianos na estimação dos componentes de variância foi realizada por meio dos programas do sistema MTGSAM, desenvolvido por Van Tassell & Van Vleck (1995).
As análises empregando o amostrador de Gibbs para obtenção das estimativas dos componentes de variância foram realizadas com base no modelo animal descrito em [1]. Admitiu-se que o vetor y de observações, condicionado aos parâmetros de locação e de dispersão, tivesse a seguinte distribuição, y|β,a,p, ~MVN [Xβ+Za+Wp,In
~MVN [Xβ+Za+Wp,In ], enquanto, para os vetores a e p, admitiram-se as seguintes distribuições a priori:
], enquanto, para os vetores a e p, admitiram-se as seguintes distribuições a priori:
Para os efeitos fixos de ambiente, foi usada distribuição vaga ou flat, portanto f(β) µ cte . Distribuições gama invertida foram usadas como distribuições a priori para obtenção dos componentes de variância genética, ambiente permanente e residual de cada elemento  ,
,  e
e  de G, P e R, respectivamente, como segue:
de G, P e R, respectivamente, como segue: ~ ΓI (
~ ΓI ( νa), de modo que f(
νa), de modo que f( |
| ,νa)∝(
,νa)∝( )-½(νa+2)×e-½(
)-½(νa+2)×e-½(
 ), em que νa = número de graus de liberdade da distribuição; e
), em que νa = número de graus de liberdade da distribuição; e  = parâmetro de escala da distribuição de
= parâmetro de escala da distribuição de  ;
; ~ΓI(
~ΓI( ,νp), de modo que f(
,νp), de modo que f( |
| ,νp)∝(
,νp)∝( )-½(νp+2)×e-½(
)-½(νp+2)×e-½(
 ), em que νp = graus de liberdade da distribuição; e
), em que νp = graus de liberdade da distribuição; e  = parâmetro de escala da distribuição de
= parâmetro de escala da distribuição de  ;
;  ~ IX-2(
~ IX-2( ,νe), de modo que f(
,νe), de modo que f( /so,νe)∝(
/so,νe)∝( )-½(νe+2)×e-½(so
)-½(νe+2)×e-½(so ). Atribuiu-se valor 3 para o grau de liberdade das distribuições iniciais, tanto nas análises utilizando-se o pedigree restrito como naquelas com o pedigree completo. Os valores a priori para os componentes de variância foram aqueles obtidos nas análises REML. Para todos os parâmetros, os valores dos hiperparâmetros foram escolhidos de forma que se tinha priori não-informativa.
). Atribuiu-se valor 3 para o grau de liberdade das distribuições iniciais, tanto nas análises utilizando-se o pedigree restrito como naquelas com o pedigree completo. Os valores a priori para os componentes de variância foram aqueles obtidos nas análises REML. Para todos os parâmetros, os valores dos hiperparâmetros foram escolhidos de forma que se tinha priori não-informativa.
O esquema de análise estabelecido incluiu amostras de uma cadeia de 550.000 iterações. O número de iterações descartadas para remover o efeito dos valores iniciais foi de 50.000 iterações com intervalo de utilização amostral de dez iterações. A monitoração de convergência das amostras das distribuições das cadeias geradas pelo GS foi feita pela biblioteca CODA (Convergence Diagnosis and Output Analysis), versão 0.4, desenvolvida por Cowles et al. (1995) usando o método de Heidelberg & Welch (1983).
Resultados e Discussão
A convergência do algoritmo pelo método Bayesiano foi alcançada em 22 das 30 cadeias de Markov geradas. Portanto, foram necessários descartes adicionais das iterações iniciais e aumento nos intervalos de retirada amostral para obtenção das densidades a posteriori de oito parâmetros nos seguintes estados e respectivo arquivo: MG/pedigree restrito, SP/pedigree completo, SC/pedigree restrito e SC/pedigree completo. Em geral, o tamanho das cadeias variou de 10.000 a 45.000, exceto para a  em SC/pedigree completo, cujo tamanho da amostra foi de 2.500.
em SC/pedigree completo, cujo tamanho da amostra foi de 2.500.
Os valores mais altos de similaridade genética foram encontrados entre os estados de Minas Gerais, São Paulo e Paraná e os demais estados agrupados (Tabela 3). Esses valores indicam que esses estados foram os que apresentaram laços genéticos mais fortes com os demais estados, provavelmente em razão do maior número de touros usados em comum entre eles. A similaridade genética é uma medida de conectabilidade genética entre as regiões. Como era esperada, a magnitude da variância genética aumentou no modelo PEDA, pois este aumento está diretamente relacionado à magnitude da similaridade genética. Rekaya et al. (1999), utilizando dados de rebanhos da raça Holandesa, encontraram valores de similaridade genética de 0,35 a 0,46 entre cinco regiões dos Estados Unidos.
As médias para PL305, com seus respectivos desvios-padrão, nos estados de Minas Gerais, São Paulo, Paraná, Santa Catarina e Rio Grande do Sul foram 4.713 ± 1.543 kg, 5.052 ± 1.590 kg, 6.327 ± 1.501 kg, 5.083 ± 1.347 kg e 4.840 ± 1.535 kg, respectivamente.
Os erros-padrão das estimativas de herdabilidade foram menores ou iguais a 0,001 (Tabela 4). Os valores das estimativas dos componentes de variância foram similares nas duas análises, ou seja, tanto considerando o pedigree restrito quanto incluindo os animais de todos os estados na matriz de parentesco, enquanto os valores de herdabilidades foram exatamente iguais nas duas análises.
A magnitude das estimativas REML de herdabilidade para PL305 nos estados de Minas Gerais, São Paulo e Paraná estão dentro dos limites observados na literatura, que variam entre 0,16 e 0,35 (Matos et al., 1996; Costa, 1999; Freitas et al., 2001). No entanto, Van Vleck & Dong (1988), Rorato et al. (1994) e Olori et al. (1999) encontraram valores de herdabilidade para produção de leite superiores a 0,36 e mais próximos das estimativas dos estados de Santa Catarina e Rio Grande do Sul encontradas neste estudo.
Em todos os estados, foram encontradas fortes evidências de que indicavam que as médias a posteriori da variância genética obtidas com o pedigree completo, foram superiores (P<0,001) àquelas obtidas utilizando o pedigree restrito (Tabela 5). Dessa forma, verificou-se aumento significativo das médias da variância genética ao incorporar na matriz de parentesco os animais de todos os estados. Os resultados deste trabalho estão de acordo com a literatura e comprovam que a inclusão da matriz de parentesco e o aumento de laços genéticos nesta matriz melhoram a acurácia das estimativas e a magnitude dos parâmetros de interesse (Pollak et al., 1977; Van Vleck & Hudson, 1982; Carlson et al., 1984).
As médias a posteriori das variâncias de ambiente permanente e residual no modelo pedigree restrito também diferiram significativamente (P<0,001) daquelas estimadas com o modelo pedigree completo (Tabela 5). A única exceção foi observada para a média da variância residual do estado do Paraná.
Altarriba et al. (1998) encontraram diferenças significativas entre as estimativas de herdabilidade para tamanho de ninhada de ovinos em duas populações simuladas, ambas com grande proporção de família de irmãos completos e que diferiam quanto à informação de pedigree. Esses autores mostraram que a herdabilidade foi superestimada na população em que o pedigree dos machos era desconhecido. Dong et al. (1988), utilizando registros de características produtivas de bovinos da raça Holandesa para avaliar os efeitos do parentesco sobre a estimação dos componentes de variância com um modelo animal, concluíram que, ao ignorar as relações genéticas para obtenção de componentes de variância, as estimativas REML de herdabilidade eram viesadas. Johnson et al. (1991) observaram que a inclusão da matriz de parentesco aditivo aumentou as estimativas de herdabilidades e dos valores genéticos de características de crescimento de bovinos Angus e Hereford.
A variância residual tendeu a ser menor para o estimador baseado no método Bayesiano, sobretudo quando considerado o pedigree completo. Esses resultados estão de acordo com aqueles encontrados por Van Tassell et al. (1995) ao compararem as estimativas do quadrado médio do resíduo obtidas pelos métodos REML, MIVQUE (Minimum Variance Quadratic Unbiased Estimation) e Bayesianos via amostrador de Gibbs a partir de dados simulados com vários esquemas de seleção e diferentes valores de herdabilidade.
As médias a posteriori das herdabilidades para PL305 em todos os estados aumentaram significativamente quando houve aumento de informações na matriz de parentesco (Tabela 5). Ressalta-se que, nos estados de Minas Gerais, Santa Catarina e Rio Grande do Sul, a baixa magnitude de  pode ter inflacionado a variância genética e, portanto contribuído com parte desse aumento na magnitude da herdabilidade.
pode ter inflacionado a variância genética e, portanto contribuído com parte desse aumento na magnitude da herdabilidade.
Os valores de herdabilidade para PL305 nos estados de Minas Gerais, São Paulo e Paraná estão dentro do intervalo registrado na literatura para esta raça (Costa, 1999; Freitas et al., 2001, Samoré et al., 2002). Os valores mais extremos de herdabilidade encontrados em Santa Catarina e Rio Grande do Sul utilizando o pedigree restrito ou o completo, e em Minas Gerais com o pedigree completo foram superiores à maioria dos descritos na literatura. Entretanto, Weigel & Rekaya (2000), Jamrozik et al. (2002) e Zwald et al. (2003) estimaram valores de herdabilidade para produção de leite variando de 0,39 a 0,56. Segundo Zwald et al. (2003), a superestimação da variância genética em rebanhos pequenos pode estar relacionada à falta de ajustamento da heterogeneidade da variância genética e leva a elevados valores de herdabilidade. Ressalta-se que neste trabalho os baixos valores  de podem também ter inflacionado
de podem também ter inflacionado  .
.
As distribuições a posteriori marginais dos componentes de variância para PL305 de Santa Catarina e Rio Grande do Sul, estimadas com o pedigree restrito e com o pedigree completo foram todas unimodais (Figura 1). As densidades a posteriori dos demais estados foram omitidas, pois não mostraram virtualmente desvios da distribuição normal, assim são bem descritas por suas médias a posteriori e respectivos desvios-padrão dos parâmetros. Em ambos os estados, as distribuições marginais a posteriori da variância genética (pedigrees restrito e completo) foram aproximadamente simétricas em torno de suas modas e as estimativas da média, moda e mediana foram similares. As densidades a posteriori obtidas com o pedigree completo apresentaram caudas mais curtas em comparação às estimadas com o pedigree restrito. Por outro lado, a assimetria da densidade a posteriori de  ficou bem evidenciada em ambos os estados. Desta forma, as estimativas da media, mediana e moda foram claramente diferentes, o que implica completa inadequacao a distribuicao normal. Essa assimetria parece refletir o limitado numero de informacoes para estimacao de
ficou bem evidenciada em ambos os estados. Desta forma, as estimativas da media, mediana e moda foram claramente diferentes, o que implica completa inadequacao a distribuicao normal. Essa assimetria parece refletir o limitado numero de informacoes para estimacao de  . Em ambos os estados, o aumento no numero de animais na matriz de parentesco provocou aumento da assimetria da distribuicao de
. Em ambos os estados, o aumento no numero de animais na matriz de parentesco provocou aumento da assimetria da distribuicao de  .
.
Apesar da pequena assimetria, as distribuições a posteriori marginais da variância residual de Santa Catarina (pedigrees restrito e completo) se ajustaram razoavelmente bem à curva normal (Figura 1). Os valores de suas médias, medianas e modas foram muito próximos. As densidades a posteriori de  no Rio Grande do Sul tiveram comportamentos similares. Nesses estados, nos arquivos de pedigree restrito e completo, as amplitudes dos coeficientes de variação a posteriori para
no Rio Grande do Sul tiveram comportamentos similares. Nesses estados, nos arquivos de pedigree restrito e completo, as amplitudes dos coeficientes de variação a posteriori para  ,
,  e
e  foram 5 a 13%. 50 a 78% e 3,5 a 4%, respectivamente. A baixa magnitude dos coeficientes de variação para
foram 5 a 13%. 50 a 78% e 3,5 a 4%, respectivamente. A baixa magnitude dos coeficientes de variação para  , segundo Wang et al. (1993), é indicativo que o método Bayesiano comumente apresenta menos dificuldade na estimação da variância residual em comparação à estimação de outros componentes de variância e parâmetros função desses componentes.
, segundo Wang et al. (1993), é indicativo que o método Bayesiano comumente apresenta menos dificuldade na estimação da variância residual em comparação à estimação de outros componentes de variância e parâmetros função desses componentes.
As inferências baseadas na teoria frequentista dependem da normalidade assimptótica dos estimadores de máxima verossimilhança. Do ponto de vista bayesiano, esta suposição não é necessária, uma vez que os parâmetros são estimados a partir da distribuição de equilíbrio de cada parâmetro. Os métodos de convergência, neste sentido, são úteis para avaliar se os algoritmos MCMC atingiram essa distribuição de equilíbrio.
A acentuada assimetria das densidades a posteriori de alguns parâmetros pode ser uma evidência da quebra da suposição de normalidade assimptótica. Desta forma, as estimativas REML dos componentes de variância em Santa Catarina e Rio Grande do Sul podem ter sido viesadas, principalmente para a  , cujas distribuições foram altamente assimétricas, o que, por si só, viola a pressuposição de normalidade, admitida para todos os efeitos aleatórios. Por outro lado, como a abordagem Bayesiana é capaz de produzir as distribuições conjunta e marginal a posteriori exatas para qualquer tamanho de amostra (Zellner, 1971; Box & Tiao, 1973), espera-se que as estimativas Bayesianas dos componentes de variância tenham sido mais acuradas.
, cujas distribuições foram altamente assimétricas, o que, por si só, viola a pressuposição de normalidade, admitida para todos os efeitos aleatórios. Por outro lado, como a abordagem Bayesiana é capaz de produzir as distribuições conjunta e marginal a posteriori exatas para qualquer tamanho de amostra (Zellner, 1971; Box & Tiao, 1973), espera-se que as estimativas Bayesianas dos componentes de variância tenham sido mais acuradas.
Apesar do tamanho da amostra usada para estimar os componentes de variância nos estados de Santa Catarina e Rio Grande do Sul, que foi relativamente pequena em comparação aos demais estados, é provável que as distribuições a priori usadas neste trabalho tenham ocasionado pouco impacto na estimação dos componentes de variância, principalmente em virtude dos elevados valores de herdabilidade encontrados.
Van Tassell et al. (1995) demonstraram que o uso de uma priori com valor esperado incorreto pode levar a estimativas viesadas dos componentes de variância. No entanto, mesmo que a distribuição a priori seja relativamente pobre, a estimativa pelo método Bayesiano, embora possivelmente viesada, pode ter quadrado médio do resíduo do componente de variância similar aos obtidos pelos métodos REML e MIVQUE. O efeito da priori, de acordo com esses autores, diminui à medida que a herdabilidade ou a quantidade de informações aumenta.
Os procedimentos Bayesianos permitem, além das estimativas pontuais, determinar intervalos de credibilidade para a distribuição a posteriori do componente de variância, sem aproximações ou o uso de pressuposições de normalidade, e representa, assim, uma vantagem sobre os métodos frequentistas. Neste estudo, os intervalos de credibilidade dos componentes de variância e de herdabilidade foram obtidos a partir das amostras geradas pelo método Bayesiano (Tabelas 6 e 7).
As estimativas mais precisas da variância genética a posteriori ocorreram nos estados com maior número de registros de lactação e animais na matriz de parentesco, ou seja, no Paraná, em São Paulo e em Minas Gerais, como se pode deduzir dos respectivos desvios-padrão e intervalos de credibilidade, que foram menores nesses estados (Tabelas 5 e 6). O intervalo de credibilidade de  no Paraná, sob pedigrees restrito, foi aproximadamente quatro vezes menor que aquele estimado no Rio Grande do Sul. A precisão dessas estimativas aumentou, ou seja, o desvio-padrão a posteriori e o intervalo de credibilidade diminuíram naqueles estados com menor número de obser-vações quando houve aumento dos laços genéticos, navs análises com o pedigree completo. O mesmo padrão foi encontrado para as estimativas das herdabilidades a posteriori. Os intervalos de credibilidade de
no Paraná, sob pedigrees restrito, foi aproximadamente quatro vezes menor que aquele estimado no Rio Grande do Sul. A precisão dessas estimativas aumentou, ou seja, o desvio-padrão a posteriori e o intervalo de credibilidade diminuíram naqueles estados com menor número de obser-vações quando houve aumento dos laços genéticos, navs análises com o pedigree completo. O mesmo padrão foi encontrado para as estimativas das herdabilidades a posteriori. Os intervalos de credibilidade de  , nos estados de Santa Catarina e Rio Grande do Sul reduziram quase pela metade quando obtidos com o pedigree completo.
, nos estados de Santa Catarina e Rio Grande do Sul reduziram quase pela metade quando obtidos com o pedigree completo.
As médias a posteriori da variância residual PL305 também foram estimadas com maior precisão nas maiores populações e com maior número de animais na matriz de parentesco como indicam os intervalos de credibilidade e desvios-padrão a posteriori. Os intervalos de credibilidade de  reduziram quando estimados sob o modelo com pedigree completo (Tabela 7). De modo geral, a incerteza sobre os parâmetros, mostrada pelo desvio-padrão a posteriori e o intervalo de credibilidade dos respectivos componentes de variância diminuíram com o aumento do número de animais na matriz de parentesco.
reduziram quando estimados sob o modelo com pedigree completo (Tabela 7). De modo geral, a incerteza sobre os parâmetros, mostrada pelo desvio-padrão a posteriori e o intervalo de credibilidade dos respectivos componentes de variância diminuíram com o aumento do número de animais na matriz de parentesco.
As estimativas dos componentes de variância encontradas neste estudo pelos métodos REML e Bayesiano sugerem que as inferências obtidas pelos dois métodos nem sempre são concordantes, principalmente para pequenas amostras. Este comportamento fica bem eviden-ciado nos estados de Minas Gerais, Santa Catarina e Rio Grande do Sul. Segundo Blasco (2001), quando um conjunto de dados é suficientemente grande, os resultados observados, tanto usando os métodos frequentistas quanto os procedimentos Bayesianos, são muito similares na maioria dos casos. Wang et al. (1993) também observaram resultados similares.
Uma das vantagens das análises Bayesianas é a possibilidade de exploração dos dados com mais elegância e detalhamento que o método REML. As análises bayesianas produziram fortes evidências de que o aumento no número de animais na matriz de parentesco resultou em diferentes estimativas dos componentes de variância, diferentemente das estimativas REML.
Conclusões
As estimativas dos componentes de variância encontradas neste estudo pelos métodos REML e Bayesiano sugerem que as inferências obtidas pelos dois métodos nem sempre são concordantes, particularmente para pequenas amostras. Os componentes de variância foram estimados com mais precisão nos conjuntos de dados com maior número de lacta-ções, pois a magnitude dos desvios-padrão e os intervalos de credibilidade foram significativamente inferiores àqueles estimados para os estados com menor número de lactações. A pressuposição de normalidade assumida para estimação dos efeitos aleatórios nos problemas de obtenção dos componentes de variância nem sempre pode ser assegurada, principalmente quando se trata de pequeno número de dados.
Agradecimentos
À EMBRAPA Gado de Leite e à Associação Brasileira de Criadores de Bovinos da Raça Holandesa, pela cessão dos dados. Aos revisores ad hoc, pelo minucioso trabalho e pelas valiosas sugestões apresentadas para redação final do trabalho.
Literatura Citada
Este artigo foi recebido em 20/6/2007 e aprovado em 27/10/2008.
Correspondências devem ser enviadas para: alencariano@uft.edu.br
- ALTARRIBA, J.; VARONA, L.; GARCIA-CORTES, L.A. et al. Bayesian inference of variance components for litter size in Rasa Aragonesa sheep. Journal of Animal Science, v.76, p.23-28, 1998.
- BLASCO, A. The Bayesian controversy in animal breeding. Journal of Animal Science, v.79, p.2023-2046, 2001.
- BOLDMAN, K.G.; KRIESE, L.A.; Van VLECK, L.D. et al. A Manual for use of MTDFREML A set of programs to obtain estimates of variance and covariances [DRAFT]. Clay Center: USDA-ARS, 1995. 120p.
- BOX, G.E.P.; TIAO, G.C. Bayesian inference in statistical analysis Reading: Addison-Wesley Publishing Co., 1973. 588p.
- CARLSON, J.P.; CHRISTIAN, L.L.; ROTHSCHILD, M.F. et al. An evaluation of four procedures to rank centrally tested boars. Journal of Animal Science, v.59, p.934, 1984.
- COSTA, C.N. An investigation into heterogeneity of variance for milk and fat yields of Holstein cows in Brazilian herd environments. Genetics and Molecular Biology, v.22, n.3, p.375-381, 1999.
- COWLES, K.; BEST, N.; VINES, K. Convergence diagnosis and output analysis Version 0.40. Cambrigde: MRC Biostatistics Unit, 1995. 48p
- COWLES, M.K.; CARLIN, B.P. Markov chain Monte Carlo convergence diagnostics: a comparative review. Delaware: Universidade de Minnesota/Divisão de Bioestatística, 1994. 52p. (Relatório técnico).
- DEMPFLE, L. Problems in the use of the relationship matrix in animal breeding. In: GIANOLA, D.; HAMMOND, K. (Eds.) Advances in statistical methods for genetic improvement of livestock Berlin: Springer-Verlag, 1990. p.454-473.
- DONG, M.C.; VAN VLECK, L.D.; WIGGANS, G.R. Effect of relationships on estimation of variance components with an animal model and restricted maximum likelihood. Journal of Dairy Science, v.71, p.3047-3052, 1988.
- FALCÃO, A.J.S.; MARTINS, E.N.; COSTA, C.N. et al. Heterocedasticidade entre estados para produção de leite em vacas da raça Holandesa, usando métodos bayesianos via amostrador de Gibbs. Revista Brasileira de Zootecnia, v.35, n.2, p.405-414, 2006.
- FREITAS, A.F.; DURÃES, M.C.; VALENTE, J. et al. Parâmetros genéticos para produção de leite e gordura nas três primeiras lactações de vacas Holandesas. Revista Brasileira de Zootecnia, v.30, n.3, p.709-713, 2001.
- GAMERMAN, D. Simulação estocástica via cadeias de Markov Rio de Janeiro: Universidade Federal do Rio de Janeiro, 1996. 196p.
- GIANOLA, D.; FERNANDO, R.L. Bayesian methods in animal breeding theory. Journal of Animal Science, v.63, p.217-277, 1986.
- HEIDELBERGER, P.; WELCH, P.D. Simulation run length control in the presence of an initial transient. Operations Research, v.31, p.1109-1144, 1983.
- HENDERSON, C.R. A simple method for computing the inverse of a numerator relationship matrix used in prediction of breeding values. Biometrics, v.32, p.69-83, 1976.
- JAMROZIK, J.; SCHAEFFER, L.R.; WEIGEL, K.A. Estimates of genetic parameters of single and multiple-country test-day models. Journal of Dairy Science, v.85, p.3131-3141, 2002.
- JOHNSON, Z.B.; WRIGHT, D.W.; BROWN, C.J. et al. Effect of including relationship in the estimation of genetic parameters of beef calves. Journal of Animal Science, v.70, n.1, p.78-88, 1991.
- KENNEDY, B.W.; MOXLEY, J.E. Comparison of genetic group and relationship methods for mixed model sire evaluation. Journal of Dairy Science, v.58, p.1507-1514, 1975.
- MARTINS, E.N.; ENGLER, E.O.; SAKAGUTI, E.S. et al. Bayesian analyses of heterogeneous variance among generations of brazilian Canchim beef calves. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 7., 2002, Montpellier. Proceedings... Montpellier, 2002. (CD-ROM).
- MATOS, R.S.; RORATO, P.R.N.; FERREIRA, G.B. et al. Parâmetros genéticos para produção de leite e gordura da raça Holandesa no Estado do Rio Grande do Sul. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 33., 1996, Fortaleza. Anais... Fortaleza: Sociedade Brasileira de Zootecnia, 1996. p.86-87.
- OLORI, V.E.; HILL, W.G.; MCGUIRK, B.J. et al. Estimating variance components for test day milk records by restricted maximum likelihood with random regression animal. Livestock Production Science, v.61, p.53-63, 1999.
- PATTERSON, H.D.; THOMPSON, R. Recovery of inter-block information when block sizes unequal. Biometrika, v.58, n.3, p.545-554, 1971.
- POLLAK, E.J.; UFFORD, G.R.; GROSS, S.J. Comparison of alternative models for within-herd genetic evaluation fo beef cattle. Journal of Animal Science, v.45, p.1010, 1977.
- REKAYA, R.; WEIGEL, K.A. GIANOLA, D. Bayesian estimation of parameters of a structural model for genetic covariances between milk yield in five regions of the United States. In: ANNUAL MEETING OF EUROPEAN ASSOCIATION FOR ANIMAL PRODUCTION, 50., 1999, Zurich. Proceeding... Zurich: European Association for Animal Production, 1999. 6p.
- RORATO, P.R.N.; LÔBO, R.B.; MARTINS FILHO, R. et al. Efeito da interação genótipo-ambiente sobre a produção de leite da raça Holandesa, no Estado do Paraná. Revista Brasileira de Zootecnia, v.23, n.5, p.859-869, 1994.
- SAMORÉ, A.B; P. BOETTCHER, P.; JAMROZIK, J. et al. Genetic parameters for production traits and somatic cell scores estimated with a multiple trait random regression model in Italian Holsteins. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 7., 2002, Montpellier. Proceeding... Montpellier, 2002. (CD-ROM).
- SCHENKEL, F.S. Effects of selection on animal genetic evaluation: a short review. In: INTERNATIONAL SYMPOSIUM ON ANIMAL BREEDING AND GENETICS, 1999, Viçosa, MG. Proceeding...Viçosa, MG: 1999.
- STATISTICAL ANALYSIS SYSTEM - SAS. SAS/STAT User's guide: statistics. versão 8.01, 4.ed. Cary: 2000. v.2, 328p.
- Van TASSELL, C.P. The use of Gibbs sampling for variance component estimation with simulated and weaning weight data using animal and maternal effects models 1994. 120f. Thesis (PhD in Animal Breeding) - Cornell University, Ithaca, 1994.
- Van TASSELL, C.P.; Van VLECK, D.L. A manual for use of MTGSAM A set of FORTRAN programs to apply Gibbs sampling to animal models for variance component estimation [DRAFT]. Lincoln: U.S. Department of Agriculture, Agricultural Research Service, 1995. 86p.
- Van TASSELL, C.P.; CASELLA, G.; POLLAK, E.J. Effects on selection on estimates of variance components using Gibbs sampling and restricted maximum likelihood. Journal of Dairy Science, v.78, p.678-692, 1995.
- Van VLECK, L.D.; DONG, M. Genetic (co)variance for milk and fat yield in California, New York, and Wisconsin for an animal model by restricted maximum likelihood. Journal of Dairy Science, v.71, p.3053-3060, 1988.
- Van VLECK, L.D.; HUDSON, G.F.S. Relationships among sires in estimating genetic variance. Journal of Dairy Science, v.65, p.1663, 1982.
- WANG, C.S.; RUTLEDGE, J.J.; GIANOLA, D. Marginal inferences about variance components in a mixed linear model using Gibbs sampling. Genetic Selection Evolution, v.25, p.41-62, 1993.
- WEIGEL, K.A.; REKAYA, R. A multiple-trait herd cluster model for international dairy sire evaluation. Journal of Dairy Science, v.83, p.815-821, 2000.
- ZELLNER, A. An introduction to Bayesian inference in econometrics New York: J. Willey and Sons, 1971. 431p.
- ZWALD, N.R.; WEIGEL, K.A.; FIKSE, W.F et al. Identification of factors that cause genotype by environment interaction between herds of Holstein cattle in seventeen countries. Journal of Dairy Science, v.86, p.1009-1018, 2003.
Efeitos do número de animais na matriz de parentesco sobre as estimativas de componentes de variância para produção de leite usando os métodos de Máxima Verossimilhança Restrita e Bayesiano
Datas de Publicação
-
Publicação nesta coleção
18 Set 2009 -
Data do Fascículo
Ago 2009
Histórico
-
Aceito
27 Out 2008 -
Recebido
20 Jun 2007