Resumos
Este estudio presenta a) dos enfoques teóricos cognitivos para abordar la resolución de problemas en física y b) un análisis del grado de adecuación de ambos enfoques a registros de estudiantes resolviendo problemas. Uno de los enfoques es la aproximación clásica basada en los resultados de los estudios de expertos y novatos. El otro, es un marco basado en un enfoque múltiple y contextualizado de la cognición. El análisis se realiza en torno a dos cuestiones clave para el estudio de la resolución de problemas: la naturaleza de los procesos que ocurren durante la tarea y del conocimiento puesto en juego. El análisis pone en evidencia las limitaciones y bondades de los enfoques para entender mejor por qué los estudiantes hacen lo que hacen cuando resuelven problemas.
Fenomenología; cognición; enseñanza de la Física
The present work is a) a comparative analysis of two theoretical approaches for cognition in Physics Problem Solving, and b) a discussion of the extent to which both of these approaches are able to account for protocols of students solving problems. One of the approaches is grounded on the classical expert-novice difference studies. The other one is a theoretical framework based on a manifold and context-sensitive view of cognition. The analysis addresses two key aspects of problem solving: the nature of the knowledge involved and the processes that takes place. The result of this analysis points out the limitations and the benefits of these approaches in order to understand why students do what they do when solving problems.
Theory; phenomenology; cognition; physics problem solving
Fenomenología; cognición; enseñanza de la Física
Theory; phenomenology; cognition; physics problem solving
Un fenómeno, dos teorías: una elección para la resolución de problemas en física1 1 Una versión preliminar de este estudio fue presentada en el IX Simposio de Investigación de Educación en Física, Rosario, octubre de 2008.
A single phenomenon, two theoretical frameworks: how to make a choice in physics problem solving
Laura Maria Buteler; Enrique Andrés Coleoni
Instituto de Física, Facultad de Matemática, Astronomía y Física (IFEG), Córdoba, Argentina <lbuteler@famaf.unc.edu.ar>; <ecoleoni@famaf.unc.edu.ar>
RESUMEN
Este estudio presenta a) dos enfoques teóricos cognitivos para abordar la resolución de problemas en física y b) un análisis del grado de adecuación de ambos enfoques a registros de estudiantes resolviendo problemas. Uno de los enfoques es la aproximación clásica basada en los resultados de los estudios de expertos y novatos. El otro, es un marco basado en un enfoque múltiple y contextualizado de la cognición. El análisis se realiza en torno a dos cuestiones clave para el estudio de la resolución de problemas: la naturaleza de los procesos que ocurren durante la tarea y del conocimiento puesto en juego. El análisis pone en evidencia las limitaciones y bondades de los enfoques para entender mejor por qué los estudiantes hacen lo que hacen cuando resuelven problemas.
Palabras clave: Fenomenología, cognición, enseñanza de la Física.
ABSTRACT
The present work is a) a comparative analysis of two theoretical approaches for cognition in Physics Problem Solving, and b) a discussion of the extent to which both of these approaches are able to account for protocols of students solving problems. One of the approaches is grounded on the classical expert-novice difference studies. The other one is a theoretical framework based on a manifold and context-sensitive view of cognition. The analysis addresses two key aspects of problem solving: the nature of the knowledge involved and the processes that takes place. The result of this analysis points out the limitations and the benefits of these approaches in order to understand why students do what they do when solving problems.
Keywords: Theory, phenomenology, cognition, physics problem solving.
Introducción
Si bien toda investigación necesita de pilares teóricos para definir sus preguntas y orientar su búsqueda, los resultados experimentales también constituyen evidencias fundamentales para reorientar la teoría. Esto, que puede parecer trivial en el desarrollo de la ciencia en general, no lo es tanto en campos interdisciplinarios -como la educación en física- en los que a menudo se observa "importación" de teorías de otras áreas de conocimiento que, aunque relacionadas con la interdisciplina, no fueron desarrolladas para dar respuesta al problema interdisciplinario en cuestión. Es allí donde la relación teoría-fenomenología adquiere fundamental relevancia y requiere, a nuestro criterio, un cuidado especial.
Distintas revisiones de estudios en resolución de problemas en física muestran que si bien las investigaciones producidas alrededor de esta área han sido abordadas desde variados referenciales teóricos, aquellas que estudian el proceso de solución y el conocimiento puesto en juego por las personas durante el mismo, se basan mayoritariamente en los resultados de los estudios denominados en la literatura como diferencias entre expertos y novatos (HSU et al., 2004; GANGOSO, 1999; COSTA; MOREIRA, 1997; COSTA, 1996; MALONEY, 1994). Los primeros estudios sobre diferencias entre expertos y novatos surgieron en el ámbito de las Ciencias Cognitivas y no tuvieron como objetivo investigar procesos de aprendizaje humanos, sino más bien, describir procesos exitosos y no exitosos. Estos estudios fueron un referente para la comunidad educativa, dando lugar a estudios comparativos tendientes a describir los comportamientos observados en novatos (estudiantes) y expertos (profesores) en esa tarea. Estos estudios han arrojado valiosa información acerca de cuáles son algunas de las dificultades que impiden a los estudiantes resolver problemas exitosamente y cuáles son algunas de las habilidades que deberían desarrollar para lograr el éxito.
Más recientemente, han surgido un conjunto de investigaciones que centran su atención en la naturaleza del conocimiento que los estudiantes de física ponen en juego al resolver problemas (DISESSA; SHERIN, 1998; REDISH, 2004; HAMMER, 2004; HAMMER et al., 2005). Este enfoque modela el conocimiento de los estudiantes en términos de elementos cognitivos más pequeños que, por ejemplo, conceptos, leyes o procedimientos de la física. Estos elementos forman una red que se activa parcialmente ante una demanda cognitiva, y tal activación depende del contexto2 2 Dentro de este enfoque, dado un individuo con respecto a un conjunto de unidades cognitivas, el contexto son las circunstancias en las que ese individuo activa confiablemente ese conjunto de unidades. . Estas investigaciones han permitido abordar la resolución de problemas en física desde una perspectiva más centrada en lo que los estudiantes saben y hacen cuando resuelven problemas, y menos en cuánto dista el proceder de los estudiantes del conocimiento de conceptos, principios y procedimientos de la física. Dentro de este enfoque, el conocimiento intuitivo no es un obstáculo para nuevos aprendizajes, sino que lo entienden como la base a partir de la cual se puede entender la construcción del conocimiento normativo de la física.
Los dos párrafos anteriores refieren a dos enfoques teóricos diferentes para estudiar la resolución de problemas en física. En las dos secciones que siguen se presentarán estos enfoques con mayor detalle. Luego se realizará un análisis comparativo entre ellos utilizando registros de estudios de campo. Se compararán los enfoques en relación a dos aspectos esenciales en el estudio de la resolución de problemas en física: A) La naturaleza de los procesos y B) La naturaleza del conocimiento puesto en juego durante esta tarea. El trabajo pretende generar una reflexión entre la relación teoría-fenomenología para el caso específico de la resolución de problemas en física, intentando mostrar cuán sensible es el resultado de la observación de los razonamientos de los estudiantes a los "lentes" teóricos que se utilizan para hacerlo. La reflexión que se pretende generar, aunque acotada a la resolución de problemas en física y a los dos enfoques elegidos, deja entrever aspectos más generales relativos al aprendizaje de la física cuando esta tarea es visualizada como un proceso en el que las personas utilizan conocimiento, que ya poseen asociado a algún contexto, para abordar una situación nueva.
El enfoque expertos y novatos
Sin intentar hacer una revisión histórica exhaustiva, lo cual excede el objetivo de este trabajo, en la década de los años ochenta aparecen un conjunto de trabajos que marcan el inicio de una línea de investigación que, con mayor o menor impronta, se extiende hasta el presente (MALONEY, 1994; LARKIN, 1983; CHI et al., 1981; CHI et al., 1982; DE JONG; FERGUSON-HESSLER, 1986; FERGUSON-HESSLER; DE JONG, 1987). Esta línea, denominada en la literatura como estudios de expertos y novatos, tiene como objetivo describir las diferencias entre expertos (usualmente profesores de física) y novatos (usualmente estudiantes), referidas tanto a su conocimiento de base como a los procedimientos que ocurren durante el proceso de solución.
Los resultados de estos estudios tuvieron un alto impacto en la comunidad de educación en física interesada en la tarea de resolución de problemas y sirvieron para construir un andamiaje teórico de numerosas investigaciones en ese campo. Algunas de ellas han servido de fundamento para orientar el desarrollo de estrategias de enseñanza cuyo fin es mejorar el desempeño de los estudiantes de física (GANGOSO et al., 2006; FOSTER, 2000; HUFFMAN, 1994; MALONEY, 1994; MESTRE, et al., 1993). Estos autores toman como punto de partida a estudiantes de física como los sujetos novatos, a quienes se instruye de manera de favorecer en ellos el desarrollo de ciertas habilidades expertas. Estos estudios centran su atención en el punto de partida (el novato y sus características) y en la meta (ciertos hábitos tipo experto).
Respecto de los tipos de conocimiento puestos en juego durante el proceso de solución, numerosos estudios enmarcados en esta perspectiva presuponen la siguiente categorización: conocimiento situacional, conocimiento conceptual, conocimiento procedimental y conocimiento estratégico. Según la revisión de De Jong y Ferguson-Hessler (1996), los estudios que refieren a esta clasificación obedecen mayoritariamente a las siguientes conceptualizaciones:
-
Conocimiento situacional: conocimiento acerca de situaciones tal como típicamente aparecen en los problemas de física. Este conocimiento permite al sujeto identificar los rasgos relevantes del enunciado del problema y, si es necesario, suplementar la información contenida en el mismo. Puede servir para crear una representación del problema, desde la cual,
si la organización del conocimiento es adecuada, se puede recuperar el conocimiento conceptual y procedimental.
-
Conocimiento conceptual: conocimiento acerca de hechos,
conceptos y principios físicos que pueden aplicarse a ciertos dominios. Este conocimiento funciona como información adicional que los sujetos incorporan al problema para resolverlo.
-
Conocimiento procedimental: conocimiento de las acciones o
manipulaciones válidas en el dominio de la física. Este conocimiento ayuda al sujeto a realizar las transiciones de un estado a otro del problema.
-
Conocimiento estratégico: ayuda a los sujetos a organizar su proceso de resolución dirigiendo los estadios que ellos
deberían transitar para alcanzar la solución. Una estrategia puede ser vista como un plan general de acción desde el cual se desprenden las actividades concretas de solución.
La segunda cuestión central que se aborda en el estudio de la resolución de problemas es la naturaleza del proceso de solución. Un modelo para el proceso de solución de problemas en física que es suficientemente representativo e influyente en investigaciones posteriores, es el de Larkin3 3 Se ha elegido el modelo de Larkin (1983) pues es suficientemente abarcativo y general respecto de la idea que se pretende poner en evidencia. Otros ejemplares pueden encontrarse en Maloney (1994). (1983). Basada en investigaciones propias y de otros colegas, ella propone un modelo para el proceso de solución que, en principio, es capaz de dar cuenta del desempeño experto y novato. La propuesta consiste en un proceso de tres estadios cada uno de los cuales implica la construcción de una representación de características propias. Estas representaciones, dan lugar a grados de abstracción cada vez mayores y el pasaje entre una y otra involucra ciertas reglas, tal como muestra la Figura 1.
Las características de estas representaciones y reglas son las siguientes:
-
. Representación ingenua: esta representación contiene entidades visibles y cotidianas mencionadas en el enunciado del problema, que interactúan entre ellas permitiendo predecir los eventos que ocurren en tiempo real. Da cuenta de un estadio para el cual no es necesario conocimiento físico formal de conceptos y principios. Esta representación guía, según Larkin, la construcción de la representación física vía las reglas de construcción.
-
. Representación física: esta representación contiene conocimiento físico formal y cualitativo. Las representaciones físicas difieren en muchos aspectos de las representaciones ingenuas. Estas son independientes del tiempo dado que incorporan los principios físicos relevantes, los cuales consisten en relaciones que pueden ser aplicadas en cualquier orden. Esas representaciones proveen suficientes fuentes de inferencias, de manera que la información puede ser determinada de numerosas maneras. Finalmente, esas representaciones contienen entidades como fuerzas, momentos y velocidad que están localizadas, es decir, los atributos de esas entidades están localizadas a las entidades mismas, y no a su entorno, como sucede con las representaciones ingenuas.
-
. Representación matemática: es el conjunto de ecuaciones que representan cuantitativamente a la representación física. La generación y comprensión de estas ecuaciones está, según Larkin, estrictamente guiada por la representación física.
-
. Reglas de construcción: estas reglas actúan sobre la representación ingenua para producir las entidades de la representación física. Estas reglas están definidas sólo en términos de conceptos y principios físicos (elementos de la representación física) sin alusión a ningún elemento de la representación ingenua.
-
. Reglas de extensión: actúan sobre la representación física para agregar nuevas entidades a esa representación. Estas reglas están definidas sólo en términos de conceptos y principios físicos (elementos de la representación física) sin alusión a ningún elemento de la representación ingenua.
Un enfoque múltiple y contextualizado de la cognición
Este enfoque modela el conocimiento de los estudiantes en términos de elementos cognitivos más pequeños que, por ejemplo, los conceptos, leyes o procedimientos de la física. Estos elementos forman una red que se activa parcialmente ante una demanda cognitiva. Esta activación depende del contexto en el que se presenta la tarea y puede presentar distintos grados de estabilidad. Distintos investigadores han conceptualizado de maneras ligeramente diferentes a estos elementos cognitivos, pero en general este tipo de aproximación al conocimiento ha sido denominado en la literatura como "conocimiento en piezas" o "enfoque múltiple y contextualizado de la cognición". Hammer (2004), Redish (2004) y Hammer y colaboradores (2005) han denominado "recursos cognitivos" a estos elementos o piezas de conocimiento, mientras que DiSessa y Sherin (1998) los llaman "primitivos fenomenológicos". Más allá de las diferencias entre ambas conceptualizaciones, en ambos casos estos elementos se consideran generados a partir de la experiencia con el mundo físico y se supone que existen porque han sido útiles para entender situaciones en determinados contextos. En este análisis se adoptará la conceptualización propuesta por Hammer (2004), Redish (2004) y Hammer et al. (2005), denominando recursos cognitivos a las piezas elementales de la cognición.
Es una visión contextualizada de la cognición porque propone que la activación de estos recursos está íntimamente relacionada con el contexto en el que ese recurso es útil. Para los autores todo recurso es útil en algún contexto, de lo contrario no existiría como tal. Es una visión múltiple de la cognición porque no presupone que los recursos cognitivos sean conceptos, principios o procedimientos físicos que están o no están en la mente de los estudiantes. En vez de ello presupone que la activación de un conjunto de recursos cognitivos puede, en un determinado contexto, dar lugar a razonamientos que están de acuerdo o no con un concepto, una ley o un procedimiento físicamente correcto. Los recursos no son correctos o incorrectos en sí mismos, sino que pueden ser valorados en términos de su adecuación o no a un contexto dado. Estos recursos cognitivos son clasificados por sus autores en conceptuales y epistémicos.
Los recursos cognitivos conceptuales son aquellos que les permiten a las personas entender una situación física. El mapeo de esos recursos (el proceso de trasladar una idea abstracta a una situación física concreta) sobre algunas magnitudes físicas puede dar lugar a una descripción que esté de acuerdo o no con algún concepto o principio físico. Por ejemplo, cuando a los estudiantes se les pregunta acerca de las causas de las estaciones del año, una respuesta bastante generalizada consiste en describir el movimiento de la tierra alrededor del sol como una elipse, estando el sol ubicado en uno de sus focos. Ellos explican que los veranos ocurren cuando la tierra está más cerca del sol y los inviernos cuando está más lejos de éste. Esta respuesta, que es incorrecta, puede explicarse a partir de la activación de los recursos "a menos, más" y "a más, menos", mapeados sobre la distancia tierra-sol y sobre la intensidad de la energía solar en la tierra. Estos dos recursos no son correctos ni incorrectos por sí mismos, y pueden dar lugar a respuestas correctas o incorrectas según el contexto en el que se activen. Pueden dar lugar a respuestas correctas si se activaran para entender la temperatura de un objeto en relación con su distancia a una fuente de calor. También podría dar lugar a una respuesta correcta si se activaran para entender la relación entre la iluminación en un punto y su distancia a la fuente, o para entender la relación entre la intensidad del campo eléctrico en un punto y la distancia desde ese punto a una distribución de cargas.
Los recursos cognitivos epistémicos son aquellos que operan sobre el conocimiento de las personas, permitiendo entender distintas formas y distintas fuentes del conocimiento a ser utilizado. Por ejemplo, un estudiante puede considerar a un determinado problema como una actividad en la cual hay que encontrar las fórmulas que relacionen los datos y las incógnitas para obtener la respuesta, o como una situación en la que no hace falta utilizar ninguna fórmula para hacer cálculos sino responder a partir del sentido común, o bien como una situación que les permite entender porqué ciertos aspectos de un concepto o principio físico son relevantes para su resolución y otros no. Estas diferentes posturas con respecto al conocimiento pueden explicarse mediante la activación de recursos epistémicos distintos, que no son correctos ni incorrectos en sí mismos, sino que pueden ser adecuados o no para resolver un determinado problema. La activación de recursos epistémicos siempre conlleva la activación de recursos conceptuales y viceversa, se trata de procesos simultáneos y complementarios. Desde esta perspectiva, una respuesta equivocada desde el punto de vista de la física podría ocurrir como consecuencia de la activación de recursos cognitivos- que en otro contexto pueden ser muy útiles- en un contexto inapropiado.
Dentro de este enfoque y con el propósito de estudiar los procesos de solución de estudiantes universitarios de física, Tuminaro (2004) desarrolló el concepto de juego epistémico. Un juego epistémico es una actividad coherente que usa tipos particulares de conocimientos y procesos, para crear conocimiento nuevo o resolver un problema. Cada juego epistémico está definido por una ontología y una estructura como muestra el Cuadro 1. La ontología está dada por los tipos de recursos cognitivos involucrados y por una forma epistémica que es un objeto que guía la búsqueda durante el juego (por ello es una componente ontológica con funciones epistémicas). La estructura de un juego epistémico está dada por las condiciones de entrada y de salida (o finalización) del juego y por los movimientos intermedios. El Cuadro 1 resume las componentes que definen a un juego epistémico.
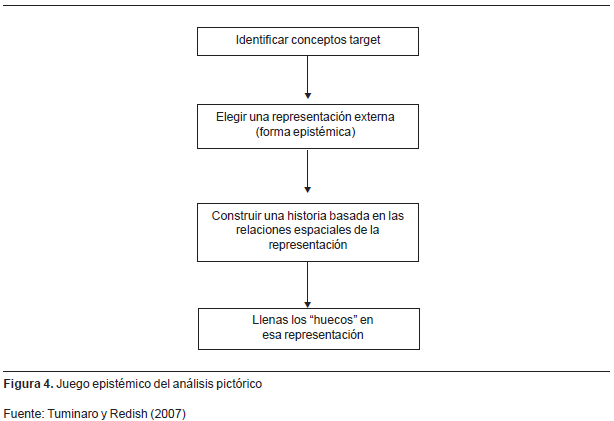
La conceptualización de los juegos epistémicos que se muestra en el Cuadro 1, le permitió a Tuminaro (2004) entender distintos procesos de solución llevados a cabo por un grupo de estudiantes universitarios de física. Cada uno de estos juegos se diferencia entre sí por alguna de sus componentes ontológicas y/o estructurales. Las figuras 2, 3 y 4 representan los movimientos de tres de estos juegos4 4 Otros juegos pueden consultarse en Tuminaro y Redish (2007). . Las formas epistémicas de esos tres juegos, es decir los elementos que guían la búsqueda durante el proceso de solución, son diferentes. En el juego de atribuir significado físico a la matemática, la forma epistémica son las ecuaciones. En el juego de los mecanismos físicos, la forma epistémica es la historia, y en el juego del análisis pictórico la forma epistémica es la representación externa.
Análisis comparativo sobre algunos ejemplos concretos
Un primer análisis comparativo entre los dos enfoques presentados permite advertir que ambos responden de modo diferente a los mismos dos aspectos centrales a considerar en el estudio de la resolución de problemas: la naturaleza del conocimiento puesto en juego durante la resolución y la naturaleza de los procesos que ocurren. En el primer enfoque, los conocimientos situacional, conceptual, procedimental y estratégico se relacionan entre sí para dar lugar a un proceso de solución.
En el segundo, los recursos conceptuales y epistémicos se relacionan entre sí para dar lugar a distintos juegos epistémicos. Es decir, las preguntas son las mismas, y en lo que sigue del trabajo se intentará mostrar cómo cambian las respuestas.
Otra cuestión que se desprende del análisis de ambos enfoques es que el primero tiene una tendencia prescriptiva y el segundo, descriptiva (al menos en lo que refiere al conocimiento de los estudiantes). En el primero, las definiciones y procesos están dados en términos del conocimiento formal de física y de características expertas de resolución. Este enfoque describe el conocimiento del principiante a partir de sus diferencias o similitudes con las características expertas. En el segundo enfoque las definiciones de conocimientos y procesos no involucran conocimiento formal de física ni procesos de solución expertos. El conocimiento y el proceder del principiante se describen en términos de recursos cognitivos y juegos epistémicos que en sí mismos no son correctos o incorrectos desde el punto de vista de la física. El primer enfoque puede ser útil para saber cuán experto es un sujeto, el segundo puede resultar más útil para investigar cómo las personas se vuelven expertas.
En el próximo apartado se intenta profundizar el análisis comparativo sobre un conjunto de registros provenientes de distintos estudios de campo referidos a la resolución de problemas en física. Se comparan las diferentes respuestas que ambos enfoques permiten dar a las mismas preguntas: A) De la naturaleza de los procesos y B) De la naturaleza del conocimiento puesto en juego durante esta tarea. Los ejemplos de las secciones A y B se individualizan por el nombre del problema que resolvían los sujetos de cada estudio. Para cada uno de los estudios sobre los que se realiza el análisis se presenta secuencialmente: a) el problema que resolvieron los estudiantes, b) los registros (verbalizaciones) obtenidos a partir de esas tareas, y c) las interpretaciones de los registros según los dos enfoques teóricos en cuestión.
A. Del proceso de solución: ¿Proceso único o varios procesos?
Ejemplo A1: El problema del choque entre dos cuerpos
-
La masa de un objeto A es la mitad de la de un objeto M. El objeto A se mueve con una velocidad constante
 en dirección al cuerpo M que está en reposo. A choca con M y como consecuencia del choque A queda en reposo. Aplique la segunda ley de Newton
en dirección al cuerpo M que está en reposo. A choca con M y como consecuencia del choque A queda en reposo. Aplique la segunda ley de Newton  a cada uno de los objetos para comparar los cambios en los momentos) de cada uno de ellos
a cada uno de los objetos para comparar los cambios en los momentos) de cada uno de ellos  debidos a la colisión.
debidos a la colisión.
Este problema fue utilizado por Tuminaro y Redish (2007) para estudiar los procesos de solución de estudiantes universitarios de física. Lo que sigue es el extracto de protocolo de los estudiantes "R", "T" y "B", resolviendo este problema:
R:Entonces la fuerza neta para A, la fuerza neta para M esta es una masa grande y esta otra es una masa chiquita y las fuerzas son iguales, entonces ésta tiene una velocidad grande y la otra una chiquita entonces el cambio en la velocidad de A tiene que ser más grande. Velocidad grande masa chica, velocidad chica, masa grande
T: si, claro
B: si
R: entonces los dos momentos son los mismos
B: sí, pero el cambio de momento del cuerpo A
R: ¡pero no pueden ser los mismos porque son opuestos!... no sé no esto no está bien
Según el modelo de Larkin (1983), la representación ingenua se construye al comienzo del proceso de solución. En este protocolo no se advierten evidencias de tal representación. Sí se advierten evidencias de la representación física durante el análisis cualitativo "[ ] esta es una masa grande y esta otra es una masa chiquita [ ]", también se evidencia la presencia de una representación matemática, porque el análisis cualitativo se realiza sobre una relación cuantitativa entre conceptos físicos (las ecuaciones dadas en el enunciado del problema). Lo que no queda claro en este protocolo es cuál es la secuencia de las representaciones física y matemática, ya que el proceso parece estar dirigido desde el comienzo por las ecuaciones para F y para Dp. Según Larkin (1983), la representación física precede a la representación matemática y guía su construcción, pero en este ejemplo la secuencia es diferente: las ecuaciones parecen preceder el análisis cualitativo y parecen dirigir el proceso de solución.
En la Figura 2 se muestra la interpretación de Tuminaro (2004, p. 70) en términos de los movimientos del juego epistémico que él denomina "atribuir significado físico a la matemática". La forma epistémica de este juego son las ecuaciones, que en este caso son dadas en el enunciado.
Este ejemplo da cuenta del juego de atribuir significado físico a la matemática, un juego en el que el primer movimiento es la identificación de aquello que se pretende encontrar y que se denomina "concepto" target (las comillas indican que este concepto no necesariamente coincide con un concepto físico). En este caso particular los dos primeros movimientos, que son la identificación de los "conceptos" target y sus relaciones, están dados en el enunciado. El tercer movimiento es el desarrollo de la historia utilizando esos "conceptos", y el cuarto movimiento es la evaluación de la historia.
Ejemplo A2: El problema del ascensor
-
Una persona está parada sobre una balanza que está en el piso de un ascensor. La persona tiene una masa de 80 kg y la balanza 7kg:
a) Dibuje las fuerzas que están actuando sobre la persona y sobre la balanza cuando el ascensor está detenido
b) El ascensor comienza a descender desde el reposo. En 6 segundos alcanza una velocidad de 8m por segundo. Suponiendo a la aceleración uniforme durante ese tiempo, ¿cuáles de las fuerzas antes dibujadas cambia? Para cada una de las fuerzas que cambia, especifique si aumenta o disminuye.
Este problema fue presentado por Tuminaro (2004) durante el mismo estudio del ejemplo anterior. Los estudiantes "L", "T" y "M", luego de realizar un diagrama de cuerpo aislado para la balanza y para la persona, continuaron resolviendo el problema para contestar el apartado b:
L : ok, ahora nosotros conocemos ellos nos dieron los pesos entonces nosotros sabemos que la persona pesa 80 kg y la balanza 7 kg y nosotros determinamos la aceleración
T: ¿necesitamos hacer algún cálculo?
L: no se
T: no se si ellos nos están pidiendo cálculos
L: Ellos no quieren números, pero nosotros no podríamos darnos cuenta de la respuesta quizás algunos números os ayudarían
T: Bueno, entonces, veamos, la normal sería ¿no creen que debería decrecer? Al principio
M: cuando se está acelerando hacia abajo, la fuerza de
T: ¡claro! Es casi lo mismo que, exagerando un poco, como si la persona se cayera y casi no siente el piso
L: ok, tiene sentido por eso la persona debería pesar menos
T: bien
L: y es lo que me acuerdo de la secundaria
La interpretación según el modelo de Larkin (1983) de este segmento de protocolo, sugiere que no hay indicios que se correspondan con una representación física y/o matemática. En cambio, todo el proceso parece estar dirigido por una única representación ingenua. A diferencia de las predicciones de la propuesta de Larkin (1983), los estudiantes resuelven exitosamente el problema a partir de una representación ingenua, sin la construcción de ninguna representación física ni matemática.
La Figura 3 muestra la interpretación de Tuminaro (2004) en términos del "juego de los mecanismos físicos". La forma espistémica de este juego es la historia desarrollada en el primer movimiento.
En este juego los estudiantes comienzan con un primer movimiento en el que construyen una historia física coherente basada en su intuición de los mecanismos físicos, para luego evaluarla en el segundo y último movimiento. Una característica distintiva de este juego es que en la historia no se hace referencia explícita a ecuaciones matemáticas ni a principios formales. "T" argumenta que no es necesario ningún cálculo para responder si las fuerzas aumentan o disminuyen.
Ejemplo A3: El problema del espejo
-
Considere una persona parada frente a una pared sobre la cual se desea colgar un espejo plano. Suponiendo que la persona mide 1,65 m y tiene los ojos a 1,55 m ¿Qué tamaño tiene que tener el espejo más chico (espejo mínimo) para que la persona pueda ver su imagen completa?
Este problema fue pensado para estudiar el conocimiento que ponían en juego estudiantes universitarios de física al resolverlo. El estudio fue llevado a cabo los autores del presente trabajo5 5 Extraído de Buteler y Coleoni (2009a). . Lo que sigue es un extracto de la entrevista del estudiante "F" y el entrevistador "E".
F: Si, para que se vea completamente tendría que ser un espejo grande, de 1.65 o más... por lo menos 1.65... O sea, también depende de la distancia a la que él esté
E: ¿o sea que vos pensás que esa respuesta depende de algo que no te están diciendo?
F: claro...si él está más cerca, por más que sea grande el espejo, se va a ver menos... y...si...me parece que esto es así
E: ¿vos crees que se podrá resolver este problema un poco más concretamente?
F: ¿cómo resolver?... ¿calcular la altura?... así no, me parece que no, porque no tengo la distancia a la que se va a colocar la persona...
E: ¿Y si tuvieras la distancia?
F: no sé como haría, bueno, no sé... O por lo menos si cuelgo el espejo acá, acá donde está él, bueno mas o menos sí lo podría calcular ... viendo más o menos los rayos... (Hace un dibujo del espejo, la persona y los rayos)...y si, pongo el espejo y saco los rayos de acá de la cabeza a la punta del espejo y los otros hacia la otra punta del espejo... es como que... si él va a estar acá donde dice el problema... y... el espejo ahí... je, je...desde el ojo, tendría que cubrir toda la imagen de él, o sea, la reflejada...
Desde el punto de vista de Larkin (1983), la primera parte del protocolo se corresponde con una representación ingenua del problema: "[ ] para que se vea completamente tendría que ser un espejo grande [ ]", y la última, con una representación física "[ ] o por lo menos si cuelgo el espejo acá donde está él, bueno más o menos sí lo podría calcular[ ]". Sin embargo, no hay evidencias de que haya alguna conexión entre ellas, más bien parece haber evidencias de lo contrario, es decir de que la representación física no está construida a partir de la representación ingenua. Cada una de ellas parece dar lugar a procesos de solución contradictorios entre sí: uno incorrecto (al principio) y otro correcto (al final).
Desde un enfoque múltiple y contextualizado de la cognición, es previsible que los sujetos cambien de juego epistémico durante la realización de un mismo problema. Estos cambios pueden producirse debido a algún cambio producido en el contexto del problema. Según este enfoque, el contexto es definido en relación al individuo: dado un individuo con respecto a un conjunto de recursos cognitivos, el contexto son las circunstancias en las que ese individuo activa confiablemente ese conjunto de recursos. Según la conceptualización de Tuminaro (2004), este sujeto percibe dos contextos distintos: uno antes y otro después de la pregunta del investigador, y utiliza dos juegos distintos durante su proceso de solución: primero el juego de los mecanismos físicos, y luego el juego del análisis pictórico (Cuadro 2).
En esta trascripción se puede observar cómo este estudiante primero juega el juego de los mecanismos físicos: construye una historia "Si, para que se vea completamente tendría que ser un espejo grande, de 1.65 o más... por lo menos 1.65... O sea, también depende de la distancia a la que él esté " y la evalúa "... y...si...me parece que esto es así" (ver los movimientos en la Figura 3). Luego juega el juego del análisis pictórico cuyos movimientos se muestran en la Figura 4.
Los movimientos de este último juego son: 1) Determinar el concepto target (tamaño del espejo): "[ ] si cuelgo el espejo acá, acá donde está él, bueno mas o menos sí lo podría calcular [ ]" 2) Elegir una representación externa que en este caso es el trazado de los rayos: "[ ]viendo más o menos los rayos [ ]." 3) Construir una historia basada en las relaciones espaciales entre los objetos involucrados en la representación externa: "[ ] y si, pongo el espejo y saco los rayos de acá de la cabeza a la punta del espejo y los otros hacia la otra punta del espejo [ ]" y 4) completar la información faltante en la representación elegida: "[ ] es como que... si él va a estar acá donde dice el problema... y... el espejo ahí... je, je...desde el ojo, tendría que cubrir toda la imagen de él, o sea, la reflejada [ ]".
La conceptualización de Tuminaro (2004) permite entender esta aparente falta de coherencia durante el proceso de solución a partir de algún cambio en el contexto del problema que da lugar a un cambio en el juego epistémico de "F". Este cambio podría ser objetado en tanto puede haber sido producto de la intervención del entrevistador sin embargo, lo que no puede objetarse es que "F" es capaz de jugar otro juego epistémico diferente del que venía jugando y que, en este caso, tal cambio lo dirige hacia la solución físicamente correcta. Este cambio no puede ser interpretado desde el modelo de Larkin (1983).
Ejemplo A4: El problema de la ventana
-
Una persona está en su habitación mirando hacia la ventana y observa a otra persona que está afuera. Ambas personas tienen la misma altura, y se encuentran a la misma distancia de la pared
1. ¿Qué tamaño mínimo debería tener la ventana para que la persona dentro de la habitación pueda observar completamente a la que está afuera?
2. Si ahora esta persona se alejara de la ventana una cierta distancia x, ¿cambiaría la respuesta anterior?
Este problema, junto con el problema del espejo, fue presentado a un grupo de estudiantes universitarios de física a los fines de estudiar si el problema de la ventana podía ayudar a que los estudiantes resolvieran exitosamente el problema del espejo6 6 Extraído de Buteler y Coleoni (2009b). . Estos dos problemas tienen la misma respuesta y el procedimiento utilizado para resolver el problema de la ventana (la construcción del cono de visión del observador) puede ser utilizado para resolver correctamente el problema del espejo. Se transcriben extractos de verbalizaciones de "L" durante la resolución del espejo y de la ventana:
L: y el tamaño mínimo tendría que ser el del hombre de la altura del hombre para que se vea todo y porque en un espejo plano la imagen no se agranda ni se achica y después en el otro punto que dice que pasa si se aleja entonces si la distancia es más grande la imagen que se forme va a ser más chiquita en el reflejo y entonces el espejo ahí no se que altura tendría que tener va a depender de la distancia
Durante la resolución del problema de la ventana:
L: claro no antes en el espejo para ver la imagen completa te hacía falta un espejo grande, del tamaño de la persona y ahora no ahora es suficiente que la ventana llegue a no sé porque lo que mide el ojo la ventana no tiene que llegar hasta el piso tendría que llegar hasta donde vos le puedas ver los pies al que está del otro lado (comienza a dibujar sobre el papel el cono de luz) queda determinada por la intersección entre lo que vos ves y la pared entonces la ventana tendría que ir desde acá hasta acá (muestra el resultado en su dibujo) y vos la verías completa a la otra persona
Según el modelo de Larkin (1983) , el proceso de solución es independiente del contexto del problema, por lo que prevé el mismo proceso de solución para ambos. En este ejemplo se puede observar que la respuesta de "L" parece estar guiada, en términos de la propuesta de Larkin (1983), por una representación ingenua cuando resuelve el problema del espejo y por una representación física cuando resuelve el problema de la ventana. El modelo de Larkin (1983) no prevé variación del proceso de solución en función del contexto, pero esta variación se observa en este ejemplo.
El enfoque múltiple y contextualizado de la cognición prevé variaciones en la activación de recursos y juegos epistémicos en función del contexto. Según la conceptualización de Tuminaro (2004), las verbalizaciones de "L" pueden interpretarse como respondiendo a distintos juegos epistémicos en cada uno de los problemas. Los juegos epistémicos y sus movimientos se señalan en el extracto de protocolo del Cuadro 3.
Este ejemplo muestra cómo "L" cambia de juego epistémico cuando resuelve problemas similares (desde el punto de vista de la física) presentados contextos diferentes. L procede con juegos diferentes ante el problema del espejo y el problema de la ventana, lo cual se contrapone con la existencia de un proceso único de solución independiente del problema a resolver.
B. Del conocimiento puesto en juego en el proceso:¿Estabilidad o variabilidad?
Ejemplo B1: El problema del bloque sobre la superficie con rozamiento
-
Una persona empuja horizontalmente un bloque que se encuentra sobre una superficie también horizontal. Luego de un tiempo el bloque queda en reposo. Diga cuáles son las fuerzas que actúan sobre el bloque y porqué se detiene. Si ahora se empuja a un bloque del mismo material pero de mayor peso sobre la misma mesa, ¿cambia en algo respecto de la situación anterior? (asuma que los dos bloques tienen la misma velocidad inicial)
Este problema fue presentado en un estudio llevado a cabo por Sherin (2006) a fin de estudiar el rol del conocimiento físico intuitivo en las prácticas expertas de solución. Se transcribe un extracto de protocolo de dos estudiantes universitarios de física resolviendo este problema:
A: si el bloque es más pesado, entonces la fuerza de roce será mayor y disminuirá la velocidad más rápidamente que para el otro caso y queda quieto antes
A pero algo parece raro porque si vos tuvieras un bloque pesado y otro más liviano que estuvieran por chocarte dos situaciones diferentes si vos quisieras frenar esos bloques hasta que queden en reposo vas a tener que hacer más fuerza para frenar el bloque más pesado que para el más liviano
B: sí, es verdad!
A: porque aunque ambos estén sobre la misma superficie, con el mismo rozamiento, lógicamente el bloque más pesado es más difícil de frenar .es como frenar una pelota de fútbol más grande
Luego, "B" escribió la ecuación F = ma y dijo:
B : la fuerza de fricción F aumenta a medida que m aumenta entonces yo creo que la distancia recorrida sí depende de la masa del cuerpo pero si F aumenta, la aceleración también aumenta!
A continuación "A" y "B" escribieron la expresión matemática para la fuerza de fricción y la reemplazaron en la ecuación F = ma, de donde obtuvieron, asombrados, que la aceleración no depende de la masa del cuerpo.
Si se utiliza la categorización de De Jong y Ferguson-Hessler (1996) podría interpretarse que al principio, el razonamiento seguido por "A" y "B" está sustentado en su conocimiento situacional del problema, y a partir de que escriben la ecuación matemática, en conocimiento conceptual y procedimental. Podría interpretarse que el conocimiento situacional referido a fuerzas, velocidades y masas, fue el sustento para recuperar el conocimiento conceptual y procedimental necesario para resolver el problema. Según la definición de conocimiento situacional éste "Puede servir para crear una representación del problema, desde la cual, si la organización del conocimiento es adecuada, se puede recuperar el conocimiento conceptual y procedimental " (de Jong y Ferguson-Hessler, 1996, p. 106) Pero, ¿Es adecuada la organización del conocimiento situacional utilizado por estos estudiantes? ¿Cómo se entiende que a partir de dos intuiciones contradictorias entre sí, construyan la solución correcta? Parece haber una inconsistencia entre un conocimiento situacional incorrecto desde el punto de vista de la física y un conocimiento conceptual correcto que los lleva hacia la solución del problema.
Desde un enfoque múltiple y contextualizado, las respuestas de los sujetos a las cuestiones planteadas pueden ser interpretadas como provenientes de la activación de dos recursos cognitivos: "a más, menos" y "a más, más", mapeados sobre el peso del bloque y la distancia recorrida por el mismo antes de detenerse.
"A": si el bloque es más pesado, entonces la fuerza de roce será mayor y disminuirá la velocidad más rápidamente que para el otro caso (a más, menos) y queda quieto antes
"A" pero algo parece raro porque si vos tuvieras un bloque pesado y otro más liviano que estuvieran por chocarte dos situaciones diferentes si vos quisieras frenar esos bloques hasta que queden en reposo vas a tener que hacer más fuerza para frenar el bloque más pesado que para el más liviano (a más, más)
"B": sí, es verdad!
"A": porque aunque ambos estén sobre la misma superficie, con el mismo rozamiento, lógicamente el bloque más pesado .es como frenar una pelota de fútbol más grande (a más, más)
Estos estudiantes activaron dos recursos que dieron lugar a dos intuiciones contradictorias entre sí, ambas con sentido para ellos. Analizando sus razonamientos bajo la segunda ley de Newton, ambas intuiciones son adecuadas a la situación, pero sus efectos se cancelan entre sí, de manera tal que la distancia recorrida por los bloques resulta independiente del peso de los mismos. Luego de algunos intentos fallidos, estos sujetos resolvieron el conflicto escribiendo matemáticamente la segunda ley de Newton para el bloque, pero no volvieron a sus intuiciones, simplemente se conformaron ante la respuesta dada por la ecuación para la fuerza. Ante estos razonamientos es difícil presuponer estabilidad estructural para el concepto Newtoniano de fuerza. Más bien, estos estudiantes parecen disponer de recursos cognitivos cuya activación es inestable pues depende fuertemente del contexto en el que son utilizadas. En este ejemplo, estos recursos parecen desactivarse a partir de que escriben la segunda ley de Newton para la fuerza de fricción. Parece más acertado hablar del conocimiento de los estudiantes en términos de recursos cognitivos que se activan contextualmente, que en términos de conocimiento situacional y conceptual tal como lo definen De Jong y Ferguson-Hessler (1996).
Ejemplo B2: El problema de la barra conductora en el campo magnético
-
Por una barra horizontal conductora de longitud l y masa m se hace circular una corriente eléctrica de intensidad i. Esta barra está en una zona del espacio donde existe un campo magnético constante y uniforme B, también horizontal y formando una ángulo q con éste. Sabiendo que i = 0.01 A, B = 0.3 T, l = 0.5 m, g = 9.8 m/s
2y m = 0.045 Kg, ¿para qué valor de
 estará la barra en equilibrio?
estará la barra en equilibrio?
Inicialmente, este problema fue presentado por los autores del presente trabajo, a un grupo de estudiantes universitarios de física, a fin de investigar algunas características del conocimiento que utilizaban estos estudiantes para resolverlo7 7 Extraído de Buteler y Coleoni (2009a). . El extracto que se muestra corresponde a la alumna "C" y el entrevistador "E".
C : hay una fuerza que tiende a alinearlo al conductor al campo
E: ¿y quién provoca esa fuerza?
C : obviamente tiene que provocarlo el campo exterior...la intensidad y la longitud de la barra...
E: ¿y donde esta aplicada esa fuerza y qué características tiene?
C : bueno, la fuerza es una magnitud vectorial, por lo tanto al ser B una magnitud vectorial, tiene que estar multiplicado por i por l y por el seno del ángulo, ¿no es así?
E: ¿y para dónde apunta esa fuerza?
C : eh, y...tendría que ser perpendicular al plano horizontal...para arriba, va haber una fuerza para arriba... yo aplico la fuerza...tendría que inclinarse para el lado del campo...
E: ¿cómo?
C : tengo la barra...no me sale con la otra forma de la mano derecha...la barra tendría que irse para allá para el lado del campo
E: ah
C : si, para donde apunta la fuerza...bueno, la fuerza si sé que tiene que ser perpendicular hacia arriba
E: bueno, ¿entonces?
C : y no, la va a desplazar hacia la dirección del campo...y el valor de tita... y va a tener que ser el seno del ángulo que forma la intensidad con el campo
La primera pregunta que surge del análisis según la categorización de De Jong y Ferguson-Hessler (1996) es ¿A qué categoría pertenece el conocimiento de que la fuerza que realiza el campo magnético externo tiende a alinear a la barra con el campo? ¿Cómo se explica la coexistencia entre esta propiedad y el que esa fuerza también sea vertical y hacia arriba (y que acuerda con lo que predice el electromagnetismo)? El conocimiento referido a una fuerza que alinea la barra con el campo no pertenece a ninguna de las definiciones dadas por De Jong y Ferguson-Hessler (1996) y además entra en contradicción con el concepto de fuerza de Lorentz, aparentemente también utilizado por este estudiante para resolver este problema.
Según un enfoque múltiple y contextualizado, la respuesta de esta estudiante se puede interpretar en términos de la activación de un recurso cognitivo denominado alineación. El recurso de alineación, según el cual existen objetos o entidades que se ubican paralelas a la dirección de algún campo de fuerzas, es un recurso útil cuando se lo activa en otros contextos. Mapeado sobre, por ejemplo, momentos dipolares (eléctricos y magnéticos) y campos (eléctricos y magnéticos respectivamente), genera respuestas que están de acuerdo con la física de las interacciones eléctricas y magnéticas. El razonamiento de "C" parece estar sustentado sobre dos ideas diferentes. Una de ellas interpretada como producto de la activación del recurso de alineación mapeado sobre la barra conductora y el campo magnético, y la otra parecería provenir de su conocimiento formal producto de la instrucción recibida. "C" parece conocer algunas de las propiedades de la fuerza sobre un conductor con corriente en un campo magnético, en particular que es una fuerza dirigida hacia arriba y perpendicular al conductor y al campo, pero a la vez piensa que el conductor debe alinearse con el campo. Hay una variabilidad entre esas dos ideas, posiblemente no percibida por ella durante la entrevista, que hace difícil (si no imposible) decidir cuál es el conocimiento conceptual involucrado en este proceso de solución. Más aún, es posible que si ella se hubiera sentido forzada a dar un resultado numérico, habría utilizado la expresión correcta para la fuerza sobre un conductor en un campo magnético y habría intentado calcular el valor para el ángulo è, aún creyendo que el conductor se alinea con el campo. No es posible decidir ante esta evidencia si esta alumna ha construido o no el concepto de fuerza de Lorentz sobre una barra conductora. Lo que sí parece ocurrir es que su razonamiento se basa alternativamente sobre la activación del recurso de alineación y la definición matemática de fuerza de Lorentz sobre la barra.
Ejemplo B3: Problema del espejo y problema de la ventana
Volvamos al ejemplo A3 (problema del espejo) de la sección anterior. "F" parece utilizar dos tipos distintos de conocimiento según la categorización de De Jong y Ferguson-Hessler (1996): al principio, conocimiento situacional: "Si, para que se vea completamente tendría que ser un espejo grande, de 1.65 o más... por lo menos 1.65... O sea, también depende de la distancia a la que él esté" y al final, conocimiento procedimental: " si cuelgo el espejo acá, acá donde está él, bueno mas o menos sí lo podría calcular ... viendo más o menos los rayos...", a partir de lo cual llega a la respuesta correcta del problema. Sin embargo, el razonamiento inicial de que el espejo tiene que ser tan grande como la persona y que puede ser más chico cuando la persona se aleja, no cumple con las características del conocimiento situacional definido según De Jong y Fergusson-Hessler (1996). Este conocimiento situacional no le permite a este sujeto recuperar el conocimiento conceptual y procedimental necesario para resolver el problema. Más bien parecen dos tipos de conocimiento desconectados entre sí.
Desde un enfoque múltiple y contextualizado, la primera parte del razonamiento de "F" puede ser interpretado como el resultado de la activación de los recursos de contenedor, según el cual la imagen debe estar contenida en el espejo, y del recurso a más, menos según el cual el tamaño mínimo del espejo es cada vez menor a medida que las personas se alejan de él. En la primera parte de su verbalización se puede observar la activación de contenedor y a más, menos mapeados en el contexto de observar la imagen propia en un espejo. Sin embargo, estos recursos parecen desactivarse en la segunda parte de su protocolo que lo lleva a una solución correcta del problema. Otra vez, es difícil saber si este estudiante tiene el concepto de, por ejemplo, reflexión de la luz. Más bien parece disponer de algunos recursos cognitivos que le permiten entender algunos fenómenos ópticos y también parece utilizar algunas ideas provenientes de su instrucción formal que, alternativamente, pasan a sustentar sus razonamientos. Ante estas evidencias es difícil describir el conocimiento de los estudiantes para resolver problemas de física en términos de conceptos y principios físicos cuya naturaleza presupone coherencia y estabilidad.
Discusión: ¿qué cambia con el cambio de perspectiva?
Los ejemplos presentados intentan poner en evidencia el peso de los datos en la reorientación de la teoría y el de la teoría sobre la interpretación de los datos. Concretamente, se ha intentado mostrar que es posible analizar el grado de ajuste de un marco teórico a unos resultados empíricos, y que hay enfoques teóricos que arrojan más información que otros, aún en un ámbito interdisciplinario como lo es la educación en física.
El modelo de Larkin (1983), que quizás sea útil para describir el proceso de solución experto, no parece serlo para describir el proceder del principiante. La representación ingenua, plausible de ser construida por sujetos principiantes, no parece serles útil para continuar con el proceso de resolución. Esta representación debería evolucionar hacia la representación física mediante la aplicación de las reglas de construcción y extensión, las cuales no están plenamente disponibles a los novatos, por estar definidas en términos de conceptos y principios físicos. Si el sujeto que resuelve no posee un manejo acabado de conceptos o principios físicos y de sus relaciones, no va a ser capaz de construir la representación física y, como ésta es condición necesaria para la representación matemática, tampoco construirá ésta última. De hecho, según este modelo, la generación y comprensión de las ecuaciones matemáticas está estrictamente guiada por la representación física. Sin embargo, se sabe que los estudiantes (sujetos con escasa formación) hacen cosas cuando resuelven problemas, despliegan estrategias, ejecutan procesos, y lo hacen utilizando herramientas que sí poseen. El modelo de Larkin (1983) no da cuenta del proceder del principiante, más bien da cuenta de lo que no hacen los estudiantes en comparación con lo que hace el experto.
Por otra parte, el trabajo teórico de Tuminaro (2004) permite poner en evidencia cuán lejos está la descripción de Larkin (1983) (único proceso de solución), de los múltiples abordajes exhibidos por los estudiantes. La variedad de juegos epistémicos, además de ajustarse mejor a las formas de proceder de los novatos, permite predecir algunas características de sujetos novatos antes ignoradas. Por un lado predice la existencia de una diversidad epistémica usualmente ignorada en las descripciones de los estudiantes al resolver problemas, es decir de capacidades que van más allá de reemplazar datos en fórmulas. También pone en evidencia información muy valiosa antes desconocida. Por ejemplo, una característica típica de los novatos dentro de la perspectiva expertos-novatos, es la ausencia de descripciones cualitativas al comienzo o durante el proceso de solución. Si nos permitimos mirar más allá del código binario correcto-incorrecto, la conceptualización de Tuminaro (2004) permite advertir lo contrario. Todos los juegos mostrados poseen un movimiento que responde a la elaboración de una historia del problema que tiene mucho que ver con los movimientos anteriores y posteriores, es decir, que son piezas heurísticamente valiosas durante el proceso de solución. Una descripción más ajustada de la realidad permite un punto más idóneo para investigar cómo estos sujetos refinan sus procedimientos durante su aprendizaje de la resolución de problemas en física.
Respecto de la naturaleza del conocimiento puesto en juego durante la resolución de problemas, se puede observar en los ejemplos propuestos, cuánto más útil resulta una descripción en términos de recursos cognitivos que no son correctos ni incorrectos en sí mismos- que en términos de las definiciones dadas dentro del enfoque expertos y novatos (situacional, conceptual, procedimental) fuertemente condicionadas al conocimiento físico formal. Estas definiciones, que posiblemente son útiles para describir el conocimiento experto, no parecen serlo tanto para describir el conocimiento del novato, ya que definen cómo debería ser el conocimiento del estudiante para abordar exitosamente la solución de un problema de física, en vez de cómo realmente es ese conocimiento. Por ejemplo, la primera definición (conocimiento situacional) es una definición condicional, es decir que no define a ese conocimiento si la organización del mismo no es la adecuada, tal como típicamente sucede en los sujetos novatos. Algo similar ocurre con la segunda (conocimiento conceptual), cuando no se dispone de adecuados conceptos o principios físicos para abordar la solución, característica también usual en principiantes. En este sentido, son definiciones útiles para valorar cuánto dista el conocimiento del novato del conocimiento experto. Las definiciones antes presentadas pueden ser más útiles para establecer metas u objetivos a largo plazo que para investigar el proceso mediante el cual se llega a tales metas.
¿Por qué es más útil una descripción en términos de recursos cognitivos? En primer lugar, porque se ajusta mejor al comportamiento observado en los estudiantes durante la resolución de un problema, el cual parece estar muy ligado al contexto y parece ser bastante inestable. La pregunta siguiente es ¿Cómo es posible que los estudiantes construyan conocimiento "experto" a partir de su conocimiento intuitivo? Descartando la respuesta no-constructivista de que el novato abandona su conocimiento intuitivo y construye conocimiento normativo desde la nada, todavía no hay una respuesta para esta pregunta. Sin embargo, para responderla es ineludible contar con una descripción lo más acabada posible del conocimiento que sí utilizan los estudiantes para aprender. Sólo así se podrá entender cómo éste conocimiento inicial se transforma y se relaciona con la nueva información. Entrando en el campo de la especulación, es plausible pensar que los conceptos físicos que manejan los expertos hayan sido construidos con la ayuda de sus recursos cognitivos desarrollados a partir del contacto con el mundo físico. Según este modelo, esos recursos son útiles antes de ser físicamente correctos o incorrectos. Los estudiantes estarían más cerca de esos elementos primitivos (recursos cognitivos) que del concepto "experto" y sobre la base de los primeros podrían construir los últimos. Esos elementos primitivos deben ser muy útiles pues sin ellos sería imposible aprender. Una idea que se desprende de lo anterior, y que plantea una pregunta sugerente, es hasta dónde es posible aprovechar productivamente la variabilidad y la contextualidad de los recursos cognitivos de los estudiantes para construir nuevo conocimiento.
En términos generales, un enfoque múltiple y contextualizado de la cognición permite acercarse más a los fenómenos cognitivos que ocurren en las mentes de los estudiantes, permitiendo entender mejor por qué se equivocan cuando se equivocan y permitiendo sugerir posibles mecanismos de aprendizaje durante la resolución de problemas. Estas características hablan de un mayor poder descriptivo y explicativo. En cuanto a las implicaciones instruccionales, entender qué ocurre cuando los estudiantes cometen "errores" permite orientar la instrucción para favorecer que los alumnos partan de esos errores para aprender.
Artigo recebido em 24/10/2010. Aceito em 14/02/2011.
- BUTELER, L.; COLEONI, E. Is there something useful in students' mistakes? : a cognitive resources-based approach. Electronic Journal of Science Education, Nevada, v. 13, n. 2, p. 117-135, 2009a.
- ______. Cómo aprovechar la naturaleza contextual del conocimiento para resolver un problema de física: un abordaje basado en recursos cognitivos. Investigações em Ensino de Ciências, Porto Alegre, v. 14, n. 1, p. 7-24, 2009b.
- CHI, M. et al. Categorization and representation of physics problems by experts and novices. Cognitive Science, Norwood, v. 5, n. 2, p. 121-152, 1981.
- CHI, M. et al. Expertise in problem solving. In: STENBERG, R. (Ed.). Advances in the psychology of human intelligence Hillsdale, NJ: Lawrence Erlbaum Associates, 1982. p. 7-75.
- COSTA, S. C. Resolução de problemas I: diferenças entre novatos e especialistas. Investigações em Ensino de Ciências, Porto Alegre, v. 1, n. 2, p. 176-192, 1996.
- COSTA, S. C.; MOREIRA, M. Resolução de problemas IV: estratégias para resolução de problemas. Investigações em Ensino de Ciências, Porto Alegre, v. 2, n. 3, p. 153-184, 1997.
- DE JONG, T.; FERGUSON-HESSLER, M. Cognitive structures of good and poor novice problem solvers in physics. Journal of Educational Psychology, Washington, v. 78, n. 4, p. 279-288, 1986.
- DE JONG, T. ; FERGUSSON-HESSLER, M. Types and qualities of knowledge. Educational Psychologist, Philadelphia, v. 31, n. 2, p. 105-113, 1996.
- DISESSA, A.; SHERIN, B. What changes in conceptual change? International Journal of Science Education, London, v. 20, n. 10, p. 1155-1191, 1998.
- FERGUSON-HESSLER, M.; DE JONG, T. On the quality of knowledge in the field of electricity and magnetism. American Journal of Physics, Melville, v. 55, n. 6, p. 492-497, 1987.
- FOSTER, T. The development of students' problem-solving skill from instruction emphasizing qualitative problem-solving 2000. Thesis (Doctor of Philosophy) -University of Minnesota, Minneapolis, 2000. Disponible en: <http://groups.physics.umn.edu/physed/People/Tom's%20Thesis/tom.html>. Acceso en: 8 set. 2009.
- GANGOSO, Z. Investigaciones en resolución de problemas en ciencias. Investigações em Ensino de Ciências, Porto Alegre, v. 4, n. 1, p. 8-50, 1999.
- GANGOSO, Z. et al. Teaching strategies for physics problem solving; relations to student performance. Journal of Science Education, Bogotá, v. 2, n. 7, p. 98-101, 2006.
- HAMMER, D. Variability of knowledge and reasoning. In: REDISH, E.; VICENTINI, M. (Ed.). Proceedings of the Enrico Fermi Summer School, Course CLVI Bologna: Società Italiana di Física, 2004. p. 321-340.
- HAMMER, D. et al. Resources, framing and transfer. In: MESTRE, J. (Ed.). Transfer of learning from a modern multidisciplinary perspective Greenwich: Information Age, 2005. p. 89-119.
- HUFFMAN, D. The effect of explicit problem solving instruction on students conceptual understanding of Newton's' Law 1994. 234f. Thesis (Doctor of Philosophy) - University of Minnesota, Minneapolis, 1994.
- HSU, L. et al. Research in problem solving. American Journal of Physics, Melville, v. 72, n. 9, p. 1147-1156, 2004.
- LARKIN, J. The role of problem representations in physics. In: GENTNER, D.; STEVENS, A.L. (Ed.). Mental models Hillsdale: Lawrence Erlbaum Associates, 1983. p. 75-97.
- MALONEY, D. Research on problem solving: physics. In: GABEL, D. (Ed.). Handbook of research on science teaching and learning New York: McMillan, 1994. p. 327-354.
- MESTRE, J. et al. Promoting skilled problem-solving behavior among beginning physics students. Journal of Research in Science Teaching, New York, v. 30, n. 3, p. 303-317, 1993.
- REDISH, E. A theorical framework for physics education research: modeling student thinking. In: REDISH, E.; VICENTINI, M. (Ed.). Proceedings of the Enrico Fermi Summer School, Course CLVI Bologna: Società Italiana di Física, 2004. p. 1-63.
- SHERIN, B. Common sense clarified: the role of intuitive knowledge in physics problem solving. Journal of Research in Science teaching, New York, v. 43, n. 6, p. 535-555, 2006.
- TUMINARO, J. A. Cognitive framework for analyzing and describing introductory students use and understanding of mathematics in physics 2004. 154f. Thesis (Doctor of Philosophy) - University of Maryland, College Park, 2004. Disponible en: <http://www.physics.umd.edu/rgroups/ripe/perg/dissertations/Tuminaro/>. Acceso: 4 out. 2011.
- TUMINARO, J.; REDISH, J. Elements of a cognitive model of physics problem solving: epistemic games. Physical Review Special Topics Physics Education Research, Melville, NY, v. 3, n. 020101, p. 1-22, 2007.
Datas de Publicação
-
Publicação nesta coleção
30 Jan 2012 -
Data do Fascículo
2011
Histórico
-
Recebido
24 Out 2010 -
Aceito
14 Fev 2011