Abstracts
This work constituted a significant contribution for more efficient use of a valuable computer program of non-parametric fitting of nonlinear multiparametric equations to experimental data. However, prerequisite in this context was the transformation of nonlinear multiparametric equations into linear hyperplane forms before their incorporation within the computer program; this latter was decisive and a matter of proper programming practice. Herein, a series of widely used equations useful in different fields of chemical processes, in biochemistry and/or in biotechnology, along with their suitable transformations as well as the appropriate programming support are being reported.
Non-parametric methods; computer program; fitting of nonlinear equations
Este trabalho constitui uma contribuição significativa para um uso mais eficiente de um programa de computador valioso do encaixe não-paramétrico de equações multiparamétricas não lineares aos dados experimentais. Entretanto, o pré-requisito neste contexto é a transformação de equações multiparamétricas não lineares em formulários lineares do hyperplano antes de sua incorporação dentro do programa de computador; este último é decisive e uma matéria da prática de programação apropriada. Nisto, nós relatamos uma série das equações extensamente usadas úteis em campos diferentes de processos químicos, em bioquímia e/ou em biotechnologia, junto com suas transformações apropriadas além a sustentação de programação apropriada.
ENGINEERING AND TECHNOLOGY
Necessary auxiliary background for efficient use of an existing computer program of non-parametric fitting of nonlinear equations
Emmanuel M. Papamichael* * Author for correspondence: epapamic@cc.uoi.gr ; Leonidas G. Theodorou
Sector of Organic Chemistry and Biochemistry; Laboratory of Enzymology; Department Chemistry; University of Ioannina 45110, Ioannina - GREECE
ABSTRACT
This work constituted a significant contribution for more efficient use of a valuable computer program of non-parametric fitting of nonlinear multiparametric equations to experimental data. However, prerequisite in this context was the transformation of nonlinear multiparametric equations into linear hyperplane forms before their incorporation within the computer program; this latter was decisive and a matter of proper programming practice. Herein, a series of widely used equations useful in different fields of chemical processes, in biochemistry and/or in biotechnology, along with their suitable transformations as well as the appropriate programming support are being reported.
Key Words: Non-parametric methods, computer program, fitting of nonlinear equations
RESUMO
Este trabalho constitui uma contribuição significativa para um uso mais eficiente de um programa de computador valioso do encaixe não-paramétrico de equações multiparamétricas não lineares aos dados experimentais. Entretanto, o pré-requisito neste contexto é a transformação de equações multiparamétricas não lineares em formulários lineares do hyperplano antes de sua incorporação dentro do programa de computador; este último é decisive e uma matéria da prática de programação apropriada. Nisto, nós relatamos uma série das equações extensamente usadas úteis em campos diferentes de processos químicos, em bioquímia e/ou em biotechnologia, junto com suas transformações apropriadas além a sustentação de programação apropriada.
INTRODUCTION
A non-parametric method of fitting nonlinear multiparametric equations to experimental data, along with a suitable computer program, has been presented in details and analyzed statistically previously. However, the transformation of nonlinear multiparametric equations into linear hyperplane forms, before their incorporation within the computer program is a prerequisite (Papamichael et al., 2000; Eisenthal and Cornish-Bowden, 1974). This latter is a matter of proper programming practice, which could obstruct the use of the non-parametric fitting program, and it is not uncommon in cases where the monitored response of a chemical, biochemical and/or biotechnological process is described by a more or less awkward equation (Theodorou et al., 2001, 2007). Herein, we report a series of widely used equations in the fields of chemistry, biochemistry and biotechnology, along with their suitable transformations and the appropriate programming support.
Equations
All nonlinear multiparametric equations appeared in Table 1 are frequently and commonly encountered in chemical, biochemical and/or biotechnological processes. As a matter of fact, a larger number of equations could be cited in this report; however we collected those which were considered as relatively more important due to their usefulness. On the other hand the transformations given below could be applied to other equations having similar forms to those cited herein.
Equations (1) to (24) are referred to chemical and/or biotechnological procedures, as the chlorination of di-chloro-hydrocarbons to tri- and tetra- analogues, and/or to yield-density, sigmoid-growth and logistic models of the development of certain organisms (Kafarov, 1976; Iglesias and Chirife, 1981; Ratkowsky, 1983; Pilling and Seakins, 1997; Papamichael et al., 2000). However, equations (25) to (33) are frequently encountered in biochemical reactions (Double-Michaelis, non-Michaelis, reversible inhibition and/or activation and uptake kinetics); equations (34) to (39) are important in proton inventories and/or in burst kinetics (Papamichael and Lymperopoulos 1988; Theodorou et al., 2001, 2007). Similarly, equations (40) and (41), including equation (29), are useful in fitting experimental data from pH-profiles, and are valuable in treating biotechnological data Theodorou et al., 2007).
Transformations
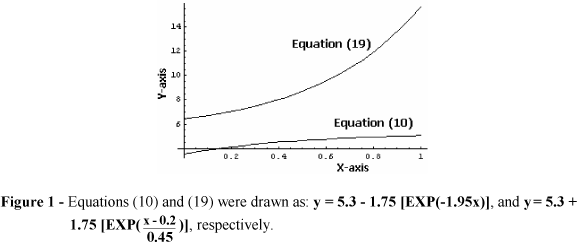
The transformations which are illustrated herein are based on the fundamental requirements of y≠0 and/or x≠0, i.e. both the dependent and the independent variables never take a zero-value, as this is valid under the experimental conditions in chemistry, biochemistry, biotechnology etc. In the same way, we should point out how simply and easily were performed all transformations depicted in Table 1. Some additional difficulties were faced in cases of equations (10), (11), (12), (14) and (19), where a parameter, namely a, was incorporated into the dependent variable during their transformation for simplicity purposes. In following are given, as examples, the transformations of equation (1), as well as of some other awkward equations.
Equation (1) can be transformed to the form axy + bx2y = x(1-x) (as y≠0 and/or x≠0); then, by dividing both members of its new form by x(1-x), and performing all necessary simplifications the suitable form  is the result.
is the result.
Alternatively, in equation (10) the first step is the separation of its variables, where a new equation a - y = b [EXP(-cx)] is formed, whose both logarithmic forms ln(a-y) = -cx + ln(b) and ln(b) - cx = ln(a-y) are valid. The transformation of equation (10) is easily obtained by dividing both members of the latter equation by ln(a-y).
In equation (11) the first step is to form the equality ln(y) = a - bcx; the separation of the variables comes next, i.e. a - ln(y) = bcx, and equation ln[a - ln(y)] = ln(b) +xln(c) is obtained which is easily transformed to its suitable form  . By performing very similar rearrangements one may transform appropriately equations (12) and (19); however, a last example should be given, that of equation (14).
. By performing very similar rearrangements one may transform appropriately equations (12) and (19); however, a last example should be given, that of equation (14).
In equation (14), both its members were divided by a to obtain  and then
and then  which was rearranged to the form
which was rearranged to the form  . If and only if 1
. If and only if 1 , then the latter equation was transformed to
, then the latter equation was transformed to  , by taking the logarithms, and then taken on its final form
, by taking the logarithms, and then taken on its final form  , as before.
, as before.
Hence, in cases of equations (10), (11), (12), (14) and (19) initial guessing values of parameter a must be obtained easily and incorporated within transformations for further use by the computer program; this holds true and it needs only a simple inspection of the experimental points in a scatter graph (Cornish-Bowden, 1995). Useful examples are depicted in Figures 1 and 2, where estimates of parameter a can be obtained: (a) as the maximum value of the independent variable y when x→∞ (asymptote parallel to abscissas i.e. the Y-axis), in cases of equations (10), (12) and (14) (Fig. 1 and 2), (b) by subtracting the value of numeric constant λ from that of the intersection of the experimental curve on the ordinate axis (Fig. 1) in case of equation (19), and (c) as the natural logarithm (ln) of the maximum value of the independent variable y when x→∞ in case of equation (11) (Fig. 2).
In this way, transformations were provided for all the above mentioned nonlinear multiparametric equations into their linear hyperplane forms. In the above equations and their transformations, λ is only a numeric constant. Additionally, care should be taken in transformations when the natural logarithm (ln) of an expression is appeared; these expressions should take on values only greater than zero.
RESULTS AND DISCUSSION
What could be deduced from the preceding section was that which has been mentioned about the prerequisites of using the previously described computer program (Papamichael et al., 2000). Therefore, in this work, a series of nonlinear multiparametric equations, useful in different fields of sciences and technology, were properly transformed into linear hyperplane forms, capable for incorporation within this program. Then, to accomplish successfully the non-parametric fitting of a nonlinear multiparametric equation, after its suitable transformation, one has only to follow the build-in instructions mentioned in the program listing.
Let us take equation (1) as an example along with its linear transformation, i.e. equation  Then, in addition to the details given previously (Papamichael et al., 2000), the program user should form carefully a system of simultaneous equations found within the multiple FOR-NEXT loops by following the appropriate syntax. In the example, the program user should type two lines as indicated below, and should not confuse e with the base of natural logarithms, in e!(i,j) statements:
Then, in addition to the details given previously (Papamichael et al., 2000), the program user should form carefully a system of simultaneous equations found within the multiple FOR-NEXT loops by following the appropriate syntax. In the example, the program user should type two lines as indicated below, and should not confuse e with the base of natural logarithms, in e!(i,j) statements:
First line: e!(1,1)=y!(op)/(1-x!(op)): e!(1,2)=x!(op)*y!(op)/(1-x!(oq))): e!(1,3)=1
Second line: e!(2,1)=y!(oq)/(1-x!(oq)): e!(2,2)=x!(oq)*y!(oq)/(1-x!(oq)): e!(2,3)=1
It should be emphasized that the Michaelis-Menten equation  , as well as equation (23) of this report, have been presented and accordingly analyzed previously (Eisenthal and Cornish-Bowden, 1974; Papamichael et al., 2000)
, as well as equation (23) of this report, have been presented and accordingly analyzed previously (Eisenthal and Cornish-Bowden, 1974; Papamichael et al., 2000)
REMARKS
The program listing has been developed under Z-BASIC compiler for Macintosh, and it is given below. However, there is a version of the Z-BASIC compiler for PC-compatible computers, and authors could help in a future appropriate transforming of the program listing.
Likewise, the principles of transformation of nonlinear multiparametric equations into linear hyperplane forms, as well as a complete statistical analysis and description and function of the computer program have been already described in details previously (Papamichael et al., 2000).
The Program Listing and an Example
REM Non-Parametric Curve Fitting. Configure ZBASIC for Integer Variables.
REM Clear, and Clear (binco+2)*(number of digits of ndp +1)*npr (see a$=. .below).
CLEAR: CLEAR 12100
ndp=14:npr=4:binco=1001:cntr=0
REM DIM's: x(ndp), y(ndp), r(ndp), e(npr+1,ndp+1), g(npr+1), pm(npr,binco), vl(npr,6), dx(npr)
DIM x!(14),y!(14),r!(14),e!(5,15),g!(5),pm!(4,1001),vl!(4,6),dx(4)
INDEX$(0)=""
FOR j=1 TO ndp
READ x!(j),y!(j)
NEXT j
CLS: PRINT TIME$: REM Time$ function Optional
FOR op=1 TO ndp
FOR oq=1 TO ndp
IF (oq=op) THEN "NextA"
FOR or=1 TO ndp
IF ((or=oq) OR (or=op)) THEN "NextB"
FOR ow=1 TO ndp
IF ((ow=or) OR (ow=oq) OR (ow=op)) THEN "NextC"
dx(1)=op
dx(2)=oq
dx(3)=or
dx(4)=ow
GOSUB "Sortindices"
a$=STR$(dx(1))+STR$(dx(2))+STR$ (dx(3))+STR$(dx(4))
REM a$ -> (number of digits of ndp +1)*npr
IF INDEXF(a$)=-1 THEN INDEX$(cntr+1)=a$ ELSE "NextC"
cntr=cntr+1
e!(1,1)=x!(op)^2/y!(op): e!(1,2)=-x!(op)^2: e!(1,3)=-x!(op): e!(1,4)=-SQR(x!(op)): e!(1,5)=1
e!(2,1)=x!(oq)^2/y!(oq): e!(2,2)=-x!(oq)^2: e!(2,3)=-x!(oq): e!(2,4)=- -SQR(x!(oq)): e!(2,5)=1
e!(3,1)=x!(or)^2/y!(or): e!(3,2)=-x!(or)^2: e!(3,3)=-x!(or): e!(3,4)= -SQR(x!(or)): e!(3,5)=1
e!(4,1)=x!(ow)^2/y!(ow):e!(4,2)=-x!(ow)^2: e!(4,3)=-x!(ow): e!(4,4)= -SQR(x!(ow)): e!(4,5)=1
GOSUB "Cholesky"
FOR os=1 TO npr
REM Assignment for future sorting of the parameters estimates.
pm!(os,cntr)=g!(os)
NEXT os
"NextC"
NEXT ow
"NextB"
NEXT or
"NextA"
NEXT oq,op
REM Procedure to Sort Parameter Estimates; Shell-Metzner Type.
FOR jj=1 TO npr: REM For All parameter series.
meo=binco
"CycA"
meo=INT(meo/2)
IF meo=0 THEN "CycE"
jaj=1:kaj=binco-meo
"CycB"
iaj=jaj
"CycC"
laj=iaj+meo
IF pm!(jj,iaj)<=pm!(jj,laj) THEN "CycD" ELSE SWAP pm!(jj,iaj),pm!(jj,laj)
iaj=iaj-meo
IF iaj<1 THEN "CycD"
GOTO "CycC"
"CycD"
jaj=jaj+1
IF jaj>kaj THEN "CycA"
GOTO "CycB"
"CycE"
meo=binco
NEXT jj
REM Calculating Subroutine. Calculates MEDIANs, IQRs, Limits etc of the parameters estimates.
PRINT TIME$: REM Time$ function Optional
ck=1
WHILE ck<=npr
LONG IF INT(cntr/2)<(cntr/2)
vl!(ck,1)=pm!(ck,(cntr+1)/2)
LONG IF INT((INT(cntr/2))/2)>=(INT(cntr/2))/2
vl!(ck,2)=pm!(ck,3*(INT(cntr/2))/2+1)-pm!(ck,(INT(cntr/2))/2+1)
vl!(ck,3)=pm!(ck,3*(INT(cntr/2))/2+1)+vl!(ck,2)*1.5
vl!(ck,4)=pm!(ck,(INT(cntr/2))/2+1)-vl!(ck,2)*1.5
XELSE
vl!(ck,2)=(pm!(ck,(3*(INT(cntr/2))+3)/2)+pm!(ck,(3*(INT(cntr/2))+3)/2-1))/2-(pm!(ck,(INT(cntr/2)+1)/2)+pm!(ck,(INT(cntr/2)+1)/2+1))/2
vl!(ck,3)=(pm!(ck,(3*(INT(cntr/2))+3)/2)+pm!(ck,(3*(INT(cntr/2))+3)/2-1))/2+vl!(ck,2)*1.5
vl!(ck,4)=(pm!(ck,(INT(cntr/2)+1)/2)+pm!(ck,(INT(cntr/2)+1)/2+1))/2-vl!(ck,2)*1.5
END IF
XELSE
vl!(ck,1)=(pm!(ck,cntr/2)+pm!(ck,cntr/2+1))/2
LONG IF INT(cntr/4)<(cntr/4)
vl!(ck,2)=pm!(ck,(3*cntr+2)/4)-pm!(ck,(cntr/2+1)/2)
vl!(ck,3)=pm!(ck,(3*cntr+2)/4)+vl!(ck,2)*1.5
vl!(ck,4)=pm!(ck,(cntr/2+1)/2)-vl!(ck,2)*1.5
XELSE
vl!(ck,2)=(pm!(ck,3*cntr/4)+pm!(ck,3*cntr/4+1))/2-(pm!(ck,cntr/4)+pm!(ck,cntr/4+1))/2
vl!(ck,3)=(pm!(ck,3*cntr/4)+pm!(ck,3*cntr/4+1))/2+vl!(ck,2)*1.5
vl!(ck,4)=(pm!(ck,cntr/4)+pm!(ck,cntr/4+1))/2-vl!(ck,2)*1.5
END IF
END IF
ck=ck+1
WEND
PRINT TIME$: REM Time$ function Optional
REM Printing Subroutine. Prints the Results.
cntr_a=0
TEXT 1,9,0,1: REM Change settings according to your display device.
CLS
PRINT %(15,30);" X - VALUES Y - VALUES Y-CALC. VALUES RESIDUALS RELATIVE RES."
PRINT %(15,45);" -"
REM Change Printing settings according to your display device.
REM Subroutine to calculate a Chi-Square Test value by Yate's correction.
FOR jm=1 TO ndp
REM The four parameters equation y = ax2/(1+bx2+cx+d√x) is portrayed below
r!(jm)=vl!(1,1)*x!(jm)^2/(vl!(2,1)*x!(jm)^2+vl!(3,1)*x!(jm)+vl!(4,1)* SQR(x!(jm))+1)
cha!=0:chb!=0:ch2!=0:d_fr=0
kr=0
DO
kr=kr+1
"A_Cycl"
LONG IF ((ABS(r!(kr))+ABS(chb!)>=5) OR (ABS(y!(kr))+ABS(cha!)>=5))
LONG IF (ABS(r!(kr))+ABS(chb!)<>0)
ch3!=ABS((ABS(y!(kr))+ABS(cha!)-ABS(r!(kr))- ABS(chb!))-.5)^2/(ABS (r!(kr))+ABS(chb!))
ch2!=ABS(ch2!)+ABS(ch3!)
d_fr=d_fr+1
XELSE
LONG IF kr=ndp
ch2!=ABS(ch2!)-ABS(ch3!)
d_fr=d_fr-1
lm=kr
"C_Cycl"
LONG IF (ABS((y!(lm))>=5) OR (ABS(r!(lm))>=5))
cha!=0:chb!=0
FOR xk=lm TO kr
cha!=ABS(cha!)+ABS(y!(xk))
chb!=ABS(chb!)+ABS(r!(xk))
NEXT xk
ch2!=ABS(ch2!)+(ABS(ABS(cha!)-ABS(chb!))-.5)^2/ ABS(chb!)
d_fr=d_fr+1
XELSE
lm=lm-1
GOTO "C_Cycl"
END IF
XELSE
END IF
END IF
XELSE
cha!=ABS(cha!)+ABS(y!(kr))
chb!=ABS(chb!)+ABS(r!(kr))
GOTO "B_Cycl"
END IF
cha!=0:chb!=0
"B_Cycl"
UNTIL kr=ndp
d_fr=d_fr-2
pr_cnt=55+30*jm
LONG IF (pr_cnt>=735)
cntr_a=cntr_a+1
IF (cntr_a=1) THEN CLS
pr_cnt=55+30*cntr_a
IF (pr_cnt>=710) THEN cntr_a=0
END IF
PRINT %(40,pr_cnt);USING ".#";x!(jm)
PRINT %(180,pr_cnt);USING ".#";y!(jm)
PRINT %(340,pr_cnt);USING " .";r!(jm)
PRINT %(520,pr_cnt);USING " #.";y!(jm)-r!(jm)
PRINT %(700,pr_cnt);USING " #.";(y!(jm)-r!(jm))/y!(jm)
NEXT jm
PRINT "Chi-Square with Yates's Correction=";ch2!,"Degrees of Freedom=";d_fr
FOR ck=1 TO npr
PRINT "Par(";ck;")="USING ".#^^^^";vl!(ck,1),"IQR="USING ".^^^^";vl!(ck,2),"Up.Lim="USING ".#^^^^";vl!(ck,3),"Lo.Lim="USING "#^^^^";vl!(ck,4)
PRINT "Par(";ck;") Lower Estimate="USING ".^^^^";pm!(ck,1),"Par(";ck;") Upper Estimate="USING ".^^^^";pm!(ck,binco)
NEXT ck
PRINT TIME$: REM Time$ function Optional
END
"Sortindices"
REM A Bubblesort Type Sorting Subroutine for the Nested FOR. . . NEXT loops.
FOR i=1 TO npr-1
FOR ij=i+1 TO npr
IF dx(i)<=dx(ij) THEN "Enlp" ELSE SWAP dx(i),dx(ij)
"Enlp"
NEXT ij,i
RETURN
"Cholesky"
REM Applies Cholesky's Method to solve a System of Linear Equations using Partial Pivoting.
FOR k=1 TO npr
pvt!=e!(k,k):il=k: REM Finds Largest Pivot.
FOR l=k+1 TO npr
IF ABS(e!(l,k))<ABS(pvt!) THEN "First"
pvt!=e!(l,k)
il=l
"First"
NEXT l
IF il=k THEN "Second"
FOR ll=1 TO npr+1
SWAP e!(k,ll),e!(il,ll)
NEXT ll
"Second"
NEXT k
FOR jk=2 TO npr+1
e!(1,jk)=e!(1,jk)/e!(1,1): REM Calculate first row.
NEXT jk
FOR l=2 TO npr: REM For all rows and columns.
FOR ik=l TO npr
sum!=0
FOR k=1 TO l-1
sum!=sum!+e!(ik,k)*e!(k,l)
NEXT k
e!(ik,l)=e!(ik,l)-sum!
NEXT ik
FOR jk=l+1 TO npr+1
sum!=0
FOR k=1 TO l-1
sum!=sum!+e!(l,k)*e!(k,jk)
NEXT k
IF e!(l,l)=0 THEN "Third"
e!(l,jk)=(e!(l,jk)-sum!)/e!(l,l)
NEXT jk
"Third"
NEXT l
REM Gets g( ) values by back substitution.
g!(npr)=e!(npr,npr+1)
FOR m=1 TO npr-1
im=npr-m
sum!=0
FOR jk=im+1 TO npr
sum!=sum!+e!(im,jk)*g!(jk)
NEXT jk
g!(im)=e!(im,npr+1)-sum!
NEXT m
RETURN
REM Put after keyword DATA your data in a xi,yi,.., successive form, as in the example
REM Experimental (x,y) data pairs
DATA 0.1,0.82,0.2,2.51,0.5,42.23,0.7,84.85,0.9,157.9,1,211.8,1.5,662.8,2,1265.6,2.5,1437.8
DATA 3,1630,3.5,1608.6,4,1679.4,4.5,1692.4,5,1711.2
REM If more than one independent variables are provided by your equation, then put your data in a x1i, x2i,...etc..yi,.., successive form, and PROVIDE as more as you need x1!(), x2!()... etc DIM in the DIM-statements line, as well as in the READ-statement line.
REM____________________________________________________________________
REM ******************** List of Variables *************
REM____________________________________________________________________
REM * ndp, & npn: Numbers of experimental data pairs, & of parameters of the nonlinear equations, respectively.
REM * binco: Binomial Coefficient for npr ways of random to ndp????.
REM * d_fr : Degrees of Freedom.
REM * x!(),y!(), & r!(): Arrays to store the experimental data pairs & the calculated response values, respectively.
REM * e!(,): A two dimensions array to store and elaborate the systems written in matrix notation.
REM * g!(): Array to store temporarily the parameter estimates from systems solutions.
REM * pm!(,) & v!(,): Two dimensions arrays to store parameter estimates & elaborate IQR etc values, respectively.
REM * dx(): An array for storing of some loop counters.
REM * cha!,chb!,ch2! & cntr: Chi-Square temporary values and/or local counters & global counter, respectively.
REM * i,j,k,l,m,ij,ik,jj,jk,jl,ll,ka,kr ck,kla : Are Loop counters of different loop kinds.
REM * il,im,iaj,kaj,laj,pr_cnt,cntr_a : Are different local counters.
REM * op,oq,or,ow,os : Are Special Loop Counters (see Program Listing).
REM____________________________________________________________________
Received: March 03, 2008;
Revised: September 03, 2008;
Accepted: December 11, 2008.
- Cornish-Bowden, A. (1995), Analysis of Enzyme Kinetic Data. Oxford University Press, Oxford, pp.3-9.
- Eisenthal, R., and Cornish-Bowden, A. (1974), Statistical considerations in the estimation of enzyme kinetic parameters by the direct linear plot and other methods. Biochem. J., 139, 721-730.
- Iglesias, H.A., and Chirife, J. (1981), An Equation for Fitting Uncommon Water Sorption Isotherms in Food. Lebens. Wiss. Technol., 14, 105-106.
- Kafarov, V. (1976), Cybernetic Methods in Chemistry & Chemical Engineering, MIR Publishers, Moscow, pp. 374-379 (Translated in English).
- Papamichael, E.M., and Lymperopoulos, K. (1998), Elastase and Cathepsin-G from Human PMN Activated by PAF: Relation between their Kinetic Behavior and Pathophysiological Role. In Advances in Biotechnology, ed. A. Pandey. Educational Publishers and Distributors, New Delhi, pp.221-234.
- Papamichael, E.M., Evmiridis, N.P., and Potosis, C. (2000), Non-parametric Fitting of Nonlinear Equations to Experimental Data without Use of Initial Guessing: A Basic Computer Program. Brazilian Archives of Biology and Technology, 43, 1-9.
- Pilling, M.J., and Seakins, P.W. (1997), Reaction Kinetics. Oxford University Press, Oxford, pp.190-200.
- Ratkowsky, D.A. (1983), Nonlinear Regression Modeling: A Unified Practical Approach. Marcel Dekker Inc, New York - Basel, pp. 49-134.
- Theodorou, L.G., Lymperopoulos, K., Bieth, J.G., and Papamichael, E.M. (2001), Insight into the Catalysis of Hydrolysis of Four Newly Synthesized Substrates by Papain: A Proton Inventory Study. Biochemistry-US, 40, 3996-4004.
- Theodorou, L.G., Perysinakis, A., Valasaki, K., Drainas, C., and Papamichael, E.M. (2007), Proton inventories constitute reliable tools in investigating enzymatic mechanisms: application on a novel thermo-stable extracellular protease from a halo-alkaliphilic Bacillus sp. J. Biochem. (Tokyo), 142, 293-300.
Publication Dates
-
Publication in this collection
06 May 2009 -
Date of issue
Apr 2009
History
-
Accepted
11 Dec 2008 -
Reviewed
03 Sept 2008 -
Received
03 Mar 2008